Suspension biomechanics of swimming microbes

Abstract

Micro-organisms play a vital role in many biological, medical and engineering phenomena. Some recent research efforts have demonstrated the importance of biomechanics in understanding certain aspects of micro-organism behaviours such as locomotion and collective motions of cells. In particular, spatio-temporal coherent structures found in a bacterial suspension have been the focus of many research studies over the last few years. Recent studies have shown that macroscopic properties of a suspension, such as rheology and diffusion, are strongly affected by meso-scale flow structures generated by swimming microbes. Since the meso-scale flow structures are strongly affected by the interactions between microbes, a bottom-up strategy, i.e. from a cellular level to a continuum suspension level, represents the natural approach to the study of a suspension of swimming microbes. In this paper, we first provide a summary of existing biomechanical research on interactions between a pair of swimming micro-organisms, as a two-body interaction is the simplest many-body interaction. We show that interactions between two nearby swimming micro-organisms are described well by existing mathematical models. Then, collective motions formed by a group of swimming micro-organisms are discussed. We show that some collective motions of micro-organisms, such as coherent structures of bacterial suspensions, are satisfactorily explained by fluid dynamics. Lastly, we discuss how macroscopic suspension properties are changed by the microscopic characteristics of the cell suspension. The fundamental knowledge we present will be useful in obtaining a better understanding of the behaviour of micro-organisms.

1. Introduction

Micro-organisms can be categorized into three major groups: bacteria, archaea and eukaryotes (Ingraham & Ingraham 2004). All bacteria and archaea prokaryotes are unicellular, varying in length from roughly 0.1 to 10 µm. Eukaryotes may be unicellular or multicellular and are typically much larger than prokaryotes. Although there is no strict limitation on size, eukaryotes smaller than several hundred micrometres are commonly considered to be micro-organisms. Micro-organisms first appeared on Earth about 3.8 billion years ago and are found almost everywhere. Since it is estimated that there are approximately 5 × 10³⁰ bacterial cells on Earth, micro-organisms constitute the majority of terrestrial life in terms of both numbers and biomass (Madigan et al. 2003).

Despite their tiny size, micro-organisms play a vital role in a wide variety of phenomena. For example, massive plankton blooms are an integral part of the oceanic ecosystem. The dependency on these populations of micro-organisms extends from the largest animals on Earth (blue whales) to the smallest nocturnal grazers that ascend from the depths of the oceans to feast on phytoplankton descending from the sea surface at night to increase their nutrient uptake. Algal cells in the ocean incorporate carbon dioxide (CO₂) from sea water, and much of this carbon dioxide comes from the atmosphere. Raven & Falkowski (1999) reported that the oceans are among the largest natural carbon sinks on Earth. Since CO₂ in the atmosphere induces global warming, the carbon cycle contributed by micro-organisms affects the global climate. Bacterial metabolites in the ocean break down not only carbon, but also nitrogen, phosphorus and sulphur. Thus, micro-organisms play an important role in global material circulation.

In the food and chemical industries, micro-organisms are used in the production of medicines and everyday foods, including beer and cheese, as well as insecticides. These products are made in bioreactors, in which control of mass transport and cell population is crucial for achieving good quality. In industrial plants, micro-organisms are often used to break down organic materials. For instance, in sewage treatment plants, micro-organisms are employed to reduce the biochemical oxygen demand of the sewage in order to protect the aquatic environment (Madigan et al. 2003). In maritime coastal regions, micro-organisms sometimes cause toxic algal blooms, such as red tides (e.g. Anderson 1997; Schrope 2008), which attack fish farms and oyster farms. Red tides can be formed from more than 200 kinds of phytoplankton and occasionally inflict serious damage on the fishing industry.

The human body hosts hundreds of species of micro-organisms (Madigan et al. 2003). The number of micro-organisms in the human body is estimated to be of the order of 10¹⁴, roughly double the number of cells in the body. To cite one specific example, in the intestines of a typical adult male, approximately 1 kg of enterobacteria form a unique ecosystem, known as bacterial flora. This system plays an important role in the digestion and absorption of food and also in protecting against infections. For instance, our bodies alone cannot synthesize vitamin K; the synthesis is actually carried out by the bacterial flora. Because of the considerable influence that micro-organisms have on human life, the study of their behaviour is an important area of scientific research.

Although biology, ecology and chemistry have all been used extensively to investigate various phenomena pertaining to micro-organisms, biomechanics is also important in understanding certain aspects of their behaviour, such as locomotion and collective motions. The locomotion mechanics of micro-organisms have been reviewed by Brennen & Winet (1977) and Fauci & Dillon (2006) and by E. Lauga and T. R. Powers (2009, unpublished data). The swimming speeds of micro-organisms range up to several hundred micrometres per second. The Reynolds number based on the swimming speed and radius of the individual is usually less than 10⁻². It can therefore be assumed that the flow field around a micro-organism is a Stokes flow and hence that the inertial force is negligible compared with the viscous force. In the Stokes flow regime, reciprocal motion cannot lead to any locomotion; this is known as Purcell's scallop theorem (Purcell 1977). In the case of ciliates, for instance, the motion of each individual cilium follows an asymmetric pattern, consisting of an effective stroke and a recovery stroke, as illustrated in figure 1a. As a result of this asymmetry, the cilium is able to generate a net thrust on the cell body.

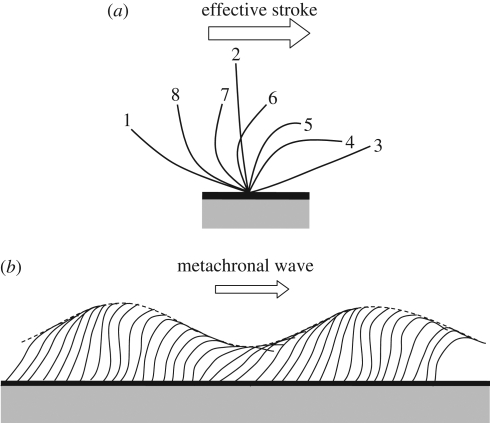
Figure 1.

Schematic of the motion of an individual cilium and the collective motion of cilia. (a) Effective stroke of an individual cilium. The numbers in the figure indicate the order of the ciliary motion. The effective stroke is defined from 1 to 3. (b) Metachronal wave generated by cilia (reproduced images from Blake & Sleigh 1974).

Propulsion by cilia and flagella may be classified into three major groups: ciliary propulsion, eukaryotic flagellar propulsion and prokaryotic flagellar propulsion. Cilia and eukaryotic flagella have essentially the same structure, and there is no clear distinction between them. Roughly speaking, eukaryotic flagella are typically long compared with the cell body, and the number of flagella per cell is small. On the other hand, cilia are typically short compared with the cell body, and the number of cilia per cell is large. A ciliate swims by synchronizing ciliary motions with slight phase differences, thus generating metachronal waves, as shown in figure 1b. A eukaryotic flagellate swims by propagating a planar wave or a helical wave along the flagella normally from the base to the tip (Fauci & Dillon 2006). Eukaryotic and prokaryotic flagella are evolutionarily unrelated structures. Prokaryotic flagella are placed outside the cytoplasmic membrane and basically resemble corkscrews. When a flagellum is rotated relative to the cell body, using a basal motor, a helical wave propagates towards the tip, and the cell is able to propel itself.

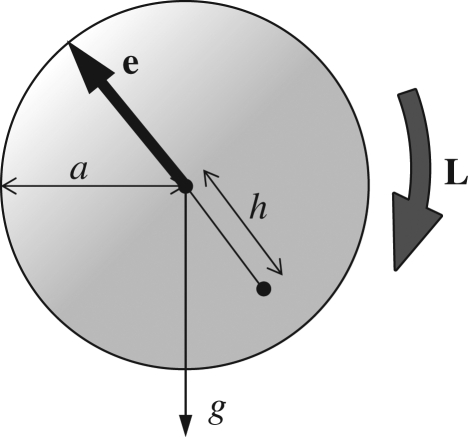
In analysing the locomotion of micro-organisms, force and torque conditions are important. Although micro-organisms might be slightly denser than water, the sedimentation velocity for typical aquatic micro-organisms is usually much less than their swimming speed. Thus, one may assume that micro-organisms have neutral buoyancy, provided that the sedimentation effect is negligible. The centre of buoyancy of a micro-organism may not coincide with its geometric centre; this is referred to as bottom heaviness. For simplicity, let a cell be a sphere with radius a, and the distance between the centre of gravity and the geometric centre be h, as shown in figure 2. Then, there is an additional torque of 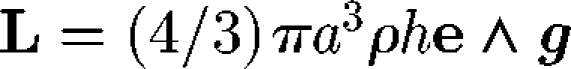, where ρ is the density, e is the orientation vector and g is the gravitational acceleration vector. This feature provides a micro-organism with a self-righting mechanism, causing it to move in a preferred direction, even if it is temporarily advected or rotated in another direction by the flow (Kessler 1985, 1986; Pedley & Kessler 1987). Brownian motion is not usually taken into account because micro-organisms are typically too large for Brownian effects to be significant. However, it should be noted that micro-organisms often appear to reorient themselves randomly while swimming, such as tumbling of bacteria, in a manner that may be analogous to a Brownian motion (Pedley & Kessler 1992; Hill & Hader 1997; Berg 2003; Vladimirov et al. 2004).

Figure 2.

A sketch of the arrangement of a bottom-heavy cell. Gravity acts in the g-direction, while the spherical cell has orientation vector e, radius a and its centre of mass distance h from its geometric centre. The torque L is exerted on the cell body.

Recently, a lot of researchers have studied the suspension biomechanics of swimming microbes. In particular, spatio-temporal coherent structures, as illustrated in figure 3, that are found in a bacterial suspension have been investigated intensely in the last few years. It has been observed experimentally that the diffusion of particles and chemical substances in such a suspension are considerably enhanced by these coherent structures and are sometimes of the order of a thousand times greater than Brownian diffusion (Wu & Libchaber 2000). Since collective motions may be biologically and evolutionarily favourable, it is important to determine whether they are formed passively owing to hydrodynamic forces or actively owing to biological communication. Recent research has shown that collective motions can be formed passively because of hydrodynamic forces (Ishikawa & Pedley 2008), and hence that biomechanics and biophysics play an important part in the behaviour of micro-organisms.

Figure 3.

Coherent structures observed in a suspension of bacterium B. subtilis. A sessile drop is viewed from below, through the bottom of a Petri dish, and the horizontal white line near the top is the air–water–plastic contact line. The central fuzziness is due to collective motion that was not completely captured at the frame rate of 1/30 s. White scale bar, 35 µm (reprinted with permission from Dombrowski et al. 2004). Copyright (2004) by the American Physical Society.

In this paper, we review recent studies on the suspension biomechanics of swimming microbes. The macroscopic properties of a suspension, such as rheological and diffusion properties, are strongly affected by meso-scale flow structures generated by the swimming microbes. Thus, in order to understand the macroscopic suspension properties, we need to improve our understanding of the meso-scale structures. Since the meso-scale flow structures are strongly affected by the interactions between microbes, a bottom-up strategy, i.e. from a cellular level to a continuum suspension level, represents the natural approach to the study of a suspension of swimming microbes. In §2, we provide a summary of existing biomechanical research on interactions between a pair of swimming micro-organisms. Since a two-body interaction is the simplest many-body interaction, we will consider it before proceeding to more general cases. Note, however, that some collective motions are the result of many-body interactions and are difficult to explain by simply exploiting the results of pairwise interactions. In §3, the collective motions formed by a group of swimming micro-organisms are discussed, including the coherent structures formed by bacteria. Since a thorough review paper on bioconvection has been recently published (Hill & Pedley 2005), the details of this topic are omitted here. In the last two sections, the macroscopic properties of a suspension of micro-organisms are considered. A fine review paper by Pedley & Kessler (1992) describes continuum models for a suspension of micro-organisms, but most of the models presented in that paper are only applicable to dilute suspensions in which cell-to-cell interactions are neglected. Recent research has revealed that the suspension properties are considerably influenced by the collective motions of micro-organisms. This research topic has also been investigated intensely in the last few years. In this paper, the focus is on the effect of cell-to-cell interactions on macroscopic properties. Rheological and diffusion properties in a suspension of micro-organisms are discussed in §§4 and 5, respectively. Section 6 provides a brief summary of conclusions.

2. Interactions between a pair of swimming micro-organisms

Before examining the many-body interactions of micro-organisms, it may be important to first have an understanding of two-cell interactions, although some collective motions, such as coherent structures in a bacterial bath, cannot be interpreted solely in terms of two-body interactions. When two micro-organisms are far apart in a dilute suspension, the translational velocity of cell A may be approximated by the summation of two velocities: the translational velocity of cell A when it is alone, i.e. no effect of cell B; and the disturbance velocity at the centre of cell A generated by cell B in the far field. A similar observation can be made for the rotational velocity. For simplicity, let cells A and B be spherical with radius a and swim in a fluid otherwise at rest. In the Stokes flow regime, the disturbance velocity u at position x generated by cell B can be expressed by the integration of the traction force f exerted on the surface of cell B (Kim & Karrila 1992; Pozrikidis 1992):

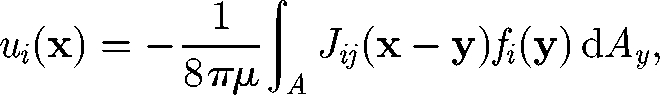2.1

where μ is the viscosity and A is the surface area of cell B. J is the Oseen tensor defined by

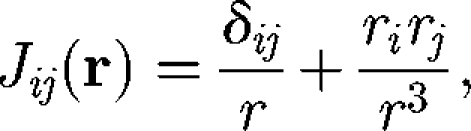2.2

where r = |r| and δ_ij is the Kronecker delta. The integral representation for the velocity field can be viewed as a restatement of the governing equation of Stokes flow from a three-dimensional partial differential equation to a two-dimensional integral equation for traction forces over the boundary of the fluid domain. By taking the Taylor series of J, the right-hand side of equation (2.1) can be expanded in moments about the centre of cell B (Durlofsky et al. 1987; Brady & Bossis 1988):

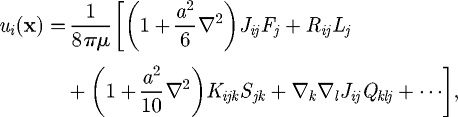2.3

where F, L, S and Q are the force (monopole), torque (antisymmetric dipole), stresslet (symmetric dipole; cf. Batchelor 1970) and the irreducible quadrupole of the traction force of cell B, respectively. The propagators are given as follows:

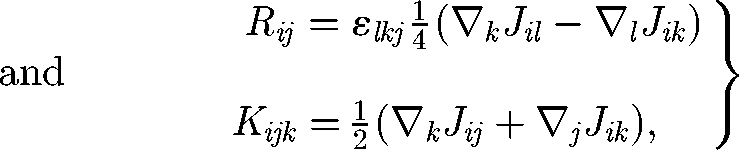2.4

where ε is the unit alternating isotropic tensor. Equation (2.3) indicates that the disturbance flow generated by high multipoles decays rapidly as r. If cell B is force free, the disturbance flow generated by the stresslet term decays as r², and the additional translational velocity of cell A caused by cell B also decays as r². The additional rotational velocity of cell A, however, decays as r³. Thus, in the far-field hydrodynamic interactions, it may be enough to consider only the first few multipoles. In other words, the effect of the detailed cell shape is unimportant in the far-field interactions, but the force, torque and stresslet conditions become important.

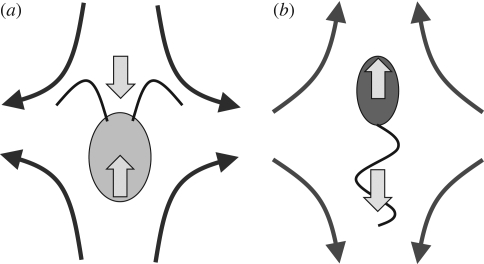
If a micro-organism is force free and torque free, the leading order term in equation (2.3) is the stresslet, i.e. force dipole. Although the stresslet is a second-order tensor, we discuss ee component of the stresslet, where e is the orientation direction of the micro-organism. The ee component of the stresslet is positive for a micro-organism that generates a thrust force in front of the body (referred to as a puller), such as the biflagellate algae Chlamydomonas, as illustrated in figure 4a. On the other hand, the ee component of the stresslet is negative for a micro-organism that generates a thrust force behind the body (referred to as a pusher), such as many types of bacteria or spermatozoa, as illustrated in figure 4b. Thus, the disturbance flow fields generated by a puller and a pusher are opposite. Two pullers swimming side-by-side repel each other, but two pushers swimming side-by-side attract each other. Guell et al. (1988) modelled a bacterium as a force dipole, similar to figure 4b, and discussed the interaction between two bacteria by calculating the disturbance flow field. They analysed the far-field interactions of magnetotactic bacteria and gave one explanation of why magnetotactic bacteria tend to form clusters.

Figure 4.

Schematic of the stresslet exerted on the fluid for two types of cells, and the far-field velocity field relative to the swimming velocities of the cells. The arrows within the cells' bodies show the bodies' direction of ‘forward’ locomotion and also the force by the cell bodies on the fluid. The external arrows show the associated forces by the flagella on the fluid. (a) Thrust generated in front of the body (puller). Typical of the algae Chlamydomonas, the return stroke, with somewhat folded flagella, reverses the arrows. The cell body then moves backward. The return stroke results in less motion than the forward stroke; the net motion over one complete cycle is forward. (b) Thrust generated behind the body (pusher).

When two micro-organisms come close, however, the high multipoles in equation (2.3) become important. In the case of lubrication flow between two near-contact surfaces, all multipoles are required. Thus, near-field interactions between two cells are difficult to solve mathematically, and we usually must employ a detailed computational analysis to solve the problem. The computational models of micro-organisms often vary with the problems to be solved; it is important to find an appropriate model for the specific problem. It is also unclear whether the near-field interactions can be described only by hydrodynamics. In the following subsections, we review some recent numerical and experimental studies on interacting pairs of micro-organisms in the near field.

2.1. Interactions between two nearby eukaryotes

While there have been numerous mathematical and numerical investigations of hydrodynamic interactions between two micro-organisms, relatively few experimental studies have thus far been carried out. Most of the existing mathematical and numerical studies have assumed that cell-to-cell interactions were purely hydrodynamic, and no biological reactions were considered. In practice, however, the behaviour of a micro-organism may be affected by the proximity of another micro-organism. It may be stimulated to engage in reproductive activity or to consume (or avoid being consumed by) its neighbour. It may also move away from other cells because of the increased competition for food. Hence, it is first necessary to investigate experimentally whether two-cell interactions can best be described as physical phenomena or biological phenomena.

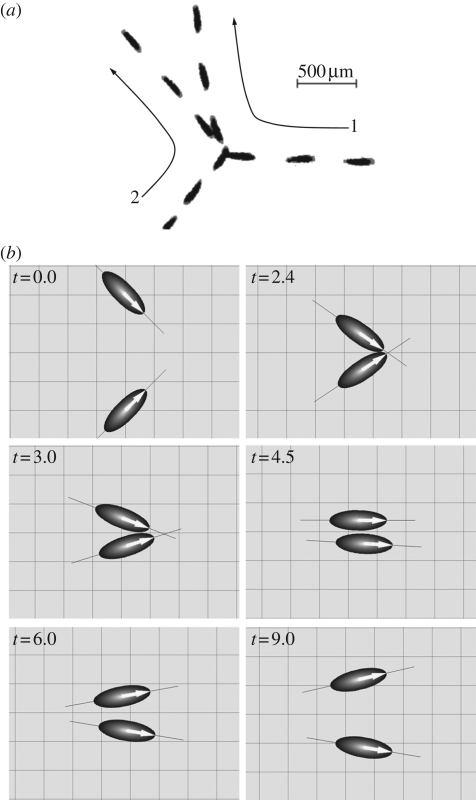
Ishikawa & Hota (2006) carried out an experimental study on the interaction of two swimming micro-organisms using the unicellular freshwater ciliate Paramecium caudatum. It is known that a solitary Paramecium cell exhibits two types of biological reactions to a mechanical stimulation, namely avoiding reactions and escape reactions (Naitoh & Sugino 1984). An avoiding reaction occurs when a cell receives a strong jolt at its anterior end. The cell first swims backward, gyrates about its posterior end and then resumes normal forward locomotion. An escape reaction occurs when the cell's posterior end is mechanically agitated. The cell momentarily increases its forward swimming velocity and then resumes normal forward locomotion. The change in the swimming motion is regulated by a change in the membrane potential, since Paramecium cells (as well as other monads) have neither nerves for transmitting stimulative information nor synapses to determine transmission direction (Machemer 1974). Ca²⁺ channels in the anterior end regulate avoiding reactions, whereas K⁺ channels in the posterior end regulate escape reactions. In the experiment by Ishikawa & Hota (2006), avoiding and escape reactions were also observed when a Paramecium cell bumped into another cell. However, in most of their experimental cases, obvious biological reactions were not observed whenever two Paramecia came into close contact. Although detailed interactions between cilia and cell membranes, such as biochemical repulsion, are still unclear, the trajectories of the cells were mainly governed by hydrodynamics. One example of the hydrodynamic interaction in a fluid layer between flat plates is shown in figure 5a. Here, the angle between the orientation vectors of the two cells is initially large. The two cells then swim nearly side-by-side and finally move away from each other at an acute angle.

Figure 5.

Comparison between experimental and numerical results for the hydrodynamic interaction between two swimming P. caudatum. (a) A sample sequence showing the hydrodynamic interaction between two swimming P. caudatum that experience a near contact in a fluid layer between flat plates. The time interval between sequential images is 1/3 s. Long arrows are added to schematically illustrate cell motion. (b) A sample sequence showing the hydrodynamic interaction between two squirmer models. The orientation vectors of the squirmers are denoted by large arrows on the ellipsoids, and a thin solid line is added so that one can easily visualize the angle between the two squirmers (reproduced with permission from Ishikawa & Hota 2006).

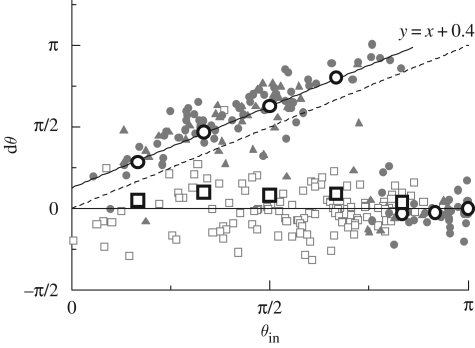
Ishikawa & Hota (2006) also performed a computational analysis of the interaction between two Paramecia. They modelled the Paramecium as a squirmer (Ishikawa et al. 2006), which propels itself by generating tangential velocities on its surface. The squirming velocity was measured experimentally using a particle image velocimetry technique. This is, in fact, a very reasonable model for describing the locomotion of ciliates, which propel themselves by means of pulsating arrays of cilia on their surfaces, as illustrated in figure 1b. In particular, the so-called symplectic metachronal wave, in which the cilia tips remain close together at all times, can be modelled simply as the stretching and displacement of the surface formed by the envelope of these tips. The squirmer model was first proposed by Lighthill (1952) and then extended by Blake (1971), Stone & Samuel (1996) and Downton & Stark (2009). Details of the squirmer model can be found in Ishikawa et al. (2006). The Stokes flow field and the squirmer motion were obtained numerically by a boundary element method. In the case of two cell surfaces in close proximity to each other, a lubrication theory was incorporated to calculate the lubrication forces and torques. No biological reaction was included in the model, and the interaction was purely hydrodynamic. Figure 5b shows the numerical results for the interaction between two squirmers, which are in close agreement with the experimental results shown in figure 5a. The relationship between θ_in and dθ was also investigated, where θ_in denotes the angle between the orientation vectors of two cells before the near contact and dθ denotes the change in the angle of cell 2 relative to cell 1 after the near contact. In figure 6, the experimental results are plotted with grey symbols, and the numerical results are plotted with large circles and squares. Head, body and tail indicate the collision position in the cell body; e.g. head–tail means that the head of cell 1 collides with the tail of cell 2. We note that for head–tail interactions, the numerical results for dθ (large white squares) cluster around dθ = 0, and the experimental results exhibit the same tendency. For head–head interactions (large white circles), the numerical results for dθ increase almost linearly with θ_in when θ_in is less than about 3π/4, and once again the experimental results exhibit the same tendency. Thus, the mathematical model correctly describes many interactions between Paramecia.

Figure 6.

Comparison of the experimental and simulation results for dθ, where dθ is the change in the angle of cell 2 relative to cell 1 after near contact, and θ_in is the angle between the orientation vectors of the cells before the near contact. The experimental results are plotted with grey symbols (filled circle, head–head; filled triangle, head–body; open square, head–tail; dotted line, y = x), and the numerical results are plotted with large circles (head–head) and squares (head–tail). The broken line with slope = 1 and the solid lines dθ = 0 and dθ = θ_in + 0.4 are added for comparison. In the figure, head, body and tail indicate the collision position on the cell body (reproduced with permission from Ishikawa & Hota 2006).

Another interesting pairwise interaction of eukaryotes is a dancing pair of Volvox. Drescher et al. (2009) recently discovered two types of dancing motion of the multicellular freshwater ciliate Volvox carteri. When suspensions of Volvox were placed in glass-topped chambers, a stable bound state of two Volvox cells orbiting each other occurred frequently near the top surface. Since the orbiting motion resembles the waltzing motion of dancers, it is termed a ‘waltzing’ motion. Near the bottom surface, on the other hand, the Volvox cells oscillate back and forth as if held together by an elastic band; this motion is called a ‘minuet’. The clustering of cells may be evolutionarily favourable to Volvox, since it increases the probability of fertilization. Thus, it becomes important to clarify whether the dancing motions occurred actively, as the result of a biological interaction (such as chemical communication), or passively, due to the hydrodynamic interaction between the Volvox. The waltzing motion was analysed mathematically using point singularities and numerically using a boundary element method, and it was concluded that the effect can be explained well in terms of hydrodynamics.

Jiang et al. (2002) numerically investigated the hydrodynamic interactions between two copepods, although the Reynolds number in this case is slightly larger than unity and the flow field is not Stokesian. Their detailed model consisted of a prosome, a urosome and two antennules and was designed to imitate the external morphology of a species of coastal water copepods. They found two beneficial roles of the hydrodynamic interactions for copepod swarms: the interactions maintained the integrity of the swarms and separated the swarming members by ensuring large nearest-neighbour distances. Although the interactions were not between eukaryotes, Barbara & Mitchell (2003) found an interesting example of a two-cell interaction between a motile alga and a bacterium. They demonstrated that some marine bacteria are able to track motile algae by a combination of direction reversal and steering. Tracking motile algae is biologically important for bacteria because they are able to ingest nutrients exuded by the algae. Locsei & Pedley (2009) investigated this phenomenon analytically and showed that a bacterial cell may exploit the vorticity and strain-rate fields generated by an algal cell in order to steer. In all these models, the interaction was assumed to be purely hydrodynamic, and no provision was made for any type of biological reaction. Although the detailed roles of biological reactions are still unclear, these findings suggest that hydrodynamics play an important part in pairwise interactions of swimming micro-organisms.

2.2. Interactions between two nearby bacteria

Aranson et al. (2007) experimentally observed two-cell interactions between Bacillus subtilis bacteria in a thin film. They observed that bacteria reoriented during collision and tended to align side-by-side afterwards. In a dense suspension of bacteria, many cells interacted significantly, and the suspension showed coherent structures (see §3.2). In order to study these bacterial interactions, various levels of mathematical models have been proposed. As mentioned earlier, Guell et al. (1988) modelled a bacterium as a force dipole and analysed the far-field interactions between bacteria. Another simple mathematical model is a linked-sphere model, which is widely used by many researchers to investigate cell–cell interactions (Hernandez-Ortiz et al. 2005; Pooley et al. 2007; Alexander & Yeomans 2008; Alexander et al. 2008, 2009; Gunther & Kruse 2008; Underhill et al. 2008). Although a linked-sphere model is not intended to specifically model a bacterium, it gives suggestive results even for bacterial interactions. Pooley et al. (2007) employed a simple swimmer model consisting of three spheres joined by thin rods that move by shortening and extending the rods in a periodic and time-irreversible manner. They showed that the interactions between two swimmers may be attractive, repulsive or oscillatory, depending on their relative displacement, orientation and phase. Hernandez-Ortiz et al. (2005) and Underhill et al. (2008) proposed two rigidly linked beads and analysed the many-body interactions. They successfully simulated coherent structures found in a dense suspension of bacteria (see §3.2). Cisneros et al. (2007) also proposed a similar model, in which a cell body is modelled by a sphere and a flagella bundle is modelled by a rod. They numerically investigated hydrodynamic interactions between several bacteria swimming near a wall.

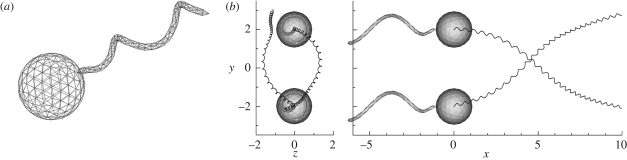
Ramia et al. (1993) and Nasseri & Phan-Thien (1997) employed a more detailed model of a bacterium as a spherical body with a rotating helical flagellum. They numerically investigated the interactions between bacteria using a boundary element method. They found attraction between two bacteria swimming side-by-side, as predicted by a far-field analysis. Keaveny & Maxey (2008) investigated interactions between two artificial micro-swimmers. Their model consisted of a series of spheres, with a magnetic drive force exerted on each sphere. Ishikawa et al. (2007b) have recently used a similar bacterial model, illustrated in figure 7a, to investigate near-field interactions. They carried out a numerical analysis of the stability of two parallel swimming bacteria using a boundary element method. Figure 7b shows a sample result for an interaction between two bacteria initially placed parallel to one another. The parallel swimming motion was demonstrated to be unstable, whereas earlier experimental research based on observations in a thin film and near a wall and analytical research using multipoles yielded the opposite result. It was concluded that the three-dimensional shape of the helical flagellum and the boundaries of their domain have an appreciable effect on the near-field interactions of bacteria.

Figure 7.

Interaction of two swimming bacterial models (cf. Ishikawa et al. 2007b). (a) Computational mesh for a bacterium model, in which 320 and 360 triangles are generated for a cell body and a flagellum, respectively. (b) Initial positions and trajectories of two interacting bacterial models. The two bacteria are initially set parallel each other, and their orientation vectors are in the x-direction.

Although the interactions were not between two bacteria, numerous investigations have focused on the interactions between a bacterium and a solid wall. These interactions are crucial to understanding the concepts such as the migration of infectious bacteria along a catheter and the formation of a biofilm. Experimental studies have shown that swimming bacteria tend to stay near a wall for a time, and their trajectory often forms a circle (Maeda et al. 1976; Berg & Turner 1990; Frymier et al. 1995; Magariyama et al. 2005). The small number of multipoles in equation (2.3) is not sufficient to analyse this phenomenon because of the small separation between them. Lauga et al. (2006) used a numerical approach called resistive-force theory, first proposed by Gray & Hancock (1955). Resistive-force theory is an approximation of slender-body theory, in which Stokes flow singularities are distributed along the centreline of the flagellum. Lauga et al. (2006) reproduced the circular trajectories of bacteria, and their results were in good agreement with the experiments. Goto et al. (2005) developed a more detailed model, similar to that of Ramia et al. (1993), and analysed the near-field interactions between a bacterium and a wall using a boundary element method. Their results revealed that bacterium motion is influenced by the angle between the boundary and the swimming direction and that forward swimming motion is more stable than backward swimming motion near a wall. These hydrodynamic models explain the behaviour of bacteria near a wall.

3. Collective motions of swimming micro-organisms

3.1. Various types of collective motions in a suspension of micro-organisms

Micro-organisms in a suspension exhibit a variety of collective motions, sometimes resulting in the formation of interesting geometric patterns. Bioconvection is the biological analogue to a physical process, such as thermal convection, that sometimes results in geometric patterns and has been investigated extensively (e.g. Wager 1911; Platt 1961; Pedley et al. 1988; Kessler et al. 1994; Bees & Hill 1997; Bearon & Grunbaum 2006; Denissenko & Lukaschuk 2007; Kitsunezaki et al. 2007). Bioconvection is observed in suspensions of algal cells and bacteria, whereby both generally swim upwards either because of bottom heaviness or the oxygen gradient produced by their own consumption, respectively. Since these micro-organisms are slightly denser than water, the upper regions of the suspension become denser than the lower regions. This leads to the development of overturning instability, analogous to Rayleigh–Benard convection, resulting in the formation of descending plumes of dense cell suspension. The mechanism of bioconvection can be satisfactorily explained in terms of hydrodynamics. For details, see Hill & Pedley (2005).

Spormann (1987), Carlile et al. (1987) and Mann et al. (1990) reported another type of migration phenomenon in dense suspensions of unidirectional magnetotactic bacteria swimming in narrow glass tubes. When such a suspension is subjected to an aligned magnetic field, thousands of cells form a stable band perpendicular to the direction of movement. Magnetotactic bacteria contain intracytoplasmic Fe₃O₄ particles, and the magnetic dipole is oriented more or less parallel to the axis of motility of the cells (Balkwill et al. 1980). There are two kinds of dipoles acting on a magnetotactic bacterium: the magnetic dipole owing to permanent magnetic particles in the cell and the hydrodynamic force dipole resulting from the swimming motion of the cell. Carlile et al. (1987) speculated that band formation is due to the magnetic interaction, whereas Guell et al. (1988) suggested that it is a consequence of the hydrodynamic interaction. Although the exact nature of the mechanism remains unclear, both hypotheses suggest that this migration phenomenon may have a biomechanical explanation.

Collective motions of spermatozoa have also been widely investigated. Moore et al. (2002) reported the probable altruistic behaviour of spermatozoa in a eutherian mammal. They showed that the spermatozoa of the common wood mouse displayed a unique morphological transformation, resulting in the cooperation in distinctive aggregations or trains of hundreds of cells. They performed a computer-assisted sperm analysis and found that the mean average path velocity of sperm trains was significantly greater than that of single spermatozoa. Eventual dispersal of sperm trains was associated with most of the spermatozoa undergoing a premature acrosome reaction. Yang et al. (2008) studied the hydrodynamic interaction and cooperation of sperm embedded in a two-dimensional fluid using a particle-based mesoscopic simulation method. Owing to the hydrodynamic effects, a multisperm system showed aggregations and swarm behaviour, similar to former experimental observations. The synchronization of sperm beats was accomplished by the hydrodynamic interactions. Similar synchronization was also found in the interactions between flagella of a bacterium (Kim et al. 2003; Kim & Powers 2004; Reichert & Stark 2005). Riedel (2005) found a self-organized vortex array of sperm cells at planar surfaces. These vortices formed an array with local hexagonal order when the sperm density was above a critical value. They also concluded that large-scale coordination of cells could be regulated hydrodynamically, and chemical signals were not required. Similar circling sperm cells in the vicinity of a wall were found numerically by using a coarse-grained model (Friedrich & Julicher 2008). These collective motions were well explained by hydrodynamic forces.

Bacterial colonies cultured on agar gels are known to exhibit fractal-like branching and complex spatio-temporal patterns. This phenomenon was first reported by Fujikawa & Matsushita (1989). Bacterial colonies respond to adverse growth conditions by sophisticated cooperative behaviour and intricate types of communication such as direct cell-to-cell physical interactions (Igoshin et al. 2004) and long-range chemotactic signalling (Bassler 2002). Shapiro & Hsu (1989) investigated cell–cell interactions in bacterial colonies of Escherichia coli. They showed that E. coli cells responded to each other and adjusted their cellular morphogenesis to form multicellular groups as they proliferated on agar. A detailed discussion of these mechanisms can be found in the excellent review papers by Ben-Jacob & Levine (2006), Ben-Jacob et al. (2000) and Copeland & Weibel (2009). In these views, it is shown that pattern formation in micro-organisms can be viewed as a result of an exchange of information between the individual cell level and the macroscopic colony level. Lega & Passot (2003, 2004, 2007) developed a hydrodynamic model for the evolution of bacterial colonies growing on soft agar plates. Their model consists of hydrodynamic equations coupled with reaction–diffusion equations for the respective concentrations of nutrients and bacteria and is capable of reproducing both the usual colony shapes and the typical hydrodynamic motions such as whirls and jets observed in wet colonies of B. subtilis (Mendelson et al. 1999). In bacterial colonies, the interactions between cells are mediated both by chemical signalling and by hydrodynamics. Recently, however, there has been a growing interest in hydrodynamic motions (such as whirls and jets), since they have a significant effect on the properties of a suspension in regions of high cell concentration.

3.2. Coherent structures in a bacterial suspension

Coherent structures in bacterial suspensions were first reported by Kessler & Wojciechowski (1997) and Kessler & Hill (1997), followed by Mendelson et al. (1999). They observed a meso-scale motion of whorls and jets generated by B. subtilis in a thin water film above an agar gel. Steager et al. (2008) also found similar swarming motion of Serratia marcescens bacteria above an agar gel. Dombrowski et al. (2004) reported meso-scale coherent structures in a concentrated suspension of B. subtilis. In a concentrated suspension, a B. subtilis cell tends to swim in much the same direction as its neighbours, generating a flow pattern larger than the scale of an individual cell, but smaller than the scale of the container used in the experiment, as shown in figure 3. The meso-scale structure changes its direction randomly, in a manner reminiscent of turbulence. The concentration dependence of the coherent structure was later reported by Sokolov et al. (2007). Liao et al. (2007) examined the pair velocity correlations among E. coli bacteria swimming freely in a microfluidic channel. A large number of bacterial tracks were obtained using a particle-tracking algorithm, and the longitudinal and transverse pair velocity correlation functions were evaluated. Their experiments indicated that the longitudinal and transverse correlation functions were positive and negative, respectively. The diffusivity of inert particles in such a suspension was investigated experimentally by Kessler (2000) and Wu & Libchaber (2000). Specifically, the latter group studied the effect of bacterial motion on the diffusivity of micro-scale polystyrene beads in a freely suspended film using a stable two-dimensional soap film seeded with bacteria (E. coli) and micro-scale beads. Interestingly enough, the diffusion of beads in the cell suspension was enhanced thousands of times compared with Brownian diffusion owing to the effect of the coherent structures. By measuring correlations of passive tracer particles in a bacterial bath, Chen et al. (2007) found that the macroscopic stress fluctuations were sensitive to the microscopic swimming behaviour of the bacteria.

Various types of mathematical and numerical models have been suggested for investigating the coherent structures and collective motions observed in suspensions of micro-organisms. These models can be classified into two major groups: continuum models and discrete models. In the case of a continuum model for a dilute suspension of micro-organisms, the bulk velocity field u is assumed to satisfy the continuity and Cauchy equations, subject to the Boussinesq approximation, given by (cf. Hill & Pedley 2005)

3.1

and

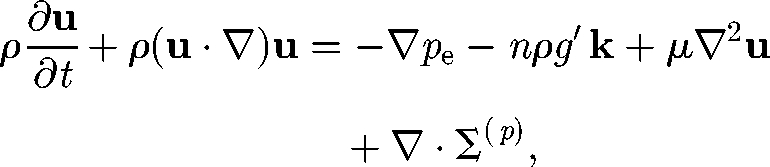3.2

where ρ is the density, p_e is the pressure excess over hydrostatic pressure, g′ is the reduced gravity, k is the vertical unit vector and μ is the viscosity. Σ^(p) is the particle stress tensor, which indicates how the stress field is affected by the swimming micro-organisms (Batchelor 1970). This single fluid model with the Boussinesq approximation has been used for the bioconvection analysis (Pedley & Kessler 1992). Although the model was successful in explaining the overturning instability resulting in the formation of descending plumes, it has not been used for simulating coherent structures in a bacterial bath.

Continuum models for dense suspensions of cells have been proposed by Simha & Ramaswamy (2002), Hatwalne et al. (2004), Toner et al. (2005), Ramaswamy & Simha (2006), Sankararaman & Ramaswamy (2009), Saintillan & Shelley (2008a,b), Aranson & Tsimring (2005), Aranson et al. (2007) and Wolgemuth (2008), as well as by other researchers such as Voituriez et al. (2006) and Liverpool & Marchetti (2006). Ramaswamy's group constructed hydrodynamic equations for suspensions of self-propelled particles. The effect of swimming particles was taken into account by adding force dipoles in the momentum equation of the fluid. Linear analysis of their model showed that nematic suspensions were unstable for certain wave angles with respect to the direction of alignment. Saintillan & Shelley (2008a,b) used a kinetic theory and performed nonlinear continuum simulations. Their results showed that the instability actually occurred for all wave angles. In their model, the dense regions of particles are typically in the form of bands, which become unstable and fold onto themselves owing to the disturbed flow. After folding, the bands break up and reorganize in the transverse direction. These dynamics may be analogous to the jetting found in a bacterial bath. Aranson et al. proposed a two-dimensional master equation for the probability density of bacterial position and orientation, derived from microscopic interaction rules dictated by experiments. By assuming a fully inelastic collision between two micro-organisms, the model could successfully reproduce the coherent structures in a bacterial bath and their cell density dependency. Wolgemuth (2008) developed a two-phase model for the collective swimming of dense colonies of bacteria. His model treats the fluid and bacteria as independent, interpenetrating continuum phases. By introducing an entropically driven tendency for the bacteria to align, similar to nematic liquid crystals, the model could reproduce coherent structures and density fluctuations in a bacterial bath. Most of the continuum models described in this paragraph have successfully reproduced coherent structures and density fluctuations found in former experiments.

The mathematical models described for the system of cell suspensions are quite similar to the work being done on active gels. Voituriez et al. (2006), Liverpool & Marchetti (2006) and Marenduzzo et al. (2007) proposed nematic hydrodynamic equations similar to continuum models for a cell suspension and discussed rheology and macroscopic phase separation of active gels or active liquid crystals. The importance of hydrodynamic interactions between particles in the fluctuations of a suspension has also been recognized in former studies on inert particles. Koch & Shaqfeh (1989) and Saintillan et al. (2006) investigated the density fluctuations in a suspension of sedimenting non-Brownian spheroids. Although the spheroids did not swim like micro-organisms, they found that the suspension was unstable to particle density fluctuations. Sedimenting suspensions of spherical particles, however, were shown to be stable in the absence of inertial effects.

Another type of model for suspensions of cells is a discrete model, in which the motions of individual cells in a suspension are solved in a discrete manner. Wide varieties of discrete models with different levels of hydrodynamics have been proposed so far. In some models, the hydrodynamics were not at all incorporated, and thus they are not applicable to a dense suspension of bacteria (Vicsek et al. 1995; Czirok et al. 1997; Gregoire & Chate 2004; Sambelashvili et al. 2007). Some other discrete models solve far-field hydrodynamics precisely, although near-field hydrodynamics are not accurately incorporated. Hopkins & Fauci (2002) solved the Navier–Stokes equations of fluid dynamics in the presence of a discrete collection of micro-organisms. These cells act as point sources of gravitational force in the fluid equations and thus affect the fluid flow. This model was not only successful in reproducing bioconvection, but also it was done in three dimensions, with good fidelity of results to both geometry and temporal dynamics. Llopis & Pagonabarraga (2006) analysed the collective dynamics of self-propelling particles using a lattice Boltzmann method. Although they reported aggregation of particles and self-diffusion over a long period of elapsed time, coherent structures were not mentioned in the paper. Hernandez-Ortiz et al. (2005) and Underhill et al. (2008) simulated the motions of large populations of confined swimming particles that interact hydrodynamically. Their model consists of two rigidly linked beads that exert equal and opposite point forces on the fluid. The swimmer moves and rotates in response to the low-Reynolds-number flow of the suspending medium, driven by all the other structures. Their model successfully reproduced coherent vortex motions in the flow, which are similar to the coherent structures observed in the experiments. Saintillan & Shelley (2007) investigated orientational order in suspensions of self-locomotive narrow spheroids using slender-body theory. In their work, a bacterium is modelled as a slender, narrow spheroid particle that propels itself by exerting an axisymmetric tangential shear stress on the fluid over a section of its body, while the remainder of its body is subject to the usual no-slip boundary condition. Coherent structures of particles appeared in their model, and they confirmed numerically that nematic suspensions of swimming particles were unstable at long wavelengths, which was reported in the former study by Simha & Ramaswamy (2002). In the models of Hernandez-Ortiz et al. (2005) and Saintillan & Shelley (2007), the coherent structures found in a bacterial bath were well reproduced. Since their models have elongated shapes (i.e. dumbbells and rods), the models tend to align to the average direction of the surrounding particles, even without precise hydrodynamics in the near field. This local alignment seems to be an important factor in the coherent structures.

Recently, discrete models with full hydrodynamics were proposed by Ishikawa et al. (2008) and Mehandia & Nott (2008). Ishikawa et al. (2008) developed an effective numerical method for investigating collective motions of swimming particles in a concentrated suspension. They used Stokesian dynamics (Brady & Bossis 1988) coupled with a boundary element method to solve the equations of near- and far-field hydrodynamics precisely. In the model of Ishikawa et al. (2008), a swimming micro-organism is assumed to be a squirming sphere with a prescribed tangential surface velocity, and no biological reactions are incorporated. Details of the squirmer model can be found in Ishikawa et al. (2006); this model was also used in the Paramecium simulations illustrated in figure 5b.

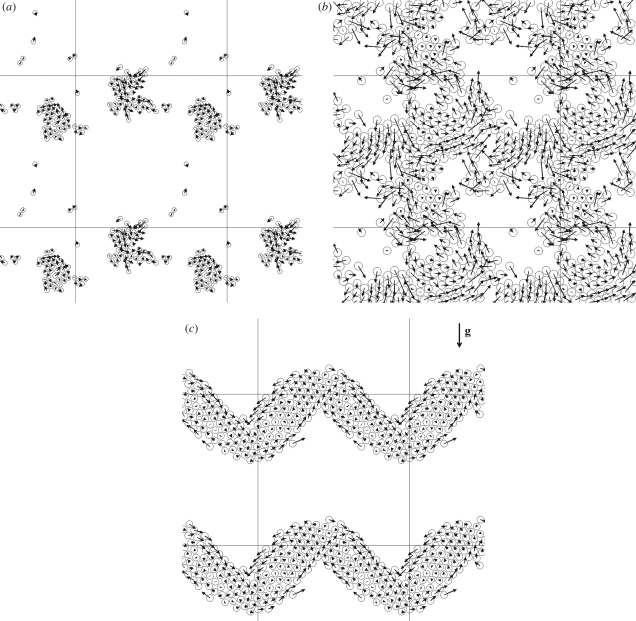
Ishikawa & Pedley (2008) calculated the motions of interacting squirmers in a monolayer, in which the centres and orientation vectors of all squirmers are on the same plane. The movement of non-bottom-heavy squirmers was computed for random initial positions and orientations. The distributions of squirmers with β = 5, as well as their velocity vectors for areal fractions of 0.1 and 0.5, are shown in figure 8a,b, where β denotes the ratio of second-mode squirming to first-mode squirming and is proportional to the squirmer's stresslet strength. In figure 8a, two large clusters are formed in a unit computational cell, which indicates that squirmers aggregate hydrodynamically in this case. In figure 8b, the clusters move together and the squirmers generate collective motions. The scale of the collective motions can be described in terms of the velocity correlations among the particles, as shown in figure 9. The velocity correlations are positive when the distances between the particles are small, indicating that neighbouring squirmers tend to swim together in a similar direction. The velocity correlations are negative when the distances are large, and thus squirmers that are far apart generally swim in opposite directions. This determines the typical scale of the coherent structures. The directions of the collective motions also changed over time, and the model was able to reproduce meso-scale spatio-temporal motions that were similar to experimental observations. Figure 8c shows the distribution and velocity vectors of bottom-heavy squirmers, relative to the average velocity. Although the squirmers were initially placed randomly, they tended to form a large band perpendicular to the gravitational direction, in a manner analogous to the band formation of magnetotactic bacteria (Carlile et al. 1987; Spormann 1987). These simulation results illustrate that various types of coherent structuring, such as aggregation, meso-scale spatio-temporal motion and band formation, can be generated by purely hydrodynamic interactions between micro-organisms.

Figure 8.

Distribution of squirmers in a monolayer and their velocity vectors. The computational cell is located at the centre as indicated by the solid lines. β is the ratio of second-mode squirming to first-mode squirming (cf. Ishikawa & Pedley 2008). (a) Aggregation of non-bottom-heavy squirmers with the areal fraction of 0.1 (β = 5). (b) Meso-scale spatio-temporal motion of non-bottom-heavy squirmers with the areal fraction of 0.5 (β = 5). (c) Band formation of bottom-heavy squirmers. Velocity vectors are taken relative to the average squirmer velocity, and vector g indicates the gravitational direction (β = 1).

Figure 9.

Correlation of the velocity of squirmers in a monolayer, with β = 5 and areal fractions of 0.1 (solid line), 0.3 (dashed line) and 0.5 (dotted line) (cf. Ishikawa & Pedley 2008).

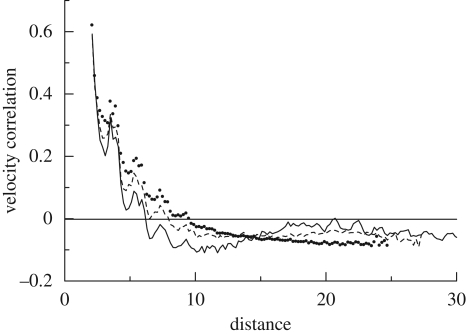
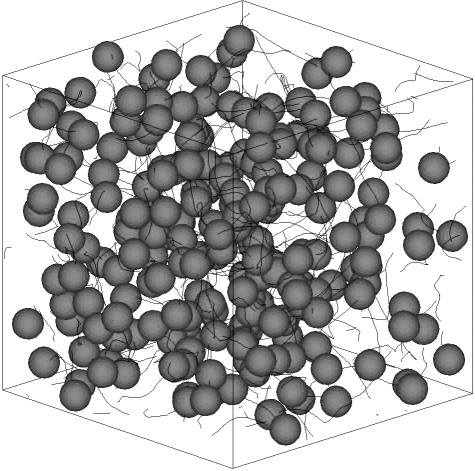
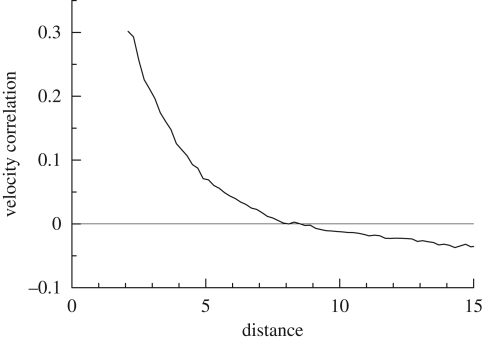
Ishikawa et al. (2008) also investigated coherent structures in three-dimensional suspensions of squirmers. The movement of 216 identical squirmers in a concentrated suspension with no imposed flow was simulated in a cubic domain with periodic boundary conditions. One realization of the instantaneous positions of the squirmers and their trajectories is shown in figure 10. The trajectories of the squirmers are not straight, since the hydrodynamic interactions between the squirmers cause them to change direction. In order to determine the scale of the collective motions, the velocity correlations between the particles were again calculated, and the results are plotted in figure 11. The velocity correlation is positive when the distance is small, indicating that neighbouring squirmers tend to move together in a similar direction, even in a three-dimensional suspension. The velocity correlation is negative when the distance is large, which is suggestive of a whirl structure. The effects of squirming velocity, volume fraction of cells and bottom heaviness on three-dimensional coherent structures were also investigated. The overall results indicated that a weak aggregation of cells appears as a consequence of the hydrodynamic interaction between cells, the cells generate collective motions via the hydrodynamic interaction and the range and duration of the collective motions depend on the volume fraction and the stresslet strength of the squirmers. These tendencies were in satisfactory qualitative agreement with previous experimental observations. In the model of Mehandia & Nott (2008), however, coherent structures similar to former experimental observations were not mentioned. The difference may have come from the near-field hydrodynamics between interacting particles. Ishikawa et al. (2008) reported that their squirmer models tend to show alignment in the average direction of surrounding cells because of the near-field hydrodynamics. Although identifying the mechanism governing coherent structures requires more detailed study, the local alignment of particles owing to the near-field hydrodynamics as well as the instability of ordered suspensions at long wavelengths could be key factors.

Figure 10.

Instantaneous position of 216 identical squirmers in a fluid otherwise at rest, with β = 5. The solid lines are the three-dimensional trajectories of the squirmers over five time intervals.

Figure 11.

Correlation of the velocities of squirmers in a three-dimensional suspension with β = 5 (cf. Ishikawa et al. 2008).

4. Rheological properties of a suspension of micro-organisms

When the size of the individual micro-organisms is much smaller than that of the flow field of interest, it is inconvenient to attempt to understand the bulk motion of the suspension from an analysis of individual cell motions. In such cases, it is better to model the suspension of micro-organisms as a continuum, in which the variables are volume-averaged quantities (Pedley & Kessler 1992). Continuum models for dilute suspensions of micro-organisms have been applied to bioconvection (Childress et al. 1975; Pedley & Kessler 1990; Hillesdon et al. 1995; Bees & Hill 1998, 1999; Metcalfe & Pedley 2001; Alloui et al. 2005; Ghorai & Hill 2005, 2007; Taheria & Bilgen 2008) and other phenomena (Metcalfe et al. 2004; Tuval et al. 2005), although cell-to-cell interactions were neglected in all cases.

The stresslet of a solitary micro-organism provides the first-order correction to the bulk stress, in terms of the volume fraction ϕ. The particle stress tensor in equation (3.2) can be expressed by using the stresslet as (Batchelor 1970)

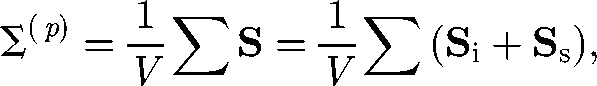4.1

where the particle stress tensor is averaged in the volume V and the sum is over all particles in V. The stresslet exerted on a particle may be split into two contributions: the stresslet generated by an inert particle in a background linear flow field, S_i, and the stresslet owing to the swimming motion of a particle in a fluid otherwise at rest, S_s. The S_i of an inert sphere with radius a in a dilute limit (i.e. no hydrodynamic interactions between particles) was first derived by Einstein (1906) as

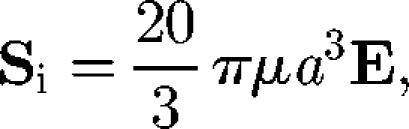4.2

where E is the rate of the strain tensor. This equation indicates that the particle stress generated by inert spheres is proportional to E in the dilute limit, and the rheology of the dilute suspension of spheres shows Newtonian properties. In the case of an ellipsoid, the angular velocity ė is given by Jeffery's equation as (Jeffery 1922)

4.3

where e is the orientation vector and Ω is the rate of rotation tensor. Here, γ is Jeffery's parameter given by 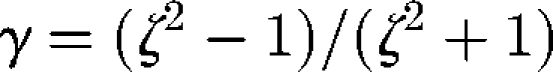, where ζ is the aspect ratio. This equation indicates that ellipsoids tend to align with the principal axis of strain. The stresslet S_i of an ellipsoid is given by 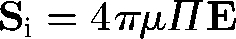, where Π is a rank 4 tensor and dependent only on the shape, size and instantaneous orientation of the particle (Batchelor 1970). Rheological properties of a dilute suspension of ellipsoids often become non-Newtonian except for some special cases, such as in an axisymmetric bulk pure straining motion.

The non-isotropic orientation of particles also results in significant change in the bulk stress field through the stresslet owing to swimming, S_s. As explained in figure 4, S_s is positive for a puller, but negative for a pusher. Ishikawa et al. (2006) derived the following equation for the stresslet S_s of a solitary spherical squirmer model:

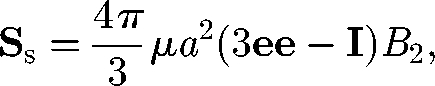4.4

where a is the radius, e is the orientation vector of the squirmer and B₂ is the coefficient of the second mode of the surface squirming velocity. Similar equations have been obtained by other researchers for an axisymmetric swimming micro-organism (Pedley & Kessler 1990; Hatwalne et al. 2004). Haines et al. (2008) investigated the effective viscosity in a dilute suspension of bacteria using a two-dimensional mathematical model. They analysed the effect of self-propulsion on the stress field and showed that the effective viscosity decreased in bacterial suspensions. They also pointed out the importance of bacterial shape to the leading order effects on the effective viscosity of dilute suspensions. In particular, a significant order ϕ effect was derived for elongated particles, such as bacteria, owing to the non-isotropic orientation distribution. D. Saintillan (2009, unpublished data) also investigated the shear viscosity of a dilute suspension of swimming particles. He found that normal stress differences appeared in a suspension subjected to a simple shear flow.

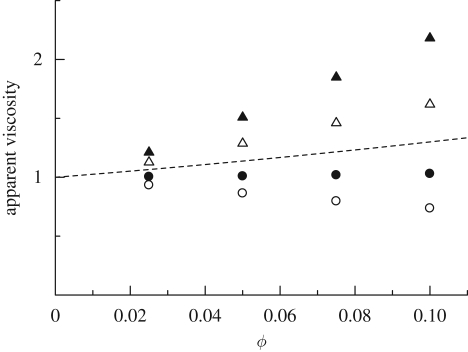
In the non-dilute regime, however, we need to accurately solve the hydrodynamics between micro-organisms interacting in the near field, which usually requires a numerical analysis. For a semi-dilute suspension of squirmers, Ishikawa & Pedley (2007a) investigated the ϕ² dependency of the asymptotic expression for the particle bulk stress in terms of ϕ. They dynamically computed the three-dimensional hydrodynamic interactions of squirmers subjected to a simple shear flow exerted in the xy-plane. For bottom-heavy squirmers, the results indicated that the stresslet generated by the squirming motion contributes to the bulk stress in direct proportion to ϕ. When the background shear flow is directed vertically, and the stresslet of a solitary squirmer is positive (puller), the apparent viscosity of the semi-dilute suspension of bottom-heavy squirmers becomes smaller than that of inert spheres, as shown in figure 12. On the other hand, when the shear flow is horizontal and varies with the vertical coordinate, the apparent viscosity becomes larger than that of inert spheres (figure 12). Thus, in the case of bottom-heavy squirmers, the suspension rheology is strongly influenced by the direction of shear relative to the gravitational direction. It is also affected by the sign of the stresslet (puller or pusher), the strength of the bottom heaviness and the shear rate. The xy- and yx-components of the stress tensor are no longer symmetric (the shear flow is in the xy-plane), and the suspension exhibits strongly non-Newtonian properties.

Figure 12.

The effect of volume fraction ϕ on the xy- and yx-components of the apparent viscosity of a suspension of bottom-heavy squirmers, under the conditions of weak shear flow and strong bottom heaviness, with β = 5. For details, see Ishikawa & Pedley (2007a). A simple shear flow is applied in the xy-plane, and the gravitational directions are taken in the −x- or −y-directions, i.e. vertical or horizontal shears. The broken line indicates the values obtained from the analytical equation of Batchelor (1977) for a suspension of Brownian spheres. Vertical: filled circle, η_xy; open circle, η_yx. Horizontal: filled triangle, η_xy; open triangle, η_yx. Dashed line, 1+2.5ϕ+5ϕ².

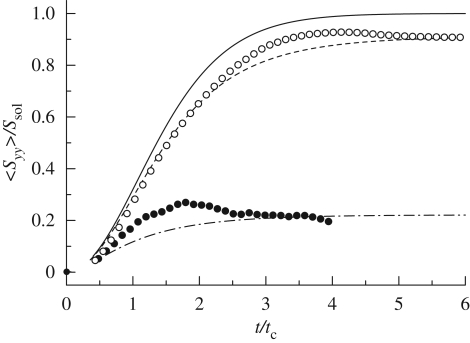
A suspension of bottom-heavy micro-organisms also shows normal stress differences and stress relaxation, analogous to a visco-elastic fluid. Ishikawa & Pedley (2007a) numerically demonstrated that in a suspension of bottom-heavy squirmers, normal stress differences appear for all relative orientations of gravity and shear flow. Ishikawa et al. (2007a) focused on the unsteady behaviour of a cell suspension and carried out analytical and numerical investigations of the orientational relaxation time, which is the time required for a micro-organism to reorient itself from a disoriented condition to its preferred direction. They assumed isotropic random orientation at t = 0 and calculated the time change of the squirmer-averaged stresslet component <S_yy>, where the gravitational direction is taken as −y. The numerical and analytical results are shown in figure 13, in which the stresslet and time are replaced by dimensionless quantities obtained by dividing the stresslet by the stresslet strength S_sol of a solitary squirmer and the time by the characteristic time t_c for reorientation. Here, t_c is defined as 6μ/ρgh, where h is the distance between the centre of gravity and the centre of the squirmer (Pedley & Kessler 1987). The results indicate that both the mean stresslet strength and the orientational relaxation time are less than those for a dilute suspension. A stress overshoot was also observed in some cases. Although these tendencies are similar to a visco-elastic fluid, the mechanism of the time variation in the stress field is different, as discussed in Ishikawa et al. (2007a).

Figure 13.

The effect of bottom heaviness on the time change of the yy-component of a squirmer-averaged stresslet, where gravity is taken in the −y-direction. S_sol is the stresslet strength of a solitary squirmer. G_bh is a dimensionless parameter for bottom heaviness, defined as 2πρgah/μB₁, where h is the distance between the centre of gravity and the centre of the squirmer, and B₁ is the first mode of the squirming velocity. The horizontal axis is calibrated in units of the time divided by the characteristic time t_c. Analytical solutions with D_rt_c = 0 (solid line), 0.03 (dashed line) and 0.35 (dashed-dotted line) are drawn for the sake of comparison, where D_r denotes the rotational diffusion. The case D_rt_c = 0 is equivalent to a dilute suspension. Simulation: open circle, G_bh = 100; filled circle, G_bh = 10 (cf. Ishikawa et al. 2007a).

In a dense suspension of bacteria, Chen et al. (2007) experimentally found stress fluctuations by using a combination of passive two-point microrheology and active response measurement. They showed that macroscopic stress fluctuations were sensitive to the microscopic swimming behaviour of bacteria. The rheology of such dense suspensions of active particles was first analysed by Hatwalne et al. (2004). They employed coarse-grained equations governing the hydrodynamic velocity, concentration and stress fields, as introduced in §3.2, although the effect of near-field hydrodynamic interactions was not incorporated in the model. They showed that an orientationally ordered state of active particles had a non-zero macroscopic stress, in contrast to thermal equilibrium nematics. Saintillan & Shelley (2008a,b) analysed the particle stress in active suspensions in more detail using a kinetic theory. In isotropic suspensions, their theory indicated the existence of an instability for the active particle stress, in which shear stresses are eigen modes and grow exponentially at long scales. They also performed nonlinear simulations and observed the growth of large-scale stress fluctuations. Interestingly, their model indicated that the active shear stresses were unstable at long wavelengths in the case of pushers, but not for pullers. Since coherent structures were found in a suspension of pushers (i.e. bacteria), essential differences may exist in terms of stability between a suspension of pushers and pullers, as predicted by them.

5. Diffusion properties of a suspension of micro-organisms

In a cell suspension, micro-organisms are dispersed by the intrinsic randomness of their swimming motion, as well as by hydrodynamic interactions. This is called self-diffusion of micro-organisms. Chemical substances in the suspension, such as oxygen and nutrients, are also diffused, both by Brownian motion and by the micro-scale flow field generated by micro-organisms. In order to understand cell distribution and mass transport in a suspension of micro-organisms, these diffusion properties must be clarified.

5.1. Self-diffusion of micro-organisms

The key equation in a continuum model of cell suspensions is the cell-conservation equation. When birth and death processes are neglected, this is given by (cf. Hill & Pedley 2005)

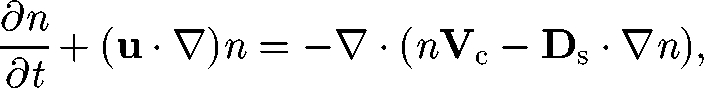5.1

where n is the number density of cells, V_c is the average cell swimming velocity, D_s is the self-diffusion tensor and the cell dispersal is modelled as a random diffusion process. Micro-organisms have some genetic randomness, in size and in shape, which may induce different swimming speeds, swimming directions and swimming trajectories for individual micro-organisms. There may also be some randomness in their reactions to light, gravity, nutrients and other micro-organisms. In the case of non-dilute suspensions of micro-organisms, the hydrodynamic interaction between cells causes frequent changes in the orientation of cells; this interaction may also be modelled as a chaotic process.

The self-diffusion of micro-organisms has been investigated analytically, numerically and experimentally by a number of researchers. One of the most intensively investigated topics is the self-diffusion of E. coli bacteria (Berg 1993). An E. coli cell has approximately six flagellar filaments on the side of its body. When these flagella turn counterclockwise, they form a synchronous bundle that pushes the body steadily forward, known as a ‘run’ motion. When they turn clockwise, the bundle comes apart and the cell body rotates in an erratic manner, known as a ‘tumble’ motion (Macnab & Ornston 1977). If a cell swims at a constant velocity U_b along a trajectory comprising a sequence of exponentially distributed straight runs of mean duration t_b, the self-diffusion D_s can be derived as (Lovely & Dahlquist 1975)

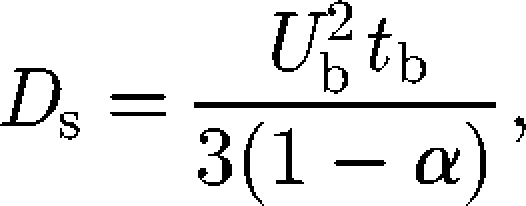5.2

where α is the mean value of the cosine of the angle between successive runs. For E. coli, α ≅ 0.33, U_b ≅ 3 × 10⁻⁵ (m s⁻¹) and t_b ≅ 1 (s), and we get D_s ≅ 4 ×10⁻¹⁰ (m² s⁻¹) (Berg 1993). Many researchers have also proposed biased random walk models for chemotactic bacteria (e.g. Alt 1980; Schnitzer 1993; Bearon 2003); these mathematical models have been recently reviewed by Codling et al. (2008) and Tindall et al. (2008a,b). These studies showed that the spreading of run-and-tumble bacteria in a dilute suspension can be well described by a random walk model.

A diffusion process was also identified for bottom-heavy algal cells in a dilute suspension. Childress et al. (1975) analysed an anisotropic self-diffusion tensor for bottom-heavy micro-organisms. They estimated the ratio of horizontal-to-vertical self-diffusions, and their results agreed with those of experiments involving Tetrahymena. Hill & Hader (1997) plotted the horizontal and vertical projections of a large number of experimentally observed individual trajectories for the bottom-heavy alga Chlamydomonas, swimming in a fluid with no imposed ambient flow. The cell trajectories showed significant randomness, and the diffusive process was described as a biased random walk. Vladimirov et al. (2000, 2004) also tracked several hundred individual Chlamydomonas and demonstrated that cell diffusion can be described again by a random walk model.

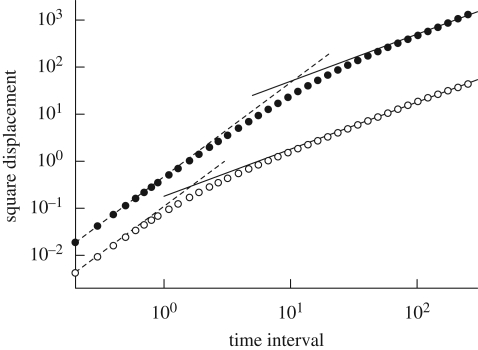
In the case of non-dilute suspensions of micro-organisms, the hydrodynamic interactions between cells play an important role in the spreading of cells. Ishikawa & Pedley (2007b) carried out analytical and numerical investigations of the self-diffusion tensor of squirmers in a semi-dilute suspension. In order to discuss the effective diffusivity, it is convenient to calculate the mean square displacement, which grows linearly over time if the dispersal is diffusive. The results for the square displacement as a function of elapsed time are shown in figure 14. The square displacement increases linearly with the squared elapsed time over short periods, which indicates that the translational and rotational velocities are relatively unchanged over short time intervals. On the other hand, for sufficiently long time intervals, both the translational and rotational square displacements increase linearly with elapsed time. Thus, the dispersal of squirmers can be accurately described as a diffusive process over a sufficiently long time interval, even though the movements of all the individual squirmers are calculated deterministically.

Figure 14.

Translational–rotational square displacements of non-bottom-heavy squirmers, with β = 5 and a volume fraction of 0.1. When the time interval is long enough, the square displacement and the time interval are proportional. Filled circle, translational; open circle, rotational; dashed line, y = cx²; solid line, y = cx.

Ishikawa & Pedley (2007b) also performed a scaling analysis. The appropriate length scale between near collisions may be the effective mean free path, l_mfp. If we assume that squirmers swim at a constant speed U_sol between collisions, then the typical time between collisions is t_mfp = l_mfp/U_sol. Also, the volume swept out by a squirmer in time t will be around V_p = πa²U_solt_mfp, where it is assumed that anything within a cylinder of radius a will be encountered. Thus, the number of particles within V_p is 3ϕU_solt_mfp/4a; if this number is assumed to be unity, we have that, in dimensionless terms, t_mfp = 4/(3ϕ). It is possible to propose scalings with ϕ for the magnitudes of the translational and rotational diffusivities, D^T and D^R, respectively. In the case of translational spreading, the random walk model suggests that D^T = U_soll_mfp/3 or, in dimensionless terms, D^T = t_mfp/3 = 4/(9ϕ). The principal prediction is that D^T is inversely proportional to ϕ. In the dilute limit (i.e. as ϕ→0), a squirmer swims at a constant velocity, and the square displacement is proportional to the square time interval. Thus, the translational diffusivity diverges when ϕ → 0, which means that the spreading of squirmers is no longer diffusive. This is because Ishikawa & Pedley (2007b) assumed that the orientational change in squirmers is caused by hydrodynamic interactions. In the rotational case, a similar random walk model implies that D^R = dθ²/(6t_mfp), where dθ² is the mean square angular displacement during one (near-)collision. The latter quantity should not depend on the distance travelled between collisions and therefore should be independent of ϕ. Thus, this model predicts that D^R∝1/t_mfp∝ϕ. These predictions were confirmed by numerical simulations.

It is also interesting to examine how bacteria spread when a suspension shows coherent structures. Hernandez-Ortiz et al. (2005) and Underhill et al. (2008) numerically analysed the self-diffusion of swimming particles, modelled as two rigidly linked beads, in a concentrated suspension. Although the swimmers formed spatio-temporal coherent structures (as discussed in §3.2), their dispersion can be well described as a diffusive process over a sufficiently long time. These studies suggest that cell dispersal can be modelled as a random diffusion process, and it is appropriate to introduce the self-diffusion tensor in equation (5.1), as long as the macroscopic time scales of interest are large enough compared with the microscopic time scales for cell reorientation and interaction.

5.2. Diffusion of tracer particles in a suspension

It is also important to understand how chemical substances and fluid particles are dispersed in a suspension of micro-organisms. In a continuum model, the mass-conservation equation for chemical substances may be expressed in a manner analogous to equation (5.1) (cf. Hill & Pedley 2005):

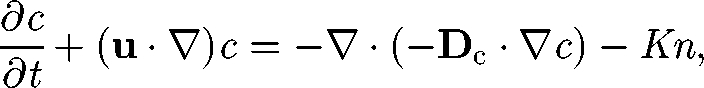5.3

where c is the concentration, D_c is the diffusion tensor for the chemical substance and −K is the production rate. In much of the earlier research, D_c is assumed to be Brownian diffusion. However, the actual diffusion may be much greater than Brownian diffusion, since micro-organisms agitate the suspension by generating a micro-scale flow field around them.

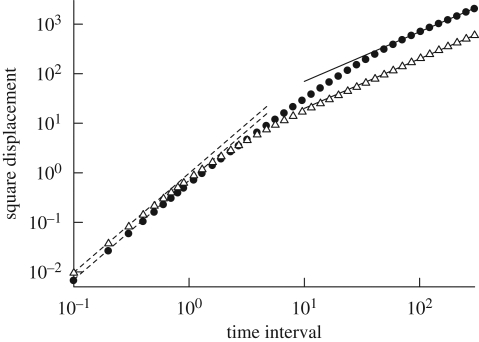
Recently, Ishikawa & Yamaguchi (2008) developed an accurate numerical technique for investigating fluid particle motions (rather than tracer particle motions) in a suspension of particles. They applied their method to fluid particle motions in a suspension of squirmers, neglecting Brownian motion. The results for the square displacement as a function of elapsed time are shown in figure 15. The square displacement of a fluid particle increased linearly with the time interval, when the time interval was long enough. Hence, the dispersal of fluid particles may again be accurately described as a diffusive process over a sufficiently long time interval. The diffusion of the fluid particles was not induced by Brownian motion, but rather by the micro-scale flow field generated by the squirmers. These findings suggest that the apparent Peclet number for mass transport may be much smaller in a suspension of micro-organisms than in a solvent fluid.

Figure 15.

Translational square displacement of non-bottom-heavy squirmers with β = 5 and fluid particles, under the condition that ϕ = 0.1. When the time interval is long enough, the square displacement and the time interval are proportional. Filled circle, squirmer; open triangle, fluid particle; dashed line, y = cx²; solid line, y = cx.

Some researchers have reported the diffusion of tracer particles in a dense suspension of bacteria. Wu & Libchaber (2000) experimentally investigated the diffusion of inert particles in a bacterial suspension. Specifically, they studied the effect of bacterial motion on the diffusivity of micro-scale polystyrene beads in a freely suspended film using a stable two-dimensional soap film seeded with bacteria (E. coli) and micro-scale beads; their observed diffusion constant was two to three orders of magnitude greater than Brownian diffusion. Kim & Breuer (2004) used E. coli to experimentally investigate the enhanced diffusion of large molecules in a bacterial suspension. They found that the effective diffusion coefficient increased linearly as the cell concentration increased. Since they used a rather small volume fraction of bacteria, coherent structures might not have appeared, and the results were thus different from those of Wu & Libchaber (2000). Saintillan & Shelley (2008a,b) used a nonlinear kinetic theory and computed the fluid mixing in a suspension of self-propelled particles. They showed that convective mixing in such suspensions was very strong as a result of the complex dynamics and flow instabilities that take place. Underhill et al. (2008) carried out a numerical investigation of the diffusion of tracer particles in a suspension of swimming particles modelled by two rigidly linked beads. Their results also indicated that collective motions of swimming particles dramatically enhance the diffusion of tracer particles. These results suggest that diffusion properties in a suspension are strongly influenced by the collective motion of micro-organisms.

6. Conclusions and prospects

In this paper, we have reviewed a number of biomechanical studies of pairwise interactions and collective motions of swimming micro-organisms. Some pairwise interactions between micro-organisms, such as Paramecia and Volvox, are adequately explained by mathematical and numerical models. These results reveal the importance of biomechanics and biophysics in understanding the behaviour of micro-organisms. Some collective motions of micro-organisms, such as coherent structures of bacterial suspensions, are also satisfactorily explained by biomechanics. Others, such as the fractal-like branching of bacterial colonies, are mediated by both hydrodynamics and chemical signalling. Although the examples of micro-organism behaviour discussed in this paper are only the tip of the iceberg, the fundamental knowledge we have obtained will be useful for a better understanding of the behaviour of micro-organisms. It will also be useful in developing micro-machines such as micro-swimmers mimicking micro-organisms (Dreyfus et al. 2005), bacterial carpets to manipulate micro-particles (Darnton et al. 2004) and micro-motors pushed by micro-organisms (Hiratsuka et al. 2006; Angelani et al. 2009).

We also discussed some of the macroscopic properties of a suspension of micro-organisms. The swimming motions of micro-organisms have a considerable influence on the rheological properties of a suspension, which affect the bulk motion of the suspension. Interactions between micro-organisms also affect the self-diffusion of micro-organisms. Moreover, the mixing caused by the swimming motion of the cells significantly enhances the diffusion of chemical substances dissolved in the suspension. Since these macroscopic properties are influenced by the microscopic characteristics of the suspension (such as individual swimming motions), they must be constructed by accurately analysing the behaviour of individual micro-organisms. Although the suspension properties considered in this paper may not be sufficient, they are useful for constructing a continuum population model for a suspension of micro-organisms.

Biomechanics and biophysics have been successfully employed to describe some of the behaviours of micro-organisms and properties of suspensions. However, many unexplained phenomena remain. One example is the biological reaction of micro-organisms to stimulations, such as chemical substances, light intensity and gravity, referred to as taxis. Gyrotaxis of micro-organisms is well described by simple mathematical models (e.g. Jones et al. 1994), but further work is required to achieve the same level of accuracy in modelling chemotaxis and phototaxis. We believe that mathematical modelling of these biological phenomena is a key issue in understanding various types of micro-organism behaviours. The immaturity of the theoretical understanding of this research field calls for theoretical physicists and biologists to continue to work together, with advances in experiments and related science supporting each other. Many researchers will undoubtedly be interested in this field and will continue to clarify the natural beauty exhibited by micro-organisms.