Modelling the effectiveness and risks of vaccination strategies to control classical swine fever epidemics

Abstract

In a recent update of the Dutch contingency plan for controlling outbreaks of classical swine fever (CSF), emergency vaccination is preferred to large-scale pre-emptive culling. This policy change raised two questions: can emergency vaccination be as effective as pre-emptive culling, and what are the implications for showing freedom of infection? Here, we integrate quantitative information available on CSF virus transmission and vaccination effects into a stochastic mathematical model that describes the transmission dynamics at the level of animals, farms and livestock areas. This multilevel approach connects individual-level interventions to large-scale effects. Using this model, we compare the performance of five different control strategies applied to hypothetical CSF epidemics in The Netherlands and, for each of these strategies, we study the properties of three different screening scenarios to show freedom of infection. We find that vaccination in a ring of 2 km radius around a detected infection source is as effective as ring culling in a 1 km radius. Feasible screening scenarios, adapted to the use of emergency vaccination, can reduce the enhanced risks of (initially) undetected farm outbreaks by targeting vaccinated farms. Altogether, our results suggest that emergency vaccination against CSF can be equally effective and safe as pre-emptive culling.

1. Introduction

Outbreaks of classical swine fever (CSF) can lead to large economic losses and have a major impact on animal welfare. A pig infected by CSF virus (CSFV) may show specific clinical symptoms (conjunctivitis, skin haemorrhages, cyanotic ears and lameness), but often the signs are aspecific (fever, dullness, diarrhoea and loss of appetite; Klinkenberg et al. 2005). Meanwhile, the infection can spread rapidly to other pigs (Laevens et al. 1998) and to other farms. At the moment the disease is first detected, a large number of farms may already be infected. To halt the epidemic, reducing the number of susceptible animals in the affected area is often required, especially in pig-dense regions. Two methods to achieve this are pre-emptive culling and emergency vaccination. Pre-emptive culling was used in the later stages of the 1997/1998 epidemic of CSF in The Netherlands, causing a large number of animals to be destroyed or prematurely slaughtered. This and subsequent experiences with foot-and-mouth disease (FMD) in 2001 and avian influenza in 2003 have caused public opinion to demand the adoption of alternative control strategies (Anon. 2007c ), in which the culling of healthy stock would be minimized. The current Dutch CSF and FMD contingency plans therefore specify that instead of culling healthy animals, they will be vaccinated. To protect pigs from CSF infection, an E2 subunit marker vaccine will be used (Bouma et al. 1999). In contrast to the classical (non-marker) C-strain vaccine, this marker vaccine has the advantage that the accompanying serological test can discriminate between infected and vaccinated animals. For this reason, the vaccinated meat will be accepted in the European common market, provided the Dutch authorities have received approval from the European Commission for an emergency vaccination plan.

Two major concerns exist about the marker vaccination strategy. First, can emergency vaccination with the marker vaccine be employed effectively to halt an epidemic? After all, vaccination will not immediately reduce epidemic spread, as it takes time to build up maximal vaccine protection (Bouma et al. 2000). Second, it is anticipated that some outbreaks occurring on (imperfectly) vaccinated farms might initially not be detected (Mangen et al. 2001; Klinkenberg et al. 2003), because the outbreak size could be limited and clinical signs in vaccinated animals are less pronounced (Bouma et al. 1999; Moormann et al. 2000). These undetected animals might pose a risk for the export position of the country. At the end of an epidemic, EU legislation requires a large-scale screening that consists of clinical inspection and serological testing of blood samples, to demonstrate (up to a certain confidence level) that the affected area is free of infection (EU Commission Decision 2002/106/EC). During this end screening a number of infected animals could escape detection again. When these are, in turn, exported and tested positive, an import ban might be the result. Therefore, a sufficiently stringent end screening must be in place to detect any seropositive animals missed during the epidemic.

Several studies have tried to answer the first question, i.e. whether marker vaccination can be an effective control strategy (Mangen et al. 2001, 2002; Klinkenberg et al. 2003). These studies model the effects of vaccinating pig farms based on the results of transmission experiments in groups of pigs vaccinated with the marker vaccine. They all consider the Dutch pig farming structure as in 1997 and study marker vaccination as an alternative to the pre-emptive culling strategy that was used in The Netherlands during the 1997/1998 epidemic. The main conclusion is that vaccination could have been effective, although the studies differ from each other in the required vaccination radius. The models used for these studies cannot be applied to study the second issue, i.e. the possibility that an infection on a vaccinated farm goes undetected, because they lack within-herd transmission dynamics. Including transmission on this level yields the number of infected animals, which is the relevant quantity for the design/study of the end screening. The within-herd transmission can be modelled implicitly (e.g. Arnold et al. 2008), but we include this transmission level explicitly, using a stochastic model description, to allow farm infections to die out, either by chance or due to the onset of vaccine protection. This is especially important for marker vaccination against CSF, as the time scale at which the virus progresses through the herd (typically four weeks; Elbers et al. 1999) is similar to the time scale at which the herd immunity against CSF infection is building up in a vaccinated population (typically two weeks; Bouma et al. 2000). Owing to these similar time scales, both timing and stochastic effects determine whether an initial infection will lead to detection or not. Thus, to quantify the risk of missing outbreaks during an epidemic, it is essential to include realistic within-herd dynamics in the model description.

In this paper, we study the effectiveness of marker vaccination against CSF and the implications for the design of the end screening to substantiate freedom of infection. For this purpose, we develop a stochastic model that includes within-herd dynamics as realistically as possible, by taking virus transmission and the effect of vaccination explicitly into account at the level of individual animals. Modelling the transmission at this level has the advantage that it can be directly linked to transmission experiments that have been performed on small animal groups. The individual-level model is coupled to models that describe transmission dynamics within a farm and on a national scale. Owing to this multi-level structure, the effect of vaccinating individual animals can be studied on the level of a nationwide epidemic, making the comparison of the culling and the vaccination strategies possible. Furthermore, the individual-based results make a comparison of different end screening scenarios possible.

Using the 2006 Dutch pig farming structure, five control strategies are compared. The EU requires the implementation of restriction zones and transport regulations, culling of detected infected herds and contact tracing (EU Council Directive 2001/89/EC). This minimal control strategy is compared to one pre-emptive ring culling strategy (in rings of 1 km radius around detected outbreaks) and to three ring vaccination strategies (in rings of 1, 2 and 5 km radius). In the results, we distinguish detected infected farms that are culled during the epidemic, and undetected infected farms that need to be detected by serological testing during the end screening. Three sampling strategies are evaluated for the end screening, which differ from each other in the number of animals to be serologically tested.

2. Classical swine fever transmission model

Before developing a transmission model for CSFV, we first investigate which data on CSFV transmission and marker vaccination are available. By first considering the information arising from these data sources in a qualitative manner, we identify the essential processes and their key parameters that inspire the structure of the transmission model.

At the individual level, a large number of transmission experiments have been conducted with vaccinated and non-vaccinated animals in direct contact (e.g. Laevens et al. 1998; Bouma et al. 2000; Moormann et al. 2000; Dewulf et al. 2001, 2004, 2005; Uttenthal et al. 2001). These show that vaccination does not have any effect in the first week after vaccination (Bouma et al. 2000). From 7 days onwards, a reduction of the infectiousness and infectious period of infected animals occurs, while the susceptibility of non-infected animals is lowered (gradual onset of vaccine protection). The longer ago animals have been vaccinated, the more pronounced these effects are. Results of transmission experiments that follow the course of infection for individual vaccinated animals (Dewulf et al. 2004) can be used to relate the length of the infectious period to the time elapsed between vaccination and (contact) infection. The effect of vaccination on the transmission rate is a combination of the reduced infectiousness of vaccinated infected animals and the reduced susceptibility of vaccinated non-infected animals. When the two effects are assumed to be separable, they can be studied separately in different types of transmission experiments. The effect of vaccination on infectiousness is assessed when vaccinated seeders infect susceptible unvaccinated animals (sentinels; Bouma et al. 1999; Moormann et al. 2000; Dewulf et al. 2005). The effect of vaccination on susceptibility is assessed when unvaccinated seeders infect vaccinated animals (Dewulf et al. 2001, 2005). These types of experiments with long vaccination-to-exposure periods have shown that a vaccinated animal will never be completely protected against infection (Dewulf et al. 2005). In transmission experiments, in a fully vaccinated population, the combined effect of vaccination on infectiousness and susceptibility is observed (Bouma et al. 2000; Moormann et al. 2000; Dewulf et al. 2004).

At the herd and livestock area level, the outbreak data of real-life CSF epidemics provide information on the within- and between-herd transmission. During the CSF epidemic in The Netherlands in 1997/1998, 429 farms were infected and 1280 were pre-emptively culled (Elbers et al. 1999). From the serological data collected during the epidemic from 82 (out of 429) infected farms, the within-farm reproduction number was estimated (Stegeman et al. 1999a ; Klinkenberg et al. 2003). For the same set of farms, the estimated infectious period (i.e. the time between estimated infection date and detection date) ranged from 10 to 57 days (Stegeman et al. 1999a ). Using the data of the full epidemic (i.e. estimated infection and removal dates for all infected and pre-emptively culled farms), combined with the location of all pig farms present at the start of the epidemic, it is possible to estimate the probability of transmission from an infected to a susceptible farm as a function of the distance between these farms (Boender et al. 2007).

Based on our inspection of the available data, we now formulate a transmission model describing the dynamics at three different levels. The highest aggregation level is a livestock area consisting of a (large) number of farms; each farm consists of a number of pens, which each holds a number of animals. In the following sections, we will describe the modelling of transmission between animals, pens and farms, together with the parameter estimation from the available data sources (summarized in table 1).

Table 1.

Parameter values and ranges for models described in §2.1–2.4.

model	parameter	value	95% CI
transmission between animals	T lat	4 days
	T inf,0	15 days	(7–25)
	T delay	6.4 days
	C inf	0.21 d−1
	T const	21 days
	β 0	6.7 d−1	(5.5–∞)
	λ inf	0.5 d−1	(0.31–0.63)
	λ sus	0.2 d−1	(0.16–0.25)
transmission between pens	R 0	2.8		for finishers and piglets
		2.9		for sows
	N p	10		for finishers and piglets
		1		for sows
	ϵ	2.8×10−3		for finishers and piglets
		2.9×10−4		for sows
detection within farms	C det	8.5		for finishers and piglets
		20.5		for sows
	r det	0.12 d−1		for finishers and piglets
		0.11 d−1		for sows
transmission between herds	α	2.2
	z 0	1 km
	k 0	0.0011 d−1

2.1. Modelling transmission between animals

We describe the transmission between animals in one and the same pen using an SEIR model. The acronym denotes the different stages of the disease: when a susceptible (S) animal is infected, it will be exposed (E) during a latent period T _lat, after which it will be infectious (I) for an infectious period T _inf until it recovers (R; or dies). In the model, the variables S, E, I and R represent the number of animals in the respective stages. The rate at which an infectious animal i infects a susceptible animal j in the same pen at time t, r _ij(t), is defined as

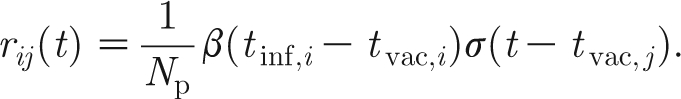2.1

Here, N _p is the total number of animals (S+E+I+R) in the pen. The function β(.) is a measure of the infectiousness of the infectious animal (in d⁻¹) that depends on the period between its vaccination time t _vac,i and its infection time t _inf,i. The function σ(.) is the relative susceptibility of the susceptible animal (0≤σ≤1), depending on its vaccination time t _vac,j. For the case of a single isolated pen, one obtains the total rate of infection at time t, r(t), by summing over all infectious animals (denoted by the set I(t)) and all susceptible animals (denoted by the set S(t)):

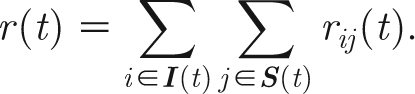2.2

For the case of a constant infectiousness β and the relative susceptibility σ equal to unity, equations (2.1) and (2.2) reduce to the well-known rate of infection of 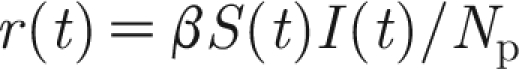for frequency-dependent transmission. As the number N _p of animals in one pen is usually small, the virus transmission can vary greatly due to stochastic effects. For this reason the model is formulated stochastically. In particular, we consider a stochastic infection process {S, E, I, R}→{.S−1, E+1, I, R} with the rate given by (2.2). This is implemented numerically in an event-driven code by giving each animal an individual infection threshold, which allows for the exact calculation of the time of the next infection (Sellke 1983).

The latent period T _lat is assumed to be fixed and independent of the time since vaccination. The mean infectious period 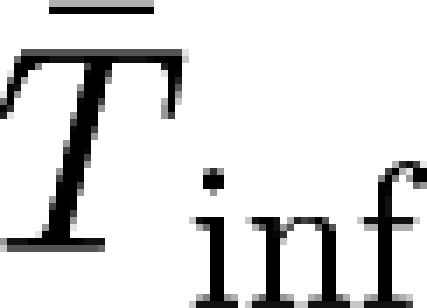is, however, assumed to decrease with the time elapsed between vaccination and infection, denoted as τ (=t _inf−t _vac). Unvaccinated animals have an average infectious period of T _inf,0, while vaccinated animals can have a shorter infectious period depending on τ. Vaccination is assumed to have no effect during a period T _delay after vaccination (Bouma et al. 2000), after which the infectious period decreases inversely proportional with time,

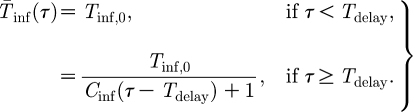2.3

The constant C _inf and the delay period T _delay are determined by fitting them to the experimental data (see below). Other functions to describe the decrease of the infectious period after T _delay (e.g. exponential, smooth Hill-type) fit the data equally well and do not alter the results. The infectious period T _inf is assumed to be distributed according to a gamma distribution with shape parameter γ and mean .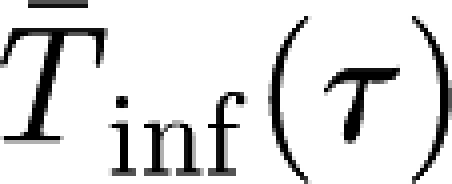

The infectiousness β and susceptibility σ are assumed to be unaffected by the vaccination for a time T _delay after which they decrease exponentially with rates λ _inf and λ _sus, respectively, similar to the function proposed by Chowell et al. (2004). Susceptibility is also assumed to remain constant and non-zero from a period of T _const after vaccination onwards.

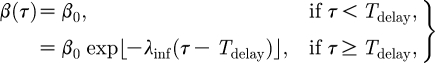2.4

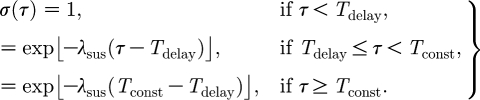2.5

Here, β ₀ denotes the infectiousness of an unvaccinated infectious animal. Multiplying this parameter by the infectious period T _inf,0 gives the reproduction number 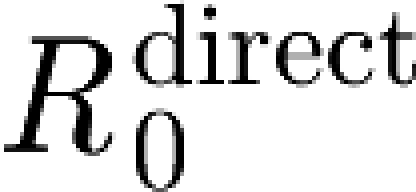, i.e. the number of secondary infections that an unvaccinated infected animal will cause when it is in direct contact with a susceptible unvaccinated population.

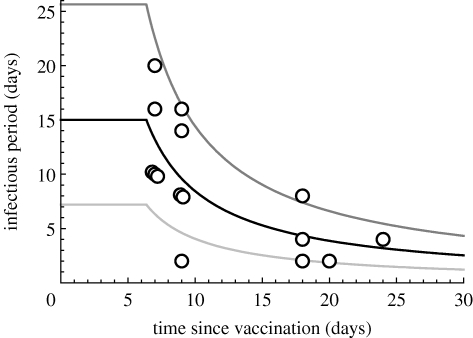
To estimate the parameters of the above model of transmission between animals kept in direct contact in a pen, we use the results of transmission experiments in which animals were also kept in direct contact in one pen. Experiments by Bouma et al. (1999) show a strong relationship between viraemia in leucocytes and transmission to sentinels, suggesting that viraemia is a necessary condition for infectiousness. Here, we simply assume that infectiousness coincides with viraemia. The latent period is assumed to be 4 days for both vaccinated and unvaccinated animals (Laevens et al. 1998; Dewulf et al. 2001, 2004, 2005). The infectious period T _inf,0 is set to 15 (7–25) days for unvaccinated animals (Dewulf et al. 2001), corresponding to a gamma distribution with mean 15 and shape parameter γ=10. Equation (2.3) that describes the relationship between infectious period and time since the vaccination is fitted to the 15 data points available from the measurements of viraemia in contact-infected animals (Dewulf et al. 2004), yielding the parameters C _inf=0.21 d⁻¹ and T _delay=6.4 days. The shape parameter for the infectious period distribution of vaccinated animals is assumed to be the same as for unvaccinated animals (i.e. γ=10). Figure 1 shows that 13 out of the 15 data points used to fit equation (2.3) are within the 95 per cent interval, which is consistent with the constant shape parameter assumption.

Figure 1.

Infectious period as a function of the time since vaccination: average infectious period (black curve) with 95% interval (between grey curves) and observations (circles; Dewulf et al. 2004).

In total, 21 published experiments (taken from Bouma et al. 1999, 2000; Moormann et al. 2000; Dewulf et al. 2004, 2005), which studied three different types of transmission (vaccinated→unvaccinated, unvaccinated→vaccinated and vaccinated→vaccinated), are used to quantify the effect of vaccination on infectiousness and susceptibility. The period after which susceptibility is constant, T _const, is assumed to be 21 days. Maximum-likelihood estimation yields the values for β ₀=6.7 (5.5–∞) d⁻¹, λ _inf=0.5 (0.31–0.63) d⁻¹ and λ _sus=0.2 (0.16–0.25) d⁻¹ (see the electronic supplementary material). The corresponding value of 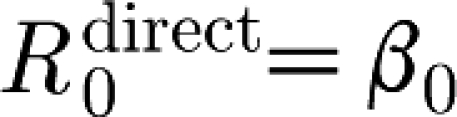T _inf,0=100 agrees well with the reported values of 81.3 (Laevens et al. 1998) and 100 (Klinkenberg et al. 2002). The effective reproduction number in a vaccinated population drops below unity approximately 10 days after the vaccination (see the electronic supplementary material). With the estimated parameter values, the model reproduces the main features of the experimental results: infected animals that are vaccinated three weeks in advance do not transmit infection to sentinels and transmission does not occur in a population that is vaccinated two weeks in advance.

2.2. Modelling transmission between pens

An infectious animal is more likely to infect a susceptible animal in its own pen than one in another pen. Owing to the lower contact rate between animals in different pens (due to the physical pen barrier, distance between pens, less direct contact, etc.) the transmission rate between pens is lower than that within pens (Klinkenberg et al. 2002; Eblé et al. 2006). Together, the between- and within-pen transmission processes determine virus spread through a pig farm. A household model (Becker & Dietz 1995) combines the two types of transmission. Each pen is considered to be a household of size N _p that has random contacts with other households. When one household member is infected, it exhibits an infectiousness β to other household members, but a reduced infectiousness ϵβ to members of other households due to the different contact rate. If the first infected member can be assumed to infect all other members in its household (i.e. 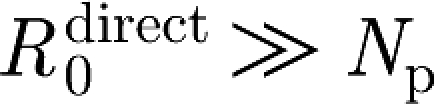), the overall within-herd reproduction ratio R ₀ can be expressed as

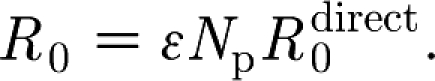2.6

We use this equation to relate the information from small-scale experiments to transmission at the farm level. From the serological data collected during the CSF epidemic in The Netherlands in 1997/1998 (Elbers et al. 1999), the within-farm reproduction number was estimated as 2.8 for finisher farms (Klinkenberg et al. 2003) and 2.9 for breeding farms (Stegeman et al. 1999a ). Using the value for finisher farms that are assumed to consist of pens holding 10 animals each (R ₀=2.8, N _p=10, 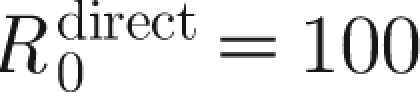), equation (2.6) gives a reduction factor of ϵ=2.8×10⁻³. For breeding sows that are held separately (R ₀=2.9, N _p=1, 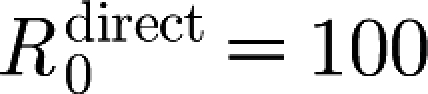), a value of ϵ=2.9×10⁻⁴ is used, which is equivalent to a homogeneously mixing population with a low transmission parameter. Clearly, these values, as they are derived from the 1997/1998 epidemic data, apply only to an unvaccinated population. In our model calculations, we assume that the reduction factor ϵ is not influenced by the vaccination. We also assume that the parameters derived for 1997/1998 adequately describe the transmission within a herd for the 2006 situation. Although pen sizes have changed in the mean time, incorporating this change in the model would require additional modelling assumptions for which a quantitative basis is lacking.

2.3. Modelling detection within farms

During an outbreak of CSF on a farm, the number of infected animals increases until the disease is diagnosed and confirmed, after which all animals on the farm will be culled. Detection is related to the number of animals showing clinical signs at a certain moment, but it also depends on tracing dangerous contacts and on the awareness of farmers and veterinarians, which can result in a large variation in the time between infection and detection. The detection time of infected farms is modelled by a parametric distribution P _det of time t since infection. This distribution was proposed for the data of the CSF epidemic in 1997/1998 in The Netherlands by Klinkenberg et al. (2003), assuming an exponential growth curve of infectious animals and a detection rate proportional to the number of infectious animals. Here, we use the proposed distribution, with a minimum detection time of two latent periods (i.e. 2T _lat=8 days),

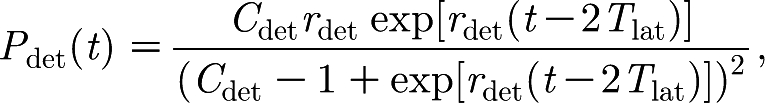2.7

in which C _det is a constant and r _det is a constant detection rate. From this distribution, an infectious period is drawn for each infected farm. When the within-herd outbreak has already ended at the resulting random detection time (i.e. a minor outbreak has occurred), the outbreak will go unnoticed and the infected animals on this farm will have to be detected during the end screening. On vaccinated farms, however, the infection rate can be so low that a within-herd outbreak is still fading out at the designated detection time. In reality, these kinds of outbreaks will not be detected at that time, but will most probably go unnoticed. To include this in our model, we require that at least 10 animals must be in the I-class (not necessarily in one pen) at the detection time. If this condition is not fulfilled, the model postpones detection until it is (or the outbreak goes undetected). This is a simple model construction to extrapolate the description of the detection process to the case of vaccinated farms. An outbreak will go unnoticed if it ends before the designated detection time, or when the requirement of 10 simultaneous infectious animals is never fulfilled.

We note that the detection threshold cannot be estimated from the data, as up until now (marker) vaccination has not been applied on Dutch pig farms. We consider the setting of this threshold at 10 simultaneous animals in the I-class as a fairly conservative choice (predicting a high number of undetected within-farm outbreaks). When the detection threshold is set even higher (we investigated thresholds of 15 and 20 animals), the model is invalidated as this alters the detection time distribution for unvaccinated infected farms (shifts to later times).

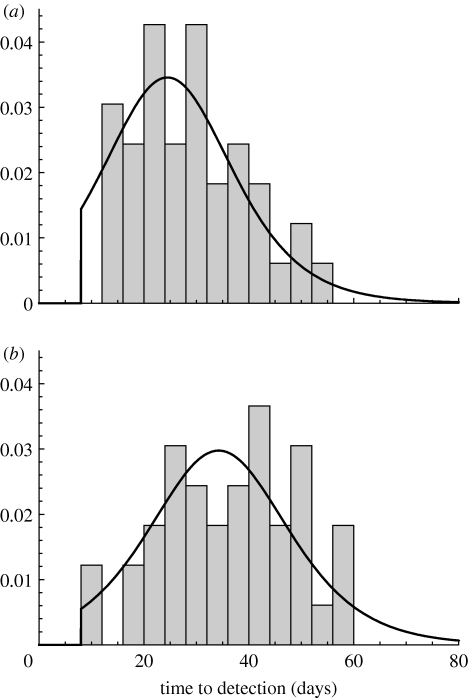
The detection time distribution (2.7) is fitted to the estimated detection times in the 1997/1998 epidemic (Stegeman et al. 1999a ). For finisher farms, the fitted parameters are C _det=8.5 and r _det=0.12 d⁻¹, with a mean detection time of four weeks after infection (figure 2 a; table 1); these parameters are also assumed to apply for piglet sections. The fitted parameters for a sow section are C _det=20.5 and r _det=0.11 d⁻¹, with a mean detection time of five weeks after infection (figure 2 b; table 1).

Figure 2.

Detection time distribution: curve described by equation (2.7) (black curve) fitted to observations (grey bars; Stegeman et al. 1999a ) for (a) finisher farms and piglet section of multiplier farms and (b) sow section of multiplier farms.

2.4. Modelling transmission between herds

The infection on one farm can spread to other farms by numerous possible infection routes. The infection probabilities through several different infection routes in the CSF epidemic in The Netherlands in 1997/1998 are investigated by Stegeman et al. (2002). After the introduction of a movement ban and enhanced biosecurity measures (i.e. after the high-risk period (HRP)) a smaller number of transmission routes remain, of which the mechanisms are not well understood. Here, we use a modelling approach that combines these remaining routes in a single transmission kernel K that only depends on the distance z between the farms. The probability p _ij that a susceptible herd j is infected by a source herd i during its infectious period T _i is

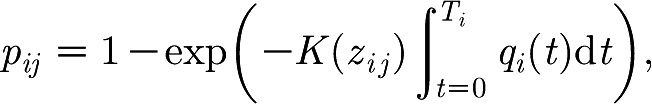2.8

where q _i(t) is the force of infection in the source herd, which is proportional to the sum of the infectiousness of all infectious animals at time t on farm i. In other words, we assume that the transmission hazard between the farms scales with the within-herd force of infection of the source herd. The transmission kernel K is parametrized as follows:

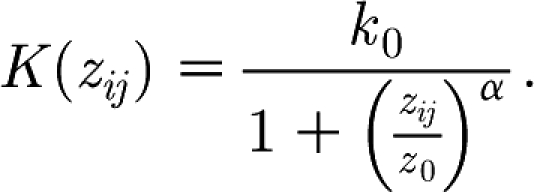2.9

The parameters α and z ₀ determine the shape of the kernel. When α>1, the probability of infection is smaller for farms that are farther apart. The point of inflection is determined by the parameter z ₀, and k ₀ is an overall multiplicative factor. For the parameter estimation, we use the data from the 1997/1998 epidemic and the location data of all Dutch pig farms at that time. The shape parameters α and z ₀ are estimated from these data by maximum likelihood in the same way as reported earlier for the transmission kernel of avian influenza (Boender et al. 2007). The multiplicative parameter k ₀ is fitted to a between-herd reproduction number of 1.3 that was estimated for the early stages of the CSF epidemic of 1997/1998 in The Netherlands (Stegeman et al. 1999b ). The kernel parameters thus found for CSF are α=2.2, z ₀=1 km and k ₀=0.0011 d⁻¹.

3. Comparing control and end screening strategies

We use the model described in §2 to compare the expected effect of different control strategies when a CSF epidemic would presently occur in The Netherlands, based on the data on the structure of Dutch pig farming in 2006. This requires the calculation of a large number of epidemic model realizations for each control strategy. Subsequently, we use these realizations to study the expected performance of different end screening strategies to detect any seropositive animals that escaped detection during the epidemic. Here, we describe the approximations used in modelling the farm structure, the way in which epidemic realizations were initialized, the parameters values defining the different control strategies and the definitions of the different end screening strategies studied.

3.1. Farm data

In 2006, 9041 pig farms were present in The Netherlands with in total 5.5 million finisher pigs, 4.6 million piglets and 1.1 million sows (Anon. 2007b ). The sows and piglets are housed together in multiplier farms, where sows produce on average 22 piglets per year. Piglets stay in multiplier farms for 70 days, until they are transported to finisher farms for fattening. There are roughly twice as many finisher farms as multiplier farms in The Netherlands (Anon. 2007b ), together with a number of farms of mixed type. In the model, we will consider only finisher and multiplier farms as separate farm types. We include 9000 model farms (with in total 11 million pigs), of which 6000 are finisher farms and 3000 are multiplier farms. Each finisher farm is assumed to consist of 900 animals that all stay in pens of 10 animals (N _p=10). Each multiplier farm consists of a piglet section of 1440 piglets (also staying in pens of 10 animals) and a sow section of 360 sows that are held separately. This results in a total population of 5.4 million finishers, 4.5 million piglets and 1.1 million sows, in agreement with the agricultural survey data above. The fixed number of animals per farm is a model simplification justified by the fact that most pig farms are sufficiently large to detect within-farm outbreaks before infection saturation effects become noticeable. As the mechanisms of transmission after the HRP are largely unknown, we assume that when a multiplier farm is infected, the chance that the virus is introduced in the sow section is 20 per cent and the chance that it is introduced in the piglet section is 80 per cent, i.e. in proportion to the number of animals.

Different livestock areas in The Netherlands differ considerably in pig farm density (Anon. 2007b ); in most areas, the density does not exceed one pig farm per square kilometre, whereas in the centre of The Netherlands, local densities of up to four pig farms per square kilometre are often encountered. As the exact locations of the pig farms were not available at the time of analysis, we randomly removed locations from an older dataset to obtain our 9000 model farms. Later comparison with the actual pig farm locations in 2006 showed a very good agreement between the spatial distributions of the actual and model farm locations.

3.2. Initialization

The model described in §2 is designed for the period after the first detection; the parameters of the detection time distribution (2.7) and transmission kernel (2.9) apply when it is confirmed that the disease is present (raising awareness) and basic measures are taken. The initial states of our calculations must therefore represent the situation at the end of the preceding period, i.e. the HRP. We consider a large set of random initial states with between 11 and 20 infected herds, covering a wide range of spatial distributions of infected farms. The range of 11–20 initially infected herds is chosen as a range of scenarios for 2006, which are similar to the actual scenario of the 1997/1998 epidemic. In that epidemic, a total of 39 herds had been infected before the end of the HRP, but as the number of pig farms in 2006 is approximately 2.4 times smaller than that in 1997, we scale down the number of initially infected herds accordingly. In the absence of an appropriate model for the transmission during the HRP, these random initial states were generated using our after-HRP model starting from one infected animal on a randomly chosen farm.

In total, 1000 stochastic realizations (runs) were calculated for each control strategy. In the week after the disease is first diagnosed, farms within 1 km of detected herds are pre-emptively culled (after 1 day) to account for the expected time elapsing until EU permission for emergency vaccination is obtained. The same set of initial states is used for each control strategy to enable proper comparison.

3.3. Control strategies

The Dutch contingency plan requires the standstill of all livestock transports for 72 hours (Anon. 2007a ) after CSF is first detected in the country. In this period, an advisory committee makes a judgement as to which areas are most at risk and how transports in and to these areas should be regulated in the following period. During the epidemic, the EU requires that infected herds that are detected are culled and that their dangerous contacts are traced and—if necessary—pre-emptively culled. We will call this the minimal control strategy; in practice, additional measures will always be taken. We compared four such additional control strategies: pre-emptive ring culling in 1 km around a detected herd and ring vaccination in 1, 2 and 5 km around a detected herd.

In modelling the vaccination strategies, we assume that the sow sections are never vaccinated with the aim to minimize the risk of carrier sow syndrome, complying with the Dutch contingency plan for CSF (Anon. 2007a ). The piglet sections are vaccinated when they fall in a vaccination circle (of 1, 2 or 5 km radius), but their vaccination degree gradually decreases because unvaccinated piglets are being born, while vaccinated piglets are being transported (within a closed compartment) to finisher farms. In 70 days, the vaccination degree decreases stepwise (by complete pens) from unity to zero. When a (partly) vaccinated multiplier farm becomes part of a new vaccination circle, the newborn piglets are vaccinated. In this way, piglets of different vaccination age can be present on a farm. Finisher farms are vaccinated only once (when they fall in a vaccination zone). Although in reality vaccinated finisher farms are allowed to admit unvaccinated piglets from within the closed compartment, we assume that their vaccination degree does not wane, as the availability of unvaccinated piglets within the compartment is likely to be small when the compartment is affected by virus spread.

In the model, we assume certain fixed intervals for responding to a detection event. When a farm is confirmed to be infected we assume it is culled the following day. When the ring culling strategy is applied, the farms around the detected farm are pre-emptively culled on the fourth day after the culling of the detected farm (Elbers et al. 1999). When a vaccination strategy is applied, the delay between the detection and the ring vaccination is taken to be 1 day.

In comparing the effectiveness of the control strategies, we consider the duration of the epidemic and the number of detected farms. The shorter an epidemic is, and the smaller the number of affected farms, the more effective the control strategy has been. An alternative quantity to measure the effectiveness of a control strategy is the effective reproduction number between herds (R _h). This is the number of secondary infections that an infected herd will cause before it is detected. When the effective reproduction number is below unity, an epidemic will die out; when it is above unity, an epidemic will grow. In this way, effectiveness is captured in one number with an objective threshold. In general, the effective reproduction number is maximal before the first detection and then gradually decreases over time until below unity, when the epidemic begins to die out. The difference between the control strategies is largest in the early stages of the detected epidemic. This is why we examine the effective reproduction number for the ‘second-generation herds’. These are the herds infected by the herds that were infectious when the epidemic was first detected. The total number of infections caused by these second-generation herds, divided by the number of second-generation herds, is the average effective reproduction number between herds for the epidemic, at the moment when control measures are first taken.

3.4. End screening

EU legislation requires that an end screening should take place at least 30 days after the last outbreak in a surveillance area (10 km around a detected and culled herd). In practice, the decision to start the end screening also depends on the number of cases, expert opinion, etc., making it difficult to model. Instead, we perform the end screening at the end of the simulated epidemics, when all infected animals have either been detected or have recovered. In this way, the end screening is focused on detecting seropositive non-infectious animals that were missed during the epidemic. Comparing the end screening results of the vaccination strategies with those of the pre-emptive culling strategy will answer the question as to whether marker vaccination increases the risk of seropositive animals remaining.

During the end screening, blood samples are taken from a number of animals per farm (depending on the end screening scenario) for serological testing. For unvaccinated animals, the conventional E2-ELISA is used, while the E^rns-ELISA serves to test vaccinated animals. The sensitivity for both tests is assumed to be 90 per cent. The specificity is set at 100 per cent, because although the ELISA tests will yield some false-positive results, the follow-up (such as PCR-testing, taking extra blood samples for antibody testing, looking for evidence of clustering) will confirm or disprove any recent CSF infections. We assume in the model that all infected animals that escaped detection during the epidemic will seroconvert and recover. These seropositive animals are usually clustered in a few pens, as few animals escape infection once a pen member is infectious. We can calculate the probability of detecting such a pen with seropositive animals, and with that the probability of detecting the farm with seropositive animals (see the electronic supplementary material). The probability of missing an infected farm is 1 minus that probability, and multiplying this with the number of seropositive animals gives the expected number of seropositive animals that remain on the farm after the end screening. The total number of seropositive animals per epidemic after the end screening is obtained by summing the number of seropositive animals per farm over all tested farms. This is a measure for the risk that seropositive animals pose, when we assume that each seropositive animal contributes equally to the total risk.

To demonstrate freedom of infection, the EU requires serological testing that would yield at least one positive test result with 95 per cent certainty when the seroprevalence is 10 per cent among finishers and piglets and 5 per cent among sows (EU Commission Decision 2002/106/EC). This minimal end screening scenario is here referred to as ES_min. A more stringent end screening scenario, ES_vac, focuses on vaccinated farms, as they are more likely to host smaller outbreaks that might lead to a within-farm prevalence below the minimal detection level. This scenario tests one animal per pen on vaccinated farms. In the ‘best case’ scenario, ES_max, one animal per pen is tested on all finisher farms and piglet sections, vaccinated and unvaccinated. As sows are never vaccinated, their sampled numbers always equal the minimum required. Table 2 summarizes the different end screening scenarios.

Table 2.

Evaluated end screening scenarios for finisher farms (900 finishers per farm) and multiplier farms (1440 piglets and 360 sows per farm).

	unvaccinated farms			vaccinated farms
scenario	type	no. of tested animals	minimal prevalencea (%)	type	no. of tested animals	minimal prevalencea (%)
ESmin	finisher	32	10.0	finisher	32	10.0
	piglet	32	10.0	piglet	32	10.0
	sow	61	5.0
ESvac	finisher	32	10.0	finisher	90b	3.3
	piglet	32	10.0	piglet	144b	2.1
	sow	61	5.0
ESmax	finisher	90b	3.3	finisher	90b	3.3
	piglet	144b	2.1	piglet	144b	2.1
	sow	61	5.0

^aMinimal seroprevalence at which at least one positive test result is expected with 95% certainty.

^bOne animal per pen is tested.

4. Results

4.1. Effectiveness of control strategies

In total, five control strategies were compared, the results of which are summarized in table 3. For each hypothetical epidemic, the duration, the number of detected infected herds, the number of undetected infected herds, the number of pre-emptively culled farms and the number of vaccinated farms are recorded. The duration and the numbers of detected, pre-emptively culled and vaccinated herds determine the socio-economic impact of an epidemic. The duration and the number of detected herds (which is a measure of the number of diseased animals) are important quantities from an animal welfare perspective. Furthermore, the number of pre-emptively culled and vaccinated herds in combination with the duration is also important to know for logistical planning purposes. Here, we will base the comparison in effectiveness on the duration and the number of detected herds of an epidemic. The results of the different control strategies are represented by their median values and a 90 per cent interval (meaning 5% of the simulations yielded a lower number than the lower limit (i.e. the 5th percentile) and 5% of the simulations yielded a higher number than the upper limit (i.e. the 95th percentile)).

Table 3.

The median values of the duration of the epidemic, the number of detected, not detected (before end screening), pre-emptively culled and vaccinated farms per epidemic and the effective reproduction number between herds (R _h) for second-generation herds (i.e. the number of herds that were infected by herds that were infectious at the time the epidemic was first detected) for different control strategies (the two-sided 90% interval is given in parentheses).

control strategy	duration (days)	no. of detected farms	no. of not detected farms	no. of pre-emptively culled farms	no. of vaccinated farms	R h
minimala	118 (39–597)	25 (10–356)	0 (0–3)	—	—	0.54 (0.07–1.76)
1 km culling	92 (39–236)	18 (10–47)	0 (0–1)	74 (32–245)	—	0.49 (0.08–1.22)
1 km vaccination	111 (42–276)	22 (10–69)	1 (0–9)	10 (2–28)	70 (22–300)	0.53 (0.09–1.30)
2 km vaccination	95 (41–203)	19 (10–43)	2 (0–8)	10 (2–28)	168 (60–457)	0.46 (0.08–1.08)
5 km vaccination	71 (38–145)	15 (9–26)	2 (0–8)	10 (2–28)	478 (197–924)	0.35 (0.05–0.84)

^aThe minimal control strategy comprises culling of infected herds, contact tracing and implementation of restriction zones and transport regulations (according to EU Council Directive 2001/89/EC).

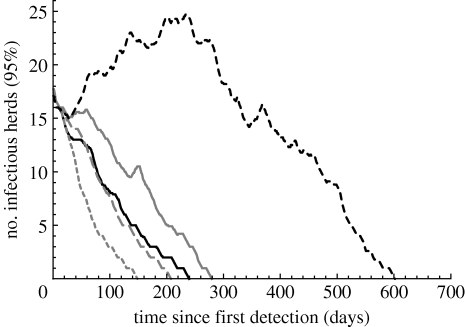
For all control strategies, the reported 90 per cent intervals are very wide and largely overlapping. These large intervals reflect the fact that a part of the simulated epidemics will die out very soon without additional control, while another part can only be contained with strict control measures. To discriminate between the different control strategies, only the epidemics in the latter category are considered in figure 3, showing the 95th percentiles of prevalence over time.

Figure 3.

The 95th percentile of number of infectious herds as a function of time since the first detection for the minimal control strategy (black dashed curve), 1 km culling (black solid curve), 1 km vaccination (grey solid curve), 2 km vaccination (grey long-dashed curve) and 5 km vaccination (grey short-dashed curve). The minimal control strategy comprises culling of infected herds, contact tracing and implementation of restriction zones and transport regulations.

Unsurprisingly, the minimal control strategy is the least effective, yielding the longest and largest epidemics. From the two strategies that are applied in a ring of 1 km around a detected herd, pre-emptive culling is more effective than vaccination. This is as expected, because the vaccination takes some time to provide protection (typically two weeks), whereas pre-emptive culling works instantaneously. The 2 km vaccination strategy yields outbreak sizes and durations comparable to the 1 km culling strategy (i.e. no significant differences in Wilcoxon signed-rank test). Finally, the 5 km vaccination strategy is the most effective of all in terms of outbreak size and duration, although not necessarily from an economic point of view.

The effective reproduction numbers show the same trend as the outbreak sizes and durations. The highest values are encountered for the minimal control strategy (table 3). For the vaccination strategies, the reproduction numbers decrease with increasing vaccination radius, and 2 km ring vaccination gives comparable results to 1 km ring culling. Although the median value for the minimal control strategy is highest, it does not differ much from the value for 1 km vaccination, which would lead one to believe that both strategies are equally effective. However, the 95th percentile for the minimal control strategy is much higher, which means that the chance of a large outbreak (where R _h>1) is higher. Of all control strategies, only the 5 km vaccination strategy produces an effective reproduction number that is significantly less than unity.

The number of pre-emptively culled herds for the vaccination strategies is listed in table 3. These are the herds that were culled in the first week after detection of the first farm. The numbers are small and identical for all the vaccination strategies, as the starting situations were identical. The number of vaccinated farms in table 3 increases with increasing vaccination radius, but not quadratically. This is because the vaccination areas can overlap and the improved control of the epidemic reduces the total affected area.

For the non-vaccination strategies, approximately 1 per cent of the infected herds escape detection before the end screening takes place. These are mainly sow sections of multiplier herds, where the infection is more likely to fade out by itself (because of the separate housing of sows). For the vaccination strategies, more of the infected herds go unnoticed, and this percentage increases with increasing vaccination radius (from 4% for 1 km ring vaccination to 12% for 5 km ring vaccination). These undetected outbreaks occur largely on vaccinated farms, where an infection is quickly contained by the vaccine protection, and affects only a small number of animals. In the model, these animals are all assumed to have seroconverted after the undetected within-herd outbreak has ended. The end screening after the nationwide epidemic is designed to detect these seropositive animals in order to minimize the risk of vaccinated infected animals remaining.

4.2. End screening

In some of the simulated epidemics, one or more within-farm outbreaks escape detection during the epidemic. The fraction of these epidemics is especially high for the vaccination strategies (table 4) and increases with increasing vaccination radius. This is not surprising, as the simulations have shown that the fraction of undetected infected farms is highest for the vaccination strategy with the largest vaccination radius (table 3). At the end of an epidemic containing undetected infected farms (but before the end screening), a number of seropositive animals will be present in these farms. The end screening should detect these animals, but how many will be detected depends on the end screening scenario used. On selecting those epidemics with undetected seropositive animals, we examine how the three end screening scenarios (table 2) reduce the total number of seropositive animals before the country is declared free of infection (table 4).

Table 4.

Average fraction of epidemics with seropositive animals and average number of seropositive animals per epidemic with seropositive animals before and after end screening (the two-sided 90% interval is given in parentheses).

		no. of seropositive animals
		before end screening	after end screening
control strategy	fraction epidemics		ESmin	ESvac	ESmax
minimal	0.29	7.6 (1–22)	5.6 (1–16)	5.6 (1–16)	1.5 (1–4)
1 km culling	0.15	5.4 (1–11)	3.9 (1–8)	3.9 (1–8)	1.0 (1–2)
1 km vaccination	0.70	40.7 (1–129)	20.6 (1–64)	3.3 (0–11)	2.6 (0–9)
2 km vaccination	0.78	43.9 (8–125)	22.1 (6–61)	3.0 (0–10)	2.7 (0–8)
5 km vaccination	0.85	43.2 (3–112)	21.7 (3–55)	2.7 (0–8)	2.6 (0–7)

Before end screening, the non-vaccination strategies will on average yield less than 10 seropositive animals per epidemic, usually on one or two farms. When one of the vaccination strategies is applied, more than 40 seropositive animals remain, distributed over three or more farms. Of course, an end screening must take place before officially substantiating freedom of infection. When the minimally required end screening is applied (ES_min), the number of seropositive animals reduces slightly for the non-vaccination strategies, whereas it is halved for the vaccination strategies. This reduction in the vaccinated farms is high because the large number of seropositive animals clustered on a few farms makes them easier to detect. The unvaccinated farms contain fewer seropositive animals, but not many of these are detected. When more effort is put into sampling the vaccinated farms by testing one animal per pen (ES_vac), the number of seropositive animals is comparable for all strategies. An even more stringent end screening (ES_max) that tests one animal per pen on all farms provides little added value because the numbers are already very low.

The number of seropositive animals after the end screening in table 4 is conditioned on the epidemics with seropositive animals, yielding a conditional risk. But when assessing the overall risk of seropositive animals, also the probability that an epidemic ends with undetected seropositive animals (i.e. the fraction in table 4) should be taken into account. Table 5 shows the average number of seropositive animals before and after end screening for all simulated epidemics that can be considered as the risk of seropositive animals that remain in the country (and that might enter food production or export), assuming that it is proportional to the number of seropositive animals present. The average risk is considerably lower for the non-vaccination strategies than for the vaccination strategies, but for the end screening scenario focused on vaccinated farms (ES_vac) the risk ranges of vaccination and non-vaccination strategies are comparable.

Table 5.

Average number of seropositive animals per epidemic (all epidemics) before and after end screening (the two-sided 90% interval is given in parentheses).

	no. of seropositive animals
	before end screening	after end screening
control strategy		ESmin	ESvac	ESmax
minimal	2.2 (0–11)	1.6 (0–8)	1.6 (0–8)	0.4 (0–3)
1 km culling	0.8 (0–10)	0.6 (0–7)	0.6 (0–7)	0.1 (0–1)
1 km vaccination	27.5 (0–110)	13.9 (0–56)	2.2 (0–9)	1.8 (0–7)
2 km vaccination	33.6 (0–114)	16.9 (0–56)	2.3 (0–8)	2.0 (0–7)
5 km vaccination	36.1 (0–105)	18.1 (0–51)	2.3 (0–7)	2.2 (0–7)

So, even though the vaccination strategies will cause more outbreaks to stay under the detection limit during the epidemic, the numbers of seropositive animals on such a farm are high enough to be easily detected during the end screening. When at least 10 per cent of the animals is tested on vaccinated farms (i.e. one animal per pen), the 95th percentile of the number of seropositive animals remaining in the country is approximately eight for both the vaccination and non-vaccination strategies.

5. Discussion

In this paper, we developed and applied a stochastic model that describes transmission of CSFV and marker vaccination on different levels of aggregation (pen, farm and livestock area). New in our approach is the use of a large number of transmission experiments to parametrize the effect of vaccination on transmission between animals. This detailed description of the within-herd dynamics allows for the simulation of minor outbreaks without additional assumptions. By combining this to large-scale transmission between herds, a comparison between not only the control strategies but also the end screening strategies becomes feasible.

Using this model and the Dutch farm structure of 2006, we compared the performance of different control strategies (the EU required strategy, additional 1 km ring culling and additional 1, 2 or 5 km ring vaccination). The results of this research indicate that vaccination will always cause fewer animals to be culled than pre-emptive culling does. The simulation results of the present study have been used for an economical evaluation of the control strategies (Bergevoet et al. 2007). From this study, it was concluded that the period between first detecting the disease and substantiating freedom of infection is the most important indicator for the economic consequences of a CSF epidemic. So, considering both animal welfare and economics, vaccination is to be preferred with a sufficiently large vaccination radius to minimize the duration of the epidemic.

The outbreak sizes and durations for 2006 presented in this paper are much smaller than those predicted for 1997 by other modelling studies (Mangen et al. 2001, 2002; Klinkenberg et al. 2003) as well as our model (Backer et al. 2007). The main reason is the reduction of farm numbers (from 21 500 farms in 1997 to 9000 farms in 2006), even though the average size of pig farms has increased (from 650 finishers per farm in 1997 to 900 finishers per farm in 2006). This finding is in agreement with Mangen et al. (2002) who showed similar differences in outbreak sizes between areas with high and low pig farm densities. The pig farm density also determines the ‘break-even’ vaccination radius at which vaccination is as effective as 1 km ring culling: this was approximately 2 km in 2006, whereas in 1997 it was between 1 and 2 km (Backer et al. 2007). The outbreak size also depends on the number of initially infected herds at the end of the HRP. For the results presented in this paper, initial states were used with 11–20 initially infected herds. Results obtained for smaller numbers of initially infected herds (2–5 and 6–10) showed smaller differences in the outcome between the control strategies, but the ordering according to effectiveness remained the same.

We note that the dependence of the model outcome on the pig farm density also illustrates the essence of the sensitivity of our model results to parameter uncertainties. Given the model assumptions of the virus having transmission characteristics similar to the 1997/1998 virus and the vaccine having the same properties in the field as under experimental conditions, the predicted effect of the control strategies considered is mainly sensitive to the magnitude of the between-farm transmission kernel. A larger/smaller magnitude would yield a similar effect as a larger/smaller farm density. The sensitivity to the uncertainties of other model parameters is very weak. This is because changes in one parameter will typically be counterbalanced by consequent changes in another due to the way we calibrate the full model to observations in experiments and in the 1997/1998 outbreak.

When vaccination is used as a control strategy, a larger number of undetected farm outbreaks during the epidemic is expected than when pre-emptive culling is used. Subsequently, the end screening should detect the infected and recovered animals on these farms on serological evidence. Our results indicate that the minimal end screening protocol required by the EU does not suffice for the vaccination strategies. When larger sample sizes are taken in vaccinated farms, the absolute number of seropositive animals which are missed by the end screening is similar for both the vaccination and culling strategies. However, this also means that when a vaccination strategy is used, the probability of finding seropositive animals during the end screening is higher. We note that finding seropositive animals automatically leads to a set-back of the infection-free status for another 30 days, which is the minimum period required between detecting the last infection and declaring the area free of infection. The planning of the end screening should consider this, e.g. by scheduling intermediate screenings as soon as seems acceptable.

Another complication for substantiating freedom of infection once the epidemic has been controlled by emergency vaccination involves retesting of positive herds. In the end screening model, we set the test specificity to 100 per cent by assuming that for each initially false positive animal the presence of CSFV will be disproved. However, this does involve retesting of the herd requiring extra time and funds. The more animals are tested, the more (initially) false positives are expected, and the more herds need to be retested. When the end screening focuses on vaccinated farms (scenario ES_vac), it is to be expected that they need more retesting than unvaccinated farms. This should be taken into account when organizing the end screening.

The modelling approach described in this paper presents a way to connect individual-based interventions to large-scale effects. The parametrization using transmission experiments allows for a reliable description of within-herd dynamics, while real outbreak data serve as a solid basis for transmission between herds. This multilevel approach represents a promising approach for studying the effectiveness and risks of emergency vaccination strategies against other infectious diseases, such as FMD and avian influenza.