A Bayesian Maximum Entropy approach to address the change of support problem in the spatial analysis of childhood asthma prevalence across North Carolina

Abstract

The spatial analysis of data observed at different spatial observation scales leads to the change of support problem (COSP). A solution to the COSP widely used in linear spatial statistics consists in explicitly modeling the spatial autocorrelation of the variable observed at different spatial scales. We present a novel approach that takes advantage of the non-linear Bayesian Maximum Entropy (BME) extension of linear spatial statistics to address the COSP directly without relying on the classical linear approach. Our procedure consists in modeling data observed over large areas as soft data for the process at the local scale. We demonstrate the application of our approach to obtain spatially detailed maps of childhood asthma prevalence across North Carolina (NC). Because of the high prevalence of childhood asthma in NC, the small number problem is not an issue, so we can focus our attention solely to the COSP of integrating prevalence data observed at the county-level together with data observed at a targeted local scale equivalent to the scale of school-districts. Our spatially detailed maps can be used for different applications ranging from exploratory and hypothesis generating analyses to targeting intervention and exposure mitigation efforts.

Introduction

Asthma, one of the most common chronic childhood diseases (Gergen et al., 1988), is an inflammatory disease characterized by symptoms that include wheezing, coughing, breathlessness, and chest tightness. Approximately 8.9% of all children (6.5 million) in the United States suffer from current asthma symptoms (NCHS, 2006), reflecting its ubiquity in affluent societies (Strachan, 1999). Estimated total costs (direct and indirect) of treating asthma range up to $12.6 billion USD per year (Weiss et al. 2004). The causes of this costly chronic disease are still unknown; however air pollution exposures (such as PM₁₀, O₃, SO₂, and NO₂ etc.) are suspects and have been extensively investigated (U.S. EPA, 1996, 2005; Gehring et al., 2002; Mortimer et al., 2002; Lewis et al., 2005).

While air pollutants have clearly been associated with exacerbations of asthma (including increased symptoms, emergency room visits, hospitalizations, and medication use), the association of air pollutants and increased asthma incidence is less clear. McConnell et al. (2002) have shown an association between asthma incidence and children exercising in high ozone areas, though conclusions were limited due to small sample sizes. Investigating the association between traffic related air pollutants and incidence of children’s asthmatic symptoms, Zmirou et al. (2004) suggest that air pollution may be a potential contributor to increasing asthma prevalence in children, while other relevant environmental risk factors, such as exposure to traffic-related air pollution near the home, have recently been investigated (Delfino et al. 2009).

Asthma maps at fine scale spatial resolution provide invaluable information that allows epidemiologists to better understand risk factors that may cause asthma, such as air pollutants, and help identify susceptible subpopulations, such as the very young, the very old, individuals with particular pre-existing health conditions and/or with specific smoking behavior and socioeconomic characteristics, etc. Additionally, more spatially detailed asthma maps are helpful for public health intervention by not only identifying areas of high prevalence and targeting health clinical facilities for susceptible populations, but also in identifying areas in which to focus efforts on abating suspected causal agents.

Geostatistics provide epidemiologists with an essential spatial estimation tool that takes into account the important spatial variability of asthma prevalence. The maps produced provide a visualization of disease prevalence that is extremely useful for health research. However, few studies on mapping asthma have been found, and existing works are often limited to an exploratory visualization of existing asthma prevalence data obtained at a single observation scale (e.g., Hernandez et al., 2000; Oyana et al., 2004).

Numerous data sources provide asthma prevalence data that can be used in mapping analysis. The asthma data can be collected in a number of ways, including random telephone surveys, questionnaire-based surveys, hospital discharge records, Medicaid claims, etc. However what is notable is the spatial aggregation scale, or observation scale, at which the data is reported, which may vary considerably from one data source to another.

One important reason for the difference in observation scale between data sources is that some data sources may have confidentiality requirements that only allow them to release data aggregated over large spatial scale (e.g. county level) to protect the privacy of the individuals who provided their health information. For example the childhood asthma Medicaid claims data analyzed by Buescher et al. (1999) are aggregated at the county level, which is a large spatial observation scale providing strong protection of individual privacy and preventing deductive disclosure. Claims data are cost effective as they are derived from a health system that is already in place. However, it is not clear how well Medicaid claims data estimate asthma prevalence at a fine spatial scale. A second source of data that we used for this study is cross-sectional asthma prevalence data obtained from a school-based asthma surveillance project, the North Carolina School Asthma Survey, or NCSAS (Yeatts et al. 2003). This project generated high quality asthma prevalence data at a fine spatial resolution. The NCSAS database provides good quality asthma prevalence estimates for the majority of middle schools in North Carolina, which corresponds to an observation scale that is much finer than that of the Medicaid data reported at the county level.

Our goal for this research is to perform an accurate mapping analysis of asthma symptom prevalence that rigorously accounts for the high natural variability of asthma prevalence across space, while efficiently integrating data collected at different observation scales. Integrating large scale data to obtain good estimate of asthma prevalence at a fine spatial resolution would lead to some substantial cost savings in North Carolina because it will enable the state health department to efficiently use data from existing systems such as Medicaid, which would reduce the need to conduct additional costly active asthma surveillance.

Gotway and Young (2002) provide an excellent review of statistical methods that address the issue of combining data obtained at different observation scales. A conceptual approach to this problem is to model observations at different observation scales as the spatial average of some fine scale process averaged over the observation areas (i.e. the support of the observation), which is referred to as the change of support problem (COSP). Many of the methods addressing the COSP rely on modeling the spatial autocorrelation of the fine scale process observed at different spatial scales of interest. The procedure consists in averaging the fine scale process covariance to obtain the point-to-area or area-to-area covariance for areas (or observation scales) of any size (Journel and Huijbregts, 1978; Gotway and Young, 2002; Goovaerts, 2006; Banerjee et al, 2004). A classical solution for the prediction problem then consists in using the point-to-area and area-to-area covariances in a linear statistical estimator (e.g. block kriging). However, the implicit implication of this approach is that we are considering estimators that are a linear combination of the process observed at different scales. On the other hand, the powerful Bayesian Maximum Entropy (BME) method of modern spatiotemporal geostatistics (Christakos, 2000) provides a non-linear non-Gaussian extension to classical linear Geostatistics that is not limited by this linear constraint. The goal of this paper is to present a novel approach to deal with the COSP using BME, which provides a framework for the non-linear integration of data obtained at different observation scales. In the following sections we present this framework, and we apply it to the problem of mapping childhood asthma across North Carolina using prevalence data aggregated over large areas (counties) together with data obtained at the fine scale of interest (school districts).

One issue that we face when mapping rare diseases is that of the small number problem, which leads to noisy spatial distribution of observed rates that may require spatial smoothing. Let y_i be the number of positive cases observed for some area i out of n_i persons at risk. The spatial variation of the rate x_i=y_i/n_i tends to be dominated for rare diseases by very high or low values observed where the denominator n_i is small, because a small change in the numerator leads to a large change of the rate, resulting in the noisy spatial distribution mentioned above. The small number problem has been widely discussed and many approaches can deal with it. A classical approach to address this problem is to assume that the disease count Y_i is Poisson distributed with a mean proportional to some measure of disease risk Ri, i.e Y_i^•~Poisson(E_iR_i), where E_i may be an expected rate or the population at risk The approach consists then in obtaining estimates of the disease risk R_i, using for example a Bayesian framework (Besag et al., 1991, Lawson et al, 2003; Zhu et al., 2000; Kelsall and Wakefield, 2002; Gotway and Young, 2002; Banerjee et al, 2004; Diggle and Ribeiro, 2007), while the more recent Poison kriging method (Goovaerts, 2006; Goovaerts and Gebreab, 2008) might provide an attractive and computationally efficient alternative. These approaches basically consist in obtaining maps of disease risk that smooth out the noise arising from the small number problem for rare diseases. For example Goovaerts and Gebreab (2008) used Poisson kriging to obtain smooth maps of the risk for cervix cancer amongst white women in Indiana, where the population weighted mortality rate is only 2.85 per 100,000 person-years. By comparison, the population weighted prevalence of wheezing symptoms amongst North Carolina school children is 26,000 per 100,000 children, which is drastically greater than that of a rare disease. As a result, the small number problem is not an issue that we have addressed in this work. By choosing to model the observed rate X rather than then the disease risk R we are able to solely focus our attention to the COSP. This allows us to focus on the novel BME solution to the COSP presented in this work, which can then be extended in future works to methods dealing with the small number problem.

Theory

Notation

Let ℝ denote the set of real numbers, s∈ℝ² be a point in space, and X(s) be a spatial random field (SRF) representing the spatial distribution of disease prevalence. Let X_map=[X₁,X₂,…,X_n] be a vector of random variables representing the SRF at points s_map=[s₁,s₂,…,s_n], i.e. X₁=X(s₁),…,X_n=X(s_n). In this article the upper case X_map represent random variables and its lower case equivalent x_map=[x₁,x₂,…,x_n] an observed sample (realization). The mean trend and covariance functions of the SRF X(s) are denoted as m_X(s)=E[X(s)] and c_X(s,s′)=cov(X(s),X(s′))=E[(X(s)−m_X(s))(X(s′) −m_X(s′))], respectively, where E[.] is the stochastic expectation operator. We let m_map and c_map be the corresponding mean vector and covariance matrix at s_map. The probability density function (PDF) of X_map will be denoted as f(x_map), while φ(x;m,c) will denote the multivariate Gaussian PDF with mean m and covariance matrix c.

In the estimation problem, the mapping points will be divided in three sets of points; s_map=[s_k,s_hard,s_soft], where s_k is the estimation point, and s_hard and s_soft are the points where hard and soft data are available, respectively. Hard data are defined as exact measured values x_hard such that Prob[X_hard=x_hard]=1, while soft data correspond to observed values with an associated measurement error that can be characterized by the PDF 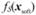defined as

$$\mathit{Prob}[X({\mathit{s}}_{\text{soft}})<\mathit{u}]={\int }_{-\infty }^{\mathit{u}}d{\mathit{x}}_{\text{soft}}{f}_{\mathcal{S}}({\mathit{x}}_{\text{soft}}).$$

The BME framework

The BME method uses epistemic principles (Christakos, 2000) to process the general knowledge ℊ characterizing trends and dependencies in the SRF, and the site-specific knowledge 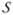consisting in the hard and soft data available. When ℊ={m_map,c_map}, the BME posterior PDF characterizing the prevalence X_k at estimation point s_k is

$$f_{\mathcal{K}}(x_{\text{k}})=A^{-1}\int \text{d}{\mathit{x}}_{\text{soft}}\phi ({\mathit{x}}_{\text{map}};{\mathit{m}}_{\text{map}},{\mathit{c}}_{\text{map}})f_{\mathcal{S}}({\mathit{x}}_{\text{soft}}),$$ (1)

where A= ∫ dx_k ∫ dx_soft φ(x_map;m_map,c_map)f_s(x_soft) is a normalization coefficient. The subscript 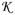=ℊ∪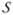 on the posterior PDF emphasizes the BME synthesis of the general knowledge ℊ and the site-specific knowledge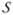. The posterior PDF provides an appropriate estimated prevalence (expected value of the posterior PDF) and estimation uncertainty (variance of the posterior PDF).

When one considers only hard data then x_map reduces to [x_k,x_hard], and the BME posterior PDF reduces to f_K(x_k)=φ(x_map;m_map,c_map)/φ(x_hard;m_hard,c_hard), which is the conditional normal PDF f_K(x_k)= φ(x_k;m_k|hard,c_k|hard) with the following conditional mean and variance

$$m_{\text{k}\mid \text{hard}}=m_{\text{k}}+{\mathit{c}}_{\text{k},\text{hard}}{{\mathit{c}}_{\text{hard},\text{hard}}}^{-1}({\mathit{x}}_{\text{hard}}-{\mathit{m}}_{\text{hard}})$$ (2)

$$c_{\text{k}\mid \text{hard}}=c_{\text{k}}+{\mathit{c}}_{\text{k},\text{hard}}{{\mathit{c}}_{\text{hard},\text{hard}}}^{-1}{\mathit{c}}_{\text{hard},\text{k}}$$ (3)

where c_k,hard=cov(X_k,X_hard) and c_hard,hard=cov(X_hard,X_hard). This estimator, obtained using epistemic principle as the linear limiting case of the BME estimator, corresponds to the classical simple, ordinary and universal kriging estimators depending on the choice of the mean trend model.

The change of support problem

Let Z(s) be defined as the average of X(s) over a 2-D spatial domain 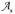centered at s

$$Z(\mathit{s})=X({\mathcal{A}}_{\mathit{s}})={•}_{\mathit{u}\in {\mathcal{A}}_{\mathit{s}}}\text{d}\mathit{u}X(\mathit{u})/\left|\right|{\mathcal{A}}_{\mathit{s}}\left|\right|.$$ (4)

We define the spatial scale R of Z(s) as the radius of a circle of same surface area as 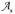, i.e. R =(||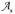||/π)^0.5. We will refer to X(s) as the prevalence observed at the local scale (i.e. R=0), while Z(s) will refer to prevalence observed at a spatial scale R>0. We are interested in the problem of estimating X_k given values observed at different spatial scales.

Area-to-point kriging provides a solution to this problem. The area-to-point kriging estimator is given by Eq. (2) and (3) where x_hard, c_k,hard and c_hard,hard are replaced with z_hard, cov(X_k,Z_hard) and cov(Z_hard,Z_hard), respectively. While area-to-point kriging has been used in other fields such as remote sensing, its use in disease prevalence estimation is only recent (Goovaerts, 2006) and is still in development, and it is therefore useful to propose alternative approaches that can complement it.

The proposed estimator

Let’s define the random variable

$$Y(\mathit{s})=X(\mathit{s})-Z(\mathit{s})$$ (5)

where Z(s) defined in Eq. (4) may have an observation domain 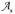that varies across space. As seen in the appendix, if X(s) is a homogeneous SRF with covariance c_X(s,s′)=c_X(|s-s′|), then Y(s) is a zero mean random variable with variance equal to

$${{\sigma }_Y}^2(\mathit{s})={{\sigma }_X}^2-2{\left|\right|{\mathcal{A}}_{\mathit{s}}\left|\right|}^{-1}{}_{\mathit{u}}\in {\mathcal{A}}_{\mathit{s}}\text{d}\mathit{u}{c}_X(\mid \mathit{s}-\mathit{u}\mid )+{\left|\right|{\mathcal{A}}_{\mathit{s}}\left|\right|}^{-2}{}_{\mathit{u}}\in {\mathcal{A}}_{\mathit{s}}\text{d}\mathit{u}{}_{{\mathit{u}}^{\prime }}\in {\mathcal{A}}_{\mathit{s}}\text{d}{\mathit{u}}^{\prime }{c}_X(\mid \mathit{u}-{\mathit{u}}^{\prime }\mid ),$$ (6)

where σ_X² =c_X(|0|) is the variance of X(s), and σ_Y²(s) is a function of s through .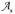

Our proposed approach relies on the model assumption that if z_soft are exact values observed at scales R>0 at points s_soft, then Y_soft=Y(s_soft) act as additive errors to the observed z_soft such that the local scale prevalence values X_soft=z_soft+Y_soft are characterized by the PDF

$$f_{\mathcal{S}}({\mathit{x}}_{\text{soft}})=f_{\mathit{Y}\text{soft}}({\mathit{x}}_{\text{soft}}-{\mathit{z}}_{\text{soft}}),$$ (7)

where f_Ysoft is the PDF for Y(s_soft). When soft data points are sufficiently far apart to be considered independent then a reasonable choice for this PDF is the product of independent Gaussian distributions with mean zero and variances given by Eq. 6.

Hence our proposed approach consist in considering exact values observed at the local scale at points s_hard as the hard data x_hard, and considering values obtained at an observation scale R>0 at points s_soft as soft data characterized by the PDF of Eq. (7). These hard and soft data are used in the BME posterior PDF of Eq. (1) to provide an estimate of prevalence at any estimation point s_k.

Our proposed approach models the uncertainty associated with the observation scale through Eq. (6). According to this equation, the larger the observation scale R is, the larger will be the uncertainty associated with the corresponding local scale prevalence. The implementation of this approach only requires calculating σ_Y² as a function of the observation scale R. Furthermore, as shown in the appendix, numerically efficient equations can be derived for the relationship between σ_Y² and R when considering nested exponential covariance functions, as is the case in this study. As a result our approach allows to conveniently integrate data at any observation scales, without having to upscale the covariance for X(s) in order to obtain that between X(s) and Z(s) as is the case in area-to-point kriging.

Validation analysis

In order to validate our proposed approach to account for observation scale in the context of mapping disease prevalence, we compare the mapping accuracy of our proposed approach with two alternative approaches that do not account for observation scale. Let x_hard be exact values of the local scale prevalence at points s_hard, and let z_soft be values of prevalence obtained at an observation scale R>0 at points s_soft. Method 1 uses the simple kriging estimator (i.e. Eq. 2–3 with m_k=0 and m_hard=0) to estimate local scale prevalence using only x_hard. Method 2 also uses the simple kriging estimator, but this time both x_hard and z_soft are treated as hard data (i.e. the uncertainty associated with the observation scale of z_soft is ignored). Finally method 3 is our proposed approach using x_hard treated as hard data, and using z_soft treated as soft data (which takes into account the uncertainty associated with the observation scale of z_soft through Eq. 6). The soft data provides, therefore, more information for BME which then should decrease the estimation error relative to that of methods 1 and 2.

We do not compare our approach with area-to-point kriging, because (i) our aim in this article is to show that our proposed approach is more accurate than two limiting methods that do not account for observation scale (by either ignoring z_soft or treating it as hard), and (ii) a comparison with area-to-point kriging will be presented in future works that will consider practical implementation aspects that cannot be covered here due to limited space, but shows that both methods are complementary. We note that Lee and Wentz (2008) also excluded area-to-point kriging when introducing the approach presented here in the different context of water resources.

The estimation error of each estimation method is measured using a validation and a cross validation procedure. In the validation procedure, x_hard is randomly split into a validation set x_validation and a training set x_training such that x_hard={x_validation,x_training}, the training set is used to obtain estimated values x_validation* of the validation set, validation errors are obtained as x_validation*-x_validation, and the mean of the square of estimation errors provide the mean square error (MSE) used to assess the estimation error of a given method. The cross validation procedure is similar, with the difference that each datum of x_hard is considered in turn as the validation set to obtain one cross-validation estimation error, and the cross validation MSE is calculated using all the cross-validation errors from x_hard.

Data

We have obtained two datasets with data on childhood asthma prevalence across North Carolina during the same time period of 1997–1999. The data with finer resolution are from a state wide public middle school asthma survey collected in the 1999–2000 school year (Yeatts et al. 2003), while the second dataset are asthma Medicaid claims from 1997–1998. (Buscher et al. 1999)

The North Carolina School Asthma Survey database

The first dataset consists in childhood asthma prevalence collected as a part of the North Carolina School Asthma Survey (NCSAS) (Yeatts et al., 2003). The NCSAS was a collaborative effort between the North Carolina Department of Health and Human Services, the North Carolina Department of Public Instruction, and the Department of Epidemiology in the University of North Carolina at Chapel Hill. This survey collected information on the breathing status of students enrolled in public 7th and 8th grades (i.e. age of 13–14) in the 1999–2000 academic school year. All 565 public middle schools (for a total of 192,248 enrolled students) were asked to participate in the survey, leading to the participation of 499 schools in the survey. We obtained data from approximately 128,556 students (i.e. 66.9% of the student population) in 493 schools (i.e. 87.3% of the school population.

The NCSAS questionnaire included internationally standardized and validated questions from the International Survey of Asthma and Allergies in Childhood (ISAAC) consisting of written and video types of questions. While the NCSAS provides several relevant asthma variables for each student, the variable we used, named “current wheezing symptom”, which characterizes the occurrence of asthma symptom prevalence, was recorded as a value of 1 for children who said “yes” to any one of four video questions describing 1) wheezing during the day, 2) wheezing induced by exercise, 3) wheezing at night, or 4) a severe wheezing attack. Using this variable, we calculated, for each of 493 schools, the asthma prevalence among children by dividing the number of children who answered yes by the total number of students surveyed in that school. For illustration purposes, we show in Fig. 1(a) a graduated color plot of childhood asthma prevalence obtained from this dataset.

Figure 1.

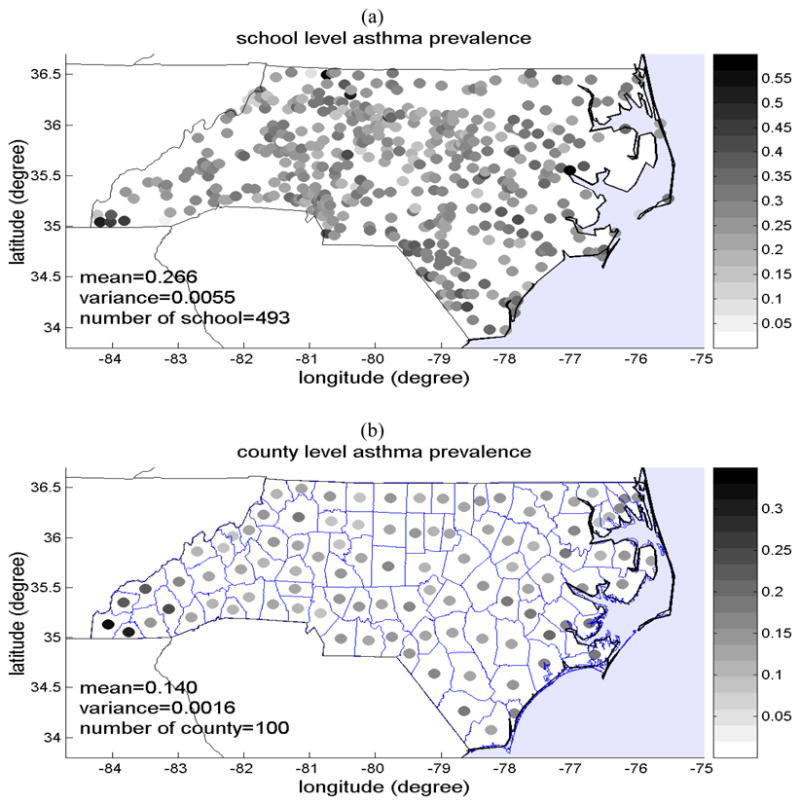
Map showing (a) the data on asthma symptoms prevalence among high school children (age 13–14) reported in the NCSAS database for most of NC schools, and (b) the county level asthma prevalence data extracted from the database of Medicaid-enrolled children age 0–14 years who suffered from asthma. The prevalence is expressed as a fraction (i.e. average childhood asthma cases per 1 child) according to the color bar next to each map.

Because of the almost-exhaustive nature and the good data quality of the NCSAS dataset, the data it provides on the prevalence of asthma symptoms among children enrolled in public 7th and 8th grades in North Carolina can reasonably be considered exact measurements of childhood asthma prevalence. Furthermore, the observation scale for this prevalence data corresponds to that of middle schools, which have a very small geographical extend relative to that of, for example, a county. Indeed, half of the average distance between schools in North Carolina and their closest neighbor is approximately 3 km, so that for the average of schools the maximum distance that children travel to go to school is on the order of 3 km. Since the children population is generally clustered around schools, the median travel distance to school must be much less than its maximum of 3 km, in the order of a fraction of the km scale. Considering the fact that children spend a portion of their day on the premises of the school itself, we can safely conclude the NCSAS data obtained at the school observation scale can reasonably be conceptualized as providing exact measurements of childhood asthma prevalence observed at the local scale, i.e. this dataset provides the hard data x_hard for the SRF X(s).

The county-level database of Medicaid-enrolled children with asthma

Buescher et al., 1999 published a document including data on Medicaid claims due to asthma in North Carolina during the state fiscal year 1997–1998. The number of childhood asthma cases in each county was recorded by counting the Medicaid-enrolled children of age 0 to 14 with asthma. According to the study, the Medicaid-enrolled children suffering from asthma were identified on the basis of paid Medicaid claims with a diagnosis of asthma as well as with prescription drugs used for treating asthma. The fraction of Medicaid-enrolled children with asthma for each of the 100 counties in North Carolina was calculated by dividing the number of Medicaid-enrolled children with asthma claims by the total number of Medicaid-enrolled children claims in each county. The location we assign for each of these fractions is the centroid of the county for which the fraction is calculated, and we represent these data in Fig. 1(b) using a graduated color plot.

The average land area for counties in North Carolina is 1363.9 km², which correspond to a radius of about 20.8 km if we assume that counties can be approximated with circles of same surface areas. This spatial scale of about 20.8 km is substantially larger than that of the NCSAS data collected at the school level, which as discussed above, is believed to be on the order of a fraction of the kilometer scale. This statement is also strengthened by the fact that most of children live close to their school, with few children living far from their school, whereas Medicaid-enrolled children can be assumed to have a much more uniform spatial distribution across the whole county. Therefore we define the fraction of Medicaid-enrolled children with asthma in a particular county as a measurement of the Z(s) observed at the county spatial scale. In other words we conceptualize the Medicaid data shown in Fig. 1(b) as being observations z_soft of the local scale childhood asthma prevalence (the NCSAS data shown in Fig. 1a) averaged at the county spatial scale. As can be seen from Fig. 1, the Medicaid data are smoother than the NCSAS data, which is consistent with our hypothesis that one corresponds to the aggregation of the other at a larger spatial scale.

There are of course many limitations in the use of the Medicaid dataset to provide values of prevalence z_soft obtained at an observation scale R>0. First, Medicaid-enrolled children are only a subgroup of the total population of children. However the advantage of this subgroup is that children enrolled in Medicaid are a group considered more “at risk” for a higher likelihood of asthma related morbidity, given the lack of economic resources and lack of consistent chronic care. Furthermore the Medicaid data was obtained in 1997–1998 while the NCSAS was obtained in 1999–2000. Nevertheless we hypothesize that the local-scale deviations in asthma prevalence between the Medicaid and NCSAS datasets average out at the county spatial scale.

Results

Trends and variability in childhood asthma prevalence

The SRF X(s) represents the spatial distribution of childhood asthma prevalence at the local scale. Its mean trend function provides a model for the systematic trends and consistent spatial structures of X(s), while its covariance function describes the inherent spatial variability of X(s).

We obtain the local scale mean trend function using a moving window average of the NCSAS data x_hard with an exponentially decaying exponential filter. This leads to the mean trend function shown in Fig. 2(a). As can be seen from this figure, the mean trend has a slightly higher prevalence along the eastern coast of North Carolina, and it decreases almost linearly from East to West. This mean trend function can be linearized within each county, and as a result the trend shown in Fig. 2(a) is also the mean trend of asthma prevalence field observed at the county spatial scale, i.e. m_Z(s)=m_X(s). A useful implication is that the framework presented in the theory section to integrate data obtained at different spatial observation scales is valid not only for the X(s) and Z(s) SRFs, but also for the mean trend removed residual fields X′(s)=X(s)−m_X(s) and Z′ (s)=Z(s)−m_Z(s) (since m_Z(s)=m_X(s)). We therefore apply our framework for the integration of data observed at different spatial scales to the residual fields X′ (s) and Z′(s).

Figure 2.

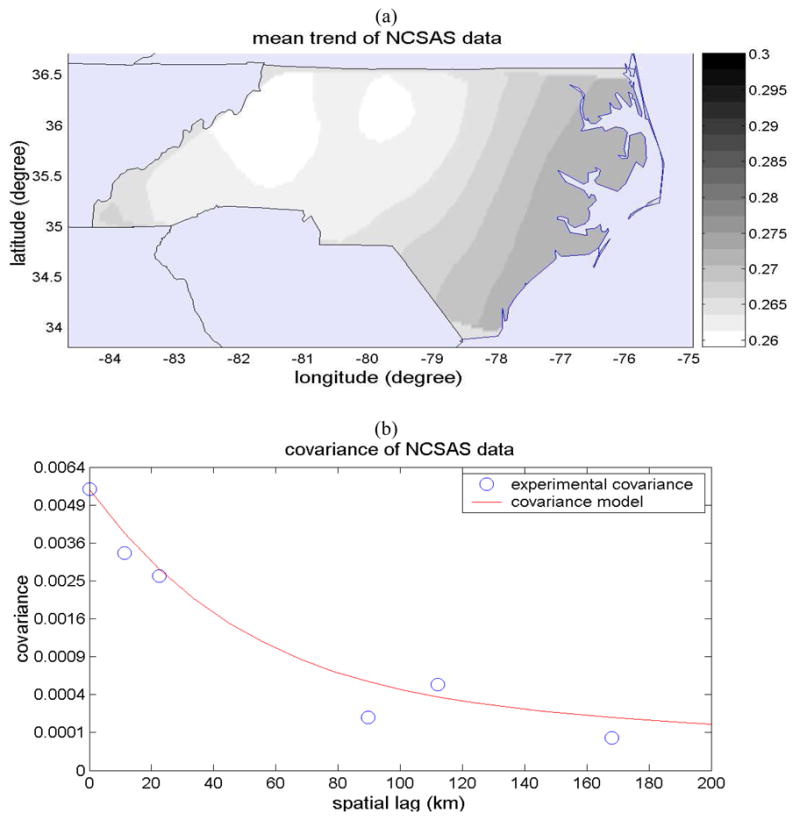
(a) Map of the local scale mean trend m_X(s) of the childhood asthma prevalence (fraction of prevalent asthma cases), and (b) plot of the covariance of the mean trend-removed local scale childhood asthma prevalence SRF X′ (s).

We obtained experimental covariances of the residual field X′ (s) and a covariance function (Eq. 8) that fits well to the experimental values (Fig. 2b).

$$c_X(r=\mid {\mathit{s}}^{\prime }-\mathit{s}\mid )=c_{01}exp\left(\frac{-3r}{a_{r1}}\right)+c_{02}exp\left(\frac{-3r}{a_{r2}}\right),$$ (8)

where c₀₁= 0.9 × σ_X², c₀₂=0.1 × σ_X², σ_X²= 0.0055 (average number of asthma cases per 1 child)², a_r1= 89.6 km, and a_r2= 448 km. The covariance model indicates that about 90 percent of the variability of the local scale childhood asthma prevalence has a spatial range (e.g. spatial clustering) of 89.6 km, while the remaining 10 percent of variability as a much larger spatial range (clustering) of 448 km. The explanation for this spatial organization of local scale asthma prevalence over rather large spatial ranges of up to a few hundred km may be manifold, and provides the basis for hypothesis generation that may be tested in future works. One such hypothesis might be that asthma among children is influenced by underlying factors that are themselves organized in space. One such factor may be the characteristics of the children population (i.e. ethnic make-up, socioeconomic status, dietary habits, proportion of children with higher asthmatic susceptibility, etc.) that may themselves have a spatial structure corresponding to the 89.6 km spatial scale. Another factor may be the exposure to environmental pollutants suspected to cause asthma, such as airborne particulate matters, ozone and lead, which may have spatial ranges in excess of 448 km (e.g. Christakos and Serre, 2000).

The mean trend function and covariance model provide the general knowledge base used in the BME analysis to produce the maps of asthma prevalence presented next.

Childhood asthma prevalence maps

Using the NCSAS data x_hard and the Medicaid data z_soft we obtain maps (Fig. 3) of childhood asthma prevalence across North Carolina with the three methods described earlier.

Figure 3.

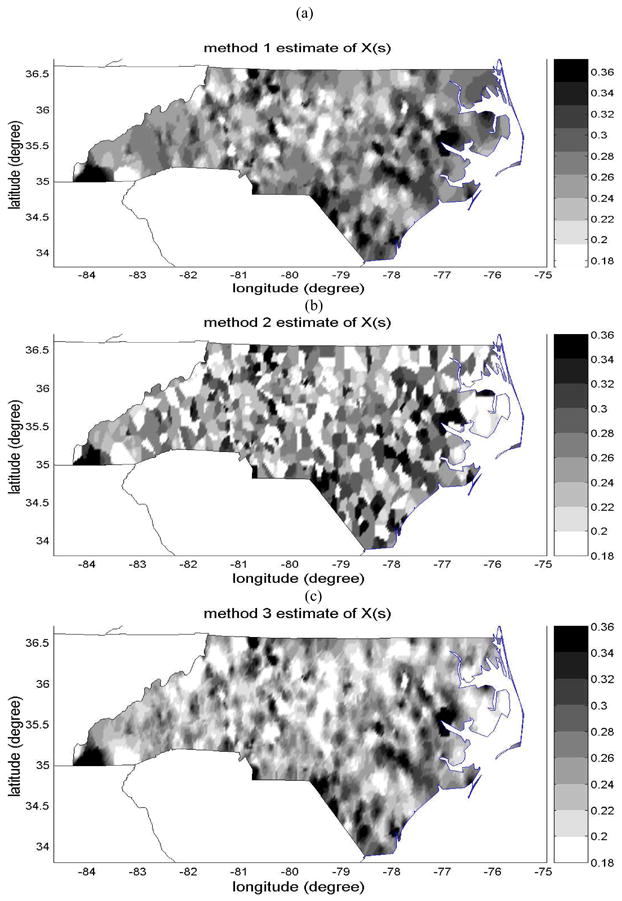
Maps of the estimates of childhood asthma symptom prevalence (average number of case per 1 child) using (a) method 1, (b) method 2, and (c) method 3.

The estimate of local scale childhood prevalence obtained with Method 1, which uses x_hard as hard data and ignores the z_soft data, is shown in Fig 3(a). The associated uncertainty (i.e. the kriging variance) is shown in Fig. 4(a). These maps interpolate the NCSAS data over all non-surveyed areas of North Carolina, with a mapping uncertainty that is zero at the spatial location of each of the NCSAS high schools, and increases away from these surveyed locations. These maps provide a baseline against which we can compare maps that attempt to integrate the additional information provided by the Medicaid childhood asthma prevalence data z_soft available at the county observation scale.

Figure 4.

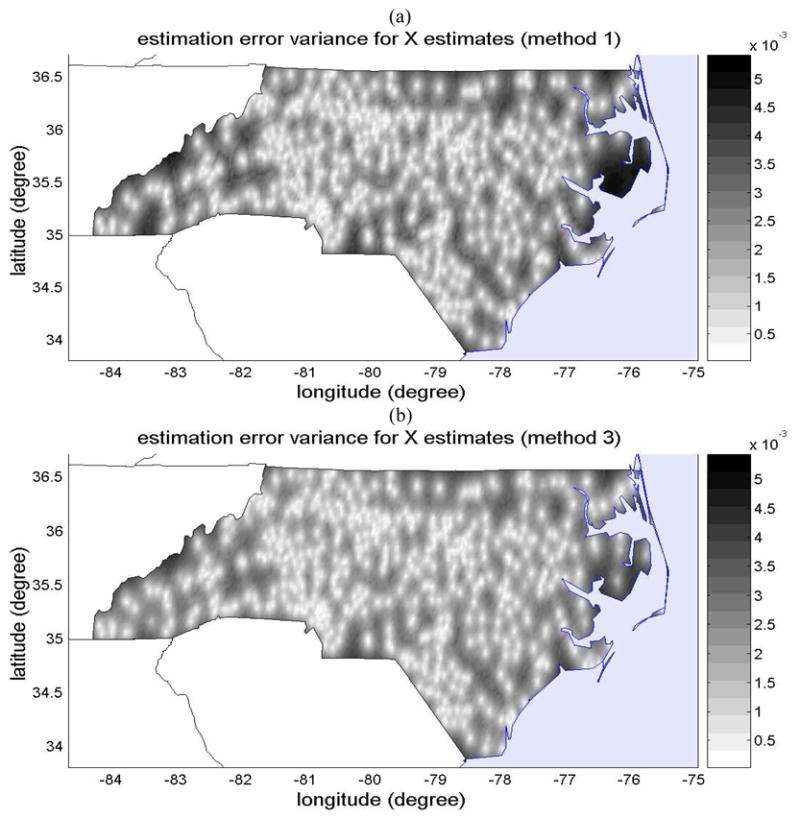
Maps of the estimation variance ([average asthma counts per 1 child]²) obtained with (a) method 1 and (b) method 3, which provides an assessment of the uncertainty associated with the estimation maps shown in Figure 3(a) and (c), respectively.

Method 2 uses both x_hard and z_soft data as hard data. By ignoring the scale effect for the Medicaid data z_soft, method 2 underestimates the uncertainty in measuring local scale asthma prevalence because of the large observation scale of that dataset. The map of the estimate obtained from method 2 is shown in Fig. 3(b). As can be seen from this figure, this map integrates more details in the spatial distribution of childhood asthma prevalence because the combined dataset is larger, leading to a spatial estimate that is quite different than that obtained with method 1. However, method 2 wrongly assumes that the scale effect of the Medicaid data can be ignored, leading to the erroneous belief that the uncertainty associated with the map of method 2 is zero at the centroid of each county where Medicaid data points are reported. As a result, method 2 is unable to provide a correct assessment of the uncertainty associated with its spatial estimate shown in Fig. 3(b).

On the other hand, method 3 accounts for the scale effect by formally processing the uncertainty associated with the observation scale of the Medicaid data. The estimate obtained from method 3 is shown in Fig. 3(c), and its estimation uncertainty (variance of the BME posterior PDF) is shown in Fig. 4(b). Method 3 integrates both datasets, extracting all the information provided by the NCSAS data obtained at the local scale, and using the Medicaid data as an approximate guess of the local scale childhood asthma prevalence away from the NCSAS data points. The resulting map has more spatial details than the map of method 1, yet it is smoother than the map of method 2. The map of the associated mapping uncertainty shows that the uncertainty is zero at the NCSAS high school location, that it is small but non zero at the centroid of counties for which the Medicaid data is available, and that it increases away from these points. Both these features result in a more realistic representation of the local scale childhood asthma prevalence than that obtained from either method 1 or 2.

The results presented illustrate that by formally accounting for the scale effect of the childhood asthma prevalence data, our proposed framework (method 3) generates a map describing the spatial distribution of childhood asthma prevalence that is substantially different and more realistic than maps obtained using methods not accounting for the scale effect. We now investigate whether this more realistic map is also substantially more accurate than the maps of method 1 or 2.

Cross-validation results

We use a cross-validation procedure to compare the accuracy of the maps obtained using methods 1, 2 and 3 by means of their MSE. The results of this cross validation procedure are shown in Table 1 in terms of the cross-validation MSE and percent reduction in MSE compared. Somewhat surprisingly, method 2 does not provide any improvement of mapping accuracy over method 1. In fact the MSE for method 2 is slightly higher than that of method 1. This result provides a striking illustration of what may happen when one attempts to mix-in data obtained at different observation scales without consideration of the scale effect, as is the case for the naïve approach used in method 2. Indeed, even though method 2 seems to provide more spatial details about childhood asthma prevalence across North Carolina, these details are actually erroneous because they do not account for the uncertainty associated with the large observation scale of the Medicaid data. Our proposed BME approach (method 3) has a MSE that is substantially smaller than that of either method 1 or 2. The sound conceptual framework we have developed in this work to integrate data obtained at different observation scale leads to a 10.2% decrease in cross-validation MSE relative to method 1, and a 11.6% decrease relative to method 2. This demonstrates that our proposed approach leads to a map of childhood asthma prevalence across North Carolina that is more realistic and more accurate than those obtained by methods that do not account for the scale effect.

Table 1.

Cross-validation results showing the cross-validation MSE for methods 1, 2 and 3, and the change in cross-validation MSE between method 1 and method 3, as well as between method 2 and method 3.

	Method 1 (simple kriging I)	Method 2 (simple kriging II)	Method 3 (BME)
MSE	4.06×10−2	4.13×1−2	3.65×10−2
${\text{r}}_{\text{MSE}}^{1,3}$		−10.21%
${\text{r}}_{\text{MSE}}^{2,3}$		−11.63%

The cross validation procedure compares the accuracy of the estimation methods when one data point is removed at a time. This comparison quantifies the gain in accuracy for the current mapping situation: We can say that the childhood asthma prevalence map (Fig. 3c) is at least 10% more accurate than maps that may have been produced to date using the traditional approach of method 1 or 2. Another comparison is through the validation procedure, which compares the mapping accuracy under other mapping situations by removing several data points at once. The next section presents validation results.

Validation results

Our validation procedure consists in removing 30% of the NCSAS data at once, and re-estimating the childhood asthma prevalence for these points using the remaining NCSAS data as well as the Medicaid data. The validation MSE obtained for estimation methods 1, 2 and 3 are shown in Table 2: When removing 30% of the NCSAS data, method 2 is slightly more accurate than method 1, and, more importantly, our soft data approach (method 3) is at least 20% more accurate than either method 1 or 2.

Table 2.

Validation results obtained when selecting a random validation set consisting of 30% of the NCSAS data. The table shows the validation MSE obtained for methods 1, 2 and 3, and the change in validation MSE between method 1 and method 3, as well as between method 2 and method 3.

	Method 1 (simple kriging I)	Method 2 (simple kriging II)	Method 3 (BME)
MSE	9.89×10−3	9.70×1−3	7.67×10−3
${\text{r}}_{\text{MSE}}^{1,3}$		−22.51%
${\text{r}}_{\text{MSE}}^{2,3}$		−20.96%

Discussion

Mapping childhood asthma prevalence (as well as other diseases) is complicated by the fact that data is often available at a variety of spatial scales. This is particularly the case because several data sources have confidentiality requirements that only allow release of information aggregated over spatial scales that are sufficiently large to ensure the privacy of the individuals who provided their health information.

We develop a mathematical framework to map the spatial distribution of childhood asthma prevalence by integrating data collected at different spatial observation scales, and we apply this framework to a real case study in North Carolina using two datasets obtained at two substantially different observation scales. We constructed our first dataset of childhood asthma prevalence using the NCSAS data that was collected as part of a previous study of one of the co-authors (Yeatts et al., 2003). By aggregating the NCSAS data at the high school spatial scale using good quality information on the prevalence of asthma symptoms among 7–8th grades, we obtained a dataset that can essentially be treated as exact measurements of childhood asthma prevalence observed at the local scale for each of 493 high-schools. While this first dataset provides a rich set of point measurements, it is inherently providing a sparse spatial coverage of North Carolina. Hence, we also included in the mapping analysis a second dataset consisting of childhood asthma prevalence calculated on the basis of Medicaid-claims aggregated at the county spatial scale (Buescher et al., 1999). While this dataset presents some limitations due to biases connected with the Medicaid-enrolled children population, we hypothesized that local errors in the Medicaid data may average out at the county spatial scale, so that this dataset provides useful information as long as the scale effect is adequately accounted for.

The conceptual framework we developed provides a rigorous mathematical formulation for the uncertainty associated with the spatial scale at which asthma prevalence data are observed. Using this framework, the NCSAS data is processed as hard data, while the Medicaid children data is used to generate soft data with an uncertainty corresponding to the county spatial scale at which these data are reported. These combined hard and soft data are then rigorously processed using the Bayesian Maximum Entropy method of modern Geostatistics, leading to an accurate estimation of the spatial distribution of childhood asthma prevalence across North Carolina.

We find that the map we obtain is substantially more realistic and accurate than the classical map obtained by ignoring entirely the county level data, or the classical map obtained by integrating the county level data without consideration of its observation scale. Our cross-validation results reveals that the childhood asthma prevalence map we generate for North Carolina has a mapping error variance that is 10% smaller than that of the classical maps obtained when ignoring the scale effect. Furthermore a partial validation analysis (using a single random selection of the validation set) indicates that under other mapping situations the drop in mapping estimation error can be in excess of 20% over the classical approaches not accounting for the scale effect. Our proposed method, therefore, provides a powerful conceptual framework to integrate data obtained at different observation scales for a wide range of asthma mapping situations.

This work provides a methodological advance that complements the area-to-point kriging method for the integration of disease prevalence data collected at different observation scales. Our approach is novel in that it uses the non-linear BME framework to integrate data collected at different observation scales. There are two aspects of this work that can be investigated in future works. First, we did not account for the small number problem because, as noted in the introduction, childhood asthma is not a rare disease. As a result our analysis interpolates the observed rate, which leads to a map that is spatially detailed (i.e. “wiggly”). This map fulfills our goal of providing a view of asthma prevalence at a fine scale, which is highly informative for the visual exploration of associations with fine scale environmental determinants such as proximity to industrial hog farms. However, future work may look at extending our novel approach to deal with both the COSP and small number problem. Second, we assumed in this work that the soft data points where independent, so that 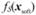(Eq. 7) can be written as the product of independent Gaussian distributions. This is a reasonable approximation in this work as the soft data points correspond to county centroids, which are about 40 km apart on average in North Carolina. However future work may consider other applications where the correlation between soft data points is taken into account.

The application of our novel approach to mapping childhood asthma prevalence is applicable nationwide. By applying this new method, we obtain a map of the distribution of childhood asthma prevalence at a finer spatial scale than that obtained using classical BME studies based on the downscaling of the covariance function and the small number problem (Choi et al., 2003). The optimal scale varies as a function of the application, but as noted earlier, our spatially detailed map of childhood asthma across North Caroline can be used to improve our understanding of possible associations between asthma and causal risk factors with fine scale spatial variations, such as air pollutants. Furthermore, we demonstrate how existing sources of asthma data such as Medicaid claims can be used to obtain good estimates of childhood asthma prevalence. These techniques could be applied to reduce the need of costly programs dedicated to asthma surveillance, so that state health departments’ limited resources can be more efficiently used for public health interventions and reduction of childhood asthma morbidity.