Cluster Morphology Analysis

Abstract

Most disease clustering methods assume specific shapes and do not evaluate statistical power using the applicable geography, at-risk population, and covariates. Cluster Morphology Analysis (CMA) conducts power analyses of alternative techniques assuming clusters of different relative risks and shapes. Results are ranked by statistical power and false positives, under the rationale that surveillance should (1) find true clusters while (2) avoiding false clusters. CMA then synthesizes results of the most powerful methods. CMA was evaluated in simulation studies and applied to pancreatic cancer mortality in Michigan, and finds clusters of flexible shape while routinely evaluating statistical power.

Introduction

A major difficulty in the geographic analysis of disease outcomes is that the patterns observed reflect the influence of a complex constellation of demographic, social, economic, cultural and environmental factors that likely change through time and space, and interact with the different types and scales of places where people live (Tunstall et al. 2004). The shape of these patterns as manifested in disease clusters may be thought of as an imperfect projection of this constellation of factors onto a map, and the clusters we observe may likely be of arbitrary shape and change dynamically through time. There thus is a need for cluster analysis approaches that detect clusters of arbitrary shape, recognize that this shape can morph through time, and shift location as underlying demographics and environmental factors wax and wane in relative importance at different places and at different times. One should also account for the known covariates and risk factors, by working with observed and expected case counts, and for uncertainties introduced by small cases counts as well as small populations at risk (e.g. small numbers problem).

The identification of sub-populations with excess disease burdens, and the detailing of disease clusters in terms of geographic extent, population impacts, and amount of excess risk, are priority issues for the National Institutes of Health (Pickle et al. 2005), and cluster studies are now routinely undertaken in cancer surveillance to focus cancer control efforts (Wheeler 2007). Yet a major barrier to the accurate identification and quantification of sub-populations with excess risk is the inability of clustering methods to find clusters of arbitrary shape and to accomplish this through time as population distributions and demography change (Jacquez 2004). In many health agencies the current state-of-the-art in disease cluster investigations employs scan statistics as are available in SatScan (Kulldorff 2004). This means only one cluster shape (circle or ellipse) is evaluated. But when this shape is not strictly correct both false positives – phantom cancer clusters – and false negatives – missed signals – can occur. This paper describes a new, meta-analytic approach to cluster analysis. This approach first conducts power comparisons using the place and disease geography of interest. Next, results from the alternative techniques are compared and contrasted using specificity, power and type 1 and type 2 error. Cluster Morphology Analysis then synthesizes the results for those techniques demonstrated to have the best power and smallest type 1 error. This is a significant advance that provides researchers with detailed knowledge of the statistical performance of clustering methods for the specific cancer outcomes, populations, spatial resolution and geography they are analyzing, and that finds clusters of arbitrary shape with high statistical power and fewer false positives than any one method considered.

The remainder of this Introduction considers the rationale for conducting cluster studies, the basics of probabilistic pattern recognition, and types of cluster tests in common use. It then describe some limitations of cluster studies and how relaxing the shape assumption allows researchers to more accurately distinguish true clusters from methodological artifacts. We then describe recent advances in space-time intelligence system software. The Methods section details the simulation approach and statistical methods, and applies the approach to white male pancreatic cancer in Michigan. Next, the results are described, and the Discussion outlines future research directions.

Objectives of Cluster Analysis

Cluster analyses evaluate both event- and population-based data. Event-based data include observed and expected counts (e.g. number of cases diagnosed within a county over a given time period, and the expected number of cases based on the state rate). Population-based data incorporate information on the at-risk population, and include cancer incidence and mortality rates. A disease cluster may be defined as an excess of cases in geographic space, in time, or in both space and time.

Cluster analysis is used to guide the construction of spatial models and in Exploratory Spatial Data Analysis (ESDA). Model construction requires an understanding of the patterns of spatial variation in order to incorporate relevant features into the model. ESDA involves the identification and description of spatial patterns and has two objectives: geographic pattern recognition and hypothesis generation to specify realistic and testable explanations for those patterns. Spatial patterns are of interest because they summarize the geographic signatures of processes, covariates, and factors (e.g. environmental exposures; access to cancer screening facilities; behaviors mediating cancer risks) that determine how disease risk varies across and is expressed within human populations.

Inference from Cluster Models

Within a hypothesis-testing framework cluster tests proceed by calculating a cluster statistic describing a relevant aspect of spatial pattern in a health outcome. The numerical value of this statistic is then compared to the distribution of that statistic under a null spatial model, providing a probabilistic assessment of how unlikely the observed cluster statistic is under the null hypothesis (Gustafson 1998; Jacquez et al. 1996b; Kulldorff et al. 2006c). Spatial cluster tests have five components (Waller and Jacquez 1995). The test statistic quantifies a relevant aspect of spatial pattern such as Cuzick and Edwards (Cuzick and Edwards 1990) T_k or the scan statistic (Kulldorff et al. 2006a; Tango and Takahashi 2005). The alternative hypothesis describes the spatial pattern the test is designed to detect. The null hypothesis describes the spatial pattern expected when the alternative hypothesis is false (e.g. uniform cancer risk). The null spatial model is a mechanism for generating the reference distribution (Goovaerts and Jacquez 2004). Most disease cluster tests employ heterogeneous Poisson and Bernoulli models for specifying null hypotheses (Lawson and Kulldorff 1999). The reference distribution is the distribution of the test statistic when the null hypothesis is true. Comparison of the test statistic to the reference distribution allows calculation of the probability of the observed value of the test statistic under the null hypothesis of no clustering. There are dozens of cluster statistics that may be categorized for convenience as global, local, and focused tests (Jacquez et al. 1996a; Jacquez et al. 1996b; Kulldorff et al. 2006c; Lawson and Kulldorff 1999). Global cluster statistics are sensitive to clustering anywhere in the study area. Local statistics such as G and G* (Ord and Getis 1995) quantify clustering around individual locations that comprise the study geography. Focused statistics quantify clustering around a specific foci (Tango 2002) and are used to explore clusters of cases near potential sources of environmental pollutants (Lawson 1989; Lawson and Waller 1996; Waller et al. 1992).

Assumptions of Clustering Methods

Hundreds of cluster investigations are recorded in the literature, are used to direct disease control activities and can initiate formal epidemiological studies to identify potential causes (CDC 1990). Cancers studied include leukemia, brain, liver, breast, prostate, bladder, lung, and colorectal cancers. Geographic patterns in therapies, screening behaviors and cancer disparities (Abe et al. 2006; Aschengrau et al. 1996; Bonner et al. 2005; Clarke et al. 2002; Fang et al. 2004; Gregorio et al. 2002; Gregorio et al. 2001; Gregorio et al. 2004; Gregorio et al. 2006; Han et al. 2004; Hsu et al. 2004; Jacquez and Greiling 2003a, b; Jemal et al. 2002; Joseph Sheehan et al. 2004; Paulu et al. 2002; Thomas and Carlin 2003; Turnbull et al. 1990; Vieira et al. 2005; Zhan 2002; Zhan and Lin 2003) are also studied. But to date many cluster studies still employ methods that assume one cluster shape (circle, ellipse, adjacency, nearest neighbors), and we do not know when a reported cluster is real, or explicable as an artifact of the shape assumption (Figure 1).

Figure 1.

Lung cancer incidence in New York. SatScan analysis found circular “clusters” that include ZIP codes with rates 50% below the state average (http://www.health.state.ny.us/nysdoh/cancer/csii/nyscsii.htm).

In addition, cluster analysis software such as SatScan (Kulldorff 2004) and Flexscan (Takahashi et al. 2004) use centroids (e.g. the center of a census unit) when constructing clusters, and these are not reasonable representations of spatial support (e.g. area) or extent. We now consider pitfalls of these strong assumptions, drawing on a published map of lung cancer in New York State (Figure 1). We use the circular scan statistic as an example because it is widely used in local and state health departments.

Assumption of Cluster Shape

The scan statistic (Kulldorff 2004) assumes circular clusters, and as a result, the clusters shown in Figure 1 are circular. Is this best explained as a methodological artifact, or do we really expect cancer clusters to be circular? Within each circular cluster a likelihood statistic is calculated from observed and expected counts, and assesses how unlikely the within-cluster risk is. This can result in false positives within clusters, since an area with a low rate – even a rate 50% below the global mean (as shown in Figure 1) – is declared part of the cluster provided the local average within the circle is sufficiently elevated. These areas of low risk are not legitimate cluster members and as false positives are methodological artifacts. A recent power study by Tango and Takahashi (Tango and Takahashi 2005) found “.... The circular spatial scan statistic tends to detect a larger cluster than the true cluster by absorbing surrounding regions where there is no elevated risk.” Returning false positives as part of a cluster appears to be a property of scan-type statistics that employ a likelihood function to average risk across cluster member candidates – it is not limited only to circular spatial scan statistics.

Assumption of Centroids – No Spatial Support

Centroids are points in the geographic space that represent the sub-areas (e.g. census blocks) that are being studied. Centroids thus ignore spatial support (geographic extent of the sub-area) and relationships between adjoining areas (common boundaries). Disease geography doesn’t stop at the edge of the study area, and the spatial extent of clusters can be biased by edge effects. For example, when a true cluster straddles a border but only half of it is analyzed (as shown in Figure 1 along the northwest border) the geographic center of the cluster may be declared to be further from the border than it really is. In addition, when centroids are used intervening geographic barriers -- such as large bodies of water -- are ignored, and clusters may straddle disjoint geographic units of disparate population characteristics. New approaches are needed that accurately detect clusters of arbitrary shape, based on realistic representations of the geography and demographics of the study populations, and that readily account for changes in disease outcomes and covariates through time.

Space Time Intelligence Systems

The representation of geographies (e.g. census units), demographics and populations as unchanging rather than dynamic is due in part to the static world-view of GIS (Geographic Information System) software, which is largely incapable of representing temporal change and is best suited to “snapshots” of static systems (Goodchild 2000; Hornsby and Egenhofer 2002; Jacquez et al. 2005). This static view hinders the mapping, representation, and analysis of dynamic health, socioeconomic, and environmental information for populations that are dispersed and mobile. Recent technological advances have resulted in Space Time Intelligence Systems (STIS) that implement constructs for representing temporal change (Avruskin et al. 2004; Greiling et al. 2005; Jacquez et al. 2005; Meliker et al. 2005). The STIS technology has the following advantages. First, it is built on true space-time data structures, enabling complex space-time queries not possible in conventional “spatial only” GIS. Second, it has space-time data models that provide realistic representations of human mobility and dynamic geography such as residential histories, geospatial lifelines and morphing polygons. Third, it incorporates statistical tests for space-time pattern such as univariate and bivariate local indicators of spatial autocorrelation. Fourth, it employs dynamic linked windows that enable both cartographic and statistical brushing. Fifth, it constructs and simulates spatio-temporal statistical models including linear, poisson and logistic regression, geographically weighted regression and space-time estimation procedures such as kriging and variogram models. Finally, it displays animated “movies” for exploring how health outcomes (e.g. maps of incidence, mortality, case counts and expectations, and clusters themselves) change through space and time.

Methods

This section describes the CMA approach, and the simulation study design used to evaluate the technique. It concludes with a description of the pancreatic cancer mortality data set used in a first application of the method.

Cluster Morphology Analysis

It should be apparent that different methods are sensitive to different aspects of clustering, since they may be founded on different null hypotheses, employ different spatial weights, and may be designed to be sensitive to different alternative hypotheses. Further, applied studies vary greatly in terms of geography (e.g. county vs. census units vs. ZIP codes), underlying risk (e.g. rare vs. common cancers) and sizes of the population at risk, and any given clustering technique cannot reasonably be expected to be the most powerful in all situations. We therefore developed CMA, whose steps are as follows.

1. Using the cancer geography of interest to the researcher, construct a cluster model incorporating the observed and expected numbers of cases, the observed at-risk populations, and the observed background risk for that cancer. Model clusters comprised of 1 or more contiguous areas with relative risks the researcher wishes to be able to detect. In this study we used pancreatic cancer in Michigan, described later.

2. Conduct a power and error analysis of alternative clustering techniques. In this study we evaluated 10 methods and a range of parameter values, for a total of 23 comparisons (shown later in Table 2).

3. Rank the methods 1^st by power and second by proportion of false positives, and select m top ranked members to use in the CMA. In this study methods for the detection of clusters of flexible shape (B, ULS, FlexScan, Kernel) and the circular scan had power=1, with false positives from 0.069 to 0.276 (we used m=5).

4. Define the set C_q to be the members of the candidate clusters found for method q. For example, if method q found a cluster of 5 counties, then the cluster set would be comprised of those 5 counties.

5. The CMA clusters are then:

   $${\mathbf{C}}_{\mathit{CMA}}={\mathbf{C}}_1\cap {\mathbf{C}}_2\cap ,\mathrm{..},\cap {\mathbf{C}}_m$$ (Equation 1)

6. Calculate Probabilities of the CMA clusters. Probabilities for the CMA clusters are then calculated as the average of the probabilities from the m clustering methods used in the CMA.

Table 2.

Classification table used in power and error calculations. See text.

		Found
		cluster	background
Truth	cluster	a	b
	background	c	d

Notice each C_q is comprised of two types of candidate clusters: true cluster members and false positives. CMA therefore reduces the number of false positives whenever the false positives found by each method are not the same over all of the m methods. There still is a tradeoff between power and type 1 error, but, because it is based on a statistical power analysis (step 2, above), under CMA this tradeoff is documented. In this study CMA had power=1 and proportion of false positives=0.017. CMA may be thought of as a meta-analysis of the results of clustering approaches found to have the best statistical performance for a given disease, geography, and at-risk population.

Simulation Design in CMA Step 1

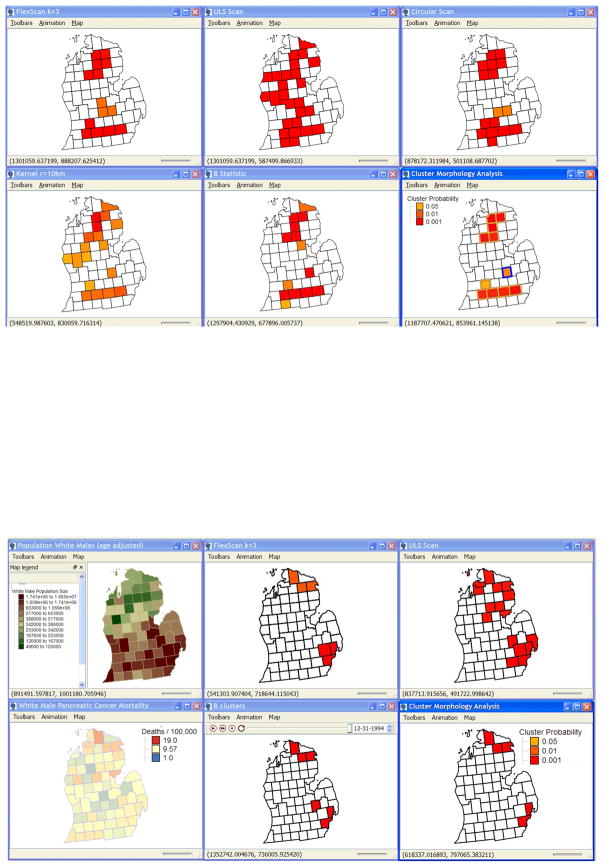
We conducted a CMA analysis that compared the statistical power of 11 methods (described below) using data from NCI’s National Atlas of Cancer Mortality for white male pancreatic cancer mortality in Michigan counties from 1970 through 1994. We used the observed age-standardized at-risk population (Figure 2, top left), and calculated the background risk of 9.57 deaths per 100,000 as the state-wide age-standardized mortality rate for white males. Next we modeled two clusters, one in the north (relative risk 2.0) and one in the south (relative risk 1.5), each comprised of five counties (Figure 2, top center) and encompassing heterogeneous rural and urban populations. We then sampled from this risk surface as a Poisson process using the population size in each county, resulting in realizations of observed deaths under the cluster model (Figure 2, top right), with variance reflecting the actual geographic heterogeneity in the at-risk population. In effect we used the modeled relative risk in each cluster/area and multiplied it by the population at risk to obtain an expected number of deaths for each county. The mean expected number of deaths was then used to sample from the population at risk as a Poisson variable to obtain the modeled number of deaths in that realization. We validated the model by plotting the expected number of deaths in each county under the model as a function of the observed number of deaths from the Atlas of Cancer Mortality (Figure 2, lower left). In Figure 2 the user has brush selected the modeled clusters to highlight them on the scattergrams, histograms and maps. Also shown is the histogram of mortality in the counties at background and in the two clusters (Figure 2, lower center); and the corresponding histogram under the Poisson model. Table 1 gives characteristics of the simulation model.

Figure 2.

Cluster model construction, pancreatic cancer mortality in white males in Michigan counties, 1970 through 1994. North and south clusters (outlined in gold) are superimposed on the white male population size (upper left map) with low population size in green and large population size shown in dark brown. The relative risk RR model (center top) shows the background RR in green, RR=2.0 in purple in the North cluster and RR=1.5 as white in the South cluster. One realization from the simulation model (top right) shows pancreatic cancer mortality rates ranging from 6.44/100,000 (pale yellow) to 25/100,000 (dark red). The user has brush selected the north and south clusters and they are shown in gold. Screen capture from the TerraSeer STIS software. See text.

Table 1.

Pancreatic cancer mortality in white males in Michigan counties from 1970 to 1994. Population at risk, mean, standard deviation, and total number of deaths observed (from the National Atlas of Cancer Mortality, cols 1–4) and expected under the simulation model (cols 5–7). Model RR (col 8) is the relative risk in the clustered and not-clustered (background) counties, “r” (col 9) is the correlation between the observed and expected deaths. The number of counties in the clusters and at background is in the last column. The model is highly realistic since it uses the actual population at risk and the correlation between modeled and actual deaths is high (col 9).

	Pop at risk (Age- adjusted)	Observed Deaths (NCI Mortality Atlas)			Expected Deaths (Model)			Model RR	r	Number of counties
		mean	std	Total	mean	std	Total
North Cluster	42,089	20.0	11.01	100	40.3	17.14	201.4	2.0	0.96	5
South Cluster	294,534	145.8	47.28	729	211.4	68.39	1057.0	1.5	0.98	5
Background	3,080,886	132.7	297.32	7,696	127.1	269.66	7,371.0	1.0	0.97	58
Michigan	3,417,509	125.4	276.53	8,525	126.9	251.93	8,629.0		0.99	68

Clustering Methods used in CMA Step 2

In CMA step 2 (above) we used 11 clustering tests: Circular scan, FlexScan, ULS scan, B-statistic, Kernel, Turnbull, Besag & Newell, local G and G*, local Moran, and wombling methods. These methods were selected because they have different alternative hypotheses and provide a practical basis for power comparison. In this study we evaluated four approaches to flexible clustering: the Upper Level Set scan statistic (Patil et al. 2006), the flexible scan statistic (Tango and Takahashi 2005); B-statistics (Jacquez et al. 2008); and probability maps from kernel-based density estimation (Rushton et al. 2004). These are now described in some detail, since they are relatively new. The other more established methods are only briefly described.

Upper Level Set (ULS) scan statistic

The basic idea is to define the shapes of the candidate clusters from a map of the data, and to then use likelihood statistics like those in Kulldorff’s scan test (Kulldorff et al. 1998; Kulldorff et al. 1997; Kulldorff et al. 2006b; Kulldorff and Nagarwalla 1995) to evaluate their significance. While ULS has been applied to crime, disease, and ecological applications, its power has yet to be evaluated, and when applied to cancer uncertainty due to spatially heterogeneous population sizes is not fully accounted for. ULS may be used to evaluate case-control clustering as a Bernoulli process, and for observed and expected counts using a Poisson framework (Modarres and Patil 2007; Patil et al. 2006). We present the Poisson version. Let c_i denote the cases within the i^th area (e.g. census block) and n_i the size of the population at risk in that area. A raw rate (e.g. incidence, mortality) is then x_i= c_i/n_i. The study region R may be divided into a zone, O, that is comprised of a spatially contiguous subset of the areas. The set of all such possible zones is denoted Ω, and represents the universe of all possible clusters of arbitrary shape and size. The problem then is to find from among this universe that set of zones that are true cancer clusters. The innovative aspect of ULS is that it uses the map of the data to prune the search space so that only a subset of Ω, denoted Ω_ULS is considered. Ω_ULS is constructed by ranking the observed rates, x_i, from highest to lowest (one also can rank the rates from smallest to largest to find “coldspots”). Membership in Ω_ULS is defined by the parameter g which is incremented sequentially over each level of the ranked x_i until the sum of the population sizes within the zones defined at the highest level of g reaches a given threshold (usually 50%) of the total population size. This defines successive closed curves on a spatial response surface in a manner analogous to the creation of “rings” in a bathtub as the water is drained. A likelihood ratio, L(O)/L_o, for each of the candidate clusters (zones) in Ω_ULS under the null hypothesis of no clustering is then calculated (Eqn 2).

$$\frac{L(O)}{L_{\text{0}}}=\frac{{\left(\frac{c_o}{e_o}\right)}^{c_o}{\left(\frac{\sum c_i-c_o}{\sum c_i-e_o}\right)}^{\sum c_i-c_o}}{{\left(\frac{\sum c_i}{\sum e_i}\right)}^{\mathrm{\sum }{c}_i}}$$ (Equation 2)

Here c_o is the observed number of cases in zone O, e_o is the expected number of cases in that zone, Σc_i is the total number of cases in the study area, and Σe_i is the covariate-adjusted expected number of cases in the entire study area under the null hypothesis. Since the analysis is conditioned on the total number of cases observed, Σc_i − e_o is the expected number of cases outside the window. Those zones with the largest likelihood ratios are deemed candidate clusters, and their significance is evaluated under randomization by repeatedly allocating the cases across the study areas, calculating the likelihood ratio, and by then accumulating them to generate the distribution of likelihood ratios under the null hypothesis of no clustering.

While able to construct clusters of arbitrary shape, ULS does not account for instability in the disease rates in the definition of the upper level sets. Hence areas with small population sizes are more likely to be deemed candidate clusters, and areas with elevated rates but large population sizes may be ignored. In this study we addressed this problem by constructing the Ω_ULS from the Poisson p-values for the rates, which takes into account both the rate and the size of the at-risk population. We then evaluated the approach in simulation studies as discussed later.

Flexible scan statistic (FlexScan)

Tango and Takahashi (Tango and Takahashi 2005) implemented a flexibly based scan statistic that constructs the set of candidate clusters by generating all possible permutations of contiguous areas up to a specified maximum cluster size, k. They found this method to have superior power relative to the circular scan statistic for non-circular clusters (Tango and Takahashi 2005), but it is computation intensive, and its power has yet to be compared to ULS. Kulldorff (Kulldorff 1997) originally made no assumptions regarding the shape of the scanning window, and circular and elliptical shapes have come into common use because of their ease of calculation. The fundamental difference between the circular, elliptical, ULS and FlexScan methods is in how the sets of candidate clusters are generated. The statistical mechanics of calculating a likelihood statistic and using it to identify the most likely cluster (MLC, that candidate cluster with the largest likelihood) are the same for circular, elliptical, the ULS and the FlexScan methods. This underlying statistical mechanism is common to all scan-type statistics and explains the tendency of scan tests to find clusters that are larger than warranted. Tango and Takahashi therefore suggested that a criterion in addition to the maximum likelihood ratio be used in cluster model selection, a suggestion that motivated the development of the B-statistic.

B-statistic

The B-statistic finds clusters of any shape by grouping adjacent areas that have similar (e.g. high or low) risks. While techniques for spatially agglomerative clustering have been available for some time (Legendre and Legendre 1987), they often do not assign probabilities to the resulting clusters. The B-statistic (Jacquez et al. 2008) detects clusters of arbitrary shape, and provides cluster probabilities under realistic null hypotheses. It works by evaluating boundaries between adjacent areas with different values, as well as links between adjacent areas with similar values. Clusters of high values (hotspots) are then constructed by joining adjacent areas that are significantly high (e.g., an unusually high disease rate) and connected through a “link” such that the values in the adjoining areas are not significantly different from one another. Coldspots are identified in an analogous fashion but by joining areas adjacent to significantly low locations. Significance is evaluated using distribution theory based on the product of two continuous (e.g. non-discrete) variables, or by a “distribution free” algorithm based on resampling of the observed values. The procedure for constructing clusters using the B-statistic is as follows.

1. Evaluate the borders between adjacent areas on the map to determine whether the rates in the two areas are significantly different from one another. The border between two areas whose rates are not significantly different is referred to as a “link”.

2. Identify areas that have significantly high or low cancer rates using the Poisson distribution to account for the size of the at risk population in that area. Each of these significantly high or low areas is referred to as a “seed”.

3. Consider each seed in turn, and deem an adjacent area to be part of the cluster only when it is connected to the seed through a link.

4. Continue growing the cluster by repeating Step 3 until no additional areas can be added to the cluster through adjacent links. The contiguous area formed by connecting the seed through the links is the spatial extent of the cluster.

Kernel density estimation

Kernel density estimation methods result in spatially continuous maps of the probability of a disease outcome (Rushton 1997; Rushton et al. 2004) and appear capable of circumscribing clusters of variable shape. The method computes, for a grid whose size is defined by the user, the local rate at each grid intersection, using a spatial filter whose properties (e.g. diameter) are also user-defined. These rates are then contoured using software for creating isarithmic maps. This technique results in probability maps whose topology can describe arbitrary shapes defined by exceeding a given probability threshold (e.g. 0.05).

Turnbull’s method (Turnbull et al. 1990) scans populations within the study area for clusters of cases. A circular window is centered on each region in turn and expanded to include neighboring regions until the total aggregated population within the window equals a user-defined threshold, R. These circular windows may overlap and the counts within the windows will not be independent. The test statistic, M_R, is the maximum number of cases observed among all windows of population size R, whereas the scan statistics presented earlier use a likelihood statistic. Turnbull’s method is most powerful when the population size at elevated risk is known a priori.

Besag & Newells method (Besag and Newell 1991; Newell and Besag 1996) is designed for case and population-at-risk data aggregated into regions with small population sizes. It evaluates local and global clustering using two statistics. The local statistic is the number of contiguous regions that need to be grouped to achieve a cluster of at least k cases. The global statistic is the total number of significant local clusters. The cluster size, k, is defined by the researcher. Waller and Turnbull (Waller and Turnbull 1993) demonstrated the power of this technique depends on how well k matches the actual scale of clustering.

The Local G and G* statistics (Getis and Ord 1992; Ord and Getis 1995) test for spatial clustering in case and population-at-risk data and assess the spatial association in risk within a particular distance of each observation. They may detect local clusters that exist despite negative tests for global spatial autocorrelation. In a study of colon cancer in counties of the south-eastern US (Greiling et al. 2005) the local G was found to give similar, but not identical results to the local Moran.

The local Moran test (Anselin 1995) evaluates clustering under the null hypothesis of no association between rates in adjacent areas. The rates are first standardized to a zero mean. The statistic is the product of the standardized rate for the location being considered and the average value for its adjacent neighbors. A negative value indicates negative local auto-correlation and the presence of a spatial outlier. Clusters of low or high values yield positive values of the statistic. In a study of incidence of breast cancer on Long Island (Jacquez and Greiling 2003b) the local Moran localized excess relative risk to the ZIP code level and confirmed clusters reported by the New York Department of Health using the circular scan statistic.

In our study statistical significance for these methods was evaluated through randomization Cluster analyses for the 10 methods were conducted in TerraSeer’s Space-Time Intelligence System software.

Power Analysis Methods used in CMA Step 3

A classification table (Table 2) was created for each method and for each model realization. For our analysis the marginal totals are the number of counties in hot spots = a+b=10, and number of counties at background = c+d=58. For a given method a is the number of counties that were correctly found to be part of a cluster; b is the number of counties that were incorrectly identified as background when they were actually part of a cluster (a false negative), c is the number of counties that were mistakenly identified as part of a cluster (a false positive), and d is the number of counties that were correctly identified as background (not part of a cluster). We then calculated Power = a/(a+b), the proportion of counties that were correctly identified as cluster members; proportion of false negatives = b/(a+b); proportion of false positives = c/(c+d); and specificity = d/(c+d), the proportion of counties that were correctly identified as background. Finally, we calculated detection accuracy = a/(a+c), the proportion of counties found to be cluster members that were within true clusters (declared clusters as a proportion of true clusters). For methods that require additional parameters (e.g. k, number of cases in the cluster for Besag & Newell) we undertook several runs using a range of parameter values to explore parameter sensitivity.

Results

We first present the CMA results for the simulation study, followed by our findings from the analysis of pancreatic cancer in white males in Michigan.

Cluster Morphology Analysis – Results for Simulated Clusters

The results of the power comparison are summarized in Table 3. To conduct CMA we ranked the results by statistical power, followed by the proportion of false positives, under the rationale that the objective of cluster-based cancer surveillance should be to (1) find the true clusters while (2) avoiding false clusters. The B-statistic, flexible scan, circular scan, kernel-based density estimation, Turnbull and ULS scan correctly identified all members of the North and South clusters. This occurred at the cost of false positives, with the B-statistic having the fewest false positives, followed by the FlexScan with cluster size set to five counties (k=5), the circular scan, FlexScan at k=7 and kernel with a radius of 10 kilometers. For FlexScan the parameter k is the maximum number of counties to include in the cluster, and this method does best when k matches the actual (but usually unobservable) cluster size. Cluster Morphology Analysis had power=1.0 with a proportion of false positives of 0.0172, substantially better than any one method in Table 3 (Figure 3, top panel). This result applies sensu strictu to (i) white male pancreatic cancer in Michigan, which is exactly what we want, since we are interested in that geography and cancer; and (ii) for the cluster sizes and relative risks modeled in the simulation, which unlike (i) are unobservable. In practice analysts will analyze sensitivity to cluster specification, an exercise readily accomplished in the Cluster Morphology Analysis software tools that are being developed at BioMedware with funding from the National Cancer Institute.

Table 3.

Results of power comparison. Results are sorted first by power, then by false positives.

Test	Parameter	Power	False negative	False positive	Specificity	Accuracy
B		1.000	0.000	0.069	0.931	0.714
FlexScan	k=3	1.000	0.000	0.086	0.914	0.667
FlexScan	k=5	1.000	0.000	0.086	0.914	0.667
Circular Scan		1.000	0.000	0.103	0.897	0.625
FlexScan	k=7	1.000	0.000	0.138	0.862	0.556
Kernel	r=10	1.000	0.000	0.138	0.862	0.556
FlexScan	k=9	1.000	0.000	0.224	0.776	0.435
Turnbull	R=2,000,000	1.000	0.000	0.276	0.724	0.385
ULS Scan RR		1.000	0.000	0.276	0.724	0.385
ULS Scan 1-p(RR)		1.000	0.000	0.310	0.690	0.357
Kernel	r=15	0.900	0.100	0.017	0.983	0.900
FlexScan	k=2	0.900	0.100	0.017	0.983	0.900
Besag & Newell	k=210 (N. cluster size)	0.700	0.300	0.052	0.948	0.700
Kernel	r=25k	0.500	0.500	0.000	1.000	1.000
Turnbull	R=400,000	0.500	0.500	0.034	0.966	0.714
Turnbull	R=800,000	0.500	0.500	0.103	0.897	0.455
Local Moran		0.400	0.600	0.000	1.000	1.000
Kernel	r=50	0.400	0.600	0.000	1.000	1.000
Kernel	r=20k	0.400	0.600	0.000	1.000	1.000
Turnbull	R=250,000	0.400	0.600	0.017	0.983	0.800
G*		0.400	0.600	0.069	0.931	0.500
G		0.400	0.600	0.069	0.931	0.500
Besag & Newell	k=1034 (S. Cluster size)	0.200	0.800	0.138	0.862	0.200

Figure 3.

Cluster Morphology Analysis (CMA) of pancreatic cancer mortality in white males, 1970–1994, for simulated clusters (above) and observed data (below). Intersection of the cluster members for the statistically most powerful methods results in a CMA. CMA of the simulated data (above, lower right map) found all 10 clustered counties (gold borders) with 1 false positive (blue border). CMA of observed mortality data found two clusters, one in the north and one in the southeast (below). The southeast cluster in Macomb and Wayne County has been validated using SEER data (see text). Different clustering methods are sensitive to different aspects of clustering, a characteristic exploited by the new approach. Screen capture from the TerraSeer STIS software.

Cluster Morphology Analysis – Results for Observed Mortality Data

Is there evidence of clusters of pancreatic cancers in white males in Michigan, and do they change through time? Findings of persistent clusters may indicate the action of a risk factor or covariate that is geographically localized and elevated through time. To address these questions we applied CMA to observed pancreatic cancer mortality data in white males for two time periods: 1950–70 and 1970–95. The ability to rapidly explore cluster change through time is available in the STIS software using the animation toolbar (Figure 3, center of bottom panel). For 1970–95 (Figure 3, bottom panel) we found two significant clusters under CMA, one in the north and one in the southeast including portions of the Detroit metropolitan area. The northern cluster is ephemeral and was not present in 1950–70. The southeast cluster consisted only of Wayne County in 1950–70 and expanded to include Macomb County in 1970–95.

Is the finding of a persistent cluster of pancreatic cancer in the Detroit metropolitan area independently confirmed by more recent incidence data of higher temporal resolution? To address this question we used incidence and mortality data from NCI’s Surveillance Epidemiology and End Results program, SEER (Ries et al. 2007). SEER provides cancer registry data for 17 areas across the United States, including Atlanta, rural Georgia, California (Bay Area, San Francisco-Oakland, San Jose-Monterey, Los Angeles and Greater California), Connecticut, Hawaii, Iowa, Kentucky, Louisiana, New Jersey, New Mexico, Seattle-Puget Sound, Utah and Detroit. For 2000–2004 of the 17 SEER areas Detroit had the highest age-adjusted incidence rate for white males at 15.0 cases per 100,000, and the second highest mortality rate at 12.9 deaths per 100,000. These compare to SEER-wide averages for white males in this period of 12.8 incident cases and 12.0 deaths per 100,000. Further, for the Detroit registry pancreatic cancer mortality for white males in this period increased 0.9% per year (Calculated by SEER*Stat from the National Vital Statistics System public use data file). The population covered by the Detroit registry in this period was 1,365,315 white males, indicating a substantial and increasing burden of pancreatic cancer in this population. The clusters found by CMA thus were independently confirmed by data from SEER and found to persist from 1950 through 2004.

Discussion

To date, one of the major deficiencies of geographic studies of disease is that they typically rely on only one clustering technique whose statistical power and type 1 error are unknown for the health outcome, at-risk population and geography being studied. This is a severe methodological shortcoming that is akin to undertaking a case-control study in the absence of a statistical power analysis of the study design. Within the context of cancer control and surveillance, the substantial benefit of the CMA approach is that it will allow cancer control professionals to detect clusters of arbitrary shape through time using a meta-analytic approach that synthesizes the results of those clustering methods found to be most powerful for a given cancer geography.

Should CMA be corrected for multiple comparisons? Adjustments for multiple comparisons are employed when a statistical procedure (e.g. clustering test) is applied to a host of different datasets (e.g. disease data from different areas, or different diseases in the same area), or when different tests are applied to the same dataset. Multiple tests are then thought of as replicates of the same or similar experiments. Given a type 1 error rate for the test of α and m datasets or tests,, one might then expect to find false positive results arising α * m times. One then would use a multiple testing procedure (e.g. Simes, Holmes, others) to obtain an adjusted type-1 error. CMA employs simulations to compare and contrast different clustering methods, hence the statistical power, type-1 error, and type-2 error are based on simulation results where the true clusters are known a priori. Correction for multiple comparisons is not needed since the true type 1 error is known from simulation.

How many cluster tests should be used in CMA? Should only a few methods be used that happen to give quite different results, the intersection rule in CMA (equation 1) at first blush appears might have low power to detect true clusters. Recall however the first step in the CMA is to undertake simulation studies to quantify the abilities of the statistical methods to detect true clustering. Methods that have low power are then excluded from the CMA when the methods are ranked after the power analysis (e.g. Table 3). In our studies at least some of the methods we’ve included in the CMA have had power=1.0. Provided power is 1.0 for all of the methods in the CMA then the intersection approach in Equation 1 will yield a CMA with power=1.0. This results in a proposed “rule-of-thumb”: Always include a sufficient number of methods/parameter sets to yield at least 5 methods that in the simulations have power=1.0. At the time of this writing we are still exploring the statistical behavior of the CMA approach, and have not further validated this recommendation.

The methods and examples presented here are for area-based data such as incidence and mortality rates. The CMA approach is directly extensible to case-control data and is a future research direction.

We currently are developing a CMA software tool that will allow cancer epidemiologists to readily construct cluster models premised on their specific cancer geography and incorporating cluster count, size, shape and relative risk as specified by the researcher; and to then automatically evaluate the statistical power of a suite of clustering methods to detect such clusters. While we have focused this software tool on the identification of cancer clusters through CMA, the software will be highly flexible and will have, through its visualization and analysis capabilities, clear applications in (a) monitoring and surveillance of cancer incidence and mortality, (b) the generation of hypotheses for in depth individual studies of risk factors that are causal, or impact survival or morbidity; and (c) establishing the rationale for targeted cancer control interventions for localized excesses in risk whose shape, extent and size will have been established and documented with an unprecedented level of statistical power and accuracy.