Abstract
Complex interactions between carbohydrate, fat, and protein metabolism underlie the body's remarkable ability to adapt to a variety of diets. But any imbalances between the intake and utilization rates of these macronutrients will result in changes in body weight and composition. Here, I present the first computational model that simulates how diet perturbations result in adaptations of fuel selection and energy expenditure that predict body weight and composition changes in both obese and nonobese men and women. No model parameters were adjusted to fit these data other than the initial conditions for each subject group (e.g., initial body weight and body fat mass). The model provides the first realistic simulations of how diet perturbations result in adaptations of whole body energy expenditure, fuel selection, and various metabolic fluxes that ultimately give rise to body weight change. The validated model was used to estimate free-living energy intake during a long-term weight loss intervention, a variable that has never previously been measured accurately.
Keywords: mathematical model, energy metabolism, macronutrient metabolism, body composition
over the past century, researchers in the fields of human metabolism and nutrition have accumulated an impressive body of quantitative knowledge regarding how dietary changes impact various aspects of metabolism, body weight, and body composition (12, 24, 38, 56, 68). But integrating this knowledge to make quantitative predictions is a formidable task given the multiple nonlinear interactions between various organ systems. Nevertheless, such an integrative approach is required to fully understand both normal physiology as well as the derangements that underlie conditions such as obesity, diabetes, and the metabolic syndrome.
Mathematical modeling and computer simulation are widely used methodologies in the engineering and physical sciences for integrating knowledge about complex systems and predicting their behavior. This approach is beginning to gain traction in the life sciences and forms a critical part of the systems biology paradigm (20, 73). In the area of human energy metabolism and body weight regulation, several mathematical models of weight change have been proposed over the past few decades (3–5, 7, 16–18, 33, 42, 44, 59, 60, 96, 110, 113). Previously, I presented the first mathematical model of the metabolism of all three macronutrients (i.e., carbohydrate, fat, and protein), and I used the model to help understand the dynamics of semistarvation and refeeding in healthy young men (42). Here, I extended my previous model to apply to both obese and nonobese men and women and validated its behavior in response to several controlled diet perturbations. The model was designed to quantitatively track the metabolism of all three dietary macronutrients and their interactions within the human body. In particular, the model describes how diet perturbations result in adaptations of energy expenditure, fuel selection, and various metabolic fluxes (e.g., lipolysis, lipogenesis, gluconeogenesis, ketogenesis, protein turnover, etc.) that ultimately give rise to changes of body weight and composition on a time scale of days and longer. The main model assumptions were that energy must be conserved and that changes of the body composition result from imbalances between the intake and utilization rates of fat, carbohydrate, and protein along with intracellular and extracellular fluid changes. The model code can be downloaded as a data supplement or at my website (http://www2.niddk.nih.gov/NIDDKLabs/LBM/LBMHall.htm; Supplemental Material for this article is available at the AJP-Endocrinology and Metabolism website).
The model was developed using published human data from more than 50 experimental studies (see appendix) and was validated by comparing model predictions with the results from several controlled feeding studies not used for model development. In this validation process, I chose to simulate human studies that carefully controlled food intake and measured changes in body weight (BW) and body fat mass (FM) as well as total energy expenditure (TEE) and resting metabolic rate (RMR). Requiring this combination of measurements dramatically narrowed the scope of possible validation studies and allowed for assessment of not only the weight change predictions but also energy partitioning and energy expenditure changes. In all cases, the measured food intake was used as a model input and included a wide range of interventions, such as overfeeding and weight gain, weight loss using a variety of diets, and adaptations of metabolic fuel selection when the dietary macronutrient proportions were altered. These validation studies were performed in several different subject groups, including lean, overweight, and obese men and women. Importantly, no model parameters were altered to fit the data other than modifying the initial conditions appropriate for modeling each subject group (e.g., initial BW and body FM).
Once the model was validated in situations where the food intake was known, I proposed that the model could be used to estimate the free-living energy intake changes underlying observed changes of body weight. In particular, I used the model to predict the energy intake required to result in the typical trajectory of weight loss and regain observed during an outpatient weight loss intervention (100). In addition to providing a novel methodology for estimating the dynamics of free-living human energy intake during weight loss and regain, the model simulations addressed the relative role of diet adherence vs. metabolic adaptation in explaining the typically observed weight loss plateau after ∼6 mo of lifestyle modification.
METHODS
The appendix provides a detailed description of the mathematical model along with the data and assumptions used in its development and calibration. Briefly, the model comprises eight ordinary differential equations and uses dietary carbohydrate, fat, and protein as model inputs. The model computes the various components of whole body energy expenditure, rates of macronutrient oxidation, respiratory exchange, lipogenesis, ketogenesis, gluconeogenesis, and turnover of fat, glycogen, and protein. Based on the computed macronutrient imbalances, along with sodium imbalances impacting extracellular fluid, the model computes dynamic changes of BW and composition.
To represent different initial conditions corresponding to different subject groups, parameter values were specified for initial BW, percent body fat, total body water, RMR, and baseline food intake. In cases where one or more of these initial parameters was unknown, the model used more common measurements of age, height, sex, and physical activity level to estimate the initial parameter values using published regression equations for body fat (50), RMR (72), and extracellular fluid (94). I also allowed for the possibility that the baseline diet may not result in a state of macronutrient balance. Rather, the parameters Fimbal, Gimbal, and Pimbal specified the initial imbalances of fat, glycogen, and protein, respectively. Other than these initial parameter values, no other model parameters were adjusted to simulate the validation experiments.
To estimate the energy intake rate underlying the weight change data of Svetkey et al. (100), I specified that the onset of the diet resulted in an immediate reduction of energy intake for a constant period followed by a linear change of energy intake until another constant period. The magnitude of the energy intake changes, along with the duration of each period, was determined using a downhill simplex algorithm (78) implemented in the Berkeley Madonna software (version 8.3; http://www.berkeleymadonna.com) to minimize the sum of squares of weighted residuals between the simulation outputs and the BW change data.
RESULTS
Metabolic Fuel Selection
When the body is in a state of energy and macronutrient balance, the intake of dietary carbohydrate, fat, and protein is matched by their rates of utilization. A useful measurement of the relative proportion of carbohydrate to fat being oxidized is provided by the RQ, where a value of 1 reflects complete reliance on carbohydrate oxidation for metabolic needs, whereas RQ = 0.7 indicates state of pure fat oxidation and intermediate values reflect a fuel selection mixture (27, 31, 37). Macronutrient balance is achieved when the RQ is equal to the food quotient (FQ), which represents the relative proportion of macronutrients in the diet. Exchanging dietary carbohydrate with fat while maintaining the same energy intake will result in a state of macronutrient imbalance until fuel selection adapts to the new FQ. Figure 1A depicts the model's predicted change of 24-h RQ in response to a high-fat isocaloric diet that resulted in a large decline of FQ. This diet perturbation was performed by Schrauwen et al. (90), and the closed squares in Fig. 1A show the measured RQ dynamics, which closely matched the model predictions. Figure 1B shows the results from a similar study performed by Smith et al. (95), with a less dramatic change of FQ. Again, the model predictions agreed with the data. Underlying these simulations were slow decreases of glycogen as well as increased lipolysis due to the reduced dietary carbohydrate (data not shown). These changes resulted in altered substrate delivery to metabolically active tissues and subsequent changes of fuel selection.
Fig. 1.
Adaptations of fuel selection following isocaloric exchange of dietary carbohydrate and fat. A: 24-h respiratory quotient (RQ) in response to switching from a 30 to a 60% fat diet. The simulated changes of RQ (dashed curve) along with the measured values (■) show a progressive approach to the food quotient (FQ; solid curve). B: simulated (dashed curve) and measured (■) 24-h RQ changes in response to a diet switch from 37 to 50% fat corresponding to the depicted changes of FQ (solid curve). Data are presented as means ± SD.
During overfeeding, the model predicts substantial changes of various whole body metabolic fluxes, including suppression of lipolysis and induction of de novo lipogenesis, that influence overall fuel selection and macronutrient balance. The imbalance between dietary macronutrients and their utilization rates determined how the energy excess was partitioned in the model. To test whether macronutrient oxidation changes were simulated correctly during overfeeding, I used the data of Jebb and colleagues (51, 52), who measured macronutrient oxidation rates during 12 days of 33% overfeeding in healthy young men that were continuously housed inside a metabolic chamber. Figure 2A, left, shows the model predictions along with the data for BW and body FM, whereas Fig. 2A, right, depicts the simulated daily macronutrient oxidation rates along with the data. The simulated gradual increase of carbohydrate oxidation reached a plateau after several days as glycogen approached a new steady state (data not shown). These results closely matched the measured carbohydrate oxidation rate shown in the closed squares in Fig. 2A, right. The simulated fat oxidation rate was suppressed at the onset of overfeeding, which matched the measurements shown in the open squares in Fig. 2A, right. The decrease of fat oxidation in the simulation corresponded to a suppression of lipolysis as a result of the increased carbohydrate intake (data not shown). The simulated protein oxidation rate remained relatively unchanged and corresponded to the measured rate shown in the open triangles in Fig. 2A, right.
Fig. 2.
Metabolic fuel selection and body composition and changes during over- and underfeeding in healthy young men. A, left: 33% overfeeding resulted in the change of simulated and measured body weight (BW; solid curve and ■, respectively) along with increased simulated and measured fat mass (FM; dashed curve and □, respectively). A, right: simulated and measured carbohydrate oxidation rates (dashed curve and ■, respectively) as well as fat oxidation (solid curve and □, respectively) and protein oxidation rates (dotted curve and ▵, respectively). B: BW, FM, and macronutrient oxidation rates in response to 67% underfeeding, where the symbols are identical to A. Data are presented as means ± SD.
Jebb and colleagues (51, 52) also performed a complementary study where energy intake was decreased by 67% for 12 days, and these results are depicted in Fig. 2B along with the corresponding model simulations. Again, the simulated changes of body composition and macronutrient oxidation rates closely matched the data and showed the opposite response to overfeeding, whereas underfeeding suppressed carbohydrate oxidation while enhancing fat oxidation.
Underfeeding and Weight Loss
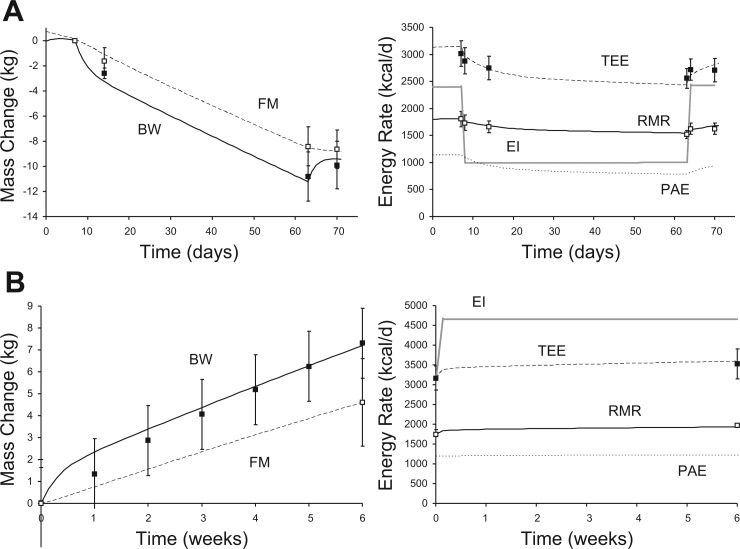
Although these results demonstrate that the model correctly simulated adaptations to short-term underfeeding in lean young men, longer-term underfeeding is required to achieve significant weight loss in overweight people. A recent 6-mo calorie restriction study investigated the metabolic effects and weight changes in healthy, sedentary, overweight men and women resulting from three strictly controlled lifestyle interventions (45, 81, 82). Figure 3A shows the effect of an 890 kcal/day very low-calorie diet followed by a maintenance diet from 3 to 6 mo. The imposed energy intake resulted in the drop of BW and FM shown in Fig. 3A, left. The simulated TEE and RMR also matched the data, which are depicted by closed and open squares, respectively, in Fig. 3A, right. Figure 3B shows the model simulations and data for a 25% reduction of calories for 6 mo, and Fig. 3C shows the results for a 12.5% caloric reduction plus a 12.5% increase of physical activity expenditure (PAE). Again, the model simulations matched the body composition and energy expenditure data remarkably well, although the initial simulated decrease in BW was slightly more rapid than the data.
Fig. 3.
Weight loss and metabolic effects of caloric restriction for 6 mo. A, left: simulated BW change (solid curve) along with the measured values (■) and the simulated FM (dashed curve) and the measured FM (□) changes resulting from a very low-calorie liquid diet followed by a weight maintenance diet. A, right: simulated (dashed curve) and measured (■) total energy expenditure (TEE) in response to the depicted changes of energy intake (EI; solid gray curve). Simulated (solid black curve) and measured resting metabolic rate (RMR; □) along with the simulated physical activity expenditure (PAE; dotted curve). B: a sustained 25% reduction of EI resulted in the simulated and measured changes of BW and FM shown at left and the corresponding TEE, RMR, and PAE changes at right. C: a sustained 12.5% reduction of EI along with a 12.5% increase of PAE resulted in the simulated and measured changes of BW and FM shown at left and the corresponding TEE and RMR changes at right. Data are presented as means ± SD.
There has been much debate surrounding the metabolic effects of weight loss diets that differ in macronutrient content. Rumpler et al. (88) investigated this issue in obese men by restricting energy intake by 50% for 4 wk using diets with either 40 or 20% of energy from dietary fat. Figure 4A, left, shows the model simulation and experimental results for the 40% fat diet, and Fig. 4B, right, shows the results for the 20% fat diet. Figure 4, A and B, top, demonstrates that the simulated body composition changes corresponded reasonably well with the data, as did the TEE and RMR changes shown in Fig. 4, A and B, middle. Figure 4, A and B, bottom, illustrates the very close agreement between the simulated and measured 24-h RQ values, demonstrating that the model appropriately represents fuel selection during weight loss diets with differing macronutrient composition in obese men.
Fig. 4.
Weight loss and metabolic changes in obese men resulting from diets with differing proportions of carbohydrate and fat. A, top: simulated and measured changes of BW and FM resulting from the 40% fat, 46% carbohydrate diet. A, middle: metabolic responses to this diet, where the symbols are identical to those in Fig. 3. A, bottom: simulated and measured changes of RQ, where the symbols are identical to Fig. 1. B, top: simulated and measured changes of BW and FM resulting from the 20% fat, 66% carbohydrate diet. B, middle: metabolic responses to this diet. B, bottom: simulated and measured changes of RQ. Data are presented as means ± SD.
The model also accurately simulated weight loss and metabolic changes in obese women consuming 1,000 kcal/day for an 8-wk period, as studied by de Boer et al. (19). Figure 5A, left, demonstrates close agreement between the simulated and measured body composition changes, whereas Fig. 5A, right, shows that the simulated TEE and RMR changes also matched the data quite well.
Fig. 5.
Weight loss and weight gain. A, left: simulated and measured changes of BW and FM resulting from a 1,000 kcal/day diet for 8 wk in obese women. A, right: simulated and measured changes of TEE, RMR, and PAE in response to imposed changes of EI, where the symbols are identical to those in Fig. 2. B, left: simulated and measured changes of BW and FM in response to 6 wk of overfeeding by 1,000 kcal/day in healthy young men. B, right: changes of TEE, RMR, and PAE, where the symbols are identical to those in Fig. 3. Data are presented as means ± SD.
Overfeeding and Weight Gain
Weight gain is the result of positive energy balance, but predicting the magnitude of weight gain for a given change of energy intake requires knowing how excess energy is partitioned between deposition of body fat and fat-free mass, which have dramatically different influences on energy expenditure and the subsequent magnitude of energy imbalance. I tested the model predictions for weight gain by simulating the 6-wk, 50% overfeeding study of Diaz et al. (21), who measured body composition changes as well as TEE and resting metabolic rate. Figure 5B, left, depicts the simulated changes of BW and FM, which clearly matched the body composition data, indicating appropriate energy partitioning and weight gain. Figure 5B, right, shows that the imposed energy intake resulted in simulated TEE and RMR changes.
I also simulated the overfeeding study of Tremblay et al. (103), who provided healthy young men with 1,000 kcal/day above baseline energy requirements 6 days/wk for 100 days. Prior to the overfeeding period, the average subject had BW = 60.3 ± 8.0 kg, FM = 6.9 ± 3.5 kg, and RMR = 1,635 ± 170 kcal/day. After 100 days of overfeeding, BW = 68.4 ± 8.2 kg, FM = 12.3 ± 4.5 kg, and RMR = 1,793 ± 190 kcal/day, which matched the following simulation results quite well: BW = 69.7 kg, FM = 12.3 kg, and RMR = 1,850 kcal/day.
Estimating the Free-Living Energy Intake Underlying Weight Loss and Regain
Maintenance of a reduced BW following weight loss is a critical issue in the treatment of obesity (44, 46, 115, 116). Most weight loss interventions result in a maximum amount of lost weight after ∼6 mo, with a gradual weight regain over the subsequent several years. But what is the mechanism of the weight loss plateau and subsequent regain? In particular, what role does metabolic adaptation play in resisting further weight loss after 6 mo?
Given that the mathematical model accurately simulates the metabolic and body composition changes in response to known changes of diet, I investigated what change of diet would be required to simulate the average weight loss and regain pattern in a group of 341 overweight and obese adults participating in a self-directed weight loss program (100). Figure 6A, left, shows the simulated weight loss and regain pattern (solid curve) which closely matched the data (closed squares), whereas the dashed curve is the predicted FM change. The solid gray curve in Fig. 6A, right, is the predicted free-living energy intake underlying the observed weight loss and regain trajectory, assuming no change of physical activity. At the onset of the intervention, the model predicted a decrease of energy intake by ∼800 kcal/day, which was maintained for only 6 wk. Subsequently, energy intake gradually increased until ∼10 mo, when it returned to the initial energy intake that resulted in energy balance at the initial BW. The simulated TEE is depicted by the dashed curve in Fig. 6A, right, and shows that negative energy balance was achieved only for ∼8 mo, after which time positive energy balance and weight regain ensued.
Fig. 6.
Weight loss and regain dynamics during an outpatient lifestyle intervention. A, left: a typical outpatient weight loss program results in the characteristic BW change trajectory, where the symbols are identical to those in Fig. 3. A, right: predicted free-living EI and TEE underlying the observed BW loss and regain trajectory. B: the model predicted that maintenance of lost BW and FM (left) would have been achieved if the EI over the last 2 yr had been decreased by 170 kcal/day. C: had the initial reduction of EI been sustained for the 3-yr period, the model predicted a progressive decrease of BW and FM shown at left and the corresponding TEE changes shown at right. Data are presented as means ± SD.
Figure 6B shows the simulated changes of energy intake required to maintain the weight loss achieved at 6 mo, which was ∼170 kcal/day less than the initial energy-balanced diet. Figure 6C shows the BW and FM changes that were predicted had the initial decrease of energy intake been maintained over the entire 3-yr period. This simulation illustrates the very long equilibration time for weight loss in obese subjects and demonstrates that the weight loss plateau observed after 6 mo cannot be a result of metabolic adaptation.
DISCUSSION
The ultimate goal of modeling is to provide physiological insights and to help design novel experiments whose results can then be integrated within the context of previous knowledge, thereby improving both the model as well as our understanding of the system. Most systems biology models of metabolism have been developed at the cellular level and are aimed at calculating steady-state flux distributions through complex metabolic networks in microorganisms (29, 30). Such models are now beginning to be applied to human metabolism (25, 92), and the model presented here represents a complementary dynamic approach to systems physiology at the level of whole body human metabolism. Other than modifying the initial model parameters to represent the various subject groups, no parameters were adjusted to simulate the validation experiments. Rather, once the initial conditions were specified, the model calculated the correct energy partitioning and metabolic adaptations required to simulate the physiological responses in lean, overweight, and obese men and women.
The model appears to accurately describe the physiology of metabolism, fuel selection, and body composition change in humans on time scales ranging from days to years. One practical use of the model would be to computationally investigate the potential of various metabolic interventions for treatment of obesity. Such a tool could help design key experiments, focus resources on areas of likely success, and help interpret experimental results. Of course, since the model presently uses food intake as an input, any adaptive changes of food intake as a result of a metabolic intervention would not be automatically accounted for, but hypotheses regarding food intake changes could be simulated.
Since the model responded accurately to known changes of food intake, I proposed that known changes of body weight and composition over long time periods could be used to estimate the underlying changes of free-living energy intake. This is an important application of the model, since free-living energy intake is notoriously difficult to measure (117) and the gold standard doubly labeled water method is valid only in situations of energy balance, when the RQ is known (102). I used the model to estimate the free-living energy intake changes underlying the typical weight loss and regain trajectory observed in an outpatient weight loss program. Surprisingly, the model predicted that the initial reduction of energy intake was maintained for only 6 wk, followed by a gradual return to baseline after 10 mo, where it remained for more than 2 years. This highlights the importance of diet adherence for successful weight loss and raises the question of why the estimated energy intake has this pattern. In other words, what internal and external factors contribute to this progressive loss of diet adherence? Although the model presented here cannot answer these questions, the ability to quantitatively predict the dynamics of free-living energy intake during weight loss and regain may have implications for the development of drug and behavioral therapies for obesity.
An important caveat regarding the model estimate of energy intake is that I assumed that the average physical activity for the group was unchanged over the course of the weight loss and regain trajectory. This does not mean that the energy cost of physical activity was unchanged, since performing the same physical activity at a different body weight has a differing energy requirement, as was demonstrated by the PAE curves in the validation simulations in Figs. 3–5. Of course, the model can be simulated for any assumed physical activity time course, and the energy intake can be recalculated, thereby providing a range of estimates for varying assumptions about physical activity. Future work will investigate the sensitivity of the energy intake estimates to various model parameters as well as the time course of body weight change.
Much work remains for improving and expanding the model. For example, although I have demonstrated that the model behaves appropriately for different groups of subjects, it is presently unclear whether individual subject responses can be predicted given sufficiently detailed information about their initial conditions. Furthermore, the model now implicitly represents the effect of hormones such as insulin, but an explicit representation of endocrine signaling along with concentrations of hormones and metabolites would be desirable, especially on shorter time scales, so that the response to individual meals could be simulated. Other additions to the model might include an explicit representation of the possible contribution of human brown adipose tissue to the overall energy expenditure and its role in adaptive thermogenesis (80). Finally, it would be particularly interesting to “close the loop” and model how internal signals from changes of metabolism and body composition combine with external factors to determine food intake. But despite the cornucopia of possible model improvements, the mathematical model presented here represents a significant step forward in a systems physiology approach to whole body human metabolism.
GRANTS
This research was supported by the Intramural Research Program of the National Institutes of Health/National Institute of Diabetes and Digestive and Kidney Diseases.
DISCLOSURES
No conflicts of interest are declared by the author.
Supplementary Material
ACKNOWLEDGMENTS
I thank Dympna Gallagher, Susan Jebb, Peter Murgatroyd, Eric Ravussin, Bill Rumpler, and Steve Smith for insightful discussions and access to their data.
APPENDIX
Detailed Description of the Mathematical Model
The individual components of the mathematical model were based on a variety of published in vivo human data, as described below. Each model component was relatively simple, and only the most important physiological effectors have been incorporated. Since continued development of the model is part of an ongoing research program, additional relevant physiological data will be incorporated within the existing computational framework to improve the realism and predictive capabilities of the model. The model code can be downloaded as a data supplement or at my website (http://www2.niddk.nih.gov/NIDDKLabs/LBM/LBMHall.htm).
The concept of macronutrient balance is an expression of energy conservation such that changes in the body's energy stores were given by the sum of fluxes entering the pools minus the fluxes exiting the pools. Thus, the mathematical representation of macronutrient balance was given by the following differential equations:
| (1) |
where ρC = 4.18 kcal/g, ρF = 9.44 kcal/g, and ρP = 4.7 kcal/g were the energy densities of carbohydrate, fat, and protein, respectively (67). MTG = 860 g/mol and MFFA = 273 g/mol were the molecular masses of triacylglycerides and free fatty acids, respectively. The efficiency of de novo lipogenesis, DNL, was represented as the dimensionless parameter εd = 0.835, which is the enthalpy of combustion of 0.37 g of fat divided by the enthalpy of combustion of the 1 g of glucose used to produce the fat (27). The efficiency of ketogenesis, KTG, was represented by the parameter εk = 0.81, calculated as the enthalpy of combustion of 4.5 mol of acetoacetate divided by the enthalpy of combustion of 1 mol of stearic acid used to produce the ketones (12). When the ketogenic rate increases, ketones are excreted in the urine at the rate KUexcr. The macronutrient intake rates CI and FI refer to the digestible energy intake of carbohydrate and fat, respectively, whereas PI refers to the digestible energy intake of protein corrected for the obligatory formation of ammonia with protein metabolism. The energy cost of ureagenesis is accounted for separately, as described below. The oxidation rates CarbOx, FatOx, and ProtOx are summed to the TEE, less the small amount of heat produced via flux through ketogenic and lipogenic pathways. Since body composition changes take place on the time scale of weeks, months, and years, the model was targeted to represent daily changes of energy metabolism and not fluctuations of metabolism that occur within 1 day. The nutrient balance equations were integrated using the fourth-order Runge-Kutta algorithm with a time step size of 0.1 days (78).
Body Composition
The BW was the sum of the FFM and the FM. FFM was computed using the following equation:
| (2) |
where the FFM is composed of BM, ECF, ECP, and LCM. LCM is composed of ICW, G, and P as well as a small contribution from nucleic acids and other ICS. The protein fraction of the lean tissue cell mass was P/LCM = 0.25, and the initial intracellular water fraction was ICW/LCM = 0.7 (13, 109). ICW was then calculated dynamically from P and G such that each gram of protein and glycogen was associated with hP and hG grams of water, respectively. IĈW was a constant amount of ICW computed to attain the appropriate initial intracellular composition, assuming that G = 500 g, hG = 2.7, and hP = 1.6 (13, 43, 71).
The initial ECF was calculated via the regression equations of Silva et al. (94), and changes of ECF were calculated as follows:
| (3) |
where [Na] = 3.22 mg/ml is the extracellular sodium concentration, ΔNadiet is the change of dietary sodium in milligrams, and ΔECF is the slow rate of increment in ECF that occurs with BW change on a very long time scale of τBW, ∼1,000 days. The value of ξBW = 0.16 ml·kg−1·day−1 was chosen so that the steady-state increment of ECF with weight change approximately matched the regression equations of Silva et al. (94). The value of ξNa was chosen according to the data of Andersen et al. (6), who measured a change of sodium excretion of 5,000 mg/day following an infusion of 1.7 liters of isotonic saline. Therefore, I assumed that a 5,000 mg/day change in sodium intake would be balanced by a 1.7-liter change of ECF giving ξNa = 3 mg·ml−1·day−1. Given that the normal sodium content of the diet is ∼4,000 mg/day and that a low-sodium diet must effectively shut off sodium excretion, I assumed that ξCI = 4,000 mg/day so that removing dietary carbohydrate doubles the sodium excretion rate compared with a very-low-sodium diet, as observed by Stinebaugh and Schloeder (98).
I assumed that BM was 4% of the initial BW, and the ECP was assumed to be a constant determined by the initial BM and ECF values, as determined by the regression equations of Wang et al. (108).
Whole Body Total Energy Expenditure
TEE was modeled by the following equation:
| (4) |
where TEF was the thermic effect of feeding, PAE was the energy expended for physical activity and exercise, and RMR was the remainder of the whole body energy expenditure, defined as the resting metabolic rate. Explicit equations for each component of energy expenditure follow.
Thermic Effect of Feeding
Feeding induces a rise of metabolic rate associated with the digestion, absorption, and short-term storage of macronutrients and was modeled by the following equation:
| (5) |
where αF = 0.025, αP = 0.25, and αC = 0.075 defined the short-term thermic effect of fat, protein, and carbohydrate feeding (12).
Adaptive Thermogenesis
Energy imbalance causes an adaptation of metabolic rate that opposes weight change (22, 23, 62). Whether or not the adaptation of energy expenditure is greater than expected based on body composition changes alone has been a matter of some debate (35, 70, 111). The so-called adaptive thermogenesis is believed to affect both resting and nonresting energy expenditure and has maximum amplitude during the dynamic phase of weight change. Adaptive thermogenesis also persists during weight maintenance at an altered body weight (85). The non-RMR component of adaptive thermogenesis may reflect either altered efficiency or amount of muscular work (63–65, 87).
The onset of adaptive thermogenesis is rapid and may correspond to altered levels of circulating thyroid hormones or catecholamines (86, 111). I defined a dimensionless adaptive thermogenesis parameter, T, which was generated by a first-order process in proportion to the departure from the baseline energy intake EIb = CIb + FIb + PIb:
| (6) |
where ΔEI was the change from the baseline energy intake, τT = 7 days was the estimated time constant for the onset of adaptive thermogenesis, and the parameters λ1 and λ2 quantified the effect of underfeeding and overfeeding, respectively, and were determined from the best fit to the Minnesota experiment data. The adaptive thermogenesis parameter T acted on both the RMR and PAE components of energy expenditure, as defined below. This simple model assumed that adaptive thermogenesis reacted to perturbations of EI and persisted as long as EI was different from baseline. Importantly, the model allowed for the possibility that no adaptive thermogenic mechanism was required to fit the data from the Minnesota experiment. The amount that the best fit values for the λ1 and λ2 parameters differ from zero provides an indication of the extent of adaptive thermogenesis that occurred during the underfeeding and overfeeding phases, respectively, of the Minnesota experiment.
Physical Activity Energy Expenditure
The energy expended for typical physical activities is proportional to the body weight of the individual (12, 105). Low-intensity physical activities may be subject to the effects of adaptive thermogenesis, whereas higher-intensity exercise appears to not be affected (87). Therefore, the following equation was used for the physical activity expenditure:
| (7) |
where δ was the nonexercise physical activity coefficient (in kcal·kg−1·day−1), υ was the exercise coefficient (in kcal·kg−1·day−1), and BW = FFM + FM was the body weight. The proportion of T that was allocated to the modification of nonexercise PAE was determined by the parameter σ. The adaptation of PAE with T did not distinguish between altered efficiency vs. amount of muscular work.
Resting Metabolic Rate
RMR includes the energy required to maintain irreversible metabolic fluxes such as de novo lipogenesis, gluconeogenesis, and ketogenesis as well as the turnover costs for protein, fat, and glycogen. The following equation included these components:
| (8) |
where εg = 0.8 was the efficiency of gluconeogenesis (12) and the constant, Ec, was a parameter chosen to ensure that the model achieved energy balance during the balanced baseline diet (see Nutrient Balance Parameter Constraints below).
The specific metabolic rate of adipose tissue was γF = 4.5 kcal·kg−1·day−1. The brain metabolic rate was γB = 240 kcal·kg−1·day−1, and its mass was MB = 1.4 kg, which does not change with weight gain or loss (26). The baseline specific metabolic rate of the fat-free mass, γ̂FFM = 19 kcal·kg−1·day−1, was determined by the specific metabolic rates of the organs multiplied by the rate of change of the organ mass with fat-free mass change according to the following equation:
| (9) |
where γi and Mi are the average specific metabolic rate and mass, respectively, of the organ indexed by i. The organs included skeletal muscle (γSM = 13 kcal·kg−1·day−1, MSM = 28 kg, dMSM/dFFM = 0.59), liver (γL = 200 kcal·kg−1·day−1, ML = 1.8 kg, dML/dFFM = 0.017), kidney (γK = 440 kcal·kg−1·day−1, MK = 0.31 kg, dMk/dFFM = 0.0038), heart (γH = 440 kcal·kg−1·day−1, MH = 0.33 kg, dMH/dFFM = 0.0029), and residual lean tissue mass (γR = 12 kcal·kg−1·day−1, MR = 23.2 kg, dMR/dFFM = 0.37), as provided by Elia (26), and the relationship between the organ masses and FFM was determined from cross-sectional body composition data (Gallagher D, personal communication). I assumed that there was no effect on RMR arising solely from changes of glycogen content, ΔG, and its associated water or changes of ECF. Adaptive thermogenesis affected the baseline specific metabolic rate for lean tissue cell mass according to the following equation:
| (10) |
The last seven terms of Eq. 8 accounted for the energy cost for urea synthesis and nitrogen excretion as well as the turnover of protein, fat, and glycogen. Urea synthesis requires 4 mol ATP/mol nitrogen excreted (76) and was represented by the parameter ηN = 5.4 kcal/g excreted nitrogen Nexcr. To calculate the energy cost for protein turnover, consider that the whole body protein pool turns over with a synthesis rate, SynthP, and a degradation rate, DP (in g/day). I assumed that it cost ηPSynthP to synthesize P and that the energy required for degradation was εPDP. Since dP/dt = SynthP − DP, the energy cost for protein turnover was given by (ηP + εP)DP + ηPdP/dt. Similar arguments led to the other terms of Eq. 8 representing the energy costs for fat and glycogen turnover, where the energy cost for degradation was negligible. The values for the parameters were ηF = 0.18 kcal/g, ηG = 0.21 kcal/g, εP = 0.17 kcal/g, and ηP = 0.86 kcal/g. These values were determined from the ATP costs for the respective biochemical pathways (i.e., 8 ATP/TG synthesized, 2 ATP/glycosyl unit of glycogen synthesized, 4 ATP/peptide bond synthesized plus 1 ATP for amino acid transport, and 1 ATP/peptide bond hydrolyzed) (12, 28). I assumed that 19 kcal of macronutrient oxidation was required to synthesize 1 mol of ATP (26).
Daily Average Lipolysis Rate
The daily average lipolysis rate, DF, was modeled as
| (11) |
where D̂F = 140 g/day was the baseline daily average TG turnover rate given by two-thirds of the fed lipolysis rate plus one-third of the overnight-fasted lipolysis rate (53). The (F/FKeys)2/3 factor accounted for the dependence of the basal lipolysis rate on the total fat mass normalized by the initial fat mass of the average Minnesota experiment subject, FKeys. The two-thirds power reflects the hypothesis that basal lipolysis scales with adipocyte surface area, which also matches the FFA rate of appearance (Ra) as a function of body fat mass observed by Bjorntorp et al. (10). The effect of diet on lipolysis, Ldiet, is determined primarily by the carbohydrate content of the diet via insulin. Furthermore, the lipolysis rate reaches half of its maximum value after ∼2 days of fasting, and the magnitude of the increase is attenuated with increasing body fat mass (58). To capture these effects, I modeled the effect of dietary carbohydrate on the daily average lipolysis rate as
| (12) |
where τL = 1/ln(2) = 1.44 days. The term in the square brackets accounted for the modulation of lipolysis by the carbohydrate content of the diet. For example, complete starvation (CI = 0) stimulated average daily lipolysis by a factor of AL = 3.1/[1 − exp(−2.5/τL)] = 3.8, as computed by the 3.1-fold increase of glycerol Ra following a 60-h fast (15) vs. the daily average glycerol Ra (53). Halving the carbohydrate content of the diet increased the average lipolysis rate by factor of 1.4, as estimated by the increased area under the circulating FFA curve following an isocaloric meal consisting of 33 vs. 66% carbohydrate (118). Given the above value for AL, the effect of halving the carbohydrate content was modeled by choosing BL = 0.9. The following choice for kL ensured that the lipolysis rate was normalized for the baseline diet:
| (13) |
Although obesity increases basal lipolysis, the stimulatory effect of decreased carbohydrate intake is impaired (120). This effect was modeled in Eq. 12 by setting KL = 4 and SL = 2 such that the curve of lipolysis vs. CI becomes flattened as FM increases and matches the data of Klein et al. (58), where long-term vs. short-term fasting stimulated lipolysis to a lesser degree in obese vs. lean subjects.
Physical activity and exercise are known to stimulate lipolysis, and this was modeled in Eq. 11 by the factor LPA as follows:
| (14) |
where ψ = 0.4 was the best fit value for the measured effect of graded exercise to increase lipolysis rates determined by FFA Ra measurements (39, 57, 84, 119).
Daily Average Ketogenesis Rate
The daily rate of ketogenesis was modeled as a function of the daily lipolysis rate, the protein content in the diet, and the glycogen level as follows:
| (15) |
where ρK = 4.45 kcal/g is the average energy density of ketones calculated as average enthalpy of combustion of β-hydroxybuterate and acetoacetate in a 2:1 ratio (12). AK = 0.8 is the maximum fraction of FFA from lipolysis converted to ketones when PI = G = 0 (9). When protein intake was at normal levels, I assumed that the maximum fraction of FFA converted to ketones was 0.4, since a protein modified fast decreases circulating ketone levels by one-half compared with fasting alone (106). Therefore, kp = ln(0.8/0.4) = 0.69. When both glycogen and protein intake are at normal levels, I assumed that the maximum fraction of FFA converted to ketones was 0.2; therefore kG = ln(0.4/0.2) = 0.69, and when the lipolysis rate was normal I assumed that 10% of FFA from lipolysis was converted to ketones such that KK =1 (9).
Daily Average Ketone Excretion Rate
Ketones are excreted in the urine when circulating levels cross the renal threshold for reuptake. I assumed that
| (16) |
where KTGthresh = 70 g/day, KUmax = 20 g/day, and KTGmax = 400 g/day such that the urinary excretion of ketones, KUexcr, matches the excretion data during various ketone infusion rates, as measured by Wildenhoff (114) and Sapir and Owen (89).
Ketone Oxidation Rate
Since ketones cannot be stored in the body in any significant quantity, I assumed that once a ketone is produced it is either oxidized or excreted. Therefore,
| (17) |
Daily Average Proteolysis Rate
The daily average protein degradation rate, DP, was given by
| (18) |
where D̂P = 300 g/day was the baseline daily protein turnover rate (107), and I assumed that the protein degradation rate was proportional to the normalized protein content of the body (112). Although it is possible that the protein content of the diet may directly influence protein turnover as represented by the parameter χ (83), the balance of the current data suggests that χ = 0 (41, 75). Nevertheless, I included this parameter in the model to allow for this possibility should new data provide further evidence for such an effect.
Daily Average Glycogenolysis Rate
The daily average glycogen degradation rate, DG, was given by the following equation:
| (19) |
where the baseline glycogen turnover rate, D̂G = 180 g/day, was determined by assuming that 70% was from hepatic glycogenolysis and 30% from skeletal muscle with the hepatic contribution computed as two-thirds of the fed plus one-third of the overnight-fasted hepatic glycogenolysis rate (69).
Daily Average Fat, Protein, and Glycogen Synthesis Rates
Mass conservation required that the daily average synthesis rates of fat, protein, and glycogen (SynthF, SynthP, and SynthG, respectively) were given by
| (20) |
Glycerol 3-Phosphate Production Rate
Because adipose tissue lacks glycerol kinase, the glycerol 3-phosphate backbone of adipose TG is derived primarily from glucose. Thus, the TG synthesis rate, SynthF, determined the rate of glycerol 3-phosphate production, G3P, according to
| (21) |
where MG = 92 g/mol and MTG = 860 g/mol are the molecular weights of glycerol and TG, respectively.
Glycerol Gluconeogenesis Rate
Lipolysis of both endogenous and exogenous TG results in the release of glycerol that can be converted to glucose via gluconeogenesis (8). Trimmer et al. (104) demonstrated that glycerol disappearance could be fully accounted for by glucose production. Therefore, I assumed that all exogenous and endogenous glycerol entered the GNG pathway according to the following equation:
| (22) |
Since glycerol cannot be used by adipose tissue for TG synthesis due to lack of glycerol kinase, all glycerol released by lipolysis is eventually oxidized (apart from a negligibly small amount incorporated into altered pool sizes of nonadipose TG). By assuming that all glycerol enters the GNG pathway, any model error was limited to an overestimate of the energy expenditure associated with glycerol's initial conversion to glucose prior to oxidation. This error must be very small, since the total energy cost for glycerol GNG in the basal state was only 25 kcal/day.
Gluconeogenesis From Amino Acids
The GNGP rate in the model referred to the net rate of gluconeogenesis from amino acid-derived carbon. Whereas all amino acids except leucine and lysine can be used as gluconeogenic substrates, the primary gluconeogenic amino acids are alanine and glutamine. Much of alanine gluconeogenesis does not contribute to the net amino acid gluconeogenic rate since the carbon skeleton of alanine is derived largely from carbohydrate precursors via skeletal muscle glycolysis (77). In an extensive review of hepatic amino acid metabolism, Jungas et al. (54) estimated that the net basal gluconeogenic rate from amino acids, GN̂Gp, was 300 kcal/day.
Several factors may regulate GNGP, but for simplicity I have assumed that GNGP was proportional to the normalized proteolysis rate and was influenced by the diet as follows:
| (23) |
where the coefficients ΓC = 0.39 and ΓP = 0.32 were determined by solving Eq. 23, using two sets of data. The first measured an initial nitrogen balance of −4 g/day upon removal of baseline dietary carbohydrate while keeping dietary protein at baseline values (47). I assumed that the negative nitrogen balance was driven largely by increased gluconeogenesis and thereby determined the value of ΓC. The second study found a 56% increase of gluconeogenesis when protein intake was increased by a factor of 2.5-fold, whereas carbohydrate intake was decreased by 20% (66). Given the value of ΓC, these data determined the value of the sum of Γp + χ and therefore ΓP.
De Novo Lipogenesis Rate
DNL occurs in both the liver and adipose tissue. Under free-living conditions, adipose DNL has recently been measured to contribute ∼20% of new TG with a measured TG turnover rate of ∼50 g/day (99). Thus, adipose DNL is ∼94 kcal/day. Measurements of daily hepatic DNL in circulating very low-density lipoproteins (VLDL) have found that ∼7% of VLDL TG occurs via DNL when a basal diet of 30% fat, 50% carbohydrate, and 15% protein is consumed (49). Given that the daily VLDL TG secretion rate is ∼33 g/day (93), this corresponds to a hepatic DNL rate of ∼22 kcal/day. For an isocaloric diet of 10% fat, 75% carbohydrate, and 15% protein, hepatic DNL increases to 113 kcal/day (49).
When carbohydrate intake is excessively large and glycogen is saturated, DNL can be greatly amplified (2). Therefore, I modeled DNL as a Hill function of the normalized glycogen content with a maximum DNL rate given by the carbohydrate intake rate:
| (24) |
I chose KDNL = 2 and d = 4 such that the computed DNL rate corresponded with measured in vivo DNL rates for experimentally determined carbohydrate intakes and estimated glycogen levels (1, 2, 49, 99).
Macronutrient Oxidation Rates
The whole body energy expenditure rate, TEE, was accounted for primarily by the sum of the heat produced from carbohydrate, fat, and protein oxidation plus the heat produced via flux through the DNL pathway (34) and ketogenesis. Furthermore, I assumed that the minimum carbohydrate oxidation rate was equal to the sum of the gluconeogenic rates less the flux required to produce glycerol 3-phosphate and that ketone oxidation was treated as fat oxidation. Thus, the remaining energy expenditure, TẼE, was apportioned between carbohydrate, fat, and protein oxidation according to the fractions fC, fF, and fP, respectively:
| (25) |
where
| (26) |
The substrate oxidation fraction for each macronutrient depends on a number of factors. First, increased lipolysis leads to concomitant increased fatty acid oxidation (15). Second, carbohydrate oxidation depends on the carbohydrate intake as well as the glycogen content (32, 61). Third, dietary protein and carbohydrate intake directly stimulate protein and carbohydrate oxidation, respectively, but dietary fat intake does not directly stimulate fat oxidation (36, 91). Fourth, I assumed that lean tissue supplies amino acids for oxidation in proportion to the proetolysis rate. Finally, although inactivity causes muscle wasting (11, 97), increased physical activity may promote nitrogen retention (14, 101, 112), and the PAE is accounted for primarily by increased oxidation of fat and carbohydrate (112). I modeled these effects by decreasing the fraction of energy expenditure derived from protein oxidation as physical activity increases.
On the basis of these physiological considerations, the substrate oxidation fractions were computed according to the following expressions:
| (27) |
where the w and S were dimensionless model parameters and ΔCI and ΔPI were changes from the basal carbohydrate intake, CIb, and protein intake, PIb, respectively. The small parameter, Gmin = 10 g, was chosen such that carbohydrate oxidation was restrained as glycogen decreases and prevents glycogen from becoming negative. The signal for dietary protein intake perturbations, Psig, changes with a time constant of τPI = 1.1 days, in accordance with the data of Rand et al. (79), and the model allows for an asymmetry between positive and negative perturbations of dietary protein. To normalize for the baseline physical activity, the constant kA was chosen such that kA = ln(SA). Z was a normalization factor equal to the sum of the numerators so that the sum of the fractions fC, fF, and fP was equal to 1.
Respiratory Gas Exchange
Oxidation of carbohydrate, fat, and protein was associated with consumption of oxygen (O2) and production of carbon dioxide (CO2) according to the stoichiometry of the net biochemical reactions (31, 37):
| (28) |
Gluconeogenesis, lipogenesis, ketogenesis (with subsequent excretion), and glycerol 3-phosphate production also contribute to gas exchange according to the following net reactions (27, 31, 37):
| (29) |
Oxidation of carbohydrate, fat, and protein can occur either directly or subsequent to intermediate exchange via lipogenesis or gluconeogenesis. In either case, the final ratio of CO2 produced to O2 consumed (i.e., the RQ) is independent of any intermediate exchanges in accordance with the principles of indirect calorimetry (27, 31, 37).
The simulated O2 consumption (V̇o2) and CO2 production (V̇co2) (in liters/day) were computed according to
| (30) |
The RQ was computed by dividing V̇co2 by V̇o2. To compute the NPRQ, the total rate of nitrogen excretion was calculated:
| (31) |
where the factor 6.25 was the number of grams of protein per gram of nitrogen.
When comparing model predictions for fuel selection with experiments employing 24-h room indirect calorimetry, I used the simulated V̇co2 and V̇o2 values from Eq. 30 and computed macronutrient oxidation rates as if they were the actual indirect calorimetry measurements.
Nutrient Balance Parameter Constraints
The baseline diet may not necessarily result in macronutrient or energy balance. Therefore, I defined the following parameters to specify the initial degree of imbalance for fat, carbohydrate, and protein: Fimbal, Gimbal, and Pimbal, respectively. Therefore, the baseline diet satisfies the following relationship: TEE + Fimbal + Gimbal + Pimbal = EIb, where the subscript b refers to the baseline state. Therefore, by explicitly expressing the TEE in the baseline state I derived the following expression:
| (32) |
which was solved for the constant Ec.
Assuming negligible baseline ketone excretion, rearrangement of the nutrient balance equations gave
| (33) |
Next, I defined the following parameters:
| (34) |
where Ω was given by
| (35) |
By substituting Eqs. 25 and 27 at the initial state, I obtained
| (36) |
where Finit, Ginit, and Pinit were the initial values for body fat, glycogen, and protein, respectively. Elementary algebra led to the following parameter constraints required to achieve the specified macronutrient imbalance:
| (37) |
where wC:G = wC/wG.
Carbohydrate Perturbation Constraint
The parameters wC and SC determined how the model adapted to changes of carbohydrate intake. I specified that an additional dietary carbohydrate intake, ΔCI, above baseline, CIb, resulted in an initial positive carbohydrate imbalance of κCΔCI, where 0 < κC < 1 specified the proportion of ΔCI directed toward glycogen storage. Thus, the glycogen increment was ΔG = κCΔCI/ρC. The goal was to solve for the parameter SC such that the correct amount of carbohydrate was oxidized and deposited as glycogen during short-term carbohydrate overfeeding. Based on the carbohydrate overfeeding study of Horton et al. (48), I chose κC = 0.5 when ΔCI = 1,500 kcal/day.
The change of TEE was given by
| (38) |
For a carbohydrate perturbation, the perturbed energy expenditure components were
| (39) |
| (40) |
| (41) |
where
| (42) |
was the average value of the thermogenesis parameter, T, over 1 day and ΔDNL was computed at the midpoint of the glycogen increment according to the following equation:
| (43) |
The change of the gluconeogenic rate, ΔGNG, was given by
| (44) |
The carbohydrate balance Eq. 1 and the carbohydrate oxidation Eq. 25 gave
| (45) |
Since I assume that the baseline diet results in a state of energy balance, I obtained the following equation for TẼE:
| (46) |
For simplicity, I assumed that
| (47) |
I define the parameter Θ as
| (48) |
Therefore, using Eq. 27, I solved Eq. 45 for SC, which gave the carbohydrate feeding constraint:
| (49) |
where
| (50) |
Protein Perturbation Constraint
The parameters wP and SP+ determined how the model adapted short-term substrate oxidation rates to changes of protein intake. In a meticulous study of whole body protein balance, Oddoye and Margen (74) measured nitrogen balance in subjects consuming isocaloric diets with moderate or high protein content. These studies found that ∼90% of the additional dietary nitrogen on the high-protein diet was rapidly excreted such that κP = 0.1 when ΔPI = 640 kcal/day, ΔCI = −310 kcal/day, and ΔFI = −330 kcal/day.
To compute the value for SP+ to match the data of Oddoye and Margen (74), I began with the protein balance Eqs. 1 and 25 to derive
| (51) |
where the changes of gluconeogenic rates were given by
| (52) |
The change of TEE was given by
| (53) |
where
| (54) |
and
| (55) |
Since the perturbed diet was isocaloric and there were no changes of physical activity,
| (56) |
I also assumed that
| (57) |
and that glycogen would change by approximately ΔG ≈ κC ΔCI/ρC, thereby altering DNL as follows:
| (58) |
Using Eq. 27, I solved Eq. 51 for SP, which gave the following constraint:
| (59) |
where Φ was defined as
| (60) |
and
| (61) |
Physical Inactivity Constraint
The parameter SA defines how the protein oxidation fraction depends on physical activity and exercise. Stein et al. (97) observed that 17 days of bed rest without a change of diet resulted in an average negative N balance: Nbal = −2 g/day. From the protein balance equation,
| (62) |
where
| (63) |
From the macronutrient oxidation Eq. 27,
| (64) |
where
| (65) |
which assumes that the approximately one-half of the energy savings due to inactivity will initially be deposited as glycogen. This results in the following expression for SA:
| (66) |
where
| (67) |
Model Parameter Values
The model parameter values listed above were obtained from the cited published literature and are listed in Table 1. The parameters, SP−, wP, wC:G, λ1, λ2, and σ, were determined using a downhill simplex algorithm (78) implemented using Berkeley Madonna software (version 8.3; http://www.berkeleymadonna.com) to minimize the sum of squares of weighted residuals between the simulation outputs and the data from the Minnesota human starvation experiment (55). I used the following measurement error estimates to define the weights for the parameter optimization algorithm: ΔBW = 0.2 kg, ΔFM = 0.5 kg, and ΔRMR = 50 kcal/day. The best fit parameter values are listed in Table 2, and the constrained parameters are listed in Table 3.
Table 1.
Model parameters determined from published data
| Parameter | Value | Description |
|---|---|---|
| ρF | 9.44 kcal/g | Energy density of F |
| ρP | 4.7 kcal/g | Energy density of P |
| ρG | 4.18 kcal/g | Energy density of G |
| ρK | 4.45 kcal/g | Energy density of ketones |
| hP | 1.6 g H2O/g | P hydration coefficient |
| hG | 2.7 g H2O/g | G hydration coefficient |
| ηF | 0.18 kcal/g | F synthesis cost |
| ηP | 0.86 kcal/g | P synthesis cost |
| εP | 0.17 kcal/g | P degradation cost |
| ηG | 0.21 kcal/g | G synthesis cost |
| ηN | 5.4 kcal/g | Urea synthesis cost/g nitrogen |
| εd | 0.835 | DNL efficiency |
| εg | 0.8 | GNG efficiency |
| εk | 0.81 | KTG efficiency |
| αF | 0.025 | TEF factor for FI |
| αC | 0.075 | TEF factor for CI |
| αP | 0.25 | TEF factor for PI |
| γF | 4.5 kcal•kg−1•day−1 | Specific RMR for adipose |
| γ̂FFM | 19 kcal•kg−1•day−1 | Basal specific RMR for FFM |
| ξBW | 0.16 | ECF response to BW changes |
| ξCI | 4000 mg/day | ECF response to CI changes |
| ξNa | 3 mg•ml−1•day−1 | ECF response to sodium changes |
| τBW | 1,000 days | ECF response time for BW changes |
| τT | 7 days | Response time for T changes |
| D̂g | 180 g/day | Baseline glycogenolysis rate |
| KDNL | 2 | Glycogen constant for DNL |
| d | 4 | Hill coefficient for DNL |
| D̂F | 140 g/day | Baseline lipolysis rate |
| AL | 3.8 | Maximum lipolysis change |
| BL | 0.9 | Minimum lipolysis change |
| τL | 1.44 days | Response time for lipolysis |
| KL | 4 | Body fat constant for lipolysis |
| SL | 2 | Hill coefficient for lipolysis |
| ψ | 0.4 | PA effect on lipolysis |
| AK | 0.8 | Maximum KTG fraction |
| kP | 0.69 | Effect of PI on KTG |
| kG | 0.69 | Effect of G on KTG |
| KK | 1 | Sets basal KTG rate |
| KTGthresh | 70 g/day | Renal threshold KTG rate |
| KUmax | 20 g/day | Maximum ketone excretion |
| KTGmax | 400 g/day | Maximum KTG |
| D̂P | 300 g/day | Baseline proteolysis rate |
| χ | 0 | Effect of PI on protein turnover |
| GN̂GP | 300 kcal/day | Basal GNGP rate |
| ΓC | 0.39 | Effect of CI on GNGP |
| ΓP | 0.32 | Effect of PI on GNGP |
| τPI | 1.1 days | Response time of ProtOx to PI changes |
See Glossary of Model Variables for definitions of the abbreviations.
Table 2.
Parameter values fit to the Minnesota experiment data
| Parameter | Value | Description |
|---|---|---|
| λ1 | 0.74 | Underfeeding adaptive thermogenesis |
| λ2 | 0.02 | Overfeeding adaptive thermogenesis |
| σ | 0.52 | Thermogenesis effect on PAE vs. RMR |
| wP | 1.1 | Weighting of ProtOx for basal PI |
| wC:G | 0.93 | Ratio of CarbOx weighting parameters |
| SP− | 1.7 | Sensitivity of ProtOx to reduced PI |
See Glossary of Model Variables for definitions of the abbreviations.
Table 3.
Parameter values determined from constraints on energy balance, nutrient balance, and physical inactivity as well as perturbations of dietary protein and carbohydrate
| Parameter | Value | Description |
|---|---|---|
| SP+ | 3.8 | Sensitivity of ProtOx to increased PI |
| SC | 0.85 | Sensitivity of CarbOx to CI changes |
| wG | 9.4 | Weighting of CarbOx for glycogenolysis |
| wF | 14.8 | Weighting of FatOx for lipolysis |
| Ec | −435 kcal/day | Constant energy expenditure offset |
See Glossary of Model Variables for definitions of the abbreviations. Other than the constant values for SC and SP+, these parameters are calculated according to the initial conditions corresponding to different subject groups. The values listed are for the average Minnesota experiment subject.
Footnotes
- BM
- Bone mineral mass in g
- BW
- Body weight in g
- CarbOx
- Rate of carbohydrate oxidation in kcal/day
- CI
- Carbohydrate intake rate in kcal/day
- DF
- Rate of endogenous lipolysis in g/day
- DG
- Rate of glycogenolysis in g/day
- DNL
- Rate of de novo lipogenesis in kcal/day
- DP
- Rate of proteolysis in g/day
- ECF
- Extracellular fluid mass in g
- ECP
- Extracellular protein mass in g
- EI
- Energy intake in kcal/day
- FM
- Body fat mass in g
- FatOx
- Rate of fat oxidation in kcal/day
- fC
- Carbohydrate oxidation fraction
- fF
- Fat oxidation fraction
- FFM
- Fat-free body mass in g
- FI
- Fat intake rate in kcal/day
- fP
- Protein oxidation fraction
- G
- Body glycogen mass in g
- G3P
- Rate of glycerol 3-phosphate synthesis in kcal/day
- GNGF
- Rate of gluconeogenesis from glycerol in kcal/day
- GNGP
- Rate of gluconeogenesis from protein in kcal/day
- ICS
- Intracellular solid mass in g
- ICW
- Intracellular water mass in g
- KetOx
- Rate of ketone oxidation in kcal/day
- KTG
- Rate of ketogenesis in kcal/day
- KUexcr
- Rate of ketone excretion in kcal/day
- LCM
- Lean tissue cell mass in g
- Nexcr
- Nitrogen excretion rate in g/day
- NPRQ
- Nonprotein respiratory quotient
- P
- Intracellular protein mass in g
- PAE
- Physical activity energy expenditure in kcal/day
- PI
- Protein intake rate in kcal/day
- ProtOx
- Rate of protein oxidation in kcal/day
- RMR
- Resting metabolic rate in kcal/day
- RQ
- Respiratory quotient
- SynthF
- Rate of fat synthesis in g/day
- SynthG
- Rate of glycogen synthesis in g/day
- SynthP
- Rate of protein synthesis in g/day
- T
- Adaptive thermogenesis
- TEE
- Total energy expenditure in kcal/day
- TEF
- Thermic effect of feeding in kcal/day
- TG
- Triacylglyceride
- V̇co2
- Rate of carbon dioxide production in liters/day
- V̇o2
- Rate of oxygen consumption in liters/day
REFERENCES
- 1. Aarsland A, Chinkes D, Wolfe RR. Hepatic and whole-body fat synthesis in humans during carbohydrate overfeeding. Am J Clin Nutr 65: 1774–1782, 1997. [DOI] [PubMed] [Google Scholar]
- 2. Acheson KJ, Schutz Y, Bessard T, Anantharaman K, Flatt JP, Jequier E. Glycogen storage capacity and de novo lipogenesis during massive carbohydrate overfeeding in man. Am J Clin Nutr 48: 240–247, 1988. [DOI] [PubMed] [Google Scholar]
- 3. Alpert SS. Growth, thermogenesis, and hyperphagia. Am J Clin Nutr 52: 784–792, 1990. [DOI] [PubMed] [Google Scholar]
- 4. Alpert SS. A limit on the energy transfer rate from the human fat store in hypophagia. J Theor Biol 233: 1–13, 2005. [DOI] [PubMed] [Google Scholar]
- 5. Alpert SS. A two-reservoir energy model of the human body. Am J Clin Nutr 32: 1710–1718, 1979. [DOI] [PubMed] [Google Scholar]
- 6. Andersen LJ, Andersen JL, Pump B, Bie P. Natriuresis induced by mild hypernatremia in humans. Am J Physiol Regul Integr Comp Physiol 282: R1754–R1761, 2002. [DOI] [PubMed] [Google Scholar]
- 7. Antonetti VW. The equations governing weight change in human beings. Am J Clin Nutr 26: 64–71, 1973. [DOI] [PubMed] [Google Scholar]
- 8. Baba H, Zhang XJ, Wolfe RR. Glycerol gluconeogenesis in fasting humans. Nutrition 11: 149–153, 1995. [PubMed] [Google Scholar]
- 9. Balasse EO, Fery F. Ketone body production and disposal: effects of fasting, diabetes, and exercise. Diabetes Metab Rev 5: 247–270, 1989. [DOI] [PubMed] [Google Scholar]
- 10. Björntorp P, Bergman H, Varnauskas E. Plasma free fatty acid turnover rate in obesity. Acta Med Scand 185: 351–356, 1969. [DOI] [PubMed] [Google Scholar]
- 11. Blanc S, Normand S, Ritz P, Pachiaudi C, Vico L, Gharib C, Gauquelin-Koch G. Energy and water metabolism, body composition, and hormonal changes induced by 42 days of enforced inactivity and simulated weightlessness. J Clin Endocrinol Metab 83: 4289–4297, 1998. [DOI] [PubMed] [Google Scholar]
- 12. Blaxter K. Energy Metabolism in Animals and Man. Cambridge, UK: Cambridge University, 1989. [Google Scholar]
- 13. Brozek J, Grande F, Anderson JT, Keys A. Densitometric analysis of body composition: revision of some quantitative assumptions. Ann NY Acad Sci 110: 113–140, 1963. [DOI] [PubMed] [Google Scholar]
- 14. Butterfield GE, Calloway DH. Physical activity improves protein utilization in young men. Br J Nutr 51: 171–184, 1984. [DOI] [PubMed] [Google Scholar]
- 15. Carlson MG, Snead WL, Campbell PJ. Fuel and energy metabolism in fasting humans. Am J Clin Nutr 60: 29–36, 1994. [DOI] [PubMed] [Google Scholar]
- 16. Chow CC, Hall KD. The dynamics of human body weight change. PLoS Comput Biol 4: e1000045, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Christiansen E, Garby L. Prediction of body weight changes caused by changes in energy balance. Eur J Clin Invest 32: 826–830, 2002. [DOI] [PubMed] [Google Scholar]
- 18. Christiansen E, Garby L, Sorensen TI. Quantitative analysis of the energy requirements for development of obesity. J Theor Biol 234: 99–106, 2005. [DOI] [PubMed] [Google Scholar]
- 19. de Boer JO, van Es AJ, Roovers LC, van Raaij JM, Hautvast JG. Adaptation of energy metabolism of overweight women to low-energy intake, studied with whole-body calorimeters. Am J Clin Nutr 44: 585–595, 1986. [DOI] [PubMed] [Google Scholar]
- 20. Di Ventura B, Lemerle C, Michalodimitrakis K, Serrano L. From in vivo to in silico biology and back. Nature 443: 527–533, 2006. [DOI] [PubMed] [Google Scholar]
- 21. Diaz EO, Prentice AM, Goldberg GR, Murgatroyd PR, Coward WA. Metabolic response to experimental overfeeding in lean and overweight healthy volunteers. Am J Clin Nutr 56: 641–655, 1992. [DOI] [PubMed] [Google Scholar]
- 22. Doucet E, Imbeault P, St-Pierre S, Almeras N, Mauriege P, Despres JP, Bouchard C, Tremblay A. Greater than predicted decrease in energy expenditure during exercise after body weight loss in obese men. Clin Sci (Lond) 105: 89–95, 2003. [DOI] [PubMed] [Google Scholar]
- 23. Doucet E, St-Pierre S, Almeras N, Despres JP, Bouchard C, Tremblay A. Evidence for the existence of adaptive thermogenesis during weight loss. Br J Nutr 85: 715–723, 2001. [DOI] [PubMed] [Google Scholar]
- 24. DuBios EF. Basal Metabolism in Health and Disease. Philadelphia, PA: Lea & Febiger, 1927. [Google Scholar]
- 25. Duarte NC, Becker SA, Jamshidi N, Thiele I, Mo ML, Vo TD, Srivas R, Palsson BO. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc Natl Acad Sci USA 104: 1777–1782, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Elia M. Organ and tissue contribution to metabolic rate. In: Energy Metabolism: Tissue Determinants and Cellular Corollaries, edited by Kinney JM, Tucker HN. New York: Raven, 1992, p. 61–79. [Google Scholar]
- 27. Elia M, Livesey G. Theory and validity of indirect calorimetry during net lipid synthesis. Am J Clin Nutr 47: 591–607, 1988. [DOI] [PubMed] [Google Scholar]
- 28. Elia M, Zed C, Neale G, Livesey G. The energy cost of triglyceride-fatty acid recycling in nonobese subjects after an overnight fast and four days of starvation. Metabolism 36: 251–255, 1987. [DOI] [PubMed] [Google Scholar]
- 29. Feist AM, Herrgård MJ, Thiele I, Reed JL, Palsson BØ. Reconstruction of biochemical networks in microorganisms. Nat Rev Microbiol 7: 129–143, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Feist AM, Palsson BØ. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat Biotechnol 26: 659–667, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Ferrannini E. The theoretical bases of indirect calorimetry: a review. Metabolism 37: 287–301, 1988. [DOI] [PubMed] [Google Scholar]
- 32. Fery F, Plat L, Balasse EO. Level of glycogen stores and amount of ingested glucose regulate net carbohydrate storage by different mechanisms. Metabolism 52: 94–101, 2003. [DOI] [PubMed] [Google Scholar]
- 33. Flatt JP. Carbohydrate-fat interactions and obesity examined by a two-compartment computer model. Obes Res 12: 2013–2022, 2004. [DOI] [PubMed] [Google Scholar]
- 34. Flatt JP. Conversion of carbohydrate to fat in adipose tissue: an energy-yielding and, therefore, self-limiting process. J Lipid Res 11: 131–143, 1970. [PubMed] [Google Scholar]
- 35. Flatt JP. Exaggerated claim about adaptive thermogenesis. Int J Obes (Lond) 31: 1626; author reply 1627–1628, 2007. [DOI] [PubMed] [Google Scholar]
- 36. Flatt JP, Ravussin E, Acheson KJ, Jequier E. Effects of dietary fat on postprandial substrate oxidation and on carbohydrate and fat balances. J Clin Invest 76: 1019–1024, 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Frayn KN. Calculation of substrate oxidation rates in vivo from gaseous exchange. J Appl Physiol 55: 628–634, 1983. [DOI] [PubMed] [Google Scholar]
- 38. Frayn KN. Metabolic Regulation: a Human Perspective. Oxford, UK: Blackwell Science, 2003. [Google Scholar]
- 39. Friedlander AL, Casazza GA, Horning MA, Buddinger TF, Brooks GA. Effects of exercise intensity and training on lipid metabolism in young women. Am J Physiol Endocrinol Metab 275: E853–E863, 1998. [DOI] [PubMed] [Google Scholar]
- 41. Garlick PJ, McNurlan MA, Patlak CS. Adaptation of protein metabolism in relation to limits to high dietary protein intake. Eur J Clin Nutr 53, Suppl 1: S34–S43, 1999. [DOI] [PubMed] [Google Scholar]
- 42. Hall KD. Computational model of in vivo human energy metabolism during semistarvation and refeeding. Am J Physiol Endocrinol Metab 291: E23–E37, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Hall KD. What is the required energy deficit per unit weight loss? Int J Obes (Lond) 32: 573–576, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Hall KD, Jordan PN. Modeling weight-loss maintenance to help prevent body weight regain. Am J Clin Nutr 88: 1495–1503, 2008. [DOI] [PubMed] [Google Scholar]
- 45. Heilbronn LK, DE Jonge L, Frisard MI, DeLany JP, Larson-Meyer DE, Rood J, Nguyen T, Martin CK, Volaufova J, Most MM, Greenway FL, Smith SR, Deutsch WA, Williamson DA, Ravussin E. Pennington CALERIE Team. Effect of 6-month calorie restriction on biomarkers of longevity, metabolic adaptation, and oxidative stress in overweight individuals: a randomized controlled trial. JAMA 295: 1539–1548, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Hill JO. Understanding and addressing the epidemic of obesity: an energy balance perspective. Endocr Rev 27: 750–761, 2006. [DOI] [PubMed] [Google Scholar]
- 47. Hoffer LJ, Bistrian BR, Young VR, Blackburn GL, Matthews DE. Metabolic effects of very low calorie weight reduction diets. J Clin Invest 73: 750–758, 1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Horton TJ, Drougas H, Brachey A, Reed GW, Peters JC, Hill JO. Fat and carbohydrate overfeeding in humans: different effects on energy storage. Am J Clin Nutr 62: 19–29, 1995. [DOI] [PubMed] [Google Scholar]
- 49. Hudgins LC, Hellerstein MK, Seidman CE, Neese RA, Tremaroli JD, Hirsch J. Relationship between carbohydrate-induced hypertriglyceridemia and fatty acid synthesis in lean and obese subjects. J Lipid Res 41: 595–604, 2000. [PubMed] [Google Scholar]
- 50. Jackson AS, Stanforth PR, Gagnon J, Rankinen T, Leon AS, Rao DC, Skinner JS, Bouchard C, Wilmore JH. The effect of sex, age and race on estimating percentage body fat from body mass index: The Heritage Family Study. Int J Obes Relat Metab Disord 26: 789–796, 2002. [DOI] [PubMed] [Google Scholar]
- 51. Jebb SA, Murgatroyd PR, Goldberg GR, Prentice AM, Coward WA. In vivo measurement of changes in body composition: description of methods and their validation against 12-d continuous whole-body calorimetry. Am J Clin Nutr 58: 455–462, 1993. [DOI] [PubMed] [Google Scholar]
- 52. Jebb SA, Prentice AM, Goldberg GR, Murgatroyd PR, Black AE, Coward WA. Changes in macronutrient balance during over- and underfeeding assessed by 12-d continuous whole-body calorimetry. Am J Clin Nutr 64: 259–266, 1996. [DOI] [PubMed] [Google Scholar]
- 53. Jensen MD. Regional glycerol and free fatty acid metabolism before and after meal ingestion. Am J Physiol Endocrinol Metab 276: E863–E869, 1999. [DOI] [PubMed] [Google Scholar]
- 54. Jungas RL, Halperin ML, Brosnan JT. Quantitative analysis of amino acid oxidation and related gluconeogenesis in humans. Physiol Rev 72: 419–448, 1992. [DOI] [PubMed] [Google Scholar]
- 55. Keys A. The Biology of Human Starvation. Minneapolis, MN: University of Minnesota, 1950. [Google Scholar]
- 56. Kleiber M. The Fire of Life: An Introduction to Animal Energetics. Malabar, FL: Robert E. Krieger Publishing; 1975. [Google Scholar]
- 57. Klein S, Coyle EF, Wolfe RR. Fat metabolism during low-intensity exercise in endurance-trained and untrained men. Am J Physiol Endocrinol Metab 267: E934–E940, 1994. [DOI] [PubMed] [Google Scholar]
- 58. Klein S, Young VR, Blackburn GL, Bistrian BR, Wolfe RR. The impact of body composition on the regulation of lipolysis during short-term fasting. J Am Coll Nutr 7: 77–84, 1988. [DOI] [PubMed] [Google Scholar]
- 59. Kozusko FP. Body weight setpoint, metabolic adaption and human starvation. Bull Math Biol 63: 393–403, 2001. [DOI] [PubMed] [Google Scholar]
- 60. Kozusko FP. The effects of body composition on setpoint based weight loss. Math Comp Model 29: 1–7, 2002. [Google Scholar]
- 61. Laurent D, Hundal RS, Dresner A, Price TB, Vogel SM, Petersen KF, Shulman GI. Mechanism of muscle glycogen autoregulation in humans. Am J Physiol Endocrinol Metab 278: E663–E668, 2000. [DOI] [PubMed] [Google Scholar]
- 62. Leibel RL, Rosenbaum M, Hirsch J. Changes in energy expenditure resulting from altered body weight. N Engl J Med 332: 621–628, 1995. [DOI] [PubMed] [Google Scholar]
- 63. Levine JA. Nonexercise activity thermogenesis (NEAT): environment and biology. Am J Physiol Endocrinol Metab 286: E675–E685, 2004. [DOI] [PubMed] [Google Scholar]
- 64. Levine JA, Eberhardt NL, Jensen MD. Role of nonexercise activity thermogenesis in resistance to fat gain in humans. Science 283: 212–214, 1999. [DOI] [PubMed] [Google Scholar]
- 65. Levine JA, Lanningham-Foster LM, McCrady SK, Krizan AC, Olson LR, Kane PH, Jensen MD, Clark MM. Interindividual variation in posture allocation: possible role in human obesity. Science 307: 584–586, 2005. [DOI] [PubMed] [Google Scholar]
- 66. Linn T, Santosa B, Gronemeyer D, Aygen S, Scholz N, Busch M, Bretzel RG. Effect of long-term dietary protein intake on glucose metabolism in humans. Diabetologia 43: 1257–1265, 2000. [DOI] [PubMed] [Google Scholar]
- 67. Livesey G, Elia M. Estimation of energy expenditure, net carbohydrate utilization, and net fat oxidation and synthesis by indirect calorimetry: evaluation of errors with special reference to the detailed composition of fuels. Am J Clin Nutr 47: 608–628, 1988. [DOI] [PubMed] [Google Scholar]
- 68. Lusk G. The Elements of the Science of Nutrition. London: Academic, 1976. [Google Scholar]
- 69. Magnusson I, Rothman DL, Jucker B, Cline GW, Shulman RG, Shulman GI. Liver glycogen turnover in fed and fasted humans. Am J Physiol Endocrinol Metab 266: E796–E803, 1994. [DOI] [PubMed] [Google Scholar]
- 70. Major GC, Doucet E, Trayhurn P, Astrup A, Tremblay A. Clinical significance of adaptive thermogenesis. Int J Obes (Lond) 31: 204–212, 2007. [DOI] [PubMed] [Google Scholar]
- 71. McBride J, Guest M, Scott E. The storage of the major liver components; emphasizing the relationship of glycogen to water in the liver and the hydration of glycogen. J Biol Chem 139: 943–952, 1941. [Google Scholar]
- 72. Mifflin MD, ST Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh YO. A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr 51: 241–247, 1990. [DOI] [PubMed] [Google Scholar]
- 73. Noble D. The rise of computational biology. Nat Rev Mol Cell Biol 3: 459–463, 2002. [DOI] [PubMed] [Google Scholar]
- 74. Oddoye EA, Margen S. Nitrogen balance studies in humans: long-term effect of high nitrogen intake on nitrogen accretion. J Nutr 109: 363–377, 1979. [DOI] [PubMed] [Google Scholar]
- 75. Pacy PJ, Price GM, Halliday D, Quevedo MR, Millward DJ. Nitrogen homeostasis in man: the diurnal responses of protein synthesis and degradation and amino acid oxidation to diets with increasing protein intakes. Clin Sci (Lond) 86: 103–116, 1994. [DOI] [PubMed] [Google Scholar]
- 76. Pattabiraman T. The energy cost of urea synthesis: a reappraisal. Biochem Ed 23: 24–25, 1995. [Google Scholar]
- 77. Perriello G, Jorde R, Nurjhan N, Stumvoll M, Dailey G, Jenssen T, Bier DM, Gerich JE. Estimation of glucose-alanine-lactate-glutamine cycles in postabsorptive humans: role of skeletal muscle. Am J Physiol Endocrinol Metab 269: E443–E450, 1995. [DOI] [PubMed] [Google Scholar]
- 78. Press W, Flannery B, Teukolsky S, Vetterling W. Numerical Recipes: The Art of Scientific Computing. New York: Cambridge University, 1986. [Google Scholar]
- 79. Rand WM, Young VR, Scrimshaw NS. Change of urinary nitrogen excretion in response to low-protein diets in adults. Am J Clin Nutr 29: 639–644, 1976. [DOI] [PubMed] [Google Scholar]
- 80. Ravussin E, Kozak LP. Have we entered the brown adipose tissue renaissance? Obes Rev 10: 265–268, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Redman LM, Heilbronn LK, Martin CK, Alfonso A, Smith SR, Ravussin E. Effect of calorie restriction with or without exercise on body composition and fat distribution. J Clin Endocrinol Metab 92: 865–872, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Redman LM, Heilbronn LK, Martin CK, de Jonge L, Williamson DA, Delany JP, Ravussin E, Pennington CALERIE Team Metabolic and behavioral compensations in response to caloric restriction: implications for the maintenance of weight loss. PLoS ONE 4: e4377, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Reeds PJ, Fuller MF. Nutrient intake and protein turnover. Proc Nutr Soc 42: 463–471, 1983. [DOI] [PubMed] [Google Scholar]
- 84. Romijn JA, Coyle EF, Sidossis LS, Gastaldelli A, Horowitz JF, Endert E, Wolfe RR. Regulation of endogenous fat and carbohydrate metabolism in relation to exercise intensity and duration. Am J Physiol Endocrinol Metab 265: E380–E391, 1993. [DOI] [PubMed] [Google Scholar]
- 85. Rosenbaum M, Hirsch J, Gallagher DA, Leibel RL. Long-term persistence of adaptive thermogenesis in subjects who have maintained a reduced body weight. Am J Clin Nutr 88: 906–912, 2008. [DOI] [PubMed] [Google Scholar]
- 86. Rosenbaum M, Hirsch J, Murphy E, Leibel RL. Effects of changes in body weight on carbohydrate metabolism, catecholamine excretion, and thyroid function. Am J Clin Nutr 71: 1421–1432, 2000. [DOI] [PubMed] [Google Scholar]
- 87. Rosenbaum M, Vandenborne K, Goldsmith R, Simoneau JA, Heymsfield S, Joanisse DR, Hirsch J, Murphy E, Matthews D, Segal KR, Leibel RL. Effects of experimental weight perturbation on skeletal muscle work efficiency in human subjects. Am J Physiol Regul Integr Comp Physiol 285: R183–R192, 2003. [DOI] [PubMed] [Google Scholar]
- 88. Rumpler WV, Seale JL, Miles CW, Bodwell CE. Energy-intake restriction and diet-composition effects on energy expenditure in men. Am J Clin Nutr 53: 430–436, 1991. [DOI] [PubMed] [Google Scholar]
- 89. Sapir DG, Owen OE. Renal conservation of ketone bodies during starvation. Metabolism 24: 23–33, 1975. [DOI] [PubMed] [Google Scholar]
- 90. Schrauwen P, van Marken Lichtenbelt WD, Saris WH, Westerterp KR. Changes in fat oxidation in response to a high-fat diet. Am J Clin Nutr 66: 276–282, 1997. [DOI] [PubMed] [Google Scholar]
- 91. Schutz Y, Flatt JP, Jequier E. Failure of dietary fat intake to promote fat oxidation: a factor favoring the development of obesity. Am J Clin Nutr 50: 307–314, 1989. [DOI] [PubMed] [Google Scholar]
- 92. Shlomi T, Cabili MN, Herrgård MJ, Palsson BØ, Ruppin E. Network-based prediction of human tissue-specific metabolism. Nat Biotechnol 26: 1003–1010, 2008. [DOI] [PubMed] [Google Scholar]
- 93. Sidossis LS, Magkos F, Mittendorfer B, Wolfe RR. Stable isotope tracer dilution for quantifying very low-density lipoprotein-triacylglycerol kinetics in man. Clin Nutr 23: 457–466, 2004. [DOI] [PubMed] [Google Scholar]
- 94. Silva AM, Wang J, Pierson RN, Jr, Wang Z, Spivack J, Allison DB, Heymsfield SB, Sardinha LB, Heshka S. Extracellular water across the adult lifespan: reference values for adults. Physiol Meas 28: 489–502, 2007. [DOI] [PubMed] [Google Scholar]
- 95. Smith SR, de Jonge L, Zachwieja JJ, Roy H, Nguyen T, Rood JC, Windhauser MM, Bray GA. Fat and carbohydrate balances during adaptation to a high-fat. Am J Clin Nutr 71: 450–457, 2000. [DOI] [PubMed] [Google Scholar]
- 96. Song B, Thomas DM. Dynamics of starvation in humans. J Math Biol 54: 27–43, 2007. [DOI] [PubMed] [Google Scholar]
- 97. Stein TP, Leskiw MJ, Schluter MD, Hoyt RW, Lane HW, Gretebeck RE, LeBlanc AD. Energy expenditure and balance during spaceflight on the space shuttle. Am J Physiol Regul Integr Comp Physiol 276: R1739–R1748, 1999. [DOI] [PubMed] [Google Scholar]
- 98. Stinebaugh BJ, Schloeder FX. Studies on the natriuresis of fasting. I. Effect of prefast intake. Metabolism 15: 828–837, 1966. [DOI] [PubMed] [Google Scholar]
- 99. Strawford A, Antelo F, Christiansen M, Hellerstein MK. Adipose tissue triglyceride turnover, de novo lipogenesis, and cell proliferation in humans measured with 2H2O. Am J Physiol Endocrinol Metab 286: E577–E588, 2004. [DOI] [PubMed] [Google Scholar]
- 100. Svetkey LP, Stevens VJ, Brantley PJ, Appel LJ, Hollis JF, Loria CM, Vollmer WM, Gullion CM, Funk K, Smith P, Samuel-Hodge C, Myers V, Lien LF, Laferriere D, Kennedy B, Jerome GJ, Heinith F, Harsha DW, Evans P, Erlinger TP, Dalcin AT, Coughlin J, Charleston J, Champagne CM, Bauck A, Ard JD, Aicher K, Weight Loss Maintenance Collaborative Research Group Comparison of strategies for sustaining weight loss: the weight loss maintenance randomized controlled trial. JAMA 299: 1139–1148, 2008. [DOI] [PubMed] [Google Scholar]
- 101. Todd KS, Butterfield GE, Calloway DH. Nitrogen balance in men with adequate and deficient energy intake at three levels of work. J Nutr 114: 2107–2118, 1984. [DOI] [PubMed] [Google Scholar]
- 102. Trabulsi J, Schoeller DA. Evaluation of dietary assessment instruments against doubly labeled water, a biomarker of habitual energy intake. Am J Physiol Endocrinol Metab 281: E891–E899, 2001. [DOI] [PubMed] [Google Scholar]
- 103. Tremblay A, Despres JP, Theriault G, Fournier G, Bouchard C. Overfeeding and energy expenditure in humans. Am J Clin Nutr 56: 857–862, 1992. [DOI] [PubMed] [Google Scholar]
- 104. Trimmer JK, Casazza GA, Horning MA, Brooks GA. Autoregulation of glucose production in men with a glycerol load during rest and exercise. Am J Physiol Endocrinol Metab 280: E657–E668, 2001. [DOI] [PubMed] [Google Scholar]
- 105. van der Walt WH, Wyndham CH. An equation for prediction of energy expenditure of walking and running. J Appl Physiol 34: 559–563, 1973. [DOI] [PubMed] [Google Scholar]
- 106. Vazquez JA, Morse EL, Adibi SA. Effect of dietary fat, carbohydrate, and protein on branched-chain amino acid catabolism during caloric restriction. J Clin Invest 76: 737–743, 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Wagenmakers AJ. Tracers to investigate protein and amino acid metabolism in human subjects. Proc Nutr Soc 58: 987–1000, 1999. [DOI] [PubMed] [Google Scholar]
- 108. Wang Z, Shen W, Kotler DP, Heshka S, Wielopolski L, Aloia JF, Nelson ME, Pierson RN, Jr, Heymsfield SB. Total body protein: a new cellular level mass and distribution prediction model. Am J Clin Nutr 78: 979–984, 2003. [DOI] [PubMed] [Google Scholar]
- 109. Wang Z, St-Onge MP, Lecumberri B, Pi-Sunyer FX, Heshka S, Wang J, Kotler DP, Gallagher D, Wielopolski L, Pierson RN, Jr, Heymsfield SB. Body cell mass: model development and validation at the cellular level of body composition. Am J Physiol Endocrinol Metab 286: E123–E128, 2004. [DOI] [PubMed] [Google Scholar]
- 110. Weinsier RL, Bracco D, Schutz Y. Predicted effects of small decreases in energy expenditure on weight gain in adult women. Int J Obes Relat Metab Disord 17: 693–700, 1993. [PubMed] [Google Scholar]
- 111. Weinsier RL, Nagy TR, Hunter GR, Darnell BE, Hensrud DD, Weiss HL. Do adaptive changes in metabolic rate favor weight regain in weight-reduced individuals? An examination of the set-point theory. Am J Clin Nutr 72: 1088–1094, 2000. [DOI] [PubMed] [Google Scholar]
- 112. Welle S. Human Protein Metabolism. New York: Springer-Verlag, 1999, p. 288. [Google Scholar]
- 113. Westerterp KR, Donkers JH, Fredrix EW, Boekhoudt P. Energy intake, physical activity and body weight: a simulation model. Br J Nutr 73: 337–347, 1995. [DOI] [PubMed] [Google Scholar]
- 114. Wildenhoff KE. Tubular reabsorption and urinary excretion of acetoacetate and 3-hydroxybutyrate in normal subjects and juvenile diabetics. Acta Med Scand 201: 63–67, 1977. [DOI] [PubMed] [Google Scholar]
- 115. Wing RR, Hill JO. Successful weight loss maintenance. Annu Rev Nutr 21: 323–341, 2001. [DOI] [PubMed] [Google Scholar]
- 116. Wing RR, Phelan S. Long-term weight loss maintenance. Am J Clin Nutr 82: 222S–225S, 2005. [DOI] [PubMed] [Google Scholar]
- 117. Winkler JT. The fundamental flaw in obesity research. Obes Rev 6: 199–202, 2005. [DOI] [PubMed] [Google Scholar]
- 118. Wolever TM, Bentum-Williams A, Jenkins DJ. Physiological modulation of plasma free fatty acid concentrations by diet. Metabolic implications in nondiabetic subjects. Diabetes Care 18: 962–970, 1995. [DOI] [PubMed] [Google Scholar]
- 119. Wolfe RR, Klein S, Carraro F, Weber JM. Role of triglyceride-fatty acid cycle in controlling fat metabolism in humans during and after exercise. Am J Physiol Endocrinol Metab 258: E382–E389, 1990. [DOI] [PubMed] [Google Scholar]
- 120. Wolfe RR, Peters EJ, Klein S, Holland OB, Rosenblatt J, Gary H., Jr Effect of short-term fasting on lipolytic responsiveness in normal and obese human subjects. Am J Physiol Endocrinol Metab 252: E189–E196, 1987. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.