Abstract
Mathematical models of water and solute transport in the kidney have significantly expanded our understanding of renal function in both health and disease. This review describes recent theoretical developments and emphasizes the relevance of model findings to major unresolved questions and controversies. These include the fundamental processes by which urine is concentrated in the inner medulla, the ultrastructural basis of proteinuria, irregular flow oscillation patterns in spontaneously hypertensive rats, and the mechanisms underlying the hypotensive effects of thiazides. Macroscopic models of water, NaCl, and urea transport in populations of nephrons have served to test, confirm, or refute a number of hypotheses related to the urine concentrating mechanism. Other macroscopic models focus on the mechanisms, role, and irregularities of renal hemodynamic control and on the regulation of renal oxygenation. At the mesoscale, models of glomerular filtration have yielded significant insight into the ultrastructural basis underlying a number of disorders. At the cellular scale, models of epithelial solute transport and pericyte Ca2+ signaling are being used to elucidate transport pathways and the effects of hormones and drugs. Areas where further theoretical progress is conditional on experimental advances are also identified.
Keywords: mathematical models, urine concentrating mechanism, tubuloglomerular feedback, glomerular filtration, epithelial transport
the role of the kidney is to maintain fluid and electrolyte homeostasis and to excrete metabolic waste products. The kidney adjusts the composition of urine so that the osmolality of blood, and thus that of surrounding tissues, stays within a narrow interval, around 300 mosmol/kgH2O in mammals. The kidney also plays an essential role in regulating the balance of sodium, potassium, and protons (1, 19, 94). Remarkably, after many decades of careful theoretical and experimental research, key physiological aspects of renal function are still poorly understood, from the microscopic to the macroscopic scale. Perhaps the central question at the macroscale is how highly concentrated urine is formed in the inner medulla. At the cellular scale, several fundamental transport mechanisms are recognized to play an important role in the pathogenesis of diseases such as proteinuria and hypertension, but they have yet to be fully elucidated.
In the search for answers to these questions, mathematical models play a role complementary to experimental investigation. Mathematical models are used to formulate and test hypotheses related to renal function, to incorporate microscale findings (i.e., at the molecular or cellular levels) into more integrated systems (such as the tubule or the whole nephron) so as to understand how the activity of these complex systems is regulated, and to predict the effects of drugs or genetic mutations.
In this review, I describe recent advances in renal transport modeling, over the past two to three years, and emphasize the physiological and pathophysiological relevance of these theoretical studies. Whereas more in-depth descriptions of the history, major assumptions, and basic equations of renal transport models can be found elsewhere (41, 76, 90, 99), I aim to identify areas where collaborations between experimentalists and modelers hold promise for accelerating progress toward a better understanding of unresolved issues.
How Can the Kidney Produce Highly Concentrated Urine?
Macroscopic mathematical models of water, NaCl, and urea transport in populations of nephrons have served to test, confirm, or refute a number of hypotheses related to the urine concentrating mechanism (UCM). In the outer medulla (OM), generation of the corticomedullary osmolality gradient has long been ascribed to the multiplication of a single effect. According to this paradigm, the active transport of NaCl out of thick ascending limbs generates a small transverse osmolality difference at each level of the OM (i.e., the single effect), which is then converted into a large axial osmolality gradient by the countercurrent flows in tubules and vessels. Mathematical models have confirmed that active NaCl reabsorption from thick ascending limbs can generate an OM osmolality gradient that is comparable to experimental measurements, as reviewed in Ref. 76.
Nevertheless, Layton et al. (37) recently suggested that the standard description of countercurrent multiplication in the OM be revised in light of several observations. In the OM of mammalian species such as rats and mice, the structural organization of tubules and vessels is highly specific. The loops of Henle and the collecting ducts (CDs) are arranged in a roughly concentric manner around tightly packed vascular bundles (32, 33). In addition, immunohistochemistry studies have shown that significant portions of short descending limbs do not express aquaporin-1 (AQP-1) water channels in rats, mice, and humans (57, 93, 106); thus water reabsorption from these segments is likely to be small. Both sets of findings suggest that radial osmolality differences between tubules and vessels at a given depth may not be small relative to the axial osmolality gradient, which contradicts the conventional interpretation of countercurrent multiplication in the OM. The region-based mathematical model of the UCM in the rat OM developed by Layton and Layton (35, 36) accounts for the specific organization of the OM by distinguishing four regions centered on a vascular bundle, thereby allowing for preferential interactions among certain tubules and vasa recta. The model predicts significantly differing NaCl and urea concentrations in adjoining regions (Fig. 1) and between tubules and vessels in a given region. In other words, the three-dimensional architecture of the rat OM is thought to generate substantial radial osmolality gradients at each level. Thus, given the significant axial and radial heterogeneities in the OM, the traditional countercurrent multiplication paradigm for the OM concentrating mechanism appears to be incorrect (37).
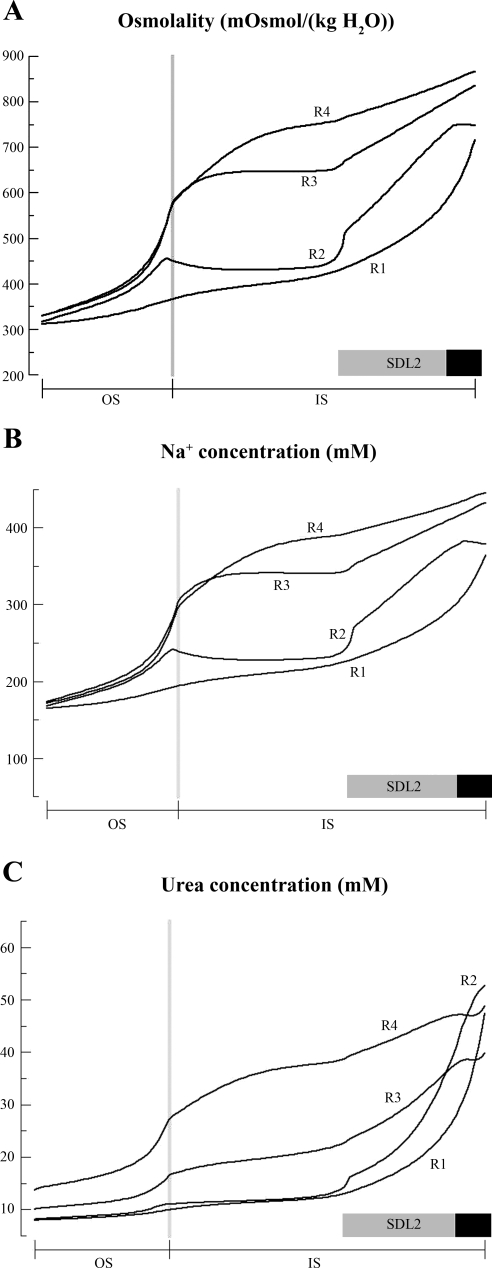
Fig. 1.
Predicted osmolality (A), Na+ concentration (B), and urea concentration profiles (C) in the interstitium of the 4 concentric regions (R1–R4) represented in the region-based model of the rat outer medulla (OM). The structural organization of the OM is represented by means of 4 concentric regions centered on a vascular bundle: an innermost region containing the central vascular bundle (R1), where long descending vasa recta are sequestered; a peripheral region of the vascular bundle (R2); a region neighboring the vascular bundle (R3), where most thick ascending limbs reside; and the region most distant from the vascular bundle (R4), where collecting ducts are located. Vertical dotted lines mark the boundary between the outer stripe (OS) and the inner stripe (IS). Horizontal shaded and solid bars correspond to positions of SDL2 (the water-impermeable, but urea-permeable, portion of the short descending limb located in the IS) and prebend segments, respectively. The region-based model predicts significantly differing NaCl and urea concentrations in adjoining regions and between tubules and vessels in a given region. [From Layton and Layton (35).]
A satisfactory understanding of the urine concentrating mechanism in the inner medulla (IM) has been a goal of several active research programs, but that understanding has yet to emerge. As described below, although computational models have invalidated, at least in part, several theories of the inner medullary UCM, they have not yet succeeded in predicting the maximal urine osmolalities that have been measured in animals. Urine osmolality can reach ∼1,000–2,000 mosmol/kgH2O in primates, ∼3,000 mosmol/kgH2O in rats, and ∼4,000 mosmol/kgH2O in mice and hamsters (76).
The passive mechanism was first proposed by Stephenson (83) and by Kokko and Rector (31). This mechanism posits that the active transport of NaCl in the OM and the cortex, in combination with the urea cycle, serves to concentrate the IM; it rests on the assumption that the urea permeability of Henle's loops is very small. If that is the case, the concentration of NaCl should be significantly greater than that of urea in the ascending limb and vice versa in the CD. Thus passive diffusion of NaCl from ascending limbs and of urea from CDs into the inner medullary interstitium should raise the osmolality of the interstitial fluid, thereby drawing water out of descending limbs and CDs and further concentrating the fluid flowing down in the descending limbs and CDs.
Simulations have shown that for the passive mechanism to operate as initially proposed, the urea permeability of Henle's loop as well as the NaCl permeability of the descending limb must be small, significantly lower in fact than measured values in the rat, hamster, and chinchilla (76). Using those measured values, existing mathematical models of the UCM are not capable of predicting physiological maximum urine osmolalities. Thus the relevance of the passive mechanism, at least in those species, has been questioned.
Nevertheless, Layton and colleagues (65) recently suggested that the passive mechanism be reconsidered in light of new observations on the IM architecture by Pannabecker and colleagues (62–64, 66). They proposed that the passive mechanism be called instead a “solute-separation, solute-mixing” (SSSM) mechanism, because it requires separation of both NaCl in loops of Henle and urea in CDs and their subsequent mixing in the interstitium and vasculature of the IM (40). Pannabecker and colleagues (61–64, 66) developed a computer-assisted process to reconstruct the vascular and tubular structures of the rat IM. Their findings on the axially variable expression of AQP-1 water channels and CLC-K1 chloride channels along thin limbs of Henle's loop (61) led to the development of two mathematical models of the UCM that incorporated these data (40). The predictions of the so-called pipe model, which is similar to the passive hypothesis, were in good agreement with in vivo micropuncture studies (67), but the model still failed to predict the very high osmolalities that have been measured in rats (40). More recent observations by Pannabecker and Dantzler (63, 64) indicate that loops and vasa recta are organized around primary clusters of CDs and that the arrangement of the CDs and some of the ascending vasa recta and ascending thin limbs inside the CD clusters forms interstitial nodal spaces (i.e., isolated microdomains) that may serve as solute-mixing compartments (Fig. 2). Their findings suggest that the concentrating mechanism in the IM may consist of three different countercurrent systems, involving different subpopulations of long loops of Henle: two in the outer portions of the IM (one in the central regions of the CD clusters, and another in the intercluster regions), and a third in the inner portion of the IM (65). A mathematical model that accounts for those highly specific anatomical features has yet to be developed.
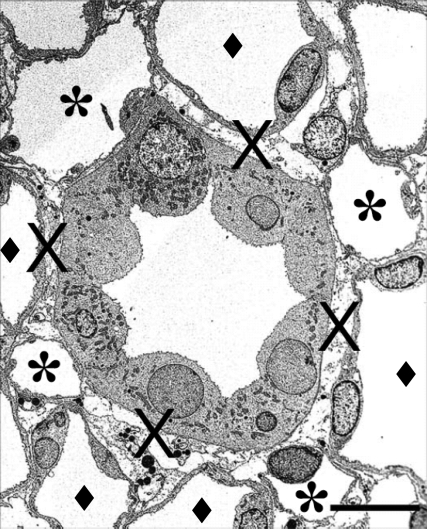
Fig. 2.
Electron micrograph showing transverse sections of collecting ducts (CDs), ascending vasa recta (AVR), and ascending thin limbs (ATLs) from 1.5 mm below the base of the inner medulla. The CD at the center is surrounded by 4 AVR (∗); other tubular structures surrounding the CD are ATLs (♦). Interstitial nodal spaces (×) are formed between CD, AVR, and ATL. Scale bar, 10 μm. It has been hypothesized that such microdomains could facilitate solute mixing and thus play an important role in generating the inner medullary osmolality gradient. [From Pannabecker and Dantzler (63) as reprinted in Pannabecker et al. (65).]
Such a model will more than likely predict higher urinary osmolalities than current approaches, but it remains unclear whether the SSSM mechanism is the main principle underlying the UCM in the inner medulla. The region-based model of the rat OM, which takes into consideration the preferential interactions between certain types of vessels and tubules in the OM (vide supra), suggests that regionalization augments the axial osmolality gradient in the OM by less than 50% (36). As noted by Layton and colleagues (37), other biophysical principles also may be fundamental to the concentrating mechanism in the IM.
It has been postulated that the rhythmic contractions of the pelvic wall contribute to the UCM in the IM. Expanding on a hypothesis first advanced by Schmidt-Nielsen (77), Knepper et al. (30) proposed that hyaluronan, the main component of the medullary interstitial matrix, can use the mechanical energy from the pelvic contractions to lower the interstitial pressure after each contraction and thereby drive water efflux from the descending limb of Henle. This would in turn raise the luminal osmolality above that of the interstitium and generate a single effect for concentration of urine. However, thermodynamic analysis of this process indicates that the pressures exerted on the inner medullary tissue can only account for a small fraction of the concentrating work in the inner medulla (70, 100). Very recently, Pinter and Shohet (69) suggested that pelvic contractions could contribute to the IM osmolality gradient via a different mechanism, one based on the Gibbs-Donnan effect between two interstitial compartments, one containing hyaluronan and the other extravasated plasma albumin. According to their hypothesis, rhythmic pressure increases could squeeze dilute fluid out of the hyaluronan compartment and simultaneously accelerate the outflow of fluid and albumin into the ascending vasa recta from the extravasated plasma albumin compartment. To date, the pressure exerted by pelvic contractions has not been measured, and no mathematical model of the UCM has formally incorporated the role of these contractions. Whether the latter can generate a single effect thus remains to be ascertained.
Several other hypotheses regarding the UCM have been put forward in the past decade or so, but none has been conclusive. Wexler and colleagues (96, 103) investigated the role of the three-dimensional organization of the renal medulla and showed that preferential interactions between tubules and vessels can, in theory, increase papillary tip concentrations of NaCl and urea. The model of Jen and Stephenson (28) demonstrated that the accumulation of an “external” osmolyte in the inner medullary interstitium could also, in principle, enhance the corticomedullary osmolality gradient by driving water out of descending limbs. Thomas and colleagues (22, 87) subsequently showed that, in theory, the accumulation of lactate via anaerobic glycolysis could indeed significantly amplify the IM accumulation of NaCl. However, the concomitant production of protons could abolish this osmotic effect, depending on the buffering ions (90). The efficient IM recycling of lactate by vascular countercurrent exchange requires that the descending vasa recta (DVR) permeability to glucose be low compared to that of other vessels, whereas the DVR permeability to lactate needs to be significantly higher than that to sodium and urea (22). Measurements of these permeabilities would therefore help to assess the lactate hypothesis.
Why Are Tubuloglomerular Feedback-Mediated Oscillations Irregular in Hypertensive Rats?
Macroscopic models of solute and water transport in the kidney also have been developed to examine other aspects of renal function, such as tubuloglomerular feedback (TGF), renal perfusion, and medullary oxygenation.
The TGF is thought to play a fundamental role in balancing the glomerular filtration rate (GFR) with transport rates across tubular epithelia and in maintaining a relatively constant delivery of water and solutes to the distal nephron. In conjunction with the myogenic mechanism, the TGF also participates in the autoregulation of renal blood flow (RBF) and protects the kidney against sudden or sizeable fluctuations in blood pressure (78). The TGF and myogenic mechanisms each generate oscillations in tubular fluid flow, at respective frequencies of 20–40 and 100–200 mHz. Since both mechanisms are mediated by constriction of the afferent arteriole, they interact: TGF modulates the amplitude and the frequency of the myogenic oscillation (81).
The observation two decades ago in spontaneously hypertensive rats that TGF-mediated oscillations are highly irregular, with a pattern suggestive of deterministic chaos (24, 105), has motivated many theoretical studies of the TGF mechanism. Possible reasons for the irregular fluctuations include temporal variations in TGF parameters and interactions between the TGF systems of nephrons originating from a common cortical radial artery. Ongoing work by Layton et al. (38, 39), as well as Marsh, Holstein-Rathlou, and colleagues (8, 51, 52), focuses on nephron-to-nephron coupling and seeks to understand why synchronization patterns are different in normotensive and hypertensive rats. The impact of irregular flow oscillations on NaCl reabsorption across the aldosterone-sensitive distal nephron, where the sodium balance is regulated, has yet to be determined. Thus it is not clear whether irregular pressure and flow patterns contribute to the renal changes in hypertension or whether they are a consequence of those changes.
How is Renal Blood Flow Regulated?
TGF models also have served to investigate the mechanisms underlying the regulation of RBF and GFR. Several theoretical studies have shown that the dynamic autoregulation of RBF is due to the combined action of TGF and the myogenic response (17, 25, 53, 58). Marsh et al. (50) developed a multiscale model of blood flow regulation, which includes a detailed description of Ca2+ dynamics in arteriolar cells, to investigate the nonlinear interactions between the two mechanisms. As shown in Fig. 3, the model predicts autoregulation of single nephron GFR over a broad range of blood pressures. Layton and colleagues investigated how physiological parameters determine the emergence of TGF-mediated oscillations in GFR (42) as well as the effects of limit-cycle oscillations, which can appear spontaneously (29), on fluid and sodium delivery to the distal tubule (43, 59, 71). Sustained perturbations in proximal tubule flow that can initiate or terminate limit-cycle oscillations are predicted to significantly affect the distal delivery of NaCl, as shown in Fig. 4. Other studies have focused on the renal myogenic response (47). A detailed model of afferent arteriole fluid dynamics and myogenic reactivity was developed to examine the importance of nitric oxide advection (80). A recent study suggests that systolic blood pressure, and not mean blood pressure, is the primary determinant of the myogenic response of the afferent arteriole (104).
Fig. 3.
Mean single nephron glomerular filtration rate (GFR) as a function of arterial blood pressure, as predicted by a model of tubuloglomerular feedback (TGF) and the myogenic mechanism in afferent arterioles (50). Results are shown for 5 different values of ξ, the coefficient coupling TGF to the myogenic mechanism. The model predicts autoregulation of GFR and renal blood flow over a broad range of blood pressure values. [From Marsh et al. (50).]
Fig. 4.
Impact of proximal tubule flow pertubations on distal water and Cl− delivery, as predicted by a model of the TGF mechanism (59). The maximum difference in percent distal delivery between the stable limit-cycle oscillation (LCO) state and the steady state is shown as a function of TGF sensitivity (κ). In the stable LCO state, a ±12 nl/min perturbation is applied to the flow in Bowman's capsule. The model predicts that LCO causes greater change in distal Cl− delivery than in distal water delivery and that this discrepancy becomes more pronounced as TGF sensitivity increases. [From Oldson et al. (59).]
Models of the medullary microvasculature have examined the contribution of vasa recta to the urine concentrating mechanism (12, 60) and the transport of nitric oxide, a potent vasodilator, in the medulla (107, 109). The contractility of resistance vessels such as DVR is regulated by the variations in intracellular Ca2+ concentration in both endothelium and smooth muscle. Some of our studies have focused on calcium transport dynamics in pericytes, the smooth muscle cells that impart contractile properties to DVR. In contrast with typical cellular representations, our pericyte model takes into account the microdomains formed through close association of the sarcoplasmic reticulum (SR) with the overlying plasma membrane (Fig. 5). Variations in microdomain Na+ pump activity, such as those induced by ouabain, are predicted to modulate both the loading of Ca2+ into SR stores and cytosolic Ca2+ concentrations (14). These studies have elucidated the mechanisms by which ouabain and angiotensin II affect Ca2+ signaling in pericytes (13, 15). A multiscale model linking cellular events to changes in vessel contractility and overall blood flow in the renal medulla has yet to be built.
Fig. 5.
Schematic representation of the pericyte cell in a model of Ca2+ signaling (13). The model distinguishes 3 compartments: bulk cytosol (CYT), microdomains (MD), and sarcoplasmic reticulum (SR). Not shown are KCa, Kir, KATP, and Kv channels and the chelating agents calmodulin and calsequestrin. Comparison between experimental Ca2+ oscillation patterns and model predictions suggests that ryanodyne receptors (RyR) and inositol trisphosphate receptors (IP3R) reside on separate SR stores in pericytes. soc, Store-operated channel; v, voltage-dependent channel. [From Edwards and Pallone (13).]
How is Kidney Oxygenation Regulated?
Both acute and chronic renal diseases are characterized by tissue hypoxia (2, 18). The availability of oxygen (O2) in the cortex and the medulla depends on the balance between supply and demand; that is, O2 distribution is regulated by renal perfusion on one hand and renal metabolic requirements (particularly for active NaCl reabsorption across thick ascending limbs) on the other hand. Evans et al. (16) recently argued that arterial-to-venous (AV) oxygen shunting could play an important role in the dynamic regulation of kidney oxygenation as well as the development of renal hypoxia in kidney disease. They proposed that RBF-dependent changes in AV O2 shunting may explain why renal oxygen tension (Po2) remains stable when RBF is varied within physiological ranges (±30% relative to basal levels) and oxygen consumption does not vary significantly. The evidence in favor of such a mechanism remains indirect thus far. Modeling studies have shown that the countercurrent arrangement of DVR and AVR in the medulla results in O2 shunting from DVR to AVR (108), similar to AV oxygen shunting in the cortex, and significantly limits O2 delivery to the deep medulla. Our recent model of oxygen transport in the OM (3, 4) suggests that the structural organization of the OM results in significant Po2 gradients in both the axial and radial directions (Fig. 6). The segregation of DVR, the main supply of O2, at the center and immediate periphery of the vascular bundles limits O2 reabsorption from long DVR, thereby preserving O2 delivery to the IM but severely restricting O2 distribution to the interbundle region where thick ascending limbs are located. The model predicts that, as a result, the concentrating capacity of the OM is significantly reduced. Further theoretical and experimental studies are needed to elucidate the contribution of cortical AV shunting to the regulation of intrarenal oxygenation.
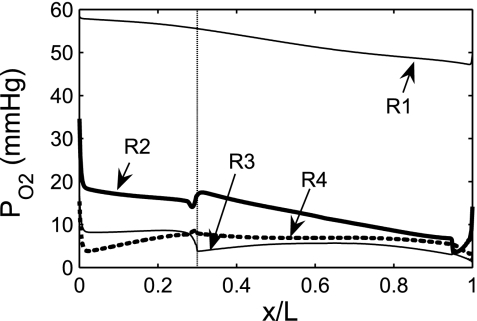
Fig. 6.
Oxygen tension (Po2) profiles predicted by a model of O2 transport in the rat OM (4). Shown is Po2 in the interstitium of the 4 concentric regions (R1–R4) distinguished in the region-based representation of the rat OM. x/L denotes the ratio of the axial coordinate to the total length of the OM. The model suggests that regionalization has a significant impact on the radial distribution of O2 and that active Na+ reabsorption across medullary thick ascending limbs is severely limited by low medullary Po2. [From Chen et al. (4).]
How Selective Is the Glomerular Filtration Barrier?
The filtration of blood by glomerular capillaries has been the object of a large modeling effort, which has significantly improved our understanding of glomerular function in both health and disease. The models developed by Deen, Myers, and colleagues have served to elucidate the mechanisms of hypofiltration in healthy, aging subjects (23), as well as the ultrastructural basis underlying a number of disorders, such as minimal change and membranous nephropathy (9, 82), IgA nephropathy (45), and preeclampsia (34). Nevertheless, the respective contribution of the three different components of the glomerular capillary wall, namely, the endothelium, the glomerular basement membrane, and the podocyte layer, remains a matter of controversy, as briefly reviewed in Ref. 54. The significance of the recently identified subpodocyte space (SPS), which covers ∼60% of the filtering portion of the glomerular filtration surface (55), also merits further investigation. A mathematical model of flow through the SPS predicts that its resistance is greater than that of the glomerular filtration barrier at physiological pressures and suggests that podocytes could play a role in regulating the rate of glomerular filtration across at least a part of the barrier by modulating the dimensions of the SPS (56).
The selectivity of the glomerular filtration barrier to albumin and the origin of proteinuria are the object of an ongoing debate (5, 6, 27) to which mathematical models have contributed. Historically, the glomerular filter has been thought to be nearly impermeable to albumin (with a glomerular sieving coefficient, or GSC, lower than 0.001) because of its large charge selectivity. The polyanionic glycoproteins that bind to the endothelial fenestrations, the glomerular membrane, and the epithelial cells are believed to strongly repel polyanions (54). However, Comper and colleagues (74, 75) have argued instead that albumin filtration is essentially determined by size selectivity alone and that the albumin GSC is orders of magnitude higher, ∼0.04. According to their hypothesis, the large amounts of filtered protein are then rapidly and efficiently removed from the tubular lumen by proximal tubular (PT) cells via endocytosis (75). This viewpoint has significant implications for the treatment of nephrotic syndrome, because it implies that albuminuria is primarily a tubular defect, not a glomerular defect (5, 7), but it remains highly controversial (5, 6, 27). The arguments and findings of Comper and colleagues have been challenged at different levels, in particular by recent measurements of albumin GSC (68, 85) and by a mathematical model of albumin reabsorption in the proximal tubule (44). To be consistent with micropuncture measurements of PT albumin concentrations, the filtered load of albumin obtained assuming a GSC of 0.04 would have to be reabsorbed in the first millimeter or so of tubule (6). However, the model of Lazzara and Deen (44) suggests that mass transfer limitations are such that the rate of albumin reabsorption by PT cells is too low to allow for the rapid retrieval of large quantities of albumin. Thus the albumin retrieval hypothesis cannot be reconciled with measurements of tubular fluid concentrations (Fig. 7). In addition, Tanner (85) recently identified several technical limitations that were likely responsible for the high albumin GSC values reported by the Comper group, including animal conditions and signal contamination by out-of-focus fluorescence. His objections have been supported by experiments conducted by Peti-Peterdi (68).
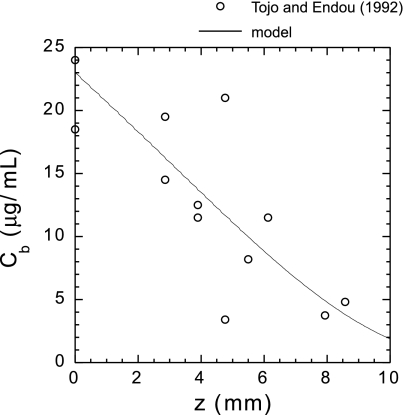
Fig. 7.
Comparison between measured and calculated bulk albumin concentration (Cb) vs. axial position (z) along the rat proximal tubule. The data points are from Tojo and Endou (91), and the predictions are from a model of albumin reabsorption along the proximal tubule (44). To be consistent with micropuncture measurements, the albumin retrieval hypothesis requires that almost all the filtered load of albumin be reabsorbed in the first millimeter or so of tubule. However, the model predicts that no more than ∼60% of filtered albumin can be reabsorbed within the first millimeter. [From Lazzara and Deen (44).]
How is Epithelial Solute Transport Regulated?
At the microscale, the reabsorption or secretion of water and solutes along the different nephron segments is mediated by epithelial transport processes. Given the many different types of channels, transporters, exchangers, and pumps that are present in a given cell and the coexistence of different cell types in some renal epithelia, mathematical models of tubular epithelial transport are necessary to understand how Na+, K+, Cl−, and acid-base fluxes are coupled and how overall cell function is regulated by molecular events. A significant body of such modeling studies, reviewed in Ref. 99, has generally been successful in predicting in vitro and in vivo transport rates while also elucidating transport pathways and the effects of hormones and drugs.
In a 2003 review of mathematical models of renal epithelial transport, Weinstein (99) summarized fundamental questions that had yet to be answered. The latter included the relative contribution of the paracellular and transcellular routes for water transport in the PT, the mechanisms underlying perfusion-absorption balance, the magnitude of in vivo and in vitro K+ fluxes in the CD, and the specific Cl− exit pathways in the OMCD. Since then, progress has been made on several of these issues.
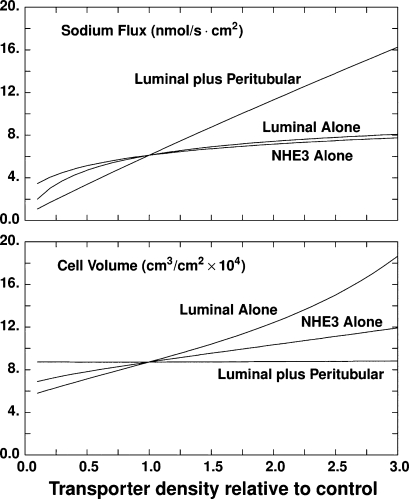
Experimental studies investigating perfusion-absorption balance, i.e., the modulation of epithelial Na+ reabsorption by luminal flow, had shown that increases in fluid velocity recruit new Na+/H+ exchangers into the luminal membrane (48, 72). Guo et al. (20) postulated that the PT brush-border microvilli could act as a mechanosensor of fluid flow. Indeed, later experiments demonstrated that Na+ and HCO3− reabsorption varies proportionally with the torque exerted on the microvilli (10, 11). The recent rat PT model developed by Weinstein et al. (102) incorporated these findings by relating the density of luminal and/or peritubular transporters to the magnitude of the microvillous torque. An important conclusion of this work was that scaling the density of luminal transporters alone could not explain experimental observations, i.e., coordinated regulation of both luminal and peritubular transporters is necessary to account for the overall impact of luminal flow on Na+ reabsorption (Fig. 8). Another recent model of PT cell homeostasis that is based on optimal control theory also suggests that to minimize variations in cell volume and composition during perfusion-absorption balance, the cell must regulate both luminal and peritubular transporter expression (101). Experimental studies are needed to elucidate the mechanisms underlying luminal-peritubular cross talk.
Fig. 8.
Impact of scaling proximal tubule transporter density with microvillous torque on transepithelial Na+ flux (top) and cell volume (bottom), as predicted by a model of rat proximal tubule (102). Calculations are done for variations in transporter density: luminal membrane type 3 Na+/H+ exchanger (NHE3) alone, all luminal membrane transporters, or coordinated scaling of luminal plus peritubular transporters. The abscissa is transporter density relative to baseline. Only a coordinated luminal plus peritubular scaling yields a linear response of the Na+ flux, as well as insignificant cell volume changes, over a broad range of axial flow values. [From Weinstein et al. (102).]
A new model of transport along the entire distal nephron has clarified the locus of K+ secretion (97). The model predicts that K+ secretion occurs primarily along the connecting tubule (CNT), that is, about five times the load delivered to the distal nephron. Thus the resulting increase in luminal K+ concentration drives diffusive K+ reabsorption in the downstream medullary segments; model results predict that one-half of the secreted K+ is reabsorbed before the final urine, in agreement with micropuncture measurements (49).
How Do Antihypertensive Thiazides Operate In the Distal Nephron?
All known Mendelian forms of hypertension and hypotension are associated with alterations in renal salt reabsorption, mainly in the distal nephron (46). Thiazides, which inhibit NaCl cotransport in the distal convoluted tubule (DCT), are often favored in the treatment of hypertension, because they reduce sodium reabsorption, plasma volume, and blood pressure. Nevertheless, the use of thiazides as the first-line treatment of hypertension remains controversial because of their negative side effects (73): thiazides exacerbate features of metabolic syndrome, increase the risk for developing diabetes, and generate acid-base disturbances. A better understanding of the underlying mechanisms could guide strategies to improve antihypertensive treatments.
The distal nephron model developed by Weinstein (97) was used to investigate the pathways leading to metabolic alkalosis with thiazides and furosemide and to metabolic acidosis with amiloride. Its results suggest that the DCT-CNT is the main site of net acid excretion (Fig. 9). Thiazides are predicted to have a local impact on acid excretion; they increase Na+/H+ exchange within the DCT but have minor effects on acid secretion in the remainder of the nephron. An interesting prediction of the model, which has yet to be verified experimentally, is that due to enhanced Cl− delivery to the CNT, the latter segment shifts from acid secretion to robust HCO3− secretion by the β-cells, thereby blunting urine acidification. A similar effect is predicted in response to furosemide, i.e., the model indicates that the increased delivery of NaCl to the CNT produces significant HCO3− secretion by β-cells so that the urine pH rises to 6.23 (97). In contrast, experimentally furosemide was found to lower the urine pH from 6.02 to 5.16 in rat micropuncture studies (26). Several hypotheses were examined in an attempt to resolve this discrepancy. The most plausible is that furosemide induces a very significant upregulation of CNT α-cell transport, perhaps as a result of increased luminal flow. Thus not only the model but also several experimental findings (reviewed in Ref. 97), suggest an adaptive response to furosemide diuresis.
Fig. 9.
Acid-base transport in the distal nephron under baseline conditions, as predicted by a model of distal nephron acidification (97). The abscissa is distance along the distal nephron (in cm). The elongated ticks mark the boundaries of the distal convoluted tubule (DCT), connecting tubule (CNT), cortical collecting duct (CCD), outer medullary collecting duct (OMCD), and inner medullary collecting duct (IMCD). Left, from top to bottom: lumen pH and concentrations of HCO3−, titrable acid (TA), and NH4+; right from top to bottom: axial flows of net acid, HCO3−, TA, and NH4+. The model predicts that the DCT-CNT is the principal locus for net acid secretion, responsible for 70% of the increase in net acid flow from the DCT to final urine. [From Weinstein (97).]
Thiazides also have been shown to inhibit NaCl reabsorption by ∼50% in the rat and mouse cortical collecting duct (CCD), downstream of the DCT, via an electroneutral pathway that is distinct from the amiloride-sensitive electrogenic pathway (45a, 86). The molecular target of thiazides in the CCD remains uncertain, but the electroneutral pathway is likely to involve pendrin, the apical Cl−/HCO3− exchanger expressed by intercalated β-cells Chloride reabsorption is abolished in pendrin knockout mice (95), and these mice are protected against hypertension induced by the aldosterone analog deoxycorticosterone pivalate (92). Experimental findings in the rabbit CCD also suggest that the most important Cl− transport pathway is through the β-cell (79). However, current mathematical models predict that the Cl− flux is predominantly paracellular in the CCD (84, 98). Further studies are needed to determine fully the ionic transport pathways in the CCD and to characterize their response to thiazides.
Conclusions
Mathematical models of renal transport continue to significantly enhance our understanding of kidney function and dysfunction. Inevitably, further progress in many areas is conditional on new experimental advances. The complexity of the kidney is such that mathematical models of renal function are highly dependent on in vivo and in vitro measurements, some of which become clear objectives only in light of the models themselves. Thus an important challenge for modelers is how to make their work more accessible, their hypotheses and suggestions more widely read, and their tools more useful to experimental researchers. The Renal Physiome Project seeks to make a major effort to facilitate access to quantitative kidney data (http://physiome.ibisc.fr/qkdb/) and to make mathematical models of the kidney part of the normal toolbox of renal research laboratories (21, 88, 89). Whether through this interface or another, greater feedback between modelers and experimentalists should increase the pace of progress toward a common goal, an improved understanding and treatment of kidney diseases.
GRANTS
This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK53775.
DISCLOSURES
No conflicts of interest are declared by the author.
REFERENCES
- 1.Bonventre JV, Leaf A. Sodium homeostasis: steady states without a set point. Kidney Int 21: 880–883, 1982 [DOI] [PubMed] [Google Scholar]
- 2.Bonventre JV, Weinberg JM. Recent advances in the pathophysiology of ischemic acute renal failure. J Am Soc Nephrol 14: 2199–2210, 2003 [DOI] [PubMed] [Google Scholar]
- 3.Chen J, Edwards A, Layton AT. A mathematical model of O2 transport in the rat outer medulla. II. Impact of outer medullary architecture. Am J Physiol Renal Physiol 297: F537–F548, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen J, Layton AT, Edwards A. A mathematical model of O2 transport in the rat outer medulla. I. Model formulation and baseline results. Am J Physiol Renal Physiol 297: F517–F536, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Christensen EI, Birn H, Rippe B, Maunsbach AB. Controversies in nephrology: renal albumin handling, facts, and artifacts. Kidney Int 72: 1192–1194, 2007 [DOI] [PubMed] [Google Scholar]
- 6.Comper WD, Haraldsson B, Deen WM. Resolved: normal glomeruli filter nephrotic levels of albumin. J Am Soc Nephrol 19: 427–432, 2008 [DOI] [PubMed] [Google Scholar]
- 7.Comper WD, Hilliard LM, Nikolic-Paterson DJ, Russo LM. Disease-dependent mechanisms of albuminuria. Am J Physiol Renal Physiol 295: F1589–F1600, 2008 [DOI] [PubMed] [Google Scholar]
- 8.Ditlevsen S, Yip KP, Marsh DJ, Holstein-Rathlou NH. Parameter estimation of feedback gain in a stochastic model of renal hemodynamics: differences between spontaneously hypertensive and Sprague-Dawley rats. Am J Physiol Renal Physiol 292: F607–F616, 2007 [DOI] [PubMed] [Google Scholar]
- 9.Drumond MC, Kristal B, Myers BD, Deen WM. Structural basis for reduced glomerular filtration capacity in nephrotic humans. J Clin Invest 94: 1187–1195, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Du Z, Duan Y, Yan Q, Weinstein AM, Weinbaum S, Wang T. Mechanosensory function of microvilli of the kidney proximal tubule. Proc Natl Acad Sci USA 101: 13068–13073, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Du Z, Yan Q, Duan Y, Weinbaum S, Weinstein AM, Wang T. Axial flow modulates proximal tubule NHE3 and H-ATPase activities by changing microvillus bending moments. Am J Physiol Renal Physiol 290: F289–F296, 2006 [DOI] [PubMed] [Google Scholar]
- 12.Edwards A, Pallone TL. Facilitated transport in vasa recta: theoretical effects on solute exchange in the medullary microcirculation. Am J Physiol Renal Physiol 272: F505–F514, 1997 [DOI] [PubMed] [Google Scholar]
- 13.Edwards A, Pallone TL. Mechanisms underlying angiotensin II-induced calcium oscillations. Am J Physiol Renal Physiol 295: F568–F584, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Edwards A, Pallone TL. Modification of cytosolic calcium signaling by subplasmalemmal microdomains. Am J Physiol Renal Physiol 292: F1827–F1845, 2007 [DOI] [PubMed] [Google Scholar]
- 15.Edwards A, Pallone TL. Ouabain modulation of cellular calcium stores and signaling. Am J Physiol Renal Physiol 293: F1518–F1532, 2007 [DOI] [PubMed] [Google Scholar]
- 16.Evans RG, Gardiner BS, Smith DW, O'Connor PM. Intrarenal oxygenation: unique challenges and the biophysical basis of homeostasis. Am J Physiol Renal Physiol 295: F1259–F1270, 2008 [DOI] [PubMed] [Google Scholar]
- 17.Feldberg R, Colding-Jorgensen M, Holstein-Rathlou NH. Analysis of interaction between TGF and the myogenic response in renal blood flow autoregulation. Am J Physiol Renal Fluid Electrolyte Physiol 269: F581–F593, 1995 [DOI] [PubMed] [Google Scholar]
- 18.Fine LG, Bandyopadhay D, Norman JT. Is there a common mechanism for the progression of different types of renal diseases other than proteinuria? Towards the unifying theme of chronic hypoxia. Kidney Int 57: S22–S26, 2000 [PubMed] [Google Scholar]
- 19.Giebisch G. Renal potassium transport: mechanisms and regulation. Am J Physiol Renal Physiol 274: F817–F833, 1998 [DOI] [PubMed] [Google Scholar]
- 20.Guo P, Weinstein AM, Weinbaum S. A hydrodynamic mechanosensory hypothesis for brush border microvilli. Am J Physiol Renal Physiol 279: F698–F712, 2000 [DOI] [PubMed] [Google Scholar]
- 21.Harris PJ, Buyya R, Chu X, Kobialka T, Kazmierczak E, Moss R, Appelbe W, Hunter PJ, Thomas SR. The virtual kidney: an eScience interface and grid portal. Philos Transact A Math Phys Eng Sci 367: 2141–2159, 2009 [DOI] [PubMed] [Google Scholar]
- 22.Hervy S, Thomas SR. Inner medullary lactate production and urine-concentrating mechanism: a flat medullary model. Am J Physiol Renal Physiol 284: F65–F81, 2003 [DOI] [PubMed] [Google Scholar]
- 23.Hoang K, Tan JC, Derby G, Blouch KL, Masek M, Ma I, Lemley KV, Myers BD. Determinants of glomerular hypofiltration in aging humans. Kidney Int 64: 1417–1424, 2003 [DOI] [PubMed] [Google Scholar]
- 24.Holstein-Rathlou NH, Leyssac PP. TGF-mediated oscillations in proximal intratubular pressure: differences between spontaneously hypertensive rats and Wistar-Kyoto rats. Acta Physiol Scand 126: 333–339, 1986 [DOI] [PubMed] [Google Scholar]
- 25.Holstein-Rathlou NH, Marsh DJ. A dynamic model of renal blood flow autoregulation. Bull Math Biol 56: 411–429, 1994 [DOI] [PubMed] [Google Scholar]
- 26.Hropot M, Fowler N, Karlmark B, Giebisch G. Tubular action of diuretics: distal effects on electrolyte transport and acidification. Kidney Int 28: 477–489, 1985 [DOI] [PubMed] [Google Scholar]
- 27.Jarad G, Miner JH. Albuminuria, wherefore art thou? J Am Soc Nephrol 20: 455–457, 2009 [DOI] [PubMed] [Google Scholar]
- 28.Jen JF, Stephenson JL. Externally driven countercurrent multiplication in a mathematical model of the urinary concentrating mechanism of the renal inner medulla. Bull Math Biol 56: 491–514, 1994 [DOI] [PubMed] [Google Scholar]
- 29.Just A, Wittmann U, Ehmke H, Kirchheim HR. Autoregulation of renal blood flow in the conscious dog and the contribution of the tubuloglomerular feedback. J Physiol 506: 275–290, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Knepper MA, Saidel GM, Hascall VC, Dwyer T. Concentration of solutes in the renal inner medulla: interstitial hyaluronan as a mechano-osmotic transducer. Am J Physiol Renal Physiol 284: F433–F446, 2003 [DOI] [PubMed] [Google Scholar]
- 31.Kokko JP, Rector FC., Jr Countercurrent multiplication system without active transport in inner medulla. Kidney Int 2: 214–223, 1972 [DOI] [PubMed] [Google Scholar]
- 32.Kriz W. Structural organization of renal medullary circulation. Nephron 31: 290–295, 1982 [DOI] [PubMed] [Google Scholar]
- 33.Kriz W. Structural organization of the renal medulla: comparative and functional aspects. Am J Physiol Regul Integr Comp Physiol 241: R3–R16, 1981 [DOI] [PubMed] [Google Scholar]
- 34.Lafayette RA, Druzin M, Sibley R, Derby G, Malik T, Huie P, Polhemus C, Deen WM, Myers BD. Nature of glomerular dysfunction in pre-eclampsia1. Kidney Int 54: 1240–1249, 1998 [DOI] [PubMed] [Google Scholar]
- 35.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol 289: F1346–F1366, 2005 [DOI] [PubMed] [Google Scholar]
- 36.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. II. Parameter sensitivity and tubular inhomogeneity. Am J Physiol Renal Physiol 289: F1367–F1381, 2005 [DOI] [PubMed] [Google Scholar]
- 37.Layton AT, Layton HE, Dantzler WH, Pannabecker TL. The mammalian urine concentrating mechanism: hypotheses and uncertainties. Physiology 24: 250–256, 2009 [DOI] [PubMed] [Google Scholar]
- 38.Layton AT, Moore LC, Layton HE. Multistability in tubuloglomerular feedback and spectral complexity in spontaneously hypertensive rats. Am J Physiol Renal Physiol 291: F79–F97, 2006 [DOI] [PubMed] [Google Scholar]
- 39.Layton AT, Moore LC, Layton HE. Multistable dynamics mediated by tubuloglomerular feedback in a model of coupled nephrons. Bull Math Biol 71: 515–555, 2009 [DOI] [PubMed] [Google Scholar]
- 40.Layton AT, Pannabecker TL, Dantzler WH, Layton HE. Two modes for concentrating urine in rat inner medulla. Am J Physiol Renal Physiol 287: F816–F839, 2004. [DOI] [PubMed] [Google Scholar]
- 41.Layton HE. Mathematical models of the mammalian urine concentrating mechanism. In: Membrane Transport and Renal Physiology: The IMA Volumes in Mathematics and Its Applications, edited by Layton HE, Weinstein AM. New York: Springer, 2002, p. 233–272 [Google Scholar]
- 42.Layton HE, Pitman EB, Moore LC. Bifurcation analysis of TGF-mediated oscillations in SNGFR. Am J Physiol Renal Fluid Electrolyte Physiol 261: F904–F919, 1991 [DOI] [PubMed] [Google Scholar]
- 43.Layton HE, Pitman EB, Moore LC. Limit-cycle oscillations and tubuloglomerular feedback regulation of distal sodium delivery. Am J Physiol Renal Physiol 278: F287–F301, 2000 [DOI] [PubMed] [Google Scholar]
- 44.Lazzara MJ, Deen WM. Model of albumin reabsorption in the proximal tubule. Am J Physiol Renal Physiol 292: F430–F439, 2007 [DOI] [PubMed] [Google Scholar]
- 45.Lemley KV, Lafayette RA, Safai M, Derby G, Blouch K, Squarer A, Myers BD. Podocytopenia and disease severity in IgA nephropathy. Kidney Int 61: 1475–1485, 2002. [DOI] [PubMed] [Google Scholar]
- 45a.Leviel F, Morla L, Pech V, Wall SM, Shull G, Chambrey R, Eladari D. Novel amiloride-resistant thiazide-sensitive electroneutral NaCl transport pathway in mouse CCD. American Society of Nephrology Annual Meeting, Renal Week 2007, San Francisco2007[Abstract SA-FC027]. [Google Scholar]
- 46.Lifton RP, Gharavi AG, Geller DS. Molecular mechanisms of human hypertension. Cell 104: 545–556, 2001 [DOI] [PubMed] [Google Scholar]
- 47.Loutzenhiser R, Bidani A, Chilton L. Renal myogenic response: kinetic attributes and physiological role. Circ Res 90: 1316–1324, 2002 [DOI] [PubMed] [Google Scholar]
- 48.Maddox DA, Fortin SM, Tartini A, Barnes WD, Gennari FJ. Effect of acute changes in glomerular filtration rate on Na+/H+ exchange in rat renal cortex. J Clin Invest 89: 1296–1303, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Malnic G, Klose RM, Giebisch G. Micropuncture study of renal potassium excretion in the rat. Am J Physiol 206: 674–686, 1964 [DOI] [PubMed] [Google Scholar]
- 50.Marsh DJ, Sosnovtseva OV, Chon KH, Holstein-Rathlou NH. Nonlinear interactions in renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol 288: R1143–R1159, 2005 [DOI] [PubMed] [Google Scholar]
- 51.Marsh DJ, Sosnovtseva OV, Mosekilde E, Holstein-Rathlou NH. Vascular coupling induces synchronization, quasiperiodicity, and chaos in a nephron tree. Chaos 17: 015114, 2007 [DOI] [PubMed] [Google Scholar]
- 52.Marsh DJ, Toma I, Sosnovtseva OV, Peti-Peterdi J, Holstein-Rathlou NH. Electrotonic vascular signal conduction and nephron synchronization. Am J Physiol Renal Physiol 296: F751–F761, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Moore LC, Rich A, Casellas D. Ascending myogenic autoregulation: Interactions between tubuloglomerular feedback and myogenic mechanisms. Bull Math Biol 56: 391–410, 1994 [DOI] [PubMed] [Google Scholar]
- 54.Navar LG. Glomerular permeability: a never-ending saga. Am J Physiol Renal Physiol 296: F1266–F1268, 2009 [DOI] [PubMed] [Google Scholar]
- 55.Neal CR, Crook H, Bell E, Harper SJ, Bates DO. Three-dimensional reconstruction of glomeruli by electron microscopy reveals a distinct restrictive urinary subpodocyte space. J Am Soc Nephrol 16: 1223–1235, 2005 [DOI] [PubMed] [Google Scholar]
- 56.Neal CR, Muston PR, Njegovan D, Verrill R, Harper SJ, Deen WM, Bates DO. Glomerular filtration into the subpodocyte space is highly restricted under physiological perfusion conditions. Am J Physiol Renal Physiol 293: F1787–F1798, 2007 [DOI] [PubMed] [Google Scholar]
- 57.Nielsen S, Pallone T, Smith BL, Christensen EI, Agre P, Maunsbach AB. Aquaporin-1 water channels in short and long loop descending thin limbs and in descending vasa recta in rat kidney. Am J Physiol Renal Fluid Electrolyte Physiol 268: F1023–F1037, 1995 [DOI] [PubMed] [Google Scholar]
- 58.Ien AH, Aukland K. A multinephron model of renal blood flow autoregulation by tubuloglomerular feedback and myogenic response. Acta Physiol Scand 143: 71–92, 1991 [DOI] [PubMed] [Google Scholar]
- 59.Oldson DR, Moore LC, Layton HE. Effect of sustained flow perturbations on stability and compensation of tubuloglomerular feedback. Am J Physiol Renal Physiol 285: F972–F989, 2003 [DOI] [PubMed] [Google Scholar]
- 60.Pallone TL, Edwards A, Ma T, Silldorff EP, Verkman AS. Requirement of aquaporin-1 for NaCl-driven water transport across descending vasa recta. J Clin Invest 105: 215–222, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Pannabecker TL, Abbott DE, Dantzler WH. Three-dimensional functional reconstruction of inner medullary thin limbs of Henle's loop. Am J Physiol Renal Physiol 286: F38–F45, 2004 [DOI] [PubMed] [Google Scholar]
- 62.Pannabecker TL, Dantzler WH. Three-dimensional architecture of collecting ducts, loops of Henle, and blood vessels in the renal papilla. Am J Physiol Renal Physiol 293: F696–F704, 2007 [DOI] [PubMed] [Google Scholar]
- 63.Pannabecker TL, Dantzler WH. Three-dimensional architecture of inner medullary vasa recta. Am J Physiol Renal Physiol 290: F1355–F1366, 2006 [DOI] [PubMed] [Google Scholar]
- 64.Pannabecker TL, Dantzler WH. Three-dimensional lateral and vertical relationships of inner medullary loops of Henle and collecting ducts. Am J Physiol Renal Physiol 287: F767–F774, 2004 [DOI] [PubMed] [Google Scholar]
- 65.Pannabecker TL, Dantzler WH, Layton HE, Layton AT. Role of three-dimensional architecture in the urine concentrating mechanism of the rat renal inner medulla. Am J Physiol Renal Physiol 295: F1271–F1285, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Pannabecker TL, Henderson CS, Dantzler WH. Quantitative analysis of functional reconstructions reveals lateral and axial zonation in the renal inner medulla. Am J Physiol Renal Physiol 294: F1306–F1314, 2008 [DOI] [PubMed] [Google Scholar]
- 67.Pennell JP, Lacy FB, Jamison RL. An in vivo study of the concentrating process in the descending limb of Henle's loop. Kidney Int 5: 337–347, 1974 [DOI] [PubMed] [Google Scholar]
- 68.Peti-Peterdi J. Independent two-photon measurements of albumin GSC give low values. Am J Physiol Renal Physiol 296: F1255–F1257, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pinter GG, Shohet JL. An inner medullary concentrating process actuated by renal pelvic/calyceal muscle contractions: assessment and hypothesis. Nephron Physiol 113: 1–6, 2009 [DOI] [PubMed] [Google Scholar]
- 70.Pinter GG, Shohet JL. Two fluid compartments in the inner renal medulla: a view through the keyhole of the concentrating process. Philos Transact A Math Phys Eng Sci 364: 1551–1561, 2006 [DOI] [PubMed] [Google Scholar]
- 71.Pitman EB, Zaritski RM, Kesseler KJ, Moore LC, Layton HE. Feedback-mediated dynamics in two coupled nephrons. Bull Math Biol 66: 1463–1492, 2004 [DOI] [PubMed] [Google Scholar]
- 72.Preisig PA. Luminal flow rate regulates proximal tubule H-HCO3 transporters. Am J Physiol Renal Fluid Electrolyte Physiol 262: F47–F54, 1992 [DOI] [PubMed] [Google Scholar]
- 73.Reungjui S, Pratipanawatr T, Johnson RJ, Nakagawa T. Do thiazides worsen metabolic syndrome and renal disease? The pivotal roles for hyperuricemia and hypokalemia. Curr Opin Nephrol Hypertens 17: 470–476, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Russo LM, Sandoval RM, Campos SB, Molitoris BA, Comper WD, Brown D. Impaired tubular uptake explains albuminuria in early diabetic nephropathy. J Am Soc Nephrol 20: 489–494, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Russo LM, Sandoval RM, McKee M, Osicka TM, Collins AB, Brown D, Molitoris BA, Comper WD. The normal kidney filters nephrotic levels of albumin retrieved by proximal tubule cells: retrieval is disrupted in nephrotic states. Kidney Int 71: 504–513, 2007. [DOI] [PubMed] [Google Scholar]
- 76.Sands JM, Layton HE. The urine concentrating mechanism and urea transporters. In: The Kidney: Physiology and Pathophysiology (4th ed.), edited by Seldin DW, Giebisch G. Philadelphia, PA: Lippincott, Williams & Wilkins, 2008, p. 1143–1178 [Google Scholar]
- 77.Schmidt-Nielsen B. August Krogh Lecture. The renal concentrating mechanism in insects and mammals: a new hypothesis involving hydrostatic pressures. Am J Physiol Regul Integr Comp Physiol 268: R1087–R1100, 1995. [DOI] [PubMed] [Google Scholar]
- 78.Schnermann J, Briggs JP. Function of the juxtaglomerulus apparatus: control of glomerular hemodynamics and renin secretion. In: The Kidney: Physiology and Pathophysiology (3rd ed.), edited by Seldin DW, Giebisch G. Philadelphia, PA: Lippincott, Williams & Wilkins, 2000, p. 945–980 [Google Scholar]
- 79.Schuster VL, Stokes JB. Chloride transport by the cortical and outer medullary collecting duct. Am J Physiol Renal Fluid Electrolyte Physiol 253: F203–F212, 1987 [DOI] [PubMed] [Google Scholar]
- 80.Smith KM, Moore LC, Layton HE. Advective transport of nitric oxide in a mathematical model of the afferent arteriole. Am J Physiol Renal Physiol 284: F1080–F1096, 2003 [DOI] [PubMed] [Google Scholar]
- 81.Sosnovtseva OV, Pavlov AN, Mosekilde E, Yip KP, Holstein-Rathlou NH, Marsh DJ. Synchronization among mechanisms of renal autoregulation is reduced in hypertensive rats. Am J Physiol Renal Physiol 293: F1545–F1555, 2007 [DOI] [PubMed] [Google Scholar]
- 82.Squarer A, Lemley KV, Ambalavanan S, Kristal B, Deen WM, Sibley R, Anderson L, Myers BD. Mechanisms of progressive glomerular injury in membranous nephropathy. J Am Soc Nephrol 9: 1389–1398, 1998 [DOI] [PubMed] [Google Scholar]
- 83.Stephenson JL. Concentration of urine in a central core model of the renal counterflow system. Kidney Int 2: 85–94, 1972 [DOI] [PubMed] [Google Scholar]
- 84.Strieter J, Stephenson JL, Giebisch G, Weinstein AM. A mathematical model of the rabbit cortical collecting tubule. Am J Physiol Renal Fluid Electrolyte Physiol 263: F1063–F1075, 1992 [DOI] [PubMed] [Google Scholar]
- 85.Tanner GA. Glomerular sieving coefficient of serum albumin in the rat: a two-photon microscopy study. Am J Physiol Renal Physiol 296: F1258–F1265, 2009 [DOI] [PubMed] [Google Scholar]
- 86.Terada Y, Knepper MA. Thiazide-sensitive NaCl absorption in rat cortical collecting duct. Am J Physiol Renal Fluid Electrolyte Physiol 259: F519–F528, 1990 [DOI] [PubMed] [Google Scholar]
- 87.Thomas SR. Inner medullary lactate production and accumulation: a vasa recta model. Am J Physiol Renal Physiol 279: F468–F481, 2000 [DOI] [PubMed] [Google Scholar]
- 88.Thomas SR. Kidney modeling and systems physiology. Wiley Interdiscip Rev Syst Biol Med 1: 172–190, 2009 [DOI] [PubMed] [Google Scholar]
- 89.Thomas SR, Baconnier P, Fontecave J, Françoise JP, Guillaud F, Hannaert P, Hernández A, Le Rolle V, Mazière P, Tahi F, White RJ. SAPHIR: a physiome core model of body fluid homeostasis and blood pressure regulation. Philos Transact A Math Phys Eng Sci 366: 3175–3197, 2008 [DOI] [PubMed] [Google Scholar]
- 90.Thomas SR, Layton AT, Layton HE, Moore LC. Kidney modelling: status and perspectives. Proc IEEE 94: 740–752, 2006 [Google Scholar]
- 91.Tojo A, Endou H. Intrarenal handling of proteins in rats using fractional micropuncture technique. Am J Physiol Renal Fluid Electrolyte Physiol 263: F601–F606, 1992 [DOI] [PubMed] [Google Scholar]
- 92.Verlander JW, Hassell KA, Royaux IE, Glapion DM, Wang ME, Everett LA, Green ED, Wall SM. Deoxycorticosterone upregulates PDS (Slc26a4) in mouse kidney: role of pendrin in mineralocorticoid-induced hypertension. Hypertension 42: 356–362, 2003 [DOI] [PubMed] [Google Scholar]
- 93.Wade JB, Lee AJ, Liu J, Ecelbarger CA, Mitchell C, Bradford AD, Terris J, Kim GH, Knepper MA. UT-A2: a 55-kDa urea transporter in thin descending limb whose abundance is regulated by vasopressin. Am J Physiol Renal Physiol 278: F52–F62, 2000 [DOI] [PubMed] [Google Scholar]
- 94.Wagner CA, Kovacikova J, Stehberger PA, Winter C, Benabbas C, Mohebbi N. Renal acid-base transport: old and new players. Nephron Physiol 103: 1–6, 2006 [DOI] [PubMed] [Google Scholar]
- 95.Wall SM, Kim YH, Stanley L, Glapion DM, Everett LA, Green ED, Verlander JW. NaCl restriction upregulates renal Slc26a4 through subcellular redistribution: role in Cl− conservation. Hypertension 44: 982–987, 2004 [DOI] [PubMed] [Google Scholar]
- 96.Wang X, Wexler AS. The effects of collecting duct active NaCl reabsorption and inner medulla anatomy on renal concentrating mechanism. Am J Physiol Renal Fluid Electrolyte Physiol 270: F900–F911, 1996 [DOI] [PubMed] [Google Scholar]
- 97.Weinstein AM. A mathematical model of distal nephron acidification: diuretic effects. Am J Physiol Renal Physiol 295: F1353–F1364, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Weinstein AM. A mathematical model of rat cortical collecting duct: determinants of the transtubular potassium gradient. Am J Physiol Renal Physiol 280: F1072–F1092, 2001 [DOI] [PubMed] [Google Scholar]
- 99.Weinstein AM. Mathematical models of renal fluid and electrolyte transport: acknowledging our uncertainty. Am J Physiol Renal Physiol 284: F871–F884, 2003 [DOI] [PubMed] [Google Scholar]
- 100.Weinstein AM. Thermodynamic relations in a system of parallel flow tubes. Math Biosci 36: 1–14, 1977 [Google Scholar]
- 101.Weinstein AM, Sontag ED. Modeling proximal tubule homeostasis: tracking changes in luminal flow. Bull Math Biol 71: 1285–1322, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Weinstein AM, Weinbaum S, Duan Y, Du Z, Yan Q, Wang T. Flow-dependent transport in a mathematical model of rat proximal tubule. Am J Physiol Renal Physiol 292: F1164–F1181, 2007 [DOI] [PubMed] [Google Scholar]
- 103.Wexler AS, Kalaba RE, Marsh DJ. Three-dimensional anatomy and renal concentrating mechanism. I. Modeling results. Am J Physiol Renal Fluid Electrolyte Physiol 260: F368–F383, 1991 [DOI] [PubMed] [Google Scholar]
- 104.Williamson GA, Loutzenhiser R, Wang X, Griffin K, Bidani AK. Systolic and mean blood pressures and afferent arteriolar myogenic response dynamics: a modeling approach. Am J Physiol Regul Integr Comp Physiol 295: R1502–R1511, 2008 [DOI] [PubMed] [Google Scholar]
- 105.Yip KP, Holstein-Rathlou NH, Marsh DJ. Chaos in blood flow control in genetic and renovascular hypertensive rats. Am J Physiol Renal Fluid Electrolyte Physiol 261: F400–F408, 1991 [DOI] [PubMed] [Google Scholar]
- 106.Zhai XY, Fenton RA, Andreasen A, Thomsen JS, Christensen EI. Aquaporin-1 is not expressed in descending thin limbs of short-loop nephrons. J Am Soc Nephrol 18: 2937–2944, 2007 [DOI] [PubMed] [Google Scholar]
- 107.Zhang W, Edwards A. A model of nitric oxide tubulovascular cross talk in a renal outer medullary cross section. Am J Physiol Renal Physiol 292: F711–F722, 2007 [DOI] [PubMed] [Google Scholar]
- 108.Zhang W, Edwards A. Oxygen transport across vasa recta in the renal medulla. Am J Physiol Heart Circ Physiol 283: H1042–H1055, 2002 [DOI] [PubMed] [Google Scholar]
- 109.Zhang W, Pibulsonggram T, Edwards A. Determinants of basal nitric oxide concentration in the renal medullary microcirculation. Am J Physiol Renal Physiol 287: F1189–F1203, 2004 [DOI] [PubMed] [Google Scholar]