Probing Substituent Effects in Aryl-Aryl Interactions Using Stereoselective Diels-Alder Cycloadditions

Abstract

Stereoselective Diels-Alder cycloadditions that probe substituent effects in aryl-aryl sandwich complexes were studied experimentally and theoretically. Computations on model systems demonstrate that the stereoselectivity in these reactions is mediated by differential π-stacking interactions in competing transition states. This allows relative stacking free energies of substituted and unsubstituted sandwich complexes to be derived from measured product distributions. In contrast to gas-phase computations, dispersion effects do not appear to play a significant role in the substituent effects, in accord with previous experiments. The experimental π-stacking free energies are shown to correlate well with Hammett σ_m constants (r = 0.96). These substituent constants primarily provide a measure of the inductive electron-donating and withdrawing character of the substituents, not donation into or out of the benzene π-system. The present experimental results are most readily explained using a recently proposed model of substituent effects in the benzene sandwich dimer in which the π-system of the substituted benzene is relatively unimportant and substituent effects arise from direct through-space interactions. Specifically, these results are the first experiments to clearly show that OMe enhances these π-stacking interactions, despite being a π-electron donor. This is in conflict with popular models in which substituent effects in aryl-aryl interactions are modulated by polarization of the aryl π-system.

I. Introduction

Non-covalent interactions (hydrogen bonding, π-stacking, cation-π, etc.) are of profound importance in molecular biology, drug design, and supramolecular chemistry.^1,2 Among non-covalent interactions, π-stacking interactions are perhaps the least well-characterized, but are key to understanding myriad phenomena. Intramolecular through-space π-π interactions have been used to alter electronic and optical properties of conjugated polymers^3,4 and intermolecular π-stacking interactions were recently exploited by Chen and McNeil in the design of a novel analyte-triggered gelation.⁵ Arene-arene interactions play a vital role in the structures and properties of DNA and RNA, in addition to the tertiary structures of proteins. ⁶ Interactions with aromatic amino acid side chains contribute to substrate binding in enzymes and were recently utilized⁷ in the computational enzyme design of a Kemp elimination catalyst. Finally, complexation of aromatic amino acid side-chains with DNA bases mediates DNA binding in anti-DNA autoantibodies, which are involved in the pathogenesis of the autoimmune disease systemic lupus erythematosus.⁸

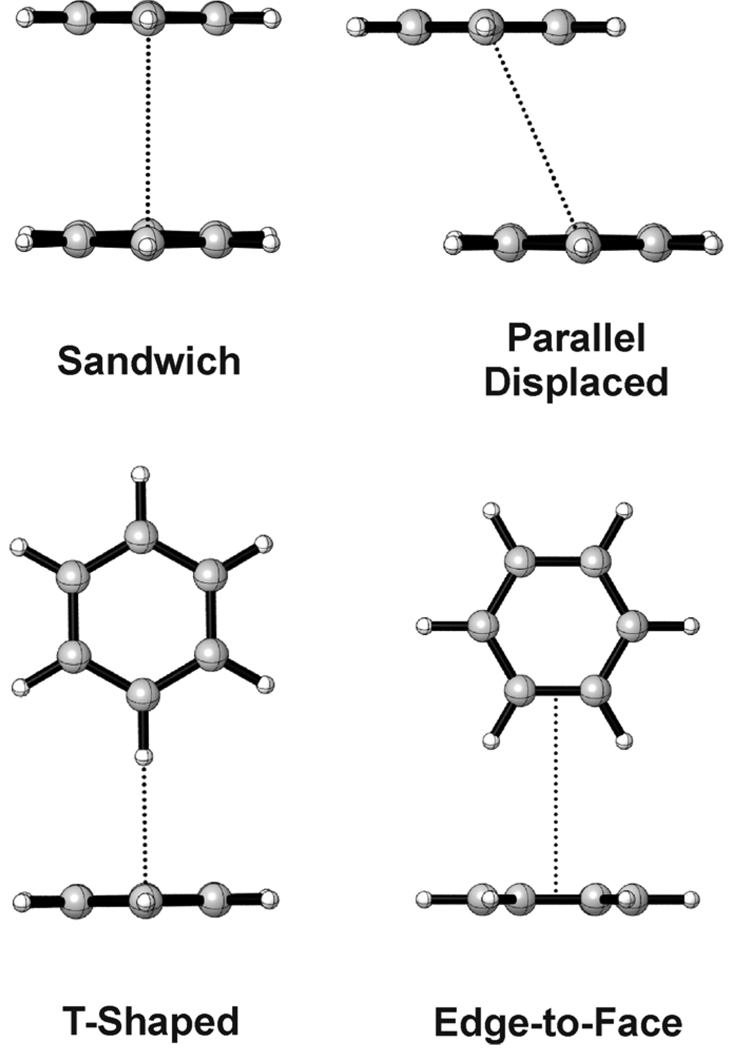
There are four prototypical structures generally considered for the simplest π-π stacked system, the benzene dimer (See Fig. 1). Benchmark ab initio results^9–13 indicate that the global minimum parallel displaced and T-shaped configurations are essentially isoenergetic and bound by 2.7 kcal mol⁻¹. The sandwich configuration lies about 1 kcal mol⁻¹ higher in energy. Although the sandwich form is not a stable minimum for the unsubstituted benzene dimer, this is a popular model system for theoretical studies of substituent effects.^9,11,14–22

Figure 1.

Prototypical benzene dimer configurations

The prevailing view of substituent effects in the benzene dimer is the polar/π model²³ espoused by Cozzi and Siegel^24–27 and Hunter et al.² This intuitive electrostatic model enjoys broad acceptance in the literature, despite numerous theoretical studies critical of this simple picture.^{9,11,16–22,28} In the polar/π model, electron-withdrawing substituents diminish the electron density in the π-cloud of the substituted ring, which decreases the electrostatic repulsion with the π-system of the interacting ring. The stacking interaction relative to the unsubstituted dimer is consequently enhanced. Conversely, π-electron-donating substituents result in weaker π-π interactions. These general trends have been born out in many experiments, ranging from studies of intramolecular stacking interactions in conformationally flexible systems^{24–27,29–31} to supramolecular host-guest complex experiments.^32–34 Gung and coworkers³⁰ utilized triptycene derivatives to study substituent effects in the parallel displaced dimer based on measured equilibria between conformations with stacked and unstacked aryl rings. Cozzi and Siegel^24–27 have introduced a number of experimental probes, including conformationally restricted polycyclic compounds yielding relative binding free energies of substituted parallel displaced dimers.²⁶ Hunter and co-workers^33,34 have quantified substituent effects on stacking interactions based on chemical double mutant cycle studies using supramolecular ‘zipper’ complexes. Results from each of these experimental probes purportedly support the polar/π model. However, as discussed below, the data of Gung and co-workers³⁰ and Hunter et al.³³ are also consistent with an alternative model.²¹ The work of Cozzi and Siegel,^24–27 on the other hand, clearly indicates that π-electron donors (CH₃, OCH₃, etc.)³⁵ decrease the π-stacking interaction in the benzene dimer while electron-withdrawing substituents (CN, NO₂, etc.) enhance the interaction, in accord with the polar/π model.

Gas-phase ab initio computations paint a different picture.¹⁷ The coupled cluster theory results of Sinnokrot and Sherrill^9,11,17 revealed enhanced stacking interactions in the sandwich dimer for all substituents studied, regardless of the electron-withdrawing or electron-donating character. Similar findings have also been reported by Kim et al.¹⁶ Ringer, Sinnokrot, Lively, and Sherrill¹⁸ further demonstrated the additivity of substituent effects in multiply-substituted benzene heterodimers. Additivity in the case of fluorine substitution has also been shown experimentally by Gung and co-workers.³⁶ Such strict additivity is contrary to expectations if π-polarization were the dominant cause of substituent effects, because the incremental polarization of the aryl π-system should decrease with each additional substituent.

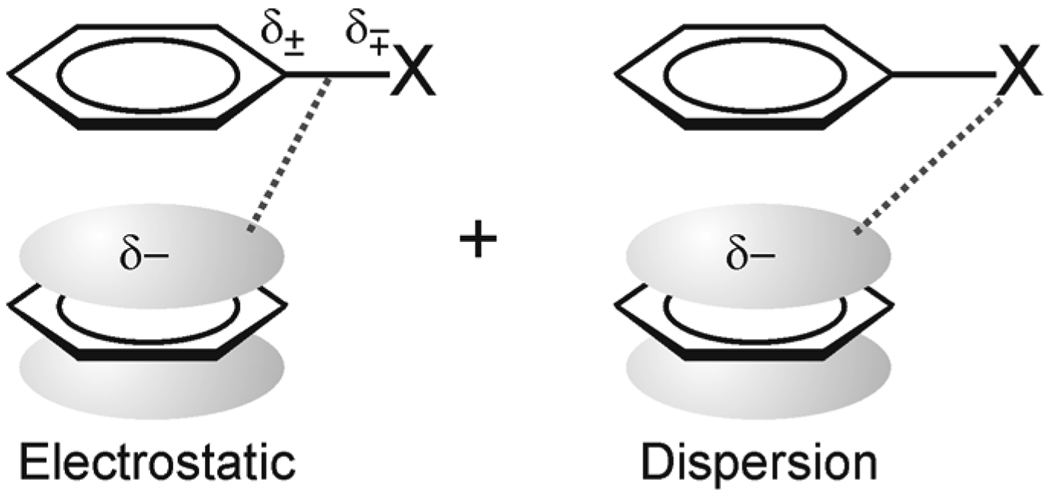
Wheeler and Houk examined substituent effects in the sandwich and edge-to-face configurations of the gas-phase benzene dimer.^21,22 For the sandwich dimer, the π-system of the substituted aryl ring is not necessary to recover substituent effects across a diverse set of 24 substituents.^21,37 Instead, substituent effects were shown to arise from direct electrostatic and dispersion interactions between the substituent and the unsubstituted ring (see Fig. 2). Rashkin and Waters²⁹ had previously invoked direct interactions between the substituent and the unsubstituted ring to account for experimental data on substituted parallel displaced benzene dimers. Sherrill and co-workers¹⁸ attributed anomalous substituent effects in T-shaped benzene dimers to direct interactions.

Figure 2.

Direct-Interaction model of substituent effects in the sandwich configuration of the benzene dimer.²¹

A consequence of the “direct-interaction” model²¹ is that σ-withdrawing character dominates substituent effects in the benzene dimer, not the extent to which substituents donate or accept π-electrons. Specifically, while the polar/π model^2,24,27 predict that π-donors³⁵ such as OMe should hinder the stacking interaction relative to the unsubstituted dimer, this new model²¹ maintains that OMe enhances the interaction due to its net withdrawing inductive/field character (the field and resonance parameters for OMe are F = 0.29 and R = −0.56, respectively).^38,39 Similarly, while the polar/π model predicts a correlation of stacking interactions with σ_p, the direct-interaction model is based on a correlation with σ_m.

A major lingering discrepancy between experimental results and gas-phase computations is the role of dispersion interactions. Sherrill and co-workers²⁰ have stressed the importance of dispersion in substituent effects in the sandwich dimer, while there is no evidence of a significant role for dispersion in available experiments.^33,40 Cockroft and Hunter⁴⁰ recently tackled this issue in an elegant paper on the role of solvent effects in edge-to-face aromatic interactions. Ultimately, it was concluded that “electrostatic effects play a dominant role in determining the properties of aromatic interactions in organic solvents,” and the predicted importance of dispersion in gas-phase computations arises from the neglect of solvent effects.

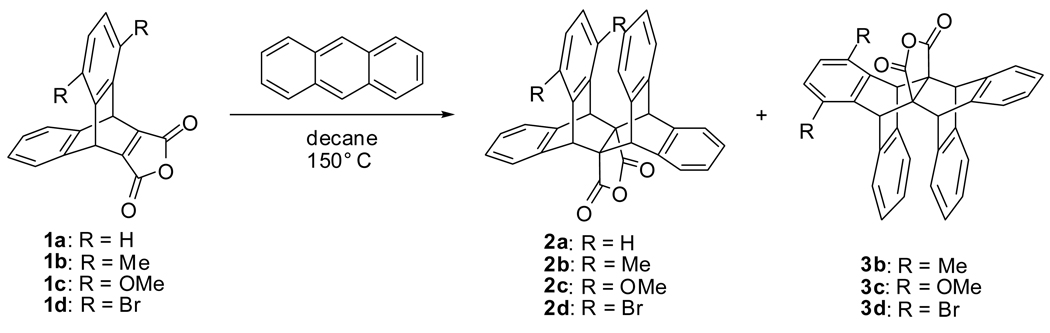
Here we present stereoselective Diels-Alder reactions (Scheme 1) that probe substituent effects in the sandwich configuration of the benzene dimer. These reactions are based on a similar stereoselective transformation utilized by Swager and co-workers in the synthesis of conjugated polymers incorporating π-stacking interactions along the polymer backbone.⁴ In contrast to previous experimental probes, the current approach quantifies substituent effects through barrier height differences of competing transition states to provide relative stacking free energies for substituted and unsubstituted benzene dimers. Computational examination of the transition states and related model systems demonstrate that the product distributions reflect differential aryl-aryl interactions.

Scheme 1.

II. Experimental Methods

Substrates 1a – 1d were prepared in two steps from substituted anthracenes and dimethyl acetylenedicarboxylate (see Supporting Information, SI). The Diels-Alder reactions were performed in decane due to its high boiling point and non-polar nature. Importantly, both starting materials were soluble at the reaction temperature (150 °C). Excess anthracene (10 equiv) was found to provide higher yields. The major products (2a, 3b, 2c, and 2d) were characterized by single-crystal X-ray analysis (see SI). The product ratios were then determined by integrating the bridgehead protons in the crude reaction mixtures via ¹H NMR spectroscopy. Average isolated yields ranged from 62% for substrate 1b to 77% for 1d. Observed product ratios varied from 1:2 to 1:4 for 1b, 4:1 to 6:1 for 1c, and 12:1 to 20:1 for 1d. The average of the measured product ratios is reported.

To verify that the product ratios reflect the kinetic selectivity (i.e., free energy differences in the transition states) and not the thermodynamic stability of the two products, we subjected product 2a to the reaction conditions using an excess of 1,4-dibromoanthracene. No crossover products were detectable by ¹H NMR after 24 h, indicating no retro-Diels-Alder reaction was occurring. Similarly, product 2c was combined with excess anthracene and heated to 150°C. NMR revealed no formation of product 3c after 24 h. These findings are consistent with computed free energy barriers for the reverse reactions, which are all in excess of 40 kcal mol⁻¹ at the M05-2X/6-31+G(d) level of theory. The reported product ratios are not the result of an equilibration.

III. Theoretical Methods

Structures of the reactants, products, and associated transition states for the Diels-Alder reactions in Scheme 1 were optimized using the B3LYP and M05-2X density functional theory (DFT) functionals^41,42 paired with either the 6-31+G(d) or AVDZ′ basis sets. Two additional substrates [1e (Cl) and 1f (F)] were also examined computationally. For each substrate (1a – 1f), transition states leading to products 2 and 3 were located, denoted by TS2 and TS3, respectively. M06-2X/6-31+G(d) single point energies⁴³ were computed at M05-2X geometries. There is no published 6-31+G(d) basis set for Br. When the M05-2X and M06-2X functionals are paired with the built-in 6-31+G(d) Br basis set in Gaussian03,⁴⁴ interaction energies for the C₆H₅Br^…C₆H₆ sandwich dimer are overestimated by 2 – 3 kcal mol⁻¹. Consequently, the AVDZ′ basis set⁹ was used for all systems that include Br. This basis set comprises the cc-pVDZ basis set on hydrogen and the aug-cc-pVDZ basis set without diffuse d-functions for other atoms.⁴⁵

Harmonic vibrational frequencies were computed for all optimized structures to characterize the stationary points. Even though B3LYP predicts C_s-symmetric transition states, M05-2X yields non-symmetric structures for TS3 for all substituents as well as TS2a and TS2b. In these cases, the C_s-symmetric structures have an additional small (< 20 cm⁻¹) imaginary vibrational frequency corresponding to rotation of the anthracene relative to the substrate. The energy differences between the C_s and C₁-symmetric stationary points were all small (<0.1 kcal mol⁻¹). Free energy corrections (423 K) were computed within the rigid-rotor/harmonic-oscillator approximation using un-scaled harmonic vibrational frequencies at the corresponding level of theory. Effects of solvent were approximately accounted for using the conductor-like polarizable continuum model (CPCM)⁴⁶ with solvent parameters for heptane (ε = 1.92, R_solv = 3.125 Å). M05-2X/6-31+G(d) free energy corrections and solvent corrections were appended to the M06-2X electronic energies.

Fine DFT integration grids (70 radial and 590 angular points) were utilized in all M05-2X and M06-2X computations, because it has previously been demonstrated that these functionals are particularly sensitive to integration grid density when applied to weakly bound complexes.⁴⁷ B3LYP and M05-2X optimizations and frequencies were carried out using Guasisan03.⁴⁴ M06-2X single point energies and constrained M05-2X optimizations on truncated structures were computed using NWChem 5.1.^48,49

IV. Results and Discussion

The Diels-Alder reactions in Scheme 1 have been examined experimentally and using modern DFT methods^42,43,50 to probe substituent effects in face-to-face aryl-aryl interactions. These reactions pose a number of difficulties for the application of standard theoretical methods. The size of the systems in Scheme 1 (63 atoms in 2c, for example) precludes the application of rigorous ab initio approaches. On the other hand the application of DFT is hampered by the need to account for the dispersion effects governing the π-stacking interactions present in TS2 and TS3. Popular DFT functionals (and B3LYP in particular) predict repulsive interaction potentials for the sandwich configuration of the benzene dimer.⁵¹ However, progress has been made in the parameterization of new functionals^42,43,50 and the development of empirical corrections to existing functionals,^15,52 opening up numerous areas of applications that were previously untenable for DFT. For example, Grimme and co-workers¹⁵ recently demonstrated the utility of empirical dispersion corrections to standard DFT functionals in capturing substituent effects in the triptycene-based probe of Gung and coworkers.³⁰

A. Validation of the Theoretical Approach

Previous benchmark studies^42,43,50,53 have demonstrated that the M05-2X and M06-2X DFT functionals^42,43 provide a satisfactory description of prototypical π-stacking interactions. These functionals were applied to C₆H₆^…C₆H₅R sandwich dimers and compared to benchmark coupled cluster results to assess their performance for substituted benzene dimers. These benchmark values, which are estimates of CCSD(T)/aug-cc-pVTZ interaction energies, arise from counterpoise-corrected CCSD(T)/AVDZ′ energies corrected for basis set incompleteness at the MP2 level of theory.⁵⁴ All interaction energies were computed within the frozen monomer approximation. Monomer geometries were optimized at the MP2/aug-cc-pVTZ level of theory for the CCSD(T) computations. Table 1 shows that M05-2X and M06-2X, when paired with a double-ζ quality basis sets, provide very accurate relative interaction energies for substituted benzene sandwich dimers.

Table 1.

Interaction energies (kcal mol⁻¹) for C₆H₆^…C₆H₅R benzene sandwich dimers, relative to the unsubstituted benzene dimer.^a Positive numbers indicate enhanced interaction relative to the unsubstituted dimer.

	Me	OH	OMe	F	Cl	Br	CN
M05-2X	0.3	0.4	0.3	0.5	0.8	1.0b	1.3
M06-2X	0.4	0.5	0.6	0.6	1.0	1.1b	1.4
CCSD(T)c	0.5d	0.4d	0.6e	0.5d	0.9e	1.1e	1.3d

^aThe interaction energy for the unsubstituted benzene dimer is −0.5 and −1.0 kcal mol⁻¹ at the M05-2X/6-31+G(d) and M06-2X/6-31+G(d) level of theory, respectively. The M05-2X/AVDZ′ and M06-2X/AVDZ′ values are −0.7 and −1.6, respectively. The CCSD(T) value from ref 9 is −1.8 kcal mol⁻¹.

^bAVDZ′ basis set.

^cEstimated CCSD(T)/aug-cc-pVTZ

^dFrom ref 9.

^eThis work.

Accurate activation barriers are also desirable in the theoretical treatment of the reactions in Scheme 1. Computed free energy barriers and reaction free energies for the 1,4-cycloaddition of maleic anhydride and benzene are given in SI Table S6, computed using M05-2X, M06-2X, and B3LYP paired with the 6-31+G(d) basis set. These DFT results are compared to benchmark CBS-QB3 predictions.⁵⁵ The M05-2X and M06-2X functionals offer a reliable description of this reaction, with the M05-2X predicted barrier (35.5 kcal mol⁻¹) falling within 0.7 kcal mol⁻¹ of the CBS-QB3 value of 34.8 kcal mol⁻¹. The B3LYP functional overestimates the free energy barrier by almost 15 kcal mol⁻¹. B3LYP similarly predicts the reaction free energy to be too large by 18 kcal mol⁻¹, while the M05-2X and M06-2X predictions of 11.0 and 12.4 kcal mol⁻¹ are in good agreement with the CBS-QB3 value (11.6 kcal mol⁻¹). These failures of B3LYP and apparent success of M05-2X and M06-2X for this cycloaddition are in accord with recent findings of Pieniazek and coworkers.⁵⁶

Because both substituent effects on aryl-aryl interactions and activation barriers are shown to be treated properly with M05-2X, this functional is used primarily for the reactions depicted in Scheme 1.

B. Product Distributions

Experimental product ratios for the reactions in Scheme 1 are provided in Table 2, along with the corresponding relative free energy barriers (ΔΔG^‡) derived from classical transition state theory. All substituents lead to pronounced stereoselectivity. Solvent-corrected free energy barriers and relative barriers from M05-2X, M06-2X, and B3LYP are also provided in Table 2. Overall, the M05-2X and M06-2X predicted ΔΔG^‡ values are in only modest agreement with the experimental results. In the case of 1b, M05-2X predicts no selectivity but experimentally product 3b is favored over 2b 3:1. For 1d, M05-2X and M06-2X underestimate the experimentally-derived ΔΔG^‡ value of 2.4 kcal mol⁻¹. The B3LYP free energies are in poorer agreement with the experimental data, predicting the opposite stereoselectivity for the OMe and Br substituted substrates than observed experimentally, although for 1d the B3LYP ΔΔG^‡ value of −0.7 kcal mol⁻¹ is fortuitously in very good agreement with the experimental value (−0.9 kcal mol⁻¹). In accord with the findings for the parent cycloaddition, B3LYP drastically overestimates these reaction barriers, predicting activation energies exceeding 60 kcal mol⁻¹ in some cases. Despite the non-polar nature of the solvent, CPCM corrections to the free energy barriers are significant. Solvent corrections generally increase both barriers, but TS2 is affected to a greater extent. The net impact on the ΔΔG^‡ values ranges from −0.1 to −2.8 kcal mol⁻¹.

Table 2.

Predicted solvent-corrected (CPCM) free energy barriers (ΔG^‡, 423K) free energy barrier differences [ΔΔG^‡ = ΔG^‡(TS3) - ΔG^‡(TS2)] along with experimentally measured 2:3 ratios and corresponding ΔΔG^‡ values. All energies given in kcal mol⁻¹.^a

Product		M05-2X		M06-2X		B3LYP		Experiment
		ΔG‡	ΔΔG‡	ΔG‡	ΔΔG‡	ΔG‡	ΔΔG‡	2:3 Ratio	ΔΔG‡
H	2a	38.1		37.4		58.5		-	-
Me	2b	36.7		35.4		60.5
	3b	36.7	0.0	36.1	0.3	59.8	−0.7	1:3	−0.9
OMe	2c	37.1		36.2		61.0
	3c	38.9	1.8	38.2	2.0	60.8	−0.2	5:1	1.4
Br	2d	33.1		32.6		60.8
	3d	34.4	1.3	34.2	1.7	60.6	−0.2	17:1	2.4
C	2e	28.4		27.5		58.9
	3e	30.6	2.2	29.9	2.4	59.8	0.9	b	b
F	2f	35.4		34.9		58.3
	3f	38.4	2.9	37.8	2.9	59.0	0.7	b	b

^aAVDZ′ basis set used for substrates 2d and 3d. 6-31+G(d) basis set used for the remaining systems.

^bSubstrates 1e and 1f were not tested experimentally.

Computed gas-phase relative enthalpy barriers (ΔΔH^‡, Table 3) exhibit much better agreement with experiment, indicating possible problems with the free energy predictions in Table 2. For systems of this size, free energy corrections computed using the standard rigid-rotor/harmonic-oscillator approximation can be problematic, particularly given the presence of very small vibrational frequencies. These small frequencies are not satisfactorily treated as harmonic oscillators and small changes in these frequencies lead to large shifts in predicted entropy contributions, exaggerating otherwise inconsequential errors in computed frequencies.

Table 3.

Predicted gas-phase enthalpy barriers (ΔH^‡, 423K) and enthalpy barrier differences [ΔΔH^‡ = ΔH^‡(TS3) - ΔH^‡(TS2)], in kcal mol⁻¹.^a

Product		M05-2X		M06-2X		B3LYP
		ΔH‡	ΔΔH‡	ΔH‡	ΔΔH‡	ΔH‡	ΔΔH‡
H	2a	13.2		12.5		35.4
Me	2b	12.3		11.4		35.8
	3b	12.4	0.1	11.7	0.4	35.1	−0.7
OMe	2c	11.3		10.5		34.6
	3c	13.9	2.5	13.2	2.7	36.0	1.3
Br	2d	9.0		8.6		32.8
	3d	12.5	3.4	12.3	3.8	34.9	2.1
Cl	2e	9.3		8.4		33.0
	3e	12.5	3.2	11.8	3.4	35.2	2.2
F	2f	10.3		9.7		33.0
	3f	12.8	2.5	12.2	2.5	35.1	2.1

^aAVDZ′ basis set used for substrates 2d and 3d. 6-31+G(d) basis set used for the remaining systems.

^bSubstrates 1e and 1f were not tested experimentally.

The M05-2X and M06-2X ΔΔH^‡ values are consistently 1.0 ± 0.1 and 1.3 ± 0.1 kcal mol⁻¹ larger than the experimental ΔΔG^‡ values. The B3LYP predicted gas-phase relative enthalpy barriers are in very good agreement with the experimental data, deviating by no more than 0.3 kcal mol⁻¹. A primary difference between the M05-2X and M06-2X methods and the B3LYP functional is the recovery of dispersion-like interactions by the former methods. The differences between the M05-2X and B3LYP predicted ΔΔH^‡ values in Table 3 are consistent with the expected size of the dispersion contribution to these relative barriers from the substituents.⁹ This is demonstrated most clearly by the series of halogen-substituted substrates (1d – 1f). The M05-2X predicted enthalpy differences decrease across the series Br > Cl > F and follow the trend in polarizabilities. The B3LYP functional predicts essentially the same ΔΔH^‡ values for all three of these species, failing to account for expected differences in dispersion interactions.

The systematic deviation of the M05-2X and M06-2X results from the experimental ΔΔG^‡ values suggests that dispersion interactions do not play a major role in the present experiment, in agreement with the recent reports of Cockroft and Hunter.⁴⁰ That the M06-2X results consistently deviate more from the experimental ΔΔG^‡ values than do the M05-2X enthalpies is also consistent with a lack of significant dispersion-like effects in the experiments, since M06-2X is known to provide a more complete recovery of dispersion effects than M05-2X.⁵⁷ Apparently, the very good agreement between the B3LYP ΔΔH^‡ values and the experimental data arises from the failure of that functional to account for the dispersion effects that are present in the gas-phase but attenuated in solution. In addition to the indirect effects of solvent on dispersion discussed by Cockroft and Hunter,⁴⁰ there is the potential for more direct solvent effects. It has previously been shown that the primary dispersion contribution to substituent effects in the gas-phase benzene sandwich dimer are the direct interactions between the substituent and the complexed ring.²¹ The presence of a polarizable solvent between the substituents and the other ring could potentially distinguish these direct dispersion interactions.⁵⁸

C. Origins of Barrier Height Differences

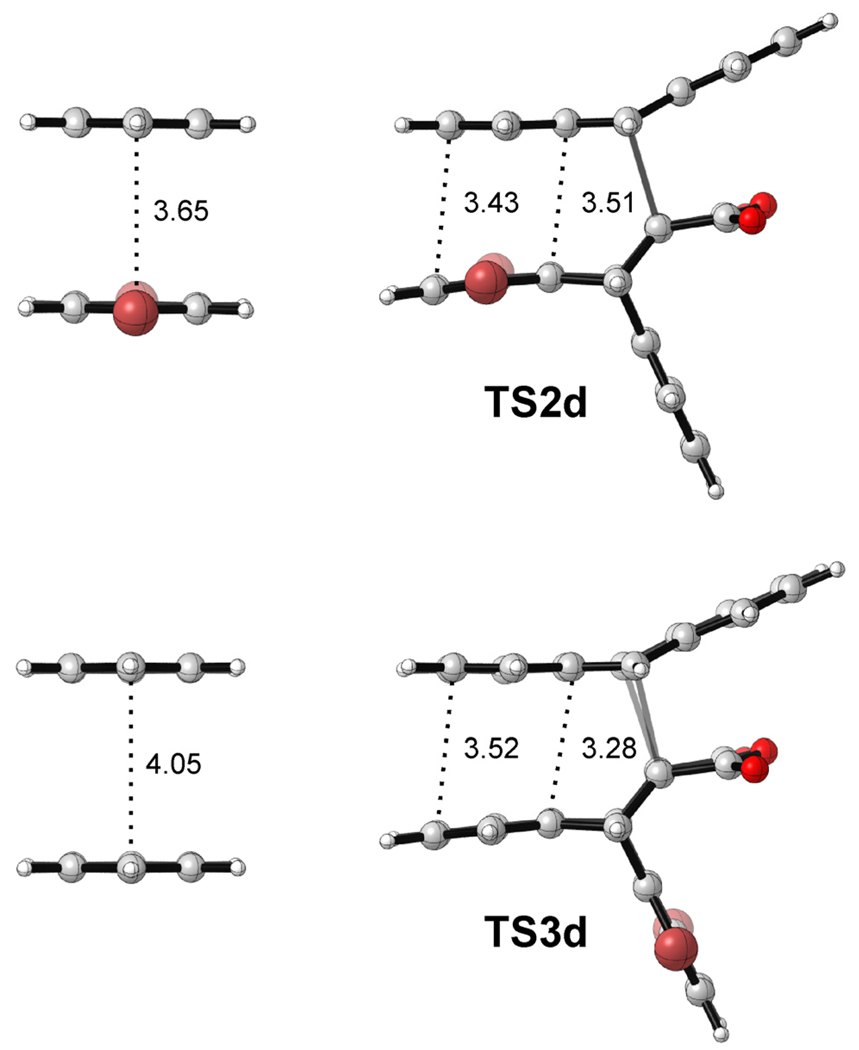
The contribution of π-stacking interactions to the energy difference between TS2 and TS3 (ΔΔE^‡) can be approximated by examining a series of model systems. In this way, it can be demonstrated that the product distributions for the reactions in Scheme 1 provide a reliable gauge of substituent effects in the benzene dimer. Fig. 3 shows the M05-2X/6-31+G(d) structures for TS2d and TS3d, along with the gas-phase C₆H₄Br₂^…C₆H₆ and C₆H₆^…C₆H₆ sandwich dimers. The arrangements of the interacting aromatic rings in these transition states are congruent with the structures of the corresponding gas-phase dimers. Inter-ring distances for all of the optimized transition states are provided in SI Table S8 along with the corresponding gas-phase dimer distances. The separations in the optimized transition states (averaging 3.4 Å) are somewhat smaller than benchmark gas-phase dimer distances (3.8 Å for the benzene dimer and slightly shorter for substituted dimers),^9–12,17,18 although they are comparable to the aryl-aryl distance in the parallel displaced benzene dimer.^10,11,19

Figure 3.

Structures of TS2d and TS3d and corresponding gas-phase sandwich configurations of the dibromobenzene-benzene and benzene-benzene dimers, optimized at the M05-2X/6-31+G(d) level of theory.

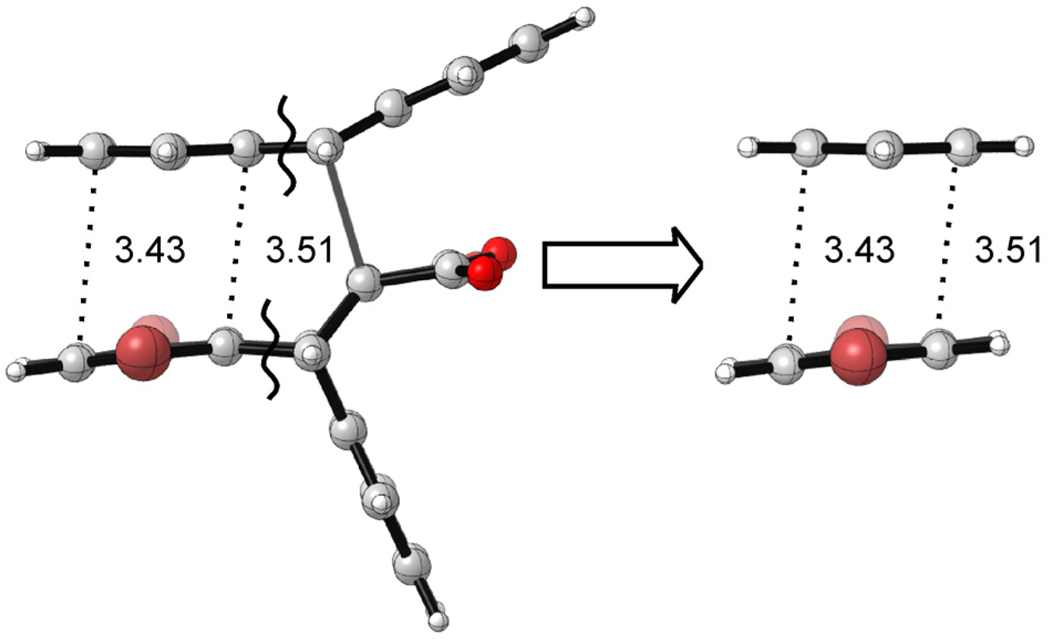
The energetic cost of these differences in the stacking interactions in TS2 and TS3 compared to the gas-phase dimers can be quantified by removing the remainder of the TS atoms and replacing the open carbon valances with hydrogens, as depicted in Fig. 4. The placement of the added hydrogens was optimized using M05-2X/6-31+G(d) while holding the remainder of the atoms fixed. Interaction energies at the geometries present in TS2 and TS3 [ΔE_stack(TS2) and ΔE_stack(TS3)] are included in Table 4. Except for the dibromobenzene and dichlorobenzene interactions present in TS2d and TS2e, the stacking interactions in the transition states are slightly repulsive energetically. This is attributed to the smaller interring distances in the transition states compared to the fully relaxed dimers. Relative interaction energies (ΔΔE_stack) for the complexes present in TS2 and TS3 are also given in Table 4, along with interaction energies for C₆H₄R₂^…C₆H₆ dimers relative to the unsubstituted sandwich dimer (ΔΔE_gas). The relative π-stacking interactions in TS2 and TS3 are in general agreement with the gas phase dimer results and follow the same trend: Me < OMe < F < Cl < Br. The deviations in inter-ring distances in TS2 and TS3 compared to the gas-phase dimers have no substantial net effect on the relative stacking energies.

Figure 4.

To isolate the relative π-stacking interactions in the transition states (ΔΔE_π), the C—C bonds in the M05-2X optimized TS2 and TS3 structures were cut as indicated by the wavy lines and replaced with hydrogens to yield a benzene dimer with the same geometry as that present in each transition state.

Table 4.

M05-2X interaction energies (kcal mol⁻¹) of 1,4-disubstitued benzene-benzene dimers relative to the unsubstituted sandwich dimer, computed at the geometries present in TS2 and TS3 (ΔΔE_π) and at the optimized gas-phase geometries (ΔΔE_gas).^a

Substituent	ΔEstack(TS1)	ΔEstack(TS2)	ΔΔEπ	ΔΔEgas
Me	1.2	1.7	0.4	0.6
OMe	0.5	1.8	1.3	0.8
Br	−1.6	1.3	2.9	2.3
Cl	−0.7	1.8	2.5	1.8
F	0.3	1.9	1.6	1.1

^aThe AVDZ′ basis set was used for dibromobenzene^…benzene dimer. The 6-31+G(d) basis set was used otherwise.

Minor complications can arise from secondary effects of the substituents on the underlying Diels-Alder reactions. The effects of the substituents on the computed transition state geometries are minor. For TS2, the length of the forming C–C bonds is 2.39Å for all of the substituted substrates, compared to 2.41 Å for TS2a. For TS3, there is a larger variation in the length of the forming C–C bonds, ranging from 2.39 Å for the Me and Br substituted substrates to 2.44 Å for TS3f. However, the positions of the Diels-Alder transition states do not correlate with the observed selectivities, and are not the origin of the barrier height differences. To quantify the effects of the substituents on the underlying Diels-Alder reaction barriers heights, the addition of 1,3-butadiene to substrates 1a – 1f was examined at the M05-2X/6-31+G(d) level of theory (see SI Scheme S1 and Table S9). The differences in electronic energy barriers (ΔΔE_sub) for the two possible cycloadditions are given in Table 5. These substituent effects on the underlying Diels-Alder reaction will also be present in the reactions given in Scheme 1.

Table 5.

Approximate decomposition of computed electronic energy barrier differences (ΔΔE^‡) into π-stacking (ΔΔE_stack, see Fig. 4) and substituent effects on the underlying Diels-Alder barriers (ΔΔE_sub) for the reactions in Scheme 1. The dominant contribution arises from ΔΔE_π.

Substrate		ΔΔE‡	≈	ΔΔEstack	+	ΔΔEsub
Me	1b	0.0		0.4		0.1
OMe	1c	2.6		1.3		1.0
Br	1d	3.5		2.9		0.9
Cl	1e	3.3		2.5		0.8
F	1f	2.6		1.6		0.3

In TS3 there is the potential for steric interactions between the substituents and the carbonyl oxygens of the maleic anhydride. In the computed transition state geometries the distance of the closest approaching atoms is always in excess of the corresponding van der Waals radii, and steric interactions are not contributing to the barrier height differences.

The contribution of π-stacking interactions (ΔΔE_stack) and secondary substituent effects (ΔΔE_sub) to the barrier height differences are given in Table 5, along with the differences in electronic energy barriers (ΔΔE^‡). For the all of the substrates except 1f, the sum of ΔΔE_stack and ΔΔE_sub is within 0.5 kcal mol⁻¹ of ΔΔE^‡. For 1f this difference is 0.7 kcal mol⁻¹. Apparently there are small additional effects that affect ΔΔE^‡ not accounted for by these simple models. Regardless, in each case the largest contributor to ΔΔE^‡ arises from differential π-stacking interactions and the measured product distributions provide a probe of substituent effects on π-stacking interactions.

V. Substituent Effects in the Benzene Dimer

The sandwich configuration of the benzene dimer is not a stable minimum, and both the parallel displaced and T-shaped structures are favored energetically. However, the sandwich dimer is the most often configuration studied theoretically,^9,11,14–22 and is the configuration depicted in qualitative models of substituent effects espoused by both Cozzi and Siegel^24–27 and Hunter et al.² The present experimental probe provides a means of testing our understanding of substituent effects in aryl-aryl sandwich complexes. The rigidity of the transition structures leading to products 2 and 3 forces one ring of the incoming anthracene into a nearly parallel arrangement with an aromatic ring of the substrate at a distance comparable to that in the gas-phase sandwich dimers (see Fig. 3). Although contaminating factors arise from secondary substituent effects and other perturbations, the bulk of the observed energy barrier differences is due to differential π-stacking interactions. Moreover, it was shown above (see Table 4) that the deviations in the stacking interactions in TS2 and TS3 from the ideal gas-phase benzene dimers have little net effect on the relative stacking energies. As a result, the measured free energy barrier differences (ΔΔG^‡) provide a measure of the relative interaction free energies (ΔΔG^stack) of the substituted sandwich dimers.

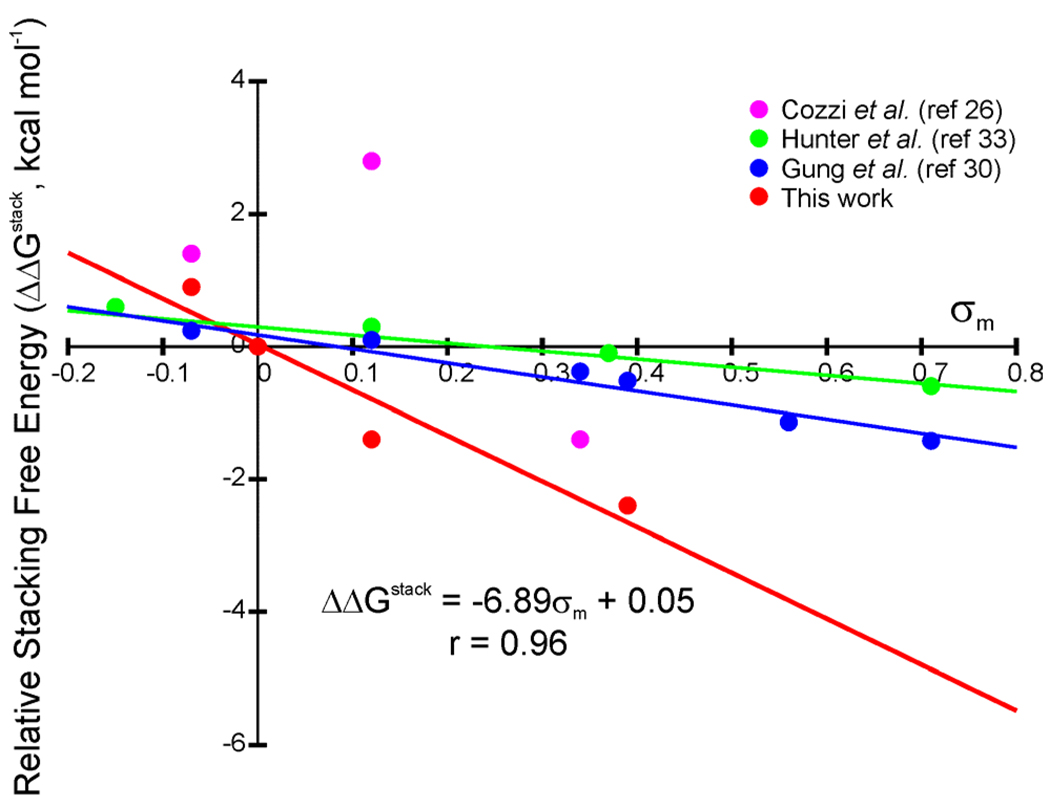
Experimental relative interaction free energies (ΔΔG^stack) for the disubstituted dimers are plotted in Fig. 5 as a function of the Hammett sigma meta constants (σ_m). These constants primarily indicate the inductive electron-donating or withdrawing character of the substituents.³⁹ There is a strong correlation (r = 0.96) between ΔΔG^stack and σ_m, in accord with recent theoretical results.²¹ The primary difference between computed gas-phase interaction energies for the benzene sandwich dimer and these ΔΔG^stack values is that in the computations substituted dimers are stabilized by on average about 0.5 kcal mol⁻¹ compared to the unsubstituted dimer. This is due to direct dispersion interactions^20,21 and leads to a y-intercept of −0.5 kcal mol⁻¹ when plotting computed interaction energies versus σ_m.²¹ In Fig. 5, the y-intercept of the best fit line for the experimental stacking free energies is essentially zero. A consequence is that even though gas-phase computations predict that all substituents stabilize the benzene dimer, experimental results indicate a net repulsive interaction between paraxylene and benzene. The direct dispersion interactions arising in gas-phase computations are diminished in the experiments, presumably due to solvent effects.^40,58

Figure 5.

Experimental stacking free energies (ΔΔG^stack, relative to R = H, in kcal mol⁻¹) versus σ_m for 1,4-disubstituted benzene dimers.³⁹ The monosubstituted results of Cozzi and Siegel,²⁶ Hunter et al.,³³ and Gung et al.³⁰ were doubled to enable direct comparison with this work.

Experimental stacking free energies from Gung and coworkers,³⁰ Cozzi and Siegel,²⁷ and Hunter et al.³³ are also included in Fig. 5. These experimental results have previously been shown to correlate well with σ_p (r = 0.98, 0.98, and 0.99 for Gung,³⁰ Cozzi,²⁷ and Hunter,³³ respectively), a feature used to support the polar/π: model.^2,24–27 However, as seen in Fig. 5, there is also a strong correlation between the data of Gung et al.³⁰ and Hunter and co-workers³³ with σ_m (r = 0.97 and 0.93, respectively). This correlation with both σ_m and σ_p arises from the similarity of σ_m and σ_p constants for most of the substituents studied in those works. The only substituent considered for which σ_m and σ_p differ qualitatively (OMe), exhibited such a small effect on the stacking interaction energy in these experiments that the sign of the effect on stacking interactions is unclear. The present experimental results show a clear correlation with σ_m, and the strong enhancement of the stacking interaction by OMe stymies any correlation with σ_p. On the other hand, the work of Cozzi and Siegel^24,26 yields a qualitatively different trend, exhibiting excellent correlation with σ_p but no correlation with σ_m.

One potential reason for the differences between the present experimental results and previous work is that the reactions in Scheme 1 probe substituent effects in the sandwich dimer, while the probes mentioned above involve parallel displaced arrangements. π-polarization effects could very well play a significant role in substituent effects in parallel displaced stacking interactions. That the present experiments probed a different dimer configuration is also one potential reason the substituent effects in the present work are significantly larger than those observed in the experiments of Gung et al.³⁰ and Hunter and co-workers.³³

VI. Conclusions

The stereoselective Diels-Alder reactions depicted in Scheme 1 have been examined experimentally and using the B3LYP, M05-2X, and M06-2X DFT functionals. Predicted solvent-corrected relative free energy barriers are in modest agreement with experimental results. Computed gas-phase relative enthalpy barriers provide much better agreement with experiment, though the M05-2X and M06-2X barriers systematically overestimate the experimental free energy differences. The deviations of the M05-2X and M06-2X results from the experimental values are attributed to dispersion effects operative in the gas phase computations but masked by solvent interactions in the experiment.

The origins of the stereoselectivities were shown to arise primarily from differential π-stacking interactions in the competing transition states. With the exception of the dimethyl case, all reactions favor the product featuring co-facial interactions between the incoming anthracene and the more heavily substituted benzene ring of the substrate. In particular, OMe, despite being a π-electron donor, enhances the interaction in aryl-aryl sandwich complexes.

The stereoselective Diels-Alder reactions depicted in Scheme 1 provide a sensitive experimental probe of substituent effects in aryl-aryl sandwich complexes, and the present results support a model of substituent effects in the sandwich configuration of the benzene dimer advanced by Wheeler and Houk.^21,22 In this model, the π-system of the substituted benzene is unimportant and substituent effects in the sandwich dimer are governed by direct interactions between the substituent and the unsubstituted aryl ring. These substituent effects correlate with σ_m, not σ_p, indicative of the dependence on inductive/field effects rather than π-polarization.

The present experimental results provide the first clear demonstration that a π-donating but σ-withdrawing substituent stabilizes π-stacking interactions in aryl-aryl sandwich complexes. This raises doubts about the popular π-polarization based models of these stacking interactions.^2,24–27 Instead, the present results are most readily explained by a new model (see Fig. 2) in which direct interactions between the substituent and the less substituted ring dominate substituent effects in the sandwich configuration of the benzene dimer. Previous experimental results of Gung et al.³⁰ and Hunter and co-workers³³ are also consistent with this new model.