Complex Geometric Models of Diffusion and Relaxation in Healthy and Damaged White Matter

Abstract

Which aspects of tissue microstructure affect diffusion weighted MRI signals? Prior models, many of which use Monte-Carlo simulations, have focused on relatively simple models of the cellular microenvironment and have not considered important anatomic details. With the advent of higher-order analysis models for diffusion imaging, such as high-angular-resolution diffusion imaging (HARDI), more realistic models are necessary. This paper presents and evaluates the reproducibility of simulations of diffusion in complex geometries. Our framework is quantitative, does not require specialized hardware, is easily implemented with little programming experience, and is freely available as open-source software. Models may include compartments with different diffusivities, permeabilities, and T2 time constants using both parametric (e.g., spheres and cylinders) and arbitrary (e.g., mesh-based) geometries. Three-dimensional diffusion displacement-probability functions are mapped with high reproducibility, and thus can be readily used to assess reproducibility of diffusion-derived contrasts.

1 Introduction

In the central nervous system, information is conveyed along axons located within the white matter. Injury to white matter occurs in disease processes with distinct pathophysiologic mechanisms. Such mechanisms include edema, demyelination, axonal transection, and cell death, as well as reparative processes such as remyelination, axon regrowth, and glial regeneration. Ascribing particular patterns of injury and repair to distinct structural and pathophysiologic mechanisms is an important clinical objective that will help to guide treatment strategies. Diffusion-weighted MRI (DWI) is exquisitely sensitive to tissue architecture on a micrometer scale. Yet current contrasts, whether from diffusion tensor imaging (DTI), the q-space formalism, high-angular-resolution diffusion imaging (HARDI), or other current analysis methods, cannot distinguish broad classes of pathological processes in white matter, especially when multiple types of damage occur together (i.e., myelin loss, axonal loss, edema, inflammation, etc.) (1–3). Thus, hypotheses about subtle structural differences cannot be tested with existing methodologies. This manuscript studies the reproducibility of simulations of diffusion in biologically relevant compartments using a cross-platform, three-dimensional computational framework. These numeric models enable in silica comparison, evaluation, and design of DWI techniques based on complex, biologically relevant geometries.

Determining whether it is possible to infer the specific mechanisms that underlie changes in the DWI signal has been an area of intense investigation, and, particularly, the focus has been on discovering DWI contrasts that are specific to particular white matter degeneration processes (4). Analytic models of restriction environments are only available for simple geometries (e.g., ellipsoids, plates, and cylinders) (5,6). Monte-Carlo simulations have been shown to be a powerful and flexible tool for examining diffusion in more complicated situations.

Norris (7) has reviewed the foundational works for modeling diffusion during MRI acquisition; a brief summary relevant to this manuscript follows. Using scans of histological sections to generate a two-dimensional pixel-based model, Lipinski (8) found that simulated diffusion in the extracellular space corresponded to a porous and isotropic medium. In their work with giant squid axons, Beaulieu and Allen (9) employed Monte-Carlo methods, with a two-dimensional hexagonal lattice of impermeable cylinders, to explore the impacts of neurofilaments on intra-axonal diffusion. Szafer et al. (10,11) explored the effects of membrane permeability, cellular volume fraction, and diffusion time by incorporating T2 relaxation and semi-permeable boundaries into a rectangular lattice model, whereas Ford and Hackney (12,13) generalized Monte-Carlo approaches to include packed-cylinder models of spinal-cord axons. More recently, several multi-compartmental hypotheses and studies, based on simulations with more involved geometries, have begun to emerge (e.g., (14,15)).

Historically, the needs for specialized software and intense computation have made more detailed, yet descriptive, studies extremely difficult, both in terms of simulation and analysis. With the advent of higher-order analysis models for diffusion imaging (16–22), emerging DWI methods appear to offer great potential for gaining insight into the intricate microstructural configurations that are clearly present in tissues. These methods have shown promise for resolution of crossing fibers in fiber tracking (23–25). Recently, advanced DWI analysis methods (e.g., (17,20)) have been applied to study the effects of white matter damage (e.g., (26)), however the conclusive assignment between structural changes and change in DWI contrasts is still lacking. While q-space, HARDI, and q-ball studies offer great potential for higher order classification of both normal anatomy and white matter damage, the relationships between the observed signal, diffusion process, and underlying biophysical processes are complex and difficult to isolate. Simulations offer an attractive and powerful manner in which to explore these phenomena and generate empirically testable hypotheses.

Very recently, a number of computational frameworks have been presented to study diffusion in differing geometric models. Hall and Alexander present a model for optimizing simulation parameters for packed and degenerating cylinders using the CAMINO software package (27). Meanwhile, Balls and Frank extended the popular MCell physiological simulation framework to allow for simulations of realistic diffusion models especially intended for high angular resolution diffusion imaging studies (28,29). Herein, we present an alternative cross-platform, three-dimensional computational framework (the random walk simulator software, RWS) for simulating restricted diffusion in multiple compartments. As this is a rapidly evolving field for software development, a direct feature comparison would quickly become obsolete. Rather, we emphasize the importance of quantitative and reproducible assessment of diffusion profiles from compartmental models of cellular arrangements. Subsets and supersets of the RWS features are available in other software packages. The results of this study are applicable to studies of diffusion in complex geometries, independent of software package. RWS supports models that may account for compartment-specific diffusivity, permeability, and T2 time-constants using both parametric (e.g., spheres, cylinders, etc.) and arbitrary (e.g., mesh-based) geometries. Note that permeability and exchange can be considered equivalent from a DWI perspective.

In this manuscript, we demonstrate the efficacy studying three-dimensional diffusion displacement probability functions with simulations for complex restriction profiles, such as bulging axons. We demonstrate that alternate models of axon degeneration (i.e., broken, crimped, bulging) may lead to significant differences in diffusion weighted (DW) contrasts.

With RWS, these computational studies can be implemented with little programming experience on standard hardware and can rapidly generate results to enable generation of hypotheses for further experimentation. The RWS software is available in open-source through the Neuroimaging Informatics Tools and Resources Clearinghouse (www.NITRC.org: project name: “DWI Random Walk Simulator”) under the Lesser GNU Public License.

This manuscript is organized as follows: Section 2 reviews the computational basis for simulating diffusion and the RWS framework. Section 3 explores the interaction of Monte-Carlo design choices (i.e., step size, number of simulated spins) with the error in estimated parameters of existing models. Section 4 demonstrates that simulations in complex, three-dimensional restriction geometries are reproducible. Finally, Section 5 discusses the implications of the findings.

2 Simulating DWI

Diffusion, also known as Brownian motion, is the random motion of particles driven by thermal energy. In free solution, diffusivity is an intrinsic property of a fluid, so that the same diffusion coefficient is observed regardless of the number of observations or the time between observations. In organized tissues, however, molecules may encounter barriers that restrict or hinder their movement. Diffusion is restricted when the maximum displacement of molecules is limited by compartment boundaries, while hindered diffusion refers to the reduction of the apparent diffusion constant. Therefore, the observed diffusivity, or apparent diffusion coefficient (ADC), may depend on the length of time over which molecular movements are observed and the direction along which that motion takes place. Over short time courses, the ADC is closely linked to the intrinsic diffusivity. However, over longer time courses, as molecules interact with local tissues, the ADC more closely reflects the structural organization of those tissues. DWI is therefore remarkably sensitive to the temporal and spatial scales of the local environment. In biologic tissues, the intracellular and extracellular environments both influence the signal arising from individual voxels.

2.1 Theory

In general, the probability that a particle (i.e., water molecule) will move from r₀ to r in time Δ can be written,

$$p(r|r_0,\mathrm{\Delta })$$ (1)

Eq. (1) is known as the motion-probability propagator. The signal observed in a diffusion-weighted experiment is generally lower than that observed without diffusion weighting due to destructive interference from the phase shifts acquired by individual spins (i.e., the magnetic moment from the hydrogen proton on water). Note that a single spin does not possess a “phase” in the sense of a magnetic resonance signal. Rather, an ensemble of spins exhibits this quantity. In this approximation, the phase-accumulation throughout a series of random walk steps is represented by an analogy in which a single particle is attributed a phase (see section 21.2 in (30)). The ratio between the signals observed with and without diffusion weighting is known as the diffusion-weighted attenuation,

$$E=\frac{S_1}{S_0}$$ (2)

where S₁ is a diffusion-weighted observation and S₀ is a non- or minimally diffusion-weighted reference.

In DWI, the echo attenuation (or diffusion sensitization) is generated by application of balanced sequences of magnetic field gradients which first introduce and subsequently reverse position-dependent phase shifts. If a water molecule moves over the course of the experiment, the two steps do not cancel and the water molecule is left with a residual phase difference. The complex-valued signal from a spin accounting for phase accrued by a spin over an experiment, neglecting position-encoding effects, is:

$$\mathrm{\psi }={\displaystyle \int e^{i2\pi q(t)·r(t)}}\mathit{\text{dt}}$$ (3)

where q is the wavenumber of the experiment, a weighting factor that captures the direction, duration, and intensity of diffusion sensitization. In traditional Stejskal-Tanner approaches, q is piecewise constant (i.e., constant gradient applied during a rephasing interval from t₀ to t₁, delay from t₁ to t₂, and a second, effectively opposite constant gradient applied during a dephasing from t₂ to t₃) so that

$$\mathrm{\psi }={\displaystyle {\int }_{t_0}^{t_1}{e}^{i2\pi q_1·r(t)}}\mathit{\text{dt}}-{\displaystyle {\int }_{t_2}^{t_3}{e}^{i2\pi q_2·r(t)}}\mathit{\text{dt}}.$$ (4)

The effects of a finite-duration pulse width are substantial in closed geometries (e.g., within pores or between plates) (31) but have been shown to have less effect in open, tortuous environments (32). However, phantom q-space experiments show better agreement with simulations that account for finite pulse duration (33).

We can approximate the diffusion sensitization as an instantaneous process (i.e., the short-gradient pulse, SGP, approximation) in order to reduce computational burden. Alternatively, the RWS framework supports specification of arbitrary (discretized) gradient waveforms; however, study of the impacts of the various forms of more realistic gradients (e.g., (34–36)) is beyond the scope of this work. Under SGP, the expected value of the echo attenuation may be explained in terms of the motion-probability propagator and the experimental parameters (37):

$$E(q,\mathrm{\Delta })=\langle p(r|r_0,\mathrm{\Delta })e^{i2\pi q·(r-r_0)}\rangle .$$ (5)

where <> indicates the ensemble average over all protons within a detected volume. To account for T2 effects, the phase must be weighted by the expected T2 signal attenuation that would occur for a displacement from r₀ to r, denoted ξ_T2,

$$E(q,\mathrm{\Delta })=\langle p(r|r_0,\mathrm{\Delta }){\xi }_{T2}(r|r_0)e^{i2\pi q·(r-r_0)}\rangle .$$ (6)

This method of modeling of T2 effects is rather naïve (e.g., it does not account for surface relaxation) . However, it provides a convenient framework in which to model very-short T2 compartments that may act as signal sinks. More complex T2 interactions are beyond the scope of this work, and T2 effects are neglected for the remainder of this manuscript. For a pulsed-gradient spin-echo (PGSE) sequence,

$$q=\frac{1}{2\pi }\gamma \delta g.$$ (7)

In general, p(r|r₀,Δ) may be a function of spatial position and diffusion time.

DWI techniques assume a particular form for the motion-probability propagator and estimate propagators through a series of carefully constructed diffusion-weighted acquisitions.

2.2 Simulation Framework

RWS is composed of an object oriented Monte-Carlo simulator (written in Java, Sun Microsystems, Santa Clara, CA) and a simple front end for specifying the experimental design and rendering results (written in Matlab, The MathWorks, Natick, MA). The simulator considers the interaction between the motion of individual, non-interacting particles (i.e., protons or spins) and the boundaries of restriction compartments (which lie within an infinite rectangular lattice). The lattice structure is a convenient representation for a space of infinite extent. Arbitrarily large movements can be simulated by realizing that a movement beyond a single lattice element can be modeled as a spin leaving one edge and “reappearing” on the opposite side. When such a “wrap-around” occurs, the initial position of the spin is moved by exactly one lattice element step in the opposite direction of the wrap-around. Thus, from the spin’s perspective, a wrap is a continuous process event. In this way, spins that finish a simulation within a lattice element may be identified regardless of where they might have started the experiment.

Spin position may be initialized uniformly or at random within a lattice block either inside all compartments, outside all compartments, or throughout the lattice element. The compartments and the extra-compartmental space have independently defined (unrestricted) diffusivities (i.e., the diffusion coefficient in the absence of barriers, D) and transverse relaxation time constants (T2); compartments also have boundary permeabilities (P).

To simulate diffusion, the simulator executes a finite, user-defined time-step (Δt) in which each spin selects a random direction and takes a step with length $l=\sqrt{6D\mathrm{\Delta }t}$. Thus, the velocity of a spin is $\nu =\sqrt{\frac{6D}{\mathrm{\Delta }t}}$. If a spin encounters a compartment boundary, the spin is either specularly reflected or transmitted, depending on the permeability, P, of the boundary and the diffusivities on either side of the boundary. To assure no net flux across the boundary (11),

$$P=\frac{1}{4}{\nu }_{\mathit{\text{in}}}{p}_{\mathit{\text{in}}\to \mathit{\text{out}}}=\frac{1}{4}{\nu }_{\mathit{\text{out}}}{p}_{\mathit{\text{out}}\to \mathit{\text{in}}}$$ (8)

where ν_in and ν_out are the spin velocities inside and outside the membrane and p_in→out and are the transmission probabilities of a particle to cross the membrane from inside or outside, respectively. This is a classic kinetics problem; one derives the fraction of particles that would hit a surface within a differential period of time and integrates over the time step. The number of collisions can be found by writing the fraction of collisions as a function of trajectory angle (because the particle must have right velocity range for the angle at which it is travelling to be within the distance of hitting the wall). The factor of ¼ arises when one integrates over all orientations (e.g., the surface of a sphere). The spins are assumed not to interact or influence each other or the boundary states.

RWS includes basic compartment geometries for spheres, cylinders, and arbitrary polyhedral meshes. Advanced compartment geometries may be generated by constructing the union, intersection, set difference, or affine transform of existing basic or advanced geometries. T2 signal loss for each spin is computed based on the relative proportion of time spent in each compartment, whereas the change in spin phase depends on the net change in position (corresponding to the short-pulse approximation). Ensemble effects are computed by integrating phase changes over all spins (i.e., Monte-Carlo integration of Eq. (5)) weighted by each spin’s net magnitude after accounting for T2 relaxation.

2.3 Software Design

RWS appears to the user as a Matlab package. The user creates compartment definitions either on the command line or through a script with the basic components (RWScreateCompartmentSphere, RWScreateCompartmentCylinder, RWScreateCompartmentMesh). The user may create new compartments by combining and/or modifying existing compartments (RWScreateCompartmentUnion, RWScreateCompartmentIntersection, RWScreateCompartmentDifference, RWScreateCompartmentAffineTransform). Each compartment has its own diffusivity, boundary permeability, and T2. Next, a simulator is created; this requires a definition of the extracompartmental diffusivity and T2 as well as the lattice block size (RWSnewSimulator). The user can add compartments (RWSaddCompartment) with the proviso that compartment boundaries may not intersect (the union/intersection operators achieve the same biophysical interpretation and ensure higher computational efficiency). The user can add any number of spins either inside compartments, outside compartments, or uniformly at random within the lattice structure (RWSaddSpins). Finally, the user can run the simulation for an arbitrary amount of time with a specified time-step (RWSsimulate). RWS includes tools to visualize and analyze the directionally dependent diffusivities and to create figures of the type shown in this manuscript. The resulting data are stored as Matlab data objects that may be manipulated and/or exported by user-generated routines or through the Matlab OpenGL visualization framework.

2.4 Performance Evaluation

RWS computes samples of spin motion according to the biophysical motion-probability propagator for the specified geometry while tracking T2 effects on individual particles. These data can be used to construct either expected signal intensities or simulated signal intensities (by the addition of noise) for DWI experiments through direct Monte-Carlo integration of Eq. (6). In turn, the simulated data can be used to assess the sensitivity and specificity of contrasts for simulated three-dimensional geometries. To investigate the applicability of RWS to the general family of DWI methods (as opposed to a specific experimental technique), we need to quantify variability and evaluate the estimation reproducibility of the underlying biophysical processes, which can be used to generate both common contrasts (i.e., fractional anisotropy, mean diffusivity, etc.) as well as novel contrasts. For the remainder of this manuscript, we focus on evaluating the intrinsic reliability of RWS, so imaging (Rician) noise is not added.

The motion-probability propagator and T2 attenuation are approximated as stationary (i.e., independent of position): p(r|r₀,Δ)=p(r-r₀|Δ)) over the field of interest – typically, a single voxel. Therefore, the signal attenuation can be rewritten in terms of T2-weighted one-dimensional projections of the motion-probability propagator,

$$\psi (\mathrm{\Delta }r,\mathrm{\Delta },g)={\displaystyle {\int }_{x:\mathrm{\Delta }r=\Vert (r-r_0)·g\Vert }p(x|r-r_0,\mathrm{\Delta })}{\xi }_{T2}(x)\mathit{\text{dx}}$$ (9)

$$E(q,g,\mathrm{\Delta })=\langle \psi (\mathrm{\Delta }r,\mathrm{\Delta },g)e^{i2\pi q\mathrm{\Delta }r}\rangle .$$ (10)

The ψ representation provides a coordinate system for convenient and meaningful comparisons of motion-probability propagators because it captures the mechanism by which spin motion interacts with applied gradients to produce diffusion sensitization. For simple and limiting cases (as in Section 3), expressions for p(x|r−r₀,Δ) are known, and we can evaluate the error of the estimated probability-density function with the RWS framework. However, this is not the case for more general geometric models.

As a surrogate for the (possibly unknown) estimated models of diffusion and diffusion-weighting paradigms (Eq. (10)), we study the reproducibility of the derived quantity ψ̈, which we define as ψ represented in spherical basis set of 258 unique directions (the vertices of an eighth order tessellation of an octahedron) at 125 linearly spaced distances between 0 µm and 30 µm. Note that ψ̈ is assumed to be symmetric. This choice of discrete representation is essentially arbitrary, but assessment of a continuous representation of ψ is not possible with Monte-Carlo methods without assuming a specific model and/or functional form. In this work, we are interested in assessing variability in a model-agnostic approach to inform future work with specific diffusion-weighting analysis approaches. We believe that this basis set affords sufficient resolution to study the models presented here; extension of these metrics to other basis sets is straightforward.

First, to assess reproducibility of ψ̈ by orientation, the angular peak signal-to-noise ratio (PSNR) is calculated as,

$${\mathit{\text{PSNR}}}_{g=}=-20{\text{log}}_{10}\frac{{\langle \text{SD}({\ddot{\psi }}_{g,r})\rangle }_r}{\underset{r}{\text{max}}{\widehat{\psi }}_{g,r}}$$ (11)

where g denotes the direction, SD indicates the standard deviation of repeated experimental measures, ψ̂_g,r indicates the empirical estimate for direction g and distance r, and <>_r indicates the average over distances. Statistics are shown as spherical maps as well as mean/standard deviation over the set of orientations. Second, to assess reproducibility of ψ̈ by distance, the radial PSNR is calculated as,

$${\mathit{\text{PSNR}}}_r=-20{\text{log}}_{10}\frac{{\langle \text{SD}({\widehat{\psi }}_{g,r})\rangle }_g}{\underset{g}{\text{max}}{\widehat{\psi }}_{g,r}}$$ (12)

where r denotes the radial distance and <>_g indicates the average over orientations.

3 Validation Experiments

3.1 Free Diffusion

When no boundaries to diffusion are present, the radial distribution (i.e., in one-dimension) of spins follows a time-varying Gaussian (μ=0, σ²=2Dt). In Monte-Carlo simulations, steps are of equal length along a random direction, chosen from a uniform distribution of orientations. The result converges to a Gaussian distribution asymptotically with the number of steps. When too few steps are taken, the random walk has not had time to converge, so the results do not represent the physical process and are biased, thereby increasing error. However, if the total number of simulation steps (i.e., number of spins times number of steps per spin) is held constant, increasing the number of steps reduces the number of spins available. Thus, the number of motion measurements will be fewer and the measured distribution will be of higher variance, also increasing total error. Hence, the optimal choice of the number of steps and spins represents a balance between sufficient steps to create representative measurements and sufficient spins to achieve an empirical measurement of low variability.

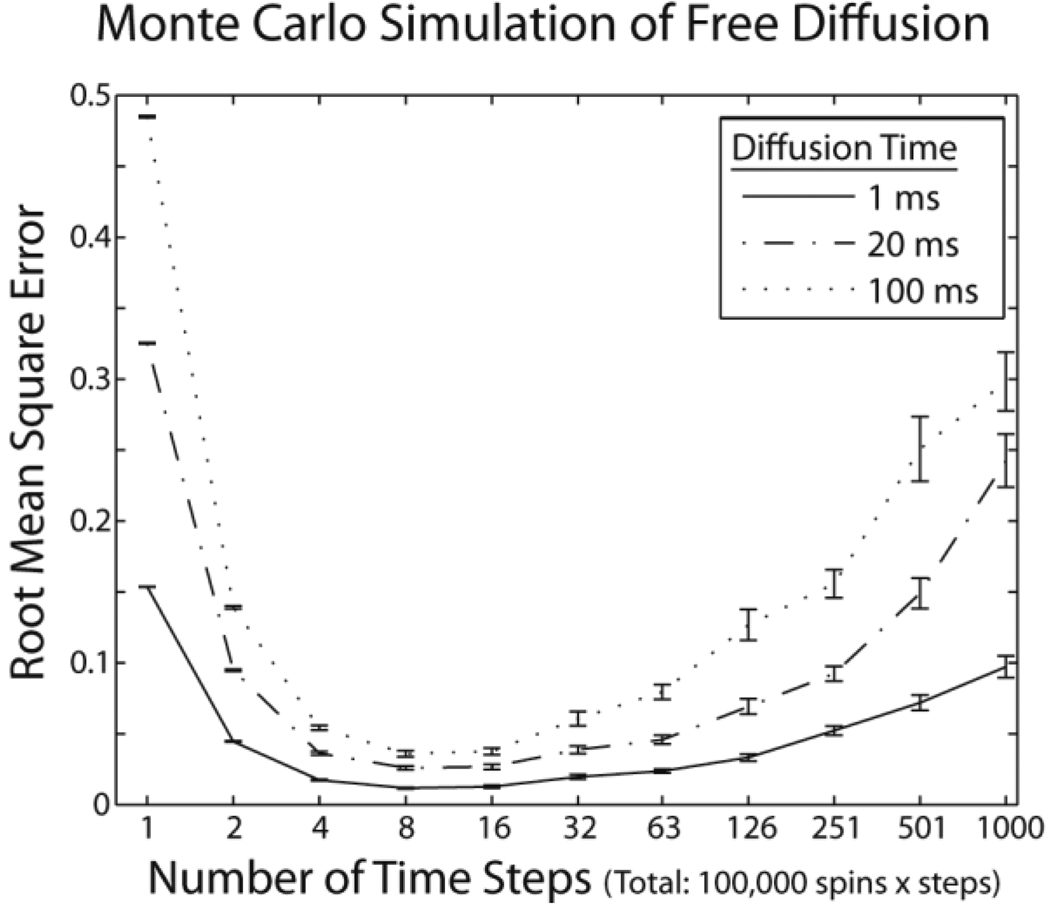
Figure 1 illustrates this phenomenon. Free diffusion (2 × 10⁻³mm²/s) was simulated for a period of 1, 20, and 100 ms with the total spins steps = 100,000. The number of steps was spaced logarithmically from 1 to 1000. To assess variability, the simulation was repeated 25 times. Error was assessed by the root-mean-square difference between the empirical cumulative-distribution function (P(x > c)=Σ_iδ(x_i > c)) and the theoretical Gaussian distribution. Simulations with few steps (<~5) resulted in increased error. Increasing the number of steps had decreasing marginal benefit and eventually (for >~10) resulted in increased error as well.

Figure 1.

Simulations of free diffusion. Error between theoretical and simulated diffusion probability-density functions was minimized with 5–10 time-steps when the number of spins × the number of time-steps was held constant. Curves show mean error ± standard error for three diffusion times.

3.2 Diffusion within Impermeable Cylinders

The probability distributions and expected echo attenuations for NMR experiments within cylindrical environments have been presented in detail (38–40). An exact expression could be derived for the ensemble propagator for perpendicular diffusion in an infinite cylinder from previously published single spin propagators (41). Here, we are interested in the effects of step size, so a direct comparison between fine-time-step and coarse-time-step simulations is of primary interest. Thus, we examine the impact of the time-step duration on the evolution of the cumulative-distribution function estimated with Monte-Carlo methods using several time-steps. A single 10 µm diameter cylinder of infinite length was simulated within a 10 × 10 × 10 µm lattice. Intra-cylinder diffusivity was set to 2 × 10⁻³ mm²/s. Simulations were run with 10,000 spins within the cylinders for diffusion times of 1 to 25 ms (expected free diffusion root mean square displacement, RMSD, of 4.5 to 14.1 µm along one dimension) using time-steps of 100 µs (Δ_0,1), 1 ms (Δ₁) and 5 ms (Δ₅), equivalent to step lengths of 0.62, 2.0, and 4.5 µm, respectively. All spins were initialized within the cylinder. Again, there were 25 repetitions.

Figure 2 illustrates that these three simulations achieve similar results at 25 ms (after 250, 25, and 5 time-steps, respectively). However, the intermediate results are quite different. After 1 ms simulation, the estimated distribution for the Δ_0,1 and Δ₁ simulations are dramatically different (the median absolute difference divided by the maximum of the empirical probability density function was greater than 17%). At 5 ms, the differences between Δ_0,1 and Δ₁ are much less apparent (approximately 1%). Similarly, the differences between Δ_0,1 and Δ₅ are substantial for 1 and 5 ms (approximately 16%), but quickly converge by 10 ms (approximately 3% by 10 ms and approximately 1% for 20 ms) (not shown). These results illustrate the need to use short time-steps for short diffusion times.

Figure 2.

Simulations of restricted diffusion. Plots illustrate the mean estimated motion-probability propagator perpendicular to the long axis of a cylinder with diameter 10 µm after 1 ms (A), 5 ms (B), and 25 ms (C) using three time-step durations. (The 5 ms time-step results are not shown in (A) because a 1 ms time-step cannot be accomplished with an integer number of 5 ms steps.) PDFs computed with different time-steps result in similar findings when at least five time-steps are performed. Note that simulated PDFs broaden with increased diffusion time. Error bars, which are smaller than the data points, indicate examples of the standard error at nine equally spaced distances.

3.3 Diffusion within Permeable Cylinders

We examined the impact of the time-step duration on the evolution of the cumulative-distribution function for particles in a permeable cylinder, using fine-grained Monte-Carlo simulations as a reference. An 8 µm diameter cylinder of infinite length was simulated within a 10×10×10 µm lattice. Intra- and extra-cylinder diffusivity was set to 2 × 10⁻³ mm²/s. Simulations used 100,000 spins uniformly distributed over the lattice volume (both inside and outside the cylinders) for diffusion times of 5 and 20 ms (expected RMSD free diffusion of 4.47 and 8.94 µm along one dimension) using time-steps of 0.1 (Δ_0.0001), 0.1 (Δ_0.001), 10 (Δ_0.01), 100 (Δ_0.1), 1000 (Δ₁), 2000 (Δ₂), and 5000 µs (Δ₅) (see Table 1). Membrane permeabilities of 0.005 cm/s and 0.01 cm/s were examined separately. These permeabilities were chosen to span the range of physiologically relevant permeabilities reported by Latour et al.(42).

Table 1.

Simulations with Permeable Cylinders

	Summary of Configurations
Time-step (µs)	0.1	1	10	100	1000	2000	5000
	Simulation Properties
Step Length (µm)	0.035	0.11	0.35	1.10	3.46	3.90	7.75
Percent collisions1(%)	0.4	1.4	4.3	13.7	42.3	59.4	95.8
	Permeability of 0.005 cm/s
5 ms Deviation2 (%)	-	2.1	1.1	1.0	3.8	11.7	31.8
20 ms Deviation2 (%)	-	1.0	0.9	0.8	2.8	4.9	4.9
	Permeability of 0.01 cm/s
5 ms Deviation2 (%)	-	2.1	1.3	1.9	4.5	14.8	34.6
20 ms Deviation2 (%)	-	2.6	2.0	1.3	5.5	9.5	12.4

¹Empirically observed fraction of simulation steps which encountered a compartment boundary during the 5 ms experiment with permeability of 0.01.

²Deviation percentages are calculated as the maximum absolute difference (between each time-step and that with a 0.1 µs time-step) divided by the maximum of the empirical probability density function with a 0.1 µs time-step.

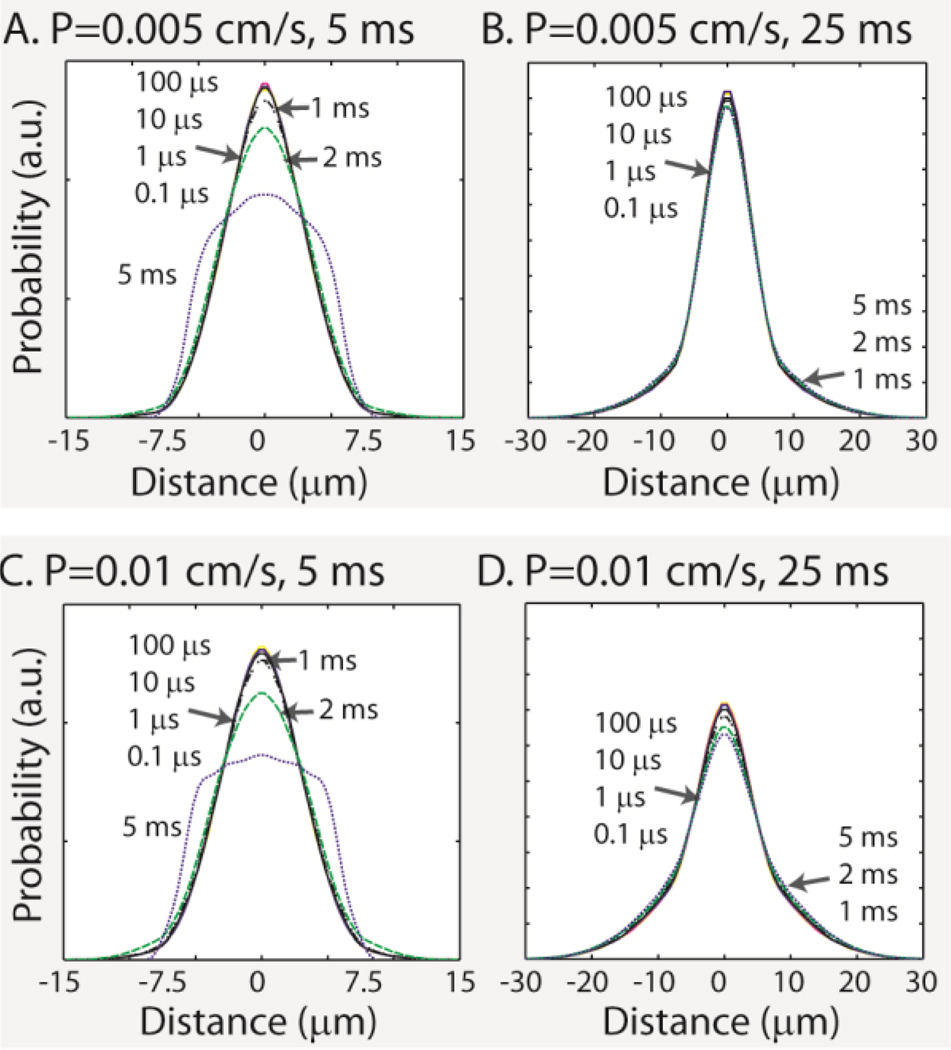
Figure 3 illustrates the impacts of step length on the estimated motion-probability propagator structure in cylinders with permeable membranes. Table 1 summarizes the deviations from the finest resolution simulations (with a time-step of 0.1 µs) for each of the simulation experiments. At both diffusion times, large time-steps lead to an overestimation of the transmission probability, and the resulting probability-density functions had heavier tails and lower peaks. Longer diffusion time mitigated the penalty in accuracy associated with longer time-steps. Similar results were observed with a range of cylinder diameters between 0.5 and 10 µm diameters (not shown).

Figure 3.

Simulations of restricted diffusion in permeable cylinders with diameter 8 µm. The estimated motion-probability propagators were consistent when the step size was much smaller than the cylinder diameter for both permeability models. Table 1 summarizes quantitative differences.

3.4 Guidelines for Monte-Carlo Simulations of Restricted Environments

Although this paper examines a small fraction of the types of simulations possible within the proposed framework, it establishes rough guidelines for planning simulations of more biologically plausible geometries. Figure 1 suggests that 5–10 steps of free diffusion phase are required for the random walk simulations to converge. This finding applies to multiple realistic MRI time scales. With fewer steps, the empirical distribution does not approximate the theoretical one; with more steps, lower total error could be achieved with more spins (in a study with the same total number of steps).

Figure 2 shows that a very similar general rule holds in impermeable environments: at least five Monte-Carlo steps are required within a fixed duration interval for the random-walk simulator to converge. In impermeable geometries, the long-time-limit diffusion behavior, where the expected diffusion is much greater than the dimensions of the restriction environment, can be accurately captured without Monte-Carlo simulation either by analytic convolution of the restriction geometric or by numeric approximation.

The situation is more complex for permeable objects because of the need to achieve close approximations for spins near and distant from boundaries at the same time. In the absence of a boundary, diffusion is Gaussian. At limiting small time-steps, all diffusion is Gaussian since the probability of encountering a wall approaches zero (as epsilon→0, the fraction of volume within epsilon distance of a solid’s surface goes to zero). As time evolves, the discrete Monte-Carlo sampling converges to the biophysical continuous process. With impermeable cylinders, we find that suitable convergence happens in approximately 5 steps (Figure 2). In a permeable cylinder, however, there is a “leak” from the perimeter and near-Gaussian spreading the in the center. Large time-steps can interfere with the convergence of the ever-changing distribution of spins.

Empirically, observed bias was minimal when the diffusion step size was much less than the width of the cylinder and, hence, less than 20 percent of spins encountered boundaries at each time-step. The bias is assessed relative to the very high temporal resolution experiments (which are assumed to be less susceptible to numerical error). The low permeability (P=0.005 cm/s) simulations exhibited a slightly lower sensitivity to temporal resolution than the high permeability (P=0.01 cm/s) simulations for longer diffusion times. Based on these observations, we advocate using a time-step that results in less than 10–20 percent boundary collisions per time-step. Of course, the choice of step size should be empirically verified by comparison of results to those from simulations with smaller step sizes.

4 Reproducibility of Diffusion Simulations in Complex Three-Dimensional Restriction Geometries

To demonstrate the utility of our approach and the potential for continuing exploration, we investigate the reproducibility of motion-probability propagators and the impacts on the DWI signal for geometric models of broken, crimped, and bulging axons. This is work is motivated by Coleman’s recent review (45) on axonal degeneration, in which he notes that “axonal spheroids, or smaller varicosities, which can be broadly termed axonal dystrophy, are almost universal in neurodegenerative diseases of the CNS, probably as manifestations of a major pathway of CNS axonal death.” The structural pathways by which varicosities arise are often unknown or poorly understood, partly due to the difficulty of observing this (often local) behavior. In separate work, we are characterizing animal models of axonal degeneration as observed with MRI. Here, we show how simulations can produce reproducible results for complex models and lead to testable empirical hypotheses.

The three models of white matter damage that we explore here are notably different from traditional models in that they are not constant along the long axis of the axons. Therefore, radial and longitudinal diffusivities are coupled to the full three-dimensional geometry, and the models do not reduce to two-dimensional problems when the radial diffusivities are considered in isolation.

4.1 Models of Axon Damage

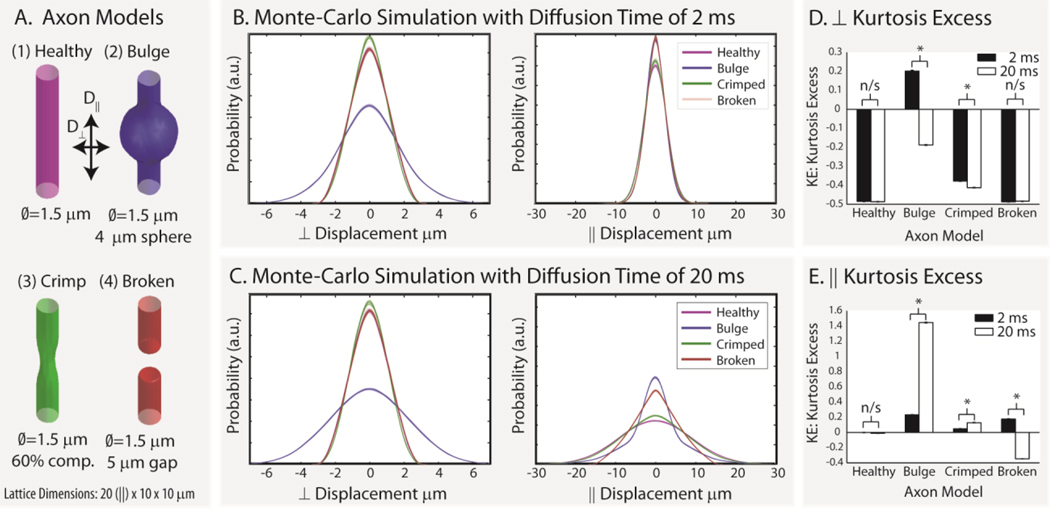
Four models of axon geometry were studied in a 20×10×10 µm lattice (as shown in Figure 4A): (1) healthy axon – a single infinite cylinder with a 1.5 µm diameter; (2) bulging axon – an infinite length of beads on a string with cylinder diameter of 1.5 µm and a spherical bulge diameter of 4 µm repeated every 10 µm; (3) crimped axon – an infinite length of repeating crimp injuries with axon diameters of 1.5 µm and two 4 µm spheres located outside of the cylinder reducing the minimum diameter to 60% of the original; and (4) broken axon – an infinite set of 15 µm cylindrical segments of 1.5 µm diameter separated by 5 µm. In the crimped axon model, the spheres were centered along the long-axis of the lattice and symmetrically positioned at 180 degrees to each other along a mid-line axis of the cylinder. In the broken axon model, diffusion is restricted by closed boundaries near the center of the lattice (shown as solid boundaries) while the ends of the lattice wrap around such that the effective segment length is 15 µm. All compartments were impermeable with a diffusivity of 2 µm²/ms and T2 of 100 ms. In 25 repetitions, 100,000 spins were initialized within each compartment and were studied for diffusion times of 2 ms and 20 ms with 250 time-steps.

Figure 4.

Simulated axon damage. Four geometrical models of axon damage (A) were simulated for 2 ms (B) and 20 ms (C) with 25 repetitions each. The resulting motion-probability propagators are shown as overlaid individual lines for parallel and perpendicular diffusivity. Note that the differences in simulated probability and kurtosis excess (D and E) depend on geometric model, diffusion time, and the displacement direction (i.e., diffusion perpendicular (⊥) or parallel (‖ to the long axis of the “axon”). Error bars in D and E show the standard deviation in kurtosis excess, and * indicates significance at the p<0.01 level.

4.2 Model Comparison

The empirical probability distributions (i.e., the distributions that would be observed with q-space or diffusion spectrum imaging) clearly disambiguate the four geometries from each other and from the free diffusion case (Figure 4B and 4C). To quantify these changes, we consider the kurtosis excess(46,47), which has been used in diffusion kurtosis imaging (48), which can also distinguish the four models studied (Figure 4D and 4E). The kurtosis excess (KE) is the difference between the kurtosis of a given probability-density function and that of a Gaussian (the probability-density function for free diffusion),

$$\mathit{\text{KE}}=\frac{E[X^4]}{E{[X^2]}^2}-3$$ (13)

where E denotes the expected value of the random variable X with the probability density function of interest. KE compares the kurtosis of a PDF to a Gaussian distribution of equivalent variance. If the peak sharpens, then the probability mass must be shifted out towards the tails at the same time to maintain equal variance. This results in a positive KE. Therefore, positive KE has both a higher peak and heavier tails. Conversely, negative KE has a broader peak. Thus, RWS results can help to accept or reject models of axonal damage in relation to empirical observations.

4.3 Simulation Reproducibility

Qualitatively, the repeated estimates of the motion probability were nearly indistinguishable (Figure 5A–D). The three nested surfaces overlay the 25 repetitions of the 10^th, 50^th, and 90^th percentile distances embodied by motion-probability propagators. Since each surface mesh is rendered semi-opaque, variability in the surfaces would visually result in a blurring and thickening of each mesh. At a visual level of precision, almost no variability is present in the simulation results. Quantitatively, the radial PSNR was 30–40 dB (31–100:1) for distances with a probability greater than ~1 × 10⁻⁶. The sharp fall off in PSNR for very unlikely events is due to undersampling (very few of the 10⁵ particles would be likely to reach such a distance) and to numerical accuracy issues in the computation of the density function. The orientation PSNR was 50–70 dB (320–3200:1) for all orientations, with lower PSNR for orientations with lower probability. Note that all orientations had significant integrated probability, so that there were no sharp drops in PSNR for unlikely events. Since the spins are treated as independent events, variability can be reduced (if needed) by increasing the number of spins. By the law of large numbers, variability approximately scales inversely with the square root of the number of spins.

Figure 5.

Reproducibility of simulated axon damage. Plots A–D show the 10^th, 50^th, and 90^th percentile isosurfaces of the motion-probability propagators estimated in each of the 25 repetitions. Nested surfaces are constructed so that local color and position of vertices indicate the distance corresponding to the indicated quantile of the probability of motion along the each direction. Repetitions of each set of surfaces are nearly identical, so the isosurfaces from the separate repetitions are difficult to distinguish except as slightly blurred lines. The spatial scales for the figures corresponding to the two diffusion times are constant across panels but are different from each other. Quantitative comparisons of the mean PSNR are shown for radial distance (E) and angular orientation (F).

4.4 Simulation Benchmarks

All simulations were run on a 2.5 GHz single-processor notebook computer running 64-bit Windows Vista. On average, tracking 100,000 particles for 250 time-steps took 39 seconds. Longer steps and more complex geometries increased the computation time due to the need to check for collisions, with the longest simulation reported here lasting 58 seconds. Table 2 provides a summary for each of the eight experiments.

Table 2.

Simulation Benchmarks

	2 ms Diffusion Time		20 ms Diffusion Time
Axon Model	Spin×Steps /s [× 105]	Collisions/Step [%]	Spin×Steps /s [× 105]	Collisions/Step [%]
Healthy	1.11 ± 0.03	10.4 ± 0.01	0.79 ± 0.02	33.0 ± 0.02
Bulge	0.86 ± 0.02	6.7 ± 0.02	0.62 ± 0.01	21.1 ± 0.02
Crimped	0.67 ± 0.02	11.7 ± 0.01	0.43 ± 0.01	37.0 ± 001
Broken	0.73 ± 0.02	11.5 ± 0.01	0.49 ± 0.01	36.3 ± 0.01

All values shown mean ± standard deviation.

4.5 Technical Demonstration

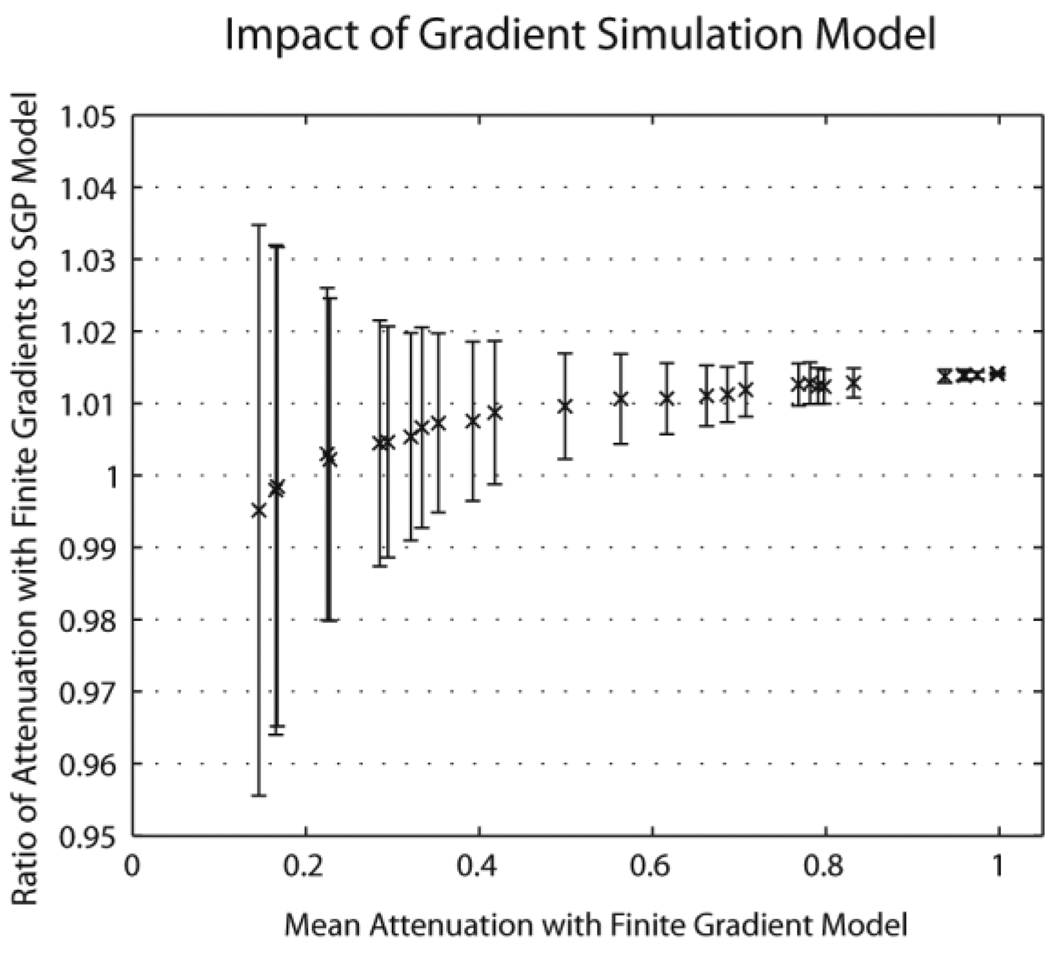
The SGP approximation may be relaxed by specifying discretized arbitrary waveform gradients in terms of the x, y, and z vector components of the effective magnetic field gradients in mT/m. Gradients must be specified prior to simulation. The framework does not take into account radio frequency pulses, so the user must adapt the sign of the waveform to compensate for these effects (hence effective gradient rather than absolute gradient). Each particle maintains a relative phase for each gradient waveform which is updated at each time-step. At the end of the simulation, each particle reports a vector of phase changes which correspond to each of the specified gradient waveforms. To illustrate these effects a simulation was conducted with a 5 µm diameter impermeable cylinder. Signal attenuation was simulated along the 30 directions specified by Jones et al. (reported in (43)) at a b-value of 1000 s/mm² with diffusion time of 100 ms (0.1 ms time-step, 10,000 spins, 50 Monte Carlo iterations) under two conditions: 1) with the SGP and 2) using a bipolar diffusion encoding gradient with 50 ms of dephasing time and 50 ms of rephasing time (rectangular gradients with infinite slew rate). Results are shown in Figure 6 and generally agree with previous finding that finite gradients result in lower signal attenuation (and perceived lower diffusion constant).

Figure 6.

Simulation of finite duration diffusion encoding gradients. For each of 30 diffusion encoding directions, the mean simulated attenuation was calculated with a finite gradient model (horizontal axis) and the SGP model was compared with each Monte Carlo simulation (vertical axis). Symbols indicate the mean difference while error bars indicate the standard deviation of the observations.

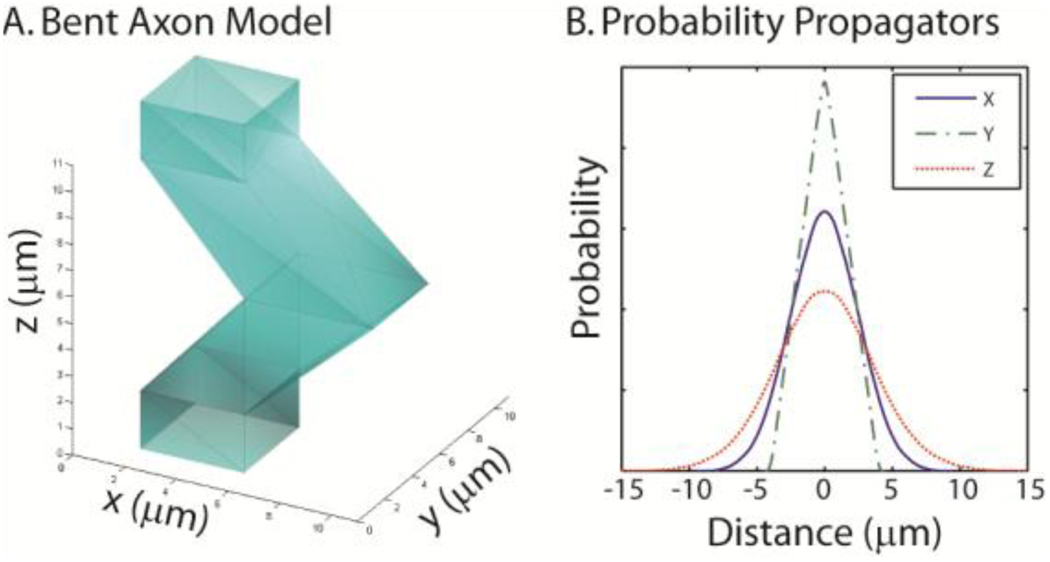
Some models of axon degeneration may involve complex changes to the global axonal shape in addition to local compression/compression. For example, the axons of the twitcher mouse are extremely wavy (i.e., saw-toothed as seen on electron microscopy) relative to a control animal (44). To illustrate the mesh-based capabilities of the RWS, we explore a simple approximation of this type of change (Figure 7). Our lattice element for the bent axon model consists of an 11 mm length with a square cross-section (4 µm per side) at the lattice boundaries. The central of the axon model had one edge pushed left 4 µm and the other edge pushed 5 µm (which resulted in a 5 µm × 4 µm cross-section at the center). The cross-section linearly varied between square at 1.1 µm from the lattice boundaries to the described rectangle at the center (as shown in Figure 7A). There were a total of 20 vertices and 36 faces. Note that each mesh model must form an enclosed polyhedron so that inside/outside tests are efficient. However, surface patches that lie outside of the lattice element are not considered during collision detection. The model in Figure 7 includes end-caps that extend beyond the lattice element. During rendering these are hidden since their location has no impact on the simulation. As with the parametric models, any intersection with the lattice boundary is considered a location for wrap-around to the next lattice element. A simulation was demonstrated with 100,000 spins diffusing inside the model for 10 ms with a time-step of 100 µs (impermeable membranes and diffusion coefficient of 1×10⁻³ µm²/µs). Simulated motion probability propagators were estimated for each of the cardinal axes (Figure 7B).

Figure 7.

Simulation of a bent axon using a mesh model. To demonstrate the ability to use arbitrary meshes, a model of a bent axon was created (A). Note that a single element of the lattice is shown and that the upper and lower square openings are continuous with the interiors of the adjacent axon elements. Plots (B) show the simulated projections of the motion probability propagator (for SGP, 10 ms diffusion time, and impermeable membranes) along x, y, and z.

5 Discussion

There has been a great deal of effort invested in understanding the biological underpinnings of the diffusion MR signal. Early studies of diffusion in normally unmyelinated garfish nerves showed that the axonal membrane is sufficient to cause significant diffusion anisotropy (2). Several current models appear to explain observed behaviors in specific disease models, but general biophysical interpretation of diffusivity remains an unsolved problem, in part due to the complex geometry of white matter. Nevertheless, ADC is often abnormal in disease and represents a clinically useful tool for diagnosis and disease monitoring (1,2,49,50).

Our results demonstrate that the empirical probability distributions (i.e., those that would be observed with q-space or diffusion-spectrum imaging) can be reliably estimated, using Monte Carlo simulations, for both traditional cylindrical and complex three-dimensional geometric models of the restriction environment. The sampling variation due to random nature of simulation experiments (i.e., 30–70 dB, 30–3200:1) was much was much less than typical noise levels in empirical studies (less than 30 dB, 30:1). Furthermore, the PSNR could be readily increased by approximately 3 dB (i.e., a factor of $\sqrt{2}$) simply by doubling the number of spins (and, in turn, the simulation time), which would remain practical and feasible on consumer hardware. Thus, it is readily feasible to use simulations of complex geometries to evaluate what real signals can actually distinguish. We emphasize that the PSNR statistics provide a means to quantify the sampling variation independent of the measure of interest (e.g., tensor FA, generalized anisotropy, etc.). In continuing work, these types of simulations may be used to study and optimize the manner in which diffusion MRI methods can be used to can disambiguate restriction environments and improve the specificity of diffusion MRI interpretation. These results can be used to investigate and design contrast mechanisms that maximize specificity and sensitivity to changes of biological interest using a minimum number of acquisitions.

RWS supports the SGP and arbitrary waveform (discretized) gradients. The system could be readily extended (at the cost of additional computational complexity) to include continuously varying and parametric gradients via extension of the finite duration gradient waveform interface. Since the full system is available in open source, anyone may use or adapt this system as desired.

Monte-Carlo simulation of individual, three-dimensional axons provides a powerful framework for evaluating potential biophysical underpinnings of diffusion. Additionally, it presents exciting opportunities layering complexity into models to recapitulate various stages of axon degeneration. For example, little is known about the content within the bulges so it would be interesting to simulate different possible events and then see which ones correlate with our observations in models. Additionally, at what scale are microscopic simulations relevant to DTI at the present clinical resolution (in which we are not looking at individual axons)? Finally, how many axons per voxel would have to demonstrate a similar pathology to become detectable, and how would distributions of similarly, but non-identically, damaged axons appear? The demonstrated RWS tool provides the numerical tools to quantitatively pursue these questions for complex geometrical models, which will present fascinating areas of continuing investigation.

In summary, RWS enables efficient, quantitative comparison of diffusion in biologically relevant restriction geometries that are not analytically accessible. This simulation framework may aid in the interpretation DTI, q-space, and higher order DWI methods as well as the optimized development of new higher-order analysis techniques targeted to specific white matter injuries.

List of abbreviations

ADC

apparent diffusion coefficient

DTI

diffusion tensor imaging

DWI

diffusion weighted MRI

HARDI

high resolution angular diffusion imaging

KE

kurtosis excess

PSNR

peak signal-to-noise ratio

RMSD

root mean square displacement

RWS

random walk simulator

SGP

short gradient pulse approximation