Abstract
Most genomes are heterogeneous in codon usage, so a codon usage study should start by defining the codon usage that is typical to the genome. Although this is commonly taken to be the genomewide average, we propose that the mode—the codon usage that matches the most genes—provides a more useful approximation of the typical codon usage of a genome. We provide a method for estimating the modal codon usage, which utilizes a continuous approximation to the number of matching genes and a simplex optimization. In a survey of bacterial and archaeal genomes, as many as 20% more of the genes in a given genome match the modal codon usage than the average codon usage. We use the mode to examine the evolution of the multireplicon genomes of Agrobacterium tumefaciens C58 and Borrelia burgdorferi B31. In A. tumefaciens, the circular and linear chromosomes are characterized by a common “chromosome-like” codon usage, whereas both plasmids share a distinct “plasmid-like” codon usage. In B. burgdorferi, in addition to different codon-usage biases on the leading and lagging strands of DNA replication found by McInerney (McInerney JO. 1998. Replicational and transcriptional selection on codon usage in Borrelia burgdorferi. Proc Natl Acad Sci USA. 95:10698–10703), we also detect a codon-usage similarity between linear plasmid lp38 and the leading strand of the chromosome and a high similarity among the cp32 family of plasmids.
Keywords: horizontal gene transfer, codon adaptation index, correspondence analysis
Introduction
Codon-usage analyses can provide insights into the functional categories and histories of genes in a genome. More information can be gained from a codon-usage analysis than a G + C analysis, and it does not require the identification of homologous proteins from other genomes, as is the case for inferring molecular phylogenies. This is particularly useful for studying mobile elements, which may be a mosaic of genes from different sources. Despite this, codon-usage analysis—as a means for assessing genome content—is underutilized and often relies on ad hoc approaches.
Early studies revealed that many genomes have a signature codon usage that is representative of the typical genes of that genome (Grantham, Gautier, et al. 1980; Grantham, Gautier, and Gouy 1980). Despite this overall signature, the gene-by-gene codon usage of most genomes is heterogeneous. In many cases, a major source of this heterogeneity is the subset of genes that exhibit high-expression codon usage. This codon usage was termed “high expression” because it is commonly exhibited by genes encoding high-abundance proteins, such as transcriptional and translational proteins (Grantham et al. 1981; Ikemura 1981a, 1981b; Gouy and Gautier 1982). It is thought that this bias reflects the “optimal” codons that provide for more efficient translation and thus greater protein abundance (Grantham et al. 1981; Ikemura 1981a, 1981b; Gouy and Gautier 1982; Grosjean and Fiers 1982). Another common source of genomic codon-usage heterogeneity is genes that have been acquired horizontally (Médigue et al. 1991). These genes can differ drastically from the native genes of the genome (both typical and high expression), potentially bearing the codon usage of their original source. Because of this, many studies consider a gene to be foreign by virtue of it not matching the high-expression or typical codon usages of the genome (e.g., Lawrence and Ochman 1997; Karlin and Mrázek 2000).
In the most common genetic code, 18 of the 20 universal amino acids can be encoded by two or more synonymous codons, resulting in a total of 59 synonymous sense codons. This high level of complexity in the data has resulted in different approaches for codon-usage analysis. One approach employs multivariate analyses—principal components analysis or factorial correspondence analysis (FCA)—to convert the 59-dimensional codon usage data into a smaller number of dimensions, while retaining the greatest variation in the data set. This has proven to be a valuable technique for visualizing codon-usage trends within a genome (e.g., Grantham, Gautier, et al. 1980; Grantham, Gautier, and Gouy 1980; Médigue et al. 1991) and has been used to study many diverse genomes, including Escherichia coli (Grantham, Gautier, et al. 1980; Grantham, Gautier, and Gouy 1980; Médigue et al. 1991), Bacillus subtilis (Kunst et al. 1997; Moszer et al. 1999), Pseudomonas aeruginosa (Grocock and Sharp 2002), and Borrelia burgdorferi (McInerney 1998a; Lafay et al. 1999). A major drawback to these multivariate analyses is that they are not clustering methods per se—further analysis is required to group the genes and associate them with biologically relevant categories (e.g., Médigue et al. 1991; Badger 1999).
Perhaps the most popular method of summarizing codon usage is the codon adaptation index (CAI) (Sharp and Li 1987). In the CAI, all of the genes in the genome are compared with an optimal codon usage inferred from a set of presumed high-expression genes. This results in a quantitative measurement of the high-expression codon usage bias exhibited by each gene in the genome. A major limitation to the CAI is that it is 1D, providing only a measure of how “high-expression-like” a gene appears. Thus, many typical and alien genes have indistinguishably low CAI values.
Karlin and Mrázek (2000) proposed a method that solves this problem, categorizing each gene in the genome as being typical, high expression or alien. If a gene is sufficiently similar to the average codon usage of the genome, yet sufficiently different from the codon usage of the high-expression genes, it is considered typical. If a gene is sufficiently similar in codon usage to two of three of their high-expression gene categories, yet sufficiently different from the average codon usage of the genome, it is considered high expression. All other genes are considered alien. Although this approach is intuitively appealing, it depends on the average not being overly affected by high expression, alien, or other aberrant genes.
We suggest that the first step in a cohesive method of codon-usage analysis should be to robustly identify those genes that are typical or most representative of the genome. In this study, we describe an approach to defining and deriving a modal codon usage—the usage that characterizes the largest number of genes. This provides a starting point for characterizing genes that are significantly different. Because the ability to calculate a modal codon usage provides a baseline for understanding genome content and horizontal gene transfer, we examined the complex bacterial genomes of Agrobacterium tumefaciens (four replicons) and B. burgdorferi (22 replicons), comparing the codon usages of the diverse genetic elements found within each of these genomes.
Materials and Methods
Sequence Data
Unless otherwise indicated, genome sequences were taken from NCBI Entrez system (Wheeler et al. 2007), and coding regions were as defined in the SEED (Overbeek et al. 2005). Genes annotated as having programmed frameshifts have been omitted.
Calculation of Codon Usage
Codon Usage Frequencies.
The codon usage of a gene does not include the initiator or terminator codons. Codons for selenocysteine and pyrrolysine, and codons with an ambiguous nucleotide were omitted. All codon-usage frequencies are expressed as relative codon usage of each of the cognate codons for the 18 amino acids with multiple codons. This choice provides a level of insensitivity to the amino acid composition of a protein because all codon-usage frequencies for a given amino acid sum to one. Due to the finite sample of codons available for computing empirical codon-usage frequencies, for each amino acid, one pseudocount has been distributed over its codons. The overall codon-usage frequencies are expressed as a 59-tuple. The average codon usage for a set of genes was found by pooling the codons of all genes.
Evaluating Gene Codon-Usage Frequencies.
The match of a gene to a set of proposed (expected) codon usage frequencies was performed by a chi-square test. The codon frequencies were used to calculate expected numbers of each of the 59 relevant codons. The resulting chi-square value has 41 degrees of freedom (59 codon counts minus 18 amino acids whose abundances were normalized). In the case of proteins that completely lack an amino acid, the amino acid was omitted from the calculation and the degrees of freedom correspondingly reduced. Chi-square P values were computed according to Zelen and Severo (1965). The consequences of applying the chi-square test with low numbers of expected counts are addressed in Results. For evaluating the match of a gene to a set of expected frequencies, a gene was classified as matching the composition if it had P ≥ 0.1 in the chi-square test.
Finding Modal Codon-Usage Frequencies.
We defined the modal codon-usage frequencies as the frequencies that match the largest number of genes in a set of genes. As outlined in Results, a direct solution is difficult. We therefore defined an optimization criterion as
where S(f,G) is the score of the codon-usage frequencies f applied to the set of genes G, p(f,i) is the chi-square P value of gene i matching frequencies f, and λ is a positive real number. It is easily seen that the larger the number of genes with large P values, the greater the sum. The value of λ affects the P values that effectively contribute to the sum; larger values of λ increase the influence for large P values relative to small P values, whereas smaller values of λ increase the ability of smaller P values to contribute to the sum. To make S(f,G) approximately equal to the number of genes with P ≥ 0.1 (the quantity that we seek to maximize), we have used a value of 0.3 for λ.
Given a set of genes, we must search for the codon-usage frequencies f that maximize S(f,G). For this, we use a version of the Simplex method (Nelder and Mead 1965). The method begins with an initial set of trial points and then seeks to improve the points (vertices) by testing new points that are a linear combination of the existing points. This is a relatively greedy algorithm. Several attempts are made to improve a given vertex, and if any attempt is successful, the vertex is replaced and a new cycle started. Generally, the vertices are prioritized from worst to best. To allow searching the full volume of the potential solution space, it is necessary to have at least one more vertex than the number of independent dimensions. Thus, we require at least 42 vertices. Generally, we found performance was better with a larger number, as many as 100. Most commonly, our starting points were based on the codon usage frequencies of actual genes. Specifically, each gene i in a set of genes G was converted to its codon frequencies, and these were scored as above. Typically, the codon-usage frequencies of the 100 highest-scoring genes were used as the initial vertices of the Simplex. When fewer than 100 genes were available, additional starting points were produced by making combinations of the frequencies from different genes, such as the alanine frequencies from gene 1, the cysteine frequencies from gene 2, etc. As might be expected in such a complex search space, no method is guaranteed to find the best solution, and even the best solution is not necessarily the mode as defined by the number of genes in G with P ≥ 0.1. Regardless, many variations in the methodology have not yielded any qualitatively different conclusions than those reported in this paper.
Distance between Codon-Usage Frequencies
We compute the distance between two codon usages in two steps. For each amino acid, we define the distance as the sum of the absolute differences in relative codon-usage frequencies (a Manhattan-metric distance). Regardless of the number of codons for the amino acid, this has the property of being 0 if the codon frequencies are identical, and 1 if there is no overlap in the codons used. Our overall distance between two codon usages is the square root of the sum of the squares of the amino acid distances (a multidimensional Euclidian distance). Thus, if all relative codon usages are identical for all amino acids, the distance is zero. If there is no overlap in the codons used for all 18 amino acids with multiple codons, the distance is the square root of 18 (∼4.2).
To find the expected distance between the modes of two sets of genes, under the assumption that they are actually drawn from a common pool, the genes of the two sets were pooled, and then randomly divided into two new sets of sizes equal to those of the original sets. The mode was determined for each shuffled gene set, and the distance between the two modes calculated. The reported values are the mean and standard deviation of the distances from 10 or more replicates.
Drawings of Genomic Codon Usage
For A. tumefaciens, the genes of the chromosomes were pooled and the genes of the plasmids were pooled and the mode of each combined set (chromosomes and plasmids) was determined. In order to reduce the number of unidentifiable genes, in this instance, the observed codon counts in the chi-square test were controlled for codon length with a cutoff of 300 observed codons. This cutoff was used to reduce the number of (long) native genes that appear foreign in the color scheme. Genome drawings were rendered in POV-Ray.
Tree Inference
Distances between codon usages were computed as described above. A Neighbor-Joining distance tree was calculated using the neighbor program in the PHYLIP package (Felsenstein 1989). Borrelia burgdorferi chromosomal genes were separated into leading versus lagging strand as in (McInerney 1998a), from the origin of replication in Picardeau et al. (1999).
Program Availability
The programs described are written in perl and C. They have been tested on PPC and i386 Macintosh computers, under OS X 10.4 and 10.5, but should work in any Unix environment. The program versions that were current at the time of submission are deposited as supplemental information, Supplementary Material online, and current versions are available through links at http://www.life.illinois.edu/gary/programs.html.
Results
Calculation of Modal Codon Usage
By defining the codon usage that is typical to the genome, it is then possible to identify those usages that are different, that is, atypical (high expression or alien). Previous studies have used the average codon usage of a genome to represent “typical” (e.g., Karlin and Mrázek 2000). Because a genome may contain disparate codon-usage types that would influence the average, we suggest that the typical codon usage could be better described as the usage that matches the most genes, that is, the modal codon usage. More precisely, we define the modal codon usage as the codon-usage frequencies from which the largest number of genes are not significantly different.
To define “significantly different,” we use a chi-square test to evaluate the agreement between the observed codon usage of a gene and an expected usage. Because we are interested in codon usage per se, as opposed to amino acid composition, the calculation of the expected number of each codon was carried out on an amino acid-by-amino acid basis (i.e., relative codon usage). This excludes methionine and tryptophan, because each has only one codon, leaving 18 amino acids encoded by 59 codons. After normalizing for each amino acid's abundance, 41 degrees of freedom remain (for proteins containing all of these amino acids). The chi-square value for the codons used in a gene having been randomly drawn from the expected codon-usage frequencies is then calculated and the corresponding P value found. Unless otherwise stated, we classified genes with P ≥ 0.1 as matching the expected usage.
Our definition of mode requires optimizing the expected codon usage. Because it involves the count of genes matching a set of frequencies, it is a discontinuous measure, making optimization difficult. To circumvent this, we define a smoothly varying approximation of the mode criterion: the sum over all genes of each of the chi-square P values raised to the 0.3 power (Materials and Methods). The more a gene differs from the mode, the lower its P value, and the lower its contribution to the sum. The power 0.3 is used because (0.1)0.3 ≈ 0.5, matching our desired P value threshold of 0.1 to the point at which a gene makes 50% of its potential contribution to the sum. This exponent has also been tested empirically on several genomes to verify that it effectively maximizes the actual count of genes with P ≥ 0.1 (data not shown).
This leaves us with the task of finding the codon-usage frequencies that maximize this sum. For simplicity, we carry out the optimization in the 59-dimensional space of relative codon-usage frequencies. The search for optimal (modal) codon usage is carried out with a Simplex method (Materials and Methods).
Our use of a chi-square test comes with caveats, especially the assumption that the expected values are “large.” To verify that violations of the assumptions do not interfere with our analyses, we tabulated the fraction of genes matching the average and modal codon usages in simulated genomes. To provide a realistic model of bacterial gene lengths and amino acid compositions, each simulated gene set was a duplicate of the E. coli K-12 protein sequence set but with each codon drawn randomly from the E. coli average codon usage for the given amino acid. The resulting simulated genes match the underlying average codon usage within statistical fluctuation. We then evaluated the chi-square P value for the fit between each individual gene in a simulated genome and the expected values based on the average codon frequencies and on the modal codon frequencies of the simulated genome. The fraction of the simulated genes with a chi-square P value greater than or equal to a given threshold was plotted versus the threshold value (supplementary fig. S1, Supplementary Material online).
When genes were compared with the average codon usage, the fraction of genes passing the chi-square test is in nearly perfect agreement with the P value in the interval 1 ≥ P ≥ 0.1. At lower P values, there is a growing excess of genes with high chi-square values. Of the genes, 5.4% have a chi-square with P ≤ 0.05; 2.5% of the genes have P ≤ 0.02, and 1.4% of the genes have P ≤ 0.01. When comparing the genes in a simulated genome to their respective modal usage (rather than their average), there is a systematic tendency for more genes to match (fewer fail the chi-square test), even though all genes are drawn from the average codon-usage pool. For example, only 7.2% of the genes have a chi-square with P ≤ 0.1, and 0.64% of the genes have a chi-square with P ≤ 0.01. These results indicate that for simulated genomes with protein sizes and amino acid compositions matched to those of E. coli, the chi-square test provides a reliable measure of matches to the average codon usage within the P value range we are using. They also show that the mode systematically matches more genes than the average (fewer genes fail the chi-square test). With a cutoff of P ≥ 0.1, 93% of the simulated genes were not significantly different from the mode calculated for the simulated genome.
The genomes of several organisms, including Wigglesworthia glossinidia, Buchnera aphidicola APS, and Rickettsia rickettsii, have been described as exhibiting little or no high-expression codon bias and lacking alien genes (Akman et al. 2002; Herbeck et al. 2003; Rispe et al. 2004). For these genomes, 87–93% of the genes are not significantly different from the corresponding modal codon usage (data not shown). Thus, the above simulations are consistent with analyses of genomes that have nearly homogeneous codon usage.
Modal versus Average Codon Usage
The most common assessment of genomic codon usage is the average, so in our initial characterization, we compared the average and modal codon usage in E. coli K-12. Of 4299 annotated K-12 genes (see Materials and Methods for details), 1,754 (40.8%) match both the average and modal codon usages; 324 genes (7.5%) match only the mode, whereas 192 genes (4.5%) match only the average. Thus, 132 more genes (3.1% of the genome complement) match the mode than the average. Although this trend should not be surprising, because it is the defined goal of finding the mode, our optimization criterion and search method are successful at increasing the number of matching genes.
In E. coli, the difference between the mode and the average is small, but there are many genomes in which the difference is large. To assess this, we compared the modal and average codon usages of 674 bacterial and archaeal genomes. In 42 of these genomes, >10% more genes in the genome match the mode than average. Table 1 gives diverse examples of genomes in which there are large differences between the number of genes matching the average and the mode. In the most extreme genome, Synechococcus elongatus PCC 6301, the mode matches 19.6% more of the genes in the genome (nearly 500 genes) than does the average. The S. elongatus PCC 6301 genome is a single small (2.7 Mbp) replicon. Few regions within the genome deviate from the average G + C of 55.5%, and G + C skew analysis does not reveal the replication origin or terminus in this organism (Sugita et al. 2007), so a strand-dependent codon bias may not be the source of this large difference. Many of the organisms in table 1 have low G + C content, but there are examples, such as S. elongatus and Pyrobaculum islandicum, where the G + C content is moderate. We have found only one genome, Burkholderia vietnamiensis, where the average outperformed the mode (by two genes).
Table 1.
Some Examples of Genomes Where There Is a Large Difference between the Average and the Mode.
| Organism | CDSa | G + Cb | G + C3c | Averaged | Moded | Difference |
| Synechococcus elongatus PCC 6301 | 2525 | 55.8 | 58.4 | 45.5 | 65.2 | 19.6 |
| Fusobacterium nucleatum subsp. nucleatum ATCC 25586 | 2075 | 27.4 | 12.5 | 66.5 | 83.1 | 16.6 |
| Ureaplasma urealyticum serovar 7 | 681 | 26.0 | 12.0 | 62.3 | 78.6 | 16.3 |
| Methanosphaera stadtmanae DSM 3091 | 1523 | 29.1 | 13.5 | 51.1 | 65.5 | 14.3 |
| Pyrobaculum islandicum DSM 4184 | 1978 | 49.5 | 53.0 | 39.3 | 52.6 | 13.3 |
| Clostridium perfringens str. 13 | 2732 | 29.4 | 16.4 | 57.0 | 69.9 | 12.9 |
| Lactobacillus acidophilus NCFM | 1866 | 35.2 | 25.0 | 44.4 | 56.1 | 11.7 |
| Staphylococcus aureus subsp. aureus COL | 2618 | 33.5 | 22.5 | 59.9 | 70.7 | 10.8 |
| Streptococcus pneumonia pneumoniae D39 | 2162 | 40.6 | 35.9 | 38.2 | 48.2 | 10.0 |
| Borrelia burgdorferi B31 | 1688 | 28.9 | 21.2 | 50.3 | 58.0 | 7.7 |
Number of coding sequences in genome (all replicons combined).
Percentage G + C for protein-encoding genes.
Mean G + C content for nucleotides in the third codon position.
Percentage of genes matching the modal or average codon usage for the entire genome of that organism.
Codon-Usage Analysis of A. tumefaciens C58
To this point, we have calculated the modal codon usage of entire genomes; however, the mode can be applied to any group of genes. This enables us to assess the codon-usage similarities and differences between the replicons comprising a given genome. To demonstrate this approach, we chose to study the genome of A. tumefaciens C58, which has two chromosomes (one circular and one linear) and two circular plasmids (Goodner et al. 2001; Wood et al. 2001). This analysis enables us to assess the relative codon-usage similarities between the chromosomes (which are topologically different), between the chromosomes and the large mobile plasmids, and between the plasmids themselves.
For each A. tumefaciens replicon, and for the combination of all replicons, the modal codon usages were determined, and the percentage of genes matching each was calculated (table 2). For each individual replicon, 60–64% of a replicon's genes match (are not significantly different from) its own modal usage. The modes of the circular and linear chromosomes are extremely similar, with only 1% more of the genes on a given chromosome matching their own mode than match the mode of the opposite chromosome. More surprisingly, the plasmids also have similar modal usages, with 55% and 61% of the genes on the At and Ti plasmids matching the mode of the opposite plasmid. In stark contrast, the chromosomal modes differ greatly from the plasmid modes. Typically, twice as many plasmid genes match a plasmid mode than match a chromosome mode and vice versa.
Table 2.
Percentage of Genes Matching the Modal Codon Usages of Replicons in Agrobacterium tumefaciens C58.
| Genes of Replicon | CDSa | Matching Mode of |
|||
| Circular Chromosome | Linear Chromosome | pAt | pTi | ||
| Circular chromosome | 2,765 | 62.2 | 61.4 | 34.9 | 30.0 |
| Linear chromosome | 1,851 | 61.2 | 62.3 | 32.5 | 27.6 |
| pAt | 542 | 26.8 | 30.1 | 64.4 | 61.3 |
| pTi | 197 | 20.8 | 24.4 | 55.3 | 59.9 |
Number of coding sequences in the replicon.
Distances between the Codon Usages of the A. tumefaciens Replicons.
The above results indicate that the genes of the chromosomes poorly match the genes of the plasmids, and vice versa. To more directly quantify the differences between replicons, we measure the distance between the modal codon usages of each replicon (table 3, column 3). The results reflect the observations made above: The distances between chromosomal modes and plasmid modes (0.390–0.469) are large compared with the distances between the two chromosomal modes (0.062) or the two plasmid modes (0.106). To assess the significance of these distances, we repeated the distance calculations but with the genes shuffled between the two replicons being compared (table 3, column 4). The results show that all replicons have at least marginally significant differences in modal codon usage, but that in both magnitude and significance, the fundamental difference is between the chromosomes and the plasmids.
Table 3.
The Distance between the Modal Codon Usages of Agrobacterium tumefaciens Replicons.
| Replicon 1 | Replicon 2 | Distance between Replicon Modes | Distance between Shuffled Repliconsa |
| Circular chromosome | Linear chromosome | 0.062 | 0.035 ± 0.006 |
| Circular chromosome | pAt | 0.423 | 0.049 ± 0.009 |
| Circular chromosome | pTi | 0.469 | 0.068 ± 0.009 |
| Linear chromosome | pAt | 0.390 | 0.053 ± 0.012 |
| Linear chromosome | pTi | 0.430 | 0.069 ± 0.008 |
| pAt | pTi | 0.106 | 0.067 ± 0.007 |
Average ± standard deviation of distances between codon-usage modes of simulated replicons with a random partitioning of the combined set of genes.
The Distribution of Codon Usages within the A. tumefaciens Replicons.
Given that A. tumefaciens genes form two main groups, “chromosome-like” and “plasmid-like,” we ask how genes matching theses two codon-usage types are distributed within the four replicons. In doing so, we note that neither high abundance nor “alien” codon usage types are analyzed here (mostly, they appear different from both chromosomal and plasmid).
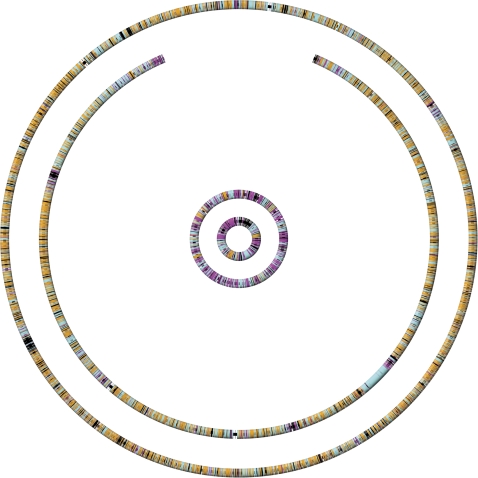
Figure 1 displays the four replicons of A. tumefaciens C58, with each gene colored according to its codon usage: similar to (not significantly different from) the chromosomal mode (orange), similar to the plasmid mode (purple), similar to both (teal), or similar to neither (black). A gene-by-gene accounting is included in the supplemental materials (supplementary table S1, Supplementary Material online). Because we do not include a category for high-expression codon usage, genes encoding highly abundant proteins tend to be black. Overall, the chromosomes are composed of chromosome-like genes, and the plasmids are composed of plasmid-like genes. One obvious exception is a concentration of plasmid-like genes near the ends of the linear chromosome. There are large stretches of genes that match neither the plasmid nor chromosome modal usages. Notably, with just the exception of rolB (Atu6003) and D protein (Atu6004), which are not significantly different from plasmid codon usage, the genes of the T-region of the Ti plasmid (the DNA transferred to plants for tumor formation and opine production) do not match either the plasmid or chromosomal usage (supplementary table S1, Supplementary Material online). Indeed, their plant-like codon usage has been previously noted (Wood et al. 2001).
FIG. 1.
Gene-by-gene plot of the codon usage of Agrobacterium tumefaciens C58. From outside to inside: circular chromosome, linear chromosome, pAt, and pTi. Each wedge represents a gene. Orange genes match the codon usage of the combined chromosomes, magenta genes match the codon usage of the combined plasmids, teal genes match both the chromosomes and plasmids, and black genes match neither.
These results indicate that the topological difference of linear and circular chromosomes introduces little or no selection on codon usage. More surprisingly, the data conflict with an image of plasmids as vehicles that promiscuously travel amongst diverse hosts, picking up and dropping off genes along the way. If this were the case, we would expect few genes within a plasmid to share a common codon usage and distinct plasmids to have distinct codon usages. Instead we observe that, despite their distinct gene contents, each plasmid has a relatively homogeneous codon usage (most genes are not significantly different from the modal usage), and the two plasmids are very similar in codon usage even though they are very far from the codon usage of the chromosomes.
Codon-Usage Analysis of B. burgdorferi
Borrelia burgdorferi offers an extreme example of a genome with many replicons: a linear chromosome, 12 linear plasmids, and 9 circular plasmids (Fraser et al. 1997; Casjens et al. 2000). Although previous studies of the B. burgdorferi chromosome have shown a significant difference in codon usage between genes on the leading and lagging strands of DNA replication (McInerney 1998a; Lafay et al. 1999), they did not address the relationships among the replicons.
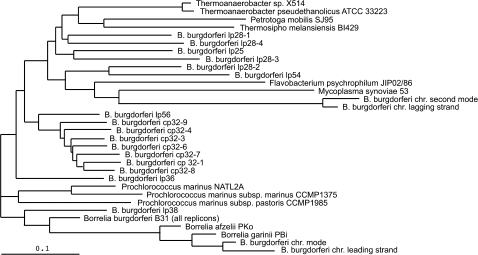
The multiplicity of elements, and the fact that their shared gene content ranges from zero to nearly complete, led us to explore an alternative to a purely tabular representation of the differences in codon usage. To display the relative similarities between the modal codon usages of the B. burgdorferi replicons, we constructed a Neighbor-Joining tree from the pairwise distances between the modal codon usages of each replicon. Replicons with fewer than 30 genes were excluded (due to statistical noise), leaving 17 replicons in the analysis. As noted above, the leading stand genes (transcribed in the direction of replication) and lagging strand genes (transcribed opposite the direction of replication) in B. burgdorferi have very distinct codon usages, so we also included the modal codon usage of each of these two gene sets. Previous observations that these latter codon usages appear bimodal in an FCA plot (McInerney 1998a; Lafay et al. 1999) led us to reason that if the data are truly bimodal, then we might directly identify the two sets of genes by identifying the modal codon usage (“first mode”), removing the genes not significantly different from this mode, and then finding the modal codon usage of the genes that remain (“second mode”). These two modes are also included in the tree. Finally, we add the most similar other (non-B. burgdorferi) genomic codon usages to provide a context and a sense of scale to the codon usage differences observed among the B. burgdorferi replicons. To do this, we compared each of the B. burgdorferi modal codon usages listed above with those of 674 other bacterial and archaeal genomes, recording the three genomes closest (least distant) in codon usage to each B. burgdorferi mode. All of these most similar genomes (11 in total) were added to the analysis (fig. 2).
FIG. 2.
Neighbor-Joining tree of codon usage of Borrelia burgdorferi replicons containing more than 30 genes. Each tip in the tree represents the modal codon usage of a replicon, genome, or set of genes (see text). For each B. burgdorferi modal codon usage, the modal codon usage of the three most similar genomes is also included to help visualize the significant groupings. The tree is shown arbitrarily rooted at its midpoint. The reference bar represents a codon usage distance of 0.1 (Materials and Methods).
The tree of modal codon usage indicates a similarity between the B. burgdorferi chromosome mode and lp38, as well as similar usages among the cp32 family of plasmids. The cluster containing the B. burgdorferi chromosome also contains the leading strand mode, the mode of the B. burgdorferi genome (all chromosomes combined) and all other Borrelia genomes. The chromosome is most similar to the leading strand mode, and both are more similar to B. garinii and B. afzelii, than they are to the entire B. burgdorferi genome (probably the result of plasmid genes “pulling” on the mode of the combined gene set). The chromosome/lp38 cluster is separated from the rest of the plasmids by a sufficient distance such that the connection is split by a branch leading to Prochlorococcus genomes. This intermixing of codon usages of distantly related organisms is an indication of the limits on divergence that can be reliably attributed to a specific relationship (i.e., the plasmids, other than lp38, are too distant to be reliably associated with the host organism on the basis of codon usage). The plasmid codon-usage cluster is sufficiently heterogeneous that it too includes interspersed genomes of distantly related organisms. The plasmids include a subgroup of cp32 family of circular plasmids and lp56 (which contains a full copy of a cp32 plasmid) (Casjens et al. 2000). The remaining plasmids (lp28 family, lp25, lp54, and lp36) are less tightly clustered, have longer branch lengths, and are interrupted by the other unrelated genomes.
The mode of the leading strand of the B. burgdorferi chromosome and the first mode of the B. burgdorferi chromosome are nearly identical. More interestingly, the same is also true of the lagging strand mode and the second mode of the chromosome. Thus, true to its design, our definition of the mode appears to be applicable to the analysis of multimodal data (a situation in which the average performs particularly badly). Our inclusion of context genomes also makes it clear that the codon usage of the lagging strand genes (and the second mode) shows no similarity to any of the other B. burgdorferi codon usages—the two closest branches correspond with the modes of Flavobacterium psychrophilum and Mycoplasma synoviae.
Discussion
Defining and Finding the Mode
Our definition and utilization of the mode involves several decisions that deserve elaboration. These begin with our working definition of a mode in 59 dimensions. With discrete data, one normally thinks of the mode as the tallest bar in a histogram. The location of the mode depends on how the underlying data are pooled into the histogram categories and depends on a number of parameters, such as the width of the categories, or how the categories are distributed (linearly, logarithmically, etc.). Visualizing our implementation in one dimension would be equivalent to moving a fixed-width bracket along the axis, and picking the point at which the bracket encompasses the most genes. Relative to a normal histogram, our bracket is unusually broad (with our P > 0.1 threshold covering 93% of the data in the case of a homogeneous genome). A tighter range (e.g., P > 0.5) might have more appeal. We chose such a large bracket for the sake of using the same criterion for finding the mode and evaluating the number of genes that are not significantly different. Our choice of P > 0.1 represents a trade-off between avoiding false positives and false negatives. A more stringent criterion will increase the number of false negatives. A more relaxed criterion would include more false positives, especially in a genome with a continuum of high-expression and alien genes, pulling the mode toward them. We have not explored the possible merits of finding the location of the mode with a more stringent criterion but then applying it to the categorization of genes with a more relaxed criterion.
Given our decision to use a P value criterion for defining the mode, we had to choose a method for evaluating the P value. We chose to use a chi-square analysis, even though its assumption of a large sample size relative to the number of categories is clearly violated. Supplementary figure S1, Supplementary Material online, provides empirical evidence that in the P value range of interest, the violation of the assumptions does not appreciably change the average behavior.
Another important issue is that the criterion that we optimize is not the number of matching genes (our actual goal) but a continuous function of the P values of the genes. Even when this function is maximized, it does not mean that we have maximized the count of genes matching at the given P value. Our data and experience suggest that it is a good compromise, but it is only an approximation of our stated criterion. A different function could easily be substituted (most appealingly, one parameterized to allow asymptotic approach to a discrete threshold).
Even with our use of a continuous function in the optimization, the process remains difficult. It is certainly possible to improve our search method, and we do occasionally modify details such as our initial selection of vertices or the step size in the simplex search. It would be straightforward to incorporate standard methods for improving the performance of heuristic searches (e.g., repeating the optimization with alternative sets of starting vertices). Although we have improved the searches during our performance of this work, we have never had an instance where it changed the biological conclusions of an analysis.
Replicon Codon Usage in A. tumefaciens C58
Our replicon-by-replicon analyses of modal codon usage reveal two distinct types of codon usage in A. tumefaciens: chromosomal-like and plasmid-like. It has been suggested that the linear chromosome has arisen from the transfer of chromosomal genes to a plasmid (Goodner et al. 2001). This has been suggested, in part, because the linear chromosome contains the plasmid replication genes repABC. Although it is unknown whether this hypothetical primordial plasmid would have had a similar codon usage with the extant plasmids, our results indicate that the present-day chromosomal repA and repB match both the chromosomal and plasmid codon usages and that repC is distinctly plasmid-like (supplementary table S1, Supplementary Material online).
The similarity in codon usages of the pAt and pTi plasmids was more surprising, given that they are independently conjugative (Genetello et al. 1977; Kerr et al. 1977; Chen et al. 2002). The matching codon usage of both plasmids suggests the coexistence and coevolution of these replicons over a long period of time. The most common explanation for the evolution of these plasmids is that the genes with plasmid-like codon usage reflect the signature codon usage of an earlier donor organism and that sufficient time has not elapsed for the plasmids to have ameliorated to the codon usage of the rest of the genome (Lawrence and Ochman 1997). In this case, it would suggest a relatively long shared history, despite their independent mobility.
The plasmids of A. tumefaciens are also remarkably homogeneous with 64% and 60% of the genes matching the mode for pAt and pTi, respectively. This level of homogeneity is similar to the chromosomes, in which 62% of the genes match the mode. Similar results were obtained for pO157 of E. coli O157:H7 Sakai, with 52% of the genes matching the mode (data not shown), and the larger B. burgdorferi plasmids (data not shown). In each of these cases, there are genes with very different codon usage from the plasmid mode, but the relative homogeneity suggests that either genes are gained from other genetic elements with similar codon usage or that the gene gains and losses have not been sufficiently frequent to obscure the presence of a core gene set.
Both the pAt and pTi plasmids contain chromosome-like genes; however, there is little indication that they are becoming chromosomes through the acquisition of chromosomal genes. There are no large blocks of genes with chromosome-like codon usage in the plasmids. Nearly half of the chromosome-like genes on pAt are annotated as ABC transporter genes. Of the 13 chromosome-like genes on pTi, six are involved in conjugal transfer: trbF, L, J, E, B, and traR. Despite their codon usages, these genes are clearly not chromosome-like in function.
Replicon Codon Usage in B. burgdorferi
The large number of B. burgdorferi replicons and their relatively small number of genes make their analysis challenging and led us to seek an alternative to presenting distances between all pairs of elements. We have explored a number of methods to assess the statistical significance of the plasmid grouping, without developing any clear and generally applicable measure. In the case of A. tumefaciens replicons, we calculated the pairwise distances between modal codon usages and compared it with the distances observed when the genes where shuffled between the replicons. Applying this to Borrelia, we would then ask if some pairs of sequences were significantly more similar than others. However, as already pointed out, this analysis breaks down when replicons contain homologous genes, biasing them to look more similar than random (because it is not random). Even if this worked, presenting a meaningful summary of so many pairs of relationships, and disentangling the multiple hypothesis testing, would be a formidable challenge. Thus, although only lp38 shows a statistically significant difference in codon usage when the plasmids are compared in this way (data not shown), it is not possible to conclude that it is the only plasmid that is significantly different.
Another approach that we examined was a resampling method in which the codon usage for each replicon was reevaluated based on a bootstrap-style resampling of its genes. Then a tree was computed from the codon usages of each resampled set of genes. With this rather brutal approach, the grouping of lp28-2 and lp54 was seen in 90% of the trees, and the grouping of the chromosome with lp38 was seen in 88% of the trees. No other group was seen more than 50% of the time (the cp32 family of plasmids was excluded from this analysis). We suspect that this provides an overly conservative assessment of the groupings seen in figure 2, but we have not come up with alternatives that correctly handle the nature of the data, particularly the fact that some of the plasmids have essentially identical gene sets, whereas others do not.
Given the problems with alternative approaches, we chose a codon-usage tree (fig. 2) to display the differences between replicon modes. Doing so comes with caveats (e.g., see the documentation for the GCUA program, McInerney 1998b). Primarily, the tree does not represent a phylogeny per se, and convergent codon usage is possible. In particular, it is likely that the non-Borrelia genomes are drawn into the tree due to convergence in codon usage, rather than any close evolutionary relationship between their genes and those of B. burgdorferi. More to the point, Thermoanaerobacter, Petrotoga, and Thermosipho are unlikely to be the source of any of the B. burgdorferi plasmids because they are thermophilic organisms found in distinct environments (Antoine et al. 1997; Lien et al. 1998; Roh et al. 2002; Onyenwoke et al. 2007). The distance between lp56 and the genome of Prochlorococcus marinus NATL2A is 0.26 and is the smallest (convergent) distance we have observed between a B. burgdorferi replicon and a genome with (presumably) unrelated codon usage. Thus, we suggest that codon-usage distances greater than 0.26 require further scrutiny (the similarity may be real or due to convergence). Despite this limitation, illustrating codon-usage similarities with a tree that includes all of the most similar codon usages observed in other genomes provides an internal scale by which to see the groups of replicons that are more like one another than they are like any other sequenced genome. That is, this method helps clarify codon-usage groups that are biologically relevant; in this case, these include the chromosome grouping with lp38 (and the complete genome, and the genomes of other Borrelia species) and the distinct cp32 group.
Previous codon-usage studies have focused on determining whether the B. burgdorferi genome has expression-related codon bias (McInerney 1998a; Lafay et al. 1999). They concluded that B. burgdorferi had no discernable expression-related bias and that the major source of codon-usage variation is caused by genes residing on the leading versus the lagging strand of DNA replication. Although we do not search for expression-related codon usage in this study, our results reinforce these earlier findings—the distance between the modes of the leading and lagging strand (or between their proxies, mode 1 and mode 2 of the chromosome) is greater than any other distance in figure 2 (including the non-Borrelia genomes). Thus, we too conclude that strand bias is the dominant source of codon-usage variation in B. burgdorferi. However, by measuring the distances between the modes of each replicon, we are also able to distinguish the more subtle differences between replicons—namely, the relationship between lp38 and the chromosome, and the cp32 group.
Barbour (1993) suggested that the B. burgdorferi linear plasmids might in fact be “mini-chromosomes,” given that they all share the same topology and copy number. If these plasmids were chromosomes, we would expect them to be chromosome-like in codon usage; however, this is not the case for any of the plasmids, except possibly lp38. Lp38 groups with the chromosome to the exclusion of other replicons, but it does not have the characteristics of a chromosome. For example, some high passage strains have lost lp38 (Norris et al. 1992). Another reason proposed for classifying the linear plasmids as chromosomes is that they carry the genes for major outer membrane proteins (Barbour 1993). This is the case for lp38, which carries ospD, an outer membrane lipoprotein that is not essential for virulence in mice but is involved in tick colonization (Norris et al. 1992; Li et al. 2007). Our data indicate that the codon usage of the ospD gene is significantly different from the modal codon usages of both lp38 and the chromosome (data not shown). It is unlikely that ospD is significantly different from the chromosome because of high-expression codon bias (above). On the basis of codon usage, our data do not suggest the classification of any of the B. burgdorferi plasmids as chromosomes.
Concluding Observations
Our observations leave several unanswered questions. The observation that most plasmids are statistically different in codon usage than their coresident chromosomes comes as no real surprise from the perspective of viewing plasmids as vehicles for gene transfer. However, all of the plasmids that we have observed show a relative homogeneity in codon usage (≥50% of the genes match the mode of the replicon). This suggests that most of the genes in any given plasmid are drawn from a common pool. Does this imply that they are more stable and less promiscuous than we originally thought? If that were so, why do we see little evidence of genes with chromosomal codon usage being transferred to the plasmids in the same lineage? This is particularly puzzling given that the similarities between plasmids within a single host would also suggest that these are not transient associations. The question of maintaining distinct codon usages seems simple in the case of abundant proteins versus “typical” proteins, but it is hard to understand why there should be any uniformity among plasmid genes. We also note that systematic differences, such as the topological, and hence supercoiling, differences between circular and linear replicons (as seen in the chromosomes of Agrobacterium and the plasmids of Borrelia), are not accompanied by corresponding differences in codon usage.
Supplementary Material
Supplementary figure S1 and supplementary table S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Supplementary Material
Acknowledgments
We wish to thank Stephen Farrand, Katherine Karberg, Andrei Kuzminov, Claudia Reich, and the anonymous reviewers for their helpful comments and suggestions with the manuscript. Portions of this material are based on work supported by the National Aeronautics and Space Administration under Grant NAG 5-12334 issued through the Exobiology Program, by the Department of Energy under Grant FG02-01ER63146 and by the National Institutes of Health under Contract HHSN266200400042C via subcontract from the University of Chicago to the University of Illinois.
References
- Akman L, Yamashita A, Watanabe H, Oshima K, Shiba T, Hattori M, Aksoy S. Genome sequence of the endocellular obligate symbiont of tsetse flies, Wigglesworthia glossinidia. Nat Genet. 2002;32:402–407. doi: 10.1038/ng986. [DOI] [PubMed] [Google Scholar]
- Antoine E, Cilia V, Muenier JR, Guezennec J, Lesongeur F, Barbier G. Thermosipho melanesiensis sp. nov., a new thermophilic anaerobic bacterium belonging to the order Thermotogales, isolated from deep-sea hydrothermal vents in the Southwestern Pacific Ocean. Int J Syst Bacteriol. 1997;47:1118–1123. doi: 10.1099/00207713-47-4-1118. [DOI] [PubMed] [Google Scholar]
- Badger JH. In: Exploration of microbial genomic sequences via comparative analysis. 1999. Multiple gene categories in microbial genomes as revealed by codon bias. [PhD Dissertation]. Urbana (IL): University of Illinois at Urbana-Champaign. p. 45–92. [Google Scholar]
- Barbour AG. Linear DNA of Borrelia species and antigenic variation. Trends Microbiol. 1993;1:236–239. doi: 10.1016/0966-842x(93)90139-i. [DOI] [PubMed] [Google Scholar]
- Casjens S, Palmer N, van Vugt R, et al. (15 co-authors) A bacterial genome in flux: the twelve linear and nine circular extrachromosomal DNAs in an infectious isolate of the Lyme disease spirochete Borrelia burgdorferi. Mol Microbiol. 2000;35:490–516. doi: 10.1046/j.1365-2958.2000.01698.x. [DOI] [PubMed] [Google Scholar]
- Chen L, Chen Y, Wood DW, Nester EW. A new type IV secretion system promotes conjugal transfer in Agrobacterium tumefaciens. J Bacteriol. 2002;17:4838–4845. doi: 10.1128/JB.184.17.4838-4845.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. PHYLIP—Phylogeny Inference Package (Version 3.2) Cladistics. 1989;5:164–166. [Google Scholar]
- Fraser CM, Casjens S, Huang WM, et al. (38 co-authors) Genomic sequence of a Lyme disease spirochaete, Borrelia burgdorferi. Nature. 1997;390:580–590. doi: 10.1038/37551. [DOI] [PubMed] [Google Scholar]
- Genetello C, Van Larebeke N, Holsters M, De Picker A, Van Montagu M, Schell J. Ti plasmids of Agrobacterium as conjugative plasmids. Nature. 1977;265:561–563. doi: 10.1038/265561a0. [DOI] [PubMed] [Google Scholar]
- Goodner B, Hinkle G, Gattung S, et al. (31 co-authors) Genome sequence of the plant pathogen and biotechnology agent Agrobacterium tumefaciens C58. Science. 2001;294:2323–2328. doi: 10.1126/science.1066803. [DOI] [PubMed] [Google Scholar]
- Gouy M, Gautier C. Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res. 1982;22:7055–7074. doi: 10.1093/nar/10.22.7055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R, Gautier C, Gouy M. Codon frequencies in 119 individual genes confirm consistent choices of degenerate bases according to genome type. Nucleic Acids Res. 1980;8:1893–1912. doi: 10.1093/nar/8.9.1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R, Gautier C, Gouy M, Jacobzone M, Mercier R. Codon catalog usage is a genome strategy modulated for gene expressivity. Nucleic Acids Res. 1981;9:r43–r74. doi: 10.1093/nar/9.1.213-b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R, Gautier C, Gouy M, Mercier R, Pave A. Codon catalog usage and the genome hypothesis. Nucleic Acids Res. 1980;8:r49–r62. doi: 10.1093/nar/8.1.197-c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grocock RJ, Sharp PM. Synonymous codon usage in Pseudomonas aeruginosa PA01. Gene. 2002;289:131–139. doi: 10.1016/s0378-1119(02)00503-6. [DOI] [PubMed] [Google Scholar]
- Grosjean H, Fiers W. Preferential codon usage in prokaryotic genes: the optimal codon–anticodon interaction energy and the selective codon usage in efficiently expressed genes. Gene. 1982;18:199–209. doi: 10.1016/0378-1119(82)90157-3. [DOI] [PubMed] [Google Scholar]
- Herbeck J, Wall D, Wernegreen J. Gene expression level influences amino acid usage, but not codon usage, in the tsetse fly endosymbiont Wigglesworthia. Microbiology. 2003;149:2585–2596. doi: 10.1099/mic.0.26381-0. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes. J Mol Biol. 1981a;146:1–21. doi: 10.1016/0022-2836(81)90363-6. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J Mol Biol. 1981b;151:389–409. doi: 10.1016/0022-2836(81)90003-6. [DOI] [PubMed] [Google Scholar]
- Karlin S, Mrázek J. Predicted highly expressed genes of diverse prokaryotic genomes. J Bacteriol. 2000;182:5238–5250. doi: 10.1128/jb.182.18.5238-5250.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunst F, Ogasawara N, Moszer I, et al. (151 co-authors) The complete genome sequence of the Gram–positive bacterium Bacillus subtilis. Nature. 1997;390:249–256. doi: 10.1038/36786. [DOI] [PubMed] [Google Scholar]
- Kerr A, Manigault P, Tempe J. Transfer of virulence in vivo and in vitro in Agrobacterium. Nature. 1977;256:560–561. doi: 10.1038/265560a0. [DOI] [PubMed] [Google Scholar]
- Lafay B, Lloyd AT, McLean MJ, Devine KM, Sharp PM, Wolfe KH. Proteome composition and codon usage in spirochaetes: species-specific and DNA strand-specific mutational biases. Nucleic Acids Res. 1999;27:1642–1649. doi: 10.1093/nar/27.7.1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence JG, Ochman H. Amelioration of bacterial genomes: rates of change and exchange. J Mol Evol. 1997;44:383–397. doi: 10.1007/pl00006158. [DOI] [PubMed] [Google Scholar]
- Li X, Neelakanta G, Liu X, Beck DS, Kantor FS, Fish D, Anderson JF, Fikrig E. Role of outer surface protein D in the Borrelia burgdorferi life cycle. Infect Immun. 2007;75:4237–4244. doi: 10.1128/IAI.00632-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien T, Madsen M, Rainey FA, Birkeland N. Petrotoga mobilis sp. nov, from a North Sea oil-production well. Int J Syst Bacteriol. 1998;48:1007–1013. doi: 10.1099/00207713-48-3-1007. [DOI] [PubMed] [Google Scholar]
- McInerney JO. Replicational and transcriptional selection on codon usage in Borrelia burgdorferi. Proc Natl Acad Sci USA. 1998a;95:10698–10703. doi: 10.1073/pnas.95.18.10698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McInerney JO. GCUA: general codon usage analysis. Bioinformatics. 1998b;14:372–373. doi: 10.1093/bioinformatics/14.4.372. [DOI] [PubMed] [Google Scholar]
- Médigue C, Rouxel T, Vigier P, Hénaut A, Danchin A. Evidence for horizontal gene transfer in Escherichia coli speciation. J Mol Biol. 1991;222:851–856. doi: 10.1016/0022-2836(91)90575-q. [DOI] [PubMed] [Google Scholar]
- Moszer I, Rocha EPC, Danchin A. Codon usage and lateral gene transfer in Bacillus subtilis. Curr Opin Microbiol. 1999;2:524–528. doi: 10.1016/s1369-5274(99)00011-9. [DOI] [PubMed] [Google Scholar]
- Nelder J, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–313. [Google Scholar]
- Norris SJ, Carter CJ, Howell JK, Barbour AG. Low-passage-associated proteins of Borrelia burgdorferi B31: characterization and molecular cloning of OspD, a surface-exposed, plasmid-encoded lipoprotein. Infect Immun. 1992;60:4662–4672. doi: 10.1128/iai.60.11.4662-4672.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onyenwoke RU, Kevbrin VV, Lysenko AM, Wiegel J. Thermoanaerobacter pseudethanolicus sp. nov, a thermophilic heterotrophic anaerobe from Yellowstone National Park. Int J Syst Evol Microbiol. 2007;57:2191–2193. doi: 10.1099/ijs.0.65051-0. [DOI] [PubMed] [Google Scholar]
- Overbeek R, Begley T, Butler RM, et al. (40 co-authors) The subsystems approach to genome annotation and its use in the project to annotate 1000 genomes. Nucleic Acids Res. 2005;33:5691–5702. doi: 10.1093/nar/gki866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picardeau M, Lobry JR, Hinnebusch BJ. Physical mapping of an origin of bidirectional replication at the centre of the Borrelia burgdorferi linear chromosome. Mol Microbiol. 1999;32:437–445. doi: 10.1046/j.1365-2958.1999.01368.x. [DOI] [PubMed] [Google Scholar]
- Rispe C, Delmotte F, van Ham R, Moya A. Mutational and selective pressures on codon and amino acid usage in Buchnera, endosymbiotic bacteria of aphids. Genome Res. 2004;14:44–53. doi: 10.1101/gr.1358104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roh Y, Liu SV, Li G, Huang H, Phelps TJ, Zhou J. Isolation and characterization of metal-reducing Thermoanaerobacter strains from deep subsurface environments of the Piceance Basin, Colorado. Appl Environ Microbiol. 2002;68:6013–6020. doi: 10.1128/AEM.68.12.6013-6020.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PM, Li W. The codon adaptation index—a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987;29:1281–1295. doi: 10.1093/nar/15.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita C, Ogata K, Shikata M, Jikuya H, Takano J, Furumichi M, Kanehisa M, Omata T, Sugiura M, Sugita M. Complete nucleotide sequence of the freshwater unicellular cyanobacterium Synechococcus elongatus PCC 6301 chromosome: gene content and organization. Photosyn Res. 2007;93:55–67. doi: 10.1007/s11120-006-9122-4. [DOI] [PubMed] [Google Scholar]
- Wheeler DL, Barrett T, Benson DA, et al. (33 co-authors) Database resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2007;35(Database issue):D5–D12. doi: 10.1093/nar/gkl1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DW, Setubal JC, Kaul R, et al. (51 co-authors) The genome of the natural genetic engineer Agrobacterium tumefaciens C58. Science. 2001;294:2317–2323. doi: 10.1126/science.1066804. [DOI] [PubMed] [Google Scholar]
- Zelen M, Severo N. Probability functions. In: Abramowitz M, Stegun IA, editors. Handbook of mathematical functions. New York: Dover Publications; 1965. pp. 925–995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.