Abstract
We use data from the National Longitudinal Study of Adolescent Health and the Adolescent Health and Academic Achievement Study to estimate how parents' union dissolution influences changes in adolescents' mathematics course work gains, overall grade point average, and course failure rates during a window of approximately 1 year (N = 2,629). A primary purpose of this study is demonstrating the utility of propensity score matching techniques for studying topics such as ours that pose methodological challenges such as dealing with endogeneity and selection bias. We compare propensity score matching techniques to ordinary least squares (OLS) regression methods to show and discuss comparability of results obtained using these different procedures. Findings suggest that associations between parents' union dissolution and achievement may be causal, regardless of method used.
Keywords: academic achievement, family structure, high school, propensity score, selection effects, union dissolution
The effect of family structure transitions on young people's school success is of interest to parents, researchers, and practitioners. Methodological challenges in this area of research arise because family structure changes are coupled with factors such as financial instability and marital stressors, which increase the risk of union dissolution and negatively affect adolescents' school performance. Disentangling the causal nature of these associations is difficult because endogeneity and selection bias likely affect results from studies of family structure and school success. Amato (2000) discusses this issue at length and offers examples of characteristics that predispose people to divorce (e.g., personal problems such as alcohol use).
Only an experiment could fully eliminate endogeneity and selection bias, but ethics prevent researchers from using this method to study the effects of union dissolution on children's well-being. No ethical researcher would propose randomly assigning children at birth to different households with similar characteristics except for their new parents' marital status. Methods that simulate an experimental design using observational data are valuable alternatives that reduce endogeneity and selection bias, therefore, producing better estimates of relationships between parents' union dissolution and educational achievement without ethical dilemmas. We utilize one such semiparametric estimation technique—propensity score matching—to reassess relationships between union dissolution and adolescents' high school achievement gains. We compare findings from this method to those obtained using traditional OLS regression methods. We also discuss how propensity score matching may help family researchers interested in other topics better assess the causal nature of relationships for which an experimental design may be inappropriate or impossible.
Background
Family Structure Change and Its Consequences
The proportion of single mother and father families has risen from 12% to 26% and 1% to 6%, respectively, from 1970 to 2003 (Fields, 2003). Estimates also suggest that since the 1990s, more than 1 million children each year experience parental divorce, and 50% – 60% of U.S. children born in the 1990s will live in a single-parent household at some point in time (Furstenberg & Cherlin, 1991). These trends have prompted a large body of research investigating how family structure influences child well-being (Amato, 2001; Hetherington & Kelly, 2002; McLanahan & Sandefur, 1994). Most studies suggest that children in single-parent households and those who experience parents' union dissolution do less well than children living with both biological parents on a host of outcomes ranging from socioeconomic well-being (Mayer, 1997) to social adjustment (Amato & Booth, 1997).
Nonetheless, controversy exists about the magnitude of these effects and whether they result from family structure itself or from other changes and problems associated with family structure. For instance, theories arguing that family structure itself leads to negative child outcomes blame the decreased resources available to children (e.g., parents' time, financial resources) that often stem from living with a single parent. Theories of family instability posit that relationships between family structure and youth outcomes stem from stressors associated with divorce and remarriage, not from family structure itself. Much of the debate between those engaged in the “Family Wars” is based on these issues (see Glenn, 1993; Popenoe, 1993; Stacey, 1993, for reviews).
Family Structure and Academic Achievement: Causation or Selection?
One youth outcome on which proponents on both sides of the family wars focus attention is educational achievement, a strong predictor of academic attainment and in turn the occupational and economic stability of the next generation of Americans. Although many studies conclude that young people in single-parent households are not as academically successful as those living with both biological parents (McLanahan & Sandefur, 1994; Pong, Dronkers, & Hampden-Thompson, 2003; Teachman, Paasch, & Carver, 1996), some research shows no significant differences in achievement between children in single- and two-parent families (Entwisle & Alexander, 1996; Marsh, 1990), especially once relevant sociodemographic and family characteristics are controlled (Grissmer, Kirby, Berends, & Williamson, 1994; Jeynes, 2000). Many factors, such as a child's age, how family structure and academic success are operationalized, and whether and when a child lived in a single-parent household, partially account for these conflicting findings. The methods and data (often cross-sectional) used to study these associations also produce these disparate findings.
Our study asks whether parents' union dissolution affects high school students' academic performance and whether this relationship is causal or the result of factors that jointly influence family structure transitions and academic success. We focus on high school achievement because this stage of schooling is characterized by increased academic stratification. Because some students simply attempt to graduate and others take demanding college preparatory classes, differences in high school achievement become greater over time (Muller & Schiller, 2000; Schiller, 1999). If students have academic problems, they tend to be apparent first in grades and course selection (Roderick, 1994). In particular, students may choose less demanding courses and courses that offer less college preparation (Schneider, Swanson, & Riegle-Crumb, 1998; Stevenson, Schiller, & Schneider, 1994).
As noted above, theories of family instability argue that it is difficult to assess whether relationships between family structure change and high school achievement are causal because a change in family structure is often coupled with factors that both increase the chances of parental union dissolution and lower students' school performance. For instance, the covariates of marital dissolution include financial instability, marital quality, negative spousal behavior, and parental fighting. These factors precede union dissolution and may lead to the end of couples' relationships. They may also influence adolescents' school performance (Demo & Acock, 1988). Thus, it is hard to discern whether union dissolution or turbulence stemming from the event leads to achievement disparities between adolescents in diverse family structures.
Methods that account for joint covariates of union dissolution and academic achievement may best assess whether relationships between the two are causal or the result of selection and endogeneity. Experiments are the gold standard for matching individuals with similar backgrounds to assess how treatments influence outcomes, but propensity score matching techniques can allow researchers to use observational data to assess how treatments predict outcomes among persons with similar backgrounds when experiments are impossible.
In our study, we match respondents using the covariates of union dissolution and school success mentioned above (financial instability, marital quality, negative spousal behavior, parental fighting) and other covariates associated with both union dissolution (Amato, 2000; Amato & Rogers, 1997; Fu, 2002) and school performance (Baker, Keller-Wolff, & Wolf-Wendel, 2000; Jeynes, 2003; Raley, Frisco, & Wildsmith, 2005). They include race and ethnicity, parental education, parental cohabitation, maternal employment, parental age, number of unions, age at first marriage, racial homogamy, and religiosity. We also account for maternal and paternal health because of their association with marital status (Lillard & Panis, 1996) and death and include key adolescent characteristics such as gender, age, and their number of reported siblings.
Propensity Score Matching Techniques
We estimate relationships between union dissolution and school performance using multiple methods. Two of these methods employ propensity score matching techniques, which can potentially address some methodological problems inherent in studies of youth outcomes following parental union dissolution when certain assumptions (discussed below) are met. First, even in large samples, few adolescents experience this event between waves in longitudinal data collection efforts. Second, the approach can help reduce bias that arises because of selection and endogeneity. Third, it provides an excellent estimation of the effect of parents' union dissolution on outcomes among adolescents who do and do not experience this event but who have similar propensities of experiencing it according to observable characteristics (the average treatment effect for the treated).
Propensity scores matching is relatively new in the field of sociology, although the method has been used in other fields, particularly in economics, for several decades (see Rosenbaum & Rubin, 1983, for one of the original pieces on this method and Dehejia & Sadek, 2002, for a more recent review). The method has been used limitedly and only more recently by researchers who study families and topics of interest to family scholars (Amato, 2003; Gertler, Levine, & Ames, 2004; Harding, 2003; King, Massoglia, & MacMillan, 2007).
Propensity score matching techniques approximate a quasi-experimental design with secondary data by comparing individuals in a “treatment group” (in this case, adolescents whose parents' union dissolves) to those in a “control group” (adolescents whose parents remain together) who have a similar likelihood of experiencing the treatment according to observable characteristics. This comparison is accomplished by using a logistic regression or probit model to estimate the propensity that adolescents will experience union dissolution. The propensity score is defined as follows (Rosenbaum & Rubin, 1983):
| (1) |
where p(T) is the propensity of experiencing parents' union dissolution, T indicates that adolescents' parents did or did not end their relationship, and S is a vector of covariates influencing union dissolution.
The propensity score is used to match adolescents who did and did not experience parents' union dissolution, our treatment and control groups, on shared observed covariates (Dehejia & Sadek, 2002; Morgan & Harding, 2005). Using propensity score matching, the mean estimated differences in academic achievement between the two groups, the average treatment effect for the treated, represents the effect of parents' union dissolution on outcomes among adolescents who do and do not experience this event but who have similar propensities of experiencing it on the basis of observable characteristics.
The success of comparing outcomes among matched respondents or groups of respondents depends upon reliably estimating a propensity score, in this case, the propensity that parents' union will end, and by not violating the Conditional Independence Assumption (i.e., all observed variables influencing both the treatment—union dissolution—and the outcome—academic achievement—must be included in the propensity score model). Some methodologists argue that models estimating propensity scores should include every variable even modestly related to the treatment (Rubin & Thomas, 1996). Others recognize that researchers are limited by available degrees of freedom and must use theory and prior research to guide model building (Dehejia & Sadek, 2002).
Once one estimates a propensity score, comparing respondents in two groups of interest is possible. In our study, these are adolescents who did and did not experience parents' union dissolution with similar propensities of experiencing this event. Several procedures match cases or groups of cases to estimate the average treatment effect for the treated. We compare a relatively common and simple method, nearest neighbor matching, to the more sophisticated kernel matching method. Other matching procedures, such as local linear matching, radius matching, and matching by stratifying respondents into different blocks of cases on the basis of their propensity to experience a treatment, were examined. Local linear matching, an alternative to kernel matching that converges faster at boundary points (when probabilities of receiving the treatment are extremely small or large), produced comparable results to those presented here, as did analysis using radius matching and matching by stratification.
Each matching method has different strengths and weaknesses and is more or less appropriate depending upon one's data and the substantive application of the matching process (Becker & Ichino, 2002; Morgan & Harding, 2005). We present estimates from nearest neighbor matching because it is widely used by researchers across different fields, relatively unbiased, and quite simple. We compare findings to those obtained using kernel matching because of this procedure's efficiency and ability to make full use of one's data in a conceptually elegant way by comparing those who experienced a treatment with all others in the control group, weighted by the similarity of propensity. Local linear regression, an alternative to kernel matching that is also highly efficient, may produce more stable estimates on the boundaries, but this is not an issue in our study. Therefore, the standard errors (derived from bootstrapping, for which some replications may approach large values on the boundary) produce slightly more conservative p values for the kernel matching method than for local linear regression.
Regardless of which matching method is used, each is ideally suited for dichotomous “treatments” such as union dissolution. For information on propensity score matching with continuous treatments, see Hirano and Imbens (2004).
Meeting certain assumptions and conducting certain procedures provides some confidence that models estimating the propensity score and the matching process itself are reliable. First, balance must be achieved between the treatment and control groups on covariates used to predict the propensity score (Rosenbaum & Rubin, 1983). In our case, matched cases with similar likelihoods of experiencing parents' union dissolution must be similar on the covariates used to predict this event. If the STATA “pscore” command is used to generate propensity scores, balance is automatically evaluated (see Becker & Ichino, 2002, pp. 12 – 14 for an example of this code and output produced by the pscore command). Balance can also be evaluated with t tests that confirm that there are no significant differences between groups of matched cases in the treatment and control group on covariates within blocks of cases with similar propensities of experiencing the treatment of interest. If differences between the treatment and control group exist, then matched cases are not similar enough to assume that all bias has been eliminated from estimates of the average treatment effect for the treated. The more unbalanced covariates one has, the greater chance that bias is still evident.
Second, sensitivity analyses must be conducted to assess how inclusion and exclusion of different variables (including interaction terms) affect the estimated propensity score and differences in outcomes between one's treatment and control group. We conducted extensive exploratory analyses to assess which covariates predicted the likelihood of parents' union dissolution, whether interactions influenced estimates of our propensity score (they did not), and whether analytic decisions influenced our estimated average treatment effect for the treated. See the Appendix for more details about these analyses.
Third, one must test whether data trimming—essentially excluding potential outliers—helps to ensure common support (i.e., that there are similar cases in matched control and treatment groups). Trimming decreases the likelihood that a few cases bias estimated differences between the treatment and control group. For example, if a few adolescents who experienced union dissolution in our study are particularly advantaged and had parents with college degrees who reported being extremely happy with their marriage, had very high incomes, and had parents who married at a very late age, they could exert undesired influence on the estimates of propensities. Excluding these outliers from analyses may lead to better estimates of the consequences of union dissolution for high school achievement gains for a typical respondent.
When utilizing propensity score methods such as kernel matching, which are dependent on the density of nearby data, different bandwidths (smoothing functions) must also be tested. Smaller bandwidths decrease the probability of introducing bias into one's analyses (DiNardo, 2002).
We reiterate that propensity score matching techniques are not a “magic bullet.” They only account for selection and endogeneity well if good data are used, one meets assumptions of conditional independence, and selection is captured well by variables predicting the propensity to experience a treatment of interest. These issues arise no matter what method one uses. Thus, it is important to test robustness of results (Frank, 2000; Frank & Min, 2002).
Nearest neighbor matching utilizes the propensity score to pair cases in the control and treatment group on the basis of their likelihood to experience a treatment. Control cases not matched with a treatment case are excluded from analyses. In our study, this procedure sets up a quasi-experimental design allowing us to compare academic outcomes among matched respondents who did and did not actually experience parents' union dissolution but who share a similar likelihood of experiencing this event given observable characteristics.
Neighbor cases can be selected in two ways. Matching using replacement allows cases in the control group to be matched to more than one case in the treatment group if that control case is a better match to multiple treatment cases than alternative cases in the control group. Replacement assures that the most similar cases are matched, although additional data are lost by excluding more cases from one's sample. This approach reduces the likelihood of bias when calculating the average treatment effect for the treated but also leads to less efficiency (Caliendo & Kopeinig, 2005).
Cases can also be matched without replacement. Each case in the treatment group is matched to a unique case in the control group. Thus, fewer cases and fewer data are excluded from analyses. Whereas this procedure decreases efficiency, it can also increase bias when calculating the average treatment effect for the treated because unique case B1 in the control group may at times be a worse match to treatment case B than control case A1 already matched to treatment case A. Nonreplacement can also produce different estimates of the average treatment effect for the treated depending on whether the program used to match respondents in the treatment and control group searches forward or backward through data for matched cases. To avoid this complication, one can specify that cases be matched randomly (Becker & Ichino, 2002).
If the propensity score distributions among the treatment and control groups are similar, then matching with and without replacement will yield similar results to each other as well as results obtained from OLS regression methods. Conversely, if the distributions are very different, then nonreplacement may yield poor matches and may increase bias in the average treatment effect for the treated.
One can match multiple cases in the control group to single cases in the treatment group when conducting nearest neighbor matching if oversampling is used (see Smith, 1997, for a discussion). This procedure also decreases efficiency, but again, at the expense of potentially introducing bias because additional cases in the control group matched to single cases in the treatment group may be poor matches. This problem is one reason to consider use of other propensity score matching techniques that allow for use of all data and available cases to estimate the average treatment effect for the treated.
Kernel matching is one approach that uses all available cases to estimate the average treatment effect for the treated. The calculated propensity score is used to match individual cases in the treatment group to a composite or weighted mean of control cases. Control cases receive weights on the basis of the distance between their propensity score and the propensity score of the treatment case to which they are being matched. All control cases potentially contribute to the weighted composite, improving the power and efficiency of estimation. This procedure is especially valuable when there are many potential matches for each treatment subject, which is the case here—only 65 of more than 2,500 respondents experienced parents' union dissolution.
Formally, define δi as the treatment effect for person i, Ti to indicate whether person i received the treatment or control (taking a value of 1 for treatment, 0 for control), nt is the number of people receiving the treatment, and ωi, j is a weight representing the similarity of respondents i and j. Then, a general matching estimator can be expressed as follows (Morgan & Harding, 2005):
| (2) |
In words, the estimated treatment effect is based on a comparison on the outcome, Y, for those who received the treatment with a weighted mean of those who received the control. Differences among matching schemes can then be expressed via ωi, j. For example, in one-to-one matching, for each i, there is only one j with a positive value of ωi, j; the rest are 0.
The kernel estimator specifies a particular form of ωi, j:
| (3) |
Here, Sj represents a set of covariates used to estimate the propensity (p); an is a bandwidth estimator, which scales the difference in the estimated propensity scores on the basis of sample size (Morgan & Harding, 2005). The larger the value of an the less important are differences in probabilities; G is a kernel function (e.g., Tricube, or Gaussian normal); Finally, k is a normalizing constant that is the sum of all G/an across all j:
| (4) |
When utilizing kernel matching, one should use bootstrap techniques to obtain standard errors because control observations contribute to more than one match, and therefore, matches are not independent, violating an assumption of ordinary parametric techniques for calculating standard errors. We use bootstrapped standard errors to make statistical inferences regarding the difference in academic achievement gains between adolescents who do and do not experience parents' union dissolution.
Comparing Methods: Propensity Score Modeling Versus OLS Regression
When comparing different modeling strategies, it is important to remember that every method depends on assumptions. In fact, “such assumptions are the strands that join the field of statistics to scientific disciplines” (Rubin, 2004, p. 345).
In addition, data limitations and survey design must always be acknowledged regardless of which method researchers use. For example, regardless of whether we use propensity score matching techniques or regression methods, we are limited by the issue of data availability. In the case of propensity score matching techniques, this limitation decreases the number of covariates that can be used to predict adolescents' propensity to experience parents' union dissolution. In the case of OLS regression models, it limits the availability of control variables that can be used in models predicting achievement gains.
Propensity score matching techniques and OLS regression methods also have unique limitations. For instance, in our study, if balance is not achieved between all covariates predicting the propensity to experience parents' union dissolution, then some bias may exist in estimated differences in achievement between adolescents with similar odds of experiencing parents' union dissolution because cases in the treatment and control group are not completely comparable on observable characteristics. For example, both parents' education level and marital happiness predict the propensity to experience union dissolution, but both covariates could have different relationships to our outcomes. If many cases in our sample have a similar propensity to experience union dissolution but do so because some respondents have highly educated parents in unhappy marriages and other respondents have less educated parents in very happy marriages, then our estimates of the average treatment effect for the treated will be biased.
Another drawback of propensity score matching techniques is that we can only calculate overall effects of one treatment—union dissolution—on high school achievement, not the effect of multiple covariates or potential interactions between union dissolution and other variables (Zanutto, 2006). Meanwhile, regression models estimating relationships between union dissolution and adolescents' achievement gains require correct specification of the functional form of data and measures.
In some cases, propensity score matching techniques may produce less biased estimates of effects of a treatment than OLS regression. There is no assumption of linear functional form, and it is easy to perform diagnostic checks for reliability (Zanutto, 2006). Zanutto also notes that by separating the process of estimating propensity scores and the average treatment effect for the treated, propensity score matching provides researchers with greater objectivity in analysis than regression methods because researchers must consider why someone would experience a treatment of interest independent of its potential effect on the outcome itself. It is also easier to discern if comparable cases in the treatment and control group exist (e.g., whether one has achieved common support).
Propensity score matching also can be used to focus on estimating a treatment for those who actually experience it, which provides a clearer picture of causal relationships between treatments and outcomes of interest. This interest derives from Heckman's (1996) interest in the treatment effect for the treated, with arguments that evaluating whether to continue existing policy targeting a specific group of interest should focus on this parameter. Conversely, if one is interested in extending policy to the population as a whole, then the parameter of interest is the average treatment effect for the population (Heckman).
We calculate both the average treatment effect for the treated and the average treatment effect for the sample. Our regression models estimate the average treatment effect of parents' union dissolution for an individual in the sample when controlling for other covariates. The treatment effect for the treated (e.g., the effect of union dissolution for respondents with a high propensity for experiencing this event according to observable characteristics), which we calculate using propensity score matching techniques, may be different from the treatment effect for the untreated (e.g., the effect of experiencing union dissolution among respondents who do not experience the event or are unlikely to experience this event) and hence the treatment effect for the total population (Morgan & Harding, 2005). This problem is particularly likely if there is not a broad area of common support (i.e., there is not considerable overlap in the propensities of those in the treatment and control group).
The Current Study
We use the methods just described to investigate whether the effects of parents' union dissolution on adolescents' high school achievement are comparable when computed using different methods. Using data from the National Longitudinal Study of Adolescent Health (Add Health) and the new education component, the Adolescent Health and Academic Achievement Study (AHAA), we estimate whether adolescents who lived with both biological (or adoptive) parents at Wave I and a single parent approximately 1 year later at Wave II make similar progress in their math curriculum, earn similar grades, and fail about the same proportion of courses when they are compared to students whose parents remain together during this time but are similar on observable characteristics.
We build on prior research in several ways. Utilizing multiple methods and testing the robustness of our results as suggested by Frank (2000) illustrates how reliable predicted estimates of union dissolution are and whether relationships between parents' union dissolution and adolescents' academic achievement are likely to be causal. This approach is an important step for better understanding the nature of short-term academic difficulty that adolescents face when their parents' union dissolves. Methodologically, our study provides readers with an example of how to use propensity score matching methods to further assess causality and shows how findings from this method compare to results from OLS regression methods.
Method
Data and Sample
The National Longitudinal Study of Adolescent Health (Add Health) is a school-based, longitudinal, nationally representative survey of 20,745 adolescents in Grades 7 through 12 from 134 public, private, and parochial schools (Bearman, Jones, & Udry, 1997). Respondents were selected using a stratified random sample of students in schools. Three waves of in-home survey data were collected in 1995, 1996, and 2000 – 2001 that contain a wealth of information on adolescents, their families, their social relationships, and their health behaviors. We use data from Waves I and II to measure parents' union dissolution and students' propensities to experience this event. The Wave II sample includes 14,736 young adults or 71% of the original Wave I sample. Roughly, 45% of this sample attrition resulted from non-follow-up of Wave I 12th graders.
The Wave III data collection effort (which included follow-up of the Wave I 12th graders) included an education component, the AHAA. High school transcript data were collected from respondents who authorized access to these data. In total, transcripts were collected and coded for approximately 81% of Wave III respondents (n = 12,258). Data were collected from all Add Health high schools except two special education schools that did not maintain students' academic transcripts and from over 1,300 additional schools where Add Health respondents last attended high school. From transcripts, researchers created indicators of academic progress designed to compare students across the nation.
We selected two samples for our study. We estimate the propensity to experience union dissolution between Waves I and II using data from the first sample and data from the second sample to estimate changes in high school achievement.
To be eligible for the first sample, respondents had to participate in the Wave I survey (n = 20,745), their parents had to complete a Wave I parent survey (n = 17,125), and indicate that they were married or cohabiting with a partner of a different gender (n = 11,974). These exclusions ensure that our base sample consists of adolescents living with a married (n = 11, 806) or cohabiting (n = 168) parent at Wave I. Analyses without adolescents living with cohabiting parents produced no significant differences in results.
Because we are interested in union dissolution between survey waves, adolescents also had to participate in the Wave II survey to be included in the base sample (n = 8,868). They also had to indicate that they lived with both biological or adoptive parents at Wave I and either both parents or only one parent at Wave II (n = 6,211).
To estimate the effects of union dissolution on academic progress, we further restrict the sample to adolescents with valid transcript data (n = 4,463), who were in Grades 9 through 11 during Wave I (n = 2,729) and who had no missing data on our three indicators of achievement gains from Wave I to Wave II (n = 2,629).
We do not constrain the sample used to construct our propensity score to the smaller sample used when matching treatment and control cases because the ideal goal of this method is to estimate individuals' true propensities or “known propensities” to receive a treatment and our estimate will typically have more precision when we use more data (Morgan & Harding, 2005; Rosenbaum & Rubin, 1983). That is, if we had data on the full population to calculate propensity, then we would certainly use those data rather than data from a sample. Using a larger sample reduces standard errors and in turn leads to a more precise estimate of the propensity score, but it may also lead to some bias. Thus, researchers must choose between potential precision versus bias. In our case, we have evidence that bias does not result from using our larger versus smaller sample because our findings do not differ substantively or statistically when using the former instead of the latter to estimate propensity scores.
Primary Dependent and Independent Variables
Academic performance
We estimate three measures of academic performance using indicators constructed as part of the AHAA study (Riegle-Crumb, Muller, Frank, & Schiller, 2005). For each indicator, we calculate the difference between the students' academic status at Wave I, before some sample members experienced parents' union dissolution, and at Wave II, after union dissolution. We assess change in achievement to take into account the respondents' academic status before parents' union transitions. We find comparable results (not shown) from lagged models in which we use OLS methods to regress Wave II academic status on the Wave I measure. One cannot produce lagged dependent variable models using kernel or nearest neighbor matching methods. This limitation shaped our decision to construct and use change scores instead. Change scores are also more appropriate than lagged dependent variable models when utilizing two panels of data to investigate how a transition affects outcomes (Johnson, 2005). We also find comparable results using propensity score matching methods when we predict Wave II outcomes and include a Wave I indicator of outcomes in our model estimating propensity scores.
Our first dependent variable taps students' level of mathematics course work completion, a strong predictor of postsecondary education preparation (Schneider, 2001). Mathematics curricula are structured such that a given course prepares students for the next course in the sequence. There is variation in the measure because in the last year or two of high school, students are typically not required to take math; approximately 60% of high school seniors do not (Schiller, 1999). In addition, all students do not enter high school taking the same math courses. The math course levels in AHAA range from no math (equal to 0) to calculus and above (equal to 9). Our indicator of change in students' level of math course work completion is the difference between the highest level of math course work completed at Waves I and II. The mean difference in our sample is 0.933, indicating that, on average, students completed almost one course more per year.
The second dependent variable is the difference in GPA for all courses taken in a given year from Wave I to Wave II, an excellent marker of students' overall achievement at each survey wave. GPA ranges from 0 (F or unsatisfactory) to 4 (A). Our constructed measure of change in GPA ranges from −3.00 to 3.69 with a mean of −0.023, indicating that, on average, students' GPAs are fairly constant across years.
Our final dependent variable, change in the proportion of courses failed each year, captures how much respondents are struggling academically. The Wave I and II indicators of course failure proportions range from 0.000, which indicates that respondents failed no classes attempted, to 1.000, which indicates that respondents failed all classes attempted. Our indicator of change in the proportion of courses failed ranges from −1.000 to 1.00, with a mean of 0.007, indicating that on average students' proportions of courses failed are fairly stable across years.
Parents' union dissolution
During the Wave I parent survey, parents reported their marital status, whether they were currently in a marriage or marriage-like relationship, and their relationship to the Add Health respondent (e.g., biological mother), by answering the following questions: “What is your current marital status?,” “Is this a marriage or marriage-like relationship?,” and “What is your relationship to NAME (the adolescent respondent)?” Most parent respondents (88%) reported that they were the biological or adoptive mother of the adolescent respondent.
Adolescents also reported who they lived with at Waves I and II by filling out an extensive household roster that asked for the gender, age, and their relationship to every person in their household. Add Health coders used data from this roster to construct detailed indicators of family structure.
Students were considered to be living with two biological or adoptive parents at Wave I if parents reported being married or cohabiting and adolescent respondents reported living with their biological (or adoptive) mother and father on the household roster. As mentioned above, only adolescents in these families at Wave I are included in our analytic sample. Adolescents' reports of who they live with at Wave II are used to construct our indicator of union dissolution (0 = teens report living with both parents, 1 = teens living with their mother or father only). Adolescents who fall into other family structure categories (such as stepfamilies) at Wave II are excluded from the sample. Few Add Health respondents (n = 60 or 2.5% of our sample) lived with both parents at Wave I and report parents' union dissolution between the two waves.
The Add Health study did not collect data from parents at Wave II nor did it ask adolescent respondents if their parents divorced between Waves I and II. Therefore, we cannot be certain that our indicator of union dissolution indicates divorce (vs. parental separation, death of a parent, or other unknown reasons), although separation usually leads to divorce and few adolescents experience parental death within a 1-year period (Casper & Bianchi, 2002; Fields & Casper, 2001). Therefore, we are confident that most cases of union dissolution represent parental separation or divorce although we acknowledge that there is potential measurement error in our indicator of parental union dissolution.
Analytic Strategy
Estimating the propensity to experience parents' union dissolution
Our first step in analysis is estimating the propensity that adolescents experienced parents' union dissolution between Waves I and II. Our model is informed by theory and previous empirical research (see Amato, 2001; Amato & Rogers, 1997; Fu, 2002 for reviews). Variables in this model can be grouped into several broad categories: parents' and children's sociodemographic characteristics, parents' relationship characteristics, parents' religiosity, parents' health status, and the duration between Waves I and II interview dates. Sociodemographic characteristics that we include are parents' race and ethnicity, parents' racial homogamy, parents' education level, family income, financial stability, parents' age, maternal employment outside the home, and adolescents' age, gender, and number of siblings.
The characteristics of parents' relationships associated with union dissolution that we include in our model are age at first marriage, if the current relationship is a first marriage or marriage-like relationship, marital status (married vs. cohabiting), marital happiness, whether the couple discussed separating, and frequent fighting. We also account for parents' religious devoutness: frequency of church attendance, importance of religion, and belief that the scriptures are the literal word of God.
To account for the possibility that parents' health influences union dissolution through either divorce or death, we include dummy variables in our model signifying serious maternal and paternal health conditions at Wave I. They indicate whether each parent suffers from obesity, asthma or emphysema, alcoholism, or diabetes (1 = yes).
Finally, we control for the duration of time between adolescents' Waves I and II interview dates in months because those with a larger gap between dates are at greater risk of experiencing parents' union dissolution. Descriptive statistics for and operationalizations of all independent variables (all measured at Wave I except for the duration of time between interviews) are shown in Table A1.
To estimate adolescents' propensities for experiencing parents' union dissolution between Waves I and II, we utilize a logistic regression model:
| (5) |
where T is the propensity of experiencing a change in family structure, α is the intercept, S is a vector of Wave I covariates described above, and β is a vector of parameter estimates.
We use mean and mode substitution to impute missing values of independent variables used to predict the propensity that respondents experience their parents' union dissolution and included dummy variables indicating where we had imputed (Cohen, Cohen, West, & Aiken, 1983). Listwise deletion produced results similar to those presented here. We do not include dummy variables representing missing cases on each independent variable in our final model for parsimony; missing data flags were not statistically significant. We do include a dummy variable indicating whether respondents had missing data on at least one independent variable to account for the possibility that missing data could represent less survey engagement because of factors related to one's propensity to experiencing parents' union dissolution.
We present a fully specified model rather that a series of nested models because of space constraints (see Table 1, described below). We conducted extensive exploratory and sensitivity analyses, though, to assess how inclusion and exclusion of different variables and blocks of variables influenced our estimated propensity score, the balance between the treatment and control groups, and estimated average treatment effects for the treated. See the Appendix for details.
Table 1. Unstandardized Regression Coefficients, Standard Errors, and Odds Ratios From Logistic Regression Models Estimating the Propensity to Experience Parents' Union Dissolution Between Waves I and IIa.
| β (SD) | Odds Ratio | |
|---|---|---|
| Family sociodemographic characteristics | ||
| Mother's race or ethnicity | ||
| Hispanic, all races | −0.064 (0.251) | 0.938 |
| African American, non-Hispanic | 0.674** (0.222) | 1.962 |
| Asian American, non-Hispanic | 0.342 (0.305) | 1.408 |
| Other, non-Hispanic | −0.212 (0.576) | 0.809 |
| White, non-Hispanic | — | |
| Parents' racial homogamy | 0.043 (0.292) | 1.044 |
| Parent has a college degree | 0.070 (0.185) | 1.072 |
| Yearly family income | −0.007* (0.003) | 0.993 |
| No reported financial distress | 0.079 (0.212) | 1.082 |
| Mother works at least part time | −0.160 (0.182) | 0.852 |
| Parent's age | −0.046* (0.018) | 0.955 |
| Parent's relationship experiences and characteristics | ||
| Parent's age at first marriage | −0.018 (0.027) | 0.982 |
| Parent is in first marriage or marriage-like relationship | −0.740* (0.309) | 0.477 |
| Parents are cohabiting, not married | 1.063** (0.380) | 2.895 |
| Marital happiness | −0.273*** (0.044) | 0.761 |
| Parents discuss separation | 0.653** (0.211) | 1.921 |
| Parents fight frequently | 0.108 (0.327) | 1.114 |
| Parent's religiosity | ||
| Frequency of church attendance | −0.011 (0.088) | 0.989 |
| Importance of religion | −0.264 (0.138) | 0.768 |
| Believes scriptures are word of god | 0.194 (0.216) | 1.214 |
| Parents' health conditions | ||
| Mother suffers from | ||
| Obesity | −0.617* (0.241) | 0.539 |
| Diabetes | 0.256 (0.396) | 1.292 |
| Emphysema or asthma | 0.167 (0.289) | 1.181 |
| Alcoholism | 0.693 (0.615) | 2.000 |
| Father suffers from | ||
| Obesity | −0.067 (0.283) | 0.935 |
| Diabetes | 0.298 (0.337) | 1.347 |
| Emphysema or asthma | −0.193 (0.357) | 0.824 |
| Alcoholism | 0.244 (0.261) | 1.276 |
| Adolescent's characteristics | ||
| Female | −0.225 (0.157) | 0.774 |
| Age | 0.093 (0.053) | 1.097 |
| Number of siblings | −0.007 (0.098) | 0.993 |
| Duration between WI and WII interview (in months) | 0.154** (0.049) | 1.167 |
| Missing data on at least one covariate | −0.225 (.187) | 0.799 |
| Intercept | −1.308 (1.276) | 0.270 |
| N | 6,211 | |
Note: Source: The National Longitudinal Study of Adolescent Health (Add Health) and Adolescent Health and Academic Achievement Study.
Either parent could respond to the Add Health Wave I parent survey, but 88% of parent respondents reported being adolescent respondents' biological mothers. We construct variables signifying mothers' characteristics and fathers' characteristics when possible but can only construct variables that refer to the parent respondent in some cases because of data limitations.
p < .05.
p < .01.
p < .001 (two-tailed test).
Calculating the average treatment effect for the treated using two propensity score matching techniques
Our second step in analysis involves estimating group differences (between those who did and did not experience parents' union dissolution) in school performance using nearest neighbor and kernel matching methods. We use a suite of programs developed for STATA by Becker and Ichino (2002) for these analyses. We conduct nearest neighbor matching with replacement using the STATA “attnw” command. This procedure results in a search for neighbor cases both forward and backward through data sorted by respondents' propensity to experience parents' union dissolution. The attnw command gives equal weight to both forward and backward potential matches. An alternative command for conducting nearest neighbor matching with replacement, attnd randomly selects either a forward or a backward match. This latter method for matching neighbor cases produced results that are substantively and statistically similar to those obtained using the attnw procedure. We use the STATA attk command to estimate differences between respondents who did and did not experience union dissolution with kernel matching. Readers interested in all options available when using these and other propensity score matching techniques should consult Becker and Ichino (2002). A second STATA component, psmatch2 can also be used to conduct propensity score matching techniques (Leuven & Sianesi, 2003) as can a SAS macro developed by Bergstralh, Kosanke, and Jacobsen (1996).
Estimating OLS regression models
Our third step in analyses is estimating the effect of experiencing parents' union dissolution on academic achievement gains using a standard OLS regression model:
| (6) |
where y is the outcome of interest, α is the constant term, each xi represents an independent variable associated with outcome y, each βi indicates the parameter estimate for each xi, and e represents an error term. The variables included in OLS models predicting achievement gains are the same measures used to estimate our propensity score and changes in achievement using propensity score matching techniques. We also control for additional variables associated with academic achievement but not with parents' odds of union dissolution (parents' and students' educational expectations, academic risk behaviors, and attachment to and engagement in school). Estimated regression coefficients from these models were neither substantively nor significantly different from models excluding these additional controls and are available upon request.
Although Add Health recommends that analyses be weighted and corrected for design effects (Chantala & Tabor, 1999), we present results from unweighted models here for comparability across methods. The STATA svy procedures used to weight and correct for design effects cannot be used with the pscore, attk, and attnw commands. Note, though, that when OLS regression models and a basic logistic regression model used to estimate propensity scores are weighted and corrected for design effects, our results are statistically and substantively similar to results presented here. (For example, estimates from OLS models weighted and corrected for design effects indicate that the average treatment effect = −0.112 for changes in math course work, −0.297 for changes in GPA, and 0.095 for changes in course failure; here, these estimates are −0.112, −0.298, and 0.082, respectively). Results from models weighted and corrected for design effects are available upon request.
Results
Predicting the Propensity to Change Family Structure
Table 1 presents coefficients, standard errors, and odds ratios (OR) from models predicting the likelihood that adolescents' experienced parents' union dissolution. They indicate that, controlling for all other variables, the odds that an adolescent with an African American mother will experience union dissolution are almost twice as high as those of adolescents with White mothers (OR = 1.962); adolescents whose parents were cohabiting rather than married at Wave I also have higher odds of living with a single parent at Wave II (OR = 2.895). The odds that teenagers' parents dissolve their union between Waves I and II are negatively related to their parent's age, reported marital happiness, their mothers' obesity status, and family income. Parental discussion of separation and the duration of time between Wave I and II interviews are also positively associated with the odds of changing family structure between waves. As noted above, space constraints lead us to present only the full model used to estimate the propensity to experience parents' union dissolution. All variables were associated with this family structure transition in reduced models in expected directions (not shown).
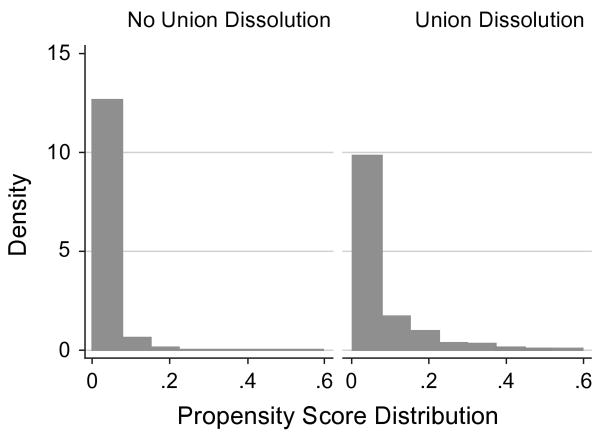
We use the propensity scores output from the model described in the previous paragraph to match cases using nearest neighbor and kernel matching. Figure 1 shows a histogram of the propensity score distribution for adolescents who did and did not experience parents' union dissolution between waves within the eight balanced blocks of matched treatment and control groups. This figure shows that there is considerable overlap in propensities in lower regions of the propensity distribution but less overlap in higher propensity blocks, which could introduce bias into estimates of the average treatment effect for the treated. We thus tested whether trimming outliers (n = 144 in our base sample, n = 39 in our second sample) influenced our findings using the comsup option available when using the STATA pscore procedure. These ancillary analyses are shown in Table A2. Estimates from these models do not statistically or substantively differ from those obtained when estimating the average treatment effect for the treated for the larger sample.
Figure 1.
Common Support Between Treatment and Control Cases Predicted to Have Similar Propensities for Experiencing Parents' Union Dissolution with Balanced Propensity Blocks.
The STATA pscore procedure (Becker & Ichino, 2002) was used to assess intrastratum differences between students who did and did not experience parents' union dissolution on covariates predicting this treatment. Results indicated no statistically significant differences in mean or modal values of covariates for our treatment and control groups within eight propensity blocks generated by the pscore procedure, which confirms balance. Although this result does not completely signify elimination of potential bias in our estimate of the average treatment effect for the treated, it suggests that bias is minimized.
Comparing Results From Propensity Matching and OLS Regression Methods
Table 2 shows the estimated differences in academic outcomes among students who did and did not experience their parents' union dissolution. Three estimates are shown: the first is the average treatment effect for the treated estimated using nearest neighbor matching, the second is the average treatment effect for the treated estimated using kernel matching, and the third is a regression coefficient from an OLS regression model. We present only the regression coefficient for parents' union dissolution because of space constraints. Estimates from the full model are available upon request.
Table 2. Comparison of Average Treatment Effects and OLS Regression Estimates of Experiencing Parents' Marital Dissolution on Academic Achievement.
| Propensity Score Matching Methods | |||
|---|---|---|---|
| Average Treatment Effect for the Treated of Experiencing Parents' Marital Dissolutiona | OLS Regression | ||
| Nearest Neighbor Matching | Kernel Matching | Estimated Effect of Experiencing Parents' Marital Dissolutiona | |
| Achievement gains from WI to WII | |||
| Math course work completed | −0.162 (0.187) | −0.173 (0.139) | −0.112 (0.222) |
| Overall GPA | −0.286*** (0.127) | −0.273*** (0.092) | −0.298* (0.119) |
| Course failure | 0.092*** (0.033) | 0.079*** (0.029) | 0.082*** (0.018) |
| Treatment observations | 65 | 65 | 65 |
| Control observations | 62 | 2,564 | 2,564 |
| Total N | 127 | 2,629 | 2,629 |
Note: Source: The National Longitudinal Study of Adolescent Health (Add Health) and Adolescent Health and Academic Achievement Study (AHAA). OLS regression models include control variables signifying the following family and parent characteristics: mother's race and ethnicity, parents' racial homogamy, parents' education level, family income, financial distress, mother' work status, parents' health conditions (obesity, diabetes, asthma or emphysema, and alcoholism), parents' relationship characteristics, parents' religiosity, parents' age, and parents' educational expectations for their child. Models also include indicators of an adolescent's age, gender, number of siblings, educational expectations, academic risk behavior, and attachment to and engagement in school. Other control variables include an indicator of the length of time between Wave I and II interviews and an indicator of missing data on any control variable in the OLS regression model.
Standard errors are given in parentheses.
p < .05.
p < .01.
p < .001 (two-tailed test).
Overall, results in Table 2 show that experiencing parents' union dissolution during the year is related to lower academic achievement at the end of that year but not to adolescents' progress through mathematics course sequences. The estimated effect of parental union dissolution is similar across the three methods used to obtain results.
Gains in students' GPA and course failures are consistently lower among students whose parents' unions ended. On average in the total sample, students' grades decline slightly (−0.018, see Table A1) from one academic year to the next, and on average, they fail fewer than 1% of their courses (0.007, see Table A1). Our estimated average treatment effects for the treated suggest that students who experience union dissolution have much larger declines in overall GPA, somewhere between around one quarter to one third (−0.286 using nearest neighbor matching, −0.273 using kernel matching) of a letter grade on average for all classes. Our OLS regression coefficient of −0.298 suggests similar declines. These estimates are quite large. They represent a full letter grade difference in one half of the students' courses during the entire year or two-letter grades (for example A vs. C) in a fourth of the classes.
Similarly, parental union dissolution also predicts failure of more classes. Depending on the method used, the failure gaps between those who did and did not experience parents' union dissolution with similar propensities for experiencing this event range from a high of 0.092 (nearest neighbor matching) to a low of 0.079 (kernel matching). This finding is noteworthy given that students attempt approximately 12 credits of course work per year (Muller, Schiller, Frank, & Riegle-Crumb, 2005). Our estimates thus suggest that students who experience parental union dissolution will fail more than one class more than students who do not.
In contrast to grades and failures, we did not find that students whose parents' unions stayed intact and those whose parents' unions dissolved completed significantly different levels of math course work 1 year later, although the difference between the groups is negative. Math curriculum is sequentially organized such that prerequisite knowledge (previous course and performance in that course) typically determines placement. Moreover, course selection is made at or before beginning of an academic year. It is possible that there are longer term effects of marital dissolution on course work that are not evident in the year long window of change that is measured in this analysis.
Discussion
In general, we find consistent results showing that adolescents whose parents' union dissolves experience poorer academic achievement: grades decline and course failures increase. Grades are a measure of how well students meet course demands, such as test taking, homework completion, and possibly other forms of behavioral expectations and course failures provide a strong signal that students are struggling. Although the point estimates for the amount of difficulty differ slightly depending upon the estimation procedure, the patterns are remarkably consistent.
We cannot be certain that parents' union dissolution causes high school academic performance to decline because we investigate a 1-year window during which time academic progress and family structure simultaneously change. Nonetheless, we are reasonably confident that union dissolution itself or the transition process leads to some level of short-term academic decline because multiple methods confirm these findings. Accounting for academic progress prior to union dissolution through use of change scores further decreases the likelihood that omitted variable bias influences our findings because accounting for Wave I outcomes absorbs much of the variance in Wave II achievement.
We also took steps to quantify potential uncertainty about causality because of either omitted variable bias or selection. In particular, we can ask what the correlations associated with an unmeasured confounding variable must be to alter causal inference. Frank's (2000) threshold for the impact of a confounding variable answers this question. The threshold for the impact of a confounding variable indicates that a hypothetical omitted confounding variable must be correlated at 0.10 with both union dissolution and GPA gains, and 0.03 with union dissolution and changes in course failures, to invalidate the inference that union dissolution has an effect on these outcomes. These correlations pertain to estimates of the average treatment effect for the treated obtained using kernel matching. The threshold for the impact of a confounding variable is quite similar when we use estimates obtained from the other two methods.
We also calculated how robust causal inference is to sample attrition using indices that estimate the correlation between parents' union dissolution and achievement outcomes among cases lost to attrition (Frank & Min, 2002). Assuming that 25% of the sample that should have been observed was lost to attrition (a rough approximation of sample attrition in Add Health from Wave I to II), then the correlation among the lost sample necessary to invalidate causal inference would have to be less than −0.13. That is, among Wave I sample members lost to attrition, students who experienced union dissolution would actually have to do better than students who did not to invalidate causal inference. Given that parents' union dissolution is typically understood to have negative effects, this is an unlikely possibility. This calculation and the fact that we lose most cases in our study when selecting our sample (and by excluding students not living with both biological parents at Wave I and 12th graders not followed up, who are a random group on all covariates except age) reassure us that sample selection is unlikely to influence our inferences to the point that they are invalid.
Although we are confident in our findings, we must reiterate that our study predicts the effect of union dissolution, not divorce. We are reasonably sure that most union dissolution represents divorce (not death) because of the low likelihood that adolescents living with both parents have of experiencing a parents' death each year (Casper & Bianchi, 2002; Fields & Casper, 2001). Nonetheless, we acknowledge this data limitation.
We also acknowledge that family structure transitions and divorce in particular are known to be processes, not single events, and academic disengagement or declines may begin to occur before one parent leaves the household. This is one primary reason why we predict changes in achievement rather than estimating achievement after a family transition. Therefore, the primary substantive contribution of our study is estimating how one part of the transition process—one parent actually leaving the household—predicts changes in achievement.
We should also note that we unfortunately could not consider racial and ethnic or gender differences in findings because we had too few cases of union dissolution. Estimating these differences should be a goal of futures studies.
Conclusions
Despite these caveats, our results substantively contribute to the body of work showing how family structure influences high school achievement. We add to evidence suggesting that academic performance declines in the short term when parents' unions dissolve. Students are not directly derailed from a core course trajectory, mathematics, but they could be derailed indirectly and in the long term because their academic performance measured in terms of grades and course failures suffers. This finding is troubling given that high school success is critical to long-term educational and occupational opportunity. These findings support other studies that find that short-term turbulence of family instability may lead to negative outcomes for adolescents.
Our study also makes methodological contributions to the field. We show how results from propensity score matching techniques compare to those obtained using more traditional OLS regression methods. Propensity score matching techniques largely confirm results obtained using OLS regression methods. This outcome likely occurs because we have relatively good common support between our treatment and control group. In addition, estimating change scores helps guard against a problem that thwarts causal inference: omitted variable bias. Accounting for Wave I achievement in our outcome helps to explain a great deal of the variance in achievement at Wave II. Thus, we have less variation on our dependent variable that can be explained by other confounding factors. Studies of other topics of interest to family scholars may not find such consistent results when utilizing OLS regression and propensity score matching techniques. This situation is most likely if the effects of a specific condition or treatment are different among one's total sample and sample members with high propensities to experience that treatment.
We also more generally introduce propensity score matching technique to family scholars and provide examples of two different approaches to this modeling strategy. This method is an exciting tool for social scientists who study families. When utilized properly, it may help researchers deal with selection and endogeniety, estimate relationships that may be best estimated with quasi-experimental research designs, provide evidence about relatively rare events, and predict outcome differences between two groups of very different sizes.
That being said, the potential utility of propensity score methods does not negate the usefulness of OLS regression methods. OLS methods use all of the available data, are asymptotically efficient in the class of unbiased estimators, and are the foundation of many other techniques (e.g., multilevel models). True, many alternative techniques improve upon OLS by focusing on specific treatment effects (e.g., propensity score matching to focus on the average treatment effect for the treated) or through attempts to reduce bias resulting from misspecification (e.g., use of instrumental variables), but these approaches may be less efficient or may require further assumptions. As an alternative that builds on common practice, one can use OLS and report the sensitivity or robustness of inferences with respect to violations of assumptions of inference (Frank, 2000; Frank & Min, 2002) as we have done here. Readers should also note that a hybrid method that uses propensity scores to weight OLS regression models is one way of drawing on the strengths of both propensity score matching techniques and regression methods (Amato, 2003; Frank, Cannata, Chard, Krause, & McCrory, 2006; Hirano & Imbens, 2001). Although no method provides researchers with a “magic bullet” to solve every methodological problem, new techniques, use of multiple methods, and procedures aimed at testing robustness of one's findings, such as those presented here, can provide valuable new evidence about some of the most important issues facing family researchers today.
Acknowledgments
The authors acknowledge the support of the Robert Wood Johnson Foundation and grants from the National Institute of Child Health and Human Development (R01 HD40428-02, PI: Chandra Muller and R01-HD050144, PI: Gary Sandefur) and the National Science Foundation (REC0126167, PI: Chandra Muller). Opinions reflect those of the authors and not necessarily those of the granting agencies. This research used data from the AHAA, funded by grants from the National Institute of Child Health and Human Development (01 HD40428-02, Chandra Muller, PI) and from the National Science Foundation (REC-0126167), Chandra Muller, PI and Pedro Reyes, Co-PI. Additionally, this study uses data from the National Longitudinal Study of Adolescent Health, a program project designed by J. Richard Udry, Peter S. Bearman, and Kathleen Mullan Harris and funded by a grant P01-HD31921 from the National Institute of Child Health and Human Development, with cooperative funding from 17 other agencies. Persons interested in obtaining data files from Add Health should contact Add Health, Carolina Population Center, 123 W. Franklin Street, Chapel Hill, NC 27516-2524 (www.cpc.unc.edu/addhealth/contract.html). We would like to thank Michael Massoglia, David Johnson, and four anonymous reviewers for their helpful comments on this and previous versions of our manuscript.
Appendix
Sensitivity Analyses Conducted as Part of Data Analysis
We conducted the following analyses to assure the reliability of the model that we use to predict respondents' propensity to experience family structure change and models assessing the average treatment effect for the treated. Note that all analyses conducted with propensity score matching techniques must include an assessment of how trimming, bandwidth adjustments, and inclusion and exclusion of different variables in models estimating the propensity score affect results. For more information on each of these issues, see Becker and Ichino (2002).
Sensitivity Analysis Used to Determine the Final Model Estimating the Propensity to Experience Parents' Union Dissolution
We used basic theory and prior research on the correlates of union dissolution to construct a base model.
We considered other factors that could contribute to the odds of parents' union dissolution and tested whether these variables should also be included in our model. They included mothers' and fathers' Wave I health status, the length of time between Waves I and II interview, and children's academic achievement at Wave I. All variables except Wave I achievement were retained in a final model.
We tested whether to include interaction terms in our model. Exploratory analysis led us to exclude interaction terms from our final model because none were statistically significant, their exclusion did not substantively change our results, and including them limited remaining degrees of freedom.
We tested whether to include flags representing missing data on each covariate in our final model. We do include a dummy variable in our final model that indicates whether respondents have missing data on at least one variable in our final model. This approach is parsimonious and saves degrees of freedom.
We estimated logistic regression models that were unweighted, weighted, and both weighted and corrected for design effects to assess whether accounting for design effects and use of sample weights significantly influenced our propensity score. Results did not differ significantly across these three approaches.
We estimated models that utilized listwise deletion and two different data imputation strategies to assess whether handling missing data differently significantly influenced the estimated propensity scores. It did not.
Sensitivity Analysis Used to Determine Final Estimation the Average Treatment Effect for the Treated
We tested whether findings differed if we included Wave I indicators of achievement in our propensity score model and predicted Wave II achievement instead of using change scores as outcomes. They did not. We estimate changes in achievement (and exclude Wave I achievement from our propensity score model) for several reasons. Substantively, there is no evidence suggesting that poor achievement predicts union dissolution, and including Wave I achievement in our analyses through use of a change score is a more aggressive approach to the problem of potential omitted variable bias (Allison, 1990). In addition, Johnson (2005) discusses in detail the strengths of using difference scores to assess change between two panels of data. Note that the propensity score modeling techniques that we utilize do not allow one to estimate lagged dependent variable models that control for Time 1 indicators of one's outcome of interest, but regression analysis conducted with this method of accounting for change produced substantively similar results.
We adjusted bandwidths to range from 0.1 to 0.8 (the default with kernel matching) to account for the possibility that our data density influenced results.
We trimmed our data at the top and bottom 1st, 5th, and 10th percentile to ensure that outliers did not significantly influence the average treatment for the treated and also conducted analyses for the full sample and for the sample in the area of common support only. Findings using the different techniques did not significantly differ.
We assessed results using multiple propensity score matching techniques including the methods presented in this paper, local linear matching, caliper matching, and matching using stratification by propensity scores. Results do not significantly differ across methods.
We estimated models that utilized listwise deletion and two different data imputation strategies to assess whether handling missing data differently significantly influenced average treatment effects for the treated. It did not.
Table A1. Descriptive Statistics for Dependent and Independent Variables for the Total Sample and by Experience of Parents' Union Dissolution.
| Total Sample | No Union Dissolution | Union Dissolution | ||||
|---|---|---|---|---|---|---|
| M or Proportion | SD | M or Proportion | SD | M or Proportion | SD | |
| Academic performance | ||||||
| Change in mathematics course enrollment | 0.908 | 0.907 | 0.912 | 0.902 | 0.738 | 1.094 |
| Change in GPA | −.018 | 0.550 | −0.012 | 0.542 | −0.285 | 0.759 |
| Change in course failure | 0.007 | 0.140 | 0.005 | 0.137 | 0.084 | 0.234 |
| Single-parent household at Wave II | 0.029 | — | — | — | — | — |
| Family sociodemographic characteristics | ||||||
| Mothers' race or ethnicity | ||||||
| White (reference) | 0.653 | — | 0.656 | — | 0.549 | — |
| Latina | 0.139 | — | 0.139 | — | 0.134 | — |
| African American | 0.119 | — | 0.116 | — | 0.212 | — |
| Asian American | 0.071 | — | 0.071 | — | 0.083 | — |
| Other | 0.018 | — | 0.018 | — | 0.022 | — |
| Parents' racial homogamy | 0.917 | — | 0.918 | — | 0.905 | — |
| Parent has a college degree | 0.409 | — | 0.411 | — | 0.335 | — |
| Yearly family income | 55.070 | 53.086 | 55.403 | 53.633 | 43.843 | 26.911 |
| No reported financial distress | 0.865 | — | 0.867 | — | 0.804 | — |
| Mother works at least part time | 0.745 | — | 0.746 | — | 0.732 | — |
| Parents' relationship experiences and characteristics | ||||||
| Parents' age at first marriage | 21.097 | 3.531 | 21.101 | 3.516 | 20.950 | 3.989 |
| Parent is in first marriage/marriage-like relationship | 0.965 | — | 0.966 | — | 0.916 | — |
| Parents are cohabiting, not married | 0.014 | — | 0.012 | — | 0.067 | — |
| Marital/relationship happiness | 8.456 | 1.584 | 8.495 | 1.539 | 7.167 | 2.352 |
| Parents discuss separation | 0.100 | — | 0.094 | — | 0.313 | — |
| Parents fight frequently | 0.025 | — | 0.023 | — | 0.089 | — |
| Parents' age | 42.175 | 5.332 | 42.212 | 5.313 | 40.932 | 5.778 |
| Parent's religiosity | ||||||
| Frequency of church attendance | 3.013 | 1.047 | 3.017 | 1.047 | 2.877 | 1.058 |
| Importance of religion | 3.591 | 0.642 | 3.593 | 0.621 | 3.503 | 0.714 |
| Believes scriptures are word of god | 0.764 | 0.425 | 0.763 | 0.425 | 0.793 | 0.406 |
| Parents' health conditions | ||||||
| Mother suffers from | ||||||
| Obesity | 0.190 | — | 0.191 | — | 0.134 | — |
| Diabetes | 0.035 | — | 0.034 | — | 0.044 | — |
| Emphysema or asthma | 0.075 | — | 0.075 | — | 0.089 | — |
| Alcoholism | 0.006 | — | 0.006 | — | 0.022 | — |
| Father suffers from | ||||||
| Obesity | 0.111 | — | 0.111 | — | 0.095 | — |
| Diabetes | 0.044 | — | 0.043 | — | 0.062 | — |
| Emphysema or asthma | 0.059 | — | 0.059 | — | 0.050 | — |
| Alcoholism | 0.057 | — | 0.054 | — | 0.134 | — |
| Adolescents' characteristics | ||||||
| Female | 0.511 | — | 0.512 | — | 0.458 | — |
| Age | 15.623 | 1.568 | 15.619 | 1.609 | 15.754 | 1.571 |
| Number of siblings | 0.826 | 0.793 | 0.825 | 0.787 | 0.877 | 0.726 |
| Months between Wave I and Wave II interview | 10.975 | 1.670 | 10.963 | 1.664 | 11.352 | 1.812 |
| Missing data on at least one covariate | 0.263 | 0.263 | 0.251 | |||
| Education variables in OLS regression models | ||||||
| R wants to go to college | 4.520 | 0.961 | 4.525 | 0.955 | 4.352 | 1.129 |
| R expects to go to college | 4.295 | 1.059 | 4.301 | 1.054 | 4.100 | 1.181 |
| Parent expects R to go to college | 2.326 | 0.701 | 2.328 | 0.698 | 2.235 | 0.772 |
| Frequently misses school | 0.113 | — | 0.112 | — | 0.140 | — |
| Suspended | 0.190 | — | 0.187 | — | 0.302 | — |
| Ever skipped a grade level | 0.017 | — | 0.018 | — | 0.000 | — |
| Ever repeated a grade level | 0.155 | — | 0.153 | — | 0.229 | — |
| School attachment | 3.846 | 0.808 | 3.849 | 0.806 | 3.752 | 0.855 |
| School engagement | 3.103 | 0.721 | 3.108 | 0.717 | 2.938 | 0.831 |
| Na | 6,211 | 6,032 | 179 | |||
Note: Source: The National Longitudinal Study of Adolescent Health (Add Health) and Adolescent Health and Academic Achievement Study (AHAA).
For indicators of academic achievement: total sample N = 2,547; no parental union dissolution = 2,487; parental union dissolution = 60.
Table A2. Comparison of Average Treatment Effects and OLS Regression Estimates of Experiencing Parents' Marital Dissolution on Academic Achievement, Analyses Constrained to Area of Common Support.
| Propensity Score Matching Methods | |||
|---|---|---|---|
| Average Treatment Effect for the Treated of Experiencing Parents' Marital Dissolutiona | OLS Regression | ||
| Nearest Neighbor Matching | Kernel Matching | Estimated Effect of Experiencing Parents' Marital Dissolutiona | |
| Achievement gains from Wave I to Wave II | |||
| Math course work completed | −0.177 (0.188) | −0.172 (0.136) | −0.091 (0.224) |
| Overall GPA | −0.283*** (0.127) | −0.273*** (0.096) | −0.301* (0.118) |
| Course failure | 0.092*** (0.033) | 0.079*** (0.028) | 0.082*** (0.018) |
| Treatment observations | 65 | 65 | 65 |
| Control observations | 62 | 2,505 | 2,505 |
| Total N | 127 | 2,570 | 2,570 |
Note: Source: The National Longitudinal Study of Adolescent Health (Add Health) and Adolescent Health and Academic Achievement Study (AHAA). OLS regression models include control variables signifying the following family and parent characteristics: mother's race and ethnicity, parents' racial homogamy, parents' education level, family income, financial distress, mother's work status, parents' health conditions (obesity, diabetes, asthma or emphysema, and alcoholism), parents' relationship characteristics, parents' religiosity, parents' age, and parents' educational expectations for their child. Models also include indicators of an adolescents' age, gender, number of siblings, educational expectations, academic risk behavior, and attachment to and engagement in school. Other control variables include an indicator of the length of time between Wave I and II interviews and an indicator of missing data on any control variable in the OLS regression model.
Standard errors are given in parentheses.
p < .05.
p < .01.
p < .001 (two-tailed test).
References
- Allison PD. Change scores as dependent variables in regression analysis. In: Clogg C, editor. Sociological methodology. Oxford, UK: Basil Blackwell; 1990. pp. 93–114. [Google Scholar]
- Amato PR. The consequences of divorce for adults and children. Journal of Marriage and the Family. 2000;62:1269–1287. [Google Scholar]
- Amato PR. Children of divorce in the 1990's: An update of the Amato and Keith meta-analysis. Journal of Family Psychology. 2001;15:355–370. doi: 10.1037//0893-3200.15.3.355. [DOI] [PubMed] [Google Scholar]
- Amato PR. Reconciling divergent perspectives: Judith Wallerstein, quantitative family research and children of divorce. Family Relations. 2003;52:332–341. [Google Scholar]
- Amato PR, Booth A. A generation at risk: Growing up in an era of family upheaval. Cambridge, MA: Harvard University Press; 1997. [Google Scholar]
- Amato PR, Rogers S. A longitudinal study of marital problems and subsequent divorce. Journal of Marriage and the Family. 1997;59:612–624. [Google Scholar]
- Baker BD, Keller-Wolff C, Wolf-Wendel L. Two steps forward, one step back: Race/ethnicity and student achievement in education policy research. Educational Policy. 2000;14:511–529. [Google Scholar]
- Bearman P, Jones J, Udry JR. The National Longitudinal Study of Adolescent Health: Research design. Chapel Hill: Carolina Population Center, University of North Carolina at Chapel Hill; 1997. [Google Scholar]
- Becker S, Ichino A. Estimation of average treatment effects based on propensity scores. STATA Journal. 2002;2:358–377. [Google Scholar]
- Bergstralh E, Kosanke J, Jacobsen S. Software for optimal matching in observational studies. Epidemiology. 1996;7:331–332. [PubMed] [Google Scholar]
- Caliendo M, Kopeinig S. Some practical guidance on the implementation of propensity score matching. Iza Bonn; Bonn, Germany: 2005. Unpublished manuscript. [Google Scholar]
- Casper L, Bianchi S. Continuity and change in American family. Thousand Oaks, CA: Sage; 2002. [Google Scholar]
- Chantala K, Tabor J. Strategies to perform a design-based analysis using the Add Health Data. Chapel Hill: Carolina Population Center, University of North Carolina-Chapel Hill; 1999. [Google Scholar]
- Cohen J, Cohen P, West S, Aiken L. Applied multiple regression/correlation analyses for the behavioral sciences. Hillsdale, NJ: Erlbaum; 1983. [Google Scholar]
- Dehejia R, Sadek W. Propensity score matching methods for non-experimental causal studies. Review of Economics and Statistics. 2002;84:151–161. [Google Scholar]
- Demo D, Acock A. The impact of divorce on children. Journal of Marriage and the Family. 1988;50:619–641. [Google Scholar]
- DiNardo J. Propensity score reweighting and changes in wage distributions. Paper presented at the Latin American Meeting of the Econometrica Society; Sao Paolo, Brazil. 2002. Jul, [Google Scholar]
- Entwisle DR, Alexander KL. Family type and children's growth in reading and math over the primary grades. Journal of Marriage and the Family. 1996;59:734–746. [Google Scholar]
- Fields J. America's families and living arrangements: 2003 (Current Population Reports, P20-553) Washington, DC: U.S. Bureau of the Census; 2003. [Google Scholar]
- Fields J, Casper L. America's families and living arrangements: Population characteristics (Current Population Reports, P20-537) Washington, DC: U.S. Bureau of the Census; 2001. [Google Scholar]
- Frank K. Impact of a confounding variable on the inference of a regression coefficient. Sociological Methods and Research. 2000;29:147–194. [Google Scholar]
- Frank K, Cannata M, Chard L, Krause A, McCrory R. Extended influence: National Board Certified Teachers as help providers. Paper presented at the American Educational Research Association; San Francisco. 2006. Mar, [Google Scholar]
- Frank K, Min K. Indices of robustness to concerns regarding the representativeness of a sample. Paper presented at the Annual Meeting of the Mid-Western Educational Research Association; Columbus, OH. 2002. Oct, [Google Scholar]
- Fu X. An interracial study of marital disruption in Hawaii: 1983-1996. Journal of Divorce and Remarriage. 2002;32:73–92. [Google Scholar]
- Furstenberg FF, Cherlin AJ. Divided families: What happens to children when parents part. Cambridge, MA: Harvard University Press; 1991. [Google Scholar]
- Gertler P, Levine DI, Ames M. Schooling and parental death. Review of Economics and Statistics. 2004;86:211–225. [Google Scholar]
- Glenn ND. A plea for objective assessment of the notion of family decline. Journal of Marriage and the Family. 1993;55:542–544. [Google Scholar]
- Grissmer DW, Kirby SN, Berends M, Williamson S. Student achievement and the changing American family (MR-488-LE) Santa Monica, CA: RAND; 1994. [Google Scholar]
- Harding DJ. Counterfactual models of neighborhood effects: The effect of neighborhood poverty on dropping out and teenage pregnancy. American Journal of Sociology. 2003;109:676–719. [Google Scholar]
- Heckman J. Randomization as an instrumental variable. Review of Economics and Statistics. 1996;78:336–341. [Google Scholar]
- Hetherington EM, Kelly J. For better or for worse: Divorce reconsidered. 1st. New York: Norton; 2002. [Google Scholar]
- Hirano K, Imbens G. Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Services and Outcomes Research Methodology. 2001;2:259–278. [Google Scholar]
- Hirano K, Imbens G. The propensity score with continuous treatments. In: Gelman TA, Meng XL, editors. Applied Bayesian modeling and causal inference from incomplete-data perspectives. New York: John Wiley; 2004. pp. 73–83. [Google Scholar]
- Jeynes WH. The effects of several of the most common family structures on the academic achievement of eighth graders. Marriage and Family Review. 2000;30:73–97. [Google Scholar]
- Jeynes WH. The effects of Black and Hispanic 12th graders living in intact families and being religious on their academic achievement. Urban Education. 2003;38:35–57. [Google Scholar]
- Johnson D. Two-wave panel analysis: Comparing statistical methods for studying the effects of transitions. Journal of Marriage and Family. 2005;67:1061–1075. [Google Scholar]
- King R, Massoglia MA, MacMillan R. Contextualizing marriage and crime: Gender, the propensity to marry, and offending in early adulthood. Criminology. 2007;45:401–434. [Google Scholar]
- Leuven E, Sianesi B. Psmatch2: STATA module to perform full mahalanobis and propensity score matching, common support graphing, and covariate imbalance testing. 2003 Retrieved December 7, 2006, from http://ideas.repec.org/c/boc/bocode/s432001.html.
- Lillard LA, Panis CWA. Marital status and mortality. The role of health. Demography. 1996;33:313–327. [PubMed] [Google Scholar]
- Marsh HW. Two-parent, stepparent, and single-parent families: Changes in achievement, attitudes, and behaviors during the last two years of high school. Journal of Educational Psychology. 1990;82:327–340. [Google Scholar]
- Mayer S. What money can't buy: Family income and children's life chances. Cambridge, MA: Harvard University Press; 1997. [Google Scholar]
- McLanahan S, Sandefur GD. Growing up with a single parent: What hurts, what helps. Cambridge, MA: Harvard University Press; 1994. [Google Scholar]
- Morgan SL, Harding DJ. Matching estimators of causal effects: From stratification and weighting to practical data analysis routines Ithaca. NY: Cornell University Department of Sociology; 2005. [Google Scholar]
- Muller C, Schiller K. Leveling the playing field? Students' educational attainment and states' performance testing. Sociology of Education. 2000;73:196–218. [Google Scholar]
- Muller C, Schiller K, Frank K, Riegle-Crumb C. User's guide for the Adolescent Health and Academic Achievement Study, First Release. Austin: Population Research Center, University of Texas-Austin; 2005. [Google Scholar]
- Pong SL, Dronkers J, Hampden-Thompson G. Family policies and children's school achievement in single- versus two-parent gamilies. Journal of Marriage and Family. 2003;65:681–699. [Google Scholar]
- Popenoe D. American family decline, 1960 – 1990: A review and appraisal. Journal of Marriage and the Family. 1993;55:527–542. [Google Scholar]
- Raley RK, Frisco ML, Wildsmith E. Maternal cohabitation and educational success. Sociology of Education. 2005;78:144–164. [Google Scholar]
- Riegle-Crumb C, Muller C, Frank K, Schiller K. National Longitudinal Study of Adolescent Health: Wave III education data. Chapel Hill: Carolina Population Center, University of North Carolina at Chapel Hill; 2005. [Google Scholar]
- Roderick M. Grade retention and school dropout: Investigating the association. American Education Research Journal. 1994;31:729–759. [Google Scholar]
- Rosenbaum PD, Rubin D. The central role of the propensity score in observational studies of causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Rubin D. Teaching statistical inference for causal effects in experiments and observational studies. Journal of Educational and Behavioral Statistics. 2004;29:343–368. [Google Scholar]
- Rubin D, Thomas N. Matching using estimated propensity scores: Relating theory to practice. Biometrics. 1996;52:249–264. [PubMed] [Google Scholar]
- Schiller K. Effects of feeder patterns on students' transition to high school. Sociology of Education. 1999;72:216–233. [Google Scholar]
- Schneider B. Educational stratification and the life course. Sociological Focus. 2001;34:463–466. [Google Scholar]
- Schneider B, Swanson C, Riegle-Crumb C. Opportunities for learning: Course sequences and positional advantages. Social Psychology of Education. 1998;2:25–53. [Google Scholar]
- Smith H. Matching with multiple controls to estimate treatment effects in observational studies. Sociological Methodology. 1997;27:325–353. [Google Scholar]
- Stacey J. Good riddance to “The Family”: A response to David Popenoe. Journal of Marriage and the Family. 1993;55:545–547. [Google Scholar]
- Stevenson DL, Schiller K, Schneider B. Sequences of opportunities for learning. Sociology of Education. 1994;67:184–198. [Google Scholar]
- Teachman JD, Paasch K, Carver K. Social capital and dropping out of school early. Journal of Marriage and the Family. 1996;58:773–783. [Google Scholar]
- Zanutto E. A comparison of propensity score and linear regression analysis of complex survey data. Journal of Data Science. 2006;4:67–91. [Google Scholar]