A quantitative comparison of bird and bat wakes

Abstract

Qualitative comparison of bird and bat wakes has demonstrated significant differences in the structure of the far wake. Birds have been found to have a unified vortex wake of the two wings, while bats have a more complex wake with gradients in the circulation along the wingspan, and with each wing generating its own vortex structure. Here, we compare quantitative measures of the circulation in the far wake of three bird and one bat species. We find that bats have a significantly stronger normalized circulation of the start vortex than birds. We also find differences in how the circulation develops during the wingbeat as demonstrated by the ratio of the circulation of the dominant start vortex and the total circulation of the same sense. Birds show a more prominent change with changing flight speed and a relatively weaker start vortex at minimum power speed than bats. We also find that bats have a higher normalized wake loading based on the start vortex, indicating higher relative induced drag and therefore less efficient lift generation than birds. Our results thus indicate fundamental differences in the aerodynamics of bird and bat flight that will further our understanding of the evolution of vertebrate flight.

1. Introduction

Active flapping flight in birds and bats represents independent evolutionary solutions to the problem of self-powered flight where the wings simultaneously generate lift and thrust. Although these different solutions to the aerodynamic demands of active flight may represent only historical constraints of the different evolutionary paths, they may still result in differences in aerodynamic performance. Qualitative differences in the wake structure between birds and bats have recently been found, including the generation of individual vortex structures from each wing in bats and a unified structure for the two wings in birds (Spedding et al. 2003; Hedenström et al. 2006a , b , 2007; Rosén et al. 2007; Henningsson et al. 2008; Johansson et al. 2008). To determine the relative merits of the solutions of birds and bats, we also need to compare the quantitative properties of aerodynamic performance. Quantitative data from bird wakes are available for several species (Spedding et al. 2003; Warrick et al. 2005; Hedenström et al. 2006a , b ; Rosén et al. 2007; Henningsson et al. 2008), but as of yet only for one bat species (Hedenström et al. 2007; Johansson et al. 2008; but see Tian et al. (2006) for some preliminary data).

Quantitative comparisons of interspecific data, where kinematics and aerodynamic mechanisms may differ between species, may seem as an impossible task. However, using circulation data obtained from the far wake eliminates some of the potential difficulties. The wake vortices contain the momentum flux associated with force generated by the wings, which is seen as changes in circulation. This means that one can ignore the details of the structure that generated the vortices, such as wing flexibility, detailed kinematics and Reynolds number (Spedding et al. 2003). Furthermore, circulation has been shown not to differ significantly when going from near to far wakes in both fixed wings and actively flying bats (Johansson et al. 2008; Spedding et al. 2008), suggesting that the actual distance between the trailing edge of the wing and the point of measurement has little influence on the results. For the present analysis, we compare the available quantitative data for the far wake of birds and bats, measured over a range of flight speeds, when the animals are flying steadily in a wind tunnel. This sums to three bird and one bat species.

2. Methods

2.1. Theory

The weight, W, of a flying animal needs to be matched by the vertical aerodynamic force produced by the wings, which can be determined from the geometry and strength of the vortex structure generated during a wingbeat as

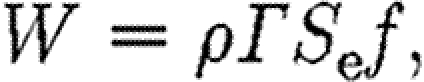2.1

where ρ is the air density; Γ is the circulation; S _e is the horizontally projected area of the wake, i.e. the area of the wake enclosed by the wing tip vortices as seen from above (ignoring the end of upstroke outer wing loop in the bats; see Hedenström et al. 2007); and f is the wingbeat frequency. A list of variables is given in table 1.

Table 1.

List of variables.

AR	aspect ratio
b	wingspan
b wake	wake width
c	mean chord
C d	body drag coefficient
C Di	induced drag coefficient
C L	mean lift coefficient
C V	vertical force coefficient
D i	induced drag
e	wing efficiency factor
f	wingbeat frequency
k	reduced frequency, fc/U
k i	induced power factor
P i	induced power
q	dynamic pressure
Q D	disc loading
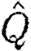
	normalized wake loading
Q wake	wake loading
Re	Reynolds number, Uc/ν
s	subscript to indicate use of the start vortex data
S	wing area
S b	body frontal area
S e	horizontally projected area of the wake
tot	subscript to indicate the use of the data of the total circulation of start sense
U	flight speed
U mp	minimum power speed
W	weight
ν	kinematic viscosity
ρ	air density
Γ	circulation
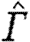
	normalized circulation

To allow for a comparison of different species, we use the circulation of the vortex structure, normalized by the flight speed, U, and the mean chord, c, as suggested by Hedenström et al. (2006a) and Rosén et al. (2007), resulting in

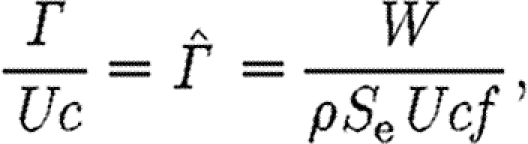2.2

where 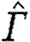is the normalized circulation. If we choose to describe the horizontally projected area of the wake, S _e, as a rectangle Ub _wake/f, where b _wake (which is a function of U) is the effective mean width of the wake, equation (2.2) becomes

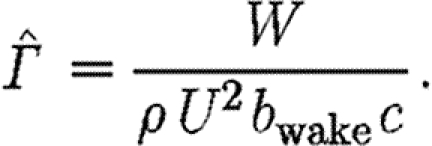2.3

According to equation (2.3), 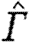is proportional to U ⁻², but the power coefficient will depend on how b _wake varies with U.

According to vortex theory (Rayner 1979) and lifting line theory (Anderson 2006), the induced power (P _i), the cost of generating lift, is proportional to the square of the wake loading (Q _wake),

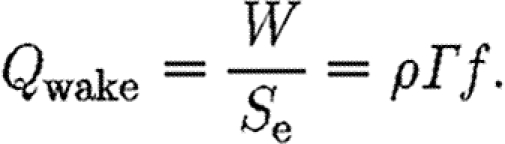2.4

This can be seen by inserting the estimate of the average lift coefficient, C _L, which, according to Hedenström et al. (2006b) and Rosén et al. (2007), can be defined as

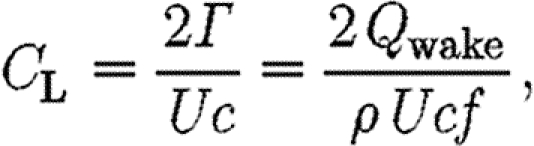2.5

into the function for induced power. According to lifting line theory, the induced power is

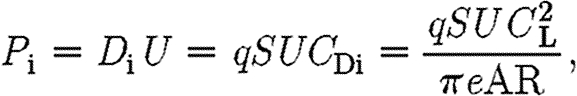2.6

where D _i is the induced drag; q (=0.5ρU ²) is the dynamic pressure; S (=bc) is the wing area; C _Di is the induced drag coefficient; e is the wing efficiency factor; and AR is the aspect ratio (=b/c). Thus, combining equations (2.5) and (2.6) yields

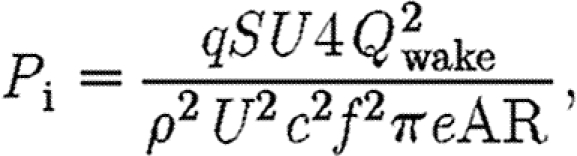2.7

which shows the relationship between P _i and Q _wake.

A high wake loading indicates a relatively small wake area (equation (2.4)) and thereby a high acceleration of the air, which thus indicate a high induced power (Rayner 1979). As we are unable to measure all the parameters necessary to calculate the induced power, we use the wake loading as an indirect measure of the cost of generating lift. We normalize Q _wake by dividing by the disc loading, Q _D=4W/πb ², to allow for the comparison of different-sized animals and wings. Disc loading is the determinant for the induced power in steady-state fixed wings (Anderson 2006),

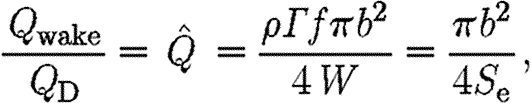2.8

where 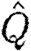is the normalized wake loading. Inserting equation (2.8) into equation (2.7) and solving for the normalized wake loading, we obtain

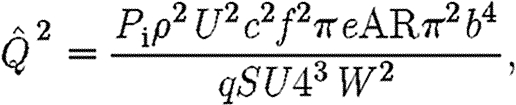2.9

which after simplification becomes

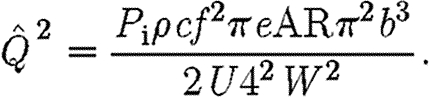2.10

Using the relationships in equations (2.1), (2.5) and (2.6), equation (2.10) can be expressed as

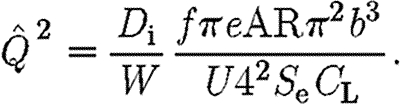2.11

Using equation (2.6), we see that

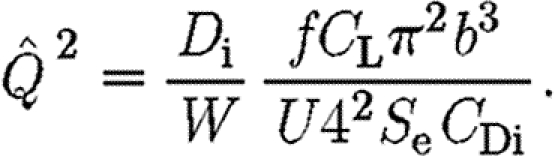2.12

From equation (2.8), we know that 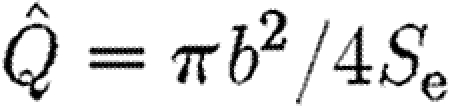, and thus equation (2.12) becomes

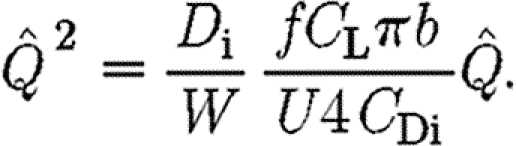2.13

We define a vertical force coefficient (C _V), which represents the steady-state lift coefficient, as

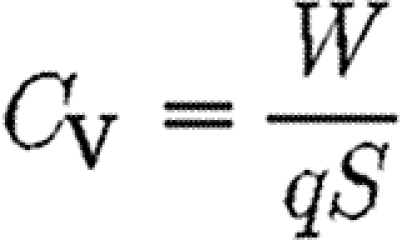2.14

and combining equation (2.13) with equation (2.14), we obtain

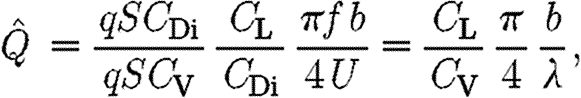2.15

where λ (=U/f) is the wavelength. The ratio can thus be interpreted as a size-independent measure of the efficiency of the wing, where relatively high values suggest high force production other than weight support (i.e. high relative drag) and/or a small wake length relative to the wingspan. High values thus represent non-economic flight, i.e. high induced drag, while low values indicate economic flight.

2.2. Data

Species characteristics are summarized in table 2. We use data of the circulation in the far wake (16–22 chord lengths downstream of the trailing edge; Johansson et al. 2008; Spedding et al. 2008) of the dominant start vortex (Γ _s) and the total circulation (Γ _tot) of the same sense in the flow fields containing the dominant start vortex (see Spedding et al. 2003). The data are from all previously published studies containing quantitative measures of the circulation over a range of flight speeds for birds and bats (TN, Luscinia luscinia, one individual (Spedding et al. 2003); HM, Delichon urbica, one individual (Rosén et al. 2007); RO, Erithacus rubecula, two individuals (Hedenström et al. 2006a ); bat, Glossophaga soricina, two individuals (Johansson et al. 2008)). For the birds, we use data from behind the body (centre plane), and for the bats we use inner wing data. Because there is a reduction in circulation along the span in bats and not in birds, using mid-body data from the bats is not justified in this comparison (Hedenström et al. 2007). Inner wing data are close to the mean circulation along the span, but slightly underestimate the mean (Johansson et al. 2008). Animals of different sizes (i.e. weight and wingspan) will have different expected at the same flight speed, and to allow for a comparison between individuals and species, we need to normalize the flight speed. Flight speed is normalized by dividing by the calculated minimum power speed, U _mp, as suggested by Rosén et al. (2007) and implemented for other interspecific comparisons (Hedenström et al. 2006b ; Rosén et al. 2007; Hedenström & Spedding 2008; Spedding et al. 2008). U _mp was estimated using Pennycuick's (1989, Flight v. 1.17) model,

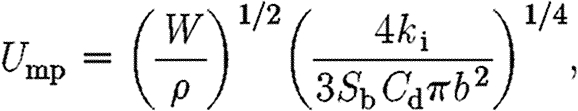2.16

where k _i (=1.2) is the induced power factor; S _b is the frontal area of the body; and C _d is the body drag coefficient. S _b was estimated using the empirically established formula S _b=0.00813×m ^0.666 (Pennycuick 1989). The calculated U _mp values are used only as a way of standardizing the flight speed, and no other inferences are made from them. We use the same parasite drag coefficient (C _d=0.1) as used in previous bird studies (Rosén et al. 2007) for both birds and bats. The choice of the same drag coefficient for both birds and bats is due to the lack of reliable estimates of drag coefficients of birds and bats in free flight. It can be argued that the body drag coefficient, C _d, of bats should be higher than for birds, due to the ‘blunt front’ of bats and protruding ears. A higher C _d for bats decreases the estimated U _mp, shifting the bat curves to the right in the graph (figure 1) without affecting the slope.

Table 2.

Species characteristics.

variables	G. soricina (bat)	D. urbica (HM)	L. luscinia (TN)	E. rebecula (RO)
mass (kg)	0.011	0.017	0.030	0.017
span, b (m)	0.24	0.30	0.26	0.22
mean chord, c (m)	0.038	0.038	0.048	0.047
AR	6.4	7.8	5.5	4.8
U mp (m s−1)	6.5	6.7	8.6	7.6
Q D (N m−2)	2.33	2.42	5.55	4.16
Re range (103)	9–15	9–23	14–26	11–25
k range	0.081–0.14	0.035–0.10	0.079–0.14	0.080–0.16

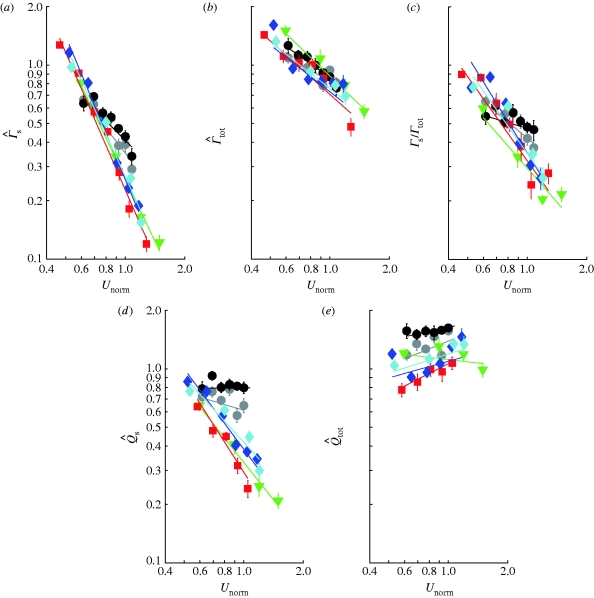
Figure 1.

Comparison of bird and bat quantitative wake data plotted against normalized flight speed (U _norm). (a) Normalized start vortex circulation, 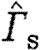. (b) Normalized total circulation of start sense, 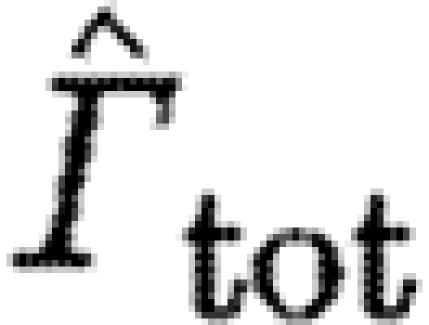. (c) The circulation of the dominating start vortex relative to the total circulation of start sense (Γ _s/Γ _tot). (d) The normalized wake loading based on start vortex circulation, , and (e) based on total circulation of start sense, . The data are means±s.e.m. and the lines are fitted power regressions for each individual (grey circles, bat 11; black circles, bat 17; green down triangles, HM; red squares, TN; blue diamonds, ROw; turquoise diamonds, ROr).

2.3. Statistics

We tested for differences between birds and bats using a linear mixed model with ln-transformed 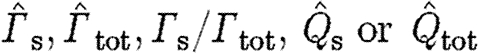as dependent variables and ln-transformed U _norm (U/U _mp) as a covariate. The subscript ‘s’ indicates that the circulation of the dominant start vortex was used in the calculation, while subscript ‘tot’ indicates that the total circulation of start sense was used. ‘Bird or bat’ (BB) and species (Sp) nested within BB were fixed factors. Individual (Ind) nested within Sp and BB was a random factor. The model included interactions between BB, Sp and Ind and the covariate. The statistical analyses were performed in JMP v. 7.0.1 (SAS Institute, Inc.).

3. Results

The bats have higher 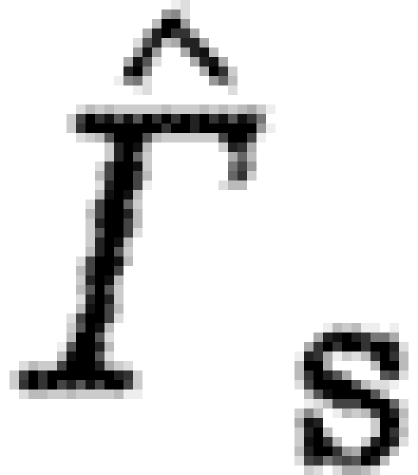than the birds at U _mp (U _norm=1), as shown by the higher intercept of the model (tables 3 and 4). Also, 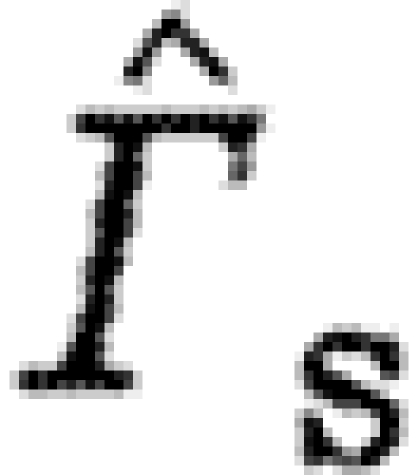varies differently with U _norm for birds and bats, with bats showing a higher exponent (less negative trend) than birds (figure 1 a; tables 3 and 4). According to equation (2.3), 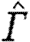should be proportional to 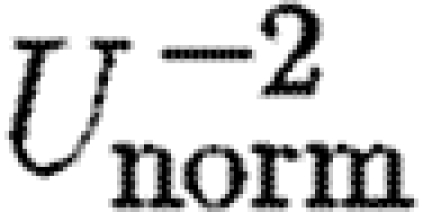. The exponent for the bats was significantly above the expected value, while birds have an exponent below the expected value, although not significantly so (table 4). For 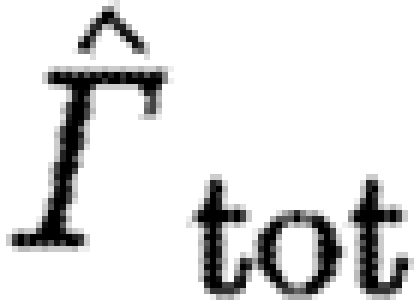, we found no differences between birds and bats (figure 1 b; table 3), but the overall exponent was significantly higher than −2. The relative contribution of the dominating start vortex to the total circulation, Γ _s/Γ _tot, differs in both exponent and intercept between birds and bats. Bats have a higher exponent (less negative slope) and a higher intercept than the birds at U _mp (figure 1 c; tables 3 and 4). The intercept differs also between the bird species (figure 1 c; table 3). The normalized wake loading also differs between birds and bats for the start vortex circulation, where bats have higher values at U _mp than birds (figure 1 d; tables 3 and 4). Also, the slope differs with bats having a higher exponent for 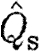(figure 1 d; tables 3 and 4) than birds. For the normalized wake loading based on the total circulation, we found no differences between the bats and the birds (figure 1 e; tables 3 and 4). However, the slopes differed between the birds (figure 1 e; table 3).

Table 3.

The p-values from the linear mixed model. (Italic fonts indicate significant differences between birds and bats.)

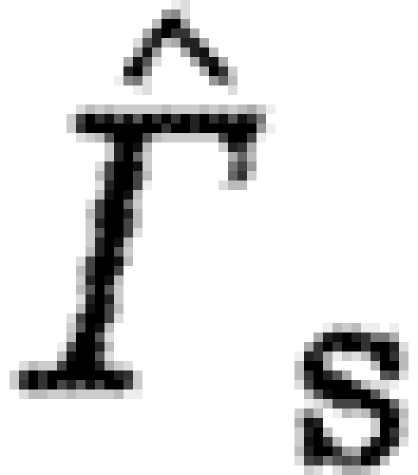
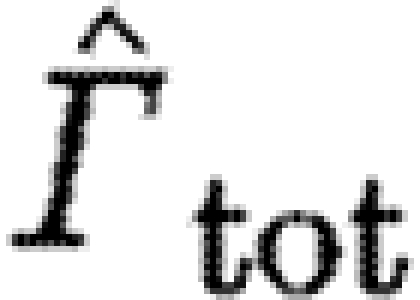
factors/dependable			Γ s/Γ tot
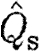
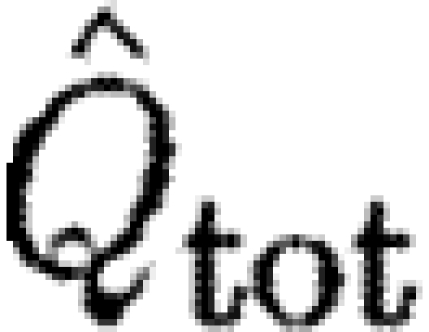
U norm	0.0001	0.0351	0.0001	0.0012	0.0001
BB	0.0053	0.1447	0.0001	0.0163	0.0738
Sp(BB)	0.2507	0.1845	0.0045	0.2701	0.8897
BB×U norm	0.0017	0.2459	0.0005	0.0026	0.5199
Sp(BB)×U norm	0.5252	0.7029	0.2411	0.4534	0.0030

Table 4.

Intercept and exponent of the power function of the linear mixed model. (Italic fonts indicate significant differences between birds and bats.)

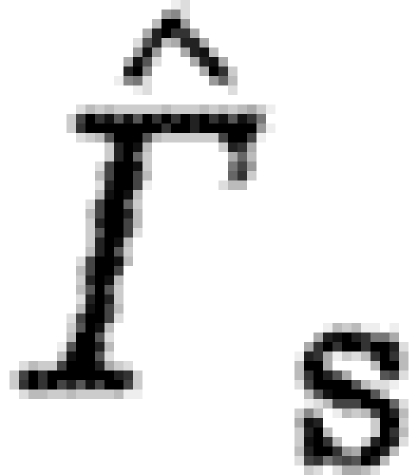
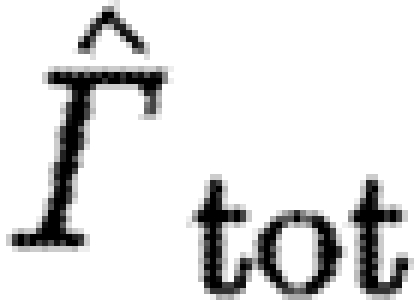
factors/dependable			Γ s/Γ tot
exponent, overall	−1.73	−0.74	−0.99	−0.77	0.28
exponent, bats	−1.17	−0.59	−0.58	−0.15	0.33
exponent, birds	−2.29	−0.89	−1.40	−1.38	0.23
intercept, overall	0.308	0.811	0.379	0.486	1.29
intercept, bats	0.379	0.852	0.446	0.698	1.51
intercept, birds	0.249	0.773	0.323	0.339	1.11

4. Discussion

Our results show that bats and birds differ in how they regulate the circulation and the wake pattern as speed changes. Birds and bats differ in the level of Γ _s/Γ _tot at U _mp as well as how Γ _s/Γ _tot varies with speed. This can be interpreted as a difference in how the circulation around the wing changes (as seen by the distribution of circulation in the wake) throughout the wingbeat. At U _mp, birds generate a weaker dominating start vortex relative to Γ _tot than do bats, indicating a more continuous change in the wing circulation as the wing stroke progresses (as in the extreme case demonstrated by the swift Apus apus; Henningsson et al. 2008). This means that a relatively larger proportion of the wake structure in bats has a higher circulation than in birds. At lower speeds, birds and bats generate a start vortex of relatively comparable strength. Γ _tot may be interpreted as a measure of the upper limit of the circulation on the wing during a downstroke because the circulation on the wing increases gradually, after shedding the start vortex, from Γ _s to some value close to Γ _tot and then decreases again at the end of the downstroke and throughout the upstroke. The difference in the exponent of the curves between birds and bats reflects differences in how the circulation around the wing is controlled during the wingbeat as a function of flight speed. The birds have a steeper reduction in the start vortex strength relative to the total circulation as flight speed increases, indicating larger changes of the aerodynamics of the wings with changes in the flight speed than for the bats. The differing pattern of circulation shedding between birds and bats may suggest some differences in the underlying mechanism of lift generation as speed increases. One such difference may be the presence or absence of leading-edge vortices, which has been demonstrated in slow-flying bats (Muijres et al. 2008). Alternatively, the flexible wings of bats (Swartz & Middleton 2008) may adapt more to the changes in flight speed than bird wings and allow for the flow to be more similar across speeds.

Bats had higher 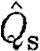than birds at U _mp, while 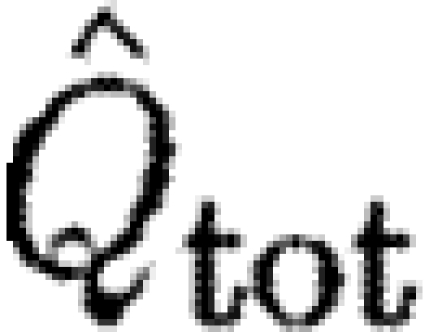did not differ significantly between birds and bats, although there is a similar pattern in the data for 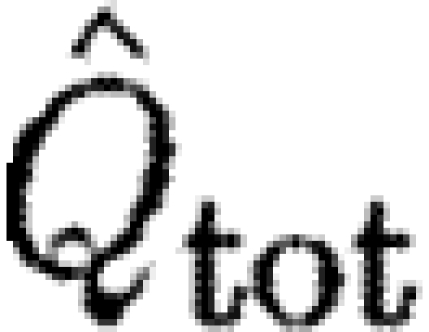as for 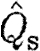. As noted above, the higher Γ _s/Γ _tot in bats suggests that a relatively larger proportion of the wake in bats will have a higher circulation than that in birds, suggesting that the results for 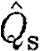are more relevant for comparison. A higher 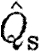in bats indicates relatively higher induced power and therefore less economic flight. According to equation (2.8), 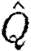can be interpreted as the inverse of the size of the horizontally projected area of the vortex structure generated during a wingbeat, corrected for the square of the wingspan. A high value thus corresponds to a relatively high induced power or, alternatively, to a relatively small projected area of the wake compared with the wingspan. A relatively smaller wake area can be the consequence of several different mechanisms, including a primarily downstroke-based wingbeat with an inactive upstroke. In the case of bats, our previous results have already suggested that the circulation along the span is not constant and that each wing generates separate vortex structures (Hedenström et al. 2007; Johansson et al. 2008), both factors that will decrease the effective horizontally projected wake area and thus the economy of flight. One intriguing question regarding the evolution of vertebrate flight is why the largest flying bird is approximately 10 times heavier than the heaviest bat (Norberg 1990). A relatively less economic flight of bats may be a candidate explanation for this difference if the available power for flight is limited. Studies of the metabolic power of flight show no difference between birds or bats (Speakman & Racey 1991) or even that bats should spend less energy than birds (Winter & von Helversen 1998). Combined with our findings, these results suggest that the conversion efficiency between metabolic and mechanical powers in birds and bats might differ in favour of bats.

Why do we find indications of less economic flight in bats? One explanation could be the difference in body shape between birds and bats. As mentioned above, the ‘blunt’ front of many bat species may result in a higher parasite drag. The nose leaf is effectively a flat plate with high drag and the ears protrude from the body to increase the frontal area and, most probably, the drag coefficient of the body. Higher parasite drag requires higher thrust production, which means that the vortex structures generated need to be tilted more. This results in a smaller horizontally projected area of the wake, which requires higher circulation to generate weight support. The higher circulation, in turn, results in a higher induced drag and less economic flight. Another potential consequence of these morphological structures in bats is that they may disturb the flow over the body, making lift production by the body less likely. This may be a reason why we find the separated vortex structures for the two wings in bats. The more streamlined body in birds might allow for higher body lift production and thus for the flow over the wings to connect more easily, resulting in a more unified vortex structure.

In this quantitative comparison of bird and bat wakes, the number of available species is limited, and therefore the results should be interpreted with some caution. However, considering that previous quantitative comparisons between bird species have failed to detect any differences between the species (Hedenström et al. 2006b ; Rosén et al. 2007), and that we here find several differences between the birds and a bat, we think that the results suggest some potentially interesting issues to be addressed in future studies. One of the areas deserving further attention includes the conversion efficiency in birds and bats and how that scales with size. Another area of interest is the dynamic flexibility of the aerodynamic mechanisms of bat and bird wings and the aerodynamics of the interaction between the body and the wings.