Dissipation and displacement of hotspots in reaction-diffusion models of crime

Abstract

The mechanisms driving the nucleation, spread, and dissipation of crime hotspots are poorly understood. As a consequence, the ability of law enforcement agencies to use mapped crime patterns to design crime prevention strategies is severely hampered. We also lack robust expectations about how different policing interventions should impact crime. Here we present a mathematical framework based on reaction-diffusion partial differential equations for studying the dynamics of crime hotspots. The system of equations is based on empirical evidence for how offenders move and mix with potential victims or targets. Analysis shows that crime hotspots form when the enhanced risk of repeat crimes diffuses locally, but not so far as to bind distant crime together. Crime hotspots may form as either supercritical or subcritical bifurcations, the latter the result of large spikes in crime that override linearly stable, uniform crime distributions. Our mathematical methods show that subcritical crime hotspots may be permanently eradicated with police suppression, whereas supercritical hotspots are displaced following a characteristic spatial pattern. Our results thus provide a mechanistic explanation for recent failures to observe crime displacement in experimental field tests of hotspot policing.

Crime is a ubiquitous feature of all modern cities, but not all neighborhoods are affected equally. In fact, serious crimes ranging from residential burglary to homicide are strongly patterned in time and space, forming crime “hotspots” (1–3). Studies show that policing actions directed at crime hotspots do lead to real reductions in offending and calls to the police for service (4, 5), while displacement of crime to adjacent settings may be less common than once thought (6–8). However, further gains in crime reduction are dependent upon gaining a quantitative understanding of the mechanisms that drive the emergence, spread, and dissipation of crime hotspots. Reaction-diffusion models, in which activators and inhibitors move, mix, and interact, provide a useful framework in which to investigate the formation of crime patterns and the impact of alternative policing strategies on crime hotspot stability. In this context, motivated offenders (activators) search their environment for suitable targets or victims (activators), which may also be mobile, following simple behavioral routines (9, 10). If an offender encounters a target in the absence of an effective security measure (inhibitor), then he is free to exploit that target. The immediate presence of security such as law enforcement is sufficient to deter that crime. Here we show that large-scale spatial crime patterns, including the formation of stationary crime hotspots, are strongly dependent upon the local diffusion of risk, driven by offender mobility in the environment, coupled with the phenomena of repeat and near repeat victimization.

Model

We study a reaction-diffusion system involving mobile criminal offenders within a square environment with periodic boundary conditions (11). Potential crime targets such as homes, automobiles, or persons, depending on crime type, are continuously distributed in space, and each location x = (x,y) is characterized by a risk of victimization, defined as a field A(x,t), representing general environmental cues about the feasibility of committing a successful crime (12–15) and/or specific knowledge offenders possess about target or victim vulnerability in the area (16–18). While A(x,t) is easiest to conceptualize in reference to stationary targets (such as homes in the case of burglary), it may also be used to represent the risk of attacks on mobile victims at any given spatial location (19, 20). Our model and its results are therefore independent of crime type.

Risk is the sum of a fixed component A⁰(x), which is stationary in time but potentially variable in space, and a dynamic component B(x,t), which evolves in time according to

[1]

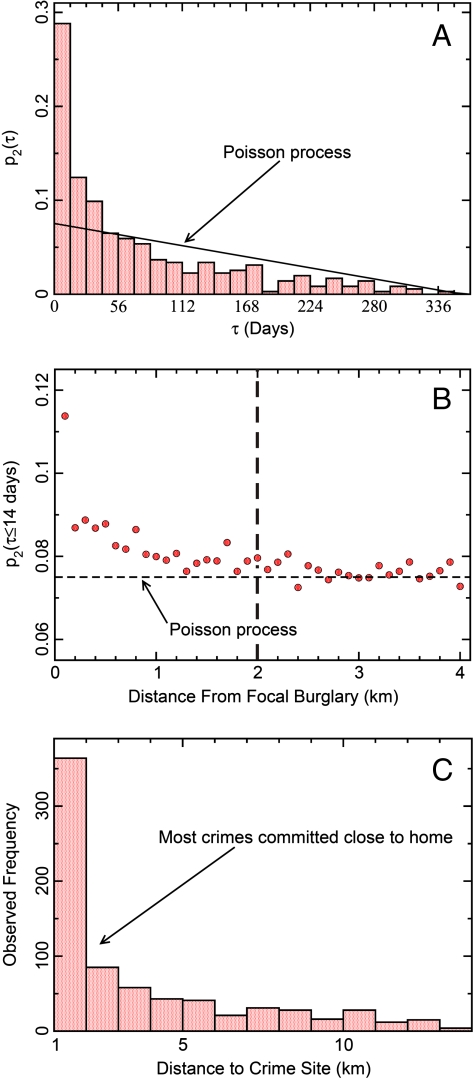
where ρ(x) is the density of criminal agents. The parameter κ measures the growth in risk at location x given crimes occurring there at a rate per unit area ρA. Thus, κ is an attractive force pulling offenders back to locations where they have successfully committed crimes, a dynamic inferred from empirical evidence for repeat crimes being concentrated in time shortly after the initial event (Fig. 1A) (SI Empirical Crime Data) (21–23). The parameter ω determines the rate at which the elevated risk decays towards the fixed environmental value A⁰(x), which generally occurs within days to weeks depending upon crime type (Fig. 1A). Finally, D, a diffusion coefficient, and η∈[0,1] control the rate of diffusive spread of crime risk within the local environment, describing a so-called “near repeat” phenomenon whereby targets within several hundred meters of an initial crime are more likely to be victimized than by chance (Fig. 1B) (19, 21, 24).

Fig. 1.

Spatio-temporal patterns of criminal behavior. Criminal offenders are more likely to return to the same and/or nearby locations to commit repeat crimes. Here we illustrate this fact through the specific example of single-family residential burglary, using data from Long Beach, California, over the years 2000–2005 (SI Empirical Crime Data). (A) The probability of observing a time separation of τ days between events at individual residences burgled exactly twice within a fixed temporal window of D = 364 days. We compare the observed distribution with an expected distribution of repeat crimes assuming they are Poisson distributed in time: p₂(τ) = 2(D - τ)/D(D + 1) (21). Repeat burglaries are much more likely to occur in the four weeks following the initial event than by chance, suggesting that burglars are biased to return to the same locations because of unique environmental cues and/or specific knowledge gained in the first burglary. (B) Repeat burglary probability in the two weeks following an initial crime as a function of distance from the initial crime. The Poisson expectation is calculated as 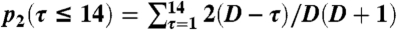. Burglaries occurring within two weeks of one another separated by more than approximately 2000 m are statistically independent (Poisson), whereas those that are closer to one another in space show strong spatial dependency; the interpretation is that the initial burglary increases the likelihood that neighbors are also victimized. Crime risk therefore spreads spatially up to distances ≤ 2000 m (dashed line). Similar repeat and near-repeat victimization dynamics are recognized for shootings (19) and insurgent attacks (23), indicating that these are generic features of a wide range of crime types. (C) Journey-to-crime distribution for residential burglars measured as the distance in kilometers from the offender’s residence to the site of a burglary. Most offenders search for targets in the immediate vicinity of home, a key activity node in their daily routine.

We assume that offenders search for criminal opportunities in the local environments surrounding the key activity nodes in their daily routines; these may include home, work, or recreation sites (Fig. 1C) (25–27). Offenders also preferentially select vulnerable targets, i.e., those with high associated risk A(x,t), usually to minimize the danger of capture or confrontation (16, 17, 28, 29). Thus the density of criminal offenders ρ at a spatial location x evolves according to

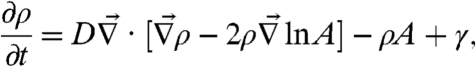[2]

where 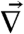is the gradient operator. Offenders move up gradients of ln A, but simply diffuse in the absence of a risk gradient. They thus seek out and victimize targets at greater risk whenever such differences are present in the environment. Offenders also exit the system at rate ρA, following commission of crimes, and are introduced at a constant, but possibly spatially variable, rate per unit area γ.

Results

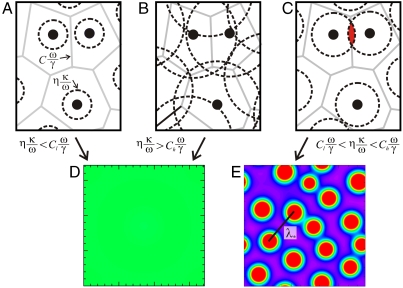
Eqs. 1 and 2 are coupled partial differential equations (PDEs) describing the space-time coevolution of crime risk and offender populations. We are interested in the conditions that cause the risk of crime, B, to be nonuniformly distributed in space. Linear stability analysis shows in fact that crime risk will form dense, well-spaced hotspots whenever the diffusion of the risk produced by individual crimes is spatially broad enough to bind local crimes together, but not so extensive that distant crimes are also connected (11). A schematic illustration of the mechanism driving crime pattern formation is shown in Fig. 2. Individual crimes are uniquely associated with a local spatial region conceptually similar to a Voronoi polygon, an area parametrically defined as Cω/γ (Fig. 2A). The inverse of this term is the average density of crime. The diffusion of risk from focal crime sites to nearby spatial locations defines a second spatial region that we term the “area of influence” of a crime given by ηκ/ω (see Fig. 1B). Crime hotspots will not emerge if the areas of influence of individual crimes do not overlap and therefore do not form risk clusters (i.e., ηκ/ω < C_lω/γ) (Fig. 2A), or conversely, if the areas of influence of individual crimes overlap with many others spreading risk evenly through the urban environment (i.e., ηκ/ω > C_hω/γ) (Fig. 2B). Thus, crime hotspots will emerge whenever C_lω/γ < ηκ/ω < C_hω/γ (Fig. 2C). The conditions necessary for crime hotspots to form hinge on the geographic nature of offender foraging behavior and underscore the importance of spatially restricted offender search in spreading risk in local neighborhoods (see Fig. 1C) (29, 30). Numerical integration of Eqs. 1 and 2 (see SI Methods) confirms that hotspots do not form when the diffusion of risk is either spatially restricted or spatially expansive (Fig. 2D) but do emerge with a distinct spatial scale set by the maximally unstable wavelength λ_∗ = 2π/|k_∗| otherwise (Fig. 2E).

Fig. 2.

The conditions for crime hotspot formation. Local diffusion of elevated risk from stochastic fluctuations in crime nucleate into crime hotspots. (A) Urban space may be thought of as being partitioned into areas uniquely associated with each individual crime (black dots), here shown as Voronoi polygons (gray lines) and described in the PDE model by average area Cω/γ. Individual crimes also produce elevated risk that diffuses out over an area (dashed circles) centered on the crime location and described in the PDE model by area ηκ/ω. If the area encompassed by diffusing risk from one crime does not overlap with the area of diffusing risk generated by another, then hotspots will not form and a spatially uniform, low equilibrium distribution of crime results. (B) If risk diffuses over a wide area, it is homogenized in space, and a spatially uniform, high equilibrium distribution of crime results. (C) Only when risk diffuses over relatively short distances, binding local crimes together but not more distant ones, do crime hotspots emerge. (D) and (E) Numerical simulations of the PDE system in a square region with periodic boundary conditions. (D) Parameters are such that ηκ/ω < C_lω/γ, or ηκ/ω > C_hω/γ giving a stable uniform crime distribution. (E) Parameters are such that C_lω/γ < ηκ/ω < C_hω/γ giving stationary crime hotspots. The spacing of hotspots is determined by the maximally unstable wavelength λ_∗ = 2π/|k_∗|. Hotspots are measured as deviations from a spatially averaged equilibrium value 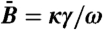(green), with maximum risk being (red) and minimum risk zero (purple).

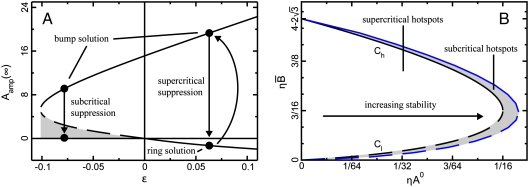
Weakly nonlinear analysis shows, however, that crime hotspots may arise as both supercritical and subcritical bifurcations, or large qualitative shifts from the homogeneous steady state (Fig. 3A). Supercritical bifurcations (ε > 0 in Fig. 3A) see the nucleation and growth of crime hotspots from small spikes in crime due to the linear instability of the system, whereas subcritical bifurcations (ε < 0 in Fig. 3A) are the result of large local spikes in crime that override linear stability. Referring to Fig. 2A, for example, crimes are sufficiently spaced such that the area of influence of a single crime generally does not overlap with that of others and the system is linearly stable with a spatially uniform crime distribution. If one location were to experience a sudden and extreme surge in crime, however, then the increased risk may suddenly spill over into the area of influence of an adjacent crime binding those areas together to create a subcritical hotspot. Alternatively, even where all crimes are bound together by the broad spatial diffusion of risk (Fig. 2B), a large surge in crime at one location may create a nucleation point pulling offenders away from a uniform distribution and causing a subcritical crime hotspot to emerge.

Fig. 3.

Crime hotspot types. Crime hotspots form in both linearly unstable and stable regimes, with correspondingly different geospatial structures. (A) The bifurcation diagram for the radially symmetric PDE system where dashed lines represent unstable branches and solid lines are stable branches. The parameter ε controls the stability of the system, with ε > 0 corresponding to linearly unstable systems and ε < 0 corresponding to linearly stable systems. A_amp(∞) measures hotspot intensity. Supercritical hotspots (ε > 0) are formed by small perturbations in crime and approach stable “bump” or “ring” solutions, shown where A_amp(∞) > 0 and A_amp(∞) < 0, respectively. Subcritical hotspots (ε < 0) are formed only by large perturbations in crime and show only a bump solution. The expected responses of supercritical and subcritical hotspots under suppression are shown by arrows (see text for discussion). (B) Parameter space for the formation of supercritical and subcritical crime hotspots for this same system. ηA⁰ is a measure of fixed (time-invariant) environmental risk, whereas 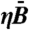represents different equilibrium values for the dynamic component of risk. Parameter regimes generating subcritical crime hotspots form an envelope surrounding the supercritical regimes suggesting that tipping of a linearly unstable regime into linear stability may still facilitate crime hotspot formation if crime events at individual locations surge in size and/or frequency. Analysis in both cases is based on a system with .

One of our key results is that subcritical hotspots may form under a wide array of conditions, paralleling those that form supercritical hotspots (Fig. 3B). The parameter combination 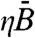describes the dynamic component of crime risk, approximately the probability of repeat victimization occurring at any given location. The variable ηA⁰ describes the fixed environmental risk of crime, approximately the probability of crimes occurring independently in space and time as a result of a stationary Poisson process. Small values of ηA⁰ describe environments characterized by very low fixed environmental risk. Small spikes in crime are easily distinguished against this background and nucleate into supercritical hotspots. As ηA⁰ increases, environments become inherently more risky and the range of values for the dynamic component of risk generating supercritical hotspots contracts. With further increases in ηA⁰ the system crosses a threshold into linear stability. At this point, small spikes in crime are insufficient to generate crime hotspots. Note, however, that for each value of 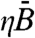capable of generating supercritical hotspots there are values of ηA⁰ describing marginally stable environments that nonetheless will support subcritical hotspots given a large enough spike in crime. The implication is that subcritical hotspots may be common in real urban settings, though the proportion of the parameter space shown in Fig. 3B that is behaviorally realistic is not presently known.

Our analysis also shows that there may be significant geospatial differences between supercritical and subcritical crime hotspots, with important implications for the response to crime hotspots of directed policing. Fig. 3A shows a bifurcation diagram for our system in a radially symmetric geometry, where A_amp(∞) is hotspot intensity and ε is a parameter that allows us to examine how system behavior changes as one moves from linearly unstable to linearly stable parameter regimes (see SI Methods). There are two spatial arrangements of crime patterns under linearly unstable conditions (ε > 0): a symmetrical “bump” solution (values of A_amp(∞) > 0) recognized as a traditional hotspot, and a “ring” solution (values of A_amp(∞) < 0). That crime patterns may form “hot rings” around a location is assumed in many individual-scale geographic profiling approaches to crime (31), but such patterns are not typically mapped in aggregate crime distributions. Conversely, linearly stable regimes (ε < 0) exhibit only the bump solution, which corresponds to a traditional hotspot pattern.

We furthermore expect supercritical and subcritical crime hotspots to respond differently to directed policing actions, such as hotspot policing. Fig. 3A indicates that suppression of supercritical crime hotspots, through police actions that drive the local hotspot intensity A_amp(∞) to zero, will first generate hot rings that subsequently break up to form hotspots of the same size and relative spatial arrangement as those prior to suppression. Conversely, we expect that subcritical crime hotspots will be eradicated by directed police action that is strong enough to drive A_amp(∞) into the gray region below the unstable branch (dashed line) of the solution shown in Fig. 3A, and that these spots will remain suppressed even after the removal of police pressure until such time as a large spike in crime overrides the linear stability of the system to form a new hotspot. The key difference in outcomes reflects the fact that focused hotspot suppression does not impact the small, stochastic fluctuations in crime occurring throughout the environment. In linearly unstable regimes, the small fluctuations are expected to quickly nucleate into new supercritical hotspots, while in linearly stable regimes the expectation is that they will not.

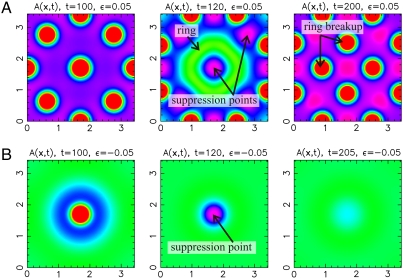
To test our theoretical expectations, we performed extensive computer simulations involving suppression of both supercritical and subcritical crime hotspots using the PDE model (see SI Methods). Crime suppression is introduced after allowing for the development of stable crime patterns using parameter combinations known to be either supercritical or subcritical. Suppression is modeled by instantaneously driving the crime rate ρA(x,t) to zero at the locations of current crime hotspots and maintaining this suppression for a fixed time period. In Fig. 4 we show that different types of crime hotspots respond differently to suppression as predicted by theory. Suppression of supercritical hotspots only temporarily results in the disruption of the crime pattern, with new hotspots emerging quickly to replace those suppressed by simulated police action (Fig. 4A). Moreover, simulations show clearly that suppression over the central area of a crime hotspot drives the elevated risk into a ring surrounding the area of suppression, corresponding to the ring solution in our nonlinear analysis. The displaced hot ring then breaks up to form independent hotspots of the stable bump solution in the nonsymmetric case. Conversely, suppression of subcritical crime hotspots does not produce displacement of crime into a ring or any other structure (Fig. 4B) and, as expected, crime hotspots do not reemerge after the cessation of crime suppression in this case.

Fig. 4.

Crime hotspot suppression. Suppression results for the PDE system with parameters chosen to generate supercritical or subcritical crime hotspots (see SI Methods). (A) Suppression of supercritical crime hotspots. Shown is the configuration of supercritical hotspots at timestep t = 100, just prior to the introduction of crime suppression. Crime suppression is then introduced over the area of each visible hotspot, leading to the eradication of the original hotspots but corresponding increases in risk in neighboring regions, seen at t = 120. The transient structure at t = 120 resembles a hot ring solution surrounding the location of the original central hotspot. By the time of the next suppression at t = 200, a new steady state featuring hotspots in positions adjacent to the original ones has been achieved. (B) Suppression of subcritical crime hotspots. Shown is a central subcritical hotspot at t = 100, just prior to the introduction of crime suppression. Crime suppression is then introduced over the area of the hotspot, leading to the eradication of the hotspot by t = 120. No transient structures appear in this case. Eventually suppression is lifted at t = 200 and the system quickly adopts the homogenous steady state. Colors scale as explained in Fig. 2.

Discussion

Our research has direct implications for the study of crime pattern formation and the mechanistic impact of policing interventions on crime. The deterministic models developed here suggest that the empirically observed reductions in crime that follow implementation of hotspot policing strategies (8, 32, 33) are not a statistical artifact but rather may reflect suppression of crime risk below some threshold level necessary to sustain a subcritical crime hotspot. Crime should remain suppressed in such situations even after the removal of law enforcement pressure, until such time as a significant cluster of crimes pushes the system towards instability. Conversely, our models also suggest that displacement of crime should result from policing actions directed at supercritical hotspots, consistent with criminological theory (34, 35). However, displacement is not commonly observed in empirical tests of hotspot policing (5, 6, 8, 32).

One possible explanation for the infrequent observation of displacement in empirical settings is that environments are sufficiently heterogeneous to limit the feasibility of offenders moving from favored habitats to adjacent areas that may be bereft of targets or victims, or may experience much higher levels of surveillance (36). Our analysis is based on a very regular, homogeneous environment where the baseline crime risk is uniformly distributed and thus displacement is not constrained by environmental structure. The assumption of environmental homogeneity could be perceived as a weakness of the modeling approach since most, if not all, real-world environments will be heterogeneous in the distribution of background crime risk (18, 37). We suggest, however, that a homogeneity assumption is useful as a theoretical baseline precisely because it is difficult to find in real-world settings. Were real-world environments as homogeneous as rendered in the current model, displacement would perhaps be much more common.

It is also possible that crime displacement has not been observed in empirical settings because controlled experiments have looked for only immediate spatial displacement in one to two block catchment areas surrounding crime suppression sites (8, 32). Displacement of supercritical hotspots in our continuum models is generally to a location midway between the hotspots being suppressed, effectively λ_∗/2, suggesting that the concern in empirical studies should be with crime displacement over intermediate distances (38).

Finally, the rarity of displacement in empirical tests of hotspot policing may mean that most real-world hotspots are subcritical rather than supercritical. However, we might also expect different crime types to generate different types of hotspots and therefore respond differently to hotspot policing actions. For example, open-air drug markets (7, 39) may require a large, initial spike in drug transactions involving multiple sellers to become established in a fixed spatial location. The failure of drug markets to reemerge following suppression, despite continued small-scale transactions on the street (40), is behavior consistent with classification of these markets as subcritical hotspots. By contrast, residential burglary or auto theft may be more likely to nucleate into supercritical hotspots, since these crimes are most often committed by either individuals acting alone or small co-offending groups (41). Displacement may be expected for these crime types since the offenders involved may be better able to respond to suppression by searching for targets in adjacent areas. However, support for such distinctions will require additional field experimentation.

We have shown that PDE reaction-diffusion models provide a mechanistic explanation for crime pattern formation given simple assumptions about the diffusion of crime risk and localized search by offenders. These models result in subtle observations about the fundamental dynamics of crime hotspots that may not be obtained through direct empirical study of crime data. The differences between supercritical and subcritical crime hotspots, for example, explain different outcomes of hotspot policing, including both hotspot suppression and displacement, and suggest that policing strategies need to be tailored to hotspot type.