Liquid crystals enable chemoresponsive reconfigurable colloidal self-assembly

Liquid crystals (LCs) and colloids have large response functions, a property that Nobel laureate Pierre-Gilles de Gennes (1) identified as the most significant unifying concept of soft matter. This strong response to external fields enables practical applications ranging from nonmechanical beam steering, to information displays, to label-free biological sensors (2–4). Poulin et al. (5) have demonstrated that colloidal particles embedded in a nematic solvent are stabilized by topological defects and interact via a new type of interactions that arise from the LC’s orientational elasticity. This seminal work initiated a great deal of excitement, and many self-assembled colloidal architectures have been reported in the bulk and at surfaces of LCs (6–14), promising a new class of reconfigurable composites that may enable mass production of tunable photonic crystals and optical metamaterials (14, 15). LC solvents can provide conceptually new means of predesigned control over self-organization of micrometer- and nanometer-sized particles that are not accessible in isotropic hosts. However, experimental demonstrations of such robust control are scarce and usually limited to the use of laser beams, electric fields, and colloidal particle shapes (6, 10–14). The study by Koenig et al. (16) in PNAS is a breakthrough in realizing a robust chemical control of colloidal self-assembly at the interface between an isotropic fluid (i.e., water) and LCs.

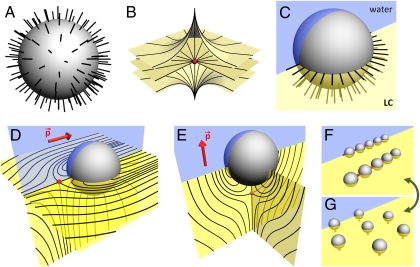
Nematic LCs are usually composed of rod-like molecules with long molecular axes aligned along a common direction described by a unit-vector with inversion symmetry n≡–n called “director” (3, 4). Anisotropic molecular interactions at LC surfaces set the boundary conditions for the director n that can be controlled by surface treatment. Colloids treated to align LC molecules and the director n orthogonally to the particle’s surface impose radial configuration of the director n resembling that around a point defect called “hedgehog” (in the core of which n is not defined) carrying topological charge “+1” (Fig. 1A) (6). Similar to their electrostatic counterparts, topological charges in a uniformly aligned LC have to be conserved; such particles are therefore accompanied by topological defects having charge of opposite sign (such as the “−1” hyperbolic point defect shown in Fig. 1B) and form elastic dipoles or quadrupoles (8–12). Koenig et al. (16) study such colloidal particles trapped at the LC–water interface and partially submerged in the nematic fluid, as shown in Fig. 1C. LC molecular alignment around such a colloidal sphere with vertical boundary conditions (Fig. 1C) resembles that around a surface point defect called “boojum” (16–18). Koenig et al. (16) show that, depending on the boundary conditions for the director n at the fluid interface, the colloids can be accompanied by either a hyperbolic boojum at the LC–water interface next to the particle (Fig. 1D) or a “−1” bulk hyperbolic point defect positioned beneath the colloid (Fig. 1E). Both structures have dipolar symmetry. The elastic dipole moment p is orthogonal to the fluid interface for the defect-particle alignment shown in Fig. 1E. However, p is parallel to this interface when the defect (boojum) is located at the LC–water interface next to the particle (Fig. 1D). By adding surfactant to the fluid interface, authors observe the director n and the dipole moment p spontaneously reorienting from the initial orientation parallel to the interface (Fig. 1D) to the orthogonal orientation (Fig. 1E) and the defect moving from the interface into the nematic bulk. This structural transformation is reversed after removing the surfactant from the fluid interface: the hyperbolic point defect moves back to the surface becoming a boojum and the dipole moment p orients parallel to the interface (Fig. 1D).

Fig. 1.

Colloidal interactions at the LC–water interface. (A) Vertical molecular alignment and radial n around a colloidal sphere resembling that around a radial point defect of charge “+1”. (B) Hyperbolic point defect of charge “−1”. (C) A colloid at the fluid interface setting vertical boundary conditions for n at the LC-submerged part of the particle; the director structure resembles that around a radial boojum. (D) A dipolar elastic configuration formed by an interface-trapped colloidal sphere and a hyperbolic boojum; the dipole moment p is parallel to the fluid interface and to the far-field director at the interface. (E) A dipolar elastic configuration formed by the colloid and a bulk hyperbolic point defect; the dipole moment p is orthogonal to the LC–water interface and along the far-field director. (F) Self-assembled linear chains of particles with elastic dipoles parallel to the interface. (G) Hexagonal arrays of colloids with the dipole moment p orthogonal to the LC–water interface. The lines in A–E show the spatial pattern of the director n. In the planes parallel and orthogonal to the fluid interface, LCs and water are shown by blue and yellow colors, respectively.

Similar to elastic interactions in the LC bulk (5), interface-trapped particles and accompanying defects introduce long-range elastic deformations and gradients in the field of the director n (16). LC elastic energy strongly depends on particles’ relative positions, giving rise to interactions mediated by the elasticity and reminiscent of electrostatic interactions between dipolar charge distributions. Colloidal elastic dipoles with the dipole moment p parallel to the LC-water interface form linear chains of particles interspaced by boojums (Fig. 1F). These surface defects prevent particle aggregation, similar to hyperbolic defects in colloidal chains assembling in the LC bulk (5). The chains are directed along the far-field director at the LC–water interface and resemble electrostatic dipolar chains that follow electric field lines. Upon adding surfactant molecules, point defects decouple from the interface and move to the positions beneath colloidal spheres (Fig.1 E and G). The surfactant monolayer at the nematic–water interface not only alters the boundary conditions for the director n but also turns the interactions from attractive dipolar interactions between colloids with the dipole moment p parallel to the interface to repulsive interactions of elastic dipoles with the dipole moment p orthogonal to this interface. The ensuing self-assembled structures gradually change from linear chains (Fig. 1F) to chains with larger interparticle distances, and then to hexagonal arrays (Fig. 1G). By varying the surfactant concentration, Koenig et al. (16) control point defects that are repeatedly forced to move from the LC bulk to the interface and back and the ensuing reconfigurable particle self-assembly. The response of this system to surfactant molecules adsorbing at the LC–water interface is perhaps another classic example of the extraordinarily strong response of soft matter (1).

Being at the nexus of several research fields, the work by Koenig et al. (16) is poised to initiate a great number of interdisciplinary studies of complex systems comprising LCs, colloids, and amphiphiles. The authors mention the need to explore how many-body elastic interactions may define the periodicity of locally hexagonal colloidal structures (Fig. 1G). It is particularly interesting to study the dynamics of reversible transformation of defect configurations. One may also explore how the addition of molecular surfactant leads to antagonistic vertical boundary conditions near the triple contact line of fluid interface and solid sphere (Fig. 1E) and how the ensuing strong elastic distortions of the director n may be relaxed by spatial redistribution of surfactant at the LC–water interface or by formation of a surface disclination ring. Both individual particles and self-assembled structures may be used in the development of new label-free chemical and biological sensors (2, 19, 20). The chemically controlled self-assembly demonstrated by Koenig et al. (16) may also guide the design of reconfigurable interfacial colloidal architectures and tunable 2D optical metamaterials (14, 15). It is therefore of great interest to explore how these interface-confined two-dimensional colloidal interactions and self-assembly will vary as a function of colloidal particle’s shape and size (especially for nanometer-sized colloids) as well as how the elasticity-mediated interactions depend on the type of the used LC mesophase (i.e., nematic vs. smectic vs. cholesteric, etc.).