Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization

Abstract

One of the best systems for exploring the origin of enzyme catalysis has been the reaction of ketosteroid isomerase (KSI). Studies of the binding of phenolates to KSI have been taken as proof that the electrostatic preorganization effect only makes a minor contribution to the binding of the real, multiring, transition state (TS). However, our simulation study has determined that the difference between the phenolates and the TS arises from the fact that the nonpolar state of the phenolate can rotate freely relative to the oxyanion hole and thus loses the preorganization contribution. A recent study explored the reactivity of both small and multiring systems and concluded that their similar reactivity contradicts our preorganization idea. Herein, we establish that the available experiments in fact provide what is perhaps the best proof and clarification of the preorganization idea and its crucial role in enzyme catalysis. First, we analyze the binding energy and the pK_a of equilenin and identify direct experimental evidence for our prediction about the differential electrostatic stabilization of the large TS and the small phenolates. Subsequently, we show that the similar reactivity of the small and large systems is also due to an electrostatic preorganization effect but that this effect only appears in the intermediate state because the TS is not free to rotate. This establishes the electrostatic origin of enzyme catalysis. We also clarify the crucial importance of having a well-defined physical concept when examining catalytic effects and the need for quantitative tools for analyzing such effects.

Elucidating the origin of the catalytic power of enzymes is a problem of great importance. Simulation and conceptual studies have suggested that electrostatic preorganization effects provide the major contributing factor in enzyme catalysis (1) and that other factors cannot give large contributions (see, e.g., ref. 2). Despite this, however, some believe that many different effects have been exploited in the evaluation of enzyme catalysis (e.g., refs. 3 and 4). Establishing the relative importance of different catalytic factors by direct experimental studies is very challenging because such an analysis requires a decomposition of the observed energetics of different contributions, and, in some cases, it is not clear how to overcome this challenge.

The electrostatic preorganization concept (5) identifies the fact that during reactions in solution, the solvent must pay the cost of reorienting its dipoles while moving from the reactant (RS) to the transition state (TS), i.e., there is a “reorganization” free energy. On the other hand, the protein active site already has partially oriented dipoles and thus has to pay a much lower energetic penalty (i.e., less reorganization energy). This concept is related to Marcus’ reorganization energy (see ref. 1), but the crucial difference is that here, the protein must have fixed dipoles rather than a nonpolar environment in order to reach both small reorganization and a stable TS. The preorganization concept can be realized by calculating the shift in the relevant Marcus parabolae or by considering the preorganization associated with binding the TS (1). (This key issue is discussed in more depth in SI Text and Fig. S1.) At any rate, the crucial difference in electrostatic preorganization between the enzyme and the reference reaction in solution (5) is arguably the most important factor in enzyme catalysis.

In light of the apparent complexity of the preorganization idea, it is fortunate that recent attempts (3, 4, 6, 7) to challenge this proposal have resulted in instructive sets of experiments that finally allow (and force) one to realize the nature of this proposal as well as the crucial need to understand this idea in any attempt to quantify enzyme catalysis. However, establishing the validity of the preorganization proposal may still be complicated by the implications (e.g., refs. 4 and 7) that this is the equivalent of the ill-defined idea of solvent exclusion (which cannot be quantified because it does not deal with the role of the enzyme as a supersolvent). The above misunderstandings cannot be resolved by attributing the electrostatic preorganization proposal to the work of Dewar (8) (who proposed that enzymes work like gas-phase systems), or, alternately, by attributing the water-exclusion gas-phase idea of Dewar to us (where we have shown that enzymes work like a supersolvent). This may compound the confusion in the field because the two proposals are mutually exclusive. Overlooking such issues makes it very hard to dissect catalytic proposals and to examine them by experimental means.

Perhaps the preorganization idea has not been widely appreciated due to the need to conceptualize it in a mathematical way, and thus it is crucial to find experimental demonstrations of the nature of this effect and to find cases that cannot be explained without considering the reorganization energy. Ketosteroid isomerase (KSI) offers perhaps the best system for illustrating the preorganization effect and is thus an excellent model system for examining the main contributing factors to enzyme catalysis (9) (see also SI Text). However, although theoretical calculations (10) have provided strong support for the electrostatic stabilization mechanism for KSI (which is further supported by the experiments in ref. 11), this enzyme has become a prototype for attempts to argue that electrostatic effects are unimportant to catalysis. In particular, a study (3) of the binding of phenolate transition state analogues (TSAs) to KSI found a small change in the binding energy upon change in the charge delocalization of the TSAs and took this as evidence that electrostatic effects do not make a major contribution to catalysis. The problems with the interpretation of the TSA experiments have been highlighted by a recent theoretical study (9) that reproduced all the experimental findings but, in contrast to the original proposal, has demonstrated that these findings are in fact quantitatively consistent with the preorganization idea. That is, a careful computational study (9) has demonstrated that the binding free energy of the enolate intermediate of KSI (and the related TS) are much larger than the corresponding binding energy of the of the phenolate TSAs. This reflects the fact that the preorganization depends on the interaction of the charged ligand with the protein configurations that are not polarized by the ligand (i.e., the configurations that correspond to the forces of the uncharged ligand). The preorganization is small in the case of the small ring of the phenolate, because this ring can freely rotate relative to the oxyanion in its uncharged form, whereas the larger multiple rings of the 5-androstene-3,17-dione (S_full^′) are unable to rotate in the active site (see SI Text for a clarification of this concept).

The persistence of arguments contrary to the points established in ref. 9 may reflect the assumption that the results of calculations and conceptual analysis do not represent solid findings. Therefore, it is crucial to revisit the case of KSI in order to demonstrate that there exists concrete experimental evidence for the fact that there is an enormous difference between the electrostatic contributions to the binding of the phenolate and to the binding of the larger steroid substrate, thus establishing our preorganization idea. Similarly, it is crucial to reanalyze the new intriguing experiment of ref. 6, which purported to provide novel evidence that KSI does not use electrostatic catalysis (see Background). This analysis is the aim of the present paper, as well as detailed clarifications aimed at preventing the propagation of misunderstandings about the presumed similarity between TSAs and TSs, which underlie the experimental work of refs. 3, 4, and 6.

We believe that further analysis and discussion of the origin of the catalytic power of KSI provides what is perhaps the best chance for communication between the school of thought that believes in a quantitative analysis of enzyme catalysis by computation of the observed effects (while dissecting them to the different contributions) and that which tries to look for alternative explanations while sometimes viewing experimental facts as being equal to the interpretation of such facts. Thus, we provide here a detailed examination of experimental observations whose direct relationship to the catalytic power of KSI has not been sufficiently appreciated or analyzed. First, we focus on the binding energy and pK_a of equilenin and establish its electrostatic origin. Furthermore, we clarify how this electrostatic effect is related to the corresponding preorganization effect. Subsequently, we provide a careful analysis of the relevant thermodynamic cycles for the binding of different TSs and TSAs, to further establish our point. Finally, we explain why the catalysis of 3-cyclohexene-1-one (S_mini) does not in any way contradict the preorganization idea. Thus, we provide direct overwhelming experimental, theoretical, and logical proof of our concept about the electrostatic origin of enzyme catalysis.

Background

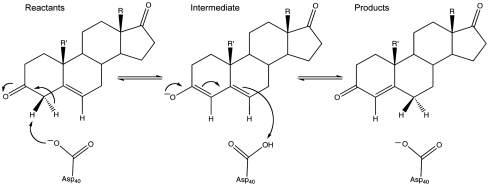
The catalytic reaction of KSI, as well as the orientation of the substrate relative to key active site residues, is schematically illustrated in Fig. 1 (see also refs. 10 and 12 for further discussion). Here, we will only consider the first step of the reaction because the two steps are thought to be similar and have similar catalytic effects (10). The first step in the chemical reaction of KSI, for the substrate S_full^′, involves a very large catalytic effect, where the activation barrier for the reaction in solution, 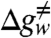, is about 21.9 kcal/mol and the chemical barrier in this enzyme is ∼10.3 kcal/mol (12). Thus, the rate acceleration, ΔΔg^≠, is 11.6 kcal/mol. The origin of this catalytic effect has been attributed to the electrostatic stabilization of the enolate intermediate by the hydrogen bonds of Tyr57 and Asp103 as well as the reduction of the reorganization energy during the reaction (10).

Fig. 1.

A schematic description of the isomerization catalyzed by KSI.

Our previous work (9) pinpointed the origin of the catalytic effect in KSI by analyzing the nature of the difference between the very large electrostatic contribution to the binding energy of the TS of KSI and the very small electrostatic contribution to the binding of the TSAs (see the Introduction). However, despite this, it appears that part of the community (e.g., refs. 3, 4, and 6) continues to search for other ways to rationalize the catalytic power of KSI (see Concluding Discussion and SI Text). These works focus on somewhat exotic options, rather than considering the works that actually quantitatively evaluated the catalytic effect. A much more direct attempt to challenge the preorganization idea (or at least as the authors understood this concept) has been advanced in a recent work (6) that examined the catalytic reaction of the large, multiring 5(10)estrene-3,17-dione (S_full) system, as well as a small ring (S_mini) system, and argued that the observation of similar rates for these systems contradicts the “prediction” of ref. 9. This remarkable observation requires careful analysis, starting with the clarification that ref. 9 never made any prediction about the reaction of S_mini or S_full but, rather, quantitatively reproduced the experimental binding of both the phenolate TSAs and the TS of S_full^′. It obviously never considered the binding energy of the TS of S_mini. As clarified in ref. 9 and below, the binding of the TS and the transition from the RS to the TS correspond to entirely different thermodynamic cycles (see Fig. S2). Furthermore, we will explain below the origin of the large catalytic effect of S_mini and explain why it has little to do with the weak electrostatic contribution to the binding of the phenolates.

Experimental Establishment of the Large Electrostatic Contribution to the Binding of Large TSAs.

In the absence of simple experiments that directly support the preorganization idea (perhaps due to the complexity of our message about the reorganization, unlike subsequent simpler but unfortunately less accurate proposals), we decided to carefully examine the available literature to see if we can find facts whose systematic analysis could provide the missing information. Fortunately, we found the relevant trend in several sources, including the work that mainly set out to challenge the electrostatic idea, namely ref. 3.

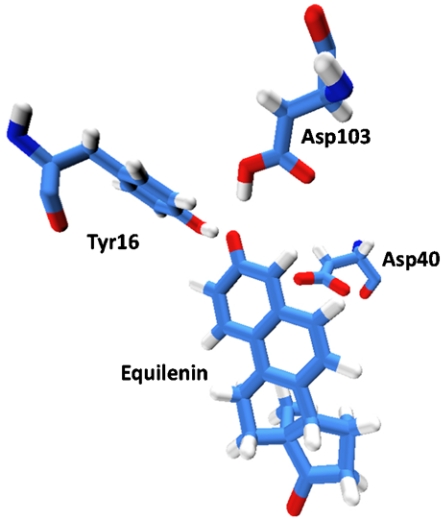
As a starting point, we have focused on the binding of equilenin, the binding configuration of which is shown in Fig. 2. In order to obtain the relevant binding energy, we followed the same type of derivation applied in ref. 3 (see the cycle of Fig. S3) and used the relationship

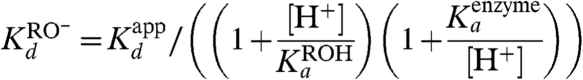1

where K_d is the actual binding of the ionized species (i.e., the RO^- form), K_a is the value of the ionization constant of the ligand, and [H⁺] is the H⁺ concentration in the bulk solution. Using the observed values of 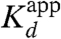of about 10^-9 M for equilenin at pH = 7 (12) (though an even smaller value is also given), at pH = 8 for the phenolate (3), and 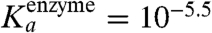(3), we obtained a K_d of 3 × 10^-14 for the equilenin and K_d = 2 × 10^-8 for the phenolate. This means that the binding free energy of the ionized forms of equilenin and phenolate are about -18.3 kcal/mol and -10.5 kcal/mol, respectively. If, as will be discussed below, the large difference (7.8 kcal/mol) is due to the change in electrostatic binding energies, then our point has been established through the experimental data.

Fig. 2.

The binding configuration of equilenin. Note that in this illustration, the residue in position 40 is an aspartate. However, experimental studies of the binding of equilenin have been performed with not only Asp40 but also a D40N mutation.

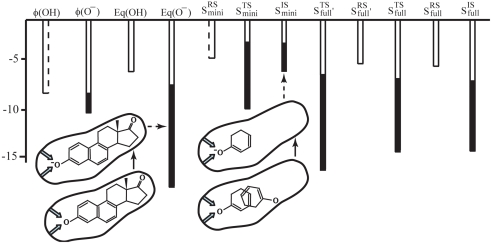
The first step in establishing the above point is our theoretical analysis of the electrostatic contribution to the binding of the phenolate and the ionized (deprotonated) equilenin, which was performed by evaluating the charging free energy of the phenolate and the ionized form of equilenin (see Methodology). The results, which are summarized in Fig. 3, Fig. S4, and Table S1, reproduce the observed trend of an extreme increase in binding energy between equilenin and the phenolate. Apparently, the difference in binding affinity is almost completely due to the change in the electrostatic contribution and the preorganization effect. This is in contrast to the case of the phenolates explored in ref. 3, in that here we have a clear example of a major increase in the electrostatic free energy, which goes in exactly the same direction as the difference between the phenolate and the TS.

Fig. 3.

The binding energies (including the relevant electrostatic contribution, highlighted in black) for the systems being considered in this work. The figure also depicts the charging step in the binding cycle for equilenin and the IS of S_mini.

One could still argue that we are only providing theoretical proof that this effect is basically electrostatic. However, this point can also be established experimentally. That is, the change in the binding energy is due to electrostatic effects if it is almost completely reflected in the change of the pK_a of the bound ligand, relative to corresponding pK_a of this ligand in water. Here, we point out that spectral data (12, 13) suggests that equilenin binds to KSI in its ionic form down to at least pH = 3.5 (as explained in SI Text, this finding is applicable to having D40 in the relevant [protonated] protonation state, as it occurs at low pH). Since the pK_a of a free equilenin is about 9, this means that the protein reduces the pK_a of this system by at least 5.5 units. This change is entirely due to an electrostatic effect (because it reflects the effect of a change in charge), and thus, from the existing data, it is experimentally established that the electrostatic contribution to binding is at least 7.6 kcal/mol. To further examine this point, we calculated the pK_a shift (upon binding to the protein) of equilenin, using the above electrostatic charging calculations. Our calculations gave a pK_a shift of about 6 pK_a units for equilenin, which falls in the same range as the observed estimate. Thus, both experiment and theory establish that the charged form of the deprotonated equilenin, which is extremely similar to the steroid enolate intermediate, is much more stable than the phenolate, due to an electrostatic effect.

Experimental and Theoretical Support from Other TSAs and TSs.

To further establish the preorganization idea, we extended our analysis, considering several TSs and TSAs, using the observed k_cat and K_D and estimating the relevant information from thermodynamic cycles when it is not directly observed. The details of this analysis are presented in SI Text and then compiled and summarized in Fig. 3. In our view, the information provided in this figure is sufficiently conclusive because it is not dependent on only a single calculation or experiment. As seen from the figure, we have enormous electrostatic transition state stabilization for the TSs of the steroids (S_full and S_full^′) and for the binding of S_mini.

Another interesting experimental point is obtained by carefully examining figure S1 of ref. 3, which illustrates the binding affinities of the ionized TSAs. As seen from the figure, the binding energy of the charged TSA increases significantly with the corresponding size. This issue was noted in ref. 3 but somehow attributed to undefined size effects without a consistent physical basis for such an attribution. That is, as explained in SI Text, whereas it may seem reasonable to attribute this to an increase in the hydrophobic contribution, such an assertion would be problematic. Apparently, the results of ref. 3 are fully consistent with the reduction in the reorganization energy when the uncharged state of the phenolate is restricted (by the larger side chain) from reorienting in the active site.

The Catalysis of S_mini and S_full Are Fully Consistent with the Preorganization Concept.

After establishing our point about the binding energies of the TSA and TS, it is important to address the current interpretation of the experimental information about the catalysis of S_mini and S_full. First (see Fig. S2), the binding of the TSA and the chemical reaction correspond to entirely different thermodynamic cycles: the first for the solvation of the negative charge, and the second for the transfer of negative charge from one center to another. Obviously, the reorganization energies are very different in each case. At any rate, we started with a careful experimentally based analysis of the actual catalytic effect (Fig. S5), establishing that the catalytic effect of S_mini is significantly smaller than that of S_full^′ (i.e., as shown in Fig. S4, the ΔΔg^≠ is different by 2.1 kcal/mol).

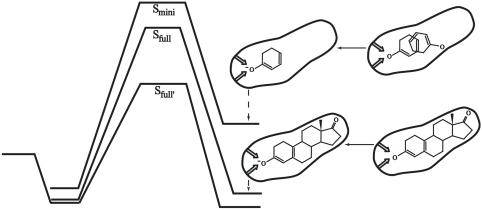
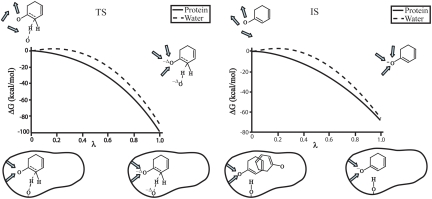
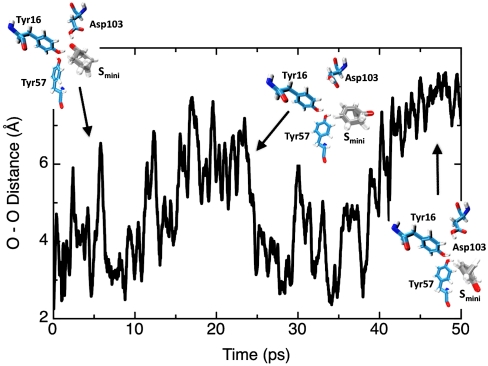
We then performed empirical valence bond (EVB) calculations and reproduced the actual catalytic effect of S_mini without adjusting any parameters upon the move from solution to the protein (see Fig. S7). Subsequently, we used EVB and charging calculations in order to explore the catalytic effects of the two systems and to relate it to the preorganization effect. The results of these calculations are summarized in Figs. 4 and 5. As seen from the figures, this paper reproduces the observed catalytic effect. More importantly, we have identified the origin of the misunderstandings in the interpretation of the relevant experiments (6). Apparently, the electrostatic stabilization of S_mini is much smaller in the intermediate state (IS) than in the TS, which lies in complete contradiction to the case in S_full. The origin of this effect is elucidated by the electrostatic calculations that are summarized in Figs. 5 and 6 and Fig. S7. As seen from the figures, the large electrostatic contribution at the TS disappears in the IS of S_mini, reflecting the large reorganization of the uncharged state of S_mini. One may wonder why the TS of S_mini has a large electrostatic contribution whereas the IS does not. The key difference here is that in the TS, we still have a partially delocalized hydrogen bond to Asp40, which prevents the large substrate rotation that determines the preorganization effect in the charging cycle, whereas the TS has small preorganization because the substrate is free to rotate. Our point about the movement of S_mini in the IS at the uncharged state is further established by the simulations shown in Fig. 6 and Fig. S7.

Fig. 4.

The energetics of the reactions of S_mini, S_full^′, and S_full. The relevant energies are taken form the analysis in Figs. S5 and S6. The figure also illustrates the preorganization effect in the charging of S_full and the IS of S_mini. In the case of equilenin, the uncharged state of the IS is fixed so that the preorganization energy is large and negative. In the case of S_mini, the uncharged state of the IS is free to rotate, leading to a very small preorganization contribution.

Fig. 5.

The nature of the electrostatic energy of the TS and IS of the reaction of S_mini. The figure presents the result of the FEP charging process for each system in water and in the protein and explains why the difference between the charging in the protein and in water is larger for the TS. As seen from the figure, the uncharged TS is not free to rotate and thus has a significant preorganization contribution, whereas the uncharged state of the IS is free to rotate in the active site.

Fig. 6.

The change in distance between the oxygen of Tyr16, and the oxygen of the IS of S_mini during simulations where the protein sees zero charge on the IS. As seen from the figure, the uncharged state of the IS is free to rotate in the active site.

The finding that S_mini has significant catalysis is, in fact, strong evidence against the idea that the phenolates are good TSAs (as was suggested in refs. 3 and 6). That is, using the analysis based on both the observed and calculated TS binding energy, and the calculations of the electrostatic contribution to this free energy, we find that the TS of S_mini has greater binding of about 6 kcal/mol than the phenolate TSA (see Fig. 3 and SI Text). Thus, the phenolates are very poor TSAs.

Discussion

Our previous study (9) has computationally established that electrostatic stabilization is the most important factor in the catalysis of KSI and that the information from small TSAs cannot be used to explore this effect. Here, we started by proving our point using available experimental facts (i.e., binding energies and pK_as) and showed that the equilenin is stabilized by about 6 kcal/mol more electrostatic energy than phenolate. Because the TS binding energy of S_full^′ is similar to the binding energy of equilenin, and because both must have similar hydrophobic contributions, they must therefore have similar electrostatic contributions. Adding to this the fact that the TS and the intermediate have similar electrostatic stabilization means that we have basically been able to use experimental facts to demonstrate that the TS binding involves very large electrostatic stabilization.

Here, we have also reanalyzed new experiments (6) that were brought as proof against the preorganization idea and established that the electrostatic contribution to the binding of the TS of S_mini is much larger than the electrostatic contribution to the binding of the phenolates as well as to that of the IS of S_mini, thus establishing that the origin of the catalytic effect in the reaction of S_mini is also the preorganization effect, which does not, however, exist in its IS. Our finding also establishes that the phenolates are very poor TSAs and highlights our point about the origin of the TS and IS binding in preorganized systems, giving further major support for the idea that electrostatic preorganization is the most important factor in enzyme catalysis (as was discussed in refs. 1, 2, and 14).

At this point, it is important to clarify the preorganization idea and its manifestation in catalysis by KSI. That is, although this idea has also received major support from our previous study of KSI and other enzymes, there have been several recent works that tried to explain the catalytic effect of KSI by various esoteric proposals. One such proposal (4) implied that the enzyme active site constrains side chain orientations in such a way as to prevent H-bonds from shortening by 0.1 Å (or less), a change that is indistinguishable by most x-ray studies. This is, in turn, assumed to provide a major catalytic effect. This work, in contrast to previous studies by the same authors (3), emphasized the preorganization effect but still involved several misunderstandings. The first of these is the fact that the authors appear to attribute the idea of TS stabilization by the preorganization effect (5) to such prominent workers as, for instance, Jencks, Polanyi, Pauling, Haldane, and Lienhard, who actually proposed ground state (GS) destabilization. This is somewhat relevant to the present issue because the authors of ref. 4 correctly wonder how preorganization can help catalysis when the substrate structural changes during the reaction are typically very small, but then this led them to incorrectly conclude that constraints on sub-Å changes are the source of these catalytic effects. Such a view overlooks the fact that the largest relevant structural changes occur in the thermodynamic cycle of the TS binding (mainly in the water reaction). In this case, one cannot observe the key changes in the uncharged form and must resort to correct thermodynamic analysis plus computational analysis as well as physically consistent analysis of indirect experimental facts (as was done in this work). In other words, we would guess that the reason for not observing the structural signature of the catalytic effect (and thus assuming that it is a very subtle change) is that the authors examined the charged system rather than the uncharged state, and of course did not examine the corresponding reaction in water (this issue was discussed in ref. 9). The difference, however, lies in the uncharged state, and the main confusion arises when looking for the preorganization effect in the enzyme with the charged TS or TSA.

The preorganization effect is associated with the reduction of the reorganization energy upon charging the TS. In water, the reorganization is very large, and in the enzyme’s active site it is much smaller. This point can be best understood if one considers the actual reaction step (i.e., the proton transfer) rather than the TS binding. To catalyze the reaction, we need to have the environment dipoles orientated in such a way as to stabilize both the RS and IS charges (because the mixture of these charges generate the TS charge). Here, we have Tyr16 and Asp104 stabilizing the enolate charge and other protein dipoles plus a water molecule stabilizing the charge of Asp40 (10). However, addressing the challenges and misunderstandings of the TSA studies requires one to consider the preorganization in terms of the TS binding (while trying not to lose the bigger picture of the reduction of the movement from the RS to the TS). Here, the difference in preorganization between the TSA (where there is no large electrostatic effect) and the real TS is associated with the freedom of motion in the uncharged state of the TSA (see ref. 9). Nevertheless, one should not lose the overall perspective and assume that the role of the enzyme is to fix the substrate TS relative to the enzyme dipoles (a problem that is highlighted in comparison to TSAs) but rather to have its dipoles pointing toward the TS charges. It is rather trivial to fix the substrate but much harder to create a preorganized polar environment around it.

At this point, we should also address attempts of ref. 6 to attribute the catalysis to remote interactions. Here, we note that the only mutations examined are local rather than remote mutations that have been examined in previous works (with similar results; see the references cited in ref. 10) and have been established to be the source of the electrostatic catalysis (9, 10). It has also been argued that the intrinsic binding energy can be used to promote catalysis (6). However, this idea has been shown to be incorrect—most glaringly in the case of orotidine decarboxylase, as was discussed in Section 5.6 of ref. 1. In fact, there is no single case where it has actually been demonstrated that the binding of the nonchemical part of the substrate leads to significant ground state destabilization (and thus an increase in k_cat). Moreover, in the case of KSI, it is not clear where these nonchemical parts can be. If one argues that they are found in the remote part of the multiring system, then why is catalysis also observed in the single-ring system? Similarly, short of electrostatic destabilization, we have not yet seen any quantitative rationalization of catalytic effects using the argument that size somehow determines catalysis, because there is no conceptual connection to how it is being done. In fact, this suggestion has been shown to lead directly to the electrostatic preorganization idea, which was elaborated on in this work.

Despite the overwhelming facts and arguments provided above, it has been maintained (6) that TSAs such as the phenolates and TSs like the KSI enolates have similarly small electrostatic contributions to binding. However, we have demonstrated here (both theoretically and through the existing experimental data) that this is not the case, and, in our view, that this is perhaps the most direct experimental demonstration of the importance of electrostatic stabilization in the whole field of enzymology. Here, the crucial and simple test is whether the binding of the TSAs depends on their ability to have large reorganization and not on the much more complicated question (that was also resolved here) of whether the reactions of S_mini and S_full have similar barriers.

In order to actually assess the relevance of the binding experiments to the catalytic effect, it is essential to use some model, and the best available ones are computational modeling approaches that can evaluate both the binding energy of the TSA and the corresponding catalytic effect. In this regard, it is important to recognize that, at present, the only rationale for the difference in electrostatic stabilization between the phenolate and the larger enolates (which was established above) comes from the preorganization concept. Furthermore, we have quantified the catalytic effect of S_mini and explained why it does not create a conflict with our preorganization idea and why it does not convert the phenolates to be good TSAs. Thus, we must consider this to be a valid concept and the best explanation for the origin of enzyme catalysis.

It is worth commenting here on the perception that the catalytic effect is due to many factors (e.g., ref. 3). Of course, this possibility should always be taken into account. However, it is essential to define, examine, and quantify each proposed catalytic contribution, as was done repeatedly in our studies (e.g., ref. 1). Even though ref. 3 does not propose any clear nonelectrostatic factor that can be computationally examined, it nevertheless concludes that electrostatic effects do not play a crucial role. Thus, it would appear that ref. 3 cannot offer any physical concept that can actually account for the large catalytic effect. In this respect, it is important to consider key experiments, such as the effects of mutating Tyr16 and Asp103, and ask what other catalytic effects except electrostatic contributions could account for the enormous effect of these residues. Here we can only point out that a previous study (10) found that the mutational effects are in fact due to electrostatic interactions, and it is very hard to see how to account for such effects by other catalytic factors. It is clearly cannot be used to invoke remote effects.

In principle, one could argue that our calculations and the reproduction of the relevant catalytic effects are “just” theoretical. However, because our arguments are based on hard experimental data, they should provide sufficient evidence for even hardened skeptics. We would also like to point out that none of the convoluted existing suggestions, such as sub-Å (4) or remote binding (6) interactions have been able to rationalize or even to suggest a very rough estimate of the magnitude of any of these observations. Perhaps the most interesting conclusion from the present work is the finding that the catalytic effect is almost entirely due to electrostatic preorganization effects. This trend has also been found in other enzymes (see, e.g., ref. 1), which indicates that enzyme catalysis is mainly associated with electrostatic factors rather than with many other small effects.

Conclusions

This work has revisited ketosteroid isomerase (KSI), as this is one of the best (and most extensively studied) systems for exploring the origin of enzyme catalysis. Specifically, we have combined recent experimental data (e.g., 3, 4, 6, 7) with a detailed theoretical and conceptual analysis, focusing particularly on examining the binding energy and pK_a of equilenin in order to conclusively establish our previous prediction (9) about the differential electrostatic stabilization of the large TS and the smaller TSAs, as well as addressing a recent experimental study (6), which argues that the similar reactivity of small (S_mini) and multi (S_full) ring systems is proof of the unimportance of electrostatic preorganization, and demonstrates that it is in fact precisely the electrostatic preorganization effect (which only appears in the IS of S_mini, as the free rotation of the TS is strongly hindered) that accounts for the reactivity of these compounds.

Of course, one could still ignore (or misunderstand) (4, 6) our points. However, it is impossible to actually explore catalysis in KSI without trying to follow the preorganization idea. This fact is amplified by the reality that none of the current alternative suggestions (SI Text) have been able to generate a way to convert a proposal to a measurable number or to an estimate of a catalytic energy contribution. As such, it is crucial to understand that proposals without a solid basis or estimate are extremely problematic, in particular when they ignore quantitative interpretations, and one should not just make suggestions as to the basis of the catalytic power of enzymes but also estimate the energetic consequences of such effects.

Finally, this paper again highlights the possibility of enormous differences between the TS and the TSA, and the fact that the nature of this difference is not only very hard to elucidate by only experimental means but also probably impossible to understand without realizing the preorganization concept. In light of this, the present work demonstrates the crucial role of computer simulations (provided there is an adequate structure available) in converting the overall observed energetics to individual energy contributions to both binding and catalysis and constructing a meaningful rationale for the enormous catalytic power of enzymes, and conclusively demonstrates the electrostatic origin of enzymatic catalysis, which would have been impossible to elucidate without a rigorous theoretical model. It is also important to note that a very recent work (17) has suddenly accepted the idea that KSI acts by major electrostatic effects by its oxyanion hole, which is in complete contradiction to the previous proposals of refs. 3, 4, 6, and 7 (which set out to disprove this idea). It is now recognized (17) that hydrogen bonds are important, and that calculations may be useful in the future, but this is stated while, as before, overlooking all the computational tools that have been developed and applied for this specific purpose (e.g. refs 1 and 10). Overall, we hope that the compelling case provided by the present study will encourage those who are interested in enzyme action to appreciate the preorganization concept.

Methodology

The charging free energies, 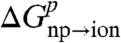and 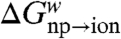were evaluated by using a standard adiabatic charging (AC) free energy perturbation (FEP) procedure (15), while changing the solute residual charges from zero to their values in the solution, 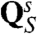, in n + 1 incremental steps. The details of this procedure are described in ref. 9. The charging of the different states of S_mini was achieved by using the EVB potential and changing the residual charges from the actual set (for the give state) to zero.

The FEP/AC calculations were performed in 30 frames of 20 ps length each, with a 1 fs time step. These calculations were then repeated 10 times with different initial conditions, and the average value of all these calculations was taken as the calculated free energy. Before performing the above simulations, we relaxed and equilibrated the simulation system by a 100 ps run. The EVB calculations were performed following the exact protocol of ref. 9, and the free energy profile (FEP/US) was evaluated in the same way as the FEP/AC calculations. The FEP/AC and FEP/US simulations were performed using the MOLARIS (17) program with an explicit simulation sphere of 18 Å, completed to 21 Å by a Langevin dipole surface and then extended to infinity by a macroscopic sphere. This system was subjected to the SCAAS (17) surface constraints and the LRF long-range treatment (17), and described by the ENZYMIX (17) force field. ESP charges were used as the EVB charges, the other EVB parameters are the same as those used in (9), and the classical part used the standard ENZYMIX parameters.