General trend for pressurized superconducting hydrogen-dense materials

Abstract

The long-standing prediction that hydrogen can assume a metallic state under high pressure, combined with arguments put forward more recently that this state might even be superconducting up to high temperatures, continues to spur tremendous research activities toward the experimental realization of metallic hydrogen. These efforts have however so far been impeded by the enormous challenges associated with the exceedingly large required pressure. Hydrogen-dense materials, of the MH₄ form (where M can be, e.g., Si, Ge, or Sn) or of the MH₃ form (with M being, e.g., Al, Sc, Y, or La), allow for the rather exciting opportunity to carry out a proxy study of metallic hydrogen and associated high-temperature superconductivity at pressures within the reach of current techniques. At least one experimental report indicates that a superconducting state might have been observed already in SiH₄, and several theoretical studies have predicted superconductivity in pressurized hydrogen-rich materials; however, no systematic dependence on the applied pressure has yet been identified so far. In the present work, we have used first-principles methods in an attempt to predict the superconducting critical temperature (T_c) as a function of pressure (P) for three metal-hydride systems of the MH₃ form, namely ScH₃, YH₃, and LaH₃. By comparing the obtained results, we are able to point out a general trend in the T_c-dependence on P. These gained insights presented here are likely to stimulate further theoretical studies of metallic phases of hydrogen-dense materials and should lead to new experimental investigations of their superconducting properties.

Hydrogen, while isoelectronic to the alkali metals, is in fact insulating under ambient conditions, which is a consequence of the comparatively high binding energy of its electron. Enormous pressure would be required to reach a hypothetical metallic phase of hydrogen (1), which remains so far elusive to the available experimental techniques. Most intriguingly, it was proposed about a decade ago that metallic hydrogen could also be superconducting up to room temperature (2), inspiring numerous studies in the direction toward realizing this goal. Hydrogen-dense materials have been recognized as a potential route to investigate such phenomena, because in these metal alloys, the combination of chemical precompression (3) from the metal host and of experimentally applied pressures could facilitate hydrogen densities in a range where metallization can occur. For example, metallization in silane (SiH₄) has been experimentally observed (4, 5) and was analyzed from a theoretical perspective by us (6).

The emergence of high-temperature superconducting phases in several pressurized hydrogen-dense materials has been predicted (7–12), but, until now, no systematic study had been carried out on how the critical temperature (T_c) of superconductivity evolves under the applied pressure. Here, we demonstrate on the examples of ScH₃, YH₃, and LaH₃, that the respective pressure dependencies of T_c exhibit remarkably similar behavior, hinting at a general rule for the MH₃ class of hydrogen-dense materials.

Many metal-hydride alloys investigated for metallization and superconductivity possess either the stoichiometry MH₃ or MH₄. The mechanism by which they are expected to conduct is markedly different: In the MH₃-type systems, M and H form a 3-D network, and both participate in the conduction process, whereas in the MH₄-type systems, M and H separate into individual layers, and conduction occurs only through the H-layers. The three isoelectronic trihydride systems that we have concentrated on in the present work, crystallize in the fcc structure when sufficiently pressurized, with the metal located at the fcc lattice sites, and two distinct groups of hydrogen atoms positioned at the octahedral (H_O) and tetrahedral interstitial sites (H_T), respectively. The M - H_T bonds form a MH₂-network that acts as a cage structure, encapsulating the H_O.

Results and Discussion

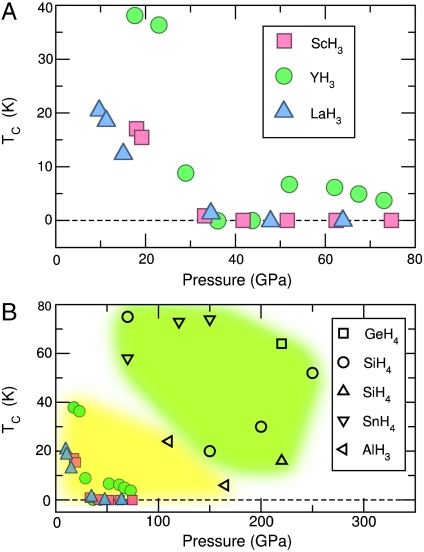
The main result of our study is presented in Fig. 1A, where we provide a summary of our calculated T_c values for ScH₃, YH₃, and LaH₃ as a function of pressure. It is important to note that several other theoretical works have predicted isolated T_c values for several tetrahydrides (7–9) and for one trihydride (AIH₃) (11), the latter having only recently been found to possess a metallic phase (13–15). Typically, these studies predicted T_c only at very few pressure values, making it difficult to discern a particular trend. For the sake of facilitating a more direct comparison, these data are put side by side in Fig. 1B with our own data. It becomes noticeable that for the MH₃-type systems investigated by us, the pressure at which superconductivity sets in (10–20 GPa) is nearly an order of magnitude lower than that for the MH₄ compounds. Around 10 GPa, fcc-LaH₃ is dynamically stabilized and possesses its highest T_c of 20 K. Slightly below 20 GPa, fcc-ScH₃ and fcc-YH₃ are stabilized and mark their highest T_c, 18 K and 40 K, respectively. This phonon-mediated superconductivity is seen to become reduced under increasing pressure, and eventually, all three MH₃ systems become normal metallic (i.e., not superconducting) around 35 GPa. In our calculations, we checked the dynamical stability of the three metal hydrides up to much higher pressure and for ScH₃ and YH₃ we did not observe any dynamical instability up to 80 GPa, but it is worth noting that LaH₃ is dynamically destabilized above 65 GPa, which implies that another high pressure phase of LaH₃ could exist in that pressure regime. We will return to a more detailed discussion of these results below. First however, let us look at some other calculated properties of the three MH₃ systems.

Fig. 1.

Calculated critical temperature of superconductivity (T_c) as a function of pressure. (A) Our predictions for ScH₃, YH₃ (12), and LaH₃. (B) The data for GeH₄ (8), SiH₄ (9, 10), SnH₄ (7), and AIH₃ (11) (Hollow Symbols), as predicted by various groups, compared with our data for the three trihydride systems (Filled Symbols). The approximate grouping of the MH₃ and MH₄ T_c - P data pairs is respectively highlighted by the yellow and green colored areas.

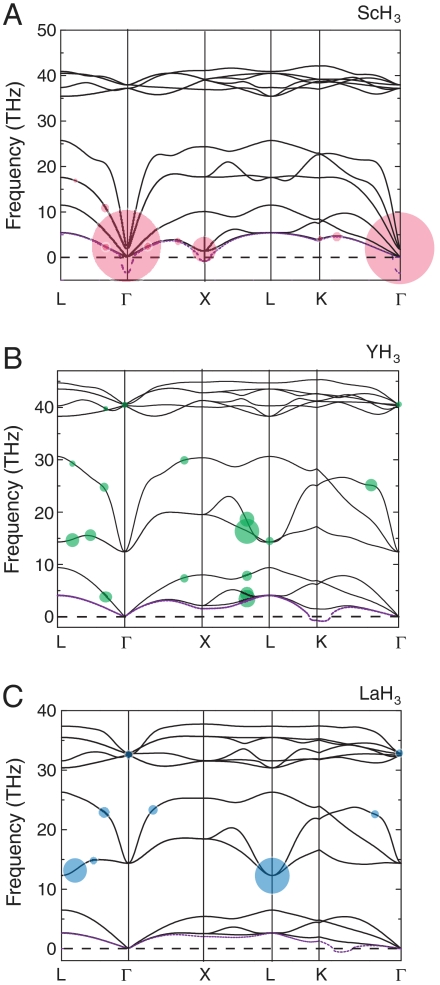
Fig. 2 shows the phonon dispersion curves that we obtained from our lattice dynamics calculations for ScH₃, YH₃, and LaH₃. For all three materials, the dispersion relation was calculated at a respective pressure that lies just slightly above the stability threshold for the corresponding metal hydride. This ensures that the phonon dispersions are captured near the onset of dynamical stability. For the case of ScH₃, dynamical stability sets in for pressures > 18 GPa. As it can be seen from the violet dashed line (drawn only for the acoustic mode below the transition pressure in the destabilized dispersion regime) in the corresponding plot of the phonon dispersion for ScH₃ in Fig. 2A, the instability is driven by the softening at both the Γ-point and the X-point. In contrast to that, one can note from Fig. 2B and C that for YH₃ and LaH₃, the instability due to softening occurs at or near the K-point. It becomes apparent that the phonon dispersion curves for YH₃ and LaH₃ are highly similar to each other, whereas they differ substantially from ScH₃. One of the main disparities lies in the much stronger dispersion at the Γ-point in ScH₃ than in YH₃ and LaH₃, which can be seen to even reach down to the acoustic phonon bands.

Fig. 2.

Phonon dispersion curves at the lowest possible stabilizing pressure plotted along high symmetry lines for (A) ScH₃ at 18 GPa, (B) YH₃ at 18 GPa, and (C) LaH₃ at 11 GPa. In all three panels, the black solid lines show the stabilized phonon dispersion relation, whereas the dashed violet line illustrates the destabilized phonon dispersion relation (shown only for the acoustic mode) at a slightly lower pressure in the dynamically unstable regime. The colored filled circles highlight points of strong electron–phonon coupling, with the radius proportional to the respective coupling strengths.

Whereas there exists no comprehensive experimental study for the low-temperature phase diagram of these trihydrides, the calculated phonon softening near the K-point in YH₃ and LaH₃ indicates equivalent structural transformations in both. For ScH₃, the situation regarding the evolution of structural changes with pressure is less clear, and it could very well be that another crystal structure may be stabilized in the pressure range below 18 GPa.

The filled circles in Fig. 2 mark the electron–phonon coupling with the radius proportional to their respective normalized strength. We see that only in the case of ScH₃, the electron–phonon coupling is very strong around the Γ-point, whereas for YH₃ and LaH₃, the strongest coupling occurs around the L-point.

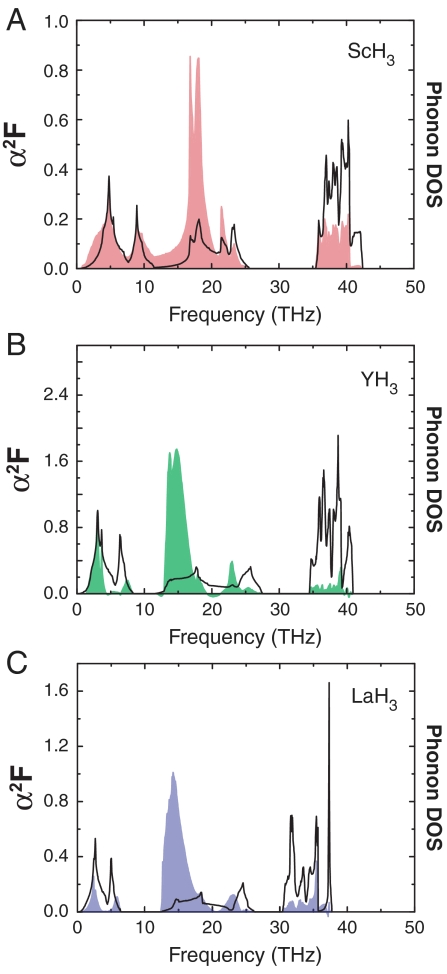
As it could already be seen above from the phonon dispersion relations (Fig. 2), the behavior of ScH₃ is markedly different from YH₃ and LaH₃. A similar conclusion can also be reached from Fig. 3, where we plot the calculated spectral functions for all three systems. We note that the acoustic band and optical band are merged together in the case of ScH₃ (Fig. 3A). Thus, Sc–Sc vibrations and Sc–H vibrations are seen to contribute equally to the spectral function. This is in contrast to the situation for YH₃ (Fig. 3B) and LaH₃ (Fig. 3C) that once again appear rather similar to each other. For a higher pressure level, the spectral function is seen to go to zero for ScH₃ and LaH₃, whereas it reappears with a finite value only for YH₃. This helps to explain the evolution of T_c with pressure as shown in Fig. 1.

Fig. 3.

The spectral function α²F is shown as colored shaded areas together with the phonon density of states (Black Curves) as a function of frequency for (A) ScH₃ at 18 GPa, (B) YH₃ at 18 GPa, and (C) LaH₃ at 11 GPa.

Let us now return to the discussion of the T_c vs. P data of Fig. 1A. Our data for the trihydrides clearly show that T_c is always highest in the vicinity of a structural transformation. This is a strong indication that the superconducting mechanism is driven by electron-phonon coupling. As we recently discussed just for the case of YH₃ (12), at the lowest possible stabilizing pressure, the electron–phonon coupling is strong for Y and Y-H_O vibrations, which couple with a high density of electronic states near the Fermi level belonging to the atomic-like H_O. With rising pressure, the coupling diminishes and the superconducting state eventually ceases to exist. Combined with the new results that we obtained for ScH₃ and LaH₃, these data suggest the rather intriguing conclusion that this general trend does in fact hold true for all MH₃ systems studied by us.

We note that for higher pressures (> 50 GPa), the superconducting phase reemerges in YH₃, but not so in ScH₃ and LaH₃. This second superconductivity region can be mostly attributed to Y-H_O vibrations coupling with the electronic states near the Fermi level (12). Because Sc, Y, and La are isoelectronic, the only essential difference between the three trihydrides is the mass of the metal. It thus appears that the mass of Y happens to fall into just the right range to generate vibrational energies of the Y-H_O mode that can give rise to this second superconducting regime. Sc and La, on the other hand, seem to have masses either too low or too high that lead to nonmatching vibrational energies, thus preventing the possibility of a reemerging second superconducting regime at higher pressure.

Conclusions

In summary, based on our first-principles calculations, we were able to identify a general trend of pressure-induced superconductivity for the metal trihydrides ScH₃, YH₃, and LaH₃, and drew comparison with other hydrogen-dense materials, including those of the MH₄ form. We found that the three transition metal hydrides studied by us possess the highest T_c at the vicinity of a structural transformation to the cubic (fcc) phase and that T_c always drops as the pressure increases, until they turn into a normal metallic state (i.e., not superconducting). A secondary superconductivity regime is seen to arise only for YH₃.

As with any other theoretical prediction, we also naturally hope that our work will not merely lead to further computational studies of related metallic hydrogen-dense materials, but actually inspire experimental measurements to test our data. Certainly, the pressure range of 10–80 GPa, for which we have predicted here superconducting states in ScH₃, YH₃, and LaH₃, is easily accessible with contemporary diamond anvil cell techniques. Rather, the challenge might actually lie in preparing metal-hydride samples of the proper stoichiometry. Even slight deviations of the perfect 1∶3 ratio of metal to hydrogen could prevent the superconducting state from emerging. Nevertheless, we hope that experimentalists will embrace this challenge to test our predictions, because we strongly believe that there is tremendous merit for the understanding of the underlying physics in metallic hydrogen-rich systems if such measurements could indeed be carried out.

Methods

Density Functional Theory and Lattice Dynamics Calculations.

Electronic structure calculations are based on the generalized gradient approximation (16) with the Perdew–Burke–Ernzerhof parametrization (17) for the exchange-correlation functional to density functional theory (18, 19). Phonon dispersion and electron–phonon calculations were performed with density functional perturbation theory (20) using the program Quantum ESPRESSO with a kinetic energy cutoff of 60 Ryd and a 24 × 24 × 24 Monkhorst–Pack mesh (21) for Brillouin zone integration. Electron–phonon coupling matrix elements were computed in the first Brillouin zone on a 8 × 8 × 8 q-mesh.

T_c Calculations.

We calculated the critical temperature for superconductivity (T_c) using the Allen–Dynes equation (22)

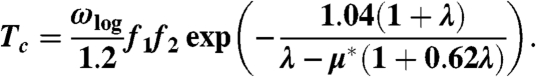[1]

In terms of the normalized weighting function that arises in Eliashberg theory,

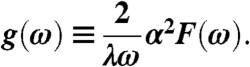[2]

The parameter λ is a dimensionless measure of the strength of α²F

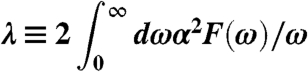[3]

and the logarithmic average frequency ω_log

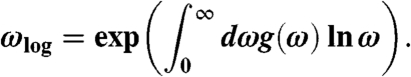[4]