Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2010 Feb 2;107(8):3645–3650. doi: 10.1073/pnas.0909910107

Translation efficiency is determined by both codon bias and folding energy

Tamir Tuller a,b,1, Yedael Y Waldman c, Martin Kupiec d, Eytan Ruppin c,e
PMCID: PMC2840511  PMID: 20133581

Abstract

Synonymous mutations do not alter the protein produced yet can have a significant effect on protein levels. The mechanisms by which this effect is achieved are controversial; although some previous studies have suggested that codon bias is the most important determinant of translation efficiency, a recent study suggested that mRNA folding at the beginning of genes is the dominant factor via its effect on translation initiation. Using the Escherichia coli and Saccharomyces cerevisiae transcriptomes, we conducted a genome-scale study aiming at dissecting the determinants of translation efficiency. There is a significant association between codon bias and translation efficiency across all endogenous genes in E. coli and S. cerevisiae but no association between folding energy and translation efficiency, demonstrating the role of codon bias as an important determinant of translation efficiency. However, folding energy does modulate the strength of association between codon bias and translation efficiency, which is maximized at very weak mRNA folding (i.e., high folding energy) levels. We find a strong correlation between the genomic profiles of ribosomal density and genomic profiles of folding energy across mRNA, suggesting that lower folding energies slow down the ribosomes and decrease translation efficiency. Accordingly, we find that selection forces act near uniformly to decrease the folding energy at the beginning of genes. In summary, these findings testify that in endogenous genes, folding energy affects translation efficiency in a global manner that is not related to the expression levels of individual genes, and thus cannot be detected by correlation with their expression levels.

Keywords: mRNA folding, protein abundance, synonymous mutations, ribosome density, translation initiation

Synonymous mutations (mutations that alter the coding DNA and RNA sequence without affecting the amino acid sequence of the protein produced) can significantly influence protein abundance via changes in translation efficiency (1 –7). Previous studies have suggested two main mechanisms by which protein abundance may be modulated by synonymous mutations: codon bias, denoting the differential usage of synonymous codons depending on the levels of their corresponding tRNAs in the cell (8), and the folding energy of the mRNA transcript, which may influence ribosome binding, and therefore translation initiation (5, 9).

Translation efficiency can be analyzed at two different levels, local and global, where the global level reflects factors that modify the translation efficiency on the transcriptome level but do not change the expression levels of single genes in a causal way (10, 11). A classic example of global mechanisms affecting translation efficiency is the correlation between mRNA levels and codon bias; the usage of efficient codons increases the elongation rate. Assuming constant flux of ribosomes, this would result in fewer ribosomes on mRNA, and thus a better allocation of ribosomes. As a result, the total rate of protein synthesis increases and cell growth is accelerated (11). Genes with higher mRNA levels potentially “consume” more ribosomes, and thus are under stronger selection for global translation efficiency. However, it should be noted that not all global effects are necessarily correlated with expression levels because they may affect translation efficiency in a uniform manner across genes irrespective of their expression levels. As we shall see, these effects play an important role in the following. In difference, factors affecting local translation efficiency are associated with a change in the levels of particular proteins, given their mRNA levels (8). The local translation efficiency of a gene is quantified by the ratio between the protein abundance and the mRNA levels of that gene. The effect of a factor on local translation efficiency can hence be traced by finding a significant correlation between this factor and the ratio between protein abundance and mRNA levels of genes or, equivalently, by finding a significant correlation between the factor and protein abundance when controlling for the mRNA level of the genes.

Recently, Kudla et al. (11) generated a library of 154 genes with different random synonymous mutations encoding the same GFP protein. Studying their influence on its protein levels in Escherichia coli, they found that the folding energy of the mRNA segment of the first ∼40 nucleotides of the transcript has a significant correlation with the GFP protein abundance, whereas codon bias, measured by the Codon Adaptation Index (12), does not exhibit a significant correlation with protein. Hence, these investigators have suggested that mRNA folding at the beginning of the sequence plays a predominant role in shaping expression levels of individual genes (i.e., local translation efficiency), whereas the previously reported correlations between codon bias and translation efficiency (13, 14) are more likely to arise as a result of selection to increase global translation efficiency across all genes by optimizing ribosome allocation.

Following this work, which focused on a single nonendogenous protein, we examine here the joint role of codon bias and folding energy in determining gene translation efficiency across a whole genome, studying their effects by considering systematically the E. coli and Saccharomyces cerevisiae transcriptomes. To this end, we employ the tRNA adaptation index (tAI) (15) (Materials and Methods,Table S1 and Table S2) as a measure of codon bias; folding energy was calculated using UNAfold software (16) (Materials and Methods).

Results

Selection Forces Act To Decrease Folding Energy at the Beginning of Genes.

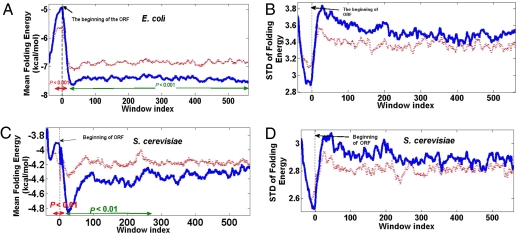
Our first step was to examine whether the mean folding energy of the first 40 nucleotides of each mRNA (of the 4,226 E. coli genes) is significantly higher than the mean folding energy of other 40-nt windows. Indeed, we find a significant difference between the first window as compared with other windows (e.g., −5 for the interval nucleotides 1–40 vs. −7.95 for nucleotides 41–80, n = 4,226; Wilcoxon test: P < 10−16; similar results were observed for other windows between 41 and 240 nucleotides; all P values were <10−16 (Fig. 1A), extending the results reported previously (11). In addition, the variance in folding energy is lower in the first window than in all other sliding windows (Fig. 1B), and further analysis of the data of Kudla et al. (11) reveals a significant positive relation between folding energy at the beginning of genes and fitness (measured by the OD of growing cultures; i.e., when there are nonfolding structures at the beginning of the GFP gene, the fitness is higher; see details in SI Note 1, Figs. S1 and S2). Similar results were obtained for the S. cerevisiae transcriptome (Fig. 1 C and D); the mean folding energy of the first 40 nucleotides is significantly higher than that of nucleotides 41–80 (−4.3580 vs. −5.1558, n = 5,869; Wilcoxon test: P < 10−16) and significantly higher than the folding energies of all other windows between 41 and 240 nucleotides (all P < 0.003). Interestingly, in both organisms, the mean folding energy of the 41–80-nt interval was lower than the mean folding energy of all other intervals, possibly to minimize the formation of potentially deleterious structures in the region of the ribosome binding site.

Fig. 1.

Fig. 1.

Open in a new tab

Endogenous genes in E. coli and S. cerevisiae. (A) Profile of folding energy (mean of sliding window of 40-nt length) across the E. coli genome (blue) vs. the profile for a randomized genome (dashed red); the window index denotes the distance (in nucleotides) from the beginning of the ORF to the beginning of the window. The figures also include the 5′-UTR near the beginning of the ORF (negative window indexes). Regions where the folding energy of the real genome is significantly higher (red) or lower (green) than the randomized genome are marked at the bottom of the figure. (B) Profile of folding energy STD across the E. coli genome (blue) vs. the profile for a randomized genome (dashed red). (C and D) Similar to A and B for the S. cerevisiae genome.

To validate further that this finding is not only a result of amino acid bias, we performed an additional test. We compared the folding profiles with those obtained for randomized versions of the genomes of the analyzed organisms, preserving the original codon bias and amino acid composition (Materials and Methods). In both E. coli and S. cerevisiae, we found that for windows more distant from the beginning of the ORF (starting from window index 18 and 10 in E. coli and S. cerevisiae, respectively; window index denotes the distance in nucleotides from the beginning of the ORF and the beginning of the window; negative window index denotes a window that begins before the beginning of the ORF), these random sequences show higher (significantly higher in most of the windows) folding energy (i.e., weaker folding) than the original profile, thus supporting previous results (17) (Fig. 1). However, when considering the windows that are close to the beginning of the ORF or even partially include the 5′-UTR near the beginning of the ORF [windows whose indexes are between −23 (i.e., they start 23 nucleotides before the first nucleotide in the ORF, and 13 in E. coli and windows whose indexes are between −13 and 6 in S. cerevisiae], these random sequences show significantly lower folding energy (i.e., stronger mRNA structures) than the original profile (Fig. 1; see SI Note 2 and Fig. S3 for a similar analysis of the terminal end of ORFs). Taken together, these results support the suggestion that the nonfolding structures at the beginning of ORFs are selected for.

There Is a Significant Association Between Codon Bias and Translation Efficiency but Not Between Folding Energy and Translation Efficiency.

Because there seems to be a selection for higher folding energy levels at the beginning of E. coli and S. cerevisiae genes, and following the findings of Kudla et al. (11) regarding the GFP gene, it is pertinent to examine how folding energy at the initial window of the transcript affects the translation efficiency across the whole transcriptome. Surprisingly, in E. coli, we do not find a significant correlation between local translation efficiency and the folding energy of the first 40 nucleotides (r = 0.019, P = 0.6971; n = 423; Fig. 2). This observation holds also when conditioning with codon bias [the partial correlation of folding energy and local translation efficiency given codon bias r(Folding Energy, Local Translation Efficiency|Codon Bias) = 0.0219; P = 0.65; n = 423] or when we examine the correlation between local translation efficiency and the folding energy of other 40-nt windows (we examined all the first 250 windows and performed false discovery rate correction for multiple hypothesis testing). Moreover, no correlation was observed when averaging all the first 250 windows in each gene. In contrast, we do find a significant correlation between local translation efficiency and codon bias [r = 0.27 and P = 1.7 × 10−8; n = 423; r(Codon Bias, Local Translation Efficiency|Folding Energy) = 0.27, P = 1.67 × 10−8; Fig. 2]. Similar results were obtained across S. cerevisiae genes [for tAI: r = 0.123 and P = 1.47 × 10−9, r(Codon Bias, Local Translation Efficiency|Folding Energy) = 0.1173 and P = 1.19 × 10−8; for folding energy: r = 0.0006 and P = 0.98, r(Folding Energy, Translation Efficiency|Codon Bias) = −0.0122 and P = 0.5553; n = 2,350]. Examining the relation with protein abundance levels directly (i.e., a measure of global translation efficiency), we again obtain similar results for both E. coli and S. cerevisiae (Fig. S4). Finally, the partial correlation between protein abundance and codon bias given the genes’ mRNA levels is significant (as opposed to the partial correlation between protein abundance and folding energy given the mRNA levels), further emphasizing the role of codon bias (rather than folding energy) in determining the local translation efficiency of endogenous genes in E. coli [r(Protein Abundance, Codon Bias|mRNA Levels) = 0.28, P = 2.74 × 10−9; r(Protein Abundance, Folding Energy|mRNA Levels) = 0.0041, P = 0.9327; n = 423] and in S. cerevisiae [r(Protein Abundance, Codon Bias|mRNA Levels) = 0.38, P = 8.54 × 10−81; r(Protein Abundance, Folding Energy|mRNA Levels) = 0.0095, P = 0.6458; n = 2,350]. These results indicate that the selection for weak mRNA folding at the beginning of genes is global and is not related to the expression level of specific genes, in contrast to codon bias.

Fig. 2.

Fig. 2.

Open in a new tab

Endogenous genes in E. coli. (A) Local translation efficiency (protein abundance/mRNA levels) vs. codon bias (tAI) for all genes. (B) Local translation efficiency vs. folding energy of the first 40 nucleotides for all E. coli genes.

Folding Energy Modulates the Relation Between Local Translation Efficiency and Codon Bias.

To elucidate the relation between codon bias, folding energy, and local translation efficiency better, we divided all E. coli genes into five equal size bins according to their folding energy and measured the correlation between codon bias or folding energy and local translation efficiency in each bin separately. As evident from Fig. 3 A and B, the codon bias and local translation efficiency correlation is significant in three of the five bins, whereas the folding energy and local translation efficiency correlation is borderline significant only in one window. Specifically, the most significant correlation between codon bias and local translation efficiency is in the bin corresponding to very high folding energy (−1.2 mean folding energy); at these levels, the mRNA folding is very weak and codon bias remains the sole determinant of local translation efficiency. Overall, the relation between codon bias and local translation efficiency as a function of folding energy is not monotonic, as can be seen from the relatively strong correlation in the second bin (−6 mean folding energy). The results for S. cerevisiae show a similar trend of more significant codon bias effects but with much lower correlation values that are more evenly distributed among the different folding energy bins (Fig. 3 C and D).

Fig. 3.

Fig. 3.

Open in a new tab

E. coli and S. cerevisiae. (A) Correlation between codon bias and local translation efficiency (y axis) for five equal-sized bins according to folding energy values (x axis). (B) Correlation between folding energy and translation efficiency (y axis) for five equal-sized bins according to folding energy values (x axis). (C and D) Same correlations (but with much lower magnitudes) are detected for S. cerevisiae.

Role of Folding Energy in Determining Global Translation Efficiency Can Be Explained by Examining the Association Between Folding Energy and Ribosomal Density.

The recent findings of Ingolia et al. (18) reporting genome-wide measurements of ribosome densities at a resolution of single nucleotides for S. cerevisiae in two conditions [growing on yeast peptone dextrose (YPD) and in starvation] may help to shed light on the findings reported in the previous section. These data have enabled us to compare the relation between the genomic profile of folding energy and the genomic profile of ribosome density. A plot of the spatial genomic ribosome density [based on the data of Ingolia et al. (18)] and the spatial mean genomic folding energy (measured in sliding windows of 40 nucleotides, as before) appears in Fig. 4. The correlation between the profile of ribosome density in YPD and the profile of folding energy is −0.63 (P = 2.4 × 10−8; n = 66); the correlation between the ribosome density in starvation and the folding energy is −0.51 (P = 1.1 × 10−5; n = 66). These inverse relations indicate that lower folding energies (which correspond to more elaborate mRNA structures) slow down the velocity of ribosomal movement on mRNA, because under the assumption of a constant flux of ribosomes, the density of ribosomes is higher for lower ribosome velocity. This result suggests that folding energy influences the rate of translation elongation (and not only translation initiation). Thus, it further demonstrates how folding energy plays a part in determining global translation efficiency.

Fig. 4.

Fig. 4.

Open in a new tab

Profile of folding energy (A) explains the profiles of ribosome density in starvation and YPD (B).

Codon Bias Better Explains Translation Efficiency and Protein Abundance Changes Across Species than Folding Energy.

Finally, we studied the influence of folding energy and codon bias on protein abundance and translation efficiency from an evolutionary standpoint. If folding energy or codon bias is a central determinant of translation efficiency (local and global) in endogenous genes, one would expect evolutionary forces to act to shape their levels according to the desired level of translation efficiency. To this end, we ranked the folding energy, codon bias, protein abundance, and local translation efficiency of endogenous genes in each of the two yeast species, S. cerevisiae and S. pombe (for which genome-wide protein abundance and mRNA data are available). Next, we measured the correlation between the change in the folding energy rank of ortholog genes between the two species and the corresponding change in their protein abundance and local translation efficiency ranks, finding it to be nonsignificant or of borderline significance (for protein abundance: r = 0.0079, P = 0.8204; for local translation efficiency: r = 0.076, P = 0.032; based on 873 gene pairs). However, a similar analysis, when performed for delineating the effects of codon bias, reveals a significant correlation between the tAI and protein abundance and local translation efficiency changes across these species (for protein abundance: r = 0.2257, P = 1.5 × 10−11; for translation efficiency: r = 0.115, P = 0.001; n = 873; see Dataset S1 for rankings of the orthologs and additional information). Thus, also from an evolutionary viewpoint, codon bias better explains protein abundance and local translation efficiency changes than folding energy. These results again show that the selection for weak mRNA folding at the beginning of genes is global and is not related to changes across evolution of the genes’ expression levels. On the other hand, codon bias does change across evolution in accordance with the changes occurring in gene expression levels.

Discussion and Conclusions

In the current study, we analyze the role of codon bias (in terms of coadaptation of the tRNA pool, the tAI measure) and folding energy in translational processes on a genome scale. We find that there is a global selection for nonfolding structures at the beginning of E. coli and S. cerevisiae genes (compared with the other parts of the coding sequences). This selection probably acts to allow faster binding of ribosomes to the transcript so as to initiate translation. In addition, in S. cerevisiae, the genomic spatial distribution of folding energy can explain the global spatial distribution of ribosomes reported (18). Thus, folding energy affects not only translation initiation but elongation speed.

When comparing between codon bias and folding energy as determinants of translation efficiency, we find the former to be more correlative with gene expression. In the case of local translation efficiency, we observe a correlation between codon bias and protein-to-mRNA level ratio, whereas a similar analysis for folding energy reveals no correlation. On a more refined level, however, when grouping the genes according to their folding energy levels, the strength of association between codon bias and local translation efficiency is dependent on the levels of folding energy. Finally, from an evolutionary standpoint, we again find that codon bias better correlates with changes across yeast species in protein abundance and protein-to-mRNA ratios than folding energy.

Our results suggest that there is selection for structures with weak folding at the beginning of genes; this selection, however, is global and not related to protein abundance or mRNA levels of genes; hence, it cannot be detected by the conventional measure of correlation with gene expression. Under the constraints of the global selection for weak folding observed at the beginning of genes in E. coli and S. cerevisiae transcriptomes, codon bias, rather than folding energy, is the rate-limiting factor in the translation process of individual genes.

These results seem to contradict those reported recently by Kudla et al. (11) regarding the fact that there is no correlation between protein abundance and codon bias in the artificial GFP gene. To explain these differences, we compared the data of Kudla et al. (11) with endogenous genes in E. coli. First, we found that the folding energy values in the artificial GFP gene are significantly lower than those of endogenous genes [mean: −8.1 vs. −5, respectively; 0.95 standard deviations (STDs) from the mean folding energy of endogenous genes; P value = 3.5 × 10−27, Wilcoxon rank sum test; n1 = 148, n2 = 4,226]. Second, we found that the partial correlation between codon bias and protein abundance given folding energy is significant [r(Local Translation Efficiency, Codon Bias|Folding Energy) = 0.17, P = 0.04; n = 148]. Finally, a detailed analysis of the correlations between codon bias, folding energy, and protein abundance across five different folding energy bins of the GFP data of Kudla et al. (11) reveals that, indeed, significant correlations between codon bias and protein abundance and nonsignificant correlations between folding energy and protein abundance can be detected in bins having folding levels in the range detected for endogenous genes (more details and further analysis are provided in SI Note 3); in addition, SI Note 4, Fig. S5 and Table S3 include specific examples from the literature in which synonymous changes (rather than folding energy) affect translation efficiency.

Thus, the differences between the findings of this global analysis and those of Kudla et al. (11) suggest that repeating the experiment of Kudla et al. (11) with a protein encoded by mRNA with higher levels of folding energy (weaker folding at the beginning) is likely to demonstrate a much stronger relation between codon bias and protein abundance than reported, as we find for both E. coli and S. cerevisiae transcriptomes. More generally, repeating the experiment of Kudla et al. (11) with different genes is likely to demonstrate different levels of correlation between translation efficiency and folding energy or codon bias. Interestingly, a recent (small-scale) study by Welch et al. (19) did not find a correlation between translation efficiency and folding energy in two endogenous E. coli genes, but in the same token, did also not find such a correlation with codon bias (though it did find a strong correlation between synonymous codon changes and protein levels). This probably indicates that there are still many open issues that need to be further studied to elucidate the determinants of translation efficiency.

Materials and Methods

Protein Abundance and mRNA Levels.

Protein abundance values and mRNA measurements of E. coli were taken from the work of Lu et al. (20); protein abundance values and mRNA levels of S. cerevisiae were taken from the work of Newman et al. (21) and Wang et al. (22), respectively; and protein abundance and mRNA values of S. pombe vs. S. cerevisiae were taken from the work of Schmidt et al. (23). We analyzed organisms whose large-scale gene expression of protein abundance and mRNA levels are available. Other recent data on protein abundance either include relatively small number of measurements (24) or do not include corresponding measurements of mRNA levels (25).

Profiles of Ribosome Density.

Profiles of ribosome density at a resolution of single nucleotides in S. cerevisiae were downloaded from the work of Ingolia et al. (18).

Coding Sequences.

Coding sequences of the fungi were taken from the work of Man and Pilpel (26), and the coding sequences of E. coli were downloaded from the National Center for Biotechnology Information (NCBI) (http://www.ncbi.nlm.nih.gov/ftp/) in August 2008.

5′-UTR Sequences.

Forty nucleotides of 5′-UTR sequences near the beginning of the ORF of S. cerevisiae and E. coli and 40 nucleotides of 3′-UTR sequences near the end of the ORF of S. cerevisiae and E. coli were taken from the NCBI (http://www.ncbi.nlm.nih.gov/ftp/) in November 2009.

Position in E. coli Operons.

Data about the order of E. coli genes in operons were downloaded from the work of Gama-Castro et al. (27). The folding profile of groups of genes that are present in the end of operons, monocistronic genes, was compared with the folding profile of genes in the beginning or middle of an operon.

tAI.

The tAI was computed following the work of dos Reis et al. (15), which defined this measure. This measure gauges the availability of tRNAs for each codon. Because codon–anticodon coupling is not unique as a result of wobble interactions, several anticodons can recognize the same codon, with different efficiency weights [see the article by dos Reis et al. (15) for all the relations between codons and anticodons].

Let ni be the number of tRNA isoacceptors recognizing codon i. Let tCGNij be the copy number of the jth tRNA that recognizes the ith codon, and let Sij be the selective constraint on the efficiency of the codon–anticodon coupling. We define the absolute adaptiveness, Wi , for each codon i as follows:

graphic file with name pnas.0909910107uneq1.jpg

From Wi, we obtain wi, which is the relative adaptiveness value of codon i by normalizing the values of Wi (dividing them by the maximal of all 61 Wis).

The final tAI of a gene, g, is the geometric mean of all its codons

graphic file with name pnas.0909910107uneq2.jpg

where ikg is the codon defined by the kth triplet on gene g and lg is the length of the gene (excluding stop codons).

For tAI calculation, tRNA copy numbers of the two fungi were downloaded from the work of Man and Pilpel (26). tRNA copy numbers of E. coli were downloaded in November 2008 from the Genomic tRNA Database (http://lowelab.ucsc.edu/GtRNAdb/) (28); tRNA copy numbers of all organisms analyzed in this study appear in Table S1.

The Sij values can be organized in a vector (S-vector) as described by dos Reis et al. (15); each component in this vector is related to one wobble nucleoside–nucleoside pairing (e.g., I:U, G:U, G:C, I:C, U:A, I:A). The wi values for all codons (except stop codons) of all organisms analyzed in this study appear in Table S2.

Ortholog Mapping.

For comparing orthologs of S. pombe and. S. cerevisiae, we used the ortholog mapping technique of Lu et al. (20).

Computing Folding Energy and Profiles of Folding Energy.

Folding energy was calculated by UNAfold software (16) for windows of 40 nucleotides along the genes’ sequences. Let Inline graphicdenote the folding energy of a window of 40-nt length, starting from the ith nucleotide of the gene.

The local profile of a gene was defined as the vector of the folding energy, FE, values assigned to the sliding windows of 40-nt length of the gene codons

graphic file with name pnas.0909910107uneq3.jpg

For a particular species, all the genes in the genome were lined up once according to their start codon and once according to their stop codon. The profiles (start and end) of mean FE were calculated as

graphic file with name pnas.0909910107uneq4.jpg

where

graphic file with name pnas.0909910107uneq5.jpg

and Genesi is the number of genes with at least i + 1 40-nt windows.

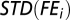Let Inline graphicdenote the STD of a vector v of real numbers; the profiles (head and tail) of the STD of FE were calculated as follows:

graphic file with name pnas.0909910107uneq6.jpg

where Inline graphic is the STD for the vector that includes the FE of the ith window of all the genes with at least I + 1 40-nt sliding windows

Randomized Profiles of Folding Energy.

To show that the profiles of folding energy (weaker folding energy at the beginning of ORF) are selected for, we compared the genomic profile of folding energy with a profile of folding energy observed for a randomization of the genome. The genome was randomized in the following way. Each codon was replaced by a random codon, according to the distribution (frequency) of codons coding the same amino acid in the genome of the organism. Thus, the randomized genomes maintained both the amino acid content of each coding sequence and the codon frequencies of the original genome. We compared the mean of 10 randomized profiles with the original profile.

Correlations and P Values.

All the correlations reported are the nonparametric Spearman correlation; P values were computed by the nonparametric Wilcoxon test. In the case of the comparison of the mean of the randomized profile energy with the original profile, we performed a Kolmogorov–Smirnov test (Wilcoxon test yields similar results) for each window index to compare the values of the folding energy of genes in the original genome with the mean folding energy of genes in the randomized genomes.

Supplementary Material

Supporting Information
supp_107_8_3645__index.html (788B, html)

Acknowledgments

We thank Prof. Plotkin for providing us with the protein abundance measurements for different synonymous mutations of the GFP protein and for helpful discussions. T.T. is a Koshland Scholar at Weizmann Institute of Science. Y.Y.W. was supported in part by a fellowship from the Edmond J. Safra Bioinformatics program at Tel-Aviv University. M.K. was supported by grants from the Israel Science Foundation and the United States–Israel Binational Fund. E.R. was supported by grants from the Israel Science Foundation and the European Union Pathogenomics consortium.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/cgi/content/full/0909910107/DCSupplemental.

References

  • 1.Zuckerkandl E, Pauling L. Molecules as documents of evolutionary history. J Theor Biol. 1965;8:357–366. doi: 10.1016/0022-5193(65)90083-4. [DOI] [PubMed] [Google Scholar]
  • 2.Ikemura T. Codon usage and tRNA content in unicellular and multicellular organisms. Mol Biol Evol. 1985;2:13–34. doi: 10.1093/oxfordjournals.molbev.a040335. [DOI] [PubMed] [Google Scholar]
  • 3.Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes. J Mol Biol. 1981;146:1–21. doi: 10.1016/0022-2836(81)90363-6. [DOI] [PubMed] [Google Scholar]
  • 4.Parmley JL, Hurst LD. How do synonymous mutations affect fitness? BioEssays. 2007;29:515–519. doi: 10.1002/bies.20592. [DOI] [PubMed] [Google Scholar]
  • 5.Nackley AG, et al. Human catechol-O-methyltransferase haplotypes modulate protein expression by altering mRNA secondary structure. Science. 2006;314:1930–1933. doi: 10.1126/science.1131262. [DOI] [PubMed] [Google Scholar]
  • 6.Boycheva S, Chkodrov G, Ivanov I. Codon pairs in the genome of Escherichia coli. Bioinformatics. 2003;19:987–998. doi: 10.1093/bioinformatics/btg082. [DOI] [PubMed] [Google Scholar]
  • 7.Coleman JR, et al. Virus attenuation by genome-scale changes in codon pair bias. Science. 2008;320:1784–1787. doi: 10.1126/science.1155761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Gustafsson C, Govindarajan S, Minshull J. Codon bias and heterologous protein expression. Trends Biotechnol. 2004;22:346–353. doi: 10.1016/j.tibtech.2004.04.006. [DOI] [PubMed] [Google Scholar]
  • 9.Hall MN, Gabay J, Débarbouillé M, Schwartz M. A role for mRNA secondary structure in the control of translation initiation. Nature. 1982;295:616–618. doi: 10.1038/295616a0. [DOI] [PubMed] [Google Scholar]
  • 10.Andersson SG, Kurland CG. Codon preferences in free-living microorganisms. Microbiol Rev. 1990;54:198–210. doi: 10.1128/mr.54.2.198-210.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kudla G, Murray AW, Tollervey D, Plotkin JB. Coding-sequence determinants of gene expression in Escherichia coli. Science. 2009;324:255–258. doi: 10.1126/science.1170160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Sharp PM, Li WH. The Codon Adaptation Index—A measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987;15:1281–1295. doi: 10.1093/nar/15.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Ghaemmaghami S, et al. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
  • 14.Tuller T, Kupiec M, Ruppin E. Determinants of protein abundance and translation efficiency in S. cerevisiae. PLoS Comput Biol. 2007;3:2510–2519. doi: 10.1371/journal.pcbi.0030248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.dos Reis M, Savva R, Wernisch L. Solving the riddle of codon usage preferences: A test for translational selection. Nucleic Acids Res. 2004;32:5036–5044. doi: 10.1093/nar/gkh834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Markham NR, Zuker M. DINAMelt web server for nucleic acid melting prediction. Nucleic Acids Res. 2005;33(Web Server issue):W577–W581. doi: 10.1093/nar/gki591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Katz L, Burge CB. Widespread selection for local RNA secondary structure in coding regions of bacterial genes. Genome Res. 2003;13:2042–2051. doi: 10.1101/gr.1257503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Ingolia NT, Ghaemmaghami S, Newman JR, Weissman JS. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science. 2009;324:218–223. doi: 10.1126/science.1168978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Welch M, et al. Design parameters to control synthetic gene expression in Escherichia coli. PLoS One. 2009;4:1–10. doi: 10.1371/journal.pone.0007002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Lu P, Vogel C, Wang R, Yao X, Marcotte EM. Absolute protein expression profiling estimates the relative contributions of transcriptional and translational regulation. Nat Biotechnol. 2007;25:117–124. doi: 10.1038/nbt1270. [DOI] [PubMed] [Google Scholar]
  • 21.Newman JR, et al. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature. 2006;441:840–846. doi: 10.1038/nature04785. [DOI] [PubMed] [Google Scholar]
  • 22.Wang Y, et al. Precision and functional specificity in mRNA decay. Proc Natl Acad Sci USA. 2002;99:5860–5865. doi: 10.1073/pnas.092538799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Schmidt MW, Houseman A, Ivanov AR, Wolf DA. Comparative proteomic and transcriptomic profiling of the fission yeast Schizosaccharomyces pombe. Mol Syst Biol. 2007;3:1–12. doi: 10.1038/msb4100117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Picotti P, Bodenmiller B, Mueller LN, Domon B, Aebersold R. Full dynamic range proteome analysis of S. cerevisiae by targeted proteomics. Cell. 2009;138:795–806. doi: 10.1016/j.cell.2009.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Malmström J, et al. Proteome-wide cellular protein concentrations of the human pathogen Leptospira interrogans. Nature. 2009;460:762–765. doi: 10.1038/nature08184. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Man O, Pilpel Y. Differential translation efficiency of orthologous genes is involved in phenotypic divergence of yeast species. Nat Genet. 2007;39:415–421. doi: 10.1038/ng1967. [DOI] [PubMed] [Google Scholar]
  • 27.Gama-Castro S, et al. RegulonDB (version 6.0): Gene regulation model of Escherichia coli K-12 beyond transcription, active (experimental) annotated promoters and Textpresso navigation. Nucleic Acids Res. 2008;36(Database issue):D120–D124. doi: 10.1093/nar/gkm994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Lowe TM, Eddy SR. tRNAscan-SE: A program for improved detection of transfer RNA genes in genomic sequence. Nucleic Acids Res. 1997;25:955–964. doi: 10.1093/nar/25.5.955. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_107_8_3645__index.html (788B, html)
0909910107_pnas.200909910SI.pdf (1.5MB, pdf)
0909910107_ds01.xls (274.5KB, xls)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES