Considerations for Thermal Injury Analysis for RF Ablation Devices

Abstract

Background:

The estimation of lesion size is an integral part of treatment planning for the clinical applications of radiofrequency ablation. However, to date, studies have not directly evaluated the impact of different computational estimation techniques for predicting lesion size. In this study, we focus on three common methods used for predicting tissue injury: (1) iso-temperature contours, (2) Cumulative equivalent minutes, (3) Arrhenius based thermal injury.

Methods:

We created a geometric model of a multi-tyne ablation electrode and simulated thermal and tissue injury profiles that result from three calculation methods after 15 minutes exposure to a constant RF voltage source. A hybrid finite element technique was used to calculate temperature and tissue injury. Time-temperature curves were used in the assessment of iso-temperature thresholds and the method of cumulative equivalent minutes. An Arrhenius-based formulation was used to calculate sequential and recursive thermal injury to tissues.

Results:

The data demonstrate that while iso-temperature and cumulative equivalent minute contours are similar in shape, these two methodologies grossly over-estimate the amount of tissue injury when compared to recursive thermal injury calculations, which have previously been shown to correlate closely with in vitro pathologic lesion volume measurement. In addition, Arrhenius calculations that do not use a recursive algorithm result in a significant underestimation of lesion volume. The data also demonstrate that lesion width and depth are inadequate means of characterizing treatment volume for multi-tine ablation devices.

Conclusions:

Recursive thermal injury remains the most physiologically relevant means of computationally estimating lesion size for hepatic tumor applications. Iso-thermal and cumulative equivalent minute approaches may produce significant errors in the estimation of lesion size.

INTRODUCTION

Radiofrequency Ablation (RFA) has become the standard of care for the treatment of primary and metastatic tumors. The goal of these treatments is to produce necrosis by raising local tissue temperatures, while limiting the collateral damage to adjacent healthy tissues. Ablation probes are positioned in the vicinity of aberrant tissues and high frequency alternating current (450-550 kHz) is delivered through an un-insulated electrode into the surrounding tissue to a dispersive ground electrode that is applied to the patient. The deposited electromagnetic energy is converted to heat which raises the temperature of the tissue and results in thermal necrosis.

While the use of radiofrequency ablation devices is well established, there is debate as to which computational method works best in estimating lesion size. Since necrosed volumes are not readily assessed under in vivo conditions, a variety of approaches are used to estimate the size of the lesion based upon temperature and exposure time. Iso-temperature contours that are derived from calculated temperature profiles, for example, have been used to estimate the tissue lesion boundary. The temperature thresholds that have been used to predict lesion size and define thermal injury are well documented in the literature [1-21]. The most common temperatures used are 43°C [22, 23], 48°C [24,25], 50°C [9,13,14], and 59°C [12]. While some of this variation is attributable to differences in tissue type (i.e. heart, liver, etc.), the literature shows broad inter-tissue variability.

Other strategies better approximate tissue injury by accounting for both exposure temperature and time [25-30]. The most common of these is the method of cumulative equivalent minutes. Several investigators have noted that for each degree increase above 43°C in temperature, there is approximately a two-fold decrease in the time required to achieve the same biological effect [28-33]. The equivalent time for each second of exposure to temperatures greater than 43°C is calculated by the isoeffect equation [33]:

$$t_{\mathit{exp}}=t_{\mathit{critical}}\ast 2^{\left(T_{\mathit{exp}}-43\right)}$$ Eq. 1

where T_exp and t_exp represent the tissue exposure temperature (in Celsius) and time, respectively. Integrating the equivalent time (t_exp) over the entire exposure time, gives the cumulative equivalent time at 43°C (CEM₄₃). When the CEM₄₃ value exceeds a critical threshold, the tissue is considered to be thermally necrosed. Thresholds for CEM₄₃ have been tabulated in the literature for several types of tissue based upon experimental observation of tissue injury at 43°C [34-37].

Another approach for approximating tissue injury utilizes the Arrhenius equation. This method establishes a first-order exponential relationship between tissue exposure temperature, exposure time, and tissue injury based upon experimental cell survivability studies. For a specified exposure temperature and time, the Arrhenius fit parameters determine the probability of cell damage. Arrhenius parameters have been determined in several body tissues, including the liver at high temperatures [31-33,38]. In the majority of studies, temperature and tissue injury profiles are calculated sequentially, meaning that Arrhenius calculations are not made until temperature calculations are completed [29-30]. A more physiologically based approach used by a few investigators has employed analytical solutions where temperature and tissue injury are calculated simultaneously [34-35]. When calculated in this manner, increased temperature causes local thermal injury which results in the localized cessation of blood flow. As a tissue lesion grows, the envelope of tissue where tissue perfusion is absent grows.

METHODS

At 450-550 kHz, the wavelength of electromagnetic energy is several orders of magnitude larger than the size of the ablation-tines. Therefore, a quasi-static approximation can be used to solve the electrical and heat conduction problems. The electric field is solved by using the generalized Laplace equation,

$$\nabla \cdot \left[\mathit{\sigma }\left(T\right)\nabla V\right]=0$$ Eq. 2

where ▽ is the gradient operator, σ(T) is the temperature-dependent conductivity (Siemens/meter), and V is the electric potential (Volts). The temperature is solved by using a modified Pennes bioheat equation [36],

$$\mathrm{\rho }C\frac{\mathit{dT}}{\mathit{dt}}=\nabla \cdot \left(k\nabla T\right)+\mathrm{\sigma }\left(T\right){\left|\nabla V\right|}^2-\mathrm{\alpha }{\mathrm{\rho }}_b{C}_b\mathrm{\omega }\left(T-T_{\mathit{amb}}\right)+Q_m$$ Eq. 3

where ρ is the density, C is the heat capacity of tissues, k is the heat conduction coefficient, ρ_b is the density of blood, C_b is the heat capacity of blood, ω is the perfusion coefficient, and α is the tissue state coefficient which varies between 0-1 depending on the normalized value of local tissue perfusion.

Iso-Temperature Contours

For this methodology, tissue damage was assumed to occur once tissue exceeded a specific temperature. Equations 2 and 3 were solved simultaneously assuming that α=1 for temperature. Iso-temperature contours at 42°C (IT42), 47°C (IT47), and 60°C (IT60) were compared.

Cumulative Equivalent Minutes (Thermal Dose)

Using the calculation method specified by Saparato and Dewey [28], the CEM₄₃ the thermal dose is defined [33] as

$${\mathit{CEM}}_{43}=\int R^{43-T\left(t\right)}\mathit{dt}$$ Eq. 4

For most biological tissues, the value of R is 0.5 for temperatures exceeding 43°C. For exposure temperatures below 43°C, the value of R is 0.25. The critical thermal dose for liver tissue is CEM₄₃ = 340 minutes [39]. Equations 2 and 3 were solved simultaneously assuming that α=1. Once the temperature was determined at each time step, the CEM₄₃ was calculated. The tissue was considered to be necrosed when the CEM₄₃ exceeded 340 minutes (C340).

Arrhenius Based Recursive Thermal Injury

Thermal injury and cell necrosis can be assessed directly by using the Arrhenius equation [34]. Although it is widely recognized that tissue injury is the result of several complex mechanisms, the progression of thermal injury can be reasonably approximated by a single process that is described by a first order kinetics expression

$$\Omega \left(t\right)=\ln \left(\frac{c\left(0\right)}{c\left(t\right)}\right)={\int }_0^t{A\cdot e}^{\frac{-\Delta E}{\mathit{RT}}}\mathit{dt}$$ Eq. 5

where Ω(t) is the degree of tissue injury, c(t) is the concentration of living cells, c(0) is the initial concentration of living cells, R is the universal gas constant, A is a "frequency" factor for the kinetic expression (s^-1), and ΔE is the activation energy for the irreversible damage reaction (J-mol^-1) [37]. The kinetic parameters account for morphologic changes in tissue relating to the thermal degradation of proteins [35]. The tissue injury integral increases as the time of exposure is increased. The critical value, Ω=1, signifies the point when thermal necrosis occurs. This corresponds to a viable cell concentration of 37%, which indicates a 63% cell necrosis volume. In its original formulation, the Arrhenius equation was associated with the percent of a volume of cells surviving a uniform exposure to temperature for a length of time. However, when the volume constitutes a single cell, the Arrhenius equation reflects the percent probability of cell survivability [34].

A known phenomenon that occurs with necrosed tissues is the transient cessation of localized blood flow during tissue heating. To adequately capture this behavior, the effective model geometry must continually change to correctly assess the level of tissue perfusion for each location in the model at each time step [40]. This significantly increases computation time and is the primary reason that simultaneous calculations have not been performed much to date. A recursive algorithm such as Gauss-Seidel, must be employed at each time step to insure that electromagnetics-thermal results change consistently with the local level of tissue perfusion. For purposes of this study, equations 2-4 were solved simultaneously using a Gauss-Seidel method. The results of the approach were previously compared directly to lesion sizes generated experimentally in liver tissue and were found to agree within 5%. In the present study, we assume that comparable levels of accuracy to experimental measurement exist. Comparisons were made assuming thermal injury thresholds of 63% (D63) and 99.99% (D100) tissue damage.

Model Geometry

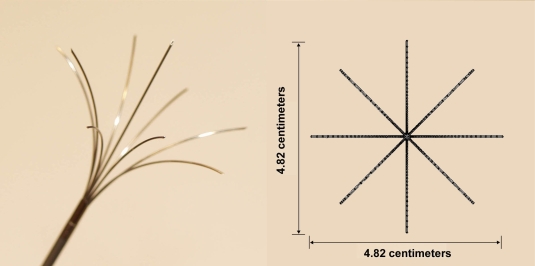
In this study, we created a model geometry similar to several commercially available multi-tine ablation electrode (Fig. 1). The model consists of 8 flexible tines that are spaced evenly at 45° angles. An additional electrode protrudes from the center of the tyne arrangement. Each tyne is 0.5 mm in diameter and 38 mm in length. When fully deployed, the 8 outer tines expand 2.41 centimeters from the center. Fig. (1) depicts the tines in a fully deployed configuration. Therapeutic treatment is achieved by applying a source voltage to the conducting tip. A conducting surface, applied to the patient skin clinically, serves as an electrical ground return.

Fig. (1).

Ablation Probe Geometry. Photograph of a multi-tine ablation electrode used for hepatic tumor ablation in a deployed orientation. The probe consists of 8 flexible tines that are spaced evenly at 45° angles. An additional electrode protrudes from the center of the tyne arrangement. Therapeutic treatment is achieved by applying a source voltage to the conducting tip. A conducting pad applied to the patient skin serves as an electrical ground return.

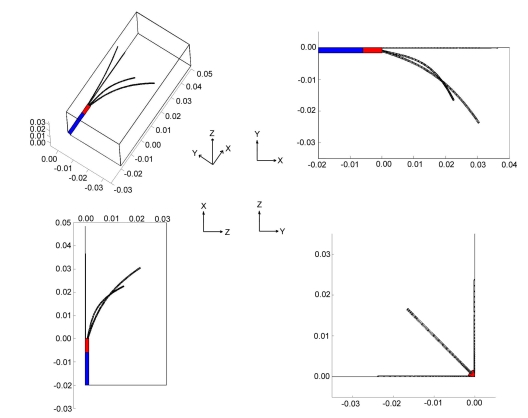
Fig. (2) depicts the model geometry used in this study. The model geometry represents a quarter of the ablation probe. Source voltage (V_o) is applied to all of the tines and the tip of the cannulating needle (red). The proximal portion of the electrode (blue) is electrically insulated with the boundary condition such that n^. (σ▽V)=0; where n is the unit vector normal to the surface, σ is the electrical conductivity, and V is the voltage at the insulating surface. The external surfaces of the model serve as a ground return (V=0).

Fig. (2).

Model Geometry. The model geometry represents a quarter of the ablation probe. Source voltage is applied to all of the tines and the tip of the canulating needle (red). The proximal portion of the electrode (blue) is electrically insulated. External surfaces of the model serve as a ground electrode and a thermal boundary condition of nominal body temperature (37°C). The entire ablation probe is assumed to be thermally insulating.

Since the thermal mass of the probe is small compared to the surrounding tissue, the entire ablation probe is assumed to be thermally insulating such that n ^. (k▽T)=0; where k is the heat conduction coefficient and T is the temperature. The initial temperature condition for hepatic tissue is assumed to be at body temperature (37°C). In addition, the outer surfaces of the model have a thermal boundary condition of T=T_amb to simulate ambient temperature of the body (37°C).

The electrical conductivity used in the model was 0.148 S/m for liver tissues at 500 kHz and 37°C, from Gabriel et al. [41]. The tissue density, 1060 kg/m³; thermal conductivity, 0.5020 W/°C-m; and tissue heat capacity, 3600 J/kg-°C were from Duck [42]. Values for the properties for blood density, 1000 kg/m³; blood heat capacity, 4180 J/kg-°C; and the perfusion coefficient 6.4 x 10^-3 (m_b³/m_t³/s) are from Tungjitkusolmun et al. [3].

The temperature-dependent behavior of liver tissue is assumed to behave in a manner similar to saline solution [34]. We used the Stogryn [43] equation for temperature-dependent behavior of sodium chloride solutions to derive the conductivity (σ) at given temperatures (T) and normalities (N):

$$\sigma \left(T,N\right)=\sigma \left(25,N\right)\left[\begin{array}{c}1.000-1.962\times {10}^{-2}\Delta +8.08\times {10}^{-5}{\Delta }^2\\ -N\Delta \left(3.020\times {10}^{-5}+3.922\times {10}^{-5}\Delta +N\left(1.721\times {10}^{-5}-6.584\times {10}^{-6}\Delta \right)\right)\end{array}\right]$$ Eq. 6

where

$\mathit{\sigma }\left(25,N\right)=N\left(\begin{array}{c}10.394-2.3776N+{0.68258N}^2\\ {-9.13538N}^3+1.0086\times {10}^{-2}{N}^4\end{array}\right)$

and Δ=25-T.

Using equation 6, which we experimentally verified to be valid from 10-90°C, we adjusted the normality to produce an equivalent electrical conductivity of liver tissues at 37°C. Sodium chloride solutions are used because liver tissue has a high water content (72-76% by volume) [42]. The electrical permittivity, which is associated with the membrane structure of cells at 500 kHz, does not contribute greatly to the overall tissue impedance and is ignored in this study.

While it is recognized that water content may also affect the ablation process, it is highly dependent on several factors such as the intensity of tissue heating, the bulk perfusion rate of body tissues, and the proximity of ablation near a vessel. In recent studies, attempts have been made to characterize the effects of tissue dessication/ vaporization by changing the electrical conductivity [39] and the heat capacity [44,45] of tissues under a variety of different physiological conditions. However, these studies do not consider the range of factors that may affect tissue re-hydration processes. As such, the majority of the studies to date have focused on ablation temperatures that do not exceed 100°C. For purposes of this study, we likewise focus on ablation phenomena below 100°C so that we avoid confounding the differences that arise between sequential and simultaneous thermal injury calculation with non-linear changes due to tissue water content.

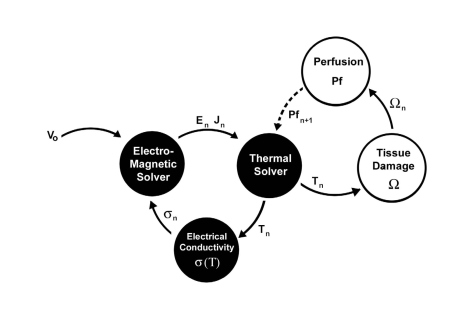
The general methodology used in our simulations is depicted in Fig. (3). The model used Femlab v2.3 (Comsol, Burlington MA, USA) and Matlab (Mathworks, Natick MA, USA) to calculate temperature and tissue injury together in a hybrid manner. A hybridized scheme was used in which both Femlab and Matlab served as co-dominant modeling algorithms for simulating tissue injury. Fig. (3) shows that the electromagnetic and thermal portions of the model were solved simultaneously in Femlab (Black) using a time dependent finite element modeling scheme, at time step n. Once convergence was reached in the electric field and temperature distribution, the results were translated into a rectilinear grid and imported into Matlab. For each time step, tissue injury and local tissue perfusion were calculated using the Arrhenius equation and time-integrated at each point in the model (White). Once the level of damage exceeded 63% cell damage, it was assumed that tissue coagulation occurred, causing a cessation in the local tissue perfusion. This level of tissue injury has been shown to correspond to the earliest onset of visible tissue coagulation in liver tissues. An updated perfusion matrix was then translated back into a finite-element grid and convergence was attained for electrical-thermal models at the subsequent time step, n+1.

Fig. (3).

Computational Technique. Diagram of data flow used in a hybrid finite element model implemented in Femlab/ Matlab to calculate temperature and tissue injury. The electromagnetic and thermal portions of the model are solved simultaneously in Femlab (black). The resulting temperature is used to calculate tissue injury in Matlab and the level of local blood perfusion (white). A tissue damage level of 63% corresponds to the onset of tissue necrosis and is associated with a cessation in local blood flow.

All simulations were performed on a dual Athlon workstation with 4 GB of RAM. The models consisted of 43,900 tetrahedral elements Femlab mode (finite element) and 31,752 rectilinear elements in the Matlab mode. Ablations were simulated using a variety of voltage source ranging from 2.5 – 30 volts for simulated ablation times of up to 30 hours, which was deemed to be steady state. The average calculation time for convergence for the simultaneous electromagnetic-thermal-tissue injury coupled model was approximately 4 hours, as compared to 1.2 hours for just the electrical-thermal model where thermal effects were calculated sequentially.

RESULTS

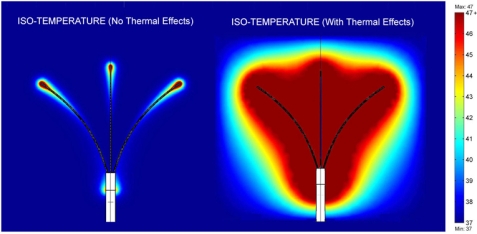
Fig. (4) shows a comparison of the temperature profiles that result from an application of a 30 volt source under steady state conditions for models that exclude (left) and include (right) recursive thermal injury calculations. The left panel was calculated using a sequential algorithm where the Arrhenius equation was solved separately from the electromagnetic-thermal equations. The right panel was calculated using a simultaneous algorithm where changes in tissue perfusion resulting from thermal injury were accounted for at each time step. Fig. (4) demonstrates that temperature patterns that include recursive thermal injury calculations far exceed the size of the profiles when recursive thermal injury is ignored.

Fig. (4).

Comparison of temperature profiles at steady state for simulations that incorporate and exclude recursive thermal effects. Figure shows a comparison of the temperature profiles that result from an application of a 30 volt source under steady state conditions (30+hours) for models that exclude and include transient changes resulting from thermal injury (recursive thermal injury). Temperature patterns that include recursive thermal injury far exceed the size of the profiles when recursive thermal injury is ignored. At each time step, the necrosed tissue volume grows, which increases the size of the area of tissue that is unperfused. This pushes the temperature envelope further away from the electrode.

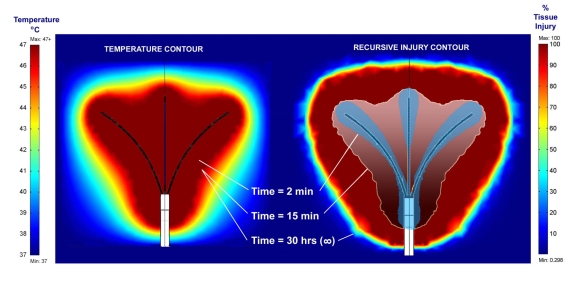
Fig. (5) shows a comparison of temperature profiles and tissue injury calculations for an application of 30 volts. The left panel shows the temperature profile after 15 minutes thermal exposure. The exposure time after 30 hours is identical to the profile at 15 minutes. The right panel shows the thermal injury profiles that corresponds to 2 min, 15 min, and 30 hour exposures to the 30 volt sources. The figure demonstrates that although temperature profiles do not vary much after 15 minutes, the corresponding tissue injury changes considerably. Under near steady state conditions, the tissue injury calculations predict a lesion size that far exceeds the size of lesions generated under more clinically relevant timeframes.

Fig. (5).

Comparison of temperature profile and tissue injury calculation. The figure shows a comparison of the temperature and its corresponding tissue injury from an application of a 30 volt source at 2 min, 15 min, and 30 hours (infinite) time calculated by considering transient changes resulting from thermal injury (recursive thermal injury). The figure demonstrates that although the temperature profile does not vary much after 15 minutes, the corresponding tissue injury changes considerably. Under steady state conditions, the tissue injury calculations predict a lesion size that far exceeds the size of lesion sizes generated under more clinically relevant timeframes.

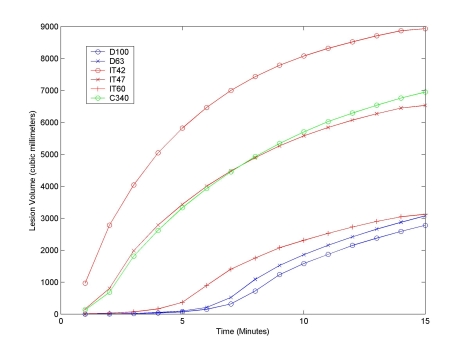
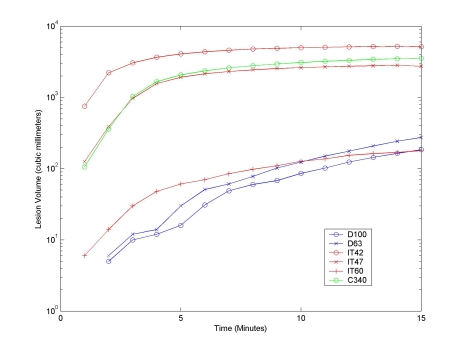
Fig. (6) shows the total volume of tissue necrosis calculated for a 15 minute unperfused ablation using a constant 22.5 volt source, using the iso-temperature contour (IT), cumulative equivalent minutes (C340), and recursive tissue injury methods (D). Fig. (7) shows a similar comparison for a 15 minute perfused ablation using a constant 22.5 volt source. The figures demonstrate that although the lesion growth rate calculated for 340 cumulative equivalent at 43°C (C340) and for an isothermal temperature of 47°C (IT47) are very similar, they grossly overestimate the rate of lesion growth. The graph shows that the isothermal temperature of 60°C (IT60) is a better approximation of modeled cell damage calculated using either the 63% (D63) or 100% (D100) recursive tissue injury contours.

Fig. (6).

Lesion Volume with No Tissue Perfusion for a 15 Minute Ablation with a Constant 22.5 Volt Source. Graph shows the total volume of tissue necroses calculated for a 15 minute ablation using a constant 22.5 volt source, using cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing (C) with no tissue perfusion. Although the lesion growth rate calculated for 340 cumulative equivalent minutes at 43°C (C340) and for an isothermal temperature of 47°C (IT47) are very similar, they grossly overestimate the rate of lesion growth. The graph shows that the IT60 curve is a better approximation of modeled cell damage calculated using either the 63% or 100% iso-damage contours methods.

Fig. (7).

Lesion Volume with 100% Normal Tissue Perfusion (6.4 x 10^-3 m_b³/m_t³/s) for a 15 Minute Ablation with a Constant 22.5 Volt Source. Graph shows the total volume of tissue necroses calculated for a 15 minute ablation using a constant 22.5 volt source, using cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing (C) with 100% normal tissue perfusion (6.4 x 10^-3 m_b³/m_t³/s). The data demonstrate that volumes calculated using traditional isothermal temperatures of 42°C and 47°C grossly overestimate the rate of lesion growth. Likewise, the volume calculated using cumulative equivalent minutes at 43°C also overestimates the rate of lesion growth. The graph shows that the IT60 curve is a better approximation of cell damage calculated using either the 63% or 100% iso-damage contours methods.

Tables 1 and 2 show the total volume of tissue necroses calculated for different source voltages for unperfused and perfused tissues ablation, respectively. The data shows that lesion volume for the unperfused simulation is grossly overestimated when calculated using isothermal temperature (97-169%) and thermal dosing (114%) descriptions. For perfused tissue, the data show more pronounced overestimations of 905-1751% for isothermal temperatures and 1165% for thermal dosing. The large discrepancy in lesion size is attributable to several mechanistic differences that are not accounted for in the isothermal and thermal dosing methods. Thus, the overestimation in lesion size is not a systematic error and a simple correction cannot be made to account for the characteristic behavior. Thermal dosing volume is calculated as the region of tissue where the cumulative equivalent minutes exceed known tissue damage at 43°C. The 63% tissue damage limit was used as a comparison to all values in the table since this approach was previously validated experimentally and found to agree within 5%. Tables 3 and 4 show the maximum lesion width and depth calculated for different source voltages for unperfused and perfused tissue ablation, respectively. The data demonstrate that lesion width and depth are relatively insensitive methods of reporting lesion growth for a multi-tyne probe geometry, since the extent of the lesion may reflect the development of several smaller lesion areas. This explains why there is virtually no transition between the absence and presence of lesions.

Table 1.

Lesion Volume with No Tissue Perfusion

Source Voltage (Volts)	D=63% (mm3)	D=100% (mm3)	IT=42°C (mm3)1	IT=47°C (mm3)1	IT=60°C (mm3)	C43=340 min (mm3)
0.0	0	0	0	0	0	0
2.5	0	0	0	0	0	0
5.0	0	0	0	0	0	0
7.5	0	0	32	0	0	0
10.0	0	0	6312	0	0	104
12.5	0	0	13790	2432	0	6704
15.0	48	32	20550	9632	32	12920
17.5	2124	744	26500	15520	1244	18530
20.0	8264	6972	31540	21060	7588	23780
22.5	13320	11950	35890	26300	12710	28560

¹The 42°C and 47°C isothermal volumes were chosen specifically because they are frequently used to establish damage thresholds in hyperthermia and radiofrequency ablation, respectively.

Values represent the total volume of tissue necroses calculated over the course of the simulated ablation using various cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing times (C₄₃) with no tissue perfusion. The data show that lesion volume is grossly overestimated when calculated using isothermal temperatures (97-169%) and thermal dosing (114%) descriptions. Thermal dosing volume is calculated as the region of tissue where the cumulative equivalent minutes exceed known tissue damage at 43°C. Since tissue damage is calculated using a first order rate law, the 63% tissue damage limit is used as a comparison to all values in the table.

Table 2.

Lesion Volume with 100% Normal Tissue Perfusion

Source Voltage (Volts)	D=63% (mm3)	D=100% (mm3)	IT=42°C (mm3)1	IT=47°C (mm3)1	IT=60°C (mm3)	C43=340 min (mm3)
0	0	0	0	0	0	0
2.5	0	0	0	0	0	0
5.0	0	0	0	0	0	0
7.5	0	0	0	0	0	0
10.0	0	0	64	0	0	0
12.5	0	0	1592	32	0	132
15.0	0	0	7404	268	0	1488
17.5	48	32	11890	2104	24	6576
20.0	236	164	16360	7144	88	10480
22.5	1136	760	21030	11420	700	14380

¹The 42°C and 47°C isothermal volumes were chosen specifically because they are frequently used to establish damage thresholds in hyperthermia and radiofrequency ablation, respectively.

Values represent the total volume of tissue necroses calculated over the course of the simulated ablation using various cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing times (C₄₃) with 100% normal tissue perfusion (6.4 x 10^-3 m_b³/m_t³/s). The data show that lesion volume is grossly overestimated when calculated using isothermal temperatures (905-1751%) and thermal dosing (1165%) descriptions. Thermal dosing volume is calculated as the region of tissue where the cumulative equivalent minutes exceed known tissue damage at 43°C. Since tissue damage is calculated using a first order rate law, the 63% tissue damage limit is used as a comparison to all values in the table.

Table 3.

Lesion Dimensions with no Tissue Perfusion

	Width (mm)						Depth (mm)
Source Voltage (Volts)	D = 63%	D = 100%	IT = 42°C1	IT = 47°C1	IT = 60°C	C43 = 340 min	D = 63%	D = 100%	IT = 42°C1	IT = 47°C1	IT = 60°C	C43 = 340 min
0	0	0	0	0	0	0	0	0	0	0	0	0
2.5	0	0	0	0	0	0	0	0	0	0	0	0
5.0	0	0	0	0	0	0	0	0	0	0	0	0
7.5	0	0	26	0	0	0	0	0	20	0	0	0
10.0	0	0	28	0	0	26	0	0	26	0	0	20
12.5	0	0	32	26	0	28	0	0	29	23	0	26
15.0	26	26	34	30	26	30	20	20	31	27	20	28
17.5	26	26	36	32	26	34	22	22	33	30	22	31
20.0	28	28	38	34	28	36	26	26	33	31	26	33
22.5	32	30	38	36	32	38	29	28	35	33	29	33

¹The 42°C and 47°C isothermal volumes were chosen specifically because they are frequently used to establish damage thresholds in hyperthermia and radiofrequency ablation, respectively.

Values represent the maximum lesion width and depth calculated over the course of the simulated ablation using various cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing times (C₄₃) with no tissue perfusion. The data show overestimations in lesion dimensions calculated using traditional isothermal temperatures of 42°C and 47°C. Similar overestimation of lesion dimensions are found with the thermal dosing method. The data demonstrate that lesion width and depth are relatively insensitive methods of reporting lesion growth for a multi-tine probe geometry, since the extent of the lesion may reflect the development of several smaller lesion areas. This explains why there is virtually no transition between the absence and presence of a lesion.

Table 4.

Lesion Volume with 100% Normal Tissue Perfusion

	Width (mm)						Depth (mm)
Source Voltage (Volts)	D=63%	D=100%	IT=42°C1	IT=47°C1	IT=60°C	C43=340 min	D=63%	D=100%	IT=42°C1	IT=47°C1	IT=60°C	C43=340 min
0	0	0	0	0	0	0	0	0	0	0	0	0
2.5	0	0	0	0	0	0	0	0	0	0	0	0
5.0	0	0	0	0	0	0	0	0	0	0	0	0
7.5	0	0	0	0	0	0	0	0	0	0	0	0
10.0	0	0	26	0	0	0	0	0	20	0	0	0
12.5	0	0	28	26	0	26	0	0	25	20	0	20
15.0	0	0	30	26	0	28	0	0	28	22	0	25
17.5	26	26	32	28	6	30	20	20	30	26	20	26
20.0	26	26	34	30	26	32	22	21	31	28	20	28
22.5	28	28	36	32	28	34	26	22	33	30	22	30

¹The 42°C and 47°C isothermal volumes were chosen specifically because they are frequently used to establish damage thresholds in hyperthermia and radiofrequency ablation, respectively.

Values represent the maximum lesion width and depth calculated over the course of the simulated ablation using various cell damage thresholds (D), isothermal temperatures (IT), and thermal dosing times (C₄₃) with 100% normal tissue perfusion(6.4 x 10^-3 m_b³/m_t³/s). The data show overestimations in lesion dimensions calculated using traditional isothermal temperatures of 42°C and 47°C. Similar overestimation of lesion dimensions are found with the thermal dosing method. The data demonstrate that lesion width and depth are relatively insensitive methods of reporting lesion growth for a multi-tyne probe geometries, since the extent of the lesion may reflect the development of several smaller lesion areas. This explains why there is virtually no transition between the absence and presence of a lesion.

DISCUSSION AND CONCLUSION

Several studies have been conducted to describe lesion growth for radiofrequency ablation devices [2,9-12,21,24,29-30,34-35]. In the majority of these cases, markers such as temperature isotherms and thermal dosing are used as the primary measure for lesion size. Only a few studies have used the Arrhenius formulation of tissue damage. Most of these, sequentially calculate the tissue damage from temperature data. Only a handful of studies calculate tissue injury simultaneously with temperature and account for physiologic change in the local perfusion due to cell necrosis [34,35,40,44]. To date, a side-by-side comparison of the effects of these calculations schemes has not been assessed. In this paper, we compare the most common methods used to computationally estimate lesions.

Our results demonstrate that sequential calculation of tissue injury following the calculation of temperature produces results that are inaccurate, regardless of whether iso-temperature contours, thermal does (cumulative equivalent minutes), or Arrhenius approaches are used. The data show that iso-temperature and thermal dosing approaches tend to overestimate lesion size. Arrhenius methods, when calculated sequentially, tend to underestimate lesion size. While it is possible to select more representative iso-temperature curves (i.e. IT60), the selection is not usually based on physiological changes but empirical observation.

The data also demonstrate that lesion width and depth are inadequate means of characterizing treatment volume for multi-tine ablation devices. Figs. (4 and 5) demonstrate that the contiguous volume seen in fully developed ablation profiles is the result of the merging of several smaller lesions that develop first at the distal end of each tine. For a multi-tine ablation device at shorter ablation times and lower source voltage, it may be difficult to assess the uniformity of lesion size by simply measuring the lesion width and depth.

DISCLAIMER

The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.