Abstract
Inverse light scattering analysis seeks to associate measured scattering properties with the most probable theoretical scattering distribution. Although Mie theory is a spherical scattering model, it has been used successfully for discerning the geometry of spheroidal scatterers. The goal of this study was an in-depth evaluation of the consequences of analyzing the structure of spheroidal geometries, which are relevant to cell and tissue studies in biology, by employing Mie-theory-based inverse light scattering analysis. As a basis for this study, the scattering from spheroidal geometries was modeled using T-matrix theory and used as test data. In a previous study, we used this technique to investigate the case of spheroidal scatterers aligned with the optical axis. In the present study, we look at a broader scope which includes the effects of aspect ratio, orientation, refractive index, and incident light polarization. Over this wide range of parameters, our results indicate that this method provides a good estimate of spheroidal structure.
1. Introduction
Inverse light scattering analysis (ILSA) is predicated on identifying the light scattering signature of an object with its shape, size, and electromagnetic properties (see Fig. 1). The signature may be identified by measurements of extinction, cross section, or the spatial light scattering distribution, among others [1]. By measuring the light scattering properties from a scatterer and comparing them to an appropriate model, its characteristics can be discerned. Since the effectiveness of ILSA in deducing the characteristics of a scatterer depends on associating a measured scattering profile with the most probable scattering geometry, finding an appropriate model is of the utmost importance. The model often used, because of its ease of implementation, is Mie theory, a spherical light scattering model that exactly predicts light scattering characteristics over a wide parameter space [2]. However, most objects in nature present geometries more complex than simple spheres, thereby creating an incompatibility between scatterer and model.
Fig. 1.
(Color online) Conceptualization of inverse light scattering analysis. Angular scattering distributions are depicted for two different spheroids as calculated by T-matrix theory. For both, the background index of refraction is 1.43 and the scattering index of refraction is 1.59. (a) Equal volume diameter, D=4.0 μm, aspect ratio ε=0.8, (b) D = 7.0 μm, ε=0.6. By measuring scattering properties and comparing to models, structural differences between two objects can be discerned.
The geometric incompatibility does not, however, obviate the use of Mie theory for ILSA of nonspherical scatterers. For example, Mie theory has been used as a model to discern the structure of spheroidal scatterers (spheroidal being defined throughout this analysis in the geometric sense) in investigations of biological cell structure and substructure [3]. In particular, the angle-resolved low-coherence-interferometry (a/LCI) technique, a platform for ILSA that uses Mie theory as a supporting model, has been used to assess the structure and structural changes in nuclear morphology of cuboidal and columnar epithelial tissues (Fig. 2) [4,5]. In these tissues, the cell nuclei present their axis of symmetry parallel to the direction of light propagation, defined here as axially symmetric, or TEM, orientation.
Fig. 2.
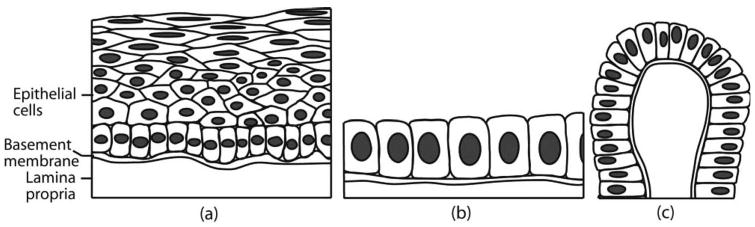
Stratified squamous (a), simple cuboidal (b), and columnar (c) epithelium. If light is incident on the surface (bottom) of tissue, stratified squamous epithelium represents axially transverse spheroids, simple cuboidal represents axially symmetric spheroids, while columnar epithelium exhibits both geometries. Figure from [6].
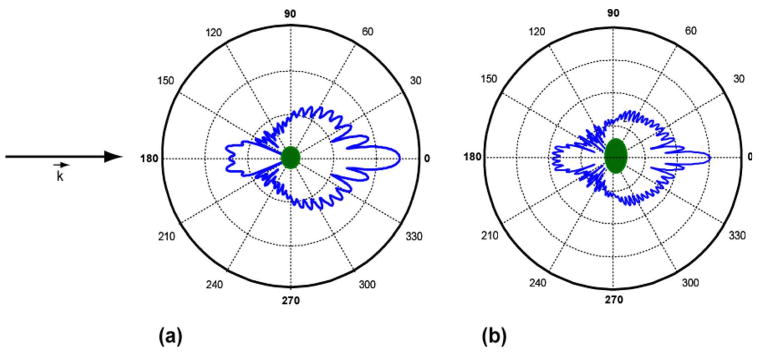
It was shown in a previous study that in the axially symmetric case, the a/LCI technique accurately measures the equatorial axis of the spheroid [6]. The a/LCI technique has also been used to experimentally determine the structure of axially transverse spheroids [3], defined as spheroids oriented with their axis of symmetry orthogonal to the direction of light propagation. In that in vitro cell experiment, spheroidal nuclear structure was evaluated for three varieties of orientations, random [Fig. 3(a)], transverse electric (TE), and transverse magnetic (TM) orientations [Fig. 3(b)]. Understanding how to evaluate the axially transverse spheroidal geometry with light scattering is also important to tissue studies; for example, cell nuclei present this geometry in squamous and columnar epithelial tissue (Fig. 2).
Fig. 3.

In vitro culture of macrophage cells in (a) random orientation and (b) oriented (orientation depends on polarization of incident light). In (b), cell nuclei are elongated in preferred direction due to nanostructural manipulation. Figure from [3] used with permission of Biophysical Journal.
The purpose of this study is to appraise the effectiveness of using Mie-theory-based ILSA (in particular the a/LCI technique) to quantify the structure of spheroidal scattering geometries. We hypothesized that the structural measurement resulting from analysis of light scattered by axially transverse spheroidal scatterers using Mie theory would yield a good estimate of one of the dimensions of the spheroid depending on orientation and incident light polarization. To test this hypothesis, we generated theoretical distributions for spheroidal scatterers using the T-matrix method [7]—which has been used with great success in light scattering studies of spheroidal geometries—to use as input test data for the a/LCI algorithm.
We expand upon our previous analysis [6] to provide a comprehensive and quantitative assessment of using the Mie-theory-based a/LCI technique to assess axially transverse spheroidal geometry and to determine the impact of scatterer orientation, aspect ratio, and incident light polarization on the accuracy of the method. To our knowledge, analysis of spheroidal scatterers using a spherical scattering model has not been explored in the backscattering geometry for large spheroidal scatterers (d≫λ). This combination is relevant to a number of light scattering applications, particularly clinical methods [8–10].
2. Background
The framework of ILSA has been developed in remote sensing [11–13] and atmospheric studies [14–16], where it has been applied successfully to large spheroidal scattering geometries. Light scattering from large spheroids (size dimensions of spheroid ≫λ) has been calculated in a number of ways [7,15,17–23]. The application of ILSA relevant to the present study is in biology and medicine, where ILSA has been used to study cell structure and substructure [24–30]. It has been used to investigate the contributions of the various cellular structures to elastic light scattering [25,29] as well as the angular dependence of light scattering from multicellular spherical aggregates [31]. The finite-difference time-domain method [32] has been used to predict light scattering from nuclei [33,34], and these models have been used to create realistic tissue phantoms [28], demonstrating a potential application for ILSA. Additionally, ILSA has been used to show that periodic variations in light scattering spectra yield the size of cell nuclei [27], to detect submicrometer structures [24], and to investigate the structure of red blood cells [35].
Another successful application of ILSA has been to detect diseased tissue states: Dysplasia in the colon, bladder, cervix and esophagus of human patients [36]; Barrett's esophagus, a metaplastic condition that can lead to dysplasia [37–39]; bladder cancer [40]; breast cancer [41]; intraoperative determination of sentinel lymph node status in the breast [42]; cervical precancers [43]; and colonic lesions [44]. It has also been used with success in diagnosing dysplasia in several animal models [4,45,46].
A specific application relevant to the present study is a/LCI, where ILSA is combined with low coherence interferometry [47] to achieve depth-resolved scattering profiles. A/LCI has been used to diagnose diseased tissue states [4,5,45], investigate cellular organization and substructure [26], and more recently to examine long range correlations due to coherent light scattering from in vitro cell arrays [30]. Additionally, a/LCI has been used to measure nuclear deformation in vitro as a response to environmental stimuli [3], which is highly relevant to the current study.
The a/LCI algorithm, which has been covered extensively elsewhere [10,48], consists of five steps: Building a database using Mie theory as the light scattering model; measuring the depth-resolved angular scattering profile of a sample; selecting from that profile an appropriate region of interest to obtain the angular scattering distribution; processing the scattering distribution to isolate the contribution to the scattering from the nucleus [30]; and comparing the processed angular scattering distribution to the database to deduce the most probable scattering geometry. The first and fifth steps are the focus of the present study.
3. Analysis
The experimental method of this study comprised the simulation of spheroidal scattering data using the T-matrix method by the means outlined in [49] and the analysis of that data using a database of light scattering distributions predicted by Mie theory. The scattering data were simulated over a range of parameters including equal-volume-sphere diameter D (which is the diameter of the sphere that will give a volume equivalent to the spheroid of interest), aspect ratio ε, and orientation [random, transverse electric (TE), or transverse magnetic (TM)] (Fig. 4). A particular scattering distribution with a chosen D,ε, and orientation was compared to a Mie theory database that was varied over a large range of nuclear diameters. The comparison yielded a best fit size z, which corresponds to the diameter of the most probable spherical scattering geometry as determined by a χ2 minimization procedure and which is described in Section 4 below.
Fig. 4.
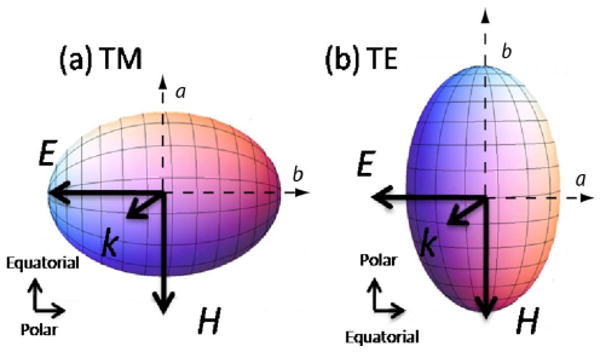
(Color online) Schematic of axially transverse spheroids in (a) TM orientation and (b) TE orientation and the dependence of orientation on incident light polarization. The axis of symmetry is the polar axis, while the axis rotated about the axis of the symmetry is the equatorial axis.
The hypothesis we sought to test was that the value of z determined by comparing the scattering distributions for the axially transverse spheroids to Mie theory corresponded to either the polar (b=Dε−2/3) or equatorial (a =Dε1/3) axis of the spheroid (Fig. 4) with an error of ±λ/nb (where nb is the refractive index of the medium surrounding the particle). The manifolds bounded by the lines a±λ/nb and b±λ/nb are called the equatorial and polar manifold, respectively. The null hypothesis was that the best fit size z is unrelated to a and b, and therefore fitting a T-matrix-generated datum to Mie theory would result in a random number in the search space. Moreover, we hypothesized that the best fit would depend on incident light polarization and orientation of the symmetry axis of the distribution of spheroids. Therefore, the effect of two linear incident light polarizations [parallel (S11) and perpendicular (S22)] was studied, as well as three different spheroidal orientations (random, TE, and TM) (see Figs. 2, 3, and 4).
This experiment was performed on two different types of scatterers to test the robustness of the results: A “cell” (which was assumed to have a background index of refraction nb=1.36 and nt=1.42, where nt is the refractive index of the scatterer) and a “phantom” (for which nb=1.43 and nt=1.59). These combinations approximate those of a cell nucleus in cytoplasm and polystyrene microspheres embedded in polydimethylsiloxane, respectively.
Spheroidal scattering distributions were generated using the following parameters: Equal volume radii of 3.0, 3.5, and 4.0 μm and aspect ratios of 0.6–1.4 in increments of 0.02. The aspect ratios and radii were chosen as a compromise between biological relevance, guided by quantitative image analysis of typical in vitro cell cultures, and computation time, which increases rapidly at extreme aspect ratios. For example, the computation time increases by an order of magnitude when computing a particle with a constant size but decreasing the aspect ratio from 0.6 to 0.5; additionally, for larger sizes (size parameter > ∼ 100), the computation may fail to converge at aspect ratios of 0.5 or less.
The scattering distributions were further parameterized (referring to Fig. 4) by incident light polarization (S22 and S11) and orientation (TE, TM, or randomly oriented, where the orientation is a superposition of 30 evenly spaced orientations between TE and TM), and were generated with a Gaussian size distribution with a 5.0% standard deviation. A size distribution is included to account for an assumed normal distribution of sizes and also the bandwidth of the low-coherence source [50]. A single combination of incident light polarization and orientation defines a configuration. The scattering angle was varied from π (backscatter) over sixty angles with an increment of 0.0103 radians for a total angular range of 0.61 radians, and the incident light wavelength was selected as 830 nm. All values were chosen by considering the parameters of the experimental a/LCI system [4,48]. Additionally, a second-order polynomial was subtracted from each scattering distribution to detrend the data, thereby isolating the oscillatory component for comparison to Mie theory. This step is an essential part of the a/LCI technique: It is included because real cell scattering data consists of contributions from small scatterers whose sizes correspond to a slowly varying trend and not an oscillatory component over the angular range in which it is investigated (for more information, see [30,48]).
In order to determine the structure of a spheroidal scatterer, each T-matrix-generated scattering distribution was treated as test data and compared to a database of Mie-theory-generated scattering distributions. Two databases of Mie-theory-generated scattering distributions were created. The first database was developed for analysis of the cell scatterers, and it was parameterized as follows: Radii ranging from 2.5 to 6.5 μm incremented in steps of 0.05 μm; refractive index combination (nb,nt) =(1.36,1.42); and a size distribution with a standard deviation of 5.0%. The second database was developed for analysis of the phantom scatterers; the only parameter distinguishing it from the cell database was that (nb,nt) =(1.43,1.59). The trend was removed from each Mie-theory-generated scattering distribution using a second-order polynomial similar to the processing of the T-matrix scattering distributions to isolate the oscillations. The scattering distribution for each spheroidal scatterer was compared to its corresponding Mie-theory database (cell or phantom scatterer) and the best fit size z was determined by using a least-squares fitting (χ2) model.
4. Statistical Methods
Spheroidal scattering data were generated for aspect ratios ε=0.6–1.4 in steps of 0.02 and compared to Mie theory to establish the best fit size z for each ε and particular combination of parameters (incident light polarization, orientation, D, and scatterer type). For each data point, a validation test was performed, and once a full data set was generated, two additional statistical tests were performed to establish the validity of the hypothesis.
A. Validation Test
A validation scheme implemented in the a/LCI technique for assessing the statistical significance of z was used. The χ2 value for the best fit was multiplied by 1.10, assigned a value χ2m=1.10χ2, and compared to all other fits χ2=χ2j in the data set. If a size determination zj existed such that |zj−z|>λ/nb and χ2j<χ2m, then the size determination for that spheroidal scatterer was deemed to be statistically invalid. In this study, 10–20% of size determinations did not meet the criterion and were not tabulated in the final results.
B. Manifold Test
For each aspect ratio, the T-matrix-generated spheroidal scattering data were fit to the Mie-theory-generated database to determine the best fit size z. As long as the validation test above was satisfied, z was tabulated in one of four categories based on the location of z in the search space: Equatorial manifold (a−λ/ns<z<a+λ/ns); polar manifold (b−λ/ns<z<b+λ/ns); both equatorial and polar manifolds; and neither equatorial nor polar manifold. Results were tabulated in the form of percentages for cells and phantoms in all configurations.
C. Squared Error Test
The second statistical test was a calculation of the squared error between z and the closest axis (a or b) for each aspect ratio (provided the validation test was passed). Subsequently, a null squared error was determined by finding the squared error between the axis and a random number in the search space. For each configuration, a distribution of squared errors and null squared errors was built; the former distribution represented the hypothesis, while the latter represented the null hypothesis. For cells and phantoms, the two distributions were compared in each configuration to determine a p value that indicates the validity of the hypothesis. Because normality of the distributions could not be assumed, all p values were calculated using a ranksum test in Matlab (The Mathworks, Natick, Massachusetts, USA). Additionally, a normalized root-mean-squared error (NRMSE) was established for each configuration from the distribution of squared errors.
5. Results
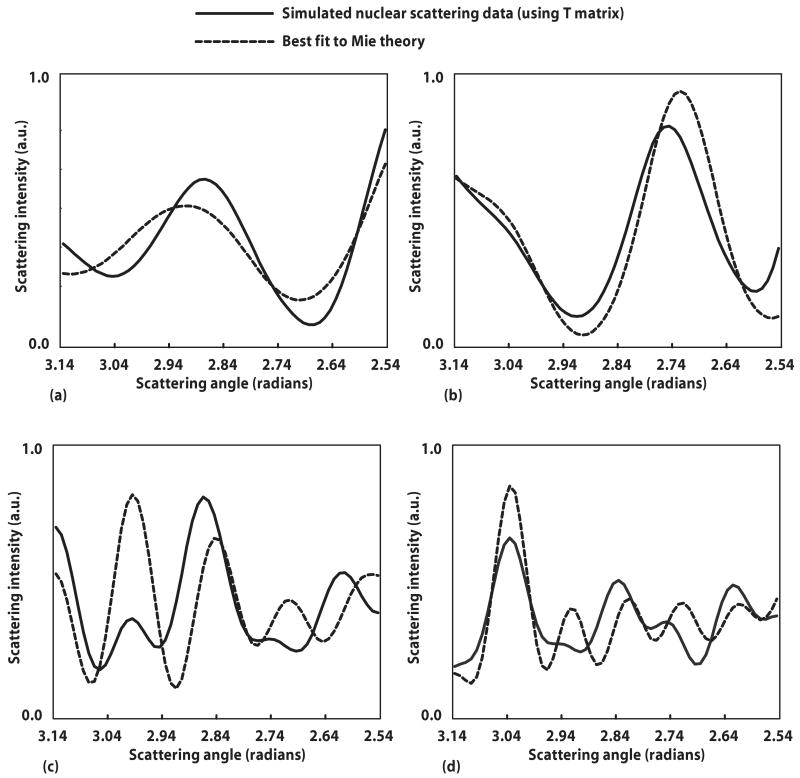
Figure 5 depicts four different T-matrix-generated spheroidal scattering distributions alongside the best fit to each obtained from Mie theory. Figures 5(a) and 5(b) represent cell scattering data for ε=0.8 and 1.2, respectively, and with D=6.0 μm. For Fig. 5(a), the best fit size z as determined by the validation test described in the Subsection 4.A is 5.4 μm, close to the equatorial axis a=5.56 μm for the corresponding aspect ratio. For Fig. 5(b), the best fit size z is 6.3 μm, close to the equatorial axis a=6.37 μm for the corresponding aspect ratio. Figures 5(c) and 5(d) represent phantom scattering data with D=7.0 μm and ε=1.2 and 0.8, respectively. For Fig. 5(c), the best fit size z is 5.9 μm, close to the polar axis a=5.81 μm for the corresponding aspect ratio. For Fig. 5(d), the best fit size z is 7.90 μm, close to the polar axis a=7.99 μm for the corresponding aspect ratio.
Fig. 5.
Spheroidal scattering data simulated by T-matrix theory alongside its best fit to Mie theory. Best fit was determined by least-squares (χ2) fitting. (a) Cell scattering with equal volume diameter D=6.0 μm and aspect ratio ε=0.8; best fit to spherical diameter of 5.4 μm (for this aspect ratio, the equatorial axis a=5.56 μm). (b) Cell scattering with D =6.0 μm and ε=1.2; best fit to spherical diameter of 6.3 μm (for this aspect ratio a=6.37 μm). (c) Phantom scattering with D=7.0 μm and ε=1.3; best fit to spherical diameter of 5.9 μm (for this aspect ratio, the polar axis b=5.81 μm). (d) Phantom scattering with D=7.0 μm and ε=0.82; best fit to spherical diameter of 7.9 μm (for this aspect ratio b=7.99 μm).
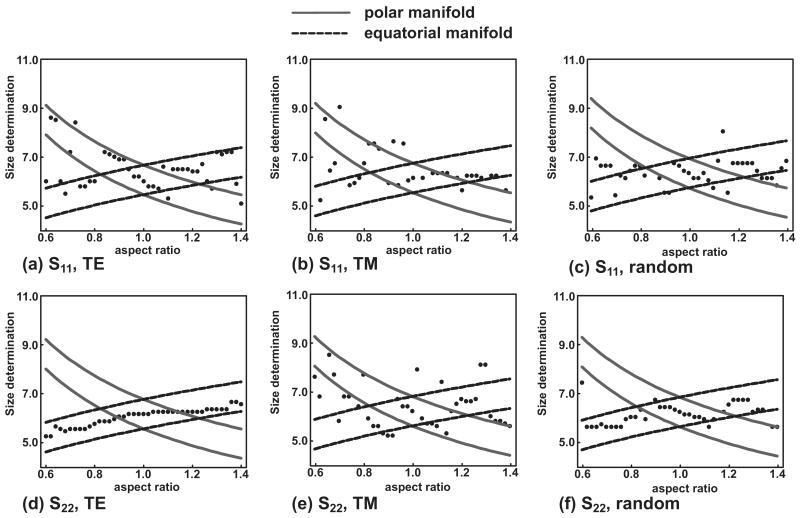
Typical comparisons across the parameter space for this study are given in Fig. 6, which is a z versus ε graph for six different configurations (defined as a single combination of incident light polarization and orientation) of a cell scatterer with equal volume diameter D=6.0 μm. To generate this figure, cell scattering data were simulated using the T-matrix approach, assuming D=6.0 μm and aspect ratios varying from 0.6–1.4. Cell scattering data corresponding to a particular aspect ratio were compared to the cell Mie-theory database, which varied in radius from 2.5 μm−6.5 μm in increments of 0.05 μm. The best fit was determined by least-squares fitting; the equatorial manifold corresponds to a±λ/ns and the polar manifold to b±λ/ns. As shown in Fig. 6, z lies largely along either the polar or equatorial manifold, but the correspondence is not consistent for all cases and configurations.
Fig. 6.
Cell scattering data were simulated with T-matrix theory in six different configurations (a)–(f), as denoted below each part, spanning three orientations (random, TE, and TM) and two linear incident light polarizations (S11 and S22). For a chosen aspect ratio, the scattering data were compared to a Mie-theory database to determine the most probable size. Each dot in the figure represents the best fit size determined by Mie theory for a given aspect ratio. The equatorial (dashed) and polar (solid) manifolds are drawn with a width of 2λ/ns.
Table 1 tabulates the results of the manifold analysis for the six different configurations and seven summary statistics. For each configuration or summary statistic given in the leftmost column, the average statistic indicated by the column heading is tabulated across all three sizes and both refractive indices. The validity of the hypothesis as determined by the manifold analysis is indicated in the final column. For all configurations and summary statistics, the hypothesis is correct at least 70% of the time.
Table 1. Results of Determining Size of Spheroidal Scatterers by Fitting Scattering Distribution to Mie Theorya.
| Equator | Polar | Both | Accuracy | ||
|---|---|---|---|---|---|
| Configuration | TE, S11 | 23 | 35 | 13 | 71 |
| TM, S11 | 46 | 17 | 18 | 79 | |
| TM, S22 | 12 | 42 | 19 | 74 | |
| TE, S22 | 67 | 1.0 | 23 | 91 | |
| random, S11 | 37 | 22 | 18 | 77 | |
| randomS22 | 52 | 13 | 24 | 89 | |
| Summary statistics | Cell | 41 | 18 | 18 | 76 |
| Phantom | 39 | 25 | 20 | 84 | |
| S11 | 36 | 24 | 14 | 75 | |
| S22 | 44 | 19 | 21 | 83 | |
| TE | 18 | 39 | 16 | 72 | |
| Random | 45 | 18 | 21 | 83 | |
| TM | 57 | 9.0 | 19 | 85 | |
Data are in percent. The average number of fits to each manifold was assessed for each configuration or summary statistic, where each manifold has a width of 2λ/nS. The final column is a measure of success for the hypothesis; namely, that the size determination is within one wavelength of one of the dimensions of the spheroidal scatterer. Data in boldface correspond to configurations or summary statistics with a normalized root mean square error (NRMSE) less than 0.1; data in lightface correspond to an NRMSE between 0.1 and 0.13. The average null NRMSE is 0.40 and always greater than 0.38. For all configurations and summary statistics, the difference between the NRMSE and the null NRMSE is statistically significant (p<10−3).
To show that our hypothesis was sufficiently conservative, the squared error test was also performed, and the hypothesis was validated for all possible cases (p<10−3 for all configurations and summary statistics). The NRMSE was between 6.0% and 13.0%; the data are in boldface if the NRMSE for a configuration or summary statistic were less than 10.0% and in lightface if the NRMSE were greater than 10.0% but less than 13.0%. The null NRMSE, on average, was 40.5% and no less than 38.0%.
We also sought to determine if the best fit size determination favored the equatorial axis, the polar axis, or either axis with equal probability. For each configuration or summary statistic given in the second column of Table 1, the manifold with the greater fitting probability was analyzed for statistical significance, and a p value was calculated based on the results of the analysis. The results are tabulated in Table 2; statistical significance is indicated by an asterisk.
Table 2. Statistical Probability That Given Configuration Favors the Equatorial Axis, the Polar Axis, or Equal Probability of Botha.
| Hypothesis | ||||
|---|---|---|---|---|
| Equator (p) |
Polar (p) |
Either (p) |
||
| Configuration | TE, S11 | 0.13 | ||
| TM, S11 | 8.7e–03* | |||
| TM, S22 | 8.9e–03* | |||
| TE, S22 | 2.2e–03* | |||
| Random, S11 | 0.017* | |||
| Random, S22 | 2.4e–03* | |||
| Summary statistics | TE | 0.012* | ||
| Random | 8.6e–05* | |||
| TM | 0.07 | |||
| S11 | 0.024* | |||
| S22 | 4.0e–03* | |||
By analyzing the squared error from each axis, a p value was established to determine if the fit to one axis were better than another in a statistically significant manner. The last column represents a case where the distance from each axis was approximately equal; therefore it could not be claimed that one axis is favored over another. Since p > 0.05, it also could not be claimed that they were equally probable.
6. Discussion
Discerning the structure of spheroidal geometries using inverse light scattering analysis is a problem of particular importance to biology, as it approximates the geometry of cell structure and substructure, including the nucleus. There are many promising methods of calculating the light scattering distributions for large spheroids; and especially as computing resources grow, those methods will garner increasing attention and study. The present study was executed to assess the utility of spherical light scattering models, supported by Mie theory (traditionally used for ILSA because of its ease of implementation), for ILSA of spheroidal geometries. This study also sought to investigate the relationship between spheroidal and spherical scattering geometries as they relate to scatterer orientation and incident polarization. The results indicate that there is a relationship between spheroidal and spherical scattering geometries, but it is not a consistent function of orientation and polarization.
In a previous study [6], it was found that using a spherical scattering model to analyze light scattered by axially oriented spheroids, such as those found in cell nuclei in cuboidal and squamous epithelium, yields a highly accurate and consistent measurement of the equatorial dimension of the spheroid. In the current study of axially transverse spheroids, there are a few observations and conclusions that can be made.
First, using S22 incident light polarization along with TE or random orientation produces fits that correspond to the equatorial manifold with remarkable consistency. This surprising result was found to be relatively independent of size and scatterer type, as seen in Table 1. Second, the results in Table 2 indicate that most configurations tested here favored fits along the equatorial manifold, but there is also the potential for measuring the polar axis using TM orientation in S22 polarization and TE orientation in S11. The former, in particular, favors a fit to the polar axis with statistical significance. Third, using our Mie-theory-based approach yields a good fit to the equatorial axis of the particles for both incident light polarizations for randomly oriented axially transverse spheroids, a geometry of interest for some epithelial tissue architectures and particularly for in vitro cell cultures. Fourth, using Mie theory to analyze scattering from spheroids yields more accurate structural information when using S22 rather than S11 incident light polarization (p=0.030).
The signal conditioning step comprising the subtraction of a second-order polynomial from both the T-matrix-generated data and the Mie-theory-generated model was essential. We did not obtain results supporting our hypothesis without this step, which indicates that there are similarities in the frequency of oscillations between spheroidal and spherical scattering data for similar objects, but there is no corresponding relationship between the general trends.
Combining the conclusions of our previous study [6] and the present study, it is clear that using Mie theory to discern the structure of spheroidal geometries can produce reasonably accurate measurements of the equator in any orientation, as long as one is careful to use the proper incident light polarization. There is a potential for measuring the polar axis of a spheroidal scattering geometry with Mie theory as well, but only in a very restricted subset of possible configurations (see Table 2). This is limiting, and ultimately points to the necessity of developing ILSA supported by an appropriate spheroidal light scattering model, such as any of the models mentioned above. However, using Mie theory for spheroidal particles may be a reasonable tradeoff in cases of geometries with large size parameters and/or extreme eccentricities, given the computational constraints of existing spheroidal light scattering models. Along these lines, the authors in [3] used Mie theory and the techniques described above to determine both the major and minor axis of macrophage cell nuclei (see Fig. 3) in a tissue engineering environment.
7. Conclusions
Analyzing backscattered light from spheroids using Mie theory yields useful information about the spheroid structure even for fairly extreme aspect ratios. For the range of aspect ratios we investigated, the size determinations were almost universally proximate to either the equatorial axis or the polar axis of the spheroid. However, the axis that was measured with the best fit size determination was not an evident function of orientation or polarization, and both dimensions contributed to the scattering in most configurations. In a scattering problem involving axially transverse spheroidal particles, an experimental configuration that acquires multiple measurements can be employed to discern the two spheroid dimensions as well as assessing outliers. Although this investigation indicates a need for improved scattering models for determining the structure of spheroids, it also shows that Mie-theory-based models can be used to estimate accurately the dimensions of spheroidal scatterers.
Acknowledgments
This work was supported by grants from the National Institutes of Health (NCI R33-CA109907) and the National Science Foundation (BES 03-48204).
References
- 1.Bohren CF, Huffman DR. Absorption and Scattering of Light by Small Particles. Wiley; 1983. pp. 1–20. [Google Scholar]
- 2.van de Hulst HC. Light Scattering by Small Particles, Structure of Matter Series. Wiley; 1957. p. 470. [Google Scholar]
- 3.Chalut KJ, Chen S, Finan JD, Giacomelli MG, Guilak F, Leong KW, Wax A. Label-free, high-throughput measurements of dynamic changes in cell nuclei using angle-resolved low coherence interferometry. Biophys J. 2008;94:4948–4956. doi: 10.1529/biophysj.107.124107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chalut KJ, Kresty LA, Pyhtila JW, Nines R, Baird M, Steele VE, Wax A. In situ assessment of intraepithelial neoplasia in hamster trachea epithelium using angle-resolved low-coherence interferometry. Cancer Epidemiol Biomarkers Prev. 2007;16:223–227. doi: 10.1158/1055-9965.EPI-06-0418. [DOI] [PubMed] [Google Scholar]
- 5.Pyhtila JW, Chalut KJ, Boyer JD, Keener J, D'Amico T, Gottfried M, Gress F, Wax A. In situ detection of nuclear atypia in Barrett's esophagus by using angle-resolved low-coherence interferometry. Gastrointest Endosc. 2007;65:487–491. doi: 10.1016/j.gie.2006.10.016. [DOI] [PubMed] [Google Scholar]
- 6.Keener JD, Chalut KJ, Pyhtila JW, Wax A. Application of Mie theory to determine the structure of spheroidal scatterers in biological materials. Opt Lett. 2007;32:1326–1328. doi: 10.1364/ol.32.001326. [DOI] [PubMed] [Google Scholar]
- 7.Mishchenko MI, Travis LD, Hovenier JW. Light Scattering by Nonspherical Particles: Theory, Measurements and Applications. Academic; 2000. pp. 147–170. [Google Scholar]
- 8.Kim YL, Liu Y, Turzhitsky VM, Wali RK, Roy HK, Backman V. Depth-resolved low-coherence enhanced backscattering. Opt Lett. 2005;30:741–743. doi: 10.1364/ol.30.000741. [DOI] [PubMed] [Google Scholar]
- 9.Mourant JR, Johnson TM, Freyer JP. Characterizing mammalian cells and cell phantoms by polarized backscattering fiber-optic measurements. Appl Opt. 2001;40:5114–5123. doi: 10.1364/ao.40.005114. [DOI] [PubMed] [Google Scholar]
- 10.Brown WJ, Pyhtila JW, Terry NG, Chalut KJ, D'Amico TA, Sporn TA, Obando JV, Wax A. Review and recent development of angle-resolved low-coherence interferometry for detection of precancerous cells in human esophageal epithelium. IEEE J Sel Top Quantum Electron. 2008;14:88–97. [Google Scholar]
- 11.Jones MR, Curry BP, Brewster MQ, Leong KH. Inversion of light-scattering measurements for particle size and optical constants: Theoretical study. Appl Opt. 1994;33:4025–4034. doi: 10.1364/AO.33.004025. [DOI] [PubMed] [Google Scholar]
- 12.Tsang L, Kong JA, Shin RT. Theory of Microwave Remote Sensing. Wiley; 1985. p. xiii.p. 613. (Wiley Series in Remote Sensing). [Google Scholar]
- 13.Wong PB, Tyler GL, Baron JE, Gurrola EM, Simpson RA. A three-wave FDTD approach to surface scattering with applications to remote sensing of geophysical surfaces. IEEE Trans Antennas Propag. 1996;44:504–514. [Google Scholar]
- 14.Shifrin KS, Tonna G. Inverse problems related to light-scattering in the atmosphere and ocean. Adv Geophys. 1993;34:175–252. [Google Scholar]
- 15.Holler S, Pan YL, Chang RK, Bottiger JR, Hill SC, Hillis DB. Two-dimensional angular optical scattering for the characterization of airborne microparticles. Opt Lett. 1998;23:1489–1491. doi: 10.1364/ol.23.001489. [DOI] [PubMed] [Google Scholar]
- 16.Pearson R, Fitzgerald RM, Polanco J. An inverse reconstruction model to retrieve aerosol size distribution from optical depth data. J Opt A, Pure Appl Opt. 2007;9:56–59. [Google Scholar]
- 17.Li X, Chen ZG, Taflove A, Backman V. Equiphase-sphere approximation for analysis of light scattering by arbitrarily shaped nonspherical particles. Appl Opt. 2004;43:4497–4505. doi: 10.1364/ao.43.004497. [DOI] [PubMed] [Google Scholar]
- 18.Marston PL. Cusp diffraction catastrophe from spheroids: Generalized rainbows and inverse scattering. Opt Lett. 1985;10:588–590. doi: 10.1364/ol.10.000588. [DOI] [PubMed] [Google Scholar]
- 19.Holler S, Surbek M, Chang RK, Pan YL. Two-dimensional angular optical scattering patterns as droplets evolve into clusters. Opt Lett. 1999;24:1185–1187. doi: 10.1364/ol.24.001185. [DOI] [PubMed] [Google Scholar]
- 20.Lock JA. Ray scattering by an arbitrarily oriented spheroid. I. Diffraction and specular reflection. Appl Opt. 1996;35:500–514. doi: 10.1364/AO.35.000500. [DOI] [PubMed] [Google Scholar]
- 21.Han YP, Wu ZS. Scattering of a spheroidal particle illuminated by a Gaussian beam. Appl Opt. 2001;40:2501–2509. doi: 10.1364/ao.40.002501. [DOI] [PubMed] [Google Scholar]
- 22.Marston PL. Catastrophe optics of spheroidal drops and generalized rainbows. J Quant Spectrosc Radiat Transf. 1999;63:341–351. [Google Scholar]
- 23.Jurgens TG, Taflove A, Umashankar K, Moore TG. Finite-difference time-domain modeling of curved surfaces. IEEE Trans Antennas Propag. 1992;40:357–366. [Google Scholar]
- 24.Backman V, Gopal V, Kalashnikov M, Badizadegan K, Gurjar R, Wax A, Georgakoudi I, Mueller M, Boone CW, Dasari RR, Feld MS. Measuring cellular structure at submicrometer scale with light scattering spectroscopy. IEEE J Sel Top Quantum Electron. 2001;7:887–893. [Google Scholar]
- 25.Mourant JR, Canpolat M, Brocker C, Esponda-Ramos O, Johnson TM, Matanock A, Stetter K, Freyer JP. Light scattering from cells: The contribution of the nucleus and the effects of proliferative status. J Biomed Opt. 2000;5:131–137. doi: 10.1117/1.429979. [DOI] [PubMed] [Google Scholar]
- 26.Wax A, Yang CH, Backman V, Badizadegan K, Boone CW, Dasari RR, Feld MS. Cellular organization and substructure measured using angle-resolved low-coherence interferometry. Biophys J. 2002;82:2256–2264. doi: 10.1016/S0006-3495(02)75571-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Perelman LT, Backman V, Wallace M, Zonios G, Manoharan R, Nusrat A, Shields S, Seiler M, Lima C, Hamano T, Itzkan I, Van Dam J, Crawford JM, Feld MS. Observation of periodic fine structure in reflectance from biological tissue: A new technique for measuring nuclear size distribution. Phys Rev Lett. 1998;80:627–630. [Google Scholar]
- 28.Sokolov K, Galvan J, Myakov A, Lacy A, Lotan R, Richards-Kortum R. Realistic three-dimensional epithelial tissue phantoms for biomedical optics. J Biomed Opt. 2002;7:148–156. doi: 10.1117/1.1427052. [DOI] [PubMed] [Google Scholar]
- 29.Mourant JR, Johnson TM, Carpenter S, Guerra A, Aida T, Freyer JP. Polarized angular dependent spectroscopy of epithelial cells and epithelial cell nuclei to determine the size scale of scattering structures. J Biomed Opt. 2002;7:378–387. doi: 10.1117/1.1483317. [DOI] [PubMed] [Google Scholar]
- 30.Pyhtila JW, Ma H, Simnick AJ, Chilkoti A, Wax A. Determining long range correlations by observing coherent light scattering from in vitro cell arrays with angle-resolved low coherence interferometry. J Biomed Opt. 2006;11:024603. doi: 10.1117/1.2209561. [DOI] [PubMed] [Google Scholar]
- 31.Mourant JR, Johnson TM, Doddi V, Freyer JP. Angular dependent light scattering from multicellular spheroids. J Biomed Opt. 2002;7:93–99. doi: 10.1117/1.1427053. [DOI] [PubMed] [Google Scholar]
- 32.Taflove A, Hagness SC. Computational Electrodynamics: The Finite-Difference Time-Domain Method. 2nd. Artech House; 2000. p. xxiii.p. 852. [Google Scholar]
- 33.Drezek R, Guillaud M, Collier T, Boiko I, Malpica A, Macaulay C, Follen M, Richards-Kortum R. Light scattering from cervical cells throughout neoplastic progression: Influence of nuclear morphology, DNA content, and chromatin texture. J Biomed Opt. 2003;8:7–16. doi: 10.1117/1.1528950. [DOI] [PubMed] [Google Scholar]
- 34.Drezek R, Dunn A, Richards-Kortum R. Light scattering from cells: Finite-difference time-domain simulations and goniometric measurements. Appl Opt. 1999;38:3651–3661. doi: 10.1364/ao.38.003651. [DOI] [PubMed] [Google Scholar]
- 35.Nilsson AMK, Alsholm P, Karlsson A, Andersson-Engels S. T-matrix computations of light scattering by red blood cells. Appl Opt. 1998;37:2735–2748. doi: 10.1364/ao.37.002735. [DOI] [PubMed] [Google Scholar]
- 36.Backman V, Wallace MB, Perelman LT, Arendt JT, Gurjar R, Muller MG, Zhang Q, Zonios G, Kline E, McGilligan JA, Shapshay S, Valdez T, Badizadegan K, Crawford JM, Fitzmaurice M, Kabani S, Levin HS, Seiler M, Dasari RR, Itzkan I, Van Dam J, Feld MS. Detection of preinvasive cancer cells. Nature (London) 2000;406:35–36. doi: 10.1038/35017638. [DOI] [PubMed] [Google Scholar]
- 37.Wallace MB, Perelman LT, Backman V, Crawford JM, Fitzmaurice M, Seiler M, Badizadegan K, Shields SJ, Itzkan I, Dasari RR, Van Dam J, Feld MS. Endoscopic detection of dysplasia in patients with Barrett's esophagus using light-scattering spectroscopy. Gastroenterology. 2000;119:677–682. doi: 10.1053/gast.2000.16511. [DOI] [PubMed] [Google Scholar]
- 38.Lovat LB, Johnson K, Novelli MR, O'Donovan M, Davies S, Selvasekar CR, Thorpe S, Bigio IJ, Bown SG. Optical biopsy using elastic scattering spectroscopy can detect high grade dysplasia and cancer in Barrett's esophagus. Gastroenterology. 2004;126:A39. doi: 10.1136/gut.2005.081497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pyhtila JW, Chalut KJ, Boyer JD, Keener J, D'Amico T, Gottfried M, Gress F, Wax A. In situ detection of nuclear atypia in Barrett's esophagus by using angle-resolved low-coherence interferometry. Gastrointest Endosc. 2007;65:487–491. doi: 10.1016/j.gie.2006.10.016. [DOI] [PubMed] [Google Scholar]
- 40.Mourant JR, Bigio IJ, Boyer J, Conn RL, Johnson T, Shimada T. Spectroscopic diagnosis of bladder cancer with elastic light scattering. Lasers Surg Med. 1995;17:350–357. doi: 10.1002/lsm.1900170403. [DOI] [PubMed] [Google Scholar]
- 41.Bigio IJ, Bown SG, Briggs G, Kelley C, Lakhani S, Pickard D, Ripley PM, Rose IG, Saunders C. Diagnosis of breast cancer using elastic-scattering spectroscopy: Preliminary clinical results. J Biomed Opt. 2000;5:221–228. doi: 10.1117/1.429990. [DOI] [PubMed] [Google Scholar]
- 42.Johnson KS, Chicken DW, Pickard DCO, Lee AC, Briggs G, Falzon M, Bigio IJ, Keshtgar MR, Bown SG. Elastic scattering spectroscopy for intraoperative determination of sentinel lymph node status in the breast. J Biomed Opt. 2004;9:1122–1128. doi: 10.1117/1.1802191. [DOI] [PubMed] [Google Scholar]
- 43.Georgakoudi I, Sheets EE, Muller MG, Backman V, Crum CP, Badizadegan K, Dasari RR, Feld MS. Trimodal spectroscopy for the detection and characterization of cervical precancers in vivo. Am J Obstet Gynecol. 2002;186:374–382. doi: 10.1067/mob.2002.121075. [DOI] [PubMed] [Google Scholar]
- 44.Dhar A, Johnson KS, Novelli MR, Bown SG, Bigio IJ, Lovat LB, Bloom SL. Elastic scattering spectroscopy for the diagnosis of colonic lesions: Initial results of a novel optical biopsy technique. Gastrointest Endosc. 2006;63:257–261. doi: 10.1016/j.gie.2005.07.026. [DOI] [PubMed] [Google Scholar]
- 45.Wax A, Pyhtila JW, Graf RN, Nines R, Boone CW, Dasari RR, Feld MS, Steele VE, Stoner GD. Prospective grading of neoplastic change in rat esophagus epithelium using angle-resolved low-coherence interferometry. J Biomed Opt. 2005;10:051604. doi: 10.1117/1.2102767. [DOI] [PubMed] [Google Scholar]
- 46.Wax A, Yang CH, Muller MG, Nines R, Boone CW, Steele VE, Stoner GD, Dasari RR, Feld MS. In situ detection of neoplastic transformation and chemopreventive effects in rat esophagus epithelium using angle-resolved low-coherence interferometry. Cancer Res. 2003;63:3556–3559. [PubMed] [Google Scholar]
- 47.Danielson BL, Boisrobert CY. Absolute optical ranging using low coherence interferometry. Appl Opt. 1991;30:2975–2979. doi: 10.1364/AO.30.002975. [DOI] [PubMed] [Google Scholar]
- 48.Pyhtila JW, Graf RN, Wax A. Determining nuclear morphology using an improved angle-resolved low coherence interferometry system. Opt Express. 2003;11:3473–3484. doi: 10.1364/oe.11.003473. [DOI] [PubMed] [Google Scholar]
- 49.Mishchenko MI. Calculation of the amplitude matrix for a nonspherical particle in a fixed orientation. Appl Opt. 2000;39:1026–1031. doi: 10.1364/ao.39.001026. [DOI] [PubMed] [Google Scholar]
- 50.Wax A. Low-coherence light-scattering calculations for polydisperse size distributions. J Opt Soc Am A. 2005;22:256–261. doi: 10.1364/josaa.22.000256. [DOI] [PubMed] [Google Scholar]