Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Mar 17.
Published in final edited form as: Appl Opt. 2009 Apr 1;48(10):D20–D25. doi: 10.1364/ao.48.000d20

Experimental verification of T-matrix-based inverse light scattering analysis for assessing structure of spheroids as models of cell nuclei

Cyrus Amoozegar 1, Michael G Giacomelli 1, Justin D Keener 1, Kevin J Chalut 1,*, Adam Wax 1
PMCID: PMC2840713  NIHMSID: NIHMS180304  PMID: 19340110

Abstract

Inverse light scattering analysis (ILSA) seeks to associate measured scattering properties with the most probable theoretical scattering distribution, making it a useful tool for assessing structure in biological materials. The accuracy of ILSA depends on the compatibility of the light scattering geometry with the light scattering model. In this study, we compare the accuracy obtained when analyzing light scattering data from spheroids using a numerical implementation of Mie theory, and the T matrix, a numerical method of solving light scattering from spheroids. Our experimental data are acquired using novel optical phantoms containing spheroidal scatterers and angle-resolved low-coherence interferometry, a depth- and angle-resolved light scattering measurement modality. The results show that Mie theory can accurately assess spheroidal structure despite the geometric incompatibility provided measurements are taken in multiple orientations of the sample relative to the incident polarization and the measured scattering angle. In comparison, analysis using the T-matrix method is highly accurate and more reliable yet requires measurements from only a single orientation.

1. Introduction

Nuclear morphology provides insight into cellular function and behavior. Nuclear size can serve as a marker for precancerous growth, with nuclear size increasing with elevating levels of precancer [1]. Nuclear deformation is also an important indicator of cellular signaling for cell mechanics studies [2,3]. However, to determine nuclear morphology in a meaningful way, accurate and reliable measurements are needed. Generally, the approach to measuring nuclear morphology involves the labeling and subsequent imaging of cell nuclei; however, this approach is slow and can arrest or interfere with cell function, making it unsuitable for sensitive studies of cellular dynamics. Light scattering techniques offer a promising alternative for measuring nuclear morphology without these drawbacks.

Angle-resolved low-coherence interferometry (a/LCI) is a light scattering approach developed to non-invasively measure nuclear morphology [4,5]. The a/LCI technique involves the measurement of the angular distribution of singly backscattered light from subsurface scatterers and the inverse light scattering analysis (ILSA) of this scattering distribution to determine the properties of the scatterers. The scattering signal is a signature of the size, shape, and optical properties of the scatterer [6]. The ILSA algorithm relies on identifying the properties of the scatterer through comparison of the scattering profile to an appropriate light scattering model. ILSA has been used to determine structure in biological materials previously [7–11]. Successful application of ILSA can yield an accurate assessment of nuclear morphology and deformations due to disease or environmental factors.

The a/LCI technique has been applied to in situ assessment of nuclear morphometry in rat esophagus epithelium [4] and in situ assessment of intraepithelial neoplasia in hamster trachea epithelium [12]. a/LCI measurements have been used to differentiate among normal tissue, low-grade dysplasia, and high-grade dysplasia in rat esophagus [13] and to assess the efficacy of chemopreventive agents [14] in the rat esophagus model of carcinogenesis. In all a/LCI studies to date, Mie theory [6] has been used as the supporting scattering model for ILSA. However, while Mie theory models light scattered by spherical objects, most cell nuclei assume nonspherical shapes, opening the question of the compatibility of this model with measurements of nuclear morphology.

Cell nuclei can be better approximated by a spheroidal geometry; light scattering from spheroidal geometries can be calculated using the T-matrix approach [15]. The T-matrix approach [15] is well characterized [16] and has been used to calculate light scattering from red blood cells [17] and other small spheroidal cell structures [18–20]. To our knowledge, the work presented here represents the first time the T-matrix approach has been experimentally validated in ILSA for large spheroidal particles (size parameter >100) in a backscattering geometry.

We have previously explored the applicability of Mie theory as a basis to analyze light scattered by spheroids. In a numerical study, we used Mie theory as the ILSA model to analyze theoretical distributions generate by T-matrix theory. This study showed that the modified Mie theory approach employed in a/LCI was able to accurately determine the average diameter of the equatorial axis of the spheroids when their axis of symmetry was oriented with the direction of incident light [20]. This geometry is relevant for nuclei in squamous and cuboidal epithelial tissues.

We have also investigated the applicability of Mie theory to analyzing spheroids in two additional orientations relevant to biological applications [21,22]. When the symmetry axis of the spheroid is oriented perpendicular to the incident light, they can either be in the transverse magnetic (TM) orientation, in which the magnetic field of the incident polarized light is transverse to the equatorial axis of the spheroids, or the transverse electric (TE) orientation, in which the electric field is transverse to the equatorial axis (see Fig. 1). In a numerical study, we used Mie theory serving as the ILSA model to analyze T-matrix-generated data of light scattered by spheroids in TE and TM orientations [21]. The results indicated that Mie theory analysis of spheroids in the TE orientation largely yields the minor axis (91% accuracy) while application in the TM orientation yields the major axis but with less reliability and accuracy (74%). In a second study, we used Mie theory to analyze light scattered by in vitro cell sample in which the cell nuclei were induced to align and elongate due to a nanopatterned substrate [22]. This study also showed that the major and minor axes of the spheroids could be determined with Mie theory but that measurements of both orientations were needed. These orientations are relevant to measurements of cell nuclei in columnar epithelium, a tissue type that is important for detecting precancerous lesions in Barrett's esophagus [23].

Fig. 1.

Fig. 1

Open in a new tab

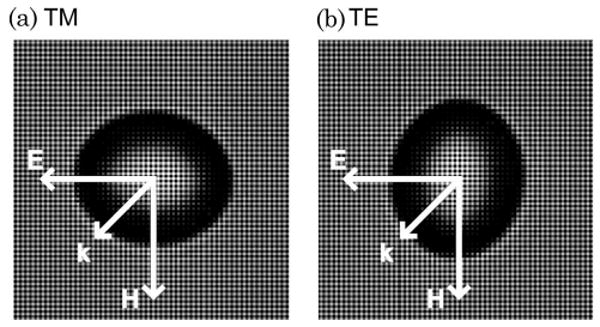
Bright-field image of a single 12 μm bead after stretching in (a) TM orientation and (b) TE orientation and diagram indicating the scattering geometries.

We present a direct comparison of the efficacy of both Mie theory- and T-matrix-based ILSA for determining the size and shape of spheroidal scatterers in TM and TE orientations. The T-matrix model is specifically developed for predicting scattering profiles from spheroidal geometries. Optical phantoms with spheroidal scatterers were developed and the size and aspect ratio of the phantoms were determined through quantitative image analysis (QIA). The angular scattering distributions of the phantoms were measured in both TE and TM orientations using a/LCI measurements and both the Mie theory and T-matrix-based ILSA models were used. The relative effectiveness of each model was determined by comparing the results from ILSA of the a/LCI measurements to the results from QIA. In the following sections we will discuss the development and measurement of the optical phantoms we used for our study as well as the results from analysis with the Mie theory and T-matrix ILSA models.

2. Materials and Methods

A. Development of Spheroidal Phantoms

Optical phantoms containing spheroidal scatterers with a refractive index mismatch similar to cells were developed through an adaptation of a preexisting technique [24]. Polystyrene microspheres (Duke Scientific, Microgenics Corporation, Fremont, California, USA) (n = 1:59) were embedded in a polydimethylsiloxane (PDMS) matrix (n = 1:44), yielding a relative refractive index difference of n = 1:10. PDMS is a silicon elastomer created by mixing a base and a curing agent (Dow Corning, Midland, Michigan, USA).

To create the phantoms, microspheres were washed to remove their surfactant coating and stirred into the PDMS base agent. The resulting solution was vortexed and sonicated in order to develop a homogeneous distribution within the PDMS. The curing agent was mixed into the homogeneous solution at a 10:1 base to curing agent ratio and was again vortexed and sonicated. The solution was poured into a chamber covered glass and placed in a vacuum chamber for 45 min in order to remove any air bubbles in the PDMS. The phantom was placed in an oven for at least 6 h at 80°–90°C in order to cure. In order to create a distinct microsphere layer in the phantom another layer of PDMS was added on top and allowed to cure the same way.

In order to create optical phantoms from polystyrene spheres the thin film of PDMS was removed and suspended by one end inside the oven. The phantom was then stretched by attaching a weight to the other end of the film and heating it for 45 min at 190°–200 °C. This temperature is above the glass transition temperature of the polystyrene such that the spheres stretch under the uniaxial tension applied to the PDMS by the attached weight. After sufficient time the sample was removed and allowed to cool at room temperature with the uniaxial force still being applied. This procedure allows creation of phantoms with spheroidal scatterers possessing aspect ratios ranging from 0.75 to 1.0, with the range limited by the mechanical properties of the PDMS. Three phantoms were prepared using this approach with different sized microspheres with NIST certified diameters of 12.0, 10.0, and 7:0 μm.

B. Quantitative Image Analysis

The scatterers in the phantoms were photographed under a bright-field microscope (40× magnification). Regions of each phantom were imaged at adequate sampling such that images of at least 30 scatterers were obtained from each. ImageJ software (NIH, Bethesda, Maryland, USA) was used to analyze the images. The lengths of the major and minor axes of 30 separate scatterers were recorded for each phantom, and this information was used to determine the average size and aspect ratio of the scatterers in each phantom.

C. a/LCI Technique

The a/LCI setup used for these studies is based on a Mach–Zehnder interferometer setup (Fig. 2) [4,22]. The light source is a Ti:sapphire laser with a low-coherence length of 30 μm centered at 830 nm. The perpendicularly polarized light is initially separated into a sample and a reference beam. In the reference arm, a retroreflector (RR) is used to take advantage of the low-coherence property of the light source to achieve optical sectioning in the sample. In the sample arm, four lenses (L2–L5) are configured such that the incident light on the sample is collimated and L4 is in the Fourier plane of the scattered light. The intensity of the scattered light is mapped out by scanning L4 transverse to the direction of incident light.

Fig. 2.

Fig. 2

Open in a new tab

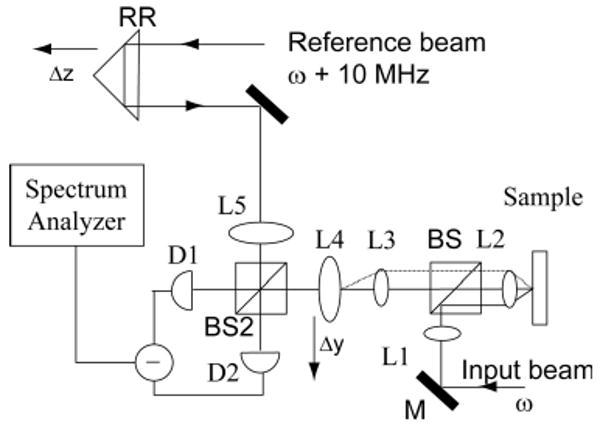
Schematic of the a/LCI system (taken from [4], with permission). Serial scanning of the retroreflector (RR) and L4 enables depth-resolved mapping of the angular light scattering distribution from the sample.

Two acousto-optic modulators are used, one in each arm, one generating a frequency shift of 100 MHz and the other a shift of 110 MHz, to establish a 10 MHz beat frequency between the reference and the sample signal when they are recombined at BS2. The combined fields are incident upon a photo-detector, and the interference signal between the two is demodulated at 10 MHz using a low noise spectrum analyzer. A map of scattering intensity as a function of both depth within the sample and scattering angle (see Fig. 3) is achieved by serially scanning both RR and L4.

Fig. 3.

Fig. 3

Open in a new tab

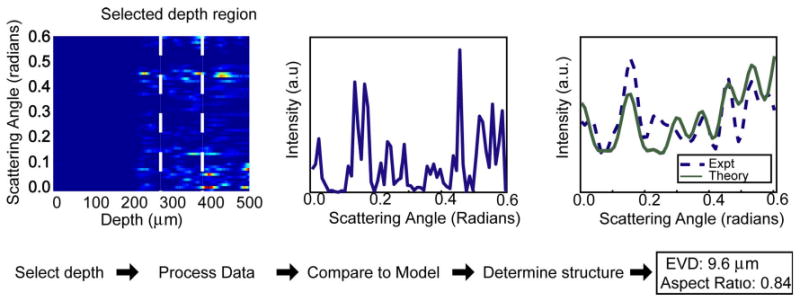
(Color online) a/LCI data processing method. The optical depth corresponding to the spheroidal scatterers is integrated to obtain scattered light intensity as a function of scattering angle. The distribution is then low-pass filtered and a second-order polynomial is subtracted to detrend the data. The processed signal is compared to a database of scattering distributions calculated by Mie theory or the T-matrix method in order to determine the properties of the scatterers. In this case, the T matrix is used, and the fitting algorithm yielded an EVD measurement of 12:3 μm with an aspect ratio of 0.86.

For each sample, the scattering profiles from the phantoms were measured in both TE and TM orientations (Fig. 1) by rotating the sample 90° between successive scans. The scattering profiles were sampled at 60 points over a range of 0:61 rad.

D. Data Analysis

Two databases were prepared for the purpose of ILSA: the first database used Mie theory as a model; the second database used the T-matrix model. The models are parameterized by the refractive index of the scatterer, the refractive index of the medium surrounding the scatterer, the distribution of scatterer sizes, the size of the scatterers (radius for Mie theory, equal volume diameter for T matrix), and, in the case of the T-matrix database, aspect ratio of the scatterers. Ranges of these values were input into the model: the input scatterer refractive indices were 1.58 and 1.59, the input background refractive indices were 1.43 and 1.44, the scatterer size distributions were 1.0% and 2.5%, and the size of the scatterers spanned from 5.0 to 16:0 μm in 0:1 μm increments. The T-matrix model was calculated in both TM and TE orientations. The input aspect ratios for the T-matrix model ranged from 0.68 to 0.98 in increments of 0.02.

The data processing and analysis procedure involves first selecting the region of interest on the previously mentioned contour plot, which consists of the scattering signal from the spheroids. The intensity at each angle is integrated over the selected depth range, and the result is the scattering profile as a function of angle (Fig. 3). A low-pass filter is then applied in order to eliminate high frequency noise [25], and then a second-order polynomial is subtracted from the scattering profile in order to detrend the data and isolate the diffractive component of the scattered light [4]. The latter step has been shown to be necessary in the application of Mie theory to spheroidal scatterers [20,22]. The subtraction of the second-order polynomial has also been applied to the T-matrix fitting as it is a vital step for biological applications. In biological studies, this step is used to separate the scattering contribution from the nucleus from the smaller scatterers in the cell, such as the mitochondria, which contribute a broad background to the scattering profiles measured here.

The experimental scattering profiles were compared to both the Mie theory and the T-matrix databases separately. A least-square-fitting algorithm is used to determine which scattering parameters yield the theoretical scattering distribution that is the best fit to the experimental scattering distribution [4].

E. Statistical Analysis

A rank-sum test (α = 0:05) was used to test for statistical significance in all analysis. A boxplot diagram was created for all the data to determine outliers. The boxplot differentiates outliers by identifying the interquartile range as the difference between the first and the third quartiles and rejecting as an outlier any data point lower or higher than 1.5 times the interquartile range.

3. Results

A. Quantitative Image Analysis

Three separate phantoms were created, each from a different size of polystyrene microsphere. Thirty spheroids from each phantom were photographed under 40× magnification (Fig. 1). The major and minor axes of these spheroids were measured, and these values were used to determine the equal volume diameter (EVD) and aspect ratio. The EVDs of phantoms 1, 2, and 3 were measured as 12:00 ± 0:07 μm, 10:01 ± 0:07 μm, and 7:03 ± 0:08 μm, respectively (mean ± SE within the 95% confidence interval), in excellent agreement with the NIST certified sizes of the microspheres used to create the spheroids. The aspect ratios of phantoms 1, 2, and 3 were found to be 0:83 ± 0:01, 0:84 ± 0:01, and 0:75 ± 0:01, respectively. These results, as well as the results of the ILSA of the experimental data, are summarized graphically in Fig. 4.

Fig. 4.

Fig. 4

Open in a new tab

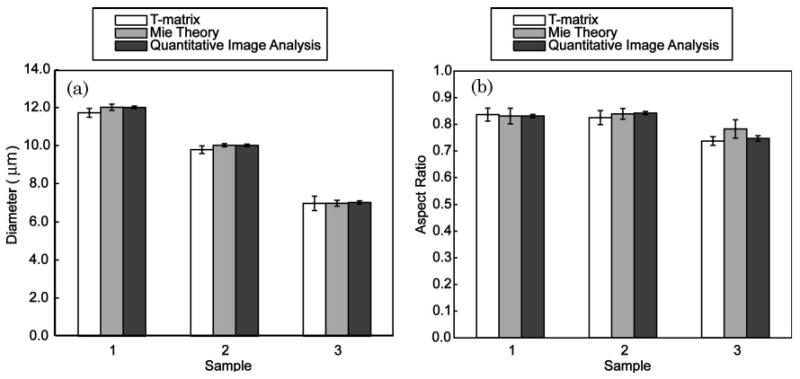
Graphic depiction of the (a) EVD and (b) aspect ratio results from T-matrix fitting, Mie theory fitting, and QIA.

B. T-Matrix Analysis

Twenty scattering profiles were measured for each phantom and compared to a database of theoretical scattering profiles determined using the T-matrix method. There was no statistically significant difference between the results for the TM and TE orientations so these were combined. Phantom 1 was found to have an EVD of 11:72 ± 0:23 μm and an aspect ratio of 0:84 ± 0:03; phantom 2 had an EVD of 9:78 ± 0:20 μm and an aspect ratio of 0:83 ± 0:02; and phantom 3 had an EVD of 6:98 ± 0:38 μm and an aspect ratio of 0:74 ± 0:02. There was no statistically significant difference between the results from fitting to the T-matrix model with the second-order polynomial subtracted and fitting to the T-matrix model without subtraction of the second-order polynomial. Because the subtraction of the second-order polynomial is needed to analyze biological materials, the results presented here include the subtraction.

C. Mie Theory

The scattering profiles of each phantom were measured in TM and TE orientations and then compared to a database of theoretical scattering profiles as determined by Mie theory. The a/LCI technique was expected to measure the minor axis when applied to TE-oriented spheroids and the major axis when applied to TM-oriented spheroids. These measurements were used to calculate the EVD and aspect ratio of the spheroids. For phantom 1, the results from the minor axis (N = 10) and major axis (N = 10) measurements indicated that the EVD was 12:01 ± 0:16 μm and the aspect ratio was 0:83 ± 0:03. For phantom 2, the results from the minor axis (N = 9) and major axis (N = 7) measurements indicated that the EVD was 10:01 ± 0:08 μm and the aspect ratio was 0:84 ± 0:02. For phantom 3, the results from the minor axis (N = 11) and major axis (N = 11) measurements indicated that the EVD was 6:99 ± 0:15 μm and the aspect ratio was 0:78 ± 0:03. The trends in fitting these experimental results were in agreement with results of a previous numerical study [21] that found that the orientation largely dictated the axis that was measured. However, these trends were not expected to be 100% accurate and for each phantom and orientation; 1–2 measurements were omitted as outliers by the boxplot analysis (a total of 8 rejected measurements).

4. Discussion

In this study, we investigated the use of T-matrix theory in an ILSA algorithm in order to determine the size and shape of spheroidal scatterers in an optical phantom. We also investigated the use of Mie theory in an ILSA algorithm to probe spheroidal scatterers, inspired by results of previous numerical studies [20,21]. It is noteworthy that, although the a/LCI technique was used for measurements in the current study, the ILSA results found here are easily generalizable to other measurement methods.

Our previous numerical study indicated that comparison of scattering data from TE-oriented spheroids to Mie theory yields the minor axis of the spheroid while that comparison for TM-oriented spheroids yields the major axis [21]. These conclusions are experimentally confirmed by the current study. Using the measurements of the minor and major axes, the average EVD and aspect ratio of the ensemble of spheroidal scatterers in the optical phantom were determined with high accuracy. One caveat concerning the use of this method is that there are some outlying data points (outliers as determined by boxplot analysis) that were discarded. Although less than 10% of the measurements were outliers, and clearly rejected by the boxplot analysis, the fact that some points did not conform to the trend emphasizes the incompatibility between the spheroidal scattering geometry and the Mie theory light scattering model, and points to a need for a more representative model.

In comparison, ILSA of a/LCI data using the T-matrix method accurately determine the aspect ratio and EVD of the optical phantoms from either TE or TM orientations and therefore offer several advantages over Mie theory for measuring nonspherical scatterers. First, comparison with the T-matrix model requires that only one orientation, TE or TM, need be scanned to measure the size and shape of the spheroidal scatterer. Comparison with the Mie theory model requires at least twice as many measurements since both TE and TM orientations are necessary to determine the major and minor axes of the spheroid. Second, in our previous numerical studies [20,21] and our study with biological cells [22], it was found that the correspondence between orientation and measured axis is not 100% for cell nuclei using Mie theory. The impact of these findings on the current study is that a small percentage of the data points measured analyzed with Mie theory produce outliers that had to be rejected via statistical analysis. This can be viewed as a lower accuracy of Mie theory analysis of spheroids compared with T-matrix-based analysis. These findings indicate that, if speed and accuracy are important experimental needs, ILSA using the T-matrix theory offers an advantage over using Mie theory based ILSA.

Mie theory does offer one significant advantage over the T-matrix method: the computation is faster, more well characterized, and easier to implement. Computation of a T-matrix database can take days to weeks to complete, and the T-matrix method becomes less accurate, or may not converge at all, for large size parameters (greater than ∼100) and extreme aspect ratios. We plan to further describe the computation of T-matrix databases and the relative advantages and disadvantages in a future publication.

In the current study, we have shown that ILSA of a/LCI measurements can determine the shape and size of spheroidal scatterers using either the T-matrix method or Mie theory. Ultimately, the choice of which theoretical framework to use depends on experimental needs. If high accuracy measurements of size and aspect ratio are desired but the experimental geometry only permits measurements to be made in a single orientation of sample and incident polarization, then the T-matrix method provides an advantage. However if measurements can be taken in multiple sample orientations, and the scatterers are nearly spherical, then the computational simplicity of Mie theory may be a suitable model for analyzing spheroids. The results presented here compare these two theoretical frameworks and show that high accuracy is obtained for the case of oriented spheroids in both cases. These results open the gateway for application of the a/LCI technique to novel experiments targeted at understanding nuclear shape deformations and more accurate assessment of nuclear morphology.

Acknowledgments

This work was supported by grants from the National Institutes of Health (NIH) (NCI R33-CA109907) and the National Science Foundation (NSF) (BES 03-48204).

References

  • 1.Boone CW, Kelloff GJ, Steele VE. Natural history of intraepithelial neoplasia in humans with implications for cancer chemoprevention strategy. Cancer Res. 1992;52:1651–1659. [PubMed] [Google Scholar]
  • 2.Guilak F. Compression-induced changes in the shape and volume of the chondrocyte nucleus. J Biomech. 1995;28:1529–1541. doi: 10.1016/0021-9290(95)00100-x. [DOI] [PubMed] [Google Scholar]
  • 3.Chen CS, Ingber DE. Tensegrity and mechanoregulation: from skeleton to cytoskeleton. Osteoarthritis Cartilage. 1999;7:81–94. doi: 10.1053/joca.1998.0164. [DOI] [PubMed] [Google Scholar]
  • 4.Pyhtila JW, Graf RN, Wax A. Determining nuclear morphology using an improved angle-resolved low coherence interferometry system. Opt Express. 2003;11:3473–3484. doi: 10.1364/oe.11.003473. [DOI] [PubMed] [Google Scholar]
  • 5.Wax A, Yang CH, Backman V, Badizadegan K, Boone CW, Dasari RR, Feld MS. Cellular organization and substructure measured using angle-resolved low-coherence interferometry. Biophys J. 2002;82:2256–2264. doi: 10.1016/S0006-3495(02)75571-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Bohren CF, Huffman DR. Absorption and Scattering of Light by Small Particles. xiv. Wiley; 1983. p. 530. [Google Scholar]
  • 7.Wilson JD, Bigelow CE, Calkins DJ, Foster TH. Light scattering from intact cells reports oxidative-stress-induced mitochondrial swelling. Biophys J. 2005;88:2929–2938. doi: 10.1529/biophysj.104.054528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Backman V, Gurjar R, Badizadegan K, Itzkan L, Dasari RR, Perelman LT, Feld MS. Polarized light scattering spectroscopy for quantitative measurement of epithelial cellular structures in situ. IEEE J Sel Top Quantum Electron. 1999;5:1019–1026. [Google Scholar]
  • 9.Bigio IJ, Bown SG, Briggs G, Kelley C, Lakhani S, Pickard D, Ripley PM, Rose IG, Saunders C. Diagnosis of breast cancer using elastic-scattering spectroscopy: preliminary clinical results. J Biomed Opt. 2000;5:221–228. doi: 10.1117/1.429990. [DOI] [PubMed] [Google Scholar]
  • 10.Sokolov K, Galvan J, Myakov A, Lacy A, Lotan R, Richards-Kortum R. Realistic three-dimensional epithelial tissue phantoms for biomedical optics. J Biomed Opt. 2002;7:148–156. doi: 10.1117/1.1427052. [DOI] [PubMed] [Google Scholar]
  • 11.Wilson JD, Giesselman BR, Mitra S, Foster TH. Lysosome-damage-induced scattering changes coincide with release of cytochrome c. Opt Lett. 2007;32:2517–2519. doi: 10.1364/ol.32.002517. [DOI] [PubMed] [Google Scholar]
  • 12.Chalut KJ, Kresty LA, Pyhtila JW, Nines R, Baird M, Steele VE, Wax A. In Situ assessment of intraepithelial neoplasia in hamster trachea epithelium using angle-resolved low-coherence interferometry. Cancer Epidemiol Biomarkers Prev. 2007;16:223–227. doi: 10.1158/1055-9965.EPI-06-0418. [DOI] [PubMed] [Google Scholar]
  • 13.Wax A, Yang CH, Muller MG, Nines R, Boon CW, Steele VE, Stoner GD, Dasari RR, Feld MS. In situ detection of neoplastic transformation and chemopreventive effects in rat esophagus epithelium using angle-resolved low-coherence interferometry. Cancer Res. 2003;63:3556–3559. [PubMed] [Google Scholar]
  • 14.Wax A, Pyhtila JW, Graf RN, Nines R, Boone CW. Prospective grading of neoplastic change in rat esophagus epithelium using angle-resolved low-coherence interferometry. J Biomed Opt. 2005;10:051604. doi: 10.1117/1.2102767. [DOI] [PubMed] [Google Scholar]
  • 15.Mishchenko MI, Travis LD, Hovenier JW. Light Scattering by Nonspherical Particles: Theory, Measurements and Applications. Academic; 2000. [Google Scholar]
  • 16.Voshchinnikov NV, Il'in VB, Henning T, Michel B, Farafonov VG. Extinction and polarization of radiation by absorbing spheroids: shape/size effects and benchmark results. J Quant Spectrosc Radiat Transfer. 2000;65:877–893. [Google Scholar]
  • 17.Nilsson AMK, Alsholm P, Karlsson A, Andersson-Engels S. T-matrix computations of light scattering by red blood cells. Appl Opt. 1998;37:2735–2748. doi: 10.1364/ao.37.002735. [DOI] [PubMed] [Google Scholar]
  • 18.Mourant JR, Johnson TM, Carpenter S, Guerra A, Aida T, Freyer JP. Polarized angular dependent spectroscopy of epithelial cells and epithelial cell nuclei to determine the size scale of scattering structures. J Biomed Opt. 2002;7:378–387. doi: 10.1117/1.1483317. [DOI] [PubMed] [Google Scholar]
  • 19.Duncan DD, Thomas ME. Particle shape as revealed by spectral depolarization. Appl Opt. 2007;46:6185–6191. doi: 10.1364/ao.46.006185. [DOI] [PubMed] [Google Scholar]
  • 20.Keener JD, Chalut KJ, Pyhtila JW, Wax A. Application of Mie theory to determine the structure of spheroidal scatterers in biological materials. Opt Lett. 2007;32:1326–1328. doi: 10.1364/ol.32.001326. [DOI] [PubMed] [Google Scholar]
  • 21.Chalut KJ, Giacomelli M, Wax A. Application of Mie theory to assess structure of spheroidal scattering in backscattering geometries. J Opt Soc Am A. 2008;25:1866–1874. doi: 10.1364/josaa.25.001866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Chalut KJ, Chen S, Finan JD, Giacomelli MG, Guilak F, Leong KW, Wax A. Label-free, high-throughput measurements of dynamic changes in cell nuclei using angle-resolved low coherence interferometry. Biophys J. 2008;94:4948–4956. doi: 10.1529/biophysj.107.124107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Pyhtila JW, Chalut KJ, Boyer JD, Keener J, D'Amico T, Gottfried M, Gress F, Wax A. In situ detection of nuclear atypia in Barrett's esophagus using angle-resolved low coherence interferometry. Gastrointest Endosc. 2007;65:487–491. doi: 10.1016/j.gie.2006.10.016. [DOI] [PubMed] [Google Scholar]
  • 24.Keville KM, Franses EI, Caruthers JM. Preparation and characterization of monodisperse polymer microspheroids. J Colloid Interface Sci. 1991;144:103–126. [Google Scholar]
  • 25.Pyhtila JW, M H, Simnick AJ, Chilkoti A, Wax A. Analysis of long range correlations due to coherent light scattering from in-vitro cell arrays using angle-resolved low coherence interferometry. J Biomed Opt. 2006;11:034022. doi: 10.1117/1.2209561. [DOI] [PubMed] [Google Scholar]

RESOURCES