Automated Multi-model Reconstruction from Single-Particle Electron Microscopy Data

Abstract

Biological macromolecules can adopt multiple conformational and compositional states due to structural flexibility and alternative subunit assemblies. This structural heterogeneity poses a major challenge in the study of macromolecular structure using single particle electron microscopy. We propose a fully automated, unsupervised method for the three-dimensional reconstruction of multiple structural models from heterogeneous data. As a starting reference, our method employs an initial structure that does not account for any heterogeneity. Then, a multi-stage clustering is used to create multiple models representative of the heterogeneity within the sample. The multi-stage clustering combines an existing approach based on Multivariate Statistical Analysis to perform clustering within individual Euler angles, and a newly developed approach to sort out class-averages from individual Euler angles into homogeneous groups. Structural models are computed from individual clusters. The whole data classification is further refined using an iterative multi-model projection matching approach. We tested our method on one synthetic and three distinct experimental datasets. The tests include the cases where a macromolecular complex exhibits structural flexibility and cases where a molecule is found in ligand-bound and unbound states. We propose the use of our approach as an efficient way to reconstruct distinct multiple models from heterogeneous data.

Introduction

Single particle electron microscopy (EM) is routinely used to resolve the three dimensional (3D) structure of large macromolecular assemblies (Sali et al., 2003). The classical single particle EM methodology assumes that all molecules have the same 3D shape, i.e., the data are homogeneous. However, in practice, some molecules can adopt different conformational states, or complexes with different compositional states may coexist. This results in heterogeneous EM data, in which individual projection images come from different 3D volumes. (Brink et al., 2004; Leschziner and Nogales, 2007; Orlova et al., 1999; Roseman et al., 2001; Staley and Guthrie, 1998; Yang et al., 2002). The use of standard analysis techniques on such data results in the reconstruction of models that are an average of all conformations. Consequently, the density map of an average structure has low or absent densities in the regions of structural variability, rendering biological interpretation difficult. In addition, heterogeneous data result in projection matching errors that lower the resolution of the single-model reconstruction (Shatsky et al., 2009). To overcome these reconstruction issues and, ultimately to understand the functional significance of structural heterogeneity it is therefore vital to develop methods that are able to resolve the heterogeneity within the data and obtain higher resolution multi-model reconstructions.

In some cases, structural heterogeneity can be approximated with discrete number of conformations. Such cases of structural variability can result from ligand bound / unbound state, alternative subunit assemblies, or a flexible region that is stabilized in a small number of conformational states. However, in a more general scenario, structural variability may result when flexible regions within a molecule are not stabilized in any particular state, but instead can occupy a continuum of structural states. Here, we assume that the heterogeneous data can be approximated by a small number of structural models (Brink et al., 2004; Leschziner and Nogales, 2007; Orlova et al., 1999; Roseman et al., 2001; Scheres et al., 2007; Staley and Guthrie, 1998; Yang et al., 2002). This assumption is correct for discrete data, but a simplification in the case of a continuous variation. The exact description of such continuous variation is problematic and presently impractical for noisy and limited EM data. However, a description by a number of intermediate structural states is practically reasonable (Siridechadilok et al., 2005).

Several attempts have been made to devise computational methods that recover multiple structural models from heterogeneous EM data. Most are based on supervised methods in which user interaction is needed in order to sort the data into multiple homogeneous subsets (Burgess et al., 2004; Fu et al., 2007; Hall et al., 2007; Penczek et al., 2006; White et al., 2004). For example a user may partition the data based on average density of class-averages (Elad et al., 2008; Penczek et al., 2006), images with larger density represent ligand-bound states and images with lower density represent unbound configurations. In another case, supervised classification is performed after a user defines references based on visual inspection (Hall et al., 2007). Obviously, a supervised approach may not work well in all the cases, can be heavily biased by assumptions that the user holds about the data, and may be exceptionally labor intensive. A way to overcome these limitations is to employ fully-automated unsupervised approaches. We are aware of only three unsupervised methods for a multi-model reconstruction. One approach resolves heterogeneity within small angular space by means of an approach called cluster tracking (Fu et al., 2007). This method allows homogeneous clusters to be obtained within a small angular neighborhood; however, no solution has been given that enables a global clustering throughout projection angular space. A second method is based on clustering the data according to the common line similarity measure (Herman and Kalinowski, 2008). However, this has not been demonstrated to work on real EM data. A third approach is based on maximum-likelihood optimization: starting with multiple models created from random subsets of the data, the raw images are iteratively assigned alignment parameters based on maximum likelihood. During each iteration the multiple models are regenerated from the realigned images. After many iterations the multiple models converge, with some models hopefully representing a different conformational state (Scheres et al., 2007). This method proved successful in several cases, however, it has a few drawbacks: its convergence depends on the starting models; it is extremely computationally expensive; and it requires a large quantity of experimental data.

Here we introduce a fully automated, unsupervised method that reconstructs multiple models from heterogeneous EM data. It is able to automatically classify the experimental images into more homogeneous subsets that produce structurally different models. Our method can be viewed as a hierarchical clustering of EM images, in which the final clustering step separates the images into homogeneous subsets.

Our method is composed of four stages. In the first stage we perform a standard projection matching procedure to assign translational and Euler angle parameters to the experimental images using an initial single 3D model. We then cluster the images that correspond to a specific Euler angle (projection direction) into a specified number, K, of classes. This results in K average images, subclass-averages, for each Euler angle. Some views show distinct structural differences while in others the structural differences may be small or indistinguishable. In related previous work (Hall et al., 2007), a manual visual inspection of subclass-averages was performed in order to pick a single representative view that shows the highest degree of variability. Here we apply a fully automated approach that considers all subclass-averages simultaneously and combines them into K groups that define K 3D models. In the last, fourth stage, we iteratively run a K-model refinement procedure that reassigns experimental images to the most similar models (Hall et al., 2007; Kostek et al., 2006).

We have tested our method, with positive results, on three single particle EM datasets and one synthetic dataset. Two cryo-EM datasets—the 70S ribosome with and without elongation factor EF-G, and human translation initiation factor eIF3 with and without internal ribosome entry site RNA (IRES)—were used to demonstrate the ability of our method to separate structures that are different in their quaternary structure composition, as well as affected by flexibility. A human RNA polymerase II cryo-EM dataset was used to demonstrate our method working with a macromolecule that exhibits global flexibility. Using a synthetic data set of the Klenow fragment of DNA polymerase I, we show that our method performs better than a supervised clustering method (Hall et al., 2007).

Methods

The input to our method is a set of n boxed projection images, {x_i}, taken from EM micrographs; an initial 3D model M₀ that roughly represents the data; and a number, K, of structurally different models that we would like to recover from the data. An initial model can be obtained from a standard single-model reconstruction procedure. The number K is not known in advance, a common problem in clustering (e.g., K-means clustering), but in practice it can be set to two and iteratively incremented until no new structurally different models are observed.

There are four major stages in our method (pseudo code of the first three is shown in Box 2 (a-b)), which are detailed below.

Box 2 (a): Pseudo code of multi-model reconstruction.

Input: K - is the number of desired models/clusters,

  M₀ - is a starting 3D model and

  {x_i: i = 1, …,n} - is the set of boxed images.

• 1){m_j : j = 1,…,p} = Evenly Spaced Forward Projections (M₀, sampling_angle)

   # Default: sampling_angle = 17°, which results in p = 98 projections.

• 2)$(\{x_i^{\ast }:i=1,\dots ,n\},f)=\text{Multi Reference Alignment}\left(\left\{m_j\right\},\left\{x_i\right\}\right)$ = Multi Reference Alignment ({m_j}, {x_i})

   # f - is a mapping from an index of image x_i to an index of the most similar

   # template projection m_j, i.e. f(i) = j.

   # $x_i^{\ast }$ is a transformed image that maximizes similarity with its assigned template m_f(i).

• 3)For each Euler angle a = 1,…, p

    Compute K clusters within given Euler angle:

     (P₁,…, P_K) = Multivariate Statistical Analysis ({x_i : f (i) = a})

     # where P_i is a subclass of images

    if exists P_i such that |P_i|< 30 then continue with next a, otherwise:

     Set subclass average images $s{i}_i^a=\text{Average Image}\left(P_i\right)$, i = 1,…,K.

  $S{I}^a=\{s{i}_i^a:i=1,\dots ,K\}$

  end for each

• 4)
  Compute similarity matrix S for each pair (u,v) of subclass averages u,v $\in \bigcup _{a}S{I}^a$:

  $$S(u,v)=\{\begin{array}{cc}0\hfill & :\exists a\mathrm{s}.\mathrm{t}u\in S{I}^a\wedge v\in S{I}^a\hfill \\ F+\mathit{CCCL}(u,v)\hfill & :\text{otherwise},\hfill \end{array}\phantom{\}}$$

    where F = 10⁶ and CCCL(u,v) is a cross – correlation coefficient of common

  1D projections of u and v.

• 5)Using S and K as parameters, run spectral clustering algorithm from Box 1 to obtain

  K clusters (C₁,…,C_K).

Box 2 (b).

• 6)Iterative improvemen t of (C₁,…,C_K):

  counter = 20

  While counter > 0

   For each $s\in \underset{a}{\overset{\bigcup }{}}S{I}^a$, ∃i s.t. s ∈ C_i

    if ∃j s.t. Ncut(C₁,…,C_i\{s},…,C_j ⋃ {s},…,C_K) <

     Ncut(C₁,…,C_K) then

    update clustering: C_i = C_i \ {s} and C_j = C _j ⋃{s}

   end for each

   counter = counter −1

  end while

• 7)Iterative improvemen t of k-tuples in (C₁,…,C_K):

  counter = 20

  While counter > 0

   For each (s₁,…,s_K) ∈ (C₁,…,C_K) s.t. ∃a s_i ∈ SI^a, i = 1,…,K

    if exists a permutatio n (s_i1,…, s_iK) s.t.

    Ncut(C₁ ⋃ {s_i1}\{s₁ }, …,C_K ⋃ {s_iK}\{s_K}) < Ncut(C₁,…,C_K) then

     update clustering : C_i = C_i ⋃ {s_ii}\{s_i}, i = 1,,…,K.

   end for each

   counter = counter −1

  end while

• 8)Apply backprojec tion reconstruc tion to compute model M_i from subclass averages

  C_i for each i = 1,…,K.

Angular assignment

Our first step is a standard projection-matching procedure commonly used in single-model reconstruction to assign Euler angles to the experimental images. Given an initial model M₀ we generate evenly spaced projections {m_j}. In practice, we generate 98 templates by projecting an initial 3D model by uniform sampling of 17 degrees (Note that the resolution can be improved at the later, fourth, stage of the multi-model refinement). The images {m_j} are then used as the templates for the multi-reference-alignment of experimental images {x_i}. In this procedure each image x_i is assigned to the most similar template m_j, thus establishing an Euler angle used in the subsequent reconstruction (this stage is depicted in the Figure 1 (a), box “Angular assignment”). Similarity between the images is measured based on the cross-correlation function which is computed over a sample of rotational and translational parameters. The final result of the multi-reference-alignment is {(x_i, j_i, T_i)}, where j_i is the index of the most similar model template which image i is assigned to and T_i is a 2D Euclidean transformation that should be applied to x_i for the alignment with m_ji.

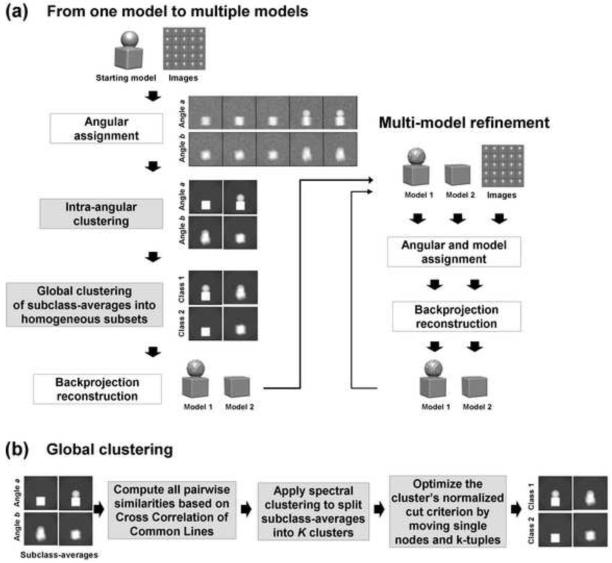
Figure 1.

(a) Method flowchart. For illustrative purposes a two-model reconstruction process is shown, though the method is generally applicable for more than two models. Grey boxes refer to new approaches introduced in this work. The input is a starting model and a set of boxed images. On the left side, the images are clustered into two groups to generate the two initial models. In the “Angular assignment” step, Euler angles are assigned to the experimental images by aligning them against the model projections. In the “Intra-angular clustering” step, we apply clustering within each Euler angle based on Multivariate Statistical Analysis (MSA) to separate all images of a specific projection direction into two homogeneous groups. This results in two subclass-average images for each Euler angle. In the “Global clustering” step, subclass-averages are grouped into two global clusters where subclass-averages from the same Euler angle are assigned to different clusters. Two initial 3D models are reconstructed from the two global clusters of subclass-averages in the “Backprojection reconstruction” step. These two initial models are improved in the iterative two-model refinement procedure, the right part of the figure. In this process, first, all experimental images are reclassified to the most similar projections of the two models. Then, new models are computed and the two-model refinement procedure is repeated. (b) More detailed algorithmic presentation of the “Global clustering” stage from (a). First, similarities between all subclass-averages are computed. Next, subclass-averages are clustered into two groups by applying the Spectral Clustering method. In the last step, two clusters are iteratively optimized by improving the score based on the normalized cut criterion.

Intra-angular clustering

The goal of this stage is to resolve heterogeneity within each Euler angle by clustering images into K groups. Our assumption is that a sufficient number of angularly similar, but structurally different projections are going to be assigned to the same projection template (Euler angle). It is not required that all Euler angles should have such a property, but since class-averages from these Euler angles are going to be used for backprojection, their number will affect the resolution of reconstructed models.

We apply clustering within each Euler angle based on Multivariate Statistical Analysis (MSA) (Borland and van Heel, 1990) to separate all images of a specific projection direction into homogeneous groups. Namely, for each model template m_t we cluster all images assigned to this template, i.e., {(x_i, j_i, T_i): j_i =t}, into K groups. Then, we compute an average image for each of the K groups (subclasses), which we term a subclass-average. In some instances, not every template has sufficient number of images assigned to it, and some of the K subclasses may be too small. We require each subclass to have a minimum number of images which by default we set to 30, otherwise, the Euler angle and all of its subclasses are disregarded from the next step. There is obvious trade-off between the number of subclasses and their SNR. More images improve SNR of the subclass-averages and therefore improve sensitivity of the following classification based on the common line similarity (discussed below). However, raising the threshold reduces the number of subclasses, which results in less Euler angles used for the reconstruction of the initial models. It has been observed (Hall et al., 2007) that sensitivity of the classification, based on the common line similarity, performs well at SNR higher than 0.5. An average SNR of the experimental cryo-EM images lies in the range of [0.05, 0.1]. Therefore, averaging at least 30 images will boost SNR to the range of [0.27, 0.55], bringing it close to the desired minimum for the classification.

The intra-angular clustering stage is depicted as box “Intra-angular clustering” in Figure 1 (a).

Global clustering of subclass-averages into homogeneous subsets

The next problem is to decide how to divide subclass-averages from all angles into K groups. This clustering stage is depicted as box “Global clustering of subclass-averages into homogeneous subsets” in Figure 1 (a) and more detail is given in Figure 1 (b). For each of the K models we need to pick one subclass-average from every Euler angle direction. There is no trivial way to perform this task. We could arbitrarily assign subclass-averages from the first Euler angle into K models, but it is not clear how to then classify the subclass-averages from subsequent Euler angles. There are two questions that need to be addressed. First, what kind of similarity function do we need in order to distinguish between subclass averages from the same or different models? Second, how to find an optimal clustering of subclass-averages into K groups?

Similarity problem

For meaningful clustering we need to define a similarity measure between the subclass-averages from different Euler angles so that more similar images are more likely to belong to the same structural model. To measure similarity between any two images, we compare their common 1D projections (Frank, 2006; van Heel, 1987) as follows. A transmission EM image is a 2D projection of a 3D object, where the normal vector of the projection plane defines the projection direction. Consider a line that is defined by the intersection between a pair of projection planes. Without loss of generality assume that the intersection line passes through the center of the coordinate system. If we perform an additional projection of any two 2D projections of the same 3D object onto their intersection line, thus generating two 1D vectors, these 1D projections will be identical. Thus, these 1D projections are called common 1D projections. The common 1D projection also corresponds to the Fourier transform of the common line defined by the intersection of two central sections of the 3D object represented in the Fourier space. For the corresponding Euler angles, the common 1D projections of more similar structures should be more similar than the common 1D projections of structurally different objects (Hall et al., 2007). Notice, for each pair of images the direction of their common 1D projections is known since we know their corresponding Euler angle from the previous stage. Let us define CCCL(u,v) as the cross-correlation coefficient between the common 1D projections of images u and v, and CCCL(u,v) is in the range of [−1,1].

Clustering problem

To solve this problem we apply a graph-theoretic approach. Let us define a graph G=(V,E), where vertices V={v₁,…,v_t} represent t subclass-averages taken from all Euler angles. Our goal is to cluster the graph nodes into K disjoint subsets C₁,…,C_K, such that a cluster C_i contains images that represent the 3D model i. We also require that no two subclass-averages from the same Euler angle are assigned to the same cluster.

Let us define a weight between the vertices of graph G as w(u,v)= F + CCCL(u,v), if u and v come from different Euler angles and w(u,v)= 0 otherwise. The weights are designed so that the clustering procedure will try to group together vertices with higher weights in-between them; thus, subclass-averages with more similar common 1D projections will be grouped together. We set F to be a large number in order to separate weights of nodes from the same and different Euler angles. This way, we encourage the clustering procedure to not group together nodes with the same Euler angle. As in our tests any value of F larger than 1 gave the same result, we set the default value of F to 10⁶. All the weights are set to be non-negative–a requirement from the clustering method explained below.

A cluster volume is defined as $\mathit{vol}\left(A\right)=\underset{u\in ,A,v\in V}{\Sigma }w(u,v)$. Notice that vol(A) includes the weights associated with intra-cluster A edges and edges connecting vertices from A with all the rest, i.e. V\A. A weight between two clusters A and B is defined as $W(A,B)=\underset{u\in A,v\in B}{\Sigma }w(u,v)$. W(A,B) measures how well two clusters are separated. Smaller W(A,B) is a feature of a better clustering. Now we are ready to define the normalized cut:

$$\mathit{Ncut}(C_1,\dots ,C_K)=\frac{1}{2}\underset{i=1}{\overset{K}{\Sigma }}\frac{W(C_i,V\backslash C_i)}{\mathit{vol}\left(C_i\right)}.$$

Our goal is to find a clustering that minimizes Ncut. Normalization by cluster volume is required to avoid clusters with very few nodes, since such clusters tend to trivially minimize the inter-cluster weights. For example, if normalization by volume is omitted, taking K-1 clusters as single nodes and putting into the K’th cluster all the rest of the graph nodes will likely create a cut with a very small weight. However, we prefer to have a more balanced clustering, where all clusters have a substantial number of nodes.

The task of finding the global minima for the normalized cut problem is computationally intractable, even for K=2 (Appendix in (Shi and Malik, 2000)). Here we apply the spectral clustering method that has been shown to give a reasonable approximation to the normalized cut criterion (Malik et al., 2001; Ng et al., 2001). Briefly, the idea of spectral clustering is to map the graph vertices into Euclidean space by projecting the vertices into an eigenvector subspace of a Laplacian matrix derived from the similarity matrix W.

After vertices are mapped onto Euclidean space a standard K-means clustering is applied. The description of spectral clustering is given in Box 1.

Box 1: Spectral clustering.

Input: S - a t×t similarity matrix, and K – number of clusters.

• 1)
  Compute the normalized graph Laplacian matrix L = I - D^−1/2 S D^−1/2, where:

  • S is the t×t non-negative matrix that describes similarity between t elements;
  • I is the t×t identity matrix with ones on its diagonal and zero elsewhere;
  • D is the t×t diagonal matrix with vertex degrees d_i on its diagonal:
    $d_i=\underset{j=1\dots t}{\Sigma }S(i,j)$, which is the total sum of similarities for the element i.
• 2)Compute K eigenvectors p₁,…,p_K corresponding to the smallest eigenvalues of L.
• 3)Construct the matrix $P\in {\Re }^{t\times K}$ where columns of P are vectors p₁,…,p_K.
• 4)Construct the matrix $P^{\ast }\in {\Re }^{t\times K}$ by normalizing the rows of ${p^{\ast }}_{ij}=p_{ij}∕{\left(\underset{k=1}{\overset{K}{\Sigma }}{p_{ik}}^2\right)}^{1∕2}$.
• 5)Define a set of t points in ${\Re }^K$ by letting y_i, i=1,…,t, be the i’th row of matrix P*.
• 6)Apply the K-means clustering algorithm to obtain K clusters C₁,…,C_K of the point set {y_i}. Consequently, the input element i belongs to cluster j if y_i belongs to cluster C_j.

Since the spectral clustering is not guaranteed to find an optimal value for the normalized cut criterion, we apply two additional local-optimization steps to improve the cut.

First, we are optimizing the cut by trying to move a single node. Find a node in the graph, by going over all graph nodes, that reduces the normalized cut score when moved to another cluster. Move this node and update the clustering. Repeat until no further improvement is possible. Even though this optimization is guaranteed to converge upon a local optima, it may require an exponential number of iterations to explore all clustering options. We limit the maximal number of iterations to 20·t, sufficient for convergence in all our experiments. At the end of this local optimization, and for all our experiments, the optimized cut resulted in equal size clusters such that the subclass-averages from the same angle are placed in different clusters. This is due to the choice of the weighting function w(u,v). Next, we are optimizing the cut by trying different permutations of subclass-averages from the same Euler angle. These two optimization procedures are given as items 6 and 7 of Box 2(b).

In our experiments for K=3 we found that we achieve better results if we do not use the clustering in its general form described above, but apply it iteratively. Namely, apply steps 1-7 to obtain two clusters and then partition the largest cluster into two more clusters. All the reported results with K>2 are obtained using iterative clustering.

Once K clusters of subclass-averages are computed, each cluster is reconstructed using standard backprojection to produce a 3D model (Figure 1 (a), box “Backprojection reconstruction”). These initial models are filtered to a low resolution (30Å is used by default in all our experiments) to prevent any noise bias in the following multi-model refinement procedure.

Multi-model refinement procedure

In the last, fourth stage, we iteratively improve the K models, {M₁,…,M_K} obtained from the previous stage (Figure 1-a, right column). All experimental images, {x_i}, are reassigned to the most similar projections of {M₁,…,M_K} by applying multi-reference alignment. K new models are computed and the refinement procedure is repeated. In our experiments we iterated up to five times. Only some percentage of the most similar images (from {x_i}), based on cross-correlation coefficients, are used for the reconstruction of each model. Only images with coefficients larger than μ+ασ are accepted, where μ and σ are the average and standard deviation of the cross-correlation coefficients. We set α to −0.8 which results in roughly 78% of the images. In the following iteration all original images are realigned against the new models. The right part of the flow chart in Figure 1 (a) depicts the multi-model refinement procedure.

Results

In our experiments below we aimed to assess the ability of a single automated protocol to produce useful results. For this reason we did not optimize parameters for each individual reconstruction. Our goal was to assess our method in this diverse set of examples using the same, fixed, set of parameters described above. We realize that in doing so we did not obtain the best possible reconstructions, but we did provide realistic results. In some cases we know the correct classification of the images (at least based on alternative sorting procedures). In order to assess a quality of partitioning by our method we calculate a classification accuracy of each reconstructed model which is measured as 100%·TP/(TP+FP), where TP are true positives and FP are false positives, and TP+FP is the total number of images used to reconstruct a particular model.

Different assemblies and a ratchet motion: 70S ribosome with and without elongation factor-G (EF-G)

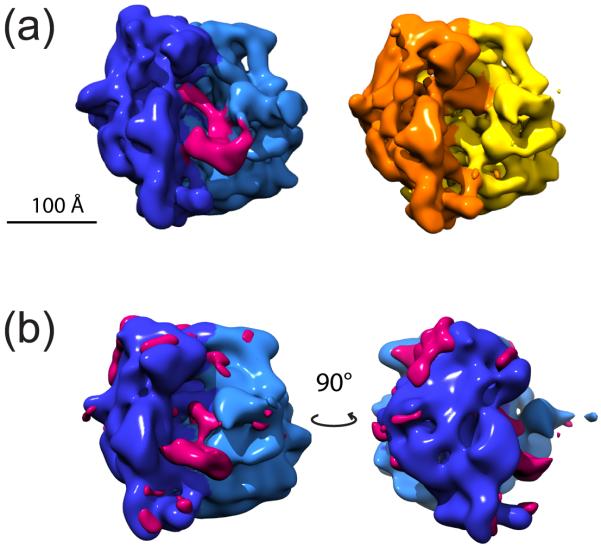
Here we analyze ten thousands cryo-EM images of 70S Escherichia coli ribosomes with either EF-G bound or absent (data were provided by J. Frank). A previous study using supervised classification (Gao et al., 2003) partitioned the data into 5,000 EF-G bound images and 5,000 EG-G absent images. The images were CTF corrected, band-pass filtered and normalized. For the starting model we used a density map of 70S ribosome from EBI Database EMDB (Tagari et al., 2002), entry EMD-1003, resolution 11.3Å (Rawat et al., 2003). We then ran our method with K=2. Assuming that the previous partition of the 10,000 images is correct, our approach clustered the images with 84% and 86% classification accuracy (100·TP/(TP+FP)). The resolution of the resulted models is 16Å (FSC at 0.5 cut-off). These two models agree very well with previously published results and are shown in Figure 2. It is clear that in one model EF-G is present, while it is absent in the other, and the binding of EF-G results in an overall structural change of the 70S ribosome called ratchet motion.

Figure 2.

Results from the reconstructions of 70S with and without EF-G. (a) shows the two reconstructions resulting from the implementation of our method, pink in the structure to the left indicates the assumed EF-G, other colors indicate the 30S and 50S subunits. (b) shows the difference map created by subtracting the structure of 70S alone from the structure assumed to contain EF-G, the difference is indicated in pink. It is clear from the difference map that not only have we captured the presence or absence of EF-G, but also a ratchet movement between the two subunits (Gao et al., 2003).

Table 1 shows a comparison of our method with the Double MSA method (Elad et al., 2008), based on manual selection of eigenvectors for the classification, and with ML3D, an implementation of a maximum likelihood approach (Scheres et al., 2007). Double MSA method shows the fastest convergence with good results after two iterations of refinement, benefiting from accurately classified sub-class averages. Our method achieved a comparable result after three more refinement iterations; however, our classification approach did not require any user supervised decisions. Maximum likelihood classification produced a broadly comparable result when using four random starting models. It should be noted that all three approaches use different multi-model refinement protocols. The percentage accuracies shown in Table 1 should not be treated as an absolute “ground-truth” assessment, since the reference classification may contain some errors with respect to presence or absence of EF-G.

Table 1.

Comparison of multimodel reconstruction methods. This is a two model reconstruction test based on the 10,000 cryo-EM images of 70S E. coli ribosomes where two halves of the images correspond to the ribosomes with and without the elongation factor-G (EF-G) (Gao et al., 2003); note that this classification should not be taken as an absolute ground truth as it may contain some errors. ML3D, which is a 3D multi-reference maximum likelihood refinement implementation (Scheres et al., 2007), has been applied using two and four starting models. For all three methods the starting models and refinement procedures are different.

		Refinement accuracy. One iteration.	Refinement accuracy. Five iterations.	Refinement accuracy. Twenty five iterations.
Our method		63 70	84 86	86 88*
Double MSA (Elad et al., 2008)		Two iterations: 85 85†
ML3D (Scheres et al., 2007)	Two models‡:	50 50	58 55	69 63
	Four models‡:	55,58 56,58	77,82 76,80	78,82 77,80

^*Twenty five iterations for our method are not required, and are only given for comparison purpose only.

^†Estimated accuracy from personal communication with Dr. Elena Orlova.

^‡From personal communication with Dr. Sjors Scheres

We also applied our method to the ribosome data setting K=3. After two iterations of the multi-model refinement one model started to converge to the EF-G absent state (92% accuracy), while the other two models started to converge to the EF-G bound conformation (92% and 60% accuracy).

Different assemblies: Human translation initiation factor eIF3 and eIF3-IRES complex

In mammalian cell protein synthesis, translation initiation factor eIF3 controls assembly of 40S ribosomal subunit on mRNA. eIF3 interacts with eIF4F bound to mRNA 5′-cap. Alternatively, a viral internal ribosome entry site (IRES) can interact with eIF3 and functionally substitutes for the eIF4F and mRNA 5′-cap complex. We analyzed two cryo-EM datasets of the human translation initiation factor eIF3 and of eIF3-IRES complex where eIF3 is bound with hepatitis C virus (HCV) internal ribosome entry site (IRES) (Siridechadilok et al., 2005). The datasets consist of 6,736 images of eIF3 and 19,027 images of eIF3-IRES, taken under the same experimental conditions. By mixing images from the two datasets we can create a model dataset with a known result for further testing our method.

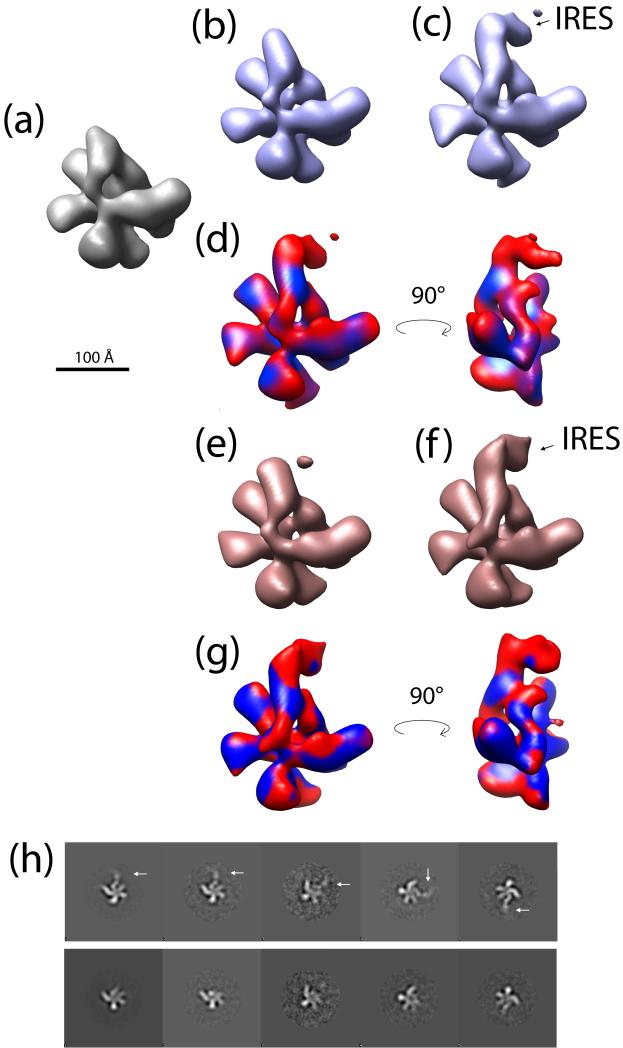
We initially mixed the 6,736 images of eIF3 and the 19,027 images of eIF3-IRES into one set and applied our method with K=2. The initial model was a previously reconstructed volume of eIF3 (EMDB entry EMD-1170). The two reconstructed models are shown in Figure 3 (b-c). The accuracy of the eIF3-IRES model is 82%, while the accuracy of eIF3 reconstruction is only 29%. The low accuracy of the eIF3 model is due to the large number (5,642) of images from the eIF3-IRES experiment’s dataset assigned to the eIF3 reconstruction. To investigate further we reconstructed a volume using only these 5,642 images from the eIF3-IRES dataset that were assigned to the eIF3 model. This reconstruction looked almost identical to the eIF3 model. Therefore we conclude that a large fraction of the images from the eIF3-IRES dataset are of unbound eIF3. This fact motivated us to apply our approach to the eIF3-IRES data alone.

Figure 3.

(a) Structure of unliganded eIF3 (EMDB entry EMD-1170) used as an initial model in our two-model reconstruction process. (b-c) Results of two-model reconstruction from a mixed set of 6,736 images of eIF3 and 19,027 images of eIF3-IRES. (d) Structure from (c) colored according to the density map difference between (c) and (b). (e-f) Results of two-model reconstruction from 19,027 images of eIF3-IRES. (g) Structure from (f) colored according to the density map difference between (f) and (e). (h) Example of five visually most distinctive subclass averages (columns) partitioned into two groups (rows). The clustering procedure clearly separated subclass averages with IRES structure (white arrows) from unliganded eIF3 (second row). Notice that the IRES is not well defined in the subclass-averages due to its high flexibility (Siridechadilok et al., 2005).

The results of two-model reconstruction from 19,027 images of eIF3-IRES dataset are shown in Figure 3 (d-e). Clearly, the RNA IRES is only present in the second model (Figure 3-e). 5,873 images were assigned to the model without IRES (Figure 3-d) and 7,994 images were assigned to the eIF3-IRES model (Figure 3-d). Therefore, we were able to partition the data into unbound eIF3 and eIF3 bound to IRES. The resolution of the two models is 34Å and 39Å correspondingly (FSC at 0.5 cut-off). We used these two models to reclassify all 19,027 images by removing the cross-correlation threshold used to select only highly correlated images during the multi-model refinement. That resulted in 6,580 (35%) images assigned to the eIF3 model and 12,449 (65%) images assigned to the eIF3-IRES model.

Different conformations: Human RNA polymerase II

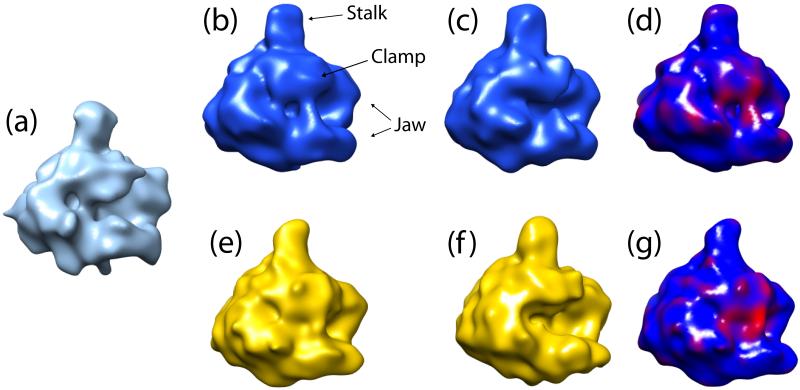
RNA polymerase II exhibits significant conformational changes during the process of transcription, for example between the transcriptional initiation (Gnatt et al., 2001) and elongation (Cheetham et al., 1999; Tahirov et al., 2002). We applied our method to 6,835 cryo-EM images of hRNAPII, that have been previously shown to exhibit flexibility (Kostek et al., 2006). A structure from a standard one model reconstruction of the data served as an initial model for the approach (Kostek et al., 2006). Figure 4 shows the results of our two-model reconstruction. The resolution of these two models is approximately 30Å (FSC at 0.5 cut-off). As it can be seen from the figure, the automated two-model reconstruction obtained with our method gave comparable results for a closed and an open conformation of hRNAPII computed with a more tedious and subjective supervised approach (Kostek et al., 2006). 2,185 images were assigned to the first model and 2,766 images were assigned to the second one.

Figure 4.

Human RNA polymerase II. (a) Reconstruction from the entire dataset. (b)-(c) Our result of the two-model reconstruction. Most of the structural changes happen in the stalk, clamp and jaw regions. (d) Structure from (b) colored according to the density map difference between (b) and (c). (e)-(f) Two previously published models that correspond to the closed and open forms (Kostek et al., 2006). The resolution of these two structures is not available. (g) Structure from (e) colored according to the density map difference between (e) and (f).

Assessment of the method components

Here we analyze how well the key components of our method contribute to the quality of the multi-model reconstruction. There are two key steps in our method, “Intra-angular clustering” and “Global clustering” (marked grey in Figure 1), that aim to resolve the heterogeneity in the data. We analyze whether each of these two stages do any better than a random partitioning. We also analyze the results when we substitute our clustering stages with a perfect clustering. For the test, we use the experimental dataset of 70S ribosome discussed above and one synthetic dataset. These two datasets model two types of heterogeneity: different quaternary structure assemblies, and structural flexibility.

We started by performing four tests on the 70S ribosome data. For each test we compute the classification accuracy for each stage of the method assuming that the true partitioning of the data is 1-5000 and 5001-10000 as reported previously. The second and the third column of Table 2 show the classification accuracy for “Intra-angular clustering” and “Global clustering”. The last column displays accuracy after all images are realigned and reassigned to the two-models obtained after the “Global clustering” stage.

Table 2.

Accuracy of two-model reconstruction. The data used for the tests are 10,000 cryo-EM images of 70S E. coli ribosomes where two halves of the images correspond to the ribosomes with and without the elongation factor-G (EF-G). “Our method” refers to the method presented in this paper. “Perfect clustering” refers to two models reconstructed from images 1-5000 and 5001-10000 after they were aligned to a density map of EMD-1003. In the “Perfect intra-angular clustering” experiment, images within each Euler angle are perfectly classified into two groups and then the “Global clustering” method is applied (third row) or subclass-averages are randomly classified (fourth row). “Random intra-angular clustering” refers to the experiment where sub-class averages were computed based on a random classification, i.e., the “Intra-angular clustering” stage is omitted. “Random global clustering” refers to the initial reconstructions computed from the random selection of subclass-averages of the “Intra-angular clustering” stage, i.e., “Global clustering” stage is omitted. “Random split” refers to the reconstructions from two randomly split datasets of 10,000 originally images, thus skipping the “Intra-angular” and “Global” clustering stages. Column “Intra-angular accuracy” shows classification accuracy within computed subclass averages. Since at this stage it is not known what subclasses belong to what model only one accuracy average for all subclasses is computed. Column “Global accuracy” is the classification accuracy after all subclasses are partitioned into two groups. “Refinement accuracy” displays the accuracy after all 10,000 images are realigned and reassigned to the two models computed in a corresponding experiment. All the randomized experiments were repeated 20 times, and its average result plus minus one standard deviation are reported.

	Intra-angular clustering accuracy	Global clustering accuracy	Refinement accuracy. One iteration.	Refinement accuracy. Five iterations
Our method	60 (average)	57 64	63 70	84 86
Perfect clustering	100	100 100	77 87	90 90
Perfect intra- angular clustering	100	97 96	80 89	91 90
Perfect intra- angular and random global clustering	100	54 ± 4 54 ± 4	58 ± 6 58 ± 6	81 ± 10 81 ± 9
Random intra- angular clustering	53.3 ± 0.4	51 ± 2 50 ± 2	52 ± 2 52 ± 2	77 ± 9 77 ± 10
Random global clustering	60 (average)	54 ± 3 55 ± 3	56 ± 6 56 ± 5	77 ± 13 76 ± 12
Random split	-	-	51 ± 2 52 ± 2	78 ± 11 78 ± 11

In the first test, “Perfect clustering”, we compute an accuracy that can be achieved at the multi-model refinement stage if we perfectly partition the data. This accuracy is not 100% since the initial model used to align images does not exactly represent any model from the data. This result represents a ceiling on what a method may be able to achieve.

In the second test, “Perfect intra-angular clustering”, we perfectly partition the data into two sub-classes within each Euler angle. Then we apply our “Global clustering” method followed by the multi-model refinement. Table 2 shows that our global clustering stage partitioned the subclass-averages into two groups with almost perfect accuracy. It made mistakes only for three pairs of subclass-averages out of 41 pairs (here we used the same set of Euler angles that passed the threshold for sufficient number of images as in our whole approach). For comparison, a random global clustering that starts from perfectly created subclass-averages achieved an average accuracy of only 54% (Table 2, fourth row). Therefore, we conclude that the “Global clustering” stage is very accurate; however, its accuracy depends on the accuracy of “Intra-angular clustering”, which remains limiting (60% on average using Multivariate Statistical Analysis (Borland and van Heel, 1990) as described above).

Next, we compare our method against random approaches. In the “Random intra-angular clustering” test we substitute “Intra-angular clustering” with a random clustering of images into two subclasses and apply our “Global clustering” method. It would naively be expected to observe a random accuracy of 50%; however, projections from the same view but from different conformations may not always match to the same model templates. Thus, some Euler angles are going to be populated with more images from one conformation than from the other. Consequently, a random clustering accuracy can be higher than 50%.

In addition we compare our method with a random partitioning of the data at the “Global clustering” stage (test “Random global clustering”). Instead of optimizing the partitioning of the subclass-averages into two groups we perform a random partitioning of the subclass-averages and compute two initial models. While the difference in accuracy between the random global clustering and our method at the level of global clustering may appear not large, it however significantly increases at the refinement stage.

In the last test, “Random split”, we measure the accuracy of a totally random approach where we randomly split the original 10,000 images into two sets and compute two initial models from each set. In this test, we skip all clustering stages.

Following the above tests we conclude that all algorithmic stages of our method contribute to achieving higher quality multi-model reconstructions compared with the randomized substitutes of the corresponding stages. Even a small improvement in accuracy of the initial models leads to a faster convergence during the multi-model refinement.

We also carried out this analysis with the synthetic data set used to model structural flexibility of a protein complex with a small flexible domain extending from the main body of the structure. We used the same dataset as in (Hall et al., 2007) in order to compare the results of our and their method. Three different synthetic conformations of the Klenow fragment of DNA polymerase I (PDB code: 1kfd, (Beese et al., 1993)) were generated and filtered to 20Å resolution (Hall et al., 2007). For each conformation they produced 150 projections at random orientations and added noise to give a final SNR of 1:1. The level of noise was chosen to resemble the level of noise of typical experimental subclass-averages. An initial model was constructed by taking all 450 images from the three structures and producing an average conformation. Angular assignment by projection matching was then carried out for the 450 images using the average conformation as the reference. Since in this experiment the images are modeled to resemble subclass-averages, we do not apply our “Intra-angular clustering” step. We also do not set to zero the weights between the images assigned to the same Euler angle, since in this experimental setup more than three images may be assigned to an Euler angle. Essentially, the only difference between the previous study (Hall et al., 2007) and the adaptation of our method for this dataset is in application of the unsupervised “Global clustering.” In the previous study (Hall et al., 2007) a supervised clustering was performed by manually picking three representative images and classifying all other images based on CCCL similarity to the picked three representatives. Their accuracy was 61%, 63%, and 77% for the corresponding three structures. We applied our “Global clustering” method and achieved a corresponding accuracy of 99%, 90%, and 98%.

From the above experiments with ribosome 70S and the Klenow fragment of DNA polymerase I we conclude that the “Global clustering” stage of our method is very accurate, while the “Intra-angular” clustering is the weakest point in our approach. However, the combination of these algorithmic steps is capable of producing starting models with sufficient differences for the multi-refinement procedure to converge. In the case of ribosome 70S data the accuracy of the first two-model refinement is 63% and 70% (Table 2), while after five refinement iterations the accuracy rises to 84% and 86% (Figure 2).

Discussion

Two extreme approaches have been proposed to solve the multi-model reconstruction problem. According to one methodology (Scheres et al., 2007) at least in some cases, and in the context of a maximum likelihood approach, it is enough to randomly partition the data into K subsets and run iterative multi-model refinement on reconstructions from these random partitions. Thus no complex clustering (“Intra-angular” and “Global” clustering stages in our method) is required to produce the starting models. The alternative methodology (Elad et al., 2008) maintains that a supervised method is necessary for an accurate classification of subclasses where a sub-classification of images from the same projection direction based on manual selection of eigenimages is performed in order to sort heterogeneity in 2D averages, similar to the reclassification of images within the same Euler angle in our method (“Intra-angular clustering”). The benefit of the first approach is its simplicity to generate K starting models, while its drawback is relatively slow execution time and dependency on the number of starting models needed for convergence. The benefit of the second approach is in its high classification accuracy within class averages, however, it requires a tedious manual selection of eigenimages for each Euler angle. Our approach falls somewhat in between. We have shown that a manual selection of the most distinguished subset of eigenimages is not required, enabling the classification to be carried out unsupervised. The results from our unsupervised classification, may not always be as accurate as a supervised classification of (Elad et al., 2008), but they are sufficient to generate starting models with significant enough differences for a multi model reconstruction procedure to converge. In addition, our method does not increase significantly the time for reconstruction, as it takes less time than a usual one iteration of a refinement procedure. For example, in the case of the 70S ribosome dataset the stages of “Intra-angular” and “Global” clustering take about one and a half hour on a single 2.2GHz AMD Opteron CPU computer.

Our method provides a multi-stage approach that addresses a classification problem of multimodel reconstruction. Several other approaches can benefit from applying our method or some of its stages to improve the multimodel reconstruction further. For example, the methods of (Hall et al., 2007) and (Elad et al., 2008) can benefit from applying “Global clustering” to perform the unsupervised clustering of class-averages into homogeneous subsets. The method of (Scheres et al., 2007) may benefit by performing its maximum likelihood refinement from the starting models produced by our method instead of the models produced from random subsets. This may allow a faster convergence for the iterative maximum-likelihood refinement.

In general, the choice of the number of clusters (i.e., the number of models) and of a clustering method can be considered as two separate computational problems, each having its own challenges. To solve the first problem one should start with answering the following question: do two given 3D structures represent the same or two different conformations? To answer this question one might consider to use a resolution (e.g., an FSC curve) of the reconstructed models as a measure of similarity. However, resolution inevitably drops when data are split into more clusters, thus making models reconstructed from fewer images artificially more distinct than the models reconstructed from more images. In this paper we have dealt only with the second problem of a clustering method, when the number of desired models is given. We estimated the differences between the models mostly based on the visual examination and compared with the previous classification. We have demonstrated that our method works for various types of heterogeneous data: macromolecules exhibiting flexible motion, complexes with variable composition, or both. Most of our results present an analysis of two-model reconstruction (K=2). Looking for an increased number of structurally different models is more challenging. The number of images needed to obtain the same signal-to-noise ratio in the class averages increases with K, and the structural differences become smaller and harder to detect. Our method can be applied to K>2 problems, given the required increase in the number of raw images, either by applying the method as described, or by running it iteratively. Namely, apply it with K=2, dividing the data into two subsets (not necessarily of equal size) and then iteratively cluster each subset separately.

The program protocol including Perl scripts, Matlab code, and instructions how to apply various stages using Spider (Frank, 2002) and Imagic (van Heel et al., 2001) software is available at http://compbio.berkeley.edu/proj/emmm/.