Abstract
The insertion of a DNA base moiety at the end of a DNA duplex to form a Watson-Crick or wobble pair during DNA annealing or replication is a step of fundamental biological importance. Therefore, we investigated the energetics of a formation of the terminal G•C, G•T and G•A base pairs in DNA containing a 5’-dangling G adjacent to the base insertion point using differential scanning calorimetry (DSC) and computer simulations. The energies calculated along classical molecular dynamics trajectories in aqueous solution were analyzed in the framework of linear-response approximation (LRA) to obtain relative free energies for the base insertion and their electrostatic, van der Waals and preorganization components. Using the generic set of LRA parameters the calculated free energies disfavored the mispair formation by 2.5 (G•C -> G•T) and 1.7 (G•C -> G•A) kcal/mol, in reasonable agreement with the experimental free energy differences of 1.8 and 1.4 kcal/mol, respectively. The calculated preorganization components of these free energies of 0.6 (G•C -> G•T) and −0.1 (G•C -> G•A) kcal/mol show that electrostatic preorganization, which is an important source of DNA replication fidelity, plays lesser role in the mispair destabilization in the absence of DNA polymerase.
Keywords: DNA melting, molecular dynamics, base stacking, thermodynamics, DNA replication fidelity
1. Introduction
The detailed knowledge of factors determining the structure and stability of DNA in aqueous solution is important for understanding and control of the transcription, replication, recombination, and preservation of genetic information 1. DNA stability can be quantitatively characterized by the free-energy change for the formation (folding) of DNA duplex from two single-stranded DNAs, or equivalently by the free-energy change for the reverse process, called DNA melting or denaturation.
The stability of a DNA duplex with N base pairs can be decomposed into the free energy for the formation of the nucleus of the first M base pairs, ΔGnuc = ΔGnuc,1 + ΔGnuc,2 + …+ ΔGnuc,M, plus the sum of N-M contributions of inserting the base at the end of the growing duplex, ΔGins,i, i=1,…,N-M. The magnitude of ΔGins,i which depends on the DNA sequence and ionic strength 2, is determined by a delicate balance of the hydrogen bonding, stacking, torsional, and solvation free energies 1,3–5.
The formation of the nucleus of the first M = 3 – 5 base pairs represents the rate-limiting step in DNA folding 1. The nucleus promotes formation of adjacent base pairs so that ΔGins,i < 0 and ΔGins,i << ΔGnuc,j., which constitutes the cooperativity of the folding process 6. Since the stacking of adjacent base pairs, being a short range interaction 7,8, is already present for M = 2 the cooperativity of DNA annealing cannot be directly attributed to DNA stacking interactions, but rather to the coupling among base stacking, base pairing, and DNA solvation in the framework of the dynamics of a solvated short-length DNA. One possible contribution lies in the preorganized electrostatics, whereby already formed base pairs, deoxyribose rings and phosphodiester bridges have dipoles oriented in directions that promote formation of adjacent base pairs. Although this contribution is explicitly determined by evaluating charge-charge interactions in the studied system (see eq 5.4d in section 2.2.), the structural underpinning of electrostatic preorganization may include van der Waals interactions and the hydrophobic effect. The electrostatic preorganization concept 9,10, which was initially advanced by likening enzyme active site to a ‘supersolvent’ 11, is the main factor in the catalytic rate-enhancement of many enzymes 9,12–14, and represents an important contribution to DNA replication fidelity achieved by DNA polymerases 15,16.
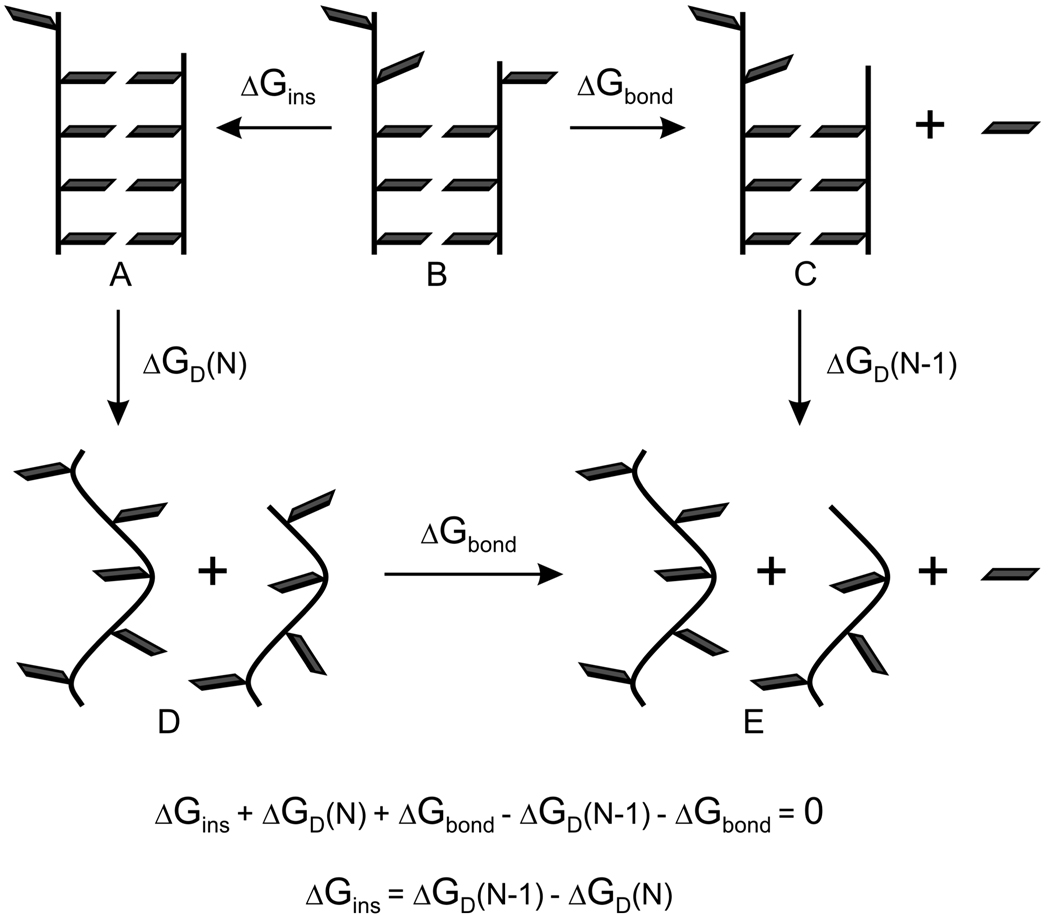
To evaluate the contribution of electrostatic preorganization to DNA stability we performed a series of molecular dynamics (MD) simulations to determine ΔGins using an LRA/α method 15,17, which combines the electrostatic and preorganization terms of Warshel’s linear-response approximation (LRA) 18,19 with the van der Waals energy component of the linear-interaction energy (LIE) method of Åqvist and coworkers 20. We also assessed the reliability of our LRA/α calculations by determining the corresponding ΔGins values using the differential scanning calorimetry (DSC). Although DSC experiments do not provide ΔGins directly, the experimental difference in melting free energies of duplex DNAs with and without the terminal base in one of its strands can be converted to ΔGins using a thermodynamic cycle (Figure 1). Abasic sites induce significant sequence-dependent reduction in thermal and thermodynamic stability of DNA 21–23 while retaining the overall B-DNA conformation. 24–26 To work with a consistent data set, experimental duplex stability parameters ΔG, ΔH and ΔS need to be extrapolated to a common reference temperature by taking into account their temperature dependences reflected in changes of the heat capacity ΔCP 27–32. This extrapolation can be rigorously achieved only for thermodynamic data obtained by calorimetric measurements 33.
Figure 1.
Thermodynamic cycle to determine a base insertion free energy (ΔGins) from the observed melting free energies for the full length DNA (ΔGD(N)) and DNA containing terminal abasic site (ΔGD(N-1)).
In this study, we used DSC to monitor the denaturation of DNA duplexes with sequences. These sequences contained the terminal Watson-Crick (B = C) or wobble (B = T) base pairs, or an abasic site (B = 0), and included 5’ dangling G nucleotide. The dangling nucleotide was included to model the product of the DNA polymerization reaction in the absence of the protein.34 This model provides an important reference state for the proofreading selectivity of DNA polymerases. 35 We determined complete thermodynamic stability profiles and described the nature of the helix-to-coil transitions of these model oligonucleotides.
In the theoretical part of this study, the MD and LRA/α 15, 19 calculations were applied to determine the relative stability of , B = 0, C, A or T, DNA duplexes. The LRA/α method has been employed because it allows for assessment of the influence of preorganized electrostatics on the DNA duplex stability. Additionally, the LRA/α can provide the electrostatic and van der Waals free-energy components for this stabilization. 36
On the other hand, the LRA/α is an empirical method, the accuracy of which relies on the parameters α and β. These parameters may differ for structurally dissimilar ligands and/or for different host molecules. 37 In this light it is important that using the generic LRA/α parameters optimized for calculations of solvation free energies of small polar molecules 15 revealed good agreement with ΔGins determined experimentally. Nevertheless, to further improve the accuracy of the LRA/α method and to extend its applicability to simulations of nucleic acids, we adjusted its empirical α and β parameters by minimizing the root mean square difference between the calculated and the experimental results.
2. Methods
2.1 Experimental Materials and Methods
Materials
Oligonucleotides used in this work were synthesized and purified by Invitrogen (Germany). The concentrations of single stranded oligonucleotides were determined by measuring absorbance at 260 nm and 25 °C (Cary Bio 100 UV spectrophotometer;Varian, Australia) using the extinction coefficients that had been calculated according to the nearest neighbor procedure. 38 We used the following extinction coefficients (M−1cm−1): 102600 for 5’-GGCGCATCAGC-3’ and 89900 (B = C), 92300 (B = T), 83800 (B = 0) for the complementary 5’-GCTGATGCGB-3’ strands. B = 0 represents the tetrahydrofuran analog of the abasic site. Biochemical studies show that DNA containing this tetrahydrofuran derivative retains its activity for DNA polymerases 39 and for apurinic/apyrimidinic endonucleases40 thus confirming its value as a model for recognition patterns associated with the natural abasic site. Buffer solutions (10 mM phosphate, [NaCl] = 100 mM, [EDTA] = 1 mM, adjusted to pH 7.0) containing equimolar amounts of the complementary single-stranded oligomers were mixed to obtain the corresponding duplex solutions. The 1:1 stechiometry of formation was for all studied duplexes verified by Job plots. 41 The duplex solutions were extensively dialyzed against the appropriate buffer (see above) and degassed at room temperature (~25 °C) for 20 min before conducting any calorimetric experiments.
Differential scanning calorimetry (DSC)
DSC measurements were performed with a Nano-II DSC scanning calorimeter (CSC, UT, USA). For each duplex (~0.24 mM) the first DSC scan was performed at a heating rate of 0.25 °C min−1. Since essentially the same thermograms were obtained by repetitive experiments at a heating rate of 1 °C min−1, the observed transitions may be considered as equilibrium processes. The DSC thermograms are presented as ΔCP = C̅P,2 - C̅P, AB versus T curves (C̅P,2 = partial molar heat capacity of DNA obtained from the raw signal corrected for the buffer contribution and normalized per mole of duplex contained in the measuring cell; C̅P, AB = partial molar heat capacity of the native (AB duplex) state extrapolated over the measured temperature range). To determine complete thermodynamic stability profiles of the model oligonucleotides the DSC thermograms were analyzed in a model-independent way. In addition, model-dependent analysis of DSC data was performed to get a deeper insight into the nature of helix-to-coil transitions for the studied oligonucleotides.
Model-independent analysis
Heat capacity of denaturation, ΔCP,D, was determined as a difference in the pre- and post-transition baselines extrapolated to a reference temperature which was for comparative purposes chosen as the melting temperature, Tm, obtained by model-dependent analysis of DSC data (see below). The enthalpy of denaturation at Tm, ΔHD,Tm, was calculated by integration of the area enclosed by the ΔCP versus T curve, the pre- and post-transition baselines and Tm. Assumptions that ΔCP,D is temperature independent quantity and that ΔHD,Tm and ΔCP,D are not functions of DNA concentration and thus equal to their values in the standard state (ΔHD,Tm = ΔHD,Tm° and ΔCP,D = ΔCP,D°) enabled the calculation of standard Gibbs free energy of denaturation, ΔGD°, as a function of T from the integrated Gibbs-Helmholtz equation:
| (1) |
Since the observed helix-to-coil transition is an equilibrium process one can express the standard Gibbs free energy of denaturation at Tm, ΔGD,Tm°, that corresponds to the AB ↔ A + B reaction performed in the 1 M standard state as: ΔGD,Tm° = -RTmln(CT/2), where CT represents the total molar concentration of DNA expressed in moles of duplex per liter. The corresponding standard thermodynamic quantities (ΔGD°, ΔHD° and ΔSD°) as functions of temperature were calculated from equation 1, from the Kirchhoff’s law ΔHD° = ΔHD,Tm° + ΔCP,D°(T – Tm) and from the general relation ΔSD° = (ΔHD° - ΔGD°)/T. The obtained thermodynamic parameters for denaturation of the model duplexes (B = C, T, 0) were used for calculation of the corresponding differential parameters ΔΔGB→X, ΔΔHB→X, ΔΔSB→X and ΔΔCP,B→X (x = C, T, 0). Since the first term of equation 1 cancels out when ΔΔ values are calculated, these differential parameters depend on the choice of neither the standard state nor the type of chemical process and can be directly compared to the complementary theoretical data. Moreover, as these differential parameters depend only on ΔHD and ΔCP,D determined directly from experimental DSC data they can be considered as model-independent quantities.
Model-dependent analysis
The monitored DNA denaturation can be described in a simplest way in terms of a reversible two state process in which DNA molecule can exist either in native duplex AB macro state or in denatured single strand A, B macro state. Such process can be presented as: AB ↔ A + B. According to this model one can express partial molar enthalpy of DNA, H̅2, in terms of the corresponding contributions H̅AB, H̅A and H̅B that characterize species AB, A and B as: H̅2 = H̅AB + αD(H̅A + H̅B – H̅AB), where αD represents a fraction of DNA molecules in the denatured state. The relative partial molar enthalpy, ΔH, can be expressed as 42
| (2) |
where ΔHD is defined as the enthalpy change accompanying the transition of 1 mole of the native AB duplex into the denatured single strands A and B. We considered ΔHD to be independent on concentration and thus equal to its value in the standard state (ΔHD = ΔHD°). The model function that describes the measured relative partial molar heat capacity of the DNA, ΔCP, can be derived from the first partial derivative of equation 2 with respect to T at constant pressure. 27,28,33,43–46
| (3) |
According to AB ↔ A + B model αD and (∂ αD/ ∂ T)P can be at any temperature expressed analytically in terms of parameters ΔHD,Tm°, ΔCP,D° and Tm (temperature at which αD = 0.5) by combination of equation 1, equation ΔHD° = ΔHD,Tm° + ΔCP,D°(T – Tm) and relation ΔGD° = −RTln[αD2CT/(1-αD)].42 For this reason, the model-dependent values of ΔHD,Tm°, ΔCP,D° and Tm can be obtained from the model function (equation 3) fitting to the experimental DSC thermograms using the Levenberg-Marquardt non-linear χ2 regression procedure. 47
2.2 LRA/α Calculations
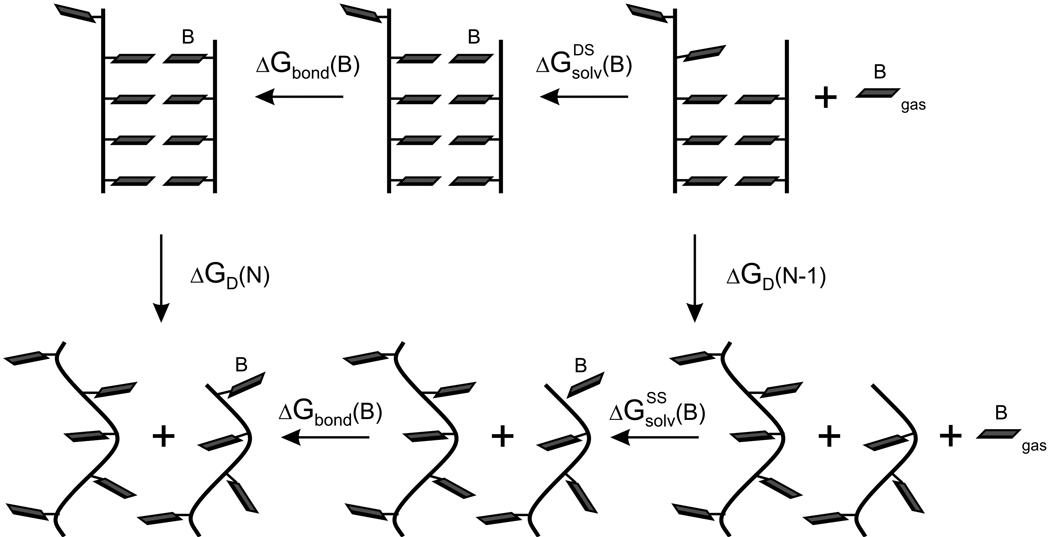
The insertion free-energy, ΔGins, could be calculated by running long MD simulations on the DNA duplex (state A in Figure 1) and counting number of occurrences of opening of the terminal base pair to form state B (Figure 1). However, such direct approach would require sampling of very long MD trajectories. Perhaps more importantly, the free energy obtained in this way would lack information about its components, including the electrostatic preorganization. Thus, we determined ΔGins for the terminal G•B base pair by combining thermodynamic cycles in Figure 1 and Figure 2 as
| (4) |
where represent the solvation free energy of the base B in hydrated double or single-stranded environment. Magnitudes of were calculated using the LRA/α method; the nucleobase B is in its terminology referred to as a probe region. 15
Figure 2.
Thermodynamic cycle for the calculation of the free energy for the DNA duplex destabilization due to the creation of a terminal abasic site, ΔGD(N) - ΔGD(N-1).
The LRA/α solvation free energy of the nucleobase B in the solvent S (either hydrated DNA duplex - DS or hydrated single stranded DNA - SS) is calculated as the sum of electrostatic , van der Waals and preorganization contributions15,19
| (5a) |
| (5b) |
| (5c) |
| (5d) |
where represent the average electrostatic and van der Waals interaction energy between the probe region and its surrounding calculated on a MD trajectory simulated using the fully charged probe. α and β denote the LRA/α empirical parameters and presents the average electrostatic interaction energy between the probe region and its surrounding calculated on a MD (ensemble) generated using the uncharged probe (nucleobase B).
The linear response part of the LRA/α expression (i.e. the sum of eq. 5b and 5d for β= 0.5) can be derived by approximating the potential energy for a charging process in solution by the intersection of two parabolas of equal curvature 15,19,20,48, or by expanding the free-energy perturbation formula for two infinitesimally close states by Taylor series 20,49. The van der Waals term (eq. 5.4c) represents an approximation to the solvation free energy of an uncharged probe 15,19 that was conveniently chosen to be the same as the corresponding term in the LIE method 20. Thus, it is only the presence of the preorganization term (eq. 5d) that distinguishes the LRA/α method from the linear interaction energy (LIE) method of Åqvist and coworkers 20. It has been argued that the preorganization term is not necessary in calculations of ligand-protein dissociation constants since its effect can be simply represented by an increased value of the coefficient β 50, but this conclusion may not be valid for all combinations of ligands and enzyme active sites. Indeed, the preorganization term did show important contribution to binding fidelity of DNA polymerases β 15 and T7 16.
The LRA/α method does not include explicit van der Waals preorganization term because it is impossible to carry out MD simulations with the whole van der Waals term turned off. Simulations carried out with only the London term absent would, apart from their unphysical nature, likely bring no qualitatively new contributions that could not be obtained by simple readjustment of the coefficient α. Similarly, a more reasonable option of adding van der Waals term sampled on the state with zero charges would likely not improve the performance of the method 19. Nevertheless, steric and dispersion forces are implicitly included in the electrostatic preorganization via the generation of the statistical ensemble used for averaging electrostatic energies in equation 5.4d.
It should be noted that the LRA approximation, despite its acronym implying a broad reach, represents a specialized version of the time-independent linear response theory 51 - specific to ligand, substrate or transition state binding and electron transfer processes 48,52. The linear response theory of hydration of ions 37,53–55 established that upon the process of solute (B) charging in water or other polar solvents approximately half of the potential energy gained from the charge dipole interaction () is spent on reorienting the water dipoles. 9,56 For example, the water hydrogen bonded pattern has to be broken in order to form good hydrogen bonds with the charged solute. This finding is reflected in the value of 0.5 chosen for the LRA/α β parameter. The generic value of 0.56 (optimized for hydration free energies of imidazole, difluorotoluene and protonated cytosine) was used for the empirical α parameter.15
Since both terms can be decomposed into three contributions according to eq 5, also their difference representing ΔGins can be subjected to such decomposition, that is
| (6a) |
where
| (6b) |
| (6c) |
| (6d) |
Hydrated single stranded DNA is very flexible, thus proper sampling of its configuration space would be computationally extremely demanding. To avoid this problem, a thermodynamic cycle was devised, which approximates the nucleobase B embedded in the hydrated single stranded DNA with the same base included in a hydrated nucleoside. 57 This reference system is denoted here dN. In order to retain the stacking interaction to the neighboring nucleobase, we used a hydrated dinucleoside monophosphate 3’-BG as an alternative reference system, and denoted it as dNpN.
Free energy is a state function. Its difference is therefore dependent only on the choice of the initial and final states. Thus, the difference in free-energy of DNA duplex annealing contributed by the formation of terminal Watson-Crick (G•C) and wobble (G•X) base pairs can be calculated as 34
| (7a) |
and analogous expressions can be formulated for its electrostatic, van der Waals and preorganization components
| (7b) |
| (7c) |
| (7d) |
2.3 Simulation Conditions
The configurational ensembles for the evaluation of free energies were generated from molecular dynamics (MD) trajectories using the AMBER58 force field implemented in the program Q59. The simulated solute molecules were immersed in a sphere (24 Å radius) of TIP3P water molecules subjected to the surface-constraint all-atom solvent (SCAAS) type boundary conditions 60,61 as implemented in the program Q 59. These constraints were designed to mimic infinite aqueous solution. Thus, the spherical models (water droplets) do not require large dimensions of the simulated systems (in comparison to simulation boxes utilizing periodic boundary conditions) to produce stable and realistic free energies.
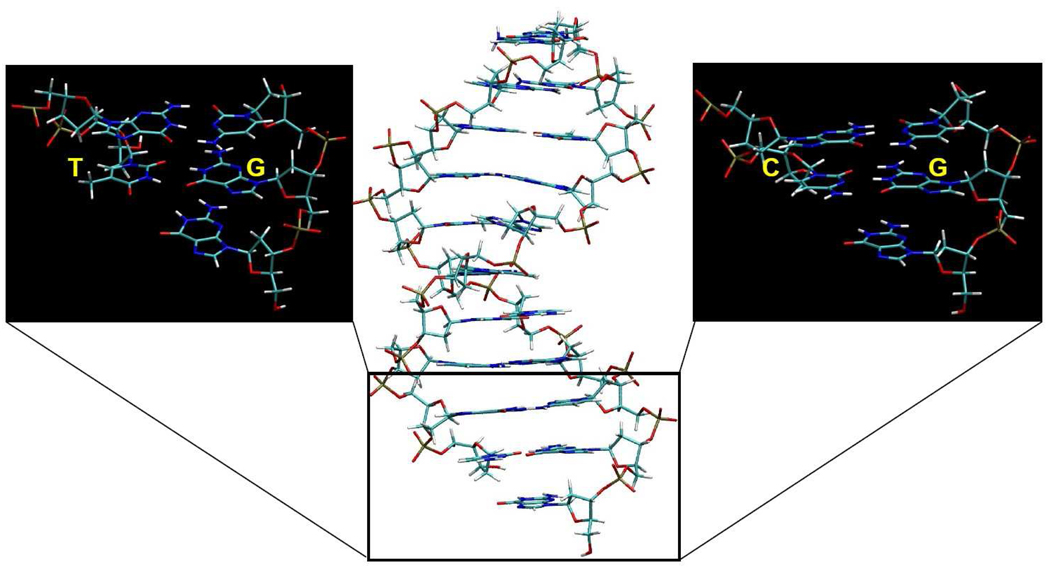
The simulations of the DNA duplexes were initiated using DNA geometry from X-ray structure of a ternary complex of DNA polymerase β (pdb code 1BPY; the structure is predominantly in the B-form which is retained during our simulations) 62, which was modified by removing all the protein, dCTP substrate, water and metal atoms. We also removed all DNA atoms upstream from guanine nucleotide that forms Watson-Crick base pair with dCTP, and, for simulations of the mispairs, manually mutated the 3’ terminal base of the primer strand to T or A. These modifications resulted in the DNA sequence, where B stands for the C, T or A nucleotides (Figure 3). DNA atoms protruding beyond the sphere boundaries were restrained to their coordinates in the 1BPY crystal structure using harmonic restraints. Nonbonding interactions of these atoms were turned off. Nonbonding interactions between other atoms inside the simulation sphere were subjected to a 10 Å cutoff. The local-reaction field (LRF) method was used to treat long-range electrostatic interactions for distances beyond this cutoff. 18,61 Non-bonding interactions of atoms forming the probe region, which was defined as nucleobase of B, were explicitly evaluated for all distances.
Figure 3.
Representative structures of the model systems used to calculate DNA melting free energy for T·G (mispair) vs C·G. Explicit water and Na+ counterions are not shown. During the production MD trajectories, the 5’-dangling guanosine was observed to sample both the stacked and unstacked configurations while the DNA remained in the B-DNA form.
The structure of all simulated systems was relaxed in a series of four 10000-and one 20000-step MD simulations at 5 K with increasing stepsize from 0.01 to 1 fs. Subsequent gradual heating of the system from 5 to 250 K in a series of five 10000-step MD simulations with 1 fs stepsize was followed by a 40 ps simulation at 298 K using a 2 fs stepsize. All production trajectories, the lengths of which were 4 ns, generated constant-temperature ensembles. The SHAKE algorithm63 was used for bonds involving hydrogen atoms. The structure and trajectory analyses were carried out using the program VMD 1.8.3. 64 Energies were sampled every 10 steps. The reported free energies and standard deviations reflect an average over four independent simulations that differed in their starting geometries, i.e. the total simulation length of 16 ns.
Sodium cations were added to the simulated system to achieve its electroneutrality. Positions of all Na+ atoms were restrained by a flat-bottom harmonic potential (force constant of 50 kcal mol−1 Å−2) that was zero for the distances less than 20 Å from the center of the simulation sphere. These potentials were applied to prevent the diffusion of the sodium ions towards the edge of the simulation sphere. No additional restraints were applied. The center of the simulation sphere was placed in the center of the studied base pair. This selection enclosed the studied base pair plus another five base pairs downstream inside the simulation sphere. Phosphate groups that were closer to the sphere boundary than 3 Å were made electroneutral by decreasing the negative charge on the oxygen atoms as described previously. 57
dNpN reference systems for simulations in aqueous solution consisted of 3’-CG, 3’-TG and 3’-AG dideoxyribonucleoside monophosphate monoanions. Each of these dinucleoside monophosphates contained 3’OH and 5’OH terminal groups and one negatively charged phosphate group neutralized by Na+. Simulations in water were also carried out for cytidine, thymidine and adenosine deoxyribonucleosides (dN). In all simulations of dNpN or dN, the C1’ atom of B was constrained in the center of the simulation sphere using a harmonic potential defined by a force constant of 50 kcal mol−1 Å−2 to prevent its diffusion towards the edge of the simulation sphere.
3. Results and Discussion
Helix-to-coil transitions of the oligonucleotides
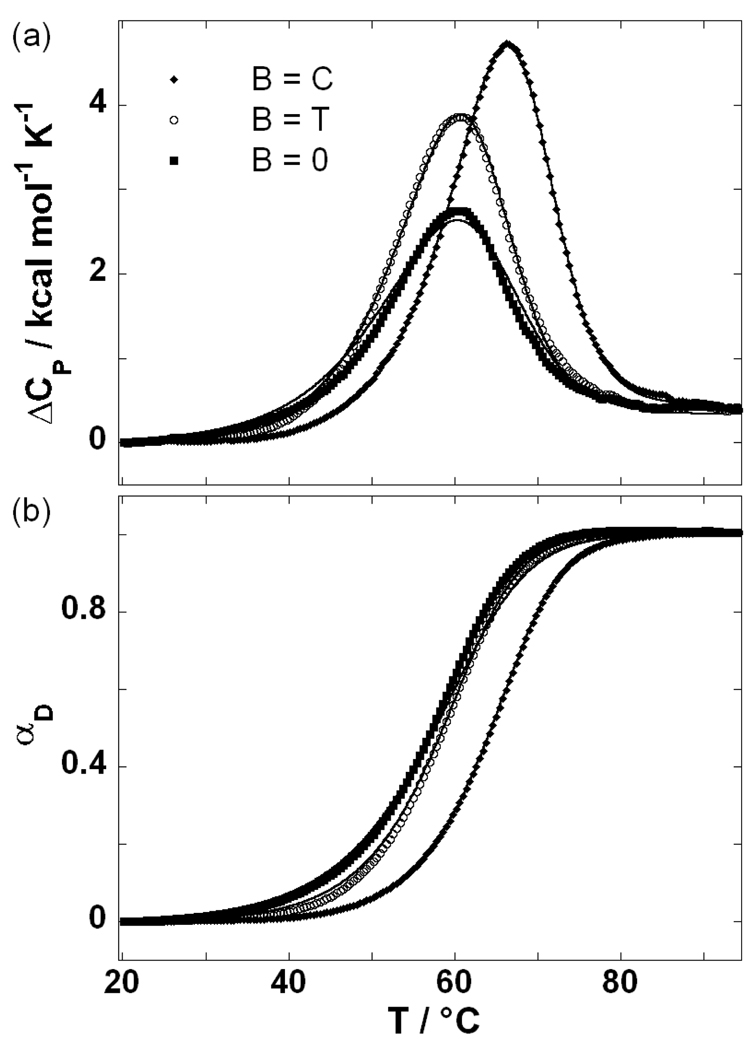
The position of the peaks of the DSC thermograms accompanying denaturation of the DNA duplexes (Figure 4) shows that the duplex with a terminal Watson-Crick base pair (B = C) exhibits the highest thermal stability (highest Tm). The Tm’s for a mismatched duplex (B = T) and a duplex containing the abasic lesion (B = 0) are similar, but significantly lower than the Tm of the B = C duplex. The two state model (equation 2 and equation 3) describes very well the transitions of B = C and B = T duplexes (Figure 4). In the case of B = 0 we observed a slight discrepancy between the model and experimental data.
Figure 4.
Experimentally monitored helix-to-coil transitions of the oligonucleotides (B = C, T, 0).
Panel a: DSC thermograms (symbols; every fourth experimental point) and the best fits of the model function (lines; see equation 3). The thermodynamic parameters characterizing the transitions monitored by DSC are presented for B = C, T and 0, respectively: Tm (°C) = 64.4, 58.6, 57.6; ΔHD,Tm (kcal mol−1) = 76.1(+0.1), 67.2(+1.2), 47.7(+6.4); ΔCP,D (kcal mol−1 K−1) = 0.43(+0.02), 0.41(+0.00), 0.44(−0.10). The values in the round brackets are the differences between the model-dependent (equation 3) and the presented model-independent thermodynamic parameters.
Panel b: Fraction of the oligonuceotides in the denatured state, αD, calculated either directly from DSC thermograms (Panel a) as a model-independent ΔH/ΔHD ratio (symbols; ΔH was obtained by integration of experimental ΔCP from the reference temperature at which all DNA molecules exist in the initial (duplex) macrostate (αD = 0) to a given T at which a certain fraction of DNA molecules exist in the final denatured (single-stranded) macrostate; ΔHD was calculated as ΔHD = ΔHD,Tm + ΔCP,D(T – Tm), see experimental materials and methods) or as the model-dependent quantity obtained from the best fit model parameters (lines).
Alternatively, the nature of a duplex denaturation process can be examined by comparing a model-dependent ΔHD,Tm° (van’t Hoff enthalpy obtained from the model function fitting) with the corresponding model-independent enthalpy. Their ratio is close to unity if the observed transition is an equilibrium two state process (AB ↔ A + B). On the other hand, the value of the ratio < 1 signifies for the presence of intermediates occurring between pure duplex and pure single-stranded DNA populations, while the ratio > 1 is indicative of a process involving double-stranded aggregates. In the case of the model oligonucleotides the ΔHD,Tm°(model-dependent)/ΔHD,Tm°(model-independent) ratio equals to 1.0 (B = C, B = T) and 1.1 (B = 0). These ratios and a good agreement between the two-state model and experiment (Figure 4) indicate that B = C duplex denaturation can be described as a cooperative process, the nature of which is not changed by the C → T mutation, and is not significantly altered by the introduction of the abasic C → 0 lesion. These findings are supported by good agreement of the two-state model with the B = C, B = T and B = 0 UV-melting curves (not shown), which results in about the same ΔHD,Tm° values as those obtained by model-dependent analysis of DSC data. Based on the analysis of thermodynamic and structural data for DNA containing abasic sites by Breslauer and coworkers 22, the observed (two-state) nature of the B = C, B = T and B = 0 denaturations suggests that the phosphodiester backbone rather than the base-sugar network, serves as primary propagation path for the communication between the cooperative DNA melting units.
Thermodynamic stability of the duplexes
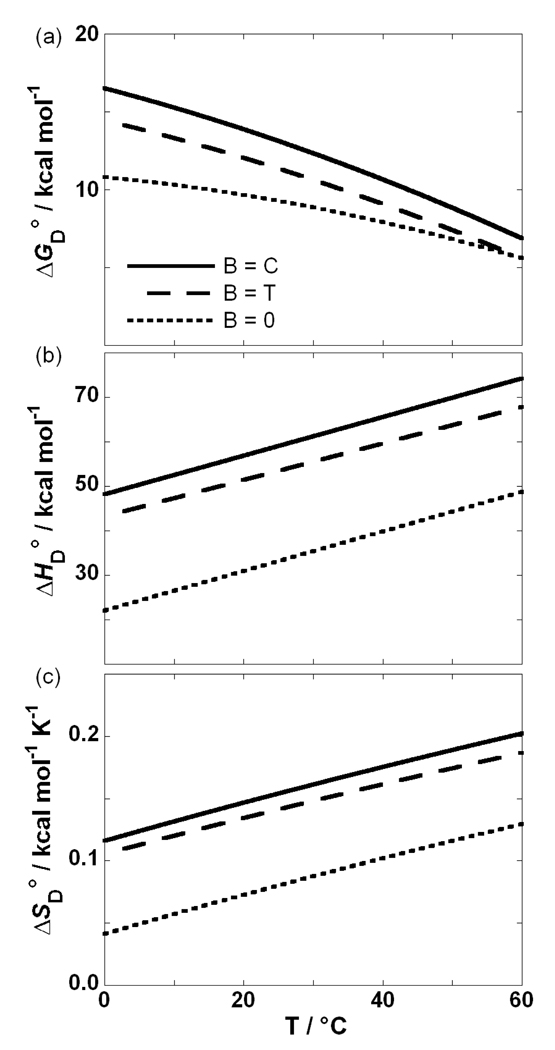
The values of ΔGD°, ΔHD° and ΔSD° are strongly temperature-dependent (Figure 5). In a temperature range of 0 to 60 °C, B = C is the most stable duplex (the highest ΔGD° value, Figure 5a) followed by the mismatched B = T duplex and the B = 0 duplex containing the abasic lesion. The observation that folding of all studied duplexes in the standard state at physiological temperatures is an enthalpy driven process accompanied by an unfavorable entropy contribution and negative heat capacity change is a general feature of polymeric and oligomeric nucleic acids. In this light, ΔHD° > 0 observed at physiological temperatures can be qualitatively explained by more energetically favorable (stacking and H-bonding) interactions formed in the duplex state, in comparison to the single stranded thermally denatured state. The corresponding ΔSD° > 0 can be explained by an increase in conformational, translational and rotational freedom of DNA upon denaturation that is accompanied by a release of a significant amount of counterions. On the other hand, ΔCP,D° > 0 is probably mainly a consequence of exposure of aromatic surfaces to water upon denaturation 65, although this contribution to ΔCP,D° is opposed by the simultaneous exposure of polar surface area (e.g. Watson-Crick face of bases). Although hydration clearly plays a major role in determining ΔCP,D° values of DNA denaturation its exact origins still remain a matter of debate 65. In this light, statistical mechanical treatments of explicitly simulated hydration may represent a promising way to the molecular understanding of ΔCP,D° values accompanying denaturation of nucleic acids and proteins 66. The average value of ΔCP,D° for denaturation of B = C, B = T and B = 0 is 0.43 (±0.03) kcal mol−1 K−1 (or 0.043 (±0.003) kcal (mol of base pairs)−1 K−1), which is consistent with the average ΔCP,D° value accompanying the denaturation of oligomeric duplexes obtained by DSC, 29 and somewhat lower than the average ΔCP,D° observed for helix-to-coil transitions of polymeric nucleic acids. 32
Figure 5.
Thermodynamic profiles of helix-to-coil transitions of the oligonucleotides (B = C, T, or 0) obtained by the model-independent analysis of DSC thermograms.
The contributions to the thermodynamic stability of the model duplexes can be discussed also in terms of the corresponding differential parameters ΔΔGB→X, ΔΔHB→X, ΔΔSB→X and ΔΔCP,B→X (x = C, T, 0) extrapolated to 25 °C using the equations described in the experimental materials and methods section (DSC model-independent analysis; see also Figure 4 and Figure 5). The ΔΔG0→C, ΔΔH0→C and ΔΔS0→C values (Table 1) for contributions of G·C base pair formation to DNA duplex annealing are in accordance with the duplex stabilizing effects presented by Vesnaver et al. 22 (ΔΔG0→T = −6.5 kcal mol−1, ΔΔH0→T = −27.2 kcal mol−1 and ΔΔS0→T = −69.2 cal mol−1 K−1). Since, in their study, the A·T base pair was formed, the gain of two hydrogen bonds should result in a less negative ΔΔG value than obtained in our study (gain of three hydrogen bonds). This apparent discrepancy can be explained by considering differences in stacking interactions. That is, since their A·T base pair is located in the middle of the duplex, its two stacking interactions lower ΔΔG and ΔΔH values more than one stacking interaction in the terminal G·C base pair. Vesnaver et al. 22 also suggested that base pair formations exert stabilizing influences that cannot be explained by simple nearest neighbor effects and may be caused by changes in solvation. In this light, the value of ΔΔCP,0→C ~ 0 estimated in our work (Table 1) may indicate that the formation of terminal G·C base pair does not significantly alter the duplex solvation.
Table 1.
Differential thermodynamic parameters for and , X = C or T, helix-to-coil transitions obtained from model-independent analysis of DSC data at 25 °C.
| B = 0 X = C |
B = 0 X = T |
B = T X = C |
|
|---|---|---|---|
| ΔΔGB→X/ kcal mol−1 | −3.9 ± 0.8 | −2.1 ± 0.5 | −1.8 ± 0.5 |
| ΔΔHB→X/ kcal mol−1 | −25.9 ± 3.2 | −20.3 ± 2.5 | −5.6 ± 2.0 |
| ΔΔSB→X/ cal mol−1 K−1 | −73.9 ± 11.1 | −61.1 ± 8.6 | −12.8 ± 6.9 |
| ΔΔCP,B→X/ kcal mol−1 K−1 | 0.01 ± 0.08 | 0.03 ± 0.06 | −0.02 ± 0.05 |
Energetic contributions to DNA duplex stability
The calculated average electrostatic, vdW and preorganization interaction energies of the C, T or A base moieties (denoted as ‘probes’) in a solvated nucleoside, dinucleoside monophosphate, or DNA environments are presented in Table 2. Regardless of the composition of the environment, the interaction energy of each probe is dominated by its electrostatic component, followed by the van der Waals and preorganization energies. The electrostatic interaction energy of cytosine is always more favorable, in agreement with its larger polarity.4 On the other hand, van der Waals interactions, which are dominated by the dispersion attraction, favor thymine and adenine due to their larger polarizability. 67
Table 2.
Averagea electrostatic, van der Waals, and preorganization interaction energies between the probe region and its surrounding ‘solvent’, and the resulting solvation free energies.b
| Solventc | Probe (B) | Interaction energy (kcal/mol) |
ΔGsolv (kcal/mol) |
||
|---|---|---|---|---|---|
| DS | C | −49.6 ± 0.2 | −15.7 ± 0.2 | 0.5 ± 0.2 | −33.3 ± 0.3 |
| T | −36.9 ± 0.2 | −18.6 ± 0.1 | −2.3 ± 0.5 | −30.0 ± 0.4 | |
| A | 36.2 ± 0.2 | −18.6 ± 0.1 | −1.0 ± 0.5 | −29.0 ± 0.4 | |
| dN | C | −45.0 ± 0.1 | −7.1 ± 0.1 | 1.5 ± 0.2 | −25.7 ± 0.2 |
| T | −36.0 ± 0.1 | −9.4 ± 0.1 | −1.4 ± 0.2 | −24.0 ± 0.2 | |
| A | −33.6 ± 0.1 | −11.1 ± 0.1 | −0.1 ± 0.2 | −23.1 ± 0.2 | |
| dNpN | C | −45.0 ± 0.2 | −11.1 ± 0.4 | 1.5 ± 0.2 | −28.0 ± 0.4 |
| T | −35.1 ± 0.1 | −14.8 ± 0.1 | −2.4 ± 0.1 | −27.0 ± 0.2 | |
| A | −32.7 ± 0.1 | −16.0 ± 0.1 | 0.2 ± 0.5 | −25.2 ± 0.4 | |
Average and standard deviation from four independent simulations.
Eq 5, α = 0.56, β = 0.5.
DNA duplex (DS), deoxynucleoside (dN) or dinucleoside monophosphate (dNpN) in aqueous solution.
The average preorganization energies, which reflect interaction of probe with its preorganized environment (i.e. environment with the geometry and polarization established in the presence of zero charges on all probe atoms), are presented in the last column of Table 2. If an uncharged solute B is immersed in water, the solvent dipoles are with respect to it randomly oriented. If the water and the solute geometries would remain unchanged during the charging process of the solute (i.e. if this process was instantaneous), the overall charge dipole interaction energy would be zero . Thus, we can say that polar solvents are not electrostatically preorganized to accommodate solute molecules. On the other hand, in proteins the binding site dipoles associated with polar groups and ionized residues may be already partially oriented towards the bound uncharged ligand B. The analogous instantaneous charging of the bound ligand may therefore yield favorable electrostatic interactions between the protein and its ligand , in which case one can claim that proteins are electrostatically preorganized to accommodate their ligands. Here, although the preorganization concept has been most frequently invoked for transition states of enzymatic reactions, the term ‘ligand‘ may represent a substrate, transition state, or an inhibitor. The electrostatic preorganization represents the main source of the catalytic power of many enzymes 52 although other factors may sometimes play important role.68 Its origin can be traced to the process of protein folding, whereby the protein attains its 3D structure and its dipoles get oriented. 12,13
The calculated preorganization contributions are negligible compared to the sum of electrostatic and van der Waals energies (Table 2). A positive preorganization energy obtained for C can be attributed to the base-deoxyribose intramolecular interactions because it has the same magnitude (1.5 kcal/mol) in both the solvated nucleoside and dinucleoside monophosphate.
Using the nucleoside model of single-stranded DNA, we obtained insertion free energies (Table 3) that were significantly more negative than experimental ΔGins. This discrepancy is likely due to the absence of the base-stacking and base-phosphate interactions in the nucleoside model. Indeed, the agreement improved for the dinucleoside monophosphate model, although C and T bases remained too stable in the duplex environment. Even though this overstabilization may still reflect the simplified nature of the reference system, it is more likely due to our use of generic LRA/α parameters, which were not optimized for the DNA environment.
Table 3.
The calculated insertion free energies and their components.
| SS modela | Bb | Free Energy (kcal/mol)c |
|||||
|---|---|---|---|---|---|---|---|
| ΔGins (B) | experimentd | ||||||
| dN | C | −2.3 ± 0.1 | −4.8 ± 0.1 | −0.5 ± 0.2 | −7.6 ± 0.4 | −3.9 ± ± 0.8 | |
| T | −0.5 ± 0.1 | −5.2 ± 0.1 | −0.4 ± 0.3 | −6.1 ± 0.5 | −2.1 ± ± 0.5 | ||
| A | −1.3 ± 0.1 | −4.2 ± 0.1 | −0.5 ± 0.3 | −6.0 ± 0.5 | |||
| dNpN | C | −2.3 ± 0.2 | −2.6 ± 0.3 | −0.5 ± 0.2 | −5.4 ± 0.7 | −3.9 ± ± 0.8 | |
| T | −0.9 ± 0.1 | −2.1 ± 0.1 | 0.1 ± 0.3 | −2.9 ± 0.5 | −2.1 ± ± 0.5 | ||
| A | −1.7 ± 0.1 | −1.4 ± 0.1 | −0.6 ± 0.5 | −3.7 ± 0.7 | |||
Although it is strictly speaking not possible to decompose free energies into additive contributions from individual molecules or force-field terms, LRA/α approximation allows to carry out such decomposition with a high rigor (12). The van der Waals term is a major contributor to the calculated ΔGins, pointing to dispersion attraction between stacked DNA bases as important source of the duplex stability. This conclusion is consistent with the results of previous computational studies, including the decomposition of the free energy change for the mutation of a terminal base of a DNA duplex to ‘nothing’ 34, and the loss of the helical structure of DNA duplex in simulations missing London term 69. The electrostatic term also stabilizes DNA duplex, but more so when a correct Watson-Crick base pair is formed. The preorganization term is negligible contributor of the stability of the duplex containing the terminal G•T base pair but contributes −0.5 kcal/mol, i.e. about 10% of the free energy of inserting C or A opposite G. However, even in this most favorable case, the magnitude of electrostatic preorganization is too small to account for the cooperativity of DNA annealing, which amounts to −2 to −3 kcal/mol per base-pair step. 70
The van der Waals components of ΔGins show a large dependence on the reference state (Table 3). For example, the insertion of C opposite G yields ΔGinsvdW of −4.8 and −2.6 kcal/mol for the dN and dNpN reference states, respectively. Because the calculated electrostatic and preorganization components of ΔGins are independent of the reference state, the model-dependent differences in ΔGins mirror those in the van der Waals term. Since there are no stacking interactions in the dN model, these differences indicate that stacking interactions in the 5’-GC, GT, and GA dinucleoside monophosphates are −2.2, −3.1 and −2.8 kcal/mol, respectively. Of course, accounting for stacking in the reference system is fundamentally important, which makes the results calculated with the dNpN model more reliable.
The order of stacking free energies is consistent with the differences in the structural flexibility of the dinucleoside monophosphates obtained by the analysis of histograms of N9-N1 or N9-N9 distances (cf. Figures 1S, 3S and 6S). Using these histograms, stacking free energies can be estimated by counting number of configurations with N9-N1(or N9-N9) distances below and above a reasonable cutoff that separates stacked and unstacked conformations 71. Using 6 Å cutoff, the stacking free energies of GC, GT and GA dinucleoside monophosphates were −1.0, −2.3, and −1.3 kcal/mol, respectively. Interestingly, the unstacked configurations of GT mostly correspond to T-shaped complexes (Figure 4S). The histogram analysis also showed that uncharging one of the bases does not significantly affect the stacking propensity of dinucleoside monophosphates (Figures 2S, 5S and 7S).
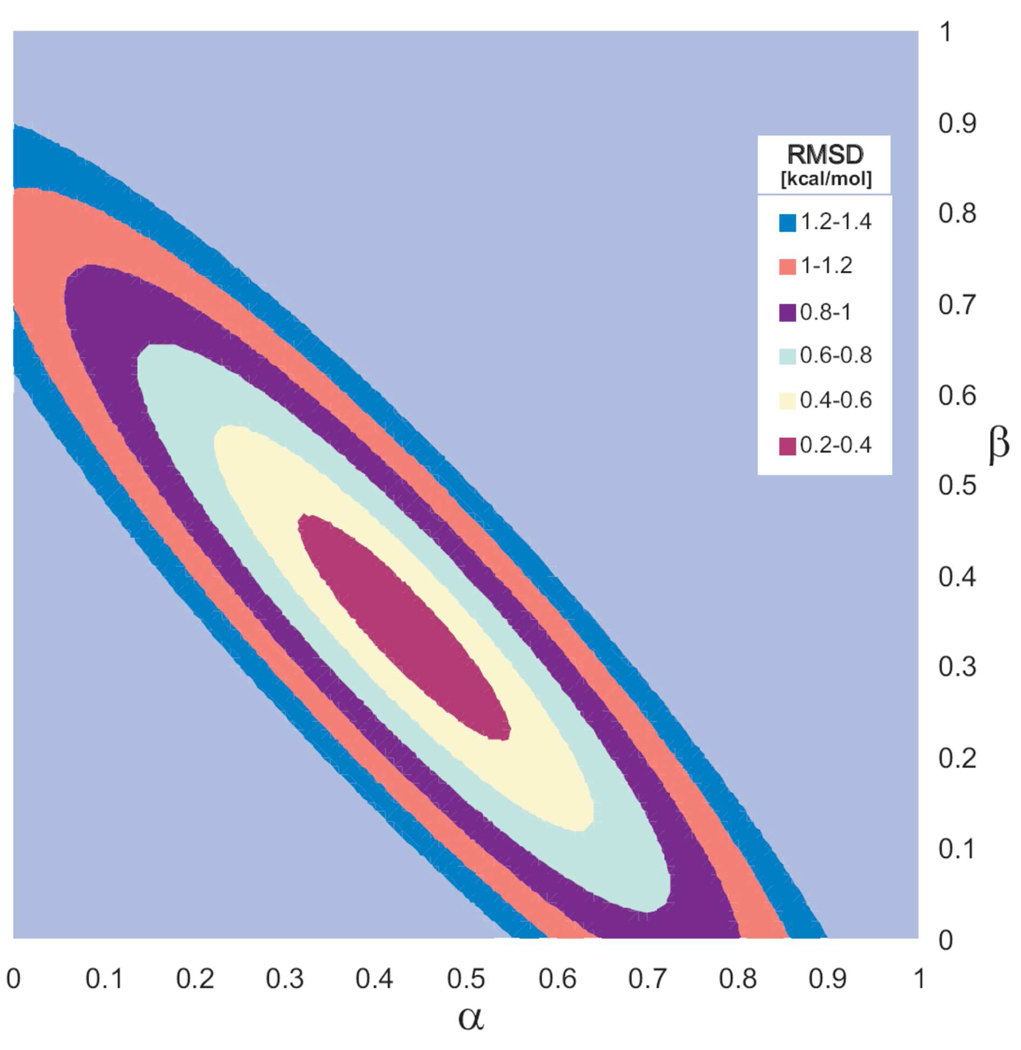
Since the differences in ΔGinsvdW for dN and dNpN reference states are larger (in absolute value) than stacking free energies determined directly by counting stacked and unstacked configurations, the coefficient α used for scaling vdW interactions in the LRA/α approximation should be decreased to better represent stacking interactions. The least-squares fit of LRA/α parameters on experimental data provided the lowest RMSD for β= 0.34 and α= 0.43 (Figure 6). Our refined LRA/α parameter β = 0.34 is consistent with the value of this parameter (β = 0.43) recommended for use in LIE calculations of protein-ligand binding free energies 50 and DNA destabilization by base substitutions 34 because a larger β compensates for the lack of the electrostatic preorganization term in the LIE method. In addition, the refined α parameter of 0.43 decreases the magnitude of ΔGinsvdW so that the LRA/α stacking free energy estimates for dinucleoside monophosphates become closer to those obtained by direct counting of stacked and unstacked configurations, or by quantum mechanical calculations combined with Langevin dipoles solvation model 4.
Figure 6.
Root mean-square deviation of the calculated and experimental insertion, ΔGins(B), as well as ΔΔGA→C and ΔΔTA→C DNA duplex stabilization free energies as a function of the LRA/α empirical parameters α and β. The calculated data were obtained using the dNpN reference state.
Although the refined LRA/α parameters are important to properly describe stacking interactions, their effect on the magnitude of the preorganization contributions to base insertion free energies is within the error bars of the values presented in Table 3, which were obtained with the generic LRA/α parameters. Similarly, the error cancellation renders the use of perfect LRA/α parameters less critical for obtaining reasonably accurate predictions of the relative insertion free energies (eq. 7, Table 4). Thus, the overall DNA duplex stabilization free energies and their components presented in Table 4 are also relatively unaffected by the choice of LRA/α parameters or models describing the single-stranded DNA.
Table 4.
The calculated DNA duplex stabilization free energies and their components.
The relative insertion free energies presented in Table 4 represent the magnitude of DNA stabilization due to replacing wobble G•T or G•A base pairs by a Watson-Crick G•C base pair at the end of DNA double helix. This stabilization is of fundamental importance for assessing intrinsic contribution of DNA polymerases to both their dNTP insertion fidelity and proofreading proficiency. In the case of G•dCTP -> G•dATP mismatch, the electrostatic preorganization was calculated to contribute 2.7 kcal/mol of the total 4.6 kcal/mol binding contribution to the fidelity of DNA replication by T7 DNA polymerase 72. Similarly, earlier LRA/α binding studies of fidelity of DNA polymerase β have shown significant preorganization effects 15, which were attributed by the free energy decomposition to the interactions between the templating base and the base of the incoming dNTP substrate. However, since these studies did not consider dNTP binding in the absence of the protein, it was not possible to convincingly attribute this preorganization to the steric and electrostatic restrictions placed upon the positioning of the template and dNTP bases by the enzyme active site. In fact, it could be argued that the template and dNTP base positioning could originate from stacking interactions with the DNA, or the restrictions imposed by the presence of the phosphodiester backbone or by strong binding of the triphosphate moiety. This possibilities have been excluded by the present calculations, which show that in the absence of the polymerase the preorganization component of the G•C -> G•A mismatch destabilization actually favors the mismatch by 0.1 kcal/mol (Table 4). Although the preorganization term does destabilize the G•T mismatch, the amount of this destabilization is relatively small in the absence of DNA polymerase. These results reinforce the notion that the electrostatic preorganization of the DNA polymerase active site represents an important contribution to DNA replication fidelity 17,73.
Supplementary Material
Acknowledgement
This work was supported by the National Institutes of Health grant 1U19CA10501 and by the Slovenian Research Agency through the Grants No. P1-0201, P1-0002, P1-0294, J1-6653 and Z1-2000 as well as by the WFS scholarship.
Footnotes
Supporting Information Available: Histograms of N9-N1 distances in solvated dinucleotides, and a T-shaped geometry of the GT dinucleotide. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Bloomfield VA, Crothers DM, Tinoco I., Jr. Nucleic Acids : Structures, Properties, and Functions. California: University Science Books: Sausalito; 2000. [Google Scholar]
- 2.SantaLucia J., Jr. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 3.Yakovchuk P, Protozanova E, Frank-Kamenetskii MD. Nucleic Acids Research. 2006;34:564. doi: 10.1093/nar/gkj454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Florián J, Sponer J, Warshel A. J. Phys. Chem. B. 1999;103:884. [Google Scholar]
- 5.Sponer J, Florián J, Ng HL, Sponer JE, Spackova N. Nucleic Acids Research. 2000;28:4893. doi: 10.1093/nar/28.24.4893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Poland D. Cooperative Equilibria in Physical Biochemistry. Oxford, UK: Clarendon Press; 1978. [Google Scholar]
- 7.Luo R, Gilson HSR, Potter MJ, Gilson MK. Biophys. J. 2001;80:140. doi: 10.1016/S0006-3495(01)76001-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Norberg J, Nilsson L. Acc. Chem.Res. 2002;35:465. doi: 10.1021/ar010026a. [DOI] [PubMed] [Google Scholar]
- 9.Warshel A. Proc. Natl. Acad. Sci. USA. 1978;75:5250. doi: 10.1073/pnas.75.11.5250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Warshel A, Naray-Szabo G, Sussman F, Hwang J-K. Biochemistry. 1989;28:3629. doi: 10.1021/bi00435a001. [DOI] [PubMed] [Google Scholar]
- 11.Warshel A. Accts. Chem. Res. 1981;14:284. [Google Scholar]
- 12.Warshel A. J. Biol. Chem. 1998;273:27035. doi: 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
- 13.Warshel A, Florián J. Proc Natl Acad Sci U S A. 1998;95:5950. doi: 10.1073/pnas.95.11.5950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cannon WR, Benkovic SJ. J. Biol. Chem. 1998;273:26257. doi: 10.1074/jbc.273.41.26257. [DOI] [PubMed] [Google Scholar]
- 15.Florián J, Goodman MF, Warshel A. J. Phys. Chem. B. 2002;106:5739. [Google Scholar]
- 16.Florián J, Warshel A, Goodman MF. J. Phys. Chem. B. 2002;106:5754. [Google Scholar]
- 17.Florián J, Goodman MF, Warshel A. Biopolymers. 2003;68:286. doi: 10.1002/bip.10244. [DOI] [PubMed] [Google Scholar]
- 18.Lee FS, Warshel A. J. Chem. Phys. 1992;97:3100. [Google Scholar]
- 19.Sham YY, Chu ZT, Tao H, Warshel A. Proteins Struct. Funct. Genet. 2000;39:393. [PubMed] [Google Scholar]
- 20.Åqvist J, Medina C, Samuelson JE. Protein Eng. 1994;7:385. doi: 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- 21.Gelfand CA, Plum GE, Grollman AP, Johnson F, Breslauer KJ. Biochemistry. 1998;37:7321. doi: 10.1021/bi9803372. [DOI] [PubMed] [Google Scholar]
- 22.Vesnaver G, Chang C, Eisenberg M, Grollman AP, Breslauer KJ. Proc. Natl. Acad. Sci. U.S.A. 1989;86:3614. doi: 10.1073/pnas.86.10.3614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gelfand CA, Plum GE, Grollman AP, Johnson F, Breslauer KJ. Biopolymers. 1996;38:439. doi: 10.1002/(SICI)1097-0282(199604)38:4%3C439::AID-BIP1%3E3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 24.Cuniasse P, Sowers LC, Eritja R, Kaplan B, Goodman MF, Cognet JAH, Le Bret M, Guschlbauer W, Fazakerley GV. Biochemistry. 1989;28:2018. doi: 10.1021/bi00431a009. [DOI] [PubMed] [Google Scholar]
- 25.Kouchakdjian M, Eisenberg M, Johnson F, Grollman AP, Patel DJ. Biochemistry. 1991;30:3262. doi: 10.1021/bi00227a014. [DOI] [PubMed] [Google Scholar]
- 26.Goljer I, Kumar S, Bolton PH. J. Biol. Chem. 1995;270:22980. doi: 10.1074/jbc.270.39.22980. [DOI] [PubMed] [Google Scholar]
- 27.Lah J, Drobnak I, Dolinar M, Vesnaver G. Nucleic Acids Res. 2008;36:897. doi: 10.1093/nar/gkm1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Drobnak I, Seručnik M, Lah J, Vesnaver G. Acta Chim. Slov. 2007;54:445. [Google Scholar]
- 29.Tikhomirova A, Beletskaya IV, Chalikian TV. Biochemistry. 2006;45:10563. doi: 10.1021/bi060304j. [DOI] [PubMed] [Google Scholar]
- 30.Mikulecky PJ, Feig AL. Biochemistry. 2006;45:604. doi: 10.1021/bi0517178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rouzina I, Bloomfield VA. Biophysical J. 1999;77:3242. doi: 10.1016/S0006-3495(99)77155-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tikhomirova A, Taulier N, Chalikian TV. J. Am. Chem. Soc. 2004;126:16387. doi: 10.1021/ja046387d. [DOI] [PubMed] [Google Scholar]
- 33.Ladbury JE, Chowdhry BZ. Biocalorimetry: Applications of calorimetry in the biological sciences. Chichester: John Wiley; 1998. [Google Scholar]
- 34.Bren U, Martinek V, Florián J. J. Phys. Chem. B. 2006;110:10557. doi: 10.1021/jp060292b. [DOI] [PubMed] [Google Scholar]
- 35.Echols H, Goodman MF. Ann. Rev. Biochem. 1991;60:477. doi: 10.1146/annurev.bi.60.070191.002401. [DOI] [PubMed] [Google Scholar]
- 36.Bren U, Martinek V, Florián J. J. Phys. Chem. B. 2006;110:12782. doi: 10.1021/jp056623m. [DOI] [PubMed] [Google Scholar]
- 37.Åqvist J, Hansson T. J. Phys. Chem. 1996;100:9512. [Google Scholar]
- 38.Cantor CR, Warshaw MM, Shapiro H. Biopolymers. 1970;9:1059. doi: 10.1002/bip.1970.360090909. [DOI] [PubMed] [Google Scholar]
- 39.Randall SK, Eritja R, Kaplan BE, Petruska J, Goodman MF. J. Biol. Chem. 1987;262:6864. [PubMed] [Google Scholar]
- 40.Takeshita M, Chang C-N, Johnson F, Will S, Grollman AP. J. Biol. Chem. 1987;262:10171. [PubMed] [Google Scholar]
- 41.Job P. Ann. Chim. (Paris) 1928;9:113. [Google Scholar]
- 42.Marky LA, Breslauer KJ. Biopolymers. 1987;26:1601. doi: 10.1002/bip.360260911. [DOI] [PubMed] [Google Scholar]
- 43.Lah J, Bester-Rogac M, Perger T-M, Vesnaver G. J. Phys. Chem. B. 2006;110:23279. doi: 10.1021/jp062796f. [DOI] [PubMed] [Google Scholar]
- 44.Lah J, Prislan I, Krzan B, Salobir M, Francky A, Vesnaver G. Biochemistry. 2005;44:13883. doi: 10.1021/bi0512952. [DOI] [PubMed] [Google Scholar]
- 45.Lah J, Simic M, Vesnaver G, Marianovsky I, Glaser G, Engelberg-Kulka H, Loris R. J. Biol. Chem. 2005;280:17397. doi: 10.1074/jbc.M501128200. [DOI] [PubMed] [Google Scholar]
- 46.Lah N, Lah J, Zegers I, Wyns L, Messens J. J. Biol. Chem. 2003;278:24673. doi: 10.1074/jbc.M303194200. [DOI] [PubMed] [Google Scholar]
- 47.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipies. Oxford: Cambridge University Press; 1992. [Google Scholar]
- 48.Lee FS, Chu ZT, Bolger MB, Warshel A. Prot. Eng. 1992;5:215. doi: 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
- 49.Levy RM, Belhadj M, Kitchen DB. J. Chem. Phys. 1991;95:3627. [Google Scholar]
- 50.Hansson T, Marelius J, Åqvist J. J. Comput.-Aided Mol. Des. 1998;12:27. doi: 10.1023/a:1007930623000. [DOI] [PubMed] [Google Scholar]
- 51.Kubo R. Journal of the Physical Society of Japan. 1957;12:570. [Google Scholar]
- 52.Warshel A, Sharma PK, Kato M, Xiang Y, Liu H, Olsson MHM. Chem. Rev. 2006;106:3210. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 53.Born M. Z. Phys. 1920;1:45. [Google Scholar]
- 54.Warshel A, Russell ST. Q. Rev. Biophys. 1984;17:283. doi: 10.1017/s0033583500005333. [DOI] [PubMed] [Google Scholar]
- 55.Roux B, Yu HA, Karplus M. J. Phys. Chem. 1990;94:4683. [Google Scholar]
- 56.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. New York: John Wiley & Sons; 1991. [Google Scholar]
- 57.Florián J, Goodman MF, Warshel A. Journal of Physical Chemistry B. 2000;104:10092. [Google Scholar]
- 58.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr., Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. [Google Scholar]
- 59.Marelius J, Kolmodin K, Feierberg I, Åqvist J. J. Mol. Graphics and Modeling. 1999;16:213. doi: 10.1016/s1093-3263(98)80006-5. [DOI] [PubMed] [Google Scholar]
- 60.King G, Warshel A. J. Chem. Phys. 1989;91:3647. [Google Scholar]
- 61.Sham YY, Warshel A. J. Chem. Phys. 1998;109:7940. [Google Scholar]
- 62.Sawaya MR, Prasad R, Wilson SH, Kraut J, Pelletier H. Biochemistry. 1997;36:11205. doi: 10.1021/bi9703812. [DOI] [PubMed] [Google Scholar]
- 63.Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Physics. 1977;23:327. [Google Scholar]
- 64.Humphrey W, Dalke A, Schulten K. J. Molec. Graphics. 1996;14.1:33. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 65.Mikulecky PJ, Feig AL. Biopolymers. 2006;81:38. doi: 10.1002/bip.20457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dill KA, Truskett TM, Vlachy V, Hribar-Lee B. Annu. Rev. Biophys. Biomol. Struct. 2005;34:173. doi: 10.1146/annurev.biophys.34.040204.144517. [DOI] [PubMed] [Google Scholar]
- 67.Johnson RC, Power TD, Holt JS, Immaraporn B, Monat JE, Sissoko AA, Yanik MM, Zagorodny AV, Cybulski SM. J. Phys. Chem. 1996;100:18875. [Google Scholar]
- 68.Sievers A, Beringer M, Rodnina MV, Wolfenden R. Proc. Natl. Acad. Sci. U.S.A. 2004;101:7897. doi: 10.1073/pnas.0402488101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cerny J, Kabelac M, Hobza P. J. Am. Chem. Soc. 2008;130:16055. doi: 10.1021/ja805428q. [DOI] [PubMed] [Google Scholar]
- 70.Porschke D. Mol. Biol. Biochem. Biophys. 1977;24:191. doi: 10.1007/978-3-642-81117-3_5. [DOI] [PubMed] [Google Scholar]
- 71.Norberg J, Nilsson L. J. A. Chem. Soc. 1995;117:10832. [Google Scholar]
- 72.Florián J, Goodman MF, Warshel A. Proc. Natl. Acad. Sci. U. S. A. 2005;102:6819. doi: 10.1073/pnas.0408173102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Martínek V, Bren U, Goodman MF, Warshel A, Florián J. FEBS Letters. 2007;581:775. doi: 10.1016/j.febslet.2007.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Peyret N, SantaLucia J., Jr. HyTher version 1.0. Wayne State University; [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.