Error Effects in Anterior Cingulate Cortex Reverse when Error Likelihood Is High

Abstract

Strong error-related activity in medial prefrontal cortex (mPFC) has been shown repeatedly with neuroimaging and event-related potential studies for the last several decades. Multiple theories have been proposed to account for error effects, including comparator models and conflict detection models, but the neural mechanisms that generate error signals remain in dispute. Typical studies use relatively low error rates, confounding the expectedness and the desirability of an error. Here we show with a gambling task and functional magnetic resonance imaging that when losses are more frequent than wins, the mPFC error effect disappears, and moreover, exhibits the opposite pattern by responding more strongly to unexpected wins than losses. These findings provide perspective on recent ERP studies and suggest that mPFC error effects result from a comparison between actual and expected outcomes.

Introduction

Medial prefrontal cortex (mPFC), and especially the anterior cingulate cortex (ACC) subregion of mPFC, is critically involved in performance monitoring and cognitive control, as revealed by ERP and functional magnetic resonance imaging (fMRI) studies (Carter et al., 1998; Botvinick et al., 1999; Gehring and Knight, 2000; MacDonald et al., 2000; Scheffers and Coles, 2000). Performance monitoring is essential to executive control wherein a central executive or supervisory attentional system takes control when detecting that automated processes (or schema) may lead to undesirable outcomes (Norman and Shallice, 1986). Perhaps the most obvious signals for the need to exert greater control are errors, which strongly activate mPFC (Gemba et al., 1986). Various theories have been proposed to account for error effects, and these can be roughly classified into categories of monitoring and detecting discrepancies (Scheffers and Coles, 2000; Oliveira et al., 2007), response conflict (Yeung et al., 2004), response sequences (Steinhauser et al., 2008), and conjunctions of events (Holroyd et al., 2005).

Theories of discrepancy detection can be further divided into error detection based on outcomes that are unintended (Scheffers and Coles, 2000) versus outcomes that are unexpected (Luu and Pederson, 2004; Holroyd and Krigolson, 2007; Oliveira et al., 2007). The distinction is subtle but leads to starkly divergent predictions. In most fMRI studies, errors are relatively infrequent, occurring on well under half of the trials (Carter et al., 1998; Kiehl et al., 2000; but see Paulus et al., 2002, 2005). Consequently, errors are both infrequent and unintended, so the two effects are confounded. Nonetheless, fMRI results show that expected errors yield smaller error effects (Brown and Braver, 2005). A recent ERP study deconfounded errors and expectancies (Oliveira et al., 2007). That study showed evidence that the ERN might reverse; i.e., the source of the ERN increased activity when an unexpected correct message was received rather than an error message; however, a similar study observed opposing results (Holroyd and Krigolson, 2007). Another fMRI study with error rates >50% used blockwise analysis, hence, the event-related responses for correct versus error trials within a block were not analyzed (Paulus et al., 2002). So it is not yet clear whether error effects seen in neuroimaging studies of mPFC will reverse when errors are more common than correct responses.

In the present study, we sought to directly discriminate among potential mechanisms for feedback error detection using fMRI and a gambling task. Crucially, subjects are motivated to choose a gamble with a low probability (LP) of winning instead of choosing a sure win, because the gamble payoff is large if won. In this way, subjects frequently chose a gamble that they intend but do not expect to win. If mPFC compares actual versus intended outcomes, then mPFC activity should be greater for losses than wins, even when losses are more likely. In contrast, if mPFC activity reflects actual versus expected outcomes, then mPFC activity should show a striking reversal effect—it should be greater for wins than losses when wins are unlikely.

Materials and Methods

Participants.

Data from 21 participants were collected; however, one individual had also participated in a behavioral-only version of the task for a previous study (Jessup et al., 2008), and consequently that participant's data were not analyzed; mean (SD) age of the remaining 20 subjects was 21.6 (3.94), of whom 10 were female. A $10 payment was provided for each hour of the experimental participation, as well as a bonus, equal to the sum of the amount that the participant won over all trials.

Procedure.

The repeated trial descriptive choice task described previously (Jessup et al., 2008) was used, in which choices were made with and without feedback, with two probability conditions—high (HP) and low (LP)—using fMRI. More details concerning the task can be found in the earlier behavioral study. Briefly, in the HP condition, subjects performed a two-alternative forced choice (2AFC) task between a certain win (sure thing) of 3 cents and a risky alternative (gamble) that paid a mean of 4 cents with probability 0.8, otherwise nothing, for an expected value of 3.2 cents per trial. In the LP condition (Fig. 1), subjects again chose between a certain win of 3 cents and a risky alternative, but the alternative now paid a mean of 64 cents with probability 0.05, otherwise nothing, for an expected value of 3.2 cents per trial. Thus, the expected values for the risky options in the HP and LP conditions were the same, but in the HP condition, subjects usually won the gamble if chosen, whereas in the LP condition, subjects usually lost the gamble if chosen. They were nonetheless motivated to choose the gamble often in both situations due to the relatively high payoff of a winning gamble in the LP condition.

Figure 1.

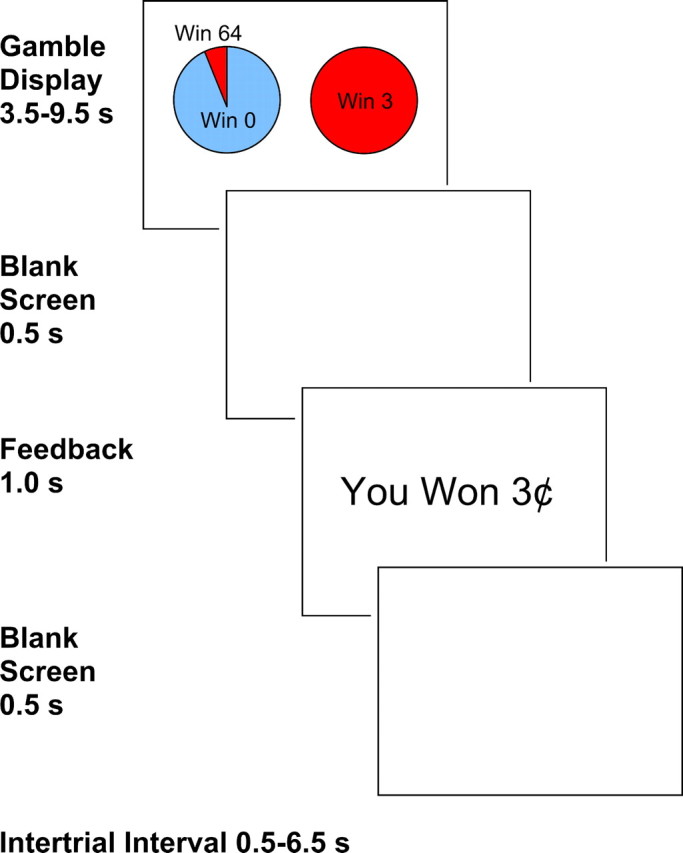
Onset and length of each trial and intertrial interval. An example choice from the LP condition is shown. After selecting an option, participants wait until the gamble display disappears and a blank screen is shown. This is followed by feedback indicating the outcome of the choice. Here, the participant chose the sure thing of 3 cents. This feedback is followed by another blank screen and then a fixation cross during the intertrial interval. The means for the pseudo-exponentially distributed gamble display and intertrial interval were 4.5 and 1.5 s, respectively.

Each participant completed one 60 trial block for each of the two different feedback conditions (feedback or none) crossed with the two probability conditions (LP or HP). On each trial participants were informed how much they could win from each option as well as the probability of winning. In this paper we are only reporting data from the feedback conditions. Each participant gave informed consent and the study was approved by the Indiana University Institutional Review Board.

Figure 1 presents the trial timing. The gamble display was shown for a variable time length (3.5–9.5 s) using a quasi-exponential distribution with a mean of 4.5 s, to allow optimal event-related estimation of the fMRI BOLD response to the gamble cue and decision (Dale, 1999). This was followed by 0.5 s of blank screen and then outcome feedback for 1 s. Last, a blank screen was presented for 0.5 s followed by a variable intertrial interval (ITI) using a quasi-exponential distribution (ITI; 0.5–6.5 s) with fixation cross resulting in a mean 1.5 s fixation (2 s mean ITI including the blank screen). The stimulus onset was timelocked to the scanner pulse. Each of the four runs lasted 9.5 min, with 30 s of fixation time at the run onset and a variable amount of fixation at the end of the run.

fMRI acquisition and data preprocessing.

The experiment was conducted with a 3 tesla Siemens Trio scanner using a phased-array eight-channel head coil and the imaging data acquired at a 30° angle from the anterior commissure–posterior commissure line to maximize orbital and ventral sensitivity (Deichmann et al., 2003), using a gradient echo T2* weighted echo planar imaging sequence, [33 × 4 mm interleaved slices; TE = 25 ms; TR = 2000 ms; matrix, 64 × 64 voxels; field of view, 192 × 192 mm]. 285 images were collected in each run for a total of 1140 functional scans. High resolution T1 weighted images for anatomical data were collected at the end of each session.

SPM5 (Wellcome Department of Imaging Neuroscience, London, UK; www.fil.ion.ucl.ac.uk/spm) was used for preprocessing and data analysis. The data for each participant was slice-time corrected, realigned using a 6 parameter rigid body spatial transformation, coregistered to their structural image, the structural was normalized to the standard Montreal Neurological Institute (MNI) space and the warps were applied to the functional images, and then the functional images were spatially smoothed using a 8 mm Gaussian kernel.

fMRI analysis.

We examined regional differences in the blood oxygenation level-dependent (BOLD) response across conditions using a general linear model (GLM) with random effects. Each estimated model included a baseline regressor applied to every scan as well as 6 movement-based regressors generated from the realignment preprocessing step. Additionally, a high pass filter cutoff of 128 and a correction for serial correlation were applied to each model estimate.

Analysis was built around the notion that two key phases existed in the neurophysiological data: a decision phase and an outcome phase. The decision phase should reflect neural activity associated with deciding on and enacting a decision whereas the outcome phase should reflect neural activity associated with observing the outcome of a choice.

For the decision phase, the model included a separate regressor for each of the 4 combinations of the Feedback and Probability factors when a choice was enacted as well as a separate regressor for each of the same 4 combinations applied to trials on which individuals did not make a choice. On trials when individuals made a choice, each of the regressors had 2 parametric modulators, one which parametrically modulated the decision regressor by the objective value of the larger outcome from the risky gamble and a second which modulated the decision regressor by the response time. This added 2 · 4 = 8 regressors. Further, a temporal modulator which allowed for a linear change in activation across all trials within a block was added to each of the 4 decision regressors, adding 1 · 4 = 4 regressors.

For the outcome phase, 3 separate regressors were applied to each of the 2 (LP and HP) feedback blocks, one for when individuals received the sure thing feedback, one for when individuals received the risky option small outcome (i.e., the “loss”) and one for when individuals received the risky option large outcome (i.e., the “win”). This last regressor was parametrically modulated by the amount won, adding 1 · 2 = 2 regressors.

Consequently, the maximum number of regressors was 20 for the decision phase and 8 during the outcome phase resulting in 28 event-based regressors, in addition to the baseline regressor which was applied to every scan and the 6 regressors representing the realignment estimates. The event-based regressors were then convolved with a canonical hemodynamic response function and then entered into the GLM matrix.

Results

Behavioral analyses

Behaviorally, individuals showed a slight preference for the sure thing option in the LP condition P(sure thing) = 0.54 and a slight preference for the risky option in the HP condition P(sure thing) = 0.48, conforming to the typical pattern for experiential choice and feedback-based decisions (Barron and Erev, 2003; Hertwig et al., 2004; Weber et al., 2004; Jessup et al., 2008) however the difference in sure thing preference between conditions was not significant.

Neuroimaging analyses

All significant regions were identified by a whole brain analysis using a Bonferroni corrected cluster threshold of p < 0.05 as calculated with SPM5, with each individual voxel within these clusters surpassing an uncorrected threshold of p < 0.001. For the sake of clarity, the presented t statistics refer to uncorrected activation values for the specified contrast on the relevant region of interest (ROI). ROIs were defined as the region of contiguous voxels (i.e., a cluster) showing a significant activation. (See Table 1 for a complete list of regions significant at the corrected cluster level.)

Table 1.

Significant clusters in the Outcome × Probability interaction and HP (Lost > Won) outcome contrasts

Cluster level			Voxel level
Contrast	p-corr	k	PFWE	pFDR	T	Z	x, y, z	L/R	Structure
Int	1.56 * 10−13	1100	0.003	0.001	11.71	5.55	[10; 14; 34]	R	ACC
Int	5.33 * 10−15	1274	0.094	0.003	8.60	4.89	[16; 8; −8]	R	Ventral striatum
Int	1.40 * 10−5	322	0.308	0.007	7.60	4.62	[−6; −32; −6]	L	Midbrain
Int	0.009	132	0.427	0.008	7.20	4.50	[−12; 2; −8]	L	Ventral striatum
Int	1.12 * 10−11	892	0.430	0.008	7.19	4.49	[−32; 16; 10]	L	Insula
HP	0.0118	132	0.6596	0.3175	6.54	4.28	[−30; 22; 0]	L	Insula
HP	0.0280	110	0.6954	0.3175	6.45	4.25	[−50; 14; 0]	L	Inferior frontal gyrus
HP	0.0181	121	0.9105	0.3175	5.82	4.02	[4; 18; 38]	R	ACC

Note. All clusters listed were significant at the p < 0.05 corrected level. p-corr, Corrected cluster p value; k, number of contiguous voxels; pFWE, family-wise error p value; pFDR, false discovery rate p value; Int, interaction.

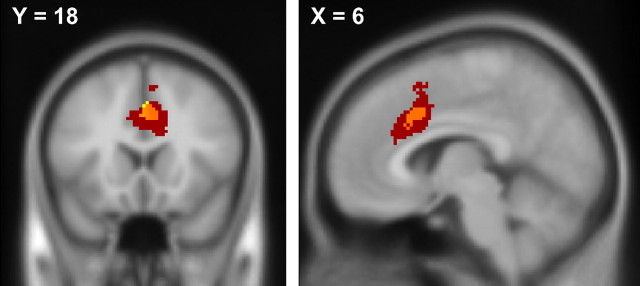
We began by examining the interaction between probability of winning (LP or HP) and outcome (won or lost) when participants chose the risky option. Because rewards were given probabilistically, it was possible for subjects to never win when choosing the risky option. In the rare win situation, this possibility of never winning increased because the likelihood of winning was lower than in the frequent win situation. Hence, only participants who won in both conditions were included in the analysis, 14 in total. The modal number of win events in the LP condition was 2, ranging from 1 to 6 (mean = 2.36, median = 2). A significant interaction of activity was observed in ACC (cluster size k = 1100, p < 5.97 * 10⁻¹⁵, contrast of activation for the cluster: t₍₁₃₎ = 6.06, p < 4.02 * 10⁻⁵, uncorrected; peak voxel MNI coordinates: [10,14,34]). Figure 2 shows the significant cluster of activity in the ACC. The mean peak activation for the four regressors in the interaction contrast as well as their time courses of activation are shown in Figure 3. Examination of the regressor magnitudes in Figure 3 revealed that this was a crossover interaction, as Lost > Won in the HP condition (t₍₁₃₎ = 3.35, p < 0.0052), but Won > Lost in the LP condition (t₍₁₃₎ = 5.96, p < 4.70 * 10⁻⁵). This finding is consistent with a comparison of actual versus expected outcomes but not with a comparison of actual versus intended outcomes.

Figure 2.

ACC significant clusters. Coronal (left) and sagittal (right) views of significant clusters of activation in the ACC for the interaction contrast between probability condition and outcome when choosing the risky option (red), the contrast between outcomes in the HP condition (yellow) which corresponds to the traditional paradigm used for testing the intended outcome discrepancy hypothesis, and where the two contrasts overlap (orange). X = 6, Y = 18, Z = 36, MNI coordinate space.

Figure 3.

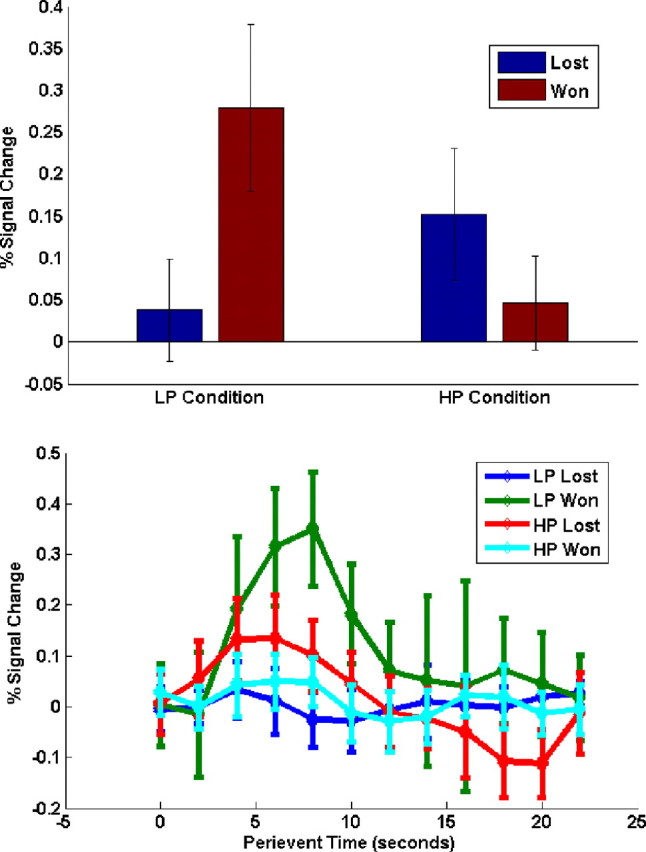
Bar plots of regressors and their time courses of activation. Upper image, Bar plots for the four regressors in the ACC ROI identified using the interaction contrast: LP Condition Won and Lost (left side) and HP Condition Won and Lost. Bars representing Won are shown in red. The right side of the image corresponds with the traditional paradigm used for testing the intended outcome hypothesis. Error bars denote 95% confidence intervals. Lower image, Fitted activation time courses for the four regressors in the ACC ROI identified using the interaction contrast: LP Lost (blue), LP Won (green), HP Lost (red), HP Won (cyan). Error bars denote 95% confidence intervals.

By comparison we also performed an analysis looking for conventional error effects. We contrasted activation on the outcome (Lost > Won) in the HP condition when choosing the risky option, for the same subjects. Note that this contrast corresponds to a more typical test of the discrepancy between actual and intended outcomes explanation for the role of mPFC function, in that errors are both less likely and less preferred than correct outcomes. The contrast revealed a significant activation in the ACC (k = 121, p < 0.0181; contrast of activation for the cluster: t₍₁₃₎ = 4.89, p < 2.95 * 10⁻⁴, uncorrected; peak voxel MNI coordinates: [4,18,38]). Of note, this region overlapped significantly with the ACC region found above via the crossover interaction of outcome and probability factors (Fig. 2). Furthermore, the magnitude and pattern of the contrasts and regressor plots support the expected outcomes over the intended outcomes hypothesis, due to the fact that the rare event in each condition elicits the larger response as opposed to the negative event.

Discussion

The results reveal a striking reversal of the error effect in ACC when losses were more likely than wins. This finding also has implications for other theories of error monitoring by mPFC.

Discrepancy detection

Work with human ERP (Hohnsbein et al., 1989; Gehring et al., 1990; Holroyd and Coles, 2002) has suggested that mPFC detects errors as discrepancies between actual and intended responses or outcomes (Scheffers and Coles, 2000), consistent with findings in monkeys (Ito et al., 2003). Nonetheless, mPFC responds to a loss even when the alternative outcome is a larger loss (Gehring and Willoughby, 2002), suggesting that mPFC responds to absolute wins and losses rather than to relative outcomes. However, in that study, the average outcome across all trials was zero net gain or loss, meaning that both wins and losses could be expected with equal probability. The present results in the context of this previous ERP work (Gehring and Willoughby, 2002) suggests that mPFC responds primarily to the unexpectedness of an event, and if both outcomes occur equally often, then mPFC activity will reflect a bias toward expecting wins rather than losses (Oliveira et al., 2007; Sharot et al., 2007).

Conflict detection

Some human fMRI and ERP studies argue that conflict effects can encompass error effects (Carter et al., 1998; Botvinick et al., 1999; MacDonald et al., 2000; Yeung et al., 2004). According to the conflict model, error effects result from the simultaneous coactivation of the conflicting error and correct responses (Yeung et al., 2004; but see Burle et al., 2005, 2008). Here it is unclear how a conflict detection mechanism could account for the findings, because the error feedback occurs well after the response has been made (Holroyd and Coles, 2002). The stimuli cueing the decision did not differ between subsequent win and loss outcomes so it is unclear how a conflict model could account for any error effects seen later at the time of outcome.

Conjunction detection

Error effects have also been attributed to a conjunction detection for events consisting of a cue followed by an incorrect response conditioned on the cue. In this case, an error signal trains mPFC to respond to conjunctions of an incorrect response to the cue (Holroyd et al., 2005). Of note, this theory should predict that as error frequency increases, so should training of conjunctive error representations. This in turn would predict that error effects should be stronger when error likelihood is higher, whereas the opposite has been found in the current study and previously (Brown and Braver, 2005; Oliveira et al., 2007).

Sequence detection

Errors in a 2AFC task are often followed by a corrective response. Lesion studies of human mPFC argue that mPFC regions showing error effects drive error correction (Modirrousta and Fellows, 2008). Thus, a recent response monitoring theory proposes that errors are detected by the correction process, in that when two actions follow in rapid succession, the first may be an error while the second is a correction response (Steinhauser et al., 2008). Therefore the occurrence of two successive actions in a trial of a 2AFC task suggests that the initial response was an error. It is not clear how the sequence detection explanation can account for the present results. We included a delay between the response cue and feedback, so it is unlikely that any rapid corrective response would account for error effects as predicted by the sequence detection theory (Steinhauser et al., 2008), although error effects based on internal detection rather than external feedback might still be accounted for by such a mechanism.

Relationship to ERP components

Evidence suggests that the ERN may originate from the ACC (Dehaene et al., 1994), in the same region where we find both error and unexpected correct effects here. While we cannot say for certain that the effects we report originate from the same neural mechanisms as the source of the ERN, there are nonetheless many points of contact between the properties of the ERN and our current findings. In particular, several ERP studies have investigated relatively high error rates, in which correct trials may be less expected. Some have found an ERN even when wins and losses were equiprobable (Gehring and Willoughby, 2002; Yeung et al., 2005), potentially reflecting an optimism bias (Oliveira et al., 2007), the basis of which has been localized in part to the ACC (Sharot et al., 2007).

While one previous ERP study has found greater negativities for unexpected correct trials consistent with the present results (Oliveira et al., 2007), other studies have contrasted wins and losses when the probabilities of each were low, ∼25%, and have found inconsistent results. Furthermore, the base-to-peak approach reported by Oliveira et al. has been criticized as potentially confounding the feedback ERN (fERN) with the P300 (Holroyd and Krigolson, 2007). Two such studies of error rates around 75% argued that unexpected errors led to a larger fERN relative to expected errors (Holroyd et al., 2003; Holroyd and Krigolson, 2007), consistent with the present findings, but without a crossover interaction of error by error probability as found here. A similar study at odds with those findings concluded that although the P300 was greater for unexpected outcomes, there was no effect of win probability on the fERN (Hajcak et al., 2005) when trial-by-trial probability cues were given. Nonetheless, a blockwise implicit manipulation of probabilities yielded a greater negativity for unexpected than expected errors (Hajcak et al., 2005), consistent with other findings from implicit blockwise manipulations of error rate (Holroyd et al., 2003; Holroyd and Krigolson, 2007). One possible reconciliation of the existing literature with our stronger finding of reversed error effects may be our use of a lower correct trial probability, which is only 5% here compared with 25% in other studies (Hajcak et al., 2005; Holroyd and Krigolson, 2007). Our lower correct trial probability may thus have induced a stronger expectation of losing, sufficient to overcome the otherwise relatively strong optimism bias.

Potential limitations

One potential limitation of our findings is the small number of wins in the LP condition. This was intentional as it was necessary to have as few LP wins as possible to make them extremely unexpected. Nonetheless, it may be argued that the small number of LP win trials may render the BOLD estimates unreliable. We suggest that the effect is robust for two reasons. First, the unexpected correct effect in the LP condition was statistically stronger than the error effects, even though the exploratory analysis only searched for regions showing an interaction of error by error probability. Typically, conditions with fewer events should have a weaker rather than stronger signal because of noisy estimates. Second, the identified region strongly overlapped with a region that showed main effects of error, consistent with a more general role in detecting unexpected outcomes.

Implications for theories of cognitive control

Taken together, the previous and current results suggest that ACC may compute an index of outcome unexpectedness. This informs a larger discussion about whether mPFC activity signals an anticipated (proactive) versus an actual (reactive) need for greater cognitive control. Our results are consistent with both possibilities (Braver et al., 2007). Reactive control signals may derive from mPFC signals reporting deviation of an actual from predicted outcome (i.e., feedback about winning or losing a gamble), and they are consistent with previous results in monkeys (Ito et al., 2003; Matsumoto et al., 2003) and humans (Holroyd and Coles, 2002). Proactive control signals may derive from mPFC signals of an anticipated outcome, as suggested by work in monkeys (Amador et al., 2000; Shidara and Richmond, 2002) and humans (Brown and Braver, 2005, 2007; Sohn et al., 2007; Aarts et al., 2008; Brown, 2009).

Our current modeling work suggests a theoretical role for these prediction and comparison signals as computed by the ACC (Alexander and Brown, 2008), and how they may contribute to cognitive processes of decision-making. ACC signals the unexpectedness of the outcomes of an action, both good and bad, similar to the prediction error observed in dopamine-mediated systems (Schultz et al., 1997; Holroyd and Coles, 2002; O'Doherty et al., 2003; Behrens et al., 2007). Of note, the expectedness of an outcome may be learned from experience of its actual probability of occurrence, but expectedness and probability are not necessarily identical, as seen in the optimism bias (Sharot et al., 2007) which may reflect greater reward sensitivity (Torrubia et al., 2001). Theoretically, signals representing expected outcomes could serve both as a basis for comparison with actual outcomes and as a forward model for cognitive and decision-making processes, analogous with motor control (Shadmehr and Wise, 2004). This would allow for taking into account the expected outcome of a planned action before execution (Haggard, 2008). Then, if an error is predicted, control may be implemented proactively (Braver et al., 2007) to avoid the risk of an error (Magno et al., 2006; Brown and Braver, 2007). Unexpected outcome signals as found here provide exactly the kind of training signal that would be needed to continually update the learned expectancies of the possible outcomes of an action, as well as drive control signals to correct errors (Modirrousta and Fellows, 2008) or avoid them in the future (Braver et al., 2007).