Quantile Regression With Measurement Error

Abstract

Regression quantiles can be substantially biased when the covariates are measured with error. In this paper we propose a new method that produces consistent linear quantile estimation in the presence of covariate measurement error. The method corrects the measurement error induced bias by constructing joint estimating equations that simultaneously hold for all the quantile levels. An iterative EM-type estimation algorithm to obtain the solutions to such joint estimation equations is provided. The finite sample performance of the proposed method is investigated in a simulation study, and compared to the standard regression calibration approach. Finally, we apply our methodology to part of the National Collaborative Perinatal Project growth data, a longitudinal study with an unusual measurement error structure.

1. INTRODUCTION AND MOTIVATION

Quantile regression, proposed by Koenker and Bassett (1978), has emerged as an important statistical methodology. By estimating various conditional quantile functions, quantile regression complements the focus of classical least squares regression on the conditional mean and offers a systematic strategy for examining how covariates influence the entire response distribution. It has been used in a wide range of applications including economics, biology, ecology, and finance.

Often, the covariates of interest, here denoted by x, are not observable and instead are measured with error. It is well known that such errors can sometimes lead to substantial attenuation of estimated effects in mean regression (Carroll et al. 2006). As we illustrate in Section 5, the regression quantiles can also be seriously biased when the covariates contain measurement errors. This paper aims at developing statistical methods and theory that yield consistent quantile estimation in the presence of covariate measurement error.

There is some work on measurement error in quantile regression. He and Liang (2000) considered the case that errors in the response y and x are independent and follow the same symmetric distribution. Their approach yields consistent estimates. However, the equal distribution assumption is very strong and difficult to verify in practice. Chesher (2001) used a small error variance approximation approach, which does not require distributional assumptions on the response y. However, it does not yield consistent estimation, and the calculation is difficult when the error distribution depends on the covariates. Hu and Schennach (2008) and Schennach (2008) proved nonparametric identification of a nonparametric quantile function under various settings where there is an instrumental variable measured on all sampling units. There are many differences between our approach and theirs in terms of generality: our model is less general. There are also differences in implementation: they use sieve-based estimation, which requires choice of tuning constants such as the number of sieve terms as well as constraints on the sieve basis functions in order to estimate densities such as that of the response given the true covariates; our method relies on a simple, straightforward but novel EM-type implementation.

We consider a family of linear quantile regression models

$$y_i={\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\tau }+{\epsilon }_i(\tau ),$$ (1)

where y_i is the response for the ith individual, x_i is its corresponding covariate, and ε_i is the error term, whose τ th quantile is zero conditional on x_i. The distribution of ε_i may depend on x_i. Moreover, we assume that Model (1) holds for all the τ’s, that is, all the conditional quantiles are linear in x_i with quantile-specific coefficient β_0,τ. A special case of Model (1) is the well-known location scale model,

$$y_i={\mathbf{x}}_i^{\top }{\mathit{\gamma }}_1+({\mathbf{x}}_i^{\top }{\mathit{\gamma }}_2){\epsilon }_i,$$ (2)

where ε_i ~ F_ε is independent of x_i. This location-scale model implies that the τ th conditional quantile coefficient ${\mathit{\beta }}_{0,\tau }={\mathit{\gamma }}_1+{\mathit{\gamma }}_2{F}_{\epsilon }^{-1}(\tau )$.

An outline of this paper is as follows. Section 2 describes the basic methodology, while in Section 3 we describe the algorithm in detail. Section 4 gives asymptotic theory. Section 5 describes a simulation study. In Section 6 we apply our methodology to the National Collaborative Perinatal Project (NCPP) investigating the effect of body size in childhood on body size in adulthood. Section 7 gives concluding remarks. Technical details are given in an Appendix.

2. SEMIPARAMETRIC JOINT ESTIMATING EQUATIONS

2.1 Preliminaries and the Case That x Is Observed

Suppose {y_i, x_i} is a random sample from Model (1) with sample size n, where x = (x₁ … x_p)^⊤ is a p-dimensional covariate. Then an estimating equation for β_0,τ can be written as

$$n^{-1}\sum _{i=1}^n{\mathrm{\Psi }}_{\tau }(y_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_{\tau }){\mathbf{x}}_i=0,$$ (3)

where Ψ_τ(u) = τ − I{u < 0}, I{·} denotes the indicator function, and β_τ ∈ R^p is a p-dimensional unknown coefficient vector. Actually, of course, the indicator function means that (3) may not have an exact zero, and what instead is done is to recast the issue as a minimization problem, and then use linear programming to solve this minimization problem. Thus, (3) is a slight abuse of notation, but since everything else involving observed data is an estimating equation that will have a zero, we will use the estimating equation nomenclature. The solution of equations (3) is proven to be a consistent estimate of β_0,τ. When x is measured with error and instead only a surrogate w_i is observed, naively replacing x_i by the observed w_i will result in substantial bias. We construct new estimating equations which take the measurement errors into account, and result in consistent estimation of β_0,τ. The new estimating equations take the form

$${\mathbf{S}}_n^0({\mathit{\beta }}_{\tau })=n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}{\mathrm{\Psi }}_{\tau }(y_i-{\mathbf{x}}^{\top }{\mathit{\beta }}_{\tau })\mathbf{x}·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i)d\mathbf{x}=0,$$ (4)

where f (x|y_i, w_i) is the conditional density of x given the observed (y_i, w_i). The integration in (4) makes the function continuous in its argument. The summand of (4) is E_x{Ψ_τ (y − x^⊤β_τ)x|y, w}, the conditional mean of the original score function given the observed y and w. Letting Ψ_new(y, w, β_τ) = ∫_x Ψ_τ(y − x^⊤β_τ)x · f (x|y, w) dx, it is easy to show that E_y[Ψ_new(y, w, β_0,τ)|w] ≡ 0 for all w. Therefore, Ψ_new(y, w, β_τ) is an unbiased estimating function, that is, has mean zero, and will be the basis for constructing estimating equations. We further impose the usual surrogacy condition that f (y|x, w) = f (y|x), which means the contaminated w does not provide additional information about the response y if the true covariate x is known.

2.2 Two Technical Challenges

Although Equation (4) provides valid estimating equations for the coefficients of interests, β_0,τ, solving such equations is challenging, mainly due to the following two reasons. First, unlike the classical approaches in mean regression, the conditional density f (x|y_i, w_i) does not have any prespecified parametric form. To get a better understanding of this, we can rewrite the conditional density f (x|y_i, w_i) under the surrogacy condition by

$$f(\mathbf{x}\mid y_i,{\mathbf{w}}_i)=\frac{f(y_i\mid \mathbf{x})f(\mathbf{x}\mid {\mathbf{w}}_i)}{{\int }_{\mathbf{x}}f(y_i\mid \mathbf{x})f(\mathbf{x}\mid {\mathbf{w}}_i)d\mathbf{x}}.$$ (5)

In the spirit of quantile regression, we leave the error distribution of ε_i in Model (1) unspecified. Therefore, f (y|x), and consequently, f (x|y_i, w_i) does not have a parametric form. However, we get around this problem by noting that we can link the conditional density f (y|x) to Model (1) by the following equation:

$$f(y\mid \mathbf{x})=\underset{\delta \to 0}{lim}\frac{\delta }{{\mathbf{x}}^{\top }[{\mathit{\beta }}_0({\tau }_y+\delta )-{\mathit{\beta }}_0({\tau }_y)]},$$ (6)

where τ_y = {τ ∈(0, 1): x^⊤β₀(τ) = y}, and β₀(τ) is the true quantile coefficient viewed as a function of τ. To make the presentation clear, we note that β(τ) = (β₁(τ), …, β_p(τ))^⊤ ∈ R^p × (0, 1) is p-dimensional quantile coefficient process on the interval (0, 1), and β_τ = (β_τ,1, …, β_τ,p)^⊤ ∈ R^p is its evaluation specifically at quantile level τ. They are unknown parameters in the estimating equations, while the previously defined β₀(τ) and β_0,τ are the corresponding true values.

Equation (6) is derived from the fact that the conditional quantile function x^⊤β₀(τ) is the inverse function of the conditional distribution function F(y|x). The density function is hence the reciprocal of the first derivative of the quantile function at the corresponding quantile level. This formulation reveals the second challenge in solving the estimating equations—the conditional density f (x|y_i, w_i) involves the entire quantile coefficient process β₀(τ). In other words, the estimating equations (4) need to be solved jointly for all the τ’s, even if one is interested in a particular quantile level τ. Following the arguments above, we extend (4) to a semiparametric joint estimating equations

$$\begin{array}{l}{n}^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}[\tau -I\{y_i-{\mathbf{x}}^{\top }\mathit{\beta }(\tau )<0\}]\\ ·\mathbf{x}·f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\beta }(\tau )\}d\mathbf{x}=0,\end{array}$$ (7)

where f {x|y_i, w_i; β(τ)} = f {y_i|x; β(τ)}f (x|w_i)/∫_xf{y_i|x; β(τ)}f (x|w_i) dx, and f {y_i|x; β(τ)} is the conditional density function of y_i given x that is induced by quantile function x^⊤β(τ), that is, f {y_i|x; β(τ)} = F′{y_i|x; β(τ)} and F{y_i|x; β(τ)} = inf{τ ∈ (0, 1): x^⊤β(τ) > y}. We use f {x|y, w; β(τ)} and f {y|x; β(τ)} to indicate their dependence on the entire unknown quantile process β(τ). The aforementioned true densities f (x|y, w) and f (y|x) can be written as f (x|y, w) = f {x|y, w; β₀(τ)} and f (y|x) = f {y|x; β ₀(τ)}. We note that the estimating function of (7), ∫_x[τ − I{y − x^⊤β(τ) < 0}] · x · f {x|y, w; β(τ)} dx, is a function of τ, and its conditional mean at β₀(τ),

$$\begin{array}{l}{E}_y[{\int }_{\mathbf{x}}[\tau -I\{y-{\mathbf{x}}^{\top }{\mathit{\beta }}_0(\tau )<0\}]\\ ·\mathbf{x}·f\{\mathbf{x}\mid y,\mathbf{w};{\mathit{\beta }}_0(\tau )\}d\mathbf{x}|\mathbf{w}]\equiv 0\end{array}$$ (8)

for all the τ and w, the estimating equations (7) are hence unbiased joint estimating equations. On the other hand, we say that the estimating equations (7) are semiparametric, since the conditional quantile function of y is a parametric function of x at given τ, but the coefficients β(τ) are nonparametric functions of τ. The estimating equations (7) involve the infinite dimensional parametric space β(τ) ∈ R^p × (0, 1).

2.3 The Continuous Case

To estimate β₀(τ), we assume that they are smooth functions on (0, 1), and approximate β(τ) in (7) by natural linear splines with common internal knots Ω = {ε = τ₁ < τ₂ < ··· < τ_kn = 1 − ε}. Let $\mathit{\theta }={({\mathit{\beta }}_{{\tau }_1}^{\top },{\mathit{\beta }}_{{\tau }_2}^{\top },\dots ,{\mathit{\beta }}_{{\tau }_{k_n}}^{\top })}^{\top }$ be the set of quantile coefficients at quantile levels Ω. We define a natural linear spline 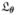(τ): [0, 1] → R^p as p continuous, piecewise linear functions on [0,1] which satisfies 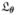(τ_k) = β_τk, and is subject to the constraints that ${\mathfrak{L}}_{\mathit{\theta }}^{\prime }(0)={\mathfrak{L}}_{\mathit{\theta }}^{\prime }(1)=\mathbf{0}$. With a sufficient numbers of knots, that is, k_n → ∞ and ε → 0, the difference between β(τ), and its spline approximation 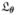(τ) is negligible (de Boor 2001). Consequently, we also approximate the conditional density function f {x|y_i, w_i; β(τ)} by

$$\begin{array}{l}f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\beta }(\tau )\}\\ \approx f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\theta })\\ \stackrel{\wedge}{=}f(y_i\mid \mathbf{x};\mathit{\theta })f(\mathbf{x}\mid {\mathbf{w}}_i)/{\int }_{\mathbf{x}}f(y_i\mid \mathbf{x};\mathit{\theta })f(\mathbf{x}\mid {\mathbf{w}}_i)d\mathbf{x},\end{array}$$ (9)

where

$$f(y_i\mid \mathbf{x};\mathit{\theta })=\sum _{k=1}^{k_n}\frac{{\tau }_{k+1}-{\tau }_k}{{\mathbf{x}}^{\top }{\mathit{\beta }}_{{\tau }_{k+1}}-{\mathbf{x}}^{\top }{\mathit{\beta }}_{{\tau }_k}}I\{{\mathbf{x}}^{\top }{\mathit{\beta }}_{{\tau }_k}\le y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{{\tau }_{k+1}}\}.$$

In other words, we approximate the quantile function x^⊤β(τ) by its spline approximation x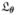^⊤ (τ). In this way, we only need to solve the estimating equations (7) for the grid of internal knots, τ_k’s. We hence reduce the infinite dimensional estimating equations (7) to a finite dimensional case

$$S_n(\mathit{\theta })=n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }\mathit{\theta })\otimes \mathbf{x}·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\theta })d\mathbf{x}=0,$$ (10)

where Ψ(y_i − x^⊤θ) = {Ψ_τ1(y_i −x^⊤β_τ1),…, Ψ_τkn(y_i − x^⊤ × β_τkn)}^⊤ is a k_n-dimensional vector, and ⊗ stands for Kronecker product. We note that Ψ(y_i − x^⊤ θ) ⊗ x is a k_n × p dimensional vector, which consists of k_n sets of original estimating functions {Ψ_τk(y_i − x^⊤β_τk)x}_{k = 1,…,kn} on quantile levels Ω; while f (x|y_i, w_i; θ) is the approximated conditional density of x given the observed (y_i, w_i). We call (10) the working estimating equations, which can be viewed as a spline approximation of the unbiased semiparametric joint estimating equations defined in (7). Solving such equations directly is not easy since they involve integration. In the next section, we outline an iterative EM-type algorithm to obtain the solution of (10).

3. ESTIMATION ALGORITHM

3.1 Preliminaries

The crux of all measurement error problems which have a likelihood flavor is the estimating of the distribution of x given w. Our method, as well as many others, depends on being able to estimate this distribution reasonably well. In practice, this distribution needs to be estimated, and estimating the distribution of x given w depends on the context of the problem.

In nutritional epidemiology, it is fairly common to use parametric and semiparametric methods to transform the observed w-data to normality, and to then assume that the measurement error model is additive with x normally distributed; see Nusser et al. (1990, 1997a, 1997b). In other cases, with replicates of the observed but error-prone predictor, the transformation is to normality and homoscedasticity of the measurement errors (Eckert, Carroll, and Wang 1997), with a flexible model for the distribution of x. See also Carriquiry (2003) for other methods. In the simulation study presented later section, we used this additive transformation model as the basis for estimating f (x|w).

In some instances, when it can be assumed that w = x + u where there are replicated values of w, the distribution of the measurement errors u as well as the latent variable x can be estimated nonparametrically (Li and Vuong 1998; Delaigle, Hall, and Meister 2008), and hence so too can the distribution of x given u be estimated nonparametrically. In the next subsection, we first assume that the crucial distribution is known, and then show how the method is modified when it is estimated. We conjecture that interesting and possibly not parametric-rate properties arise when the distribution of x given w is estimated non-parametrically.

3.2 Basic Algorithm

In this section, we outline an iterative algorithm to obtain a solution of the working estimating equations (10). We will establish in the next section the consistency property of the resulting estimates. The algorithm can be viewed as an nonparametric analogue of the EM algorithm, since the basic components involve iteratively updating the conditional distribution f (x|y_i, w_i, θ) and quantile coefficients θ. However, we do not have specific likelihood functions to work with as in classical EM algorithms. Let ν be the indicator of iteration steps, the main steps of the algorithm are the following:

• Step 1. Set initial values of θ based on uncorrected quantile regression.

• Step 2. Update the distribution f (^ν)(x|y_i, w_i) based on the ${\widehat{\mathit{\theta }}}^{(\nu -1)}=({\widehat{\mathit{\beta }}}_{{\tau }_1}^{(\nu -1)},\dots ,{\widehat{\mathit{\beta }}}_{{\tau }_{k_n}}^{(\nu -1)})$, that is,

  $$f^{(\nu )}(\mathbf{x}\mid y_i,{\mathbf{w}}_i)=\frac{f(y_i\mid \mathbf{x},{\widehat{\mathit{\theta }}}^{(\nu -1)})f(\mathbf{x}\mid {\mathbf{w}}_i)}{{\int }_{\mathbf{x}}f(y_i\mid \mathbf{x},{\widehat{\mathit{\theta }}}^{(\nu -1)})f(\mathbf{x}\mid {\mathbf{w}}_i)dx},$$
  where

  $$\begin{array}{l}f(y_i\mid \mathbf{x},{\widehat{\mathit{\theta }}}^{(\nu -1)})=\sum _{k=1}^{k_n}\frac{{\tau }_k-{\tau }_{k-1}}{{\mathbf{x}}^{\top }({\widehat{\mathit{\beta }}}_{{\tau }_k}^{(\nu -1)}-{\widehat{\mathit{\beta }}}_{{\tau }_{k-1}}^{(\nu -1)})}\\ \times I({\mathbf{x}}^{\top }{\widehat{\mathit{\beta }}}_{{\tau }_{k-1}}^{(\nu -1)}\le y_i<{\mathbf{x}}^{\top }{\widehat{\mathit{\beta }}}_{{\tau }_k}^{(\nu -1)}).\end{array}$$
• Step 3. Estimate ${\widehat{\mathit{\theta }}}^{(\nu )}=({\widehat{\mathit{\beta }}}_{{\tau }_1}^{(\nu )},\dots ,{\widehat{\mathit{\beta }}}_{{\tau }_{k_n}}^{(\nu )})$ based on the new estimating function Ψ_new(y_i, w_i;β_τ) evaluated at f (^ν)(x|y_i, w_i). In order to perform this step, we have to make a numerical approximation to an integral. We do this via translating the problem into a weighted quantile regression problem. Let x̃_i = (x̃_i,1, x̃_i,2, …, x̃_i,m) is a fine grid of possible x_i values, akin to a set of abscissas in Gaussian quadrature. Then the new sample estimating equations are

  $$\begin{array}{l}\sum _{i=1}^n\sum _{j=1}^m{\mathrm{\Psi }}_{{\tau }_k}(y_i-{\stackrel{\sim }{\mathbf{x}}}_{i,j}^{\top }{\mathit{\beta }}_{{\tau }_k}){\stackrel{\sim }{\mathbf{x}}}_{i,j}{f}^{(\nu )}({\stackrel{\sim }{x}}_{i,j}\mid y_i,{\mathbf{w}}_i)=0,\\ k=1,\dots ,k_n,\end{array}$$

  which is a weighted quantile regression with response y_i over the covariates x̃_i,j with weights f (^ν)(x_i,j|y_i, w_i).

Note that the original quantile regression estimating function Ψ_τ(y − x^⊤β_τ)x can be viewed as the first derivative of the logarithm of an asymmetric Laplace distribution (Koenker and Machado 1999)

$$f(y\mid \mathbf{x};{\mathit{\beta }}_{\tau })=\frac{\tau (1-\tau )}{\sigma }exp\left[-\frac{y-{\mathbf{x}}^{\top }{\mathit{\beta }}_{\tau }}{\sigma }\{\tau -I(y-{\mathbf{x}}^{\top }{\mathit{\beta }}_{\tau }\le 0)\}\right]$$

with respect to β_τ. The convergence of the proposed algorithm follows from classical results on the EM algorithm (McLachlan and Krishnan 2008, page 19).

The estimation algorithm involves a turning parameter, the number of quantile levels. The necessary number of quantile levels depends on the underlying distribution of y. In our numerical investigations, we found 40 evenly spaced quantile levels worked well even for heavy-tail distributions such as the log-normal. However, when the dimension of x exceeds 2, evaluating f (^ν)(x|y, w) on a fine grid of x in Step 3 could be computationally undesirable. Instead, we can simulate x̃_i,j from the conditional density of x given w to ensure a sufficient number of x̃_i,j with high densities, and then use importance weights to adjust the bias due to the difference between f (^ν)(x|y, w) and f (x|w). This Monte Carlo integration approach can be implemented to reduce the computational burden. We delay until Section 6 the details of this modified algorithm implementing MC integration.

3.3 When the Distribution of x Given w Is Estimated

Denoting f̃ (x|w) as the estimated conditional distribution of x given w, we further approximate the working estimating equations (10) by

$${\stackrel{\sim }{S}}_n(\mathit{\theta })=n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }\mathit{\theta })\otimes \mathbf{x}·\stackrel{\sim }{f}(\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\theta })d\mathbf{x}=0,$$ (11)

in which f̃ (x|y_i, w_i; θ) is the conditional distribution of x given y_i and w_i with f̃(x|w_i) and θ. The working estimating equations (11) involve two approximations: (a) β(τ) is approximated by a linear spline; and (b) the conditional density f (x|w) is approximated by its estimator. The estimation algorithm remains unchanged except that we need to replace the f (x|w_i) in Step 2 by f̃(x|w_i). Once f (x|w) is estimated, it stays the same in all the iterations. The iteration converges to the solution of the approximated working estimation equations (11), which we denote as θ̂_n. Let β̂_n(τ) = 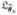(τ) be the natural linear spline extended from θ̂_n. We show in next section that β̂_n(τ) is a consistent estimator of β₀(τ) under certain conditions, especially that f̃ (x|w) is a consistent estimator of f (x|w), k_n → ∞ and k_nn⁻¹ → 0.

4. ASYMPTOTIC PROPERTIES

For a vector x, we use ||x|| to denote its Euclidean norm, and use |x| for its componentwise absolute values. By |a| < 1, we mean that each component of a is bounded by ±1.

In this section, we first list and discuss sufficient conditions for the consistency of β̂_n(τ), with the main result summarized in Theorem 1. We first introduce the conditions on the covariates (x, w).

Assumption 1

The covariate x has bounded support 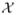, and:

1. the conditional density f (x|w) is bounded away from infinity for all (x, w);

2. there exists a consistent estimator f̂(x|w) of f (x|w), such that, ∀x,

   $$\underset{\mathbf{w}}{sup}\mid \widehat{f}(\mathbf{x}\mid \mathbf{w})-f(\mathbf{x}\mid \mathbf{w})\mid =o_p(1).$$

Remark 1

Assumption 1(i) is quite mild. The assumption that x has compact support is needed in the proof, but we think the reason is more to do with the method of proof than to the actual requirement. Our simulations does not obey this restriction, although due to the nature of the data, our empirical example does obey the restriction.

Recall that β₀(τ) is the true quantile coefficient function, and β_0,τ is the true value at quantile level τ, then for any x ∈ 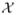, x^⊤β₀(τ) defines a conditional quantile function. We further define a functional $h_{\mathbf{x}}(\tau )=1/{\mathbf{x}}^{\top }{\mathit{\beta }}_0^{\prime }(\tau )$, which is the density of y given x at the τ th quantile. We call this the conditional quantile density function. Its reciprocal is known as the sparsity function (Welsh 1988 and Koenker and Xiao 2004). With these definitions, we now introduce the smoothness conditions on β₀(τ).

Assumption 2

The true coefficient β₀(τ) are smooth functions on (0, 1), and for any x ∈ ,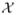

1. 0 < h_x(τ) < ∞ and lim_τ→0 h_x(τ) = lim_τ→1 h_x(τ) = 0;

2. there exist constants M and ν₁,ν₂ > −1 such that its first derivative is bounded by

   $$\underset{\mathbf{x}}{sup}{h}_{\mathbf{x}}^{\prime }(\tau )<M{\tau }^{{\nu }_1}{(1-\tau )}^{{\nu }_2}.$$ (12)

Remark 2

The first condition of Assumption 2 implicitly assumes that the conditional density f (y|x) is continuous, bounded away from zero and infinity, and diminishes to zero as τ goes to 0 and 1. The assumption that 0 < h_x(τ) < ∞ is fairly standard. The equivalent version of this assumption is that 0 < f (ε_i) < ∞, and this is commonly assumed in the quantile regression literature; see, for example, Portnoy (2003) and Koenker (2004). The second condition is on the tail behavior of f (y|x), noting that $h_{\mathbf{x}}^{\prime }(\tau )$ determines how smooth the density function diminishes as the quantile level goes to the two ends. The condition (12) is fairly general, and covers a wide range of distribution families, such as exponential, Gaussian, and Student t distributions.

We now make two further definitions:

• Recall that ${\mathbf{S}}_n^0({\mathit{\beta }}_{\tau })$ is defined at (4), and let ${\mathbf{S}}^0({\mathit{\beta }}_{\tau })=E\{{\mathbf{S}}_n^0({\mathit{\beta }}_{\tau })\}$ be it expectation at the τ th quantile.

  Recall that S_n(θ) is defined at (10). Let S_n(β_τ) be the p× 1 subset of S_n(θ) that corresponds to the τ th quantile, and let S(β_τ) = E{S_n(β_τ)} be its expectation.

We make the following assumptions.

Assumption 3

The true coefficient β_0,τ is the unique solution to the equation S⁰(β_τ) = 0, for all τ ∈ (0, 1), and there exist a ${\mathit{\beta }}_{\tau }^{\ast }$ that uniquely solves the equation S(β_τ) = 0, for all τ ∈ (0, 1).

Assumption 4

There exists a compact set Θ ∈ R^p, such that

$$\mid {\stackrel{\sim }{\mathbf{S}}}_n({\widehat{\mathit{\theta }}}_n)\mid \le \underset{\mathit{\theta }\in \mathbf{\Theta }\times \mathrm{\Omega }}{inf}\mid {\stackrel{\sim }{\mathbf{S}}}_n(\mathit{\theta })\mid +o_p(1).$$

Remark 3

Assumption 3 is the identifiability condition that is commonly assumed in the quantile regression literature, while Assumption 4 is used to ensure that the solution to the approximated working estimating equations is confined to a compact set Θ, which is a standard condition for M and Z estimators.

Moreover, if we are willing to assume that the difference between the true coefficient process β₀(τ) and its spline approximation is negligible, that is, β₀(τ) are linear natural splines with a fixed number of knots K, we obtain the asymptotic normality of θ̂_n. The results are summarized in Theorem 2 below. Additional assumptions for asymptotic normality are listed as follows.

Assumption 2*

The coefficients β₀(τ) are continuous linear splines on [0, 1] with internal knots Ω= {0 < τ₁ < τ₂ < ··· < τ_K<1}.

Let Ψ_new(y_i, w_i, θ) = ∫_xΨ(y_i − x^⊤ θ) ⊗ x · f (x|y_i,w_i; θ) dx, then $S_n(\mathit{\theta })=n^{-1}{\sum }_{i=1}^n{\mathrm{\Psi }}_{\text{new}}(y_i,{\mathbf{w}}_i,\mathit{\theta })$. We further denote V_n = var{S_n(θ₀)} and ${\mathbf{D}}_n=\frac{\partial }{\partial {\mathit{\theta }}_0}{S}_n({\mathit{\theta }}_0)$. We make the following additional assumptions.

Assumption 5

There exists a nonnegative definite matrix V such that V_n → V as n → ∞.

Assumption 6

There exists a positive definite matrix D, such that D_n → D in probability as n → ∞.

Theorem 1

Under Assumptions 1–4, for k_n → ∞, k_nn⁻¹ → 0, β̂_n (τ) is a consistent estimator of β₀(τ), that is,

$$\underset{\tau \in [1/(k_n+1),k_n/(k_n+1)]}{sup}\left|\right|{\widehat{\mathit{\beta }}}_n(\tau )-{\mathit{\beta }}_0(\tau )\left|\right|=o_p(1).$$

Theorem 2

Under Assumptions 1, 2^*, and 3–6,

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)\to \text{N}(0,\mathbf{\sum }),$$

in distribution as n → ∞, where Σ = D⁻¹VD⁻¹.

The proofs of the two theorems are provided in the Appendix.

5. SIMULATION STUDY

5.1 Model Setup

To understand the effects of measurement errors and to demonstrate the performance of our method, we used a location-scale quantile regression model

$$y_i={\beta }_1+{\beta }_2{x}_i+({\gamma }_1+{\gamma }_2{x}_i){\epsilon }_i,$$ (13)

where ε_i = Normal(0, 1). It follows that the actual quantile function of y given x is β_{τ, 1} + β_{τ, 2}x with β_{τ, 1} ≡ 0 and β_{τ, 2} = 2 + 0.5Φ⁻¹(τ). We further assume that the x_i’s are measured with error following one of two models:

Model I (Additive).

$$w_i=x_i+U_i,\text{with}{x}_i\sim \text{N}(4,1)\text{and}{U}_i\sim \text{N}(0,{\sigma }_u^2).$$

Model II (Multiplicative).

$$\begin{array}{l}log(w_i)=log(x_i)+U_i,\\ \text{with}log(x_i)\sim \text{N}(2,1)\text{and}{U}_i\sim \text{N}(0,{\sigma }_u^2).\end{array}$$

In Model I, w and x follow normal distributions, while in Model II, they follow log-normal distributions. We kept the variances of x in Model I or log(x) in Model II and ε to be 1, so that the two models have a constant signal-noise ratio. For each model, we assumed the measurement error U_i follows a normal distribution with mean 0 and variances ${\sigma }_u^2=0.25$ and 0.5. These choices correspond to moderate and larger attenuation which equal R = 4/5 and R = 2/3, respectively.

Regression model scale

It is important to note that the model (13) for the quantile regression function is in the original scale of x_i. In Model II, we are merely stating that the measurement errors are multiplicative.

5.2 Estimation of f (x|w)

To estimate the conditional density of x given w, we assume that the w_i’s were observed from the following model:

$$\begin{array}{l}\mathrm{\Lambda }(w_i,\lambda )=\mathrm{\Lambda }(x_i,\lambda )+U_i,\\ U_i\sim \text{N}(0,{\sigma }_u^2)\text{and}\mathrm{\Lambda }(x_i,\lambda )\sim \text{N}(0,{\sigma }_x^2),\end{array}$$ (14)

where the function Λ(·) is the Box–Cox transformation function, that is, Λ(Z, λ) = log(Z) if λ= 0 and = (Z^λ − 1)/λ otherwise.

The true power parameters λ in Models I and II are 1 and 0, respectively, but are assumed unknown. We estimate λ by maximizing the log-likelihood function of the w_i’s, that is,

$$\begin{array}{l}\widehat{\lambda }=arg\underset{\lambda }{max}{L}_n(\lambda )\\ =-\frac{n}{2}\sum _{i=1}^n\frac{{[\mathrm{\Lambda }(w_i,\lambda )-\overline{\mathrm{\Lambda }}(·,\lambda )]}^2}{n}+(\lambda -1)\sum _{i=1}^{n}log(w_i),\end{array}$$

where Λ̄ is the sample mean. This is a transformation that tries to make Λ (w, λ) = Normal(μ, σ²). For understanding the measurement error, we assume that there exists a subset of 100 replicates (w_i,1, w_i,2) for estimating ${\sigma }_u^2$. With replicates, the variance ${\sigma }_u^2$ can be estimated by half of the sample variance of the difference of the transformed w_i,1 and w_i,2, that is, Λ(w_i,1, λ̂) − Λ(w_i,2, λ̂), so that

$${\widehat{\sigma }}_u^2=\widehat{var}\{\mathrm{\Lambda }(w_{i,1},\widehat{\lambda })-\mathrm{\Lambda }(w_{i,2},\widehat{\lambda })\}/2.$$

With the estimated λ̂ and σ̂², the estimated f (x|w) is

$$\widehat{f}(x\mid w)={\widehat{s}}^{-1}\mathrm{\Phi }\left(\frac{\mathrm{\Lambda }(x,\widehat{\lambda })-\widehat{\mu }}{\widehat{s}}\right)x^{\widehat{\lambda }-1},$$ (15)

where Φ(·) is the density function of the standard normal distribution, and μ̂ and ŝ are the estimated conditional mean and standard deviation of the transformed Λ(x, λ̂) given the observed w. Let Λ̄_w and ${\widehat{\sigma }}_w^2$ be the sample mean and variance of Λ(w_i, λ̂). Then ${\widehat{\sigma }}_x^2={\widehat{\sigma }}_w^2-{\widehat{\sigma }}_u^2$ is an unbiased estimator of the variance of x. It then follows that μ̂ and ŝ in the density (15) are

$$\begin{array}{l}\widehat{\mu }={\overline{\mathrm{\Lambda }}}_w+({\widehat{\sigma }}_x^2/{\widehat{\sigma }}_w^2)\{\mathrm{\Lambda }(w,\widehat{\lambda })-{\overline{\mathrm{\Lambda }}}_w\},\\ \widehat{s}=\sqrt{{\widehat{\sigma }}_x^2\{1-({\widehat{\sigma }}_x^2/{\widehat{\sigma }}_w^2)\}}.\end{array}$$

5.3 Estimators Considered

We performed 100 simulations with n = 500 for each of these models, and computed four estimators:

1. the naive estimator that replaces x by w;

2. the regression calibration estimator, which replaces x by an estimate mean of x given w via the linear regression of x on w, or log(x) on log(w). Specifically, we replace x_i in Model I by (1 − R̂)w̄ + R̂w_i, and replace x_i in Model II by $exp\{(1-\widehat{R})\overline{log(w)}+\widehat{R}log(w_i)+{\widehat{\sigma }}_u^2/2\}$, where R̂ and ${\widehat{\sigma }}_u^2$ and are estimated based on the set of replicates. When applied to ordinary linear regression, the regression calibration estimator is consistent for estimating (β₁, β₂), that is, for the mean regression curve;

3. our method with 40 evenly spaced quantile levels (internal knots), but assuming f (x|w) is known;

4. our method with 40 evenly spaced quantile levels (internal knots), and the conditional density f (x|w) is estimated based on Model (14).

When applying the proposed estimation algorithm, we chose Ω to be a set of 40 evenly spaced quantile levels, the convergence criterion is set to be the average of |θ̂^(ν) − θ̂^(ν−1)| < 0.01, and the maximum iteration steps is 50. In approach (d), the power λ is estimated using the w_i’s, while the variance ${\widehat{\sigma }}_u^2$ is estimated using the 100 pairs of replicates ( $w_{i,1}^{\ast },w_{i,2}^{\ast }$).

5.4 Simulation Results and Discussion

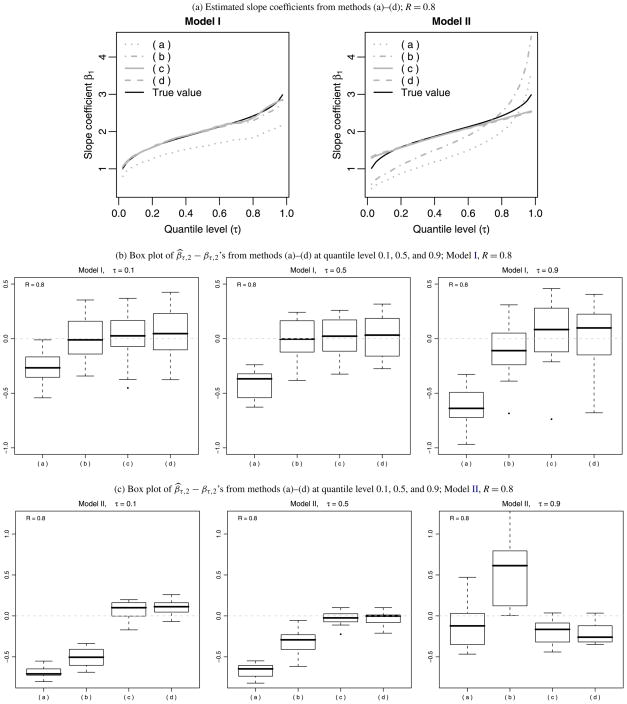
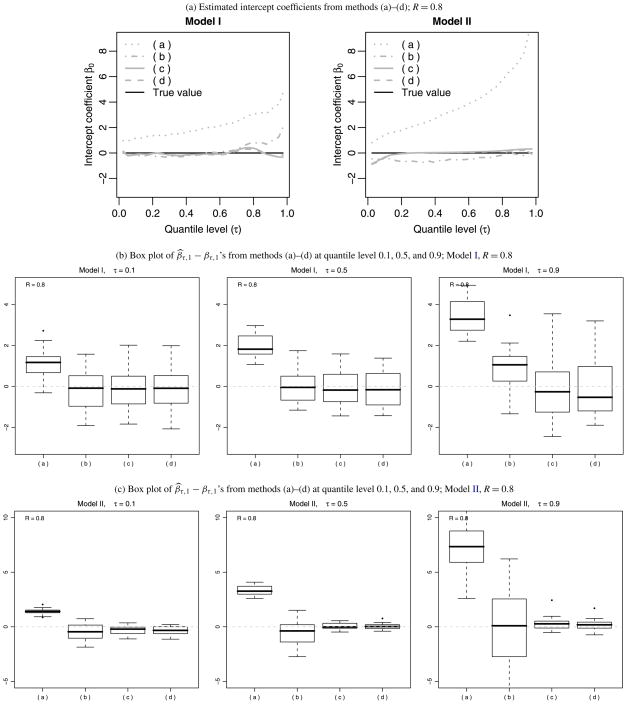
In Figures 1 and 2, we present the resulting estimated slope (Figure 1) and intercept (Figure 2) functions from the four approaches, both Models I and II and with attenuation R = 4/5. The top panel plots the mean of the estimated slope functions with the red solid line representing the true slope function. The middle panel illustrates the sample distributions of β̂_τ,(k) − β_τ from approaches (a)–(d) under Model I at selected quantile levels 0.1, 0.5, and 0.9, where β̂_τ,(k) is the estimated coefficient from the kth Monte Carlo sample, and β_τ is the true value. The bottom panel is its counterpart for Model II. As expected, the naive estimator (dotted gray lines) is badly biased for both normally distributed x and skewed x. The regression calibration estimator (dashed gray lines) worked fairly well for normally distributed x, however, it is badly biased for skewed x. Such bias is more evident under more severe contamination. The proposed method successfully corrected the bias, and brings the estimates fairly close to the true values with all the quantile levels. Moreover, the difference between the estimates using the true f (x|w) and the estimated f (x|w) are small. Similar results (not presented in this paper) were obtained for the more severe attenuation rate R = 2/3.

Figure 1.

Comparison of the estimated slope coefficients from methods (a)–(d) under the contamination rate R = 0.8. In sub-figure (a), the black curve is the true coefficient function. The gray solid and dashed lines are the estimated coefficient functions from the proposed method using the true and estimated f (x|w) respectively. The gray dotted line is the estimated coefficients from the naive method; the gray dash-dotted line is that of the regression calibration method. Note that the box plots are box plots of biases.

Figure 2.

Comparison of the estimated intercept coefficients from methods (a)–(d) under the contamination rate R = 0.8. In sub-figure (a), the black curve is the true coefficient function. The gray solid and dashed lines are the estimated coefficient functions from the proposed method using the true and estimated f (x|w), respectively. The gray dotted line is the estimated coefficients from the naive method; the gray dash-dotted line is that of the regression calibration method. Note that the box plots are box plots of biases.

5.5 Simulation When the Estimated f (x|w) Deviates From the True Function

In the previous simulation study, the conditional density f (x|w) is estimated in the correct model setting. The mean difference between the estimates from the true density and the estimated density is rather small. It is of interest to assess how sensitive the method is to the estimation of f (x|w). To do this, we replace the density function of U in both Models I and II by a t distribution with 3 degrees of freedom, that is:

Model I^*.

$$w_i=x_i+U_i,\text{with}{x}_i\sim \text{N}(4,1)\text{and}{U}_i\sim ({\sigma }_u/\sqrt{3})t_3.$$

Model II^*.

$$\begin{array}{l}log(w_i)=log(x_i)+U_i,\\ \text{with}log(x_i)\sim \text{N}(2,1)\text{and}{U}_i\sim ({\sigma }_u/\sqrt{3})t_3.\end{array}$$

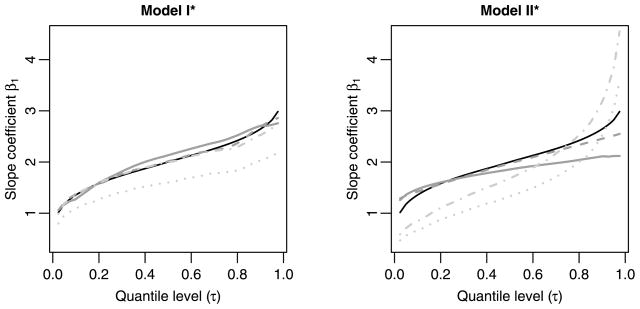
The scalar ${\sigma }_u/\sqrt{3}$ is used to maintain the same error variance as in the previous simulation. We repeated exactly the same estimation procedure (d) assuming U is Gaussian. Consequently, the estimated f (x|w) deviates systematically from the underlying true density. In Figure 3, we plot the resulting estimated slope functions under misspecified Models I and II with attenuation R = 4/5, and compare them with the naive and regression calibration estimates. The solid dark-gray lines are estimated coefficients from the misspecified f (x|w), and the long-dashed dark-gray lines are those from the correctly estimated ones. As expected, the estimated coefficients from the misspecified f (x|w) do exhibit some modest bias, but still much less biased than the naive estimates (the dotted light-gray lines) and those from regression calibration (the dot-dashed light-gray lines).

Figure 3.

Comparison of the estimated slope coefficients when the measurement error model is misspecified with moderately contaminated rate R = 4/5. The subfigure on the left compares the estimated slope functions of Model I, while the one on the right compares those Model II. In all the subfigures, the sold black lines are the true slope coefficients. The solid dark-gray lines are estimators using the proposed method but with the misspecified f (x|w), and the dashed dark-gray ones are estimators using the proposed method for the correct model. As a comparison, the dotted light-gray lines are the naive estimates and the dot-dashed light-gray ones are from regression calibration.

6. APPLICATION

6.1 Data, Model, and Algorithm

We applied our method to part of the National Collaborative Perinatal Project (NCPP; Terry, Wei, and Essenman 2007). The data set included 232 women who were born at Columbia Presbyterian Medical Center from 1959–1963. Their growth measurements, weight, and height were carefully taken by clinical researchers at birth and at 4 months, 1 year, and 7 years. These ages are known to be critical times for growth. The public health researchers were interested in studying the long-term impact of early growth on adult body size. We consider therefore the quantile regression model

$$Q_{\tau }(Y)={\beta }_{\tau ,0}+{\beta }_{\tau ,1}{\mathbb{S}}_{t_1}+{\beta }_{\tau ,2}{\mathbb{S}}_{t_2}+{\beta }_{\tau ,3}{\mathbb{S}}_{t_3}+{\beta }_{\tau ,4}{\mathbb{S}}_{t_4},$$ (16)

where Y is an individual subject’s body mass index (BMI) at age 20, 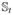stands for her weight at age t, and (t₁, t₂, t₃, t₄) are the four target ages at birth, 4 months, 1 year, and 7 years.

However, these subjects did not in fact all attend clinic at exactly these scheduled times. Since children grow relatively quickly especially at young ages, one or two week’s deviation from the target time may result in substantial measurement error in S_t. If we pretend the actual observation times are the true ones, the coefficient estimates will therefore be biased, as we have demonstrated in our simulations. We apply our method to obtain consistent estimation of the β_τ’s.

Model for f (x|w)

Suppose 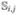is the jth measurement of the ith subject taken at age t_i,j. We assume that they are observed from a underlying weight path of the ith subject, denoted as 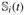. Let T₀ = (t₁, t₂, t₃, t₄) be the set of target ages; and T_i = (t_i,₁, t_i,2, t_i,3, t_i,4) be the actual measurement ages of the ith subject. Note that 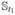is birth weight and is accurately measured at birth, that is, t_i,1 ≡ t₁. We have three covariates of interest that are unobserved, denoted as x_i = {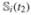, , 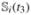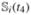}^⊤. In addition, we denote w_i = 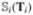= {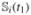, , 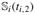, 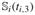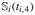}^⊤ as the actual weights at birth and the individual measurement times t_i,2, t_i,3, and t_i,4. Finally, we estimate the density f (x_i|w_i) by the following linear mixed model:

$$\begin{array}{l}log({\mathbb{S}}_{i,j})={\alpha }_{i,0}+{\alpha }_{i,1}{t}_{i,j}+{\alpha }_{i,2}{t}_{i,j}^2+{\alpha }_{i,3}{\mathbb{S}}_{i,1}+e_{i,j},\\ i=1,\dots ,n\text{and}j=2,3,4.\end{array}$$ (17)

We further assume that

$$\begin{array}{l}{({\alpha }_{i,0},{\alpha }_{i,1},{\alpha }_{i,2},{\alpha }_{i,3})}^{\top }=\text{N}\{{({\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3)}^{\top },{\mathrm{\sum }}_{\alpha }\},\\ e_{i,j}=\text{N}(0,{\sigma }_{\gamma }^2).\end{array}$$

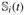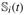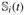Model (17) assumes that the logarithm of is a Gaussian process with mean μ_i(t) = α_i,0 + α_i,1t + α_i,2t² + α_i,3 and variance $(1,t,t^2,{\mathbb{S}}_{i,1}){\mathrm{\sum }}_{\alpha }{(1,t,t^2,{\mathbb{S}}_{i,1})}^{\top }+{\sigma }_{\gamma }^2$. The covariance between and 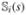is (1, t, t², 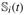)Σ_α (1, s, s², 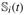)^⊤. The log-transform on 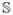is used due to the skewness of weight.

It then follows that x_i has a log-normal distribution, that is,

$$log({\mathbf{x}}_i)\sim \text{N}({\widehat{\mathit{\mu }}}_i,{\widehat{\mathbf{\sum }}}_i),$$ (18)

where

$$\begin{array}{l}{\widehat{\mathit{\mu }}}_i={\mathit{\mu }}_i({\mathbf{T}}_0)+{\mathbf{\sum }}_i({\mathbf{T}}_0,{\mathbf{T}}_i){\mathbf{\sum }}_i{({\mathbf{T}}_i)}^{-1}\{{\mathbf{w}}_i-\mathit{\mu }({\mathbf{T}}_i)\},\\ {\widehat{\mathbf{\sum }}}_i=\mathbf{\sum }({\mathbf{T}}_0)-{\mathbf{\sum }}_i({\mathbf{T}}_0,{\mathbf{T}}_i){\mathbf{\sum }}_i{({\mathbf{T}}_i)}^{-1}{\mathbf{\sum }}_i{({\mathbf{T}}_0,{\mathbf{T}}_i)}^{\top }.\end{array}$$

Algorithmic Details

We choose $\mathrm{\Omega }=\{\frac{1}{41},\frac{2}{41},\dots ,\frac{40}{41}\}$ to be a set of 40 evenly spaced quantile levels. The initial estimate ${\widehat{\theta }}_n^{(0)}$ is obtained by regressing Y over the observed weights assuming the all the t_i,j = t_j, the target ages. Note that x is three dimensional in this example, so evaluating f (x_i|w_i) on a three-dimensional grid can be computationally undesirable. Consequently, we modify Step 3 in our iterative algorithm by using an importance sampling strategy as follows:

• Step 3′(a). For each subject i, generate m = 500 x̃_i,_j’s from the log-normal distribution in (18), the conditional distribution of x_i given w_i.

• Step 3′(b). Calculate the importance sampling weights forx̃_i,j as

  $$\begin{array}{l}{\delta }_{i,j}=\frac{f^{(\nu )}({\stackrel{\sim }{\mathbf{x}}}_{i,j}\mid {\mathbf{w}}_i,y_i)}{f({\stackrel{\sim }{\mathbf{x}}}_{i,j}\mid {\mathbf{w}}_i)}\\ =\frac{f^{(\nu )}(y_i\mid {\stackrel{\sim }{\mathbf{x}}}_{i,j},w_{i,1})}{\int f^{(\nu )}(y_i\mid {\stackrel{\sim }{\mathbf{x}}}_{i,j},w_{i,1})f({\stackrel{\sim }{\mathbf{x}}}_{i,j}\mid {\mathbf{w}}_i)d{\mathbf{x}}_i}.\end{array}$$
• Step 3′(c). Estimate ${\widehat{\mathit{\beta }}}_{{\tau }_k}^{(\nu )}$’s by solving the following weighted estimating equations:

  $$\begin{array}{l}\sum _{i=1}^n\sum _{j=1}^m{\mathrm{\Psi }}_{{\tau }_k}\left(y_i-(1,w_{i,1},{\stackrel{\sim }{\mathbf{x}}}_{i,j}^{\top }){\mathit{\beta }}_{{\tau }_k}\right){(1,w_{i,1},{\stackrel{\sim }{\mathbf{x}}}_{i,j}^{\top })}^{\top }{\delta }_{i,j}=0,\\ k=1,\dots ,k_n.\end{array}$$

We used the same convergence rule as in the simulation study.

6.2 Results

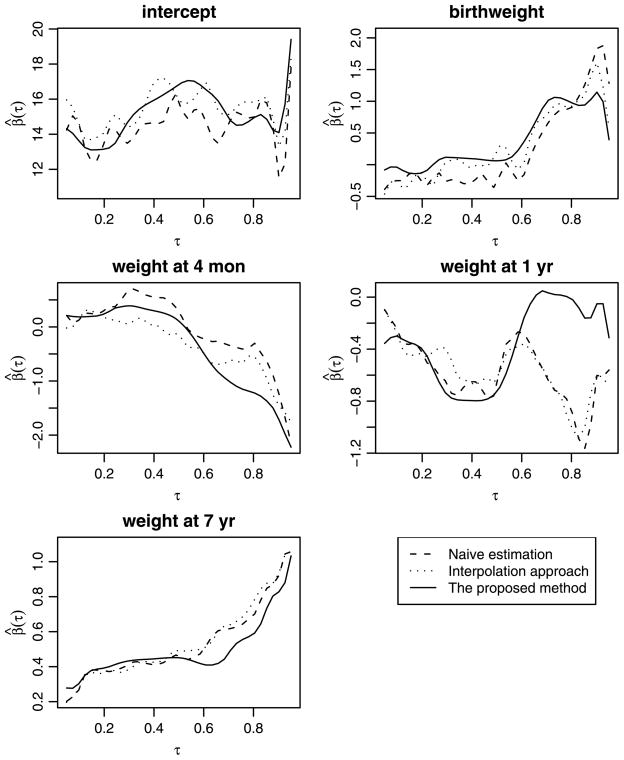
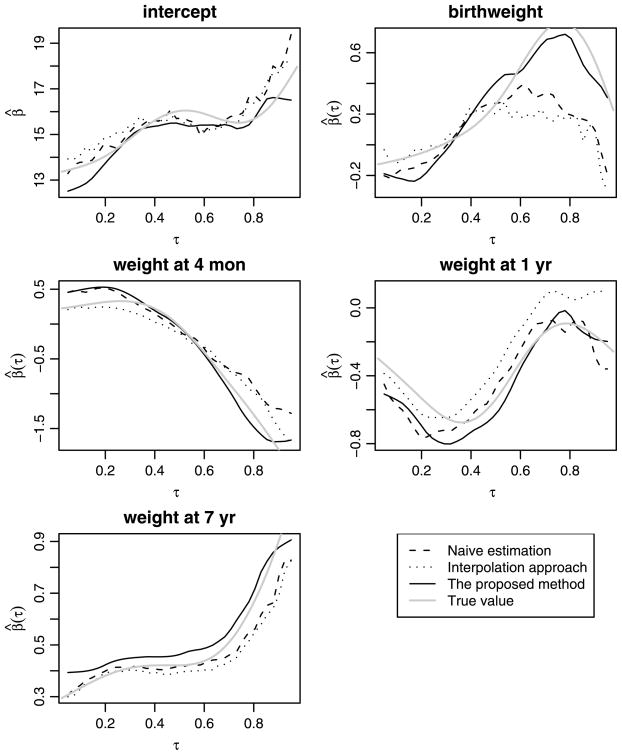
The resulting coefficient estimates are presented in Figure 4 (the solid lines). In Figure 4, for comparison we also plot the estimated coefficients from two alternative approaches. The long-dashed lines are the estimated coefficients from the original uncorrected quantile regression. Another possible approach to correct for measurement error is to fit an interpolation spline for each individual growth path, and use its fitted values at the target ages (t₂, t₃, t₄) as x, the true weights of interests. This approach smooths individual paths to reduce the measurement errors, and has been used in Terry, Wei, and Essenman (2007). The resulting coefficient estimates using this interpolation approach are displayed in Figure 4 as short-dashed lines. We note that the estimated coefficients from our method differ considerably from the naive estimator, especially the coefficients for weights at 1 year and 7 years. In contrast, the fits from the interpolation approach agree with the naive estimators fairly well. Comparing with our estimates, both the naive estimates and the interpolation approach appear to underestimate the impact of weight at age 4 months at upper quantiles, but overestimate the impact of weights at 1 and 7 years at upper quantiles. We performed a bootstrap analysis and found that the differences between two estimates for weight at 1 year are significantly different from each other at quantile levels from 0.71 to 0.85 (as presented in Table 1). The observed differences for weight at 7 years are comparably smaller, and not of statistical significance.

Figure 4.

Estimated coefficients in the NCPP study and its comparison to original QR estimates and the interpolation approach.

Table 1.

Differences between naive and the proposed estimates, and their bootstrap standard errors. β̂ is the estimated coefficient using the proposed method, while β̂_(a) is that from the naive estimation. The standard error of (β̂ − β̂_(a)) is calculated based on 50 bootstrap sample

		Quantile level (τ)
Weight at		0.66	0.68	0.71	0.73	0.76	0.78	0.80	0.83	0.85
1 yr	β̂ − β̂(a)	0.48	0.61	0.66	0.76	0.74	0.79	0.84	1.04	0.98
	Bootstrap SE	0.40	0.41	0.37	0.36	0.39	0.42	0.40	0.40	0.50
	p-value	0.114	0.069	0.038	0.019	0.029	0.030	0.018	0.005	0.024
7 yrs	β̂ − β̂(a)	−0.19	−0.17	−0.12	−0.09	−0.08	−0.12	−0.09	−0.16	−0.12
	Bootstrap SE	0.10	0.10	0.10	0.10	0.11	0.10	0.09	0.09	0.15
	p-value	0.969	0.960	0.883	0.827	0.767	0.881	0.828	0.958	0.973

6.3 Further Investigation via Simulated NCPP-Like Data

To understand the observed differences seen in the NCPP example, we generated synthetic data sets based on the estimated models (16), (17), and (18). To mimic the NCPP data, we chose the same sample size, n = 232, and use the original birth weight 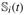and actual measurement ages t_i,2, t_i,3, and t_i,4 for all the subjects. We then generated the weights 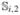, , 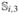and 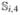from the estimated model (17). In addition, we generated x_i, the underlying “true” weights at ages 4 months, 1 year, and 7 years from the estimated model (17). Finally, we generated BMI at 20 years from the estimated quantile model (16) by

$$Y_i^{\ast }={\widehat{\beta }}_0(u_i)+{\widehat{\beta }}_1(u_i){\mathbb{S}}_{i,1}+{\widehat{\beta }}_2(u_i){\mathbb{S}}_{i,2}+{\widehat{\beta }}_3(u_i){\mathbb{S}}_{i,3}+{\widehat{\beta }}_4(u_i){\mathbb{S}}_{i,4},$$

where β̂_k(·) are smoothed the quantile coefficient process from the estimated quantile models (16), and u_i are iid random draws from Uniform(0, 1). The generated datasets follow the distribution characterized by Models (16), (17), and (18).

We generated 20 synthetic data sets, and repeatedly estimated the coefficients using the naive approach, the interpolation approach and our proposed method. The results are presented in Figure 5. In Figure 5, the solid gray line represents the true co-efficient process that is used to generate the synthetic data sets. The solid black lines are the estimated coefficients using our approach, the long-dashed lines are those from naive estimation, and the short-dashed lines used the interpolation approach. The naive estimates are close to the true values except for the birth weight coefficient, for which the naive estimates seriously underestimated the efficient at the upper quantiles. In contrast, our method appeared to largely correct the bias, as we had hoped and as the simulation led us to expect.

Figure 5.

Estimated coefficients using synthetic data sets and its comparison to original QR estimates and the interpolation approach.

7. DISCUSSION

In this paper, we have proposed a new method to estimate linear quantile regression models when the covariates are measured with error. The method is based on constructing estimating equations jointly for all quantile levels τ ∈ (0, 1), and avoids specifying a distribution for the response given the true covariates. The heart of the algorithm is an EM-type computation. The resulting estimated coefficients are consistent and, if the underlying function is characterized by a spline, asymptotically normally distributed. Numerical results show that the new estimator is promising in terms of correcting the bias arising from the errors-in-covariates, and compares favorably with alternative approaches.

In both simulation studies and an empirical data example, we estimated the conditional density f(x|w) based on a Gaussian model with appropriate transformation to accommodate possible heteroscedasticity and skewness. There are many other ways to estimate this distribution when the scale is known such that w has mean x, for example, deconvolution with or without heteroscedasticity; see Staudenmayer, Ruppert, and Buonaccorsi (2008) for multiple references to the rapidly growing de-convolution literature as well as a semiparametric Bayesian approach. Our results show that use of these methods will still lead to consistent estimation of the quantile function, although asymptotic distributions would have to be addressed separately if such deconvolution approaches were to be used.

The methodology can be extended to longitudinal or clustered data within the working independence context; see for example He, Zhu, and Fung (2002). In such an approach, one ignores the correlations but fixes up the estimated covariance matrix to account for the correlated responses, using so-called sandwich method. That is, each individual contributes an estimating function to the overall estimating equation, and it is those estimating functions to which the sandwich method is applied.

APPENDIX

Recall that β(τ) is a (p + 1) dimensional unknown quantile co-efficient function on (0, 1), and θ = {β_τk:τ_k ∈ Ω} is the set of its quantile coefficients on the quantile level set Ω. Without loss of generosity, we assume in our proof that τ_k = k/(k_n +1) such that Ω = {1/(k_n +1), 2/(k_n +1), …, k_n/(k_n +1)}. Recall that S_n(θ) are the working estimating equations defined in (10), and S(θ) is its expectation. Similarly, we denote $S_n^0(\mathit{\theta })$ as the estimating equations defined in (4) at quantile levels Ω, and S⁰(θ) its expectation. With this notation, we introduce Lemmas A.1 and A.2 which will be used for the proof of consistency.

Lemma A.1

Under Assumptions 1–2, we have

$$k_n^{-1}\left|\right|S({\mathit{\theta }}_0)-S^0({\mathit{\theta }}_0)\left|\right|=o(1).$$ (A.1)

Proof

We first decompose ||S(θ₀)− S⁰(θ₀)|| as

$$\begin{array}{l}\left|\right|S({\mathit{\theta }}_0)-S^0({\mathit{\theta }}_0)\left|\right|\\ =\Vert n^{-1}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }{\theta }_0)\\ \times \mathbf{x}\left[f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\theta }_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\right]d\mathbf{x}|{\mathbf{w}}_i\}\Vert \\ =\Vert n^{-1}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }{\theta }_0)\\ \times \mathbf{x}\left[f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\theta }_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\right]\\ ·I\left\{{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,1/(k_n+1)}<y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}d\mathbf{x}|{\mathbf{w}}_i\}\Vert \\ +\Vert n^{-1}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }{\theta }_0)\\ \times \mathbf{x}\left[f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\theta }_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\right]\\ ·I\left\{y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}d\mathbf{x}|{\mathbf{w}}_i\}\Vert \\ +\Vert n^{-1}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }{\theta }_0)\\ \mathbf{x}\left[f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\theta }_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\right]\\ ·I\left\{y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,1/(k_n+1)}\right\}d\mathbf{x}|{\mathbf{w}}_i\}\Vert \\ \stackrel{\wedge}{=}I+II+\mathit{III}.\end{array}$$ (A.2)

By construction, f(x|y_i, w_i, θ₀) = 0 for y_i ≥ x^⊤β_0,kn/(kn+1), therefore,

$$\begin{array}{l}II=\Vert n^{-1}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}\mathrm{\Psi }(y_i-{\mathbf{x}}^{\top }{\mathit{\theta }}_0)\mathbf{x}f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\\ ·I\left\{y_i>{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}d\mathbf{x}|{\mathbf{w}}_i\}\Vert \\ \le n^{-1}\sum _{k=1}^{k_n}\sum _{i=1}^n{E}_{y_i}\{E_{\mathbf{x}}\{\left|\right|{\mathrm{\Psi }}_{k/(k_n+1)}(y_i-{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k/(k_n+1)})\mathbf{x}\left|\right|\\ ·I\left\{y_i>{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}\mid y_i,{\mathbf{w}}_i\}\}\\ =n^{-1}\sum _{k=1}^{k_n}\sum _{i=1}^n{E}_{\mathbf{x}}\{E_{y_i}\{\left|\right|{\mathrm{\Psi }}_{k/(k_n+1)}(y_i-{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k/(k_n+1)})\mathbf{x}\left|\right|\\ ·I\left\{y_i>{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}\mid \mathbf{x},{\mathbf{w}}_i\}\mid {\mathbf{w}}_i\}\\ \le n^{-1}{k}_n\sum _{i=1}^n{E}_{\mathbf{x}}\left\{2p\left|\right|\mathbf{x}\left|\right|E_{y_i}\left\{·I\left\{y_i>{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}\mid \mathbf{x},{\mathbf{w}}_i\right\}\mid {\mathbf{w}}_i\right\}\\ =n^{-1}{k}_n\sum _{i=1}^n{E}_{\mathbf{x}}\left\{2p\left|\right|\mathbf{x}\left|\right|\text{Prob(}{y}_i>{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\mid \mathbf{x})\mid {\mathbf{w}}_i\right\}\\ =n^{-1}{k}_n/(k_n+1)\sum _{i=1}^n{E}_{\mathbf{x}}(2p|\left|\mathbf{x}\right||\mid {\mathbf{w}}_i)\\ =O(1).\end{array}$$ (A.3)

The second last equation above is followed by the surrogacy condition, and the last equation is due to the fact that Prob(y_i > x^⊤β_0,kn/(kn+1) = 1/(k_n+1) for all i’s. Since E_x(||x|| |w_i) is bounded for all the i’s according to Assumption 1, it follows that $k_n^{-1}II=o(1)$. Using similar arguments, we can also show that $k_n^{-1}\mathit{III}=o(1)$. In what follows, we show that $k_n^{-1}I=o(1)$. Note that I can be bounded by

$$\begin{array}{l}I\le n^{-1}\sum _{k=1}^{k_n}\sum _{i=1}^n{E}_{y_i}\{{\int }_{\mathbf{x}}2p\left|\right|\mathbf{x}\left|\right|\mid f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\theta }}_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\mid \\ \times I\{{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,1/(k_n+1)}\le y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\}d\mathbf{x}\}.\end{array}$$

Since x has bounded support as indicated in Assumption 1, a sufficient condition for $k_n^{-1}I=o(1)$, according to Scheffe’s theorem (Scheffe 1947), is that, for any x ∈ 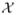, the following holds:

$$\begin{array}{l}\underset{i}{max}\mid f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\theta }}_0)-f\{\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\beta }}_0(\tau )\}\mid \\ \times I\left\{{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,1/(k_n+1)}\le y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}=o_p(1).\end{array}$$

Since f(x|y_i, w_i; θ₀) = f(y_i|x; θ₀)f(x|w)/∫_xf(y_i|x; θ₀)f(x|w) dx and f(x|y_i, w_i;β₀(τ)}= f{y_i|x; β₀(τ)}f(x|w)/∫_xf{y_i|x; β₀(τ)}f(x|w)dx, it again suffices to show that ∀x ∈ ,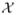

$$\begin{array}{l}\underset{i}{max}\mid f(y_i\mid \mathbf{x};{\mathit{\theta }}_0)-f\{y_i\mid \mathbf{x};{\mathit{\beta }}_0(\tau )\}\mid \\ \times I\left\{{\mathbf{x}}^{\top }{\mathit{\beta }}_{0,1/(k_n+1)}\le y_i\le {\mathbf{x}}^{\top }{\mathit{\beta }}_{0,k_n/(k_n+1)}\right\}=o_p(1).\end{array}$$ (A.4)

Let F_x(y_i)= inf{τ: x^⊤β_0,τ ≥ y_i} be the quantile rank of y_i with respect to the probability measure induced by the quantile function x^⊤β₀(τ), and let $h_{\mathbf{x}}(\tau )=1/{\mathbf{x}}^{\top }{\mathit{\beta }}_0^{\prime }(\tau )$ be the density of y at the τ th quantile. For any y_i that is bounded between x^⊤β_0,1/(kn+1) and x^⊤β_0,kn/(kn+1), there exist a k_i such that x^⊤β_0,ki/(kn+1) ≤ y_i ≤ (x^⊤β_{0,(ki+1)/(kn+1)}. Consequently, the left side of (A.4) is equivalent to

$$\begin{array}{l}\underset{i}{max}\left|\frac{1}{k_n{\mathbf{x}}^{\top }({\mathit{\beta }}_{0,(k_i+1)/(k_n+1)}-{\mathit{\beta }}_{0,k_i/(k_n+1)})}-\frac{1}{{\mathbf{x}}^{\top }{\mathit{\beta }}_0^{\prime }\{F_{\mathbf{x}}(y_i)\}}\right|\\ =\underset{i}{max}\mid h_{\mathbf{x}}({\tau }_i\ast )-h_{\mathbf{x}}\{F_{\mathbf{x}}(y_i)\}\mid \\ \text{for}\text{some}{k}_i/(k_n+1)<{\tau }_i\ast <(k_i+1)/(k_n+1)\\ =\underset{i}{max}\mid h_{\mathbf{x}}^{\prime }\{k_i/(k_n+1)\}O(k_n^{-1})\mid .\end{array}$$ (A.5)

According to Assumption 2,

$$\begin{array}{l}{h}_{\mathbf{x}}^{\prime }\{k_i/(k_n+1)\}<M{\left(\frac{k_i}{k_n+1}\right)}^{{\nu }_1}{\left(1-\frac{k_i}{k_n+1}\right)}^{{\nu }_2}\\ <M{\left(\frac{1}{k_n+1}\right)}^{{\nu }_1}{\left(1-\frac{1}{k_n+1}\right)}^{{\nu }_2}\\ +M{\left(\frac{k_n}{k_n+1}\right)}^{{\nu }_1}{\left(1-\frac{k_n}{k_n+1}\right)}^{{\nu }_2}\\ =O(k_n^{-{\nu }_1})+O(k_n^{-{\nu }_2}).\end{array}$$ (A.6)

Since ν₁, ν₂ > −1, (A.4) is implied by (A.6) and (A.5). The proof of Lemma A.1 is hence complete.

Lemma A.2

Recall that S̃_n(θ) and S_n(θ) are two sets of score functions defined in (10) and (11), respectively. Let S(θ) be the expectation of S_n(θ). Then under Assumptions 1–4, for k_n → ∞, k_nn⁻¹→ 0, we have the following uniform convergence:

$$\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\stackrel{\sim }{\mathbf{S}}}_n(\mathit{\theta })-\mathbf{S}(\mathit{\theta })\left|\right|=o_p(1)\text{as}n\to \infty .$$ (A.7)

Proof

We first bound the left side of (A.7) by

$$\begin{array}{l}\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\stackrel{\sim }{\mathbf{S}}}_n(\mathit{\theta })-\mathbf{S}(\mathit{\theta })\left|\right|\\ \le \underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\stackrel{\sim }{\mathbf{S}}}_n(\mathit{\theta })-{\mathbf{S}}_n(\mathit{\theta })\left|\right|+\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\mathbf{S}}_n(\mathit{\theta })-\mathbf{S}(\mathit{\theta })\left|\right|.\end{array}$$

According to Assumption 1, f(x|w) is bounded away from infinity, and sup_w |f̃(x|w) − f(x|w)| → 0 for any x as n goes to infinity. Therefore, for any i,

$$\mid f(y_i\mid \mathbf{x};\mathit{\theta })\stackrel{\sim }{f}(\mathbf{x}\mid {\mathbf{w}}_i)-f(y_i\mid \mathbf{x};\mathit{\theta })f(\mathbf{x}\mid {\mathbf{w}}_i)\mid =o_p(1),$$

which further implies that |f̃(x|y_i, w_i; θ) − f(x|y_i, w_i; θ)= o_p(1) for all i. Due to the boundness of x, it follows from Sheffe’s theorem that

$$\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\stackrel{\sim }{\mathbf{S}}}_n(\mathit{\theta })-{\mathbf{S}}_n(\mathit{\theta })\left|\right|=o_p(1).$$ (A.8)

Therefore, to show (A.7), we only need to show that, for any ε,

$$\text{pr}\left(\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{sup}{k}_n^{-1}\left|\right|{\mathbf{S}}_n(\mathit{\theta })-\mathbf{S}(\mathit{\theta })\left|\right|>\epsilon \right)\to 0,$$ (A.9)

as n → ∞. In what follows, we will show (A.9) using Huber’s chaining augment. Without loss of generality, we assume Θ × Ω= ∪_k{β: |β − β_0,τk| < 1}. We partition the parameter space Θ × Ω into L_n disjoint small cubes Γ_l with diameters less than q_n = C₁k_n/n, for some constant C₁. Let ξ_l be the center of the lth cube Γ_l. The probability of the left side of (A.9) is bounded by the sum of the following two probabilities, P₁ + P₂, where

$$\begin{array}{l}{P}_1=\text{pr}\left(\underset{1\le l\le L_n}{max}\underset{\mathit{\theta }\in {\mathrm{\Gamma }}_l}{sup}{k}_n^{-1}\left|\right|S_n(\mathit{\theta })-S_n({\mathit{\xi }}_l)-S(\mathit{\theta })+S({\mathit{\xi }}_l)\left|\right|>\epsilon /2\right);\\ P_2=\text{pr}\left(\underset{1\le l\le L_n}{max}{k}_n^{-1}\left|\right|S_n({\mathit{\xi }}_l)-S({\mathit{\xi }}_l)\left|\right|>\epsilon /2\right).\end{array}$$

We first note that

$$\begin{array}{l}\left|\right|S_n(\mathit{\theta })-S_n({\mathit{\xi }}_l)\left|\right|\\ \le \Vert n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}\{{\mathrm{\Psi }}_{\tau }(y_i-{\mathbf{x}}^{\top }\mathit{\theta })-{\mathrm{\Psi }}_{\tau }(y_i-{\mathbf{x}}^{\top }{\mathit{\xi }}_l)\}\mathbf{x}\\ ·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)d\mathbf{x}\Vert \\ +\Vert n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}{\mathrm{\Psi }}_{\tau }(y_i-{\mathbf{x}}^{\top }\mathit{\theta })\mathbf{x}\\ ·\{f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;\mathit{\theta })-f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)\}d\mathbf{x}\Vert \\ =S{S}_1+S{S}_2.\end{array}$$

Moreover, under Assumption 1, there exist a constant C such that

$$\begin{array}{l}\underset{l}{max}\underset{\mathit{\theta }\in {\mathrm{\Gamma }}_l}{sup}S{S}_1\\ \le \underset{l}{max}\underset{\mathit{\theta }\in {\mathrm{\Gamma }}_l}{sup}\Vert n^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}I\left\{\mid {\mathbf{x}}^{\top }{\mathit{\xi }}_l-y_i\mid \le \mid {\mathbf{x}}^{\top }({\mathit{\xi }}_l-\mathit{\theta })\mid \right\}{\mathbf{1}}_{k_n}·\mathbf{x}\\ ·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)d\mathbf{x}\Vert \\ \le k_n\underset{l}{max}{n}^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}I\{\mid {\mathbf{x}}^{\top }{\mathit{\xi }}_l-y_i\mid \le |\left|\mathbf{x}\right||q_n\}\left|\right|\mathbf{x}\left|\right|·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)d\mathbf{x}\\ \le C·k_n·\underset{l}{max}{n}^{-1}\sum _{i=1}^n{\int }_{\mathbf{x}}I\{\mid {\mathbf{x}}^{\top }{\mathit{\xi }}_l-y_i\mid \le C·q_n\}\\ ·f(\mathbf{x}\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)d\mathbf{x}\\ =C·k_n·\underset{l}{max}{n}^{-1}\sum _{i=1}^n\text{pr}\{\mid {\mathbf{x}}^{\top }{\mathit{\xi }}_l-y_i\mid \le C·q_n\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l\}.\end{array}$$

Let g_i(z) be the density of (x^⊤ ξ_l −y_i) given (y_i, ξ_l, w_i). Then g_i(z) is also continuous and bounded away from zero and infinity. Following the mean value theorem, for any i there exist $z_i^{\ast }$ such that $\text{pr}(\mid {\mathbf{x}}^{\top }{\mathit{\xi }}_l-y_i\mid \le C{q}_n\mid y_i,{\mathbf{w}}_i;{\mathit{\xi }}_l)=2{Cq}_n{g}_i(z_i^{\ast })$. It follows that ${max}_l{sup}_{\mathit{\beta }\in {\mathrm{\Gamma }}_l}{k}_n^{-1}S{S}_1=O_p(q_n)$.

On the other hand, a sufficient condition for $k_n^{-1}S{S}_2=o_p(1)$ is that max_i |f(x|y_i, w_i; θ) − f(x|y_i, w_i; ξ_l)| = o_p(1). Due to the boundedness of f(x|w), it again suffices to show that

$$\underset{i}{max}\mid f(y_i\mid \mathbf{x};\mathit{\theta })-f(y_i\mid \mathbf{x};{\mathit{\xi }}_l)\mid =o_p(1),$$

where f(y|x; θ) and f(y|x; ξ_l) are two density functions that are induced by the quantile functions x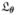^⊤ (τ) and x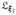^⊤(τ). Moreover, denote F_θ(y) = inf{τ: x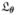^⊤ (τ) > y} and F_ξl(y) = inf{τ: x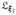^⊤(τ)>y} as the inverse functions of x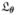^⊤ (τ) and x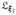^⊤(τ). Since |θ − ξ_l| = O(k_n/n), sup_τ|x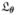^⊤ (τ) − x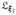^⊤(τ)| = o(1). Let θ[k] and ξ_l[k] stand for the subset of coefficients θ and ξ_l at the quantile level k/(k_n+1), then by construction,

$${\mathfrak{L}}_{\mathit{\theta }}(\tau )=\{\begin{array}{ll}\mathit{\theta }[1],\hfill & \tau <1/(k_n+1)\hfill \\ \mathit{\theta }[k_n],\hfill & \tau >k_n/(k_n+1)\hfill \\ \begin{array}{l}\mathit{\theta }[\lfloor \tau k_n\rfloor ]+\frac{\mathit{\theta }[\lfloor \tau k_n\rfloor +1]-\mathit{\theta }[\lfloor \tau k_n\rfloor ]}{1/k_n}\\ \times \left(\tau -\frac{\lfloor \tau k_n\rfloor }{k_n+1}\right),\end{array}\hfill & \text{else}.\hfill \end{array}$$

And 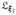(τ) has the same format. The difference between x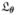^⊤ (τ) and x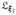^⊤(τ) is then bounded by

$$\begin{array}{l}\mid {\mathbf{x}}^{\top }{\mathfrak{L}}_{\mathit{\theta }}(\tau )-{\mathbf{x}}^{\top }{\mathfrak{L}}_{{\mathit{\xi }}_l}(\tau )\mid \\ \le \{\begin{array}{ll}\mid {\mathit{\xi }}_l[1]-\mathit{\theta }[1]\mid ,\hfill & \tau <1/(k_n+1)\hfill \\ \mid {\mathit{\xi }}_l[k_n]-\mathit{\theta }[k_n]\mid ,\hfill & \tau >k_n/(k_n+1)\hfill \\ \begin{array}{l}2\mid {\mathit{\xi }}_l[\lfloor \tau k_n\rfloor ]-\mathit{\theta }[\lfloor \tau k_n\rfloor ]\mid \\ +\mid {\mathit{\xi }}_l[\lfloor \tau k_n\rfloor +1]-\mathit{\theta }[\lfloor \tau k_n\rfloor +1]\mid ,\end{array}\hfill & \text{else}.\hfill \end{array}\end{array}$$

Since |θ − ξ_l|O(k_n/n) implies max_k |θ[k] − ξ_l[k]| = O(k_n/n), then the boundness above implies sup_τ|x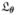^⊤ (τ) − x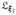^⊤(τ)| = o_p(1). Consequently, if we denote L_n = min(x^⊤ θ[1], x^⊤ξ_l[1]) and U_n =max(x^⊤θ[k_n], x^⊤ξ_l[k_n]), then we have sup_y∈[Ln,Un]|F_θ(y) − F_ξl(y)| = o(1). Since we can write $f(y\mid \mathbf{x};\mathit{\theta })=1/{\mathbf{x}}^{\top }{\mathfrak{L}}_{\mathit{\theta }}^{\prime }\{F_{\mathit{\theta }}(y)\}$ and $f(y\mid \mathbf{x};{\mathit{\xi }}_l)=1/{\mathbf{x}}^{\top }{\mathfrak{L}}_{{\mathit{\xi }}_l}^{\prime }\{F_{{\mathit{\xi }}_l}(y)\}$ for y ∈ [L_n, U_n]. sup_y∈[Ln,Un]|f(y|x; θ) − f(y|x; ξ_l) = o(1). Moreover, by construction, f(y|x; θ) = f(y|x; ξ_l) = 0 for any y > U_n or y < L_n. Combining these facts, we have max_i |f(y_i|x; θ) − f(y_i|x; ξ_l)|=o_p(1), which in turn implies k_nSS₂ =o_p(1). Following a similar argument, we can also show that, sup_{θ∈Γ l}||S(θ) − S(ξ_l)|| = o(1). It then follows that P₁ = o(1).

Let 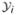(l, k, m) = ∫_xΨ_τ(y_i − x^⊤β_{τ k})x_m · f(x|y_i, w_i; θ) dxIθ ∈ Γ_l. A sufficient condition for P₂ = o(1) is that, for any β_τk and x_m,

$$\text{pr}\{\underset{1\le l\le L_n;1\le k\le k_n;1\le m\le p}{max}\left|\sum _{i=1}^n{\mathcal{Y}}_i(l,k,m)-E\{{\mathcal{Y}}_i(l,k,m)\}\right|>\epsilon \}=o(1).$$

Under Assumption 5, |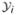(l, k, m)| < C for all the i’s. Applying Bernstein’s inequality to the probability term above, we have

$$\begin{array}{l}\text{pr}\left(\underset{1\le l\le L_n;1\le k\le k_n;1\le m\le p}{max}{n}^{-1}\left|\sum _{i=1}^n{\mathcal{Y}}_i(l,k,m)-E{\mathcal{Y}}_i(l,k,m)\right|>\epsilon \right)\\ \le k_n·p·L_n·\text{pr}\left(n^{-1}\left|\sum _{i=1}^n{\mathcal{Y}}_i(l,k,m)-E{\mathcal{Y}}_i(l,k,m)\right|>\epsilon \right)\\ \le k_n·p·L_n·exp\left\{-\frac{n^2{\epsilon }^2}{2n{C}^2+(2/3)Cn\epsilon }\right\}=o(1).\end{array}$$

We now have shown that both P₁ and P₂ =o(1), which in turn implies that the uniform convergence (A.7) holds. Lemma A.2 is hence proved.

Proof of Consistency

Recall that β̂_τk is the (p + 1)-dimensional estimated coefficient vector at quantile level τ_k based on the working estimating equations (10), and β̂_{j, τk} is its jth component. We further define β_j(τ) as the piece-wise linear function with β̂_j(τ_k) = β̂_j,τk, ∀,τ_k ∈ Ω. To simplify the notation, we also denote ${\widehat{\mathit{\theta }}}_n={({\widehat{\mathit{\beta }}}_{{\tau }_1}^{\top },{\widehat{\mathit{\beta }}}_{{\tau }_2}^{\top },\dots ,{\widehat{\mathit{\beta }}}_{{\tau }_{k_n}}^{\top })}^{\top }$ as the p × k_n dimensional estimated coefficient matrix.

For any δ > 0, we define a compact set B_τ ={β ∈ ℝ^p+1:||β − β_0,τ||<δ}, where β_0,τ is the true coefficients at the quantile level τ. We denote $B_{\tau }^c$ as its complementary set. Note that S_n(θ) are the working estimating equations defined in (10), and let S(θ) be its expectation. We define the distance

$$d_n(\delta )=k_n^{-1}\left\{\underset{\mathit{\theta }\in \{\mathrm{\Theta }\cap B_{\tau }^c\}\otimes \mathrm{\Omega }}{min}\left|\right|S(\mathit{\theta })\left|\right|-\left|\right|S({\mathit{\theta }}_0)\left|\right|\right\}$$ (A.10)

between the norm of the working estimating equations evaluated at the true coefficients θ₀ and the minimized norm when θ stays outside of B_τ ⊗ Ω. In what follows, we show that d_n(δ) > 0 under Assumptions 1 to 4.

Recall in Assumption 3 that θ₀ is the unique solution of S⁰(θ) =0, we have S⁰(θ₀) = 0. Therefore, the convergence of (A.1) stated in Lemma A.1 is equivalent to $k_n^{-1}\left|\right|S({\mathit{\theta }}_0)\left|\right|=o(1)$. Moreover, since ${\mathit{\theta }}^{\ast }=({\mathit{\beta }}_{{\tau }_1}^{\ast },\dots ,{\mathit{\beta }}_{{\tau }_{k_n}}^{\ast })$ is the unique solution of S(θ) = 0 according to Assumption 3, it follows that $k_n^{-1}\left|\right|S({\mathit{\theta }}_0)-S({\mathit{\theta }}^{\ast })\left|\right|\to 0$. Due to the continuity of S(·) and the uniqueness of θ^*, we have $k_n^{-1}\left|\right|{\mathit{\theta }}^{\ast }-{\mathit{\theta }}_0\left|\right|\to 0$, as n goes to infinity. Consequently, there exist K_δ, such that when k_n > K_δ, we have that $k_n^{-1}\left|\right|{\mathit{\theta }}^{\ast }-{\mathit{\theta }}_0\left|\right|<\delta /2$, in other words, θ^* ∈ B_τ × Ω for k_n > K_δ. Due to the uniqueness of θ^*, for any k_n > K_δ, we have

$$d_n^{\ast }(\delta )=k_n^{-1}\left\{\underset{\mathit{\theta }\in \{\mathrm{\Theta }\cap B_{\tau }^c\}\otimes \mathrm{\Omega }}{min}\left|\right|S(\mathit{\theta })\left|\right|-\left|\right|S({\mathit{\theta }}^{\ast })\left|\right|\right\}>0.$$ (A.11)

On the other hand, due to the continuity of S(·), for sufficiently larger k_n, we also have

$$k_n^{-1}\left|\right|S({\mathit{\theta }}^{\ast })-S({\mathit{\theta }}_0)\left|\right|<d_n^{\ast }(\delta )/2,$$ (A.12)

Combining these (A.12) and (A.11), we have

$$d_n(\delta )=k_n^{-1}\left[\underset{\mathit{\theta }\in \mathrm{\Theta }\cap B_{\tau }^c}{min}\left|\right|S(\mathit{\theta })\left|\right|-\left|\right|S({\mathit{\theta }}_0)\left|\right|\right]>d_n^{\ast }(\delta )/2>0.$$ (A.13)

for sufficiently large k_n.

We now define the random event that

$$E_n=\left\{k_n^{-1}\underset{\mathit{\theta }\in \mathrm{\Theta }\times \mathrm{\Omega }}{max}\left[\left|\right|{\stackrel{\sim }{S}}_n(\mathit{\theta })-S(\mathit{\theta })\left|\right|\right]>d_n(\delta )/3\right\},$$

which, together with Assumption 4, implies that

$$k_n^{-1}\left|\right|S({\widehat{\mathit{\theta }}}_n)\left|\right|\le k_n^{-1}\left|\right|{\stackrel{\sim }{S}}_n({\widehat{\mathit{\theta }}}_n)\left|\right|+d_n(\delta )/3$$ (A.14)

and

$$k_n^{-1}\left|\right|{\stackrel{\sim }{S}}_n({\mathit{\theta }}_0)\left|\right|\le k_n^{-1}\left|\right|S({\mathit{\theta }}_0)\left|\right|+d_n(\delta )/3.$$ (A.15)

Since θ̂_n is the minimizer of ||S̃_n(θ)||, we have ||S̃_n(θ̂_n)|| < ||S̃_n(θ₀)||, which, together with (A.14), shows that $k_n^{-1}\left|\right|S({\widehat{\mathit{\theta }}}_n)\left|\right|\le k_n^{-1}\left|\right|{\stackrel{\sim }{S}}_n({\mathit{\theta }}_0)\left|\right|+d_n(\delta )/3\le k_n^{-1}\left|\right|S({\mathit{\theta }}_0)\left|\right|+2d_n(\delta )/3$. Following Lemma A.2, lim_{n → ∞} pr(E_n) = 1, which implies

$$\underset{n\to \infty }{lim}\text{pr}\{k_n^{-1}\left|\right|S({\widehat{\mathit{\theta }}}_n)\left|\right|\le k_n^{-1}\left|\right|S({\mathit{\theta }}_0)\left|\right|+2d_n(\delta )/3\}\ge \underset{n\to \infty }{lim}\text{pr}(E_n)=1.$$

By the definition of B_τ and the fact that $d_n(\delta )>d_n^{\ast }(\delta )/2>0$, this in turn implies that lim_n→∞pr(θ̂_n ∈ B_τ) = 1, that is,

$$\underset{\tau \in [1/(k_n+1),k_n/(k_n+1)]}{sup}\left|\right|{\widehat{\mathit{\beta }}}_n(\tau )-{\mathit{\beta }}_0(\tau )\left|\right|=o_p(1).$$

The consistency of β̂_n(τ) is hence proved.

Proof of Asymptotic Normality

Recall that $S_n(\mathit{\theta })=n^{-1}{\sum }_{i=1}^n{\mathrm{\Psi }}_{\text{new}}(y_i,{\mathbf{w}}_i,\mathit{\theta })$, where Ψ_new(y_i, w_i, θ) =∫_xΨ(y_i −x^⊤ θ) ⊗ x · f(x|y_i, w_i; θ) dx, and S̃_n(θ) is its approximation replacing f(x|w_i) in f(x|y_i, w_i; θ) by its estimate f̃(x|w_i). Following a similar argument as in Lemma A.2, we can show that for any decreasing sequence d_n →0, we have

$$\underset{\left|\right|\mathit{\theta }-{\mathit{\theta }}_0\left|\right|<d_n}{sup}{n}^{1/2}\left|\right|S_n(\mathit{\theta })-S_n({\mathit{\theta }}_0)-S(\mathit{\theta })+S({\mathit{\theta }}_0)\left|\right|=o_p(1).$$ (A.16)

Theorem 1 implies, for fixed K, that θ̂_n is a consistent estimator of θ₀. The uniform convergence (A.16) hence implies

$$n^{1/2}\left|\right|S_n({\widehat{\mathit{\theta }}}_n)-S_n({\mathit{\theta }}_0)-S({\widehat{\mathit{\theta }}}_n)+S({\mathit{\theta }}_0)\left|\right|=o_p(1).$$ (A.17)

Note that n^1/2S̃_n(θ̂_n)= o_p(1), and ||S̃_n(θ̂_n) − ||S̃_n(θ̂_n)|| = o_p(1), which is implied by (A.8) and Assumption 4, it follows that S_n(θ̂_n) ≈ 0 for large enough n. On the other hand, S(θ₀) = 0 under Assumption 3. Therefore, the convergence (A.17) is equivalent to

$$n^{1/2}\left|\right|S_n({\mathit{\theta }}_0)-S({\widehat{\mathit{\theta }}}_n)\left|\right|=o_p(1).$$

Taylor expanding S(θ̂_n) around S(θ₀), we have

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)=-{\mathbf{D}}_n^{-1}{S}_n({\mathit{\theta }}_0)+o_p(1).$$

Theorem 2 follows immediately from the Central Limit Theorem.