An integrative genomics approach to infer causal associations between gene expression and disease

Abstract

A key goal of biomedical research is to elucidate the complex network of gene interactions underlying complex traits such as common human diseases. Here we detail a multistep procedure for identifying potential key drivers of complex traits that integrates DNA-variation and gene-expression data with other complex trait data in segregating mouse populations. Ordering gene expression traits relative to one another and relative to other complex traits is achieved by systematically testing whether variations in DNA that lead to variations in relative transcript abundances statistically support an independent, causative or reactive function relative to the complex traits under consideration. We show that this approach can predict transcriptional responses to single gene–perturbation experiments using gene-expression data in the context of a segregating mouse population. We also demonstrate the utility of this approach by identifying and experimentally validating the involvement of three new genes in susceptibility to obesity.

In the past few years, gene-expression microarrays and other general molecular profiling technologies have been applied to a wide range of biological problems and have contributed to discoveries about the complex network of biochemical processes underlying living systems¹, common human diseases^2,3 and gene discovery and structure determination^4–6. Microarrays have also helped to identify biomarkers⁷, disease subtypes^3,8,9 and mechanisms of toxicity¹⁰ and, more recently, to elucidate the genetics of gene expression in human populations^11,12 and to reconstruct gene networks by integrating gene-expression and genetic data¹³. The use of molecular profiling technologies as tools to identify genes underlying common, polygenic diseases has been less successful. Hundreds or even thousands of genes whose expression changes are associated with disease traits have been identified, but determining which of the genes cause disease rather than respond to the disease state has proven difficult.

Microarray data have recently been combined with other experimental approaches to facilitate identification of key mechanistic drivers of complex traits^3,13–17. One such technique involves treating relative transcript abundances as quantitative traits in segregating populations. In this method, chromosomal regions that control the level of expression of a particular gene are mapped as expression quantitative trait loci (eQTLs). Gene-expression QTLs that contain the gene encoding the mRNA (cis-acting eQTLs) are distinguished from other (trans-acting) eQTLs. cis-acting eQTLs that colocalize with chromosomal regions controlling a complex trait of interest are identified. The identification of a common chromosomal location for both cis-acting eQTLs and disease trait QTLs, especially in cases where the corresponding expression and disease traits are correlated, is used to nominate genes in the disease-susceptibility locus, bypassing fine mapping of the region altogether^{2,3,11,12,16,17}.

Here we present a multistep variation to this approach to identifying key drivers of complex traits that further exploits the naturally occurring DNA variation observed in segregating populations, and the association that DNA variations can have with changes in expression and other complex traits. We use gene-expression cis- and trans-acting eQTL data as well as complex-trait QTL data to identify expression traits that sit between the complex-trait QTL and complex trait. We validated the utility of this process on simulated data and known relationships among gene expression traits and applied it to large-scale genotypic, gene-expression and complex-trait data to identify known and new genes involved in susceptibility to obesity.

RESULTS

DNA variation enhances ability to order complex traits

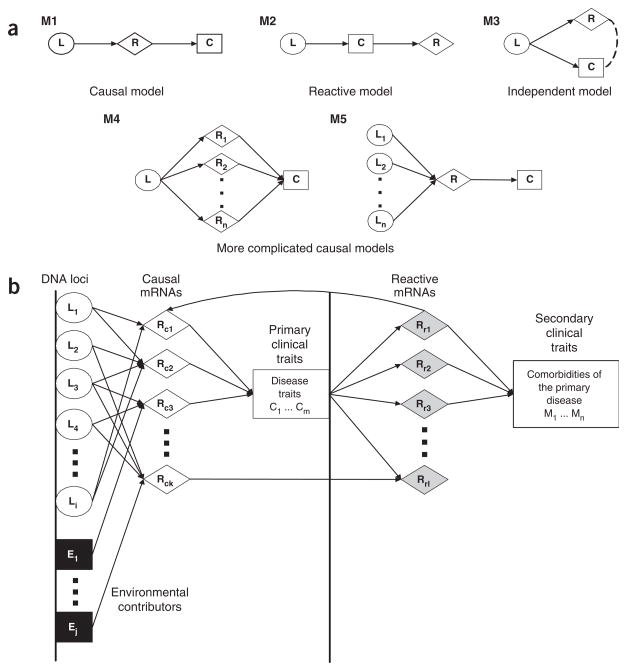
Standard gene-expression experiments can not easily distinguish variations in RNA levels that are causal for other complex traits from those that are reactive to other traits. Given two traits that are at least partially controlled by the same DNA locus, however, only a limited number of relationships between the traits are possible. We use several graphical models to represent these relationships (Fig. 1a). It is advantageous to establish relationships among complex traits in segregating populations because the associations between a locus L and two traits R and C under the control of that locus can be directed unambiguously (Fig. 1b). One method to identify the model best supported by the data uses conditional correlation measures¹⁸. We developed a likelihood-based causality model selection (LCMS) test that uses conditional correlation measures to determine which relationship among traits is best supported by the data. Likelihoods associated with each of the models are constructed and maximized with respect to the model parameters, and the model with the smallest Akaike Information Criterion (AIC) value¹⁹ is identified as the model best supported by the data.

Figure 1.

Using QTL data to infer relationships between RNA levels and complex traits. (a) Possible relationships between QTLs, RNA levels and complex traits once the expression of a gene (R) and a complex trait (C) have been shown to be under the control of a common QTL (L). Model M1 is the simplest causal relationship with respect to R, in which L acts on C through transcript R. Model M2 is the simplest reactive model with respect to R, in which R is modulated by C. Model M3 is the independent model, in which the QTL at locus L acts on these traits independently. Model M4 is a more complicated causal diagram in which a QTL at locus L affects the expression of multiple transcripts (R₁ through R_n), and these RNAs in turn act on a complex trait C. Finally, model M5 is the ideal causal diagram for target identification, in which multiple QTLs (L₁ through L_n) explain a significant amount of the genetic variance in a complex trait C, where the QTLs act on C through a convergence on a single transcript R. (b) Hypothetical gene network for disease traits and related comorbidities. The QTL (L_i) and environmental effects (E_j) represent the most upstream drivers of the disease. These components, in turn, influence one set of transcript levels (R_Ck), which in turn lead to the disease state (measured as disease traits, C_m). Variations in the disease traits affect reactive RNA levels (R_RI), which then lead to comorbidities of the disease traits or to positive or negative feedback control to the causal pathways.

Validating the LCMS procedure

To validate the LCMS procedure, we tested it using simulated data and an experimental data set in which the relationship among the expression traits was known. First, we simulated genotypes and quantitative traits in the context of an F₂ population with 360 individuals, assuming different relationships among quantitative traits (Supplementary Methods online). The results indicated good power to detect the true model in the simulated data. When the locus genotypes explained 7%, 10% or 20% of the variation in one of the two simulated traits (corresponding to lod scores of 5.2, 6.3 and 9.5, respectively), there was ~80% power at the 0.05 significance level to detect the true relationship between the two traits when the locus genotypes explained only 1–2% of the variation in the second trait (Supplementary Fig. 1 online). For all models, nearly 100% power was realized when the locus genotypes explained at least 4% of the variation in the second trait.

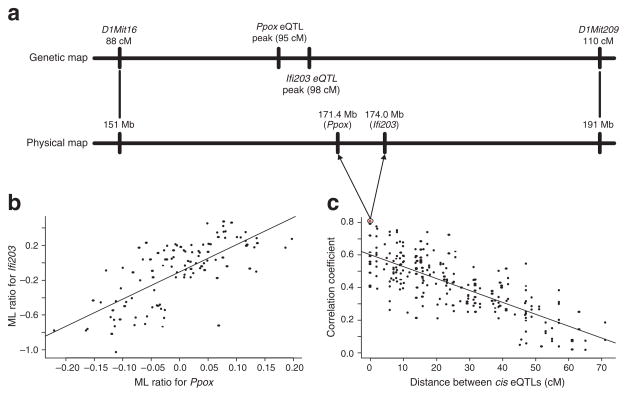
To assess the power of the LCMS procedure using experimental data, we exploited one of the features of F₂ populations, strong linkage disequilibrium over local regions that make it difficult to resolve QTLs accurately, as a more realistic way to ‘simulate’ independence relationships among complex traits. That is, if two gene-expression traits are each driven by a strong cis-acting eQTL, and these eQTLs are closely linked, they will induce a correlation structure between the two traits (Fig. 2), as we show for the previously described BXD data set³. The pattern of correlation (Fig. 2c) is a consequence of linkage disequilibrium in the BXD cross, an effect that is particularly pronounced in such populations because all mice are descended from a single F₁ founder, with only two meiotic events separating any two mice in the population.

Figure 2.

Strong gametic phase disequilibrium between genes with significant cis-acting eQTLs simulates independence events. (a) The Ppox and Ifi203 gene expression traits have strong cis-acting eQTLs with lod scores of 29.2 and 17.4, respectively, at the positions indicated. The physical locations of these genes on chromosome 1 are also shown aligned next to the genetic map. (b) Scatter plot of the mean-log (ML) expression ratios for Ppox and Ifi203 in the BXD data set. The two genes are positively correlated, with a correlation coefficient of 0.75. This correlation is probably induced by the two genes having closely linked eQTLs and not a result of any functional relationship. (c) Twenty-one genes physically residing on chromosome 1 were identified with strong cis-acting eQTL (corresponding lod scores > 10.0)³. Pearson correlation coefficients were computed for the mean log expression ratios between each of the 210 possible pairs of genes. The absolute value of each of the correlations is plotted here against the distance (cM) separating the cis-acting eQTLs for each pair. The pattern in this plot indicates that the magnitude of correlation is directly proportional to the distance between the cis-acting eQTLs, which are coincident with the physical locations of the genes (correlation coefficient = 0.82). This is precisely the relationship we would expect if the correlation structures were attributed to linkage disequilibrium between the eQTLs. The Ppox-Ifi203 pair is highlighted by the red dot.

If genes with strong cis-acting eQTLs are selected such that minimal recombination in the population has occurred between any two eQTLs, then the eQTLs will often be indistinguishable using standard methods to test for pleiotropic effects²⁰. Consequently, the two closely linked traits will seem to be independently driven by a single QTL. To assemble this set, we identified all possible gene pairs from the set of 557 gene-expression traits previously detected in the BXD data set with cis-acting eQTLs (lod > 7.0)³. Of the 154,846 possible gene pairs, 175 pairs were physically separated by <5,000,000 bp (Fig. 2a,b), with a median distance of 835,500 bp (<1 cM). On average, we would expect roughly one recombination event between the genes for each of the 175 gene pairs in the 111 F₂ mice making up the BXD cross. We used a standard test to assess whether each gene pair was driven by two closely linked QTLs or by a single QTL with pleiotropic effects²⁰ and found that only 20% of the pairs were driven by closely linked QTLs.

We fit the likelihoods for the three models (Fig. 1a) to the gene-expression data for each of the 175 gene pairs twice: once for each QTL position for each of the two gene-expression traits. We computed the AIC values for each fit and identified the model giving the lowest AIC value for both QTL positions as the model best supported by the data. Of the 175 gene pairs tested, 158 pairs (90%, compared with 20% using the standard pleiotropy test) were best supported by the independence model. This result is consistent with the fact that we selected the pairs as gene-expression traits driven by distinct, but closely linked, eQTLs and provides direct experimental support that the correlation structure among gene-expression traits and between gene-expression traits and QTL genotypes can be used to identify the correct relationship between the genes.

A multistep procedure to identify causal genes for obesity in mice

Next, we applied the LCMS procedure to the omental fat pad mass (OFPM) and liver gene-expression data in the BXD data set^3,21 to identify key drivers of the OFPM trait. We defined a broader process, a series of heuristic filters, to identify those expression traits most significantly associated with the OFPM trait (Supplementary Fig. 2 online).

The first step in the process is to build a genetic model for the OFPM trait, identifying the underlying QTLs that reflect the initial perturbations that give rise to the genetic components of the trait. We constructed the OFPM genetic model by following a previously established stepwise regression procedure that produces reliable models in this context^22,23.

We considered epistatic interactions among all pairs of positions tested in the genome for both the OFPM and expression traits. These interactions were very small compared with the additive and dominance effects. For the OFPM trait, no significant pairwise interactions between any two genome positions gave rise to lod scores >2. Therefore, epistatic interactions were not considered further in these analyses. The chromosome 6 and chromosome 19 QTLs were fixed in the OFPM genetic model, because they were previously identified as major-effect QTLs for fat mass traits in the BXD set^3,21. The chromosome 6 and chromosome 19 linkage regions are hot-spot regions for eQTL activity and are enriched for pathways underlying metabolic traits^24,25. Our stepwise regression procedure yielded a genetic model for OFPM that consisted of four QTLs located on chromosomes 1 at 95 cM, 6 at 43 cM, 9 at 8 cM and 19 at 28 cM. The model explained 39.3% of the variation in the OFPM trait and had an associated P value equal to 0.0007, with all individual terms significant at the 0.05 significance level.

Expression traits that causally explain a significant proportion of the correlation between variations in DNA and the OFPM trait should also be correlated with the OFPM trait. Therefore, we wanted to exclude expression traits that are not significantly correlated with the OFPM trait. We computed the Pearson correlation coefficients for the OFPM trait and the 4,423 gene-expression traits that were significantly differentially expressed in at least 10% of the samples profiled and found that 440 expression traits had P values corresponding to Pearson correlation coefficients of <0.001 (Supplementary Table 1 online). We permuted the OFPM trait 1,000 times and computed the Pearson correlation for the permuted OFPM vector and each of the 4,423 expression traits. The mean number of expression traits over all permutation runs with P values < 0.001 was 11, yielding a false discovery rate²⁶ (FDR) of 2.5%.

If an expression trait is causal for the OFPM trait, then at least one of the QTLs underlying the OFPM trait must also underlie the expression trait. Therefore, we applied another filtering step to identify those genes in the association set with eQTLs that coincided with the OFPM QTL. We computed lod scores for the 440 expression traits at the four OFPM QTLs. For expression traits giving rise to significant eQTLs at any of the locations (at the 0.01 level), we determined the peak eQTL position and carried out a slight generalization of the multivariate ‘pleiotropy versus close linkage’ test²⁰ to establish whether the data supported pleiotropic effects of a single QTL affecting the expression and OFPM traits (Supplementary Methods online).

There were 113 expression traits with at least two significant eQTLs overlapping the OFPM QTL, where the overlapping QTLs were supported as a single QTL with pleiotropic effects (Supplementary Table 2 online). These 113 genes gave rise to 267 eQTLs overlapping the OFPM QTL. The requirement that the two traits share two or more QTLs resulted in a FDR of 0.4% (compared with 15% when requiring only one shared QTL), computed by permuting the QTL genotypes 100 times and carrying out QTL analysis at the four OFPM QTLs for each of the expression traits. The resulting 113 transcripts are the most significant candidate causative genes with respect to the OFPM genetic model, given that an expression trait can be causal in the network associated with OFPM (Fig. 1b) only if the expression trait is affected by one or more of the genetic components driving the OFPM trait.

For each overlapping expression-OFPM QTL in the set of 113 genes, we fit the corresponding QTL genotypes, gene-expression data and OFPM data to the independent, causal and reactive likelihood models. The causal model had the smallest AIC value in 134 cases (50%), whereas the reactive model was the best in 23 cases (9%), and the independent model was the best in the remaining cases. We then rank-ordered the 113 genes according to the percentage of genetic variance in the OFPM trait that was causally explained by variation in their transcript abundances (Supplementary Table 2 online). The ten most highly ranked genes (Table 1) are the strongest causal candidates for the OFPM trait in this mouse population. Of these genes, Hsd11b1 was one of the best candidates.

Table 1.

Top ten gene-expression traits correlated with and supported as causal candidates for the OFPM trait

Accession number	Gene	Gene-expression correlation coefficient (P value)	Overlapping QTLs	Overlapping QTLs testing causal	Genetic variation in OFPM causally explained (%)
NM_011764	Zinc finger protein 90 (Zfp90)	0.45 (6.8 × 10−5)	3	3	68
AY027436	Kruppel-like factor 6 (Klf6)	0.42 (2.1 × 10−4)	3	3	68
AI506234	NA	0.49 (1.3 × 10−5)	3	3	68
NM_008288	Hydroxysteroid 11-beta dehydrogenase 1 (Hsd11b1)	0.51 (5.4 × 10−6)	4	3	61
AK004942	Glutathione peroxidase 3 (Gpx3)	0.43 (1.4 × 10−4)	4	4	61
NM_030717	Lactamase beta (Lactb)	0.54 (1.3 × 10−6)	3	2	52
NM_026508	TNF receptor-associated protein 1 (Trap1)	0.50 (8.6 × 10−6)	3	2	52
AK004980	Malic enzyme (Mod1)	0.40 (4.1 × 10−4)	3	2	52
NM_008194	Glycerol kinase (Gyk)	0.57 (2.6 ×10−7)	4	2	46
NM_08509	Lipoprotein lipase (Lpl)	0.49 (1.3 × 10−5)	3	2	46

NA, not applicable.

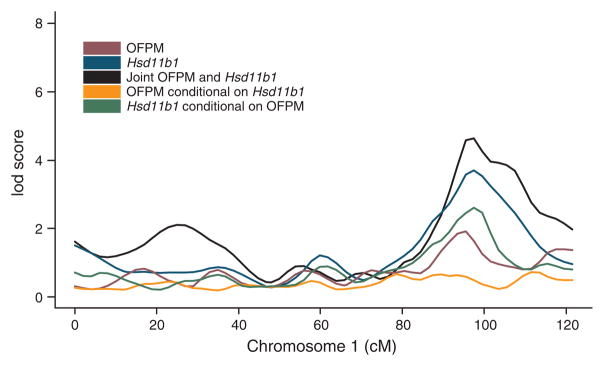
Notably, Hsd11b1 was ranked 152 of the 440 genes in the association set. This difference in ranking between the LCMS-generated list and that generated by standard Pearson correlations highlights the chief advantage of this approach: the covariance structure for two traits can be decomposed into causal and reactive components, providing a new rank-ordering scheme based on the percentage of variance in one trait causally explained by another. An intuitive view of Hsd11b1 as a causal candidate for the OFPM trait, involving standard partial correlation arguments, is depicted in Figure 3 and Table 2. The independence of QTL genotypes and OFPM conditional on Hsd11b1 expression, and the lack of independence of QTL genotypes and Hsd11b1 expression conditional on OFPM, supports the idea that Hsd11b1 is causal for the OFPM trait¹⁸. The association of Hsd11b1 with the OFPM trait was previously established in a transgenic mouse overexpressing Hsd11b1 in adipose tissue²⁷. HSD11B1 activity levels and mRNA levels are significantly correlated with fat mass and insulin sensitivity in humans²⁸.

Figure 3.

Use of conditional correlations support Hsd11b1 as causal for OFPM at the chromosome 1 OFPM QTL. The blue curve represents the lod score curve for Hsd11b1; the red curve represents the lod score curve for OFPM; and the black curve represents the lod score curve for Hsd11b1 and OFPM considered simultaneously, indicating that the two traits considered together provide a significant QTL at the chromosome 1 locus. The green line represents the lod score curve for Hsd11b1 after conditioning on OFPM; the orange line represents the lod score curve for OFPM after conditioning on Hsd11b1. Because the lod score effectively drops to 0 in the case of the orange curve and is significantly greater than 0 in the case of the green curve, a causal relationship is supported.

Table 2.

Overlapping QTLs for Hsd11b1 expression and OFPM and testing for causal associations

OFPM QTL location*	OFPM lod score	Hsd11b1 QTL location*	Hsd11b1 lod score	Hsd11b1-OFPM joint QTL lod score	Causal P value	Reactive P value
1 (95)	2.10	1 (97)	3.87	5.2	0.29	0.001
6 (43)	2.84	6 (39)	2.43	4.7	0.04	0.05
9 (8)	2.53	9 (1)	3.48	5.4	0.21	0.04
19 (28)	1.92	19 (35)	3.10	4.8	0.17	0.02

^*Chromosome location is given first, followed by centimorgan position in parentheses.

The causal P value was computed under the null hypothesis that there is no significant linkage of OFPM to the indicated position once we condition on Hsd11b1 expression (causal). Similarly, the reactive P value was computed under the null hypothesis that there is no significant linkage of Hsd11b1 to the indicated position once we condition on OFPM (reactive).

Transcriptional responses driven by perturbations to Hsd11b1

Given the causal association between expression of Hsd11b1 and the OFPM trait, we wanted to elucidate the transcriptional network associated with Hsd11b1. We applied the LCMS procedure to the Hsd11b1 expression trait and all other gene-expression traits to identify genes predicted to respond to Hsd11b1. To validate these genes, we carried out an independent Hsd11b1 perturbation experiment in mouse, identified the liver transcriptional response to this perturbation and then assessed whether the predicted Hsd11b1 reactive gene set overlapped with that observed from the Hsd11b1 perturbation experiment. We used a specific Hsd11b1 inhibitor(similar to one previously described^29,30) to decrease Hsd11b1 activity (A.H.V. et al., personal communication) in mice to assess the transcriptional response in liver tissue to this single gene perturbation.

The genetic model for the Hsd11b1 expression trait consisted of six eQTLs. We determined the overlap between the Hsd11b1 eQTLs and each of the other 23,573 genes represented on the array as described for OFPM. We then applied the LCMS test to all expression traits with eQTLs overlapping the Hsd11b1 eQTLs. Of the 23,574 genes tested, 3,277 (~14%) had eQTLs overlapping at least four of the six Hsd11b1 eQTLs and testing as reactive to the Hsd11b1 expression trait. To approximate the null distribution, we permuted the expression data 100 times such that the correlation structure among the expression traits was preserved. The mean number of genes identified as reactive to Hsd11b1 over the 100 permutations was 75 (FDR of 2.3%).

We identified 532 genes as being significantly differentially regulated in liver, relative to control mice, in at least one of the three mice treated with Hsd11b1 inhibitor at the 0.05 significance level. By chance, we would have expected 74 genes to overlap, given the overall 14% rate estimated above; however, we observed 143 genes overlapping the 3,277 gene set. The probability of seeing 143 genes by chance is 1.3 × 10⁻¹⁵ using Fisher’s exact test. In comparison, when we searched for enrichment between the expression traits significantly correlated with Hsd11b1 and the Hsd11b1 inhibitor set, we identified the P value threshold for the Pearson correlation coefficient that maximized the enrichment between these two sets. The maximum enrichment occurred at a P value cut-off of 7.1 × 10⁻⁶; 5,404 genes were correlated with Hsd11b1 at this level (FDR = 0.02%), and 156 of these overlapped the Hsd11b1 inhibitor signature set, giving an enrichment P value of 0.0003. These results indicate that the LCMS procedure is able to enrich for the correct relationship among gene-expression traits significantly beyond what can be realized using the Pearson correlation alone.

Validating Zfp90, C3ar1 and Tgfbr2 as causal for obesity

Ninety genes tested as causal for the OFPM trait at one or more QTLs (Supplementary Table 2 online). The gold standard for validating this type of prediction is the construction of animals that are genetically altered with respect to the activity of the gene of interest followed by screens for variations in the trait of interest. C3ar1 and Tgfbr2 (numbers 14 and 29 in the list, respectively) knockout mice were commercially available. For Zfp90 (number 1 in the list), we constructed a BAC transgenic mouse. Liver expression of these three genes was significantly correlated with the OFPM trait in the BXD set, and each gene could causally explain at least 45% of the genetic variance in the OFPM trait. Therefore, we predicted that eliminating or significantly increasing the activity of these genes would lead to significant variation in the OFPM trait.

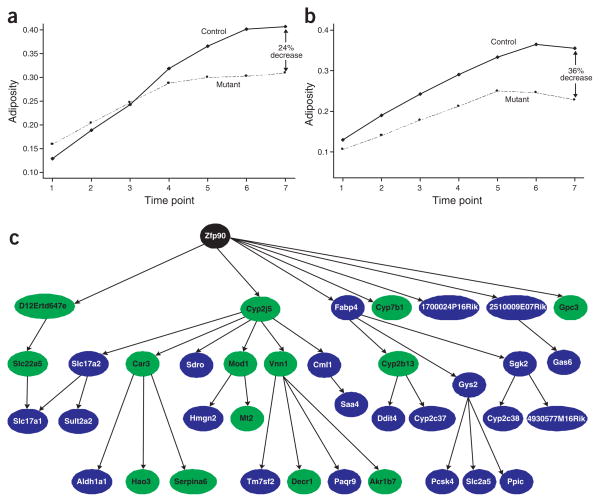
We recorded weight, fat mass and lean mass for male homozygous C3ar1^−/− (n = 5–7), heterozygous Tgfbr2^+/− (n = 5–7; Tgfbr2^−/− mice died) and wild-type littermate control (n = 5–10) mice every 2 weeks starting at 10 weeks of age for 12 weeks using quantitative nuclear magnetic resonance. The growth curves for C3ar1^−/− and Tgfbr2^+/− mice were significantly different from those of controls (Fig. 4a,b), and at each subsequent time point, the difference in fat mass increased. At the final quantitative nuclear magnetic resonance measurement on 22-week-old mice, the mean fat mass to lean mass ratios were significantly different in C3ar1 and Tgfbr2 knockout mice versus their respective wild-type controls (Table 3), validating the predictions made from the BXD cross.

Figure 4.

Three genes in the OFPM causality list achieve validation in genetically modified mice. (a,b) Growth curves for C3ar1^−/− (a) and Tgfbr2^+/− (b; mutant) and control mice over seven time points. Growth is given on the y axis as the fat mass to lean mass ratio. At each time point the mean ratio is plotted for each group. The significance of the mean ratio differences at time point 7 is given in Table 3. (c) Genetic subnetwork for liver expression in the BXD cross previously described¹³ highlights Zfp90 (black node) as a central node in the liver transcriptional network of this cross. This subnetwork was obtained from the full liver expression network previously described¹³ by identifying all nodes in this network that were descended from and within a path length of 3 of the Zfp90 node. Nodes highlighted in green represent genes testing as causal for fat mass (Supplementary Table 2 online).

Table 3.

Mean fat mass to lean mass ratios for Zfp90 transgenic, C3ar1^−/− and Tgfbr2^+/− mice

Mouse model	Mutant n (control n)	Fat mass to lean mass ratio in mutants (mean ± s.d.)	Fat mass to lean mass ratio in controls (mean ± s.d.)	Fat mass difference P valuea	Mutant versus control P value
Zfp90 transgenic versus high-fat controlb	3 (12)	0.45 ± 0.05	0.15 ± 0.06d	NA	6.5 × 10−7
Zfp90 transgenic versus chow controlc	3 (8)	0.45 ± 0.05	0.27 ± 0.07d	NA	0.0021
C3ar1−/−	5 (7)	0.31 ± 0.11a	0.41 ± 0.10	0.0026	NA
Tgfbr2+/−	7 (7)	0.23 ± 0.09a	0.36 ± 0.10	1.3 × 10−6	NA

^aComputed from final measurements at week 12.

^b32-week-old Zfp90 transgenic mice compared with 22-week-old FVB mice on a high-fat diet.

^c32-week-old Zfp90 transgenic mice compared with 32-week-old FVB mice on a chow diet.

^dComputed from FVB/NJ controls.

Mean differences were tested using a standard t-test. Significant differences in the mean for mutant and control mice were tested using the ARMAX procedure. P values correspond to the null hypothesis that there is no difference in the means between the control and mutant mice.

Tgfbr2 is active in the TGF-β signaling pathway, which regulates cell proliferation and differentiation and extracellular matrix production. Although no direct evidence for the involvement of Tgfbr2 in obesity has been previously established, elevated expression of TGF-β and TGF-β polymorphisms have been associated with body mass index, obesity (including abdominal obesity) and type 2 diabetes^31–34. Therefore, the association between TGF-β and obesity suggests that Tgfbr2 may have a role in obesity development through the TGF-β signaling pathway. C3ar1 is active during complement activation, and C3ar1 knockout mice are protected against airway hyper-responsiveness in response to challenge with an antigen. Similarly, although there is no direct evidence supporting the role of C3ar1 in obesity, indirect evidence from its ligand C3a suggests a link between C3ar1 and obesity-related traits. For example, injecting C3a in the hypothalamic region of rats increased their food and water intake in response to catecholamine stimulation³⁵. In addition, increased levels of C3a are correlated with obesity, cholesterol, lipid levels and familial combined hyperlipidemia^36–38.

Construction of Zfp90 transgenic mice resulted in two males and one female transgenic with respect to the human ZFP90 gene. After 20 weeks of breeding the transgenic mice to wild-type mice, no litters were produced. The failure of these mice to breed could be related to the fact that this gene product is predicted to be involved in spermatogenesis³⁹. We took quantitative nuclear magnetic resonance measurements of the three transgenic mice at 32 weeks of age. Their fat mass to lean mass ratios were nearly three times higher than those of 22-week-old control mice that had been on a high-fat diet for 14 weeks and were nearly 1.7 times higher than those of age-matched control mice (Table 3). These preliminary data suggest that Zfp90 may have an uncharacterized role in the regulation of obesity traits. To identify genes that are closely related to Zfp90, we examined the previously described genetic network constructed from the BXD liver expression data¹³. Zfp90 is a central node in this liver transcriptional network (Fig. 4c). Zfp90 falls upstream of several key genes predicted to be causally associated with the OFPM trait, including Mod1, Hao3, Vnn1 and Car3 (Supplementary Table 2 online). This represents a very significant enrichment for obesity-related genes in this independently derived liver-specific genetic network driven by Zfp90.

DISCUSSION

We describe a multistep process to extract causal information from gene-expression data related to complex phenotypes such as obesity and gene expression. Central to this process is a likelihood-based test for causality that takes into account genotypic, RNA and clinical data in a segregating population to identify genes in the trait-specific transcriptional network that are under the control of multiple QTLs for the trait of interest but still upstream of the trait. Whereas previous methods allow for tests of pleiotropy versus close linkage to determine whether multiple traits are under the control of common QTLs²⁰, the LCMS procedure described here allows for the possibility to unravel the nature of such associations.

We applied the LCMS procedure to a segregating mouse population phenotyped for OFPM and identified known (Hsd11b1) and new susceptibility genes (Tgfbr2, C3ar1 and Zfp90) for fat mass in this population, in addition to significantly predicting the transcriptional response to perturbation of Hsd11b1. The three new susceptibility genes that we identified have not previously been directly associated with obesity-related traits. In addition to these three genes, a SNP in lipoprotein lipase (ranked number 9 in Table 2) was recently reported to be associated with obesity and other components of the metabolic syndrome in a human population⁴⁰.

Our results indicate that integrating genotypic and expression data may help the search for new targets for common human diseases. But certain issues surrounding this process will require more careful consideration. One such issue is the dependency of the LCMS procedure on measurement and modeling errors. Suppose RNA trait R is causal for trait C, but the measurement errors related to the expression of R far exceed that of C. This might lead to a failure to detect R as causal for C or, worse, incorrectly identify C as causal for R. A second issue is that the LCMS procedure will fail to discriminate between traits that are very highly correlated (Supplementary Fig. 3 online). Thus, for cases in which a causal gene is almost completely correlated with a complex trait of interest or tightly regulates the expression of other genes unrelated to the complex trait, the power to resolve the true relationships will be reduced. Furthermore, our procedure introduces a very simplistic view of the gene networks associated with disease, focused on identifying genes in the causal-reactive interval. The true situation is more complicated, however, because the causal-reactive genes are interacting in a larger network and may be subject to negative and positive feedback control. Finally, the high-dimensional nature of this problem, involving potentially tens of thousands of molecular profiling traits, combined with the complexities of genetic model selection procedures, has only recently begun to be explored in this context. Many statistical issues remain to be addressed^41–43, and many of the steps in our overall process that are herein only heuristically justified will require more careful statistical consideration before the approach can be automatically applied to general data sets.

Despite these and other issues, the ability to partition genes into causal and reactive sets and identify those targets from the causal set that are optimally placed in the gene network associated with complex traits of interest with respect to therapeutic intervention offers a promising approach to understanding the complex network of gene changes that are associated with complex traits such as common human diseases and, in the process, identifying new ways to combat these diseases.

METHODS

The BXD data set

The F₂ mouse population and associated liver gene-expression data used in this study have been previously described^3,21 (GEO accession GSE2008). An F₂ population consisting of 111 mice was constructed from two inbred strains of mice, C57BL/6J and DBA/2J. Only female mice were maintained in this population. Mice were on a rodent chow diet up to 12 months of age and then switched to an atherogenic high-fat, high-cholesterol diet for another 4 months. At 16 months of age, the mice were killed and their livers extracted for gene-expression profiling. The mice were genotyped at 139 microsatellite markers uniformly distributed over the mouse genome to allow for the genetic mapping of the gene-expression and disease traits.

Treatment of mice with Hsd11b1 inhibitor

We placed six male C57BL/6J mice on an obesity-inducing diet for 8 weeks starting at 12 weeks of age. At 18 weeks and 3 d of age, half of the mice had the Hsd11b1 inhibitor compound introduced into their feed for 11 d, whereas the other mice were treated as controls for the same period of time. After the 11-d treatment, all mice were killed and RNA was extracted from the livers of each animal for profiling on gene-expression microarrays.

Preparation of labeled cDNA

We removed livers from control mice and mice treated with Hsd11b1 inhibitor for expression profiling, immediately flash-froze them in liquid nitrogen and stored them at −80 °C. We purified total RNA from 25-mg portions using an RNeasy Mini kit in accordance with the manufacturer’s instructions (Qiagen). We prepared liver cDNA in the same fashion as for the F₂ mice in BXD cross, as described previously³. We hybridized RNAs from each treated mouse against a pool of RNAs constructed from equal aliquots of RNA from each control mouse.

Analysis of expression data

We processed array images as previously described to obtain background noise, single-channel intensity and associated measurement error estimates³. Expression changes between two samples were quantified as log₁₀(expression ratio), where the expression ratio was taken to be the ratio between normalized, background-corrected intensity values for the two channels (red and green) for each spot on the array. We applied an error model for the log ratio as described⁴⁴ to quantify the significance of expression changes between two samples.

Probe selection for mouse gene expression arrays

The mouse microarray used for the BXD cross has been previously described³. The mouse microarray used for the present studies is an updated version, containing 23,574 non-control oligonucleotide probes for mouse genes and 2,186 control oligonucleotides. We extracted full-length mouse sequences from Unigene clusters (build 168, February 2004), combined with RefSeq mouse sequences (release 3, January 2004) and RIKEN full-length sequences (version fantom1.01). We clustered this collection of full-length sequences and selected one representative sequence per cluster. To complete the array, we selected 3′ expressed-sequence tags from Unigene clusters that did not cluster with any full-length sequence from Unigene, RefSeq or RIKEN. To select a probe for each gene sequence, we used a series of filtering steps, taking into account repeat sequences, binding energies, base composition, distance from the 3′ end, sequence complexity and potential crosshybridization interactions⁴⁵. For each gene, we examined every potential 60-bp sequence and printed the 60-bp oligonucleotide that best satisfied the criteria on the microarray. All microarrays used in this study were manufactured by Agilent Technologies, Inc.

Statistical analyses: the LMCS procedure

Assuming standard Markov properties for the simple graphs (Fig. 1a), the joint probability distributions for the three models are as follows:

$$\begin{array}{l}\text{M}1.P(\text{L},\text{R},\text{C})=P(\text{L})P(\text{R}\mid \text{L})P(\text{C}\mid \text{R})\\ \text{M}2.P(\text{L},\text{R},\text{C})=P(\text{L})P(\text{C}\mid \text{L})P(\text{R}\mid \text{C})\\ \text{M}3.P(\text{L},\text{R},\text{C})=P(\text{L})P(\text{C}\mid \text{L})P(\text{R}\mid \text{C},\text{L})\end{array}$$

The term P(R|C,L) in model M3 reflects the fact that the correlation between R and C may be explained by other shared loci or common environmental influences, in addition to locus L. We assume Markov equivalence between R and C for model M3 so that P(C|L) P(R|C,L) = P(R|L) P(C|R,L). P(L) is the genotype probability distribution for locus L and is based on a previously described recombination model⁴⁶. The random variables R and C are taken to be normally distributed about each genotypic mean at the common locus L, so that the likelihoods corresponding to each of the joint probability distributions are based on the normal probability density function, with mean and variance for each component given by the following equations: for P(R|L), the mean and variance are E(R|L) = μ_RL and $\mathit{Var}(\text{R}\mid \text{L})={\sigma }_{\text{R}}^2$, respectively; for P(C|L), the mean and variance are E(C|L) = μ_CL and $\mathit{Var}(\text{R}\mid \text{L})={\sigma }_{\text{C}}^2$, respectively; and for P(R|C), the mean and variance are $\text{E}(\text{R}\mid \text{C})={\mu }_{\text{R}}+\rho \frac{{\sigma }_{\text{R}}}{{\sigma }_{\text{C}}}(\text{C}-{\mu }_{\text{C}})$ and $\mathit{Var}(\text{R}\mid \text{C})=(1-{\rho }^2){\sigma }_{\text{R}}^2$, respectively; where ρ represents the correlation between R and C and μ_RL and μ_CL are the genotype-specific means for R and C, respectively. The mean and variance for P(C|R) follow similarly from those for P(R|C). From these component pieces, the likelihoods for each model are formed by multiplying the densities for each of the component pieces across all the individuals in the population. The exact forms of these likelihoods for the F₂ cross are given in Supplementary Methods online.

For each model, the corresponding likelihood is maximized and parameters are estimated using standard maximum likelihood methods. We then compute the AIC values for each model as two times the negative of log likelihood, maximized over the parameters, plus two times the number of parameters. The model associated with the smallest AIC value is the one best supported by the data.

We are able to constrain attention to three models (Fig. 1a) because of the requirement that R and C be driven by a common L for each position tested. Without this requirement, other biologically plausible models would be possible. Also, although additional models taking into account feedback control are possible, in the context of a single cross we assume that a given direction will dominate (given the set of perturbations in the cross acting on R and C), so that the best model represents this dominant direction. Further, for model M3, we made simplifying assumptions on the residual correlation structure between R and C after conditioning on L that allowed us to consider only a single independence model for the purpose of estimating the likelihood. In fact, model M3 represents a number of different models regarding the relationship between R and C, conditional on L.

Detecting QTL and genetic model selection

We used a forward stepwise regression framework to build up genetic models for the OFPM and Hsd11b1 traits, based on a previously described least squares QTL mapping strategy⁴⁷. Given the marker map for the BXD set²¹, we estimated QTL genotype probabilities at 1-cM intervals over the length of the genome, conditional on marker genotypes. We then constructed explanatory variables for the additive and dominance terms for each position from the estimated genotype probabilities and used them in the regression analysis. We used generalized linear models to assess the degree of epistatic interactions among all pairwise positions used in the genome-wide scan for the OFPM and Hsd11b1 traits. We then constructed the best genetic model for OFPM and Hsd11b1 using Efroymson’s stepwise regression method⁴⁸, limiting the number of QTLs that were allowed to be introduced into the model to six and thereby restricting attention to the most important effects. We added variables to the model if the associated F statistic was greater than 3 and, similarly, deleted them from the model if the associated F statistic was less than 3. This model-building procedure is similar to that used by others who showed that such methods lead to robust, highly predictive models in this context^22,23. Furthermore, this type of forward selection is consistent in the genetics context⁴⁹. To compute the eQTLs at the four OFPM and six Hsd11b1 QTL positions, we used generalized linear models to regress expression values onto the additive and dominance indicator variables described above for each position.

Construction of Zfp90 transgenic, C3ar1^−/−, Tgfbr2^+/− and control mice

Details of the construction of the Zfp90 transgenic, C3ar1^−/− and Tgfbr2^+/− mice are given in Supplementary Methods and Supplementary Figures 2, 4 and 5 online. All procedures were done in accordance with the National Research Council and the Guide for the Care and Use of Laboratory Animals and were approved by the University of California Los Angeles Animal Research Committee.