Abstract
Quantitative analysis of the staining of cell membranes with the cationic amphimphile, octadecyl rhodamine B (R18) is confounded by probe aggregation and changes to the probes' absorption cross-section and emission quantum yield. In this paper flow cytometry, quantum dot based fluorescence calibration beads and FRET to were used examine real time transfer of octadecyl rhodamine B (R18) from water to two limiting models of the cellular plasma membrane, namely a single component disordered membrane, dioleoyl-L-α-phosphatidylcholine (DOPC), and a ternary mixture of DOPC, cholesterol and sphingomyelin (DSC) membranes, reconstituted on spherical and monodisperse glass beads (lipobeads). The quenching of R18 was analyzed as the probe concentration is raised from 0 to 10 mol% in membranes. The data show a > 2-fold enhancement in the quenching level of the probes that are reconstituted in DSC relative to DOPC membranes at the highest concentration of R18. We have parameterized the propagation of concentration dependent quenching as a function of real-time binding of R18 to lipobeads. In this way, phenomenological kinetics of serum albumin mediated transfer of R18 from the aqueous phase to DOPC and DSC membranes could be evaluated under optimal conditions were the critical aggregation concentration (CAC) of the probe is defined as 14nM. The mass action kinetics of association of R18 with DOPC and DSC lipobeads are shown to be are similar. However, the saturable capacity for accepting exogenous probes is found to be 37% higher in DOPC relative to DSC membranes. The difference is comparable to the disparity in the average molecular areas of DOPC and DSC membranes. Finally this analysis shows little difference in the spectral overlap integrals of the emission spectrum of a fluorescein derivative donor and the absorption spectrum of either monomeric or simulated spectrum of dimeric R18. This approach represents a first step towards a nano-scale probing of membrane heterogeneity in living cells by analyzing differential local FRET among sites of unique receptor expression in living cells.
Introduction
Octadecyl rhodamine B (R18) is a cationic amphiphile used in numerous studies including electronic energy transfer in organized molecular assemblies,1-4 membrane structure,5-13 and distances of closest approach between protein domains and membranes.14-17 18-20 In a series of papers,14-17 we have described the use of R18 as an acceptor in fluorescence resonance energy transfer (FRET) experiments where we examined the dynamic structural transformation of a cell adhesion molecule, α4β1 integrin in living cells. In these studies,17 the expression of α4β1 integrins on the cell surface was presented in terms of a fluorescence measurement of an α4-specific peptide derivative 4-((N′-2-methylphenyl)ureido)-phenylacetyl-L-leucyl-L-aspartyl-L-valyl-L-prolyl-L-alanyl-L-alanyl-L-lysine (LDV-FITC). Using the LDV-FITC probe as a donor we developed a FRET assay where R18 partitions from the aqueous phase into cell membranes. The resultant FRET is analyzed in terms of a model that interprets acceptor surface density, and transfer efficiency with respect to separation distances or distances of closest approach (rc1 in Fig. 1)21 between the LDV-FITC probe and multiple R18 acceptors incorporated into the plasma membrane.
Figure 1.
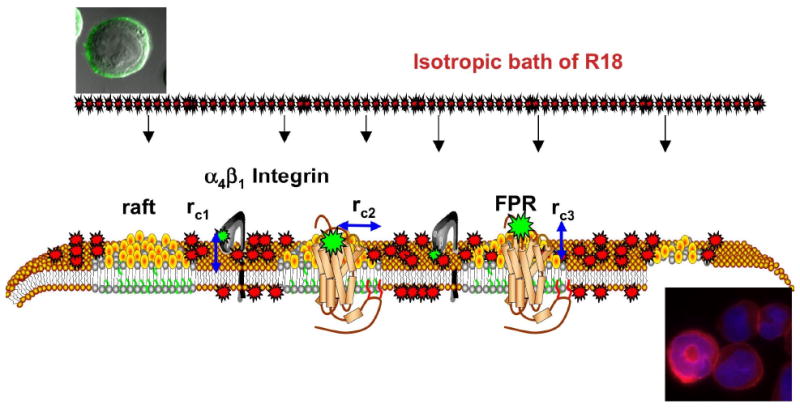
Model representation of exposure of cells to an isotropic environment of R18 results in spatio-temporally heterogeneous staining of the cell membranes in a manner that reflects heterogeneity of the plasma membrane. Sites of receptor expression are presented as fluorescently labeled ligands bound to α4β1 integrin localized in liquid disordered domains and formyl peptide receptor (FPR) localized in membrane rafts. Lipid components of membrane rafts such as cholesterol and sphingomyelin are believed to confer membrane-condensing properties that make them less permeable to exogenous probes.31-33 rci are the distances of closest approach between the FRET donor, FITC labeled ligands and R18 acceptors incorporated into the membrane. For the integrin rc1 = 25Å is equivalent to the vertical separation between the integrin headgroup that bears LDV-FITC and the membrane.17 For the FPR rci has vertical (height of the receptor binding site above the membrane, rc2 = 0) and lateral (width of the receptor and lipid raft that excludes R18 rc3 = 13Å) components. rci are based on X-ray crystal structure of the GPCR rhodopsin II (PDB # 1h68). Micrographs show a cell bearing LDV-FITC before and after mixing with R18.
The plasma membrane is a system in which there is environmental heterogeneity. Lateral heterogeneity in membranes is broadly defined in terms of the coexistence of ordered (saturated lipids and cholesterol) and disordered (unsaturated lipids) liquid phases of lipids.22-25 One essential element associated with heterogeneity among membrane lipids is the presence of submicroscopic, transient domains around proteins and protein aggregates in signaling rafts.22 While there appears to be some consensus agreement regarding the existence of raft domains, questions still remain due to lack of direct visual evidence in living cells. When exogenous R18 is added to membranes, it is expected to distribute to varying extents among the environments in the plasma membrane. With this in mind we have begun to study the coexistence of lipid domains in live cell membranes by using FRET to report, in real time, the differential distribution of R18 acceptors at the loci of two receptor sites in resting cells as illustrated in Fig. 1. The sites are defined by an α4β1 integrin, previously proposed by us to be confined to liquid disordered domains17 and the formyl peptide receptor (FPR) localized in liquid ordered domains in the plasma membranes of the same population of U937 cells (see Fig. 1).26
Progress in this work has been hindered by physiochemical characteristics of R18 that have produced confounding effects on our ability to analyze the transfer of R18 from the aqueous phase to local membrane sites. Issues of concern are as follows. 1). In the aqueous phase, amphiphilic R18 has an unknown critical aggregation concentration and exists in equilibrated monomeric and aggregated forms8,27 even at nM concentrations. As for this problem, Vaz and coworkers,28,29 have used a strategy by which amphiphile aggregation is circumvented by presenting the probe as a protein–(serum albumin) bound species. However, the mechanism (optimal reagent stoichiometry, kinetic and equilibrium constants) of this process has not been defined for R18. 2). R18 aggregates that are formed in water or in membranes have different spectroscopic properties than the monomers.30 Therefore, if used as an acceptor in a FRET experiment, changes in the absorption cross-section are likely to affect the degree of spectral overlap (JDA term in Eqn. 3) and thus the efficiency of FRET. It is therefore important to set quantitative limits on the membrane surface concentration of acceptors, where formation of dimers is deemed to be significant in order to establish appropriate constraints for accuracy in the analysis of FRET. On problem 2, several studies have described the propagation of concentration quenching of R18 in single component and cholesterol containing model membranes, including viral envelope membranes.5-13 It has been shown that in general cholesterol and membrane condensing lipids31,32 (i.e. lipids that confer a reduction of average molecular area per lipid in the bulk membrane)33 effect a notable enhancement of self-quenching of R18 compared to unsaturated phospholipids. 8
In anticipation of a rational use of R18 to stain live cell membranes, we have undertaken the present work to: a) define in a model system, the conditions under which monomeric R18 can be delivered to membranes and b) define the limiting surface density conditions, for the onset of probe aggregation that causes significant changes to spectra and random distribution on the membrane surface.1 Accordingly, in this paper we have examined the transfer of R18 into two limiting models of the plasma membrane, namely a single component disordered membrane comprised of dioleoyl-L-α-phosphatidylcholine (DOPC) and a canonical raft model34 ternary mixture of DOPC, cholesterol and sphingomyelin (DSC) lipids, reconstituted on spherical and monodisperse glass beads (lipobeads).35 Quantitative flow cytometry measurements, relying on a novel set of quantum dot based fluorescence calibration beads 36,37 and FRET were used to quantify the surface labeling of model membranes with exogenous R18 probes. As a result, we define the phenomenological kinetics of serum-mediated transfer of monomeric R18 to lipobeads under optimal conditions, where the CAC is defined. The data also reveals that lipobeads accept a limited number of exogenous amphiphile probes and that, DOPC membranes hold 37% more probes than DSC membranes, which is consistent with the relative average molecular areas of the model systems.38 Subsequent studies will use the model framework developed here to analyze differential local FRET, at sites of receptor expression (Fig. 1).
Experimental Section
A. Materials
1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(carboxyfluorescein) (fluorescein PE), 1,2-Dioleoyl-sn-Glycero-3-Phosphoethanolamine-N-(Lissamine Rhodamine B Sulfonyl) (rhodamine PE), and dioleoyl-L-a-phosphatidylcholine (DOPC), cholesterol, egg sphingomyelin: 83.9% C16:0, 6.3% C18.0 and other minor longer chains (SM), were purchased from Avanti Polar Lipids, Inc. (Alabaster, AL). 5μm diameter glass beads were obtained in dry form from Duke Scientific Corp (Palo Alto, CA), octadecyl rhodamine B chloride (R18), and 5-octadecanoylaminofluorescein (F18) were purchased from Molecular Probes (Eugene, OR) and used without further purification. Streptavidin coated polystyrene particles (6.7 μm in diameter, 0.5% w/v) were purchased from Spherotech Inc. (Libertyville, IL). Streptavidin coated quantum dots, QD585, were purchased from Invitrogen Corp (Carlsbad, CA). Phosphate-buffered saline (PBS) was purchased from Mediatech, Inc, Herndon, VA). TRIS (10 mM or 25 mM Tris, 150 mM NaCl, pH 7.5) and HHB (30 mM HEPES, 110 mM NaCl, 10 mM KCl, 1 mM MgCl26H2O and 10 mM glucose, pH 7.4) buffer were used in the presence or absence of 0.1% human serum albumin (HSA). The human monoblastoid U937 cell line was purchased from ATCC (Rockville, MD).
B. Qdot-labeled Microbeads
A detailed description of the preparation of fluorescence calibration beads can be found elsewhere. 36 Fluorescence calibration beads can be made for any fluorophore, under the rationale that the fluorescence intensity of any given molecule is proportional to, I0εϕ; I0 is the intensity of the light source, ε is the absorption coefficient and ϕ is the quantum yield of the fluorophore.
C. Determination of probe quantum yields
Absorption and spectrofluorometric measurements were performed using a Hitachi model U-3270 spectrophotometer (San Jose, CA) and a Photon Technology International QuantaMaster™ Model QM-4/2005 spectrofluorometer (Lawrenceville, NJ) respectively. QD585, fluorescein, fluorescein, rhodamine B, R18 and F18 solutions were prepared in detergent micelle (1% Triton X -100) and vesicle suspensions. The optical densities at the absorption maxima of all solutions were kept at ≤ 0.02 where the error due to inner filter effects is 2%. 39 Excitation and emission spectra were collected for all samples. Fluorescence intensity data were collected at each fluorophore's emission maxima using appropriate bandpass filters (Corion Corp., Holliston, MA; CVI Laser, Albuquerque, NM).
D. Supported Bilayer Membranes on Glass Beads
Lipid-coated glass beads (lipobeads) were prepared as previously described. 35 For the present study lipobeads of various lipid compositions were prepared for the following applications: a) To analyze the progression of self quenching of R18 as a function of its mole fraction (0-10 mol%) in a single component, DOPC lipid bilayer membrane and a 1:1:1 ternary mixture of DOPC/sphingomyelin/cholesterol (DSC) lipid membranes. b) To analyze realtime FRET quenching of 0.025 mole% fluorescein PE doped in DOPC and DSC membranes. c) To analyze lateral separation of lipid phases in DSC bilayers doped with 0.25 mol% rhodamine PE.
Briefly, small unilamellar vesicles (SUVs) were prepared from 1 mM solutions of DOPC or 1:1:1 D/S/C in chloroform (210 μL total volume) in microfuge tubes. Fluorescent probes were added to the solution in the appropriate mole fraction as needed. The chloroform was removed by vacuum drying the samples using a CentriVap Benchtop Centrifugal Vacuum Concentrator (Labconco, Kansas City, MO) at room temperature for an hour. After addition of 200 μL of Tris buffer (pH 7.5), the vesicle suspension was sonicated to optical clarity using a Branson sonifier (Branson Cleaning Equipment Co., Shelton CT). Acid and peroxide-cleaned mono disperse glass beads35 were then added to the SUV suspension with vortexing for 5 minutes. The lipobeads were then washed and resuspended in 1% HSA buffer a minimum of 5 times to remove excess vesicles. 1% HSA was added as a lipid binding scavenger protein to facilitate the removal of vesicles (see Section K for context). The final wash was performed in serum free buffer. For long-term storage, beads were stored at 20°C under Argon or N2 degassed conditions.
E. Fluorescence dequenching measurements
Unless otherwise specified, bead suspensions were used at 1,000 beads/μL. The bead samples were transferred to cuvettes in 400 μl volumes with mini magnetic stir bars to maintain beads in suspension for fluorescence measurements using a Photon Technology International QuantaMaster™ Model QM-4/2005 spectrofluorometer (Lawrenceville, NJ), following standard protocols for such measurements.36,37 With the instrument set in kinetic mode, fluorescence intensities of the quenched R18-bearing lipobead suspensions were measured as a time course for 30 seconds, after which a 20 μl aliquot of 20% Triton X-100 was added to the bead suspension. In this way the supported bilayer was completely solubilized, with the concomitant 100% dequenching of R18. The increase in fluorescence intensity of the samples was corrected for dilution, and then correlated to the degree of self-quenching of R18 at the various mole fractions in membranes. The results were plotted as a graph representing relative quantum yield versus mole-fraction of R18. This graph (see Fig. 3) was used to estimate the quantity of R18 associated with beads after a time course measurement. This analysis involved the centrifugation of and washing of beads after incubation with R18 for a desired time. The re-suspended beads where then read at the spectrofluorometer before and after addition of Triton-X 100 as described above. The increase in fluorescence intensity was correlated to the mole fraction of R18 on the standard curve.
Figure 3.
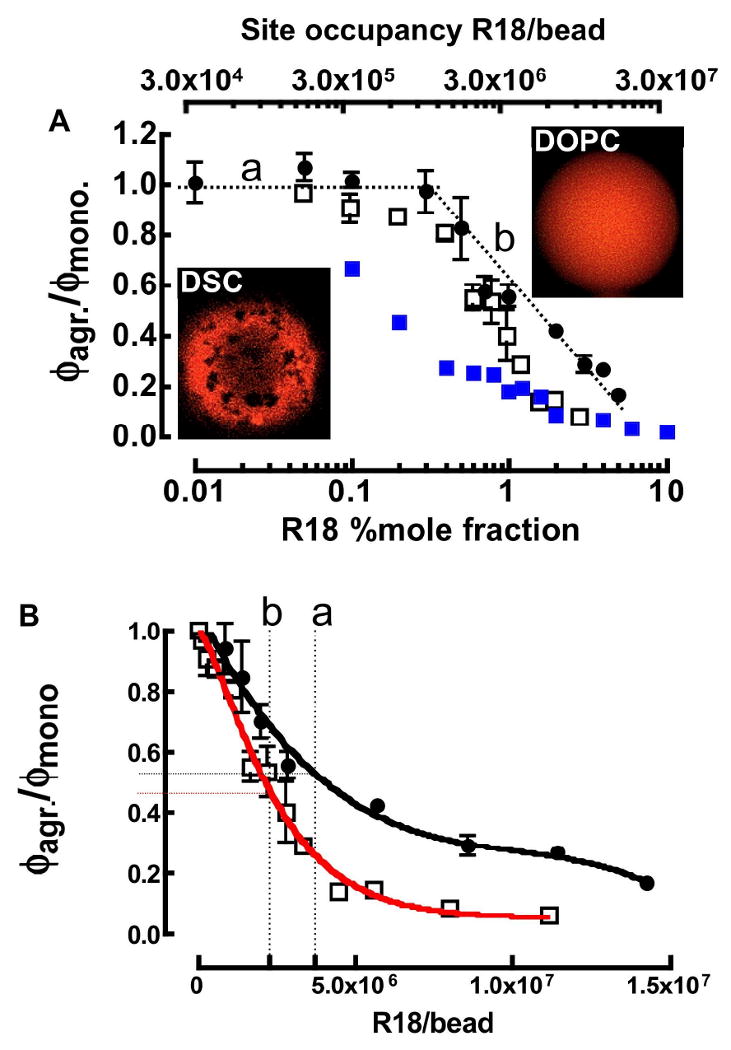
A. Confocal micrographs of DOPC (top) and DSC beads (bottom) at 20°C. Relative quantum yield ϕagr/ϕmonomer of R18 solubilized in supported lipid membrane bilayers: (filled circles) DOPC at 37°C, (open squares) DSC at 37°C and (filled squares) DSC at 20°C on beads. ϕmonomer refers to the quantum yield of soluble rhodamine B or R18 in Triton X-100. (a) Dotted line marks site occupancy/mole fraction region below the onset of self-quenching. (b) Line shows site occupancy/mole fraction region in which the self-quenching of R18 in DOPC membranes changes linearly on log scale. B. Relative quantum yield ϕbead/ϕmonomer of R18 on DOPC (filled circles) and DSC (open squares) lipobeads as a function of site coverage at 37°C. The curves represent theoretical fits to the data using Eqns. 8 and 9 respectively. The vertical dotted lines refer to the maximum site occupancy numbers of R18 at the end of a binding time course (in Figure 5) for (a) DOPC and (b) DSC beads. Horizontal tie lines to the y-axis represent the degree of self-quenching in R18 occupied DOPC and DSC lipobeads.
F. Measurement of the transfer of R18 from the aqueous phase into bead supported membranes
Flow cytometric measurements were performed on a Becton-Dickinson FACScan flow cytometer (Sunnyvale, CA) interfaced to a G4 Macintosh using the CellQuest software package. The FACScan is equipped with a 15 mW air-cooled Argon ion laser. The laser wavelength is fixed at 488 nm. The time course of association between R18 and beads was typically measured by acquiring a 30 s baseline of donor fluorescence on beads or cells then adding an aliquot of R18 to the sample, briefly vortexing, (creating a 5-10 s gap in the time course) and resuming data collection continuously to some desired time (e.g., 150-300 s). Detailed protocols have been described elsewhere.14,17 The data output from a flow cytometer is normally expressed in terms of the mean fluorescence intensity of a population of cells or particles (mean channel fluorescence- MCF). Standard fluorescence calibration beads are used to convert the MCF value of cells to number of fluorophore equivalents using Eqn. 1, where: Ii are the measured intensities of the
| (1) |
R18-bearing beads (1) and standard QD585 quantum dot bearing beads (2) irradiated by the same 488nm, 15 mW laser; ελex,i are the molar extinction coefficients of R18 (4,750 M-1cm-1) and QD585 quantum dots (530,000 M-1cm-1) at the excitation wavelength; ϕi are the respective quantum yields of R18 and QD585 dots, lot# 452664A (see Table 1); It is important to note that the emission quantum yield of quantum dots varies from batch to batch 36,37 hence the lot number of the streptavidin functionalized dots used to tag our calibration beads is given here. The intrinsic quantum yield of R18 is 0.3 36,37 which decreases in proportion to the degree of self-quenching as will be shown in the results section. ρi are the site densities of R18 on the beads and quantum dots on the calibration beads respectively; %T is the percent fraction of fluorescence light transmitted through the bandpass filter and is used to account for the spectral mismatch between R18 fluorophore and QD585 Quantum dots. The values of these parameters are given in Table 1.
Table 1.
Some Spectroscopic Characteristics of Molecular Probes.
| Parameter | F18 | QD585 (lot#45264A) |
R18 |
|---|---|---|---|
| λmax =498 | - | λmax =564 | |
| λex =488 | λex =488 | λex =488 | |
| Molar absorptivity i, | |||
| ε(M-1cm-1)@,λmax | 80,000ia | - | 95,400ic |
| ε(M-1cm-1)@λex | 72,600 | 530,000 | 4,750 |
| Quantum yield (ϕs) ii | 0.88iia | 0.12iic | 0.3iid |
| λem max. (nm) | 520iiia | 585 | 585 |
| Bandpass %T iii | 37 | 65 | 51 |
| Overlap integral | |||
| JD-R18 (cm3M-1) iv | 3.35×10-13 iva | - | 3.75×10-13 iva |
| 1.96×10-13 ivb | 3.40×10-13 ivb | ||
| 2.8×10-13 ivc | 3.09×10-13 ivc | ||
| R0-R18 (Å) v | 61.0va | 52.2va, 51.5±1v′ | |
| 56.3vb | 51.3vb | ||
| 57.3vc | 48.0vc | ||
Notes.
Extinction coefficients obtained from www.probes.invitrogen.com. (a) The extinction coefficients of fluorescein and derivatives vary from 85,000 for the NIST fluorescein solution standard reference material SRM 1932 to 75,000 for some FITC derivatives, and values are pH dependent. We have selected a median number here. (b) ibid. (c) Taken from ref (Cerione, R. A., McCarty, R. E., and Hammes, G. G. (1983) Biochemistry 22,769–776).
Relative quantum yields, , were calculated using the integrated intensity of sample relative to fluorescein, φref = 0.93; or rhodamine B (0.31 in water (Magde et. al., Photochem. Photobiol. 1999) Is and Iref are the integrated band intensities. The optical densities (OD) of the sample (s) and reference (ref) were kept close. n is the index of refraction of the solvent; 1.32 for water. The experiments were perfomed in: (a) ethanol/PBS, (b) water (c) water, ϕs is accurate for the given lot number and excitation wavelength (see text and Wu et al Anal. Biochem. 2007, 364, 193-203 for details). (d) vesicles.
Bandpass filters used in a standard model BD FACScan flow cytometer (c.f. Figure 2 and Figure 4 in ref (Wu et al Anal. Biochem. 2007, 364, 193-203).
Calculated using Eqn. 3.(a) Overlap with absorption spectrum of R18 in Triton X-100. (b) R18 Spectrum in water. (c) Spectrum of H-dimer.
(a-c) Calculated using J values derived from iv. v′ Taken from Edinger, M.D., Domingue, R.P., Fayer, M.D. J. Chem. Phys. 1984, 80, 1246-1253.
G. Calculation of R0
The characteristic distance at which the efficiency of energy-transfer is 50% is defined as R0. R0 is calculated (in Å units) using Eqn. 2.
| (2) |
where, QD is the quantum yield of the donor in the absence of acceptors, κ2 is the geometric factor that depends on the relative orientation of the donor and acceptor transition dipoles. κ2 is usually assumed to be 2/3, a value which corresponds to the randomization of donor-acceptor orientations by their rotation or diffusion, n is the refractive index (1.33) of the medium between the donor and acceptor moieties. JDA is the overlap integral that expresses the degree of overlap between the donor emission and acceptor absorption.
| (3) |
FD (λ) is dimensionless intensity, representing a corrected emission spectrum of the donor normalized to unity at the band maximum, ε(λ) is an extinction coefficient expressed in units of M-1cm-1, λ is wavelength that is expressed in units of cm, thus the overall units of J are M-1cm3. Calculated values of R0 for probes used herein are given in Table 1.
H. Random energy transfer to multiple acceptors in two dimensions
Energy transfer data were analyzed using the formalism developed by Wolber and Hudson, 21 which involves the steady state intensity of randomly distributed donor molecules quenched by acceptor molecules on an infinite plane. This is given by the expression in Eqn. 4a.
| (4a) |
| (4b) |
QDA and QD are the respective quantum yields of the donor in the presence and absence of acceptors λ=t/τ is the ratio of time t, and the intrinsic lifetime τ of donor molecules. Γ(2/3) is the standard mathematical gamma function and c is the two dimensional concentration of acceptors per unit area, expressed in terms of R02 or C = R02c. Equation 4 is applicable for values of C the range 0<C< 0.5. 21 Eqn. 4b represents an approximate solution to the numerical integration of Eqn 4a where the coefficients corresponds to an exact solution for the series approximation for the value of the distance of closet approach, rc = 0 between randomly distributed donors and acceptors on an infinite plane. rc = 0 is applicable to DOPC membranes where the donor and acceptor probes are both randomly distributed in a homogeneous membrane without the presence of boundary lipid (membrane raft), which excludes or hinders the partitioning of R18 such as DSC membranes (cf. Fig. 3).
I. Incorporation of R18 into and dissociation from bead supported DOPC membranes
To measure the dissociation of R18 from beads, a relatively low concentration of 0.44 μM R18 was added to a suspension of 2×106 beads in 0.1% HSA HHB buffer and allowed to incubate at 37°C for a minute. The sample was then centrifuged and the beads were resuspended in 1mL HHB buffer containing 1% HSA. Once again, a high concentration of HSA was used here to capture the desorbing R18 probes, thus minimizing probe rebinding. To analyze the dissociation kinetics of R18 from resuspended beads, fluorescence intensity of the beads was measured using a flow cytometer at regular intervals over a period of over thirty hours, the beads were kept at 37°C and in suspension by stirring in a temperature controlled sample holder.
J. Confocal Microscopy Imaging
Beads were placed in a sample chamber (Model PDMI-2 Open Perfusion Microincubator). Confocal microscope imaging was performed on a Zeiss 510 LSM inverted microscope at 20°C as previously described.35
K. Kinetic Analysis of the association of R18 and beads
Most amphiphiles (phospholipids and their derivatives, long-chain fatty acids, etc.) are predisposed to aggregate in aqueous solution, when used at concentrations that are higher than their critical aggregation or micelle concentration (CAC or CMC).28,29 Serum albumin is the principal physiological carrier of highly insoluble long chain fatty acids (≥C14) in the circulation.40-43 Consumption for energy metabolism requires the rapid transport of fatty acids between serum and cells. Consequently the characteristic time of approach to binding equilibrium must be extremely fast and is typified by a rapid on-rate and a relatively rapid dissociation rate to facilitate the delivery of the fatty acids to their metabolic sites.42,44-46 Accordingly, serum albumin has been used in membrane staining buffers, to reduce the concentration of free amphiphile to some desired level below the cmc.28,29 The free monomeric amphiphile that transfers from the aqueous phase to the membrane is continuously replenished with amphiphiles that dissociate from the protein-bound state.28,29 This process is represented in a mass action based kinetic model as shown in Eqn. 6.
| (6a) |
| (6b) |
The kinetic interaction of serum albumins with amphiphile probes or various fatty acids is well studied and as such, we have relied upon the conceptual framework established by Vaz and coworkers28,29,47 for our kinetic analysis. To that purpose, for Eqn. 6a an intrinsically fast binding rate constant (k1≥106 M-1s-1) and dissociation rate constant (0.1≤k-1 ≤0.9s)42 is expected (vide supra). These interactions are largely driven by hydrophobic interactions such that a limiting range of values can be estimated based on chain lengths.43,48 For the practical purpose of maintaining a monomeric concentration of free R18, the relative concentrations of serum albumin and R18 must be, ([HSA]0 ≫[R18]0) such that [HSA] remains unchanged throughout the course of the experiments. Each HSA molecule is assumed to bear six receptor sites for long chain (>C14) fatty acids/amphiphiles.40,42,43 Our analysis makes the simplifying assumption that the kinetic differences among the intra-protein binding sites cannot be resolved by our experimental method in line with single exponential dissociation characteristics of fatty acids from serum albumin.42
In Equation 6B, lipids represents “free volume” units or holes of dimensions approximately equal to or greater than the cross-sectional area of the R18 probes that represent binding sites in the lipid bilayer membrane.49,50 The definition of a binding site in lipid membranes is complicated and often the formalism that is used depends on the experimental situation.51 The most common model treatment of the partitioning of a probe into lipid membranes is one that is expressed in terms of a ratio of membrane-associated probes and probes in the aqueous phase i.e. [R18]membrane/[R18]aq. This model contains no explicit information on binding sites and is, in principle most applicable when the probe concentration is much smaller than the quantity of membrane lipids.51 Several approaches, that include the concept of binding sites have been discussed in a book by Gennis.51 Our experimental situation is mitigated by the use of mono disperse sized beads, which present a defined supporting platform for a finite quantity of membrane lipids. Quantitative assessment of probe binding to measurable and finite binding sites on beads allows us to treat our data using a homogeneous kinetic model based on mass action. In view of that, the association of R18 with beads was then analyzed using a set of coupled ordinary differential rate equations derived from Equation 6.
| (7a) |
| (7b) |
Results
A. Spectroscopic properties of R18 relative to quantum dot fluorescence calibration beads
Figure 2A shows a graph of superimposed absorption (left axis) and emission spectra (right axis) of R18 and 585 nm quantum dots. The emission spectra are scaled such that the peak value represents the maximum quantum yield values of R18 and QD585 respectively. Spectroscopic data are summarized in Table 1.
Figure 2.
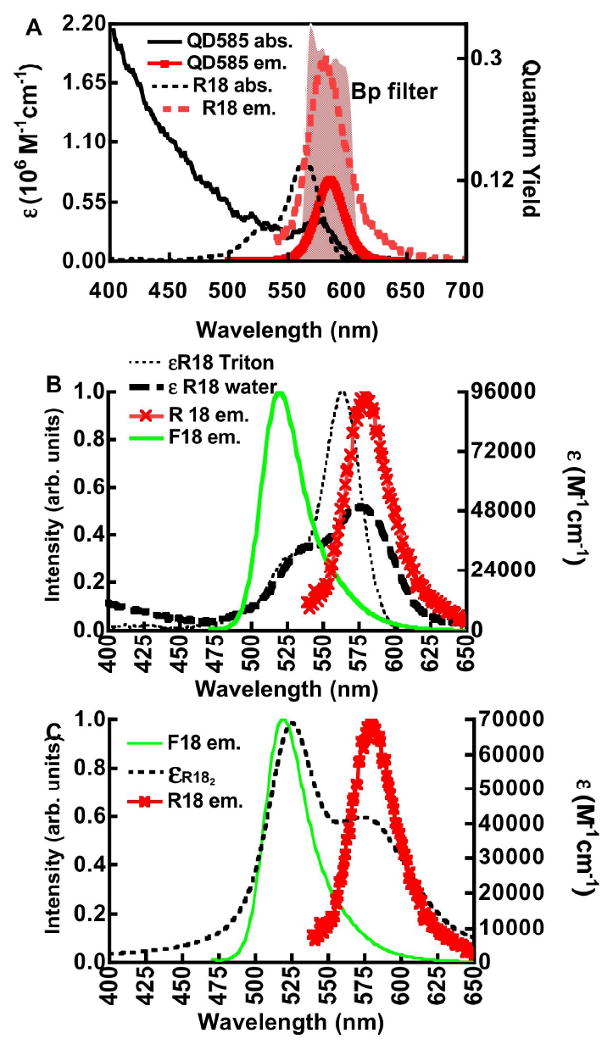
A. Fluorescence calibration and spectroscopic properties of R18 and QD585 dots. Right hand ordinate. Plot of absorption spectra of R18 (R18 abs.) and QD585 quantum dots (QD585 abs.). Left ordinate. Plot of quantum distribution functions of emission of R18 (R18 em.) and QD585 (QD585 em.) normalized by the maximum quantum yield of each probe. The shaded spectral region represents a bandpass filter centered at 580 nm and a component of one of 3 detection channels of a BD flow cytometer. B. Left ordinate. Plot of normalized emission spectra of F18 (F18 em.) and R18 (R18 em.). Right ordinate. Plot of absorption spectra of R18 solubilized in Triton X-100 (εR18 Triton) and neat buffer (εR18 water). C. Left ordinate. Plot of normalized emission spectra of F18 (F18 em.) and R18 (R18 em.). Right ordinate. Resolved spectrum of R18 H-dimer (εR182) modeled from the compound spectrum of R18 aggregates (εR18 water) in Figure 2B using parameters (λmax, ε, and bandwith FWHM) taken from Selwyn and Steinfeld (see text for details).30
Numerous studies have shown that xanthene dyes such as rhodamine B, tend to form aggregates in the aqueous phase. 30,52-56 These aggregates exist as either nonfluorescent “H-dimers” or fluorescent “J-dimers” depending on the geometry adopted by the monomer constituents.57 H-dimers are formed when two monomer transition moments are in coplanar geometry whereas, J-dimers are at oblique angles.53,57 H-dimers of rhodamine B, are formed in polar solvents such as water whereas J-dimers dominate in non-polar environments such as ethanol.30 Elucidation of the spectral characteristics of R18 under our experimental conditions is important to establish the modes of self-quenching.
The absorption spectra of 1×10-6 M R18 in 1% Triton X-100 and regular buffer are shown in Fig. 2B. The emission spectra of F18 and R18 are also presented for the purpose of displaying spectral overlap with the absorption spectra (vide infra). The absorption cross-section and emission properties of monomeric R18, solubilized in vesicles or Triton X-100, are close to those of the parent molecule, rhodamine B. 58 Some differences can be found in the absorption maxima and extinction coefficients of the rhodamine B (λmax = 554nm; ε = 120,000 M-1cm-1)30 and R18 (λmax = 565nm; ε = 95,400 M-1cm-1).59 In 1% Triton X-100 R18 aggregates are solubilized, to the extent that they exist in monomeric form. In water the absorption spectrum of R18 aggregates is characterized by a significant loss in the oscillator strength of the lowest energy band (0-0 transition)60 centered at 570 nm. Others 30,54 have shown that rhodamine B forms ground state complexes with an average association constant (Ka) of ≈ 104 M. Based on the putative Kd one would expect only a small fraction of the dye to be dimerized at 1μM. Nevertheless, for R18, the C18 long acyl chain on R18 is expected to confer surfactant-like properties, such that aggregation occurs at much lower concentrations.61 Selwyn and Steinfeld 30 have examined the absorbance of rhodamine B over the concentration range 10-7 M to 10-3 M. From these measurements they resolved the absorption spectra of H-and J-aggregates. Spectral parameters (e.g. λmax, bandwidth (FWHM), ε,) of the absorbance spectrum of an H dimer from Selwyn and Steinfeld30 were used to resolve the absorption spectrum of H-dimers in our compound spectrum of monomers and aggregates using Igor Pro Software package (Lake Oswego, OR). The absorption spectrum of R182 consists mainly of two overlapping bands with peak wavelengths fixed at 524nm and 574nm. The bandwidths were estimated to be 50 nm and 90 nm respectively. The extinction coefficients at the two peaks which are given by Selwyn and Steinfeld30 relative to rhodamine B monomers (1.2 × 105 M-1cm-1) were then scaled relative to the extinction coefficient of R18 of 9.54 × 104 M-1 cm-1 at 564 nm.59 The simulated absorption spectrum of an R182 H-dimer is shown in Figure 2C.
B. Calculation of R0
The overlap integrals (JDA in Eqn. 3), for F18 and R18 donor emission and R18, and (R18)2 acceptor absorption spectra were calculated and the results are summarized in Table 1. The outcome shows very little distinction in the relative magnitudes of JDA for monomeric or dimeric forms of R18. Because of the inverse 6th power dependence (Eqn. 2) of dipole-dipole interactions changes in the relative size of parameters such as κ2 and JDA have little effect on the magnitude of R0. Thus, a 64-fold change in JDA is necessary to effect a 2-fold change in the numerical value of R0 if all other parameters in Eqn. 2 are held constant. The magnitude of κ2 normally spans the 0≤ κ2 ≤ 4 range. The values of 0 and 4 correspond to the cases where the donor and acceptor dipole moments are orthogonal and comprise a mixture of parallel and antiparallel moments respectively.62 Two common values of κ2 in membranes are 0.667 corresponding to the randomization of donor-acceptor orientation by rotational diffusion of donors and acceptors before FRET, and 0.476 the static randomization of donor-acceptor orientations, that otherwise remain constant during the lifetime of the donor.62,63 The value for static randomization normally applies to 3D measurements whereas 0.405 has been suggested as the more appropriate value for 2D membrane surface measurements.64 The most commonly used approximate value of 0.667 yields a maximum error of 35%. These limiting values of κ2 produce a variation in the value of R0 of ≈ 5%. The usual error encountered in most experiments is no more than 10%. 62 The applicability of 0.667 to our data is later demonstrated in Figure 8.
Figure 8.
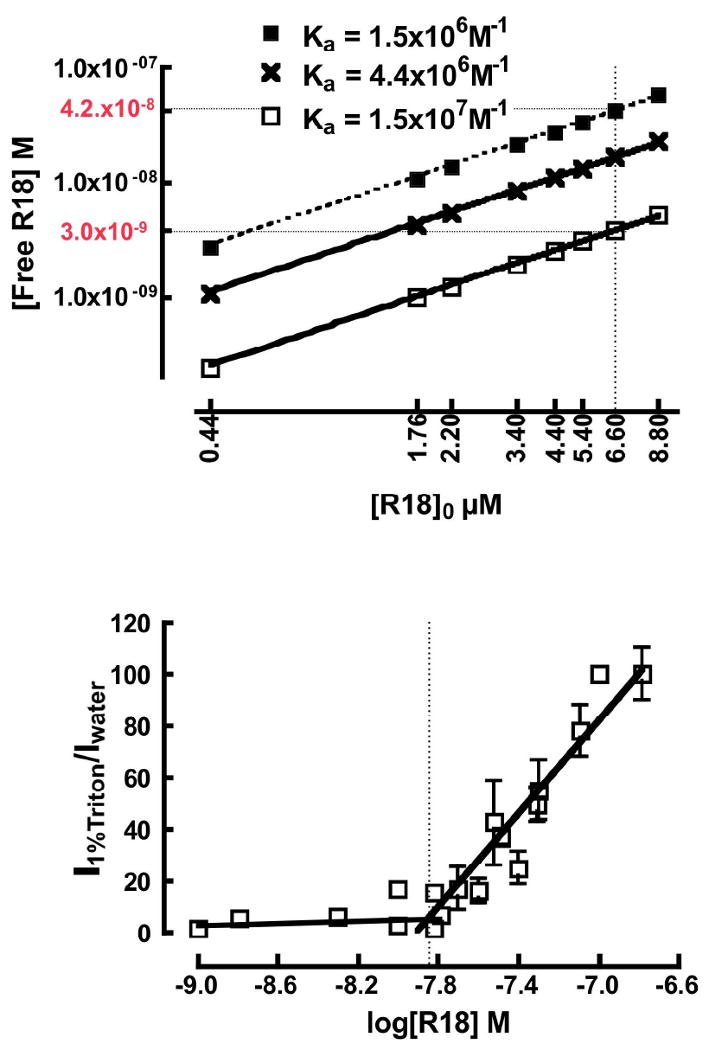
A. Plot of free [R18]eq. versus [R18]0. Values of [R18]eq. were calculated using three values of Ka derived from theoretical fits of experimental data (see Fig. 5). Top and bottom curves represent the upper and lower limits of Ka based on the uncertainty in the rate parameters. The middle curve represents the Ka value based on the CAC determination (see text for details). The vertical dotted line marks the concentration of bulk R18 at which probe aggregation was inferred. The limiting values of [R18]eq are identified along the lower and upper curves by dotted lines that intersect the y-axis at 3 nM and 42nM as shown. B. Determination of CAC from a plot of the ratiometric assay of the fluorescence intensity of R18 solublized in 1%Triton X-100 and water versus log [R18]. The inflection point is equal to the CAC value of ≈14nM.
C. R18 in bead supported bilayer membranes
Bead supported bilayer membranes were formed by vesicle fusion on hydrophilic glass surfaces as previously described.35,65 Depending on composition and temperature, the typical membrane is separated from the substrate by a thin (10-30 Å) layer of water and, like natural membranes possesses macroscopically long range fluidity with mobile components of both leaflets freely diffusing over the entire surface of the support.35,66,67 68Figure 3 shows confocal fluorescence micrographs of DOPC and DSC bilayer membranes supported on 5μm glass beads. DOPC (C18:1- C18:1) has two unsaturated acyl chains, with a low chain melting temperature (-20°C). SM (C16:0) has saturated chains that melt at 40° C.69 The (1:1:1) ternary mixture of DOPC, SM and cholesterol has two coexisting phases, namely liquid ordered (Lo) SM and cholesterol enriched, and liquid disordered (Ld), DOPC and cholesterol depleted phases, below the miscibility transition temperature of Tm = 35-40°C.69 At 20°C, phase separated Lo and Ld domains are recorded by the acyl chain-unsaturated fluorescent probe 18:1 rhodamine PE that is excluded from SM-rich Lo and co-localizes with the DOPC-rich Ld domain.24
D. Self-quenching of R18 is enhanced in DSC membranes relative to DOPC membranes
Figure 3A shows a plot of the relative quantum yield of bead-borne R18 as a function of its % mole fraction (%χ) in the DOPC and DSC bilayer membranes. A comparison of our DOPC data to vesicle data (e.g. see Figure 5 from Johansson and Niemi58) shows that the onset and degree of self-quenching of R18 over a 0 - 10%χ range is enhanced by a factor of 2 on beads compared to vesicles. It turns out that on beads, R18 is effectively localized in the outer leaflet of the membrane, and not randomized in both leaflets, as is the case in vesicles. This was confirmed by a potassium iodide collisional-quenching experiment,60 where the addition of 100 mM KI quenched nearly all fluorescence. The efficient quenching was taken to be consistent with the localization of R18 headgroup at the membrane/water interface in the outer leaflet where it is exposed to collisional encounter with KI. The localization R18 in the outer leaflet is likely to be imposed by the unfavorable steric interaction of the chromophore with the bead surface, as the water layer does not provide sufficient separation between bulk membranes and the substrate surface.68 Self-quenching in DOPC membranes is constant between room temperature and 37°C whereas in DSC membranes, partial exclusion of R18 from the gel-like Lo phase at temperatures below the 35-41°C miscibility transition temperature 69 yields a significant increase in quenching because of the increase in the surface concentration of R18 in the Ld domains.
Figure 5.
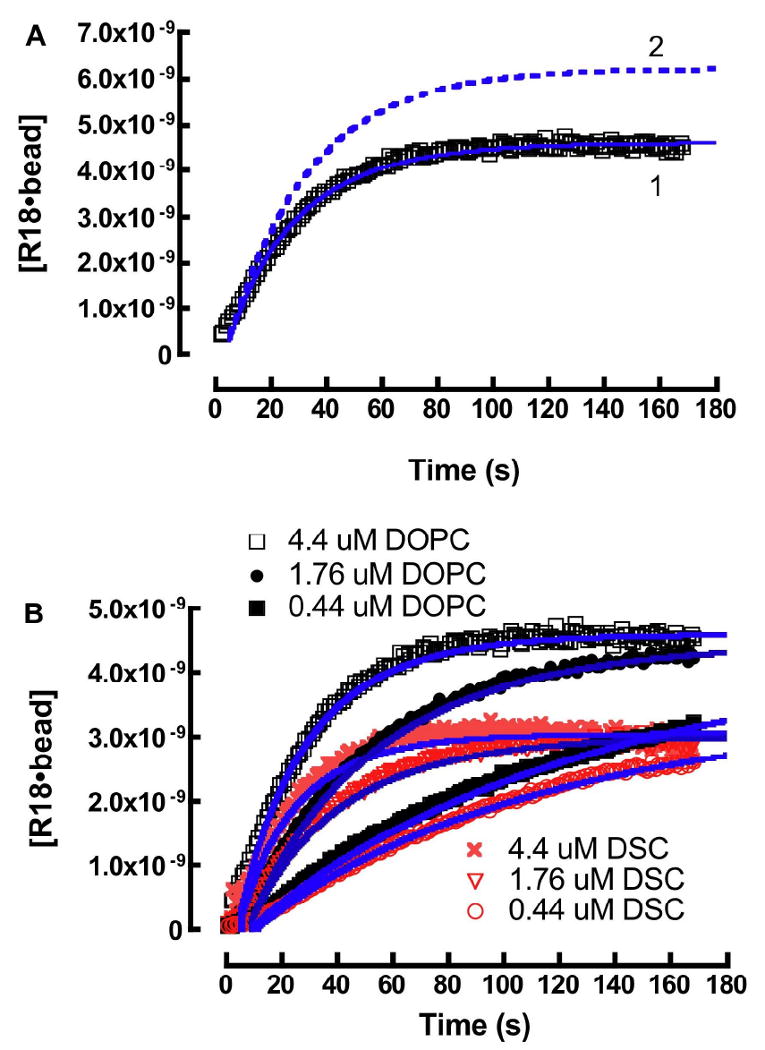
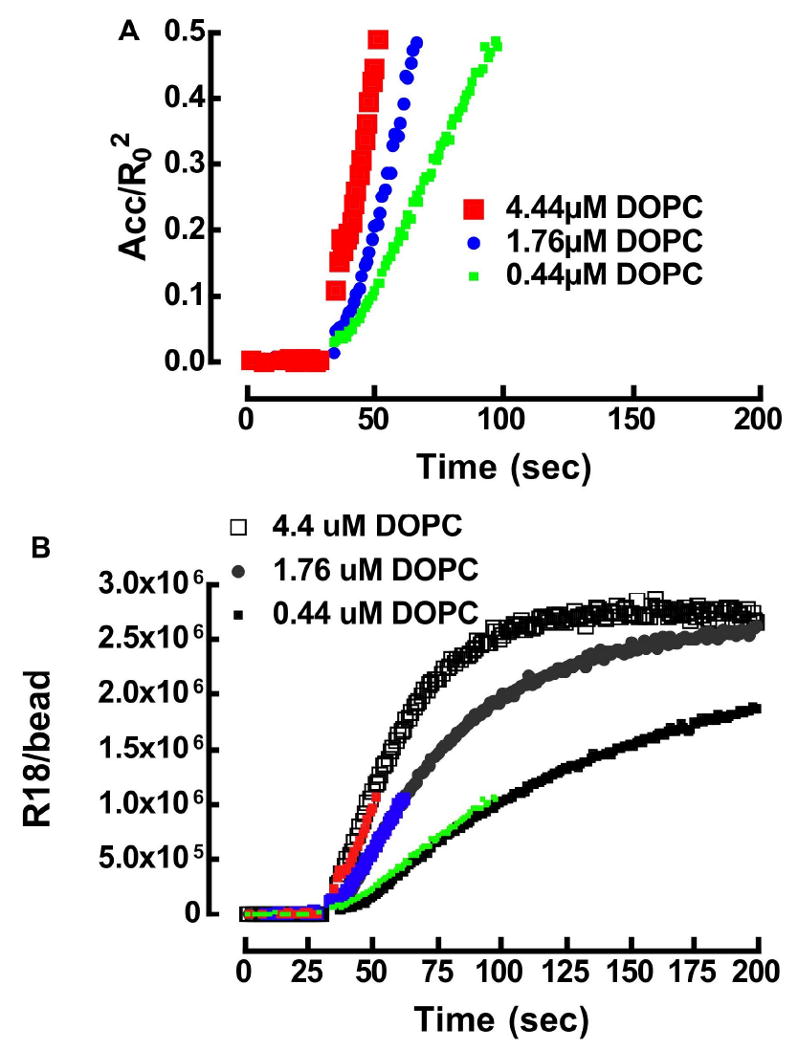
A. Kinetic analysis of real time association of R18 with DOPC beads. A theoretical fit of the data set was derived from the following rate constants: k1 = 1.0 ×106 M-1s-1, k-1 = 0.73 s-1, k2 = 1.2 ×106 M-1s-1, and k-2 = 1.2×10-5 s-1. (1) Theoretical fit (Eqn. 12) of experimental data describing the association and self-quenching of 4.4μM R18 with DOPC beads. (2) Simulation of the propagation of unquenched [R18] on DOPC beads. B. Kinetic analysis and simulation of the association of 0.44 μM, 1.76 μM, and 4.4 μM R18 and 400,000 lipobeads bearing DOPC and DSC membranes in 400 μL buffer containing 0.1% HSA.
Cholesterol or membrane condensing lipids (with relatively small molecular area footprints)33,38 significantly enhance quenching due to relatively higher surface concentration of probes in the condensed membranes.8 Figure 3B shows a plot of relative quantum yield of R18 versus numbers of R18 on beads at 37°C. For later convenience, it is useful to represent the propagation of self-quenching as a function of site occupancy, on a bead, by some empirical formalism that best fits the data points. The DOPC data were fit to a third order polynomial (Equation 8) while the DSC data were fit to a double exponential function (Equation 9).
| (8) |
| (9) |
For use in a kinetic model, it is practical to represent Eqns. 8 & 9 in terms of molar concentration at 1×109 beads/L as used in our experiments.
| (10) |
| (11) |
E. Quantification of bound R18 using fluorescence calibration beads
Flow cytometry is a multi-parameter measurement tool that enables the simultaneous analysis of light scatter and several colors.70 The measurements are based on the analysis of quenching of the emission of the donor probe excited with the 488 nm line of an Argon ion laser. There is sufficient off-resonance absorbance (ε = 4,750M-1cm-1 cf. Table 1) of the blue tail of the R18 acceptor at 488 nm. It is important to note that the magnitude of fluorescence intensity from direct excitation is experimentally demonstrated to be orders of magnitude larger than what one would expect from sensitized emission. Accordingly, the partitioning of R18 into membranes was concurrently measured as the emission output of direct excitation of R18 at 488 nm as well as energy transfer quenching of donor fluorescence. The data are shown in Fig. 4. To the casual observer, the association of R18 with DOPC and DSC lipobeads appears to be governed by similar kinetics where, the number of saturable “binding sites” on DOPC beads turns out to be higher than DSC. Turning to the FRET data, it is unfortunate that full donor quenching is realized at a relatively low surface concentration of R18, which constitutes a small fraction of the time course. The quantitation of R18 on beads by calibration beads will be presented first, while some quantitative aspects of the FRET assay will be examined later.
Figure 4.
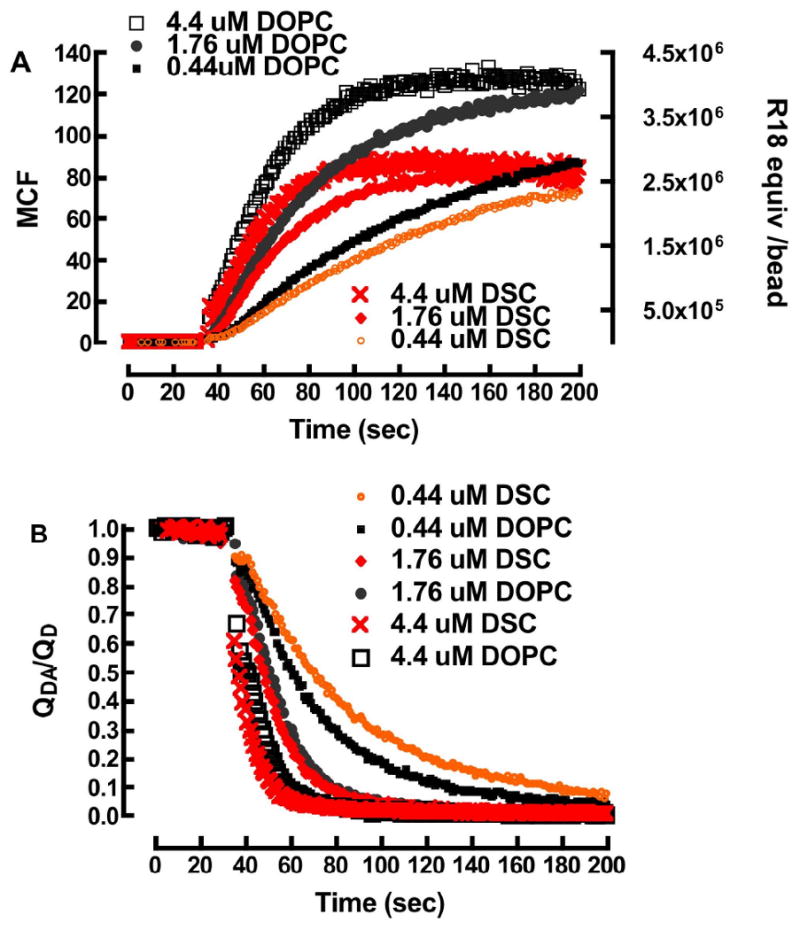
Partitioning of R18 into membranes: A. Direct excitation of R18. Left y-axis, plot of mean channel fluorescence (MCF) versus time, readings for partitioning of R18 into DOPC and DSC membranes. Right y-axis, nominal site occupancy of R18 equivalents on self quenched beads, derived from fluorescence calibration beads B. FRET time-course of FRET-quenching of F18 after addition of R18.
Equation 1 (see Table 1 for parameter values) was used to convert the raw mean channel fluorescence data to effective numbers of R18 probes/bead. At this time, the quantum yield of monomeric R18 was applied throughout the time course, without correcting for the self-quenching that is known to propagate with increasing surface concentration (cf. Fig. 3). The data were plotted as shown in Figure 4. The effective occupancies/bead were then converted to effective molar concentration units on 1×109 beads/L. Eqn. 12 was used to analyze the kinetics of association of R18 with lipobeads.
| (12) |
where, is represented by Eqns. 10 and 11 for DOPC and DSC respectively.
Finally, Eqn. 12 and all of the rate equations for the variable parameters of the kinetic scheme shown in Eqn. 6 were solved numerically using the Runge-Kutta method for values of reaction rate constants ki and k-i using Berkeley Madonna Software (Berkeley, CA) or Scientist Software (Micromath, St. Louis, MO)).
The dissociation rate constant, k-2, of R18 from lipobeads was determined by measuring the desorption of low surface concentration R18 (i.e. below the self-quenching regime) from beads over a 30-hour period, and analyzing the loss of fluorescence intensity of washed lipobeads (not shown). The t1/2 for the desorption of R18 from beads was ≈17 hours or k-2 = 1.2×10-5s-1. In context, it is worth noting that shorter single chain amphiphiles (≤C14 chain) are very labile71 and readily desorb from membranes (t1/2 ≈ 0.02 secs) 72 while double chain amphiphiles of the same length are slow (t1/2 ≈ 10-5 secs).73 The well documented strong interaction between R18 and membranes12,74 is attributable in part to the length of its C18 acyl chain and headgroup.12,75 The surface concentration of R18 at the end of the time course (i.e. t = 200 sec.) was estimated by correlating the degree of dequenching of the beads (after detergent solubilization) to R18/bead from readout of our standard curves in Fig. 3.
Under our experimental conditions it was not possible to experimentally measure the other three unknown rate parameters. Constraints were placed on the values of k1 and k-1 based on literature values for long chain fatty acids (C16-18:0) (k1: 1 ×106 - 107 M-1s-1) and k-1 (0.1 - 0.9s-1) 42,76 only k2 was unconstrained. Thus, the rate parameters k1, k-1 and k2, are nominally defined to within an order of magnitude. In this way, a theoretical fit of the [R18]0 = 4.4 μM data set yielded the following nominal rate constants: k1 = 1.0 ×107M-1s-1, k-1 = 0.73 s-1, k2 = 1.2 ×106M-1s-1, and experimentally measured k-2 = 1.2×10-5s-1. The rate constants used here represent an upper limit in the constraints placed on k1. The analysis is summarized in Figure 5A. Curve 1 shows an overlay of the quenched experimental data with a theoretical fit to Eqn. 12. Curve 2 represents the evolution of (unquenched) [R18•lipids] derived from the theoretical fit when the self-quenching term in Eqn. 12 is fixed to unity. The derived rate parameters were then fixed and used to simulate the [R18]0 = 0.44 μM and 1.76 μM DOPC data sets. The DSC data sets were analyzed using the same rate constants. As shown in Figure 5B, the simulated curves are reasonably correlated to the experimental data. The correlation between the early kinetic data, <10 sec, and theoretical fits was generally poor because of deadtime and laminar flow recovery time of the flow cytometer.77 At this time, it is important to note that a different combination of rate parameters, which fall within an order of magnitude of the ones given here, can fit the data just as well. To limit the number of unknown variables we considered applying quasi-stationary or steady state kinetics.78 To demonstrate conditions for the applicability of quasi-steady state treatment, it is useful to show the distribution of [R18]0 = 4.4 μM among 97.0 μM HSA, free R18 monomers, and DOPC membranes over, the experimental time course, using the nominal rate parameters from the kinetic model so far. As shown in Fig. 6, the rate parameters for Eqn. 6a allow for an a priori prediction of a subsecond characteristic time for equilibration (i.e. teq= 5t1/2= 3.5/(k1[R18]0+k-1))79 (see a in Fig. 6). The 2.5 nanomolar-range, working concentration of the free probe, [R18]eq, is maintained at a constant value throughout the time course, (i.e. when [R18]0 ≫ [lipids]) as the probe that is consumed by the beads is replenished by the dissociation of monomeric R18 from HSA•R18 complexes (cf. Eqn. 6a).28,29
Figure 6.
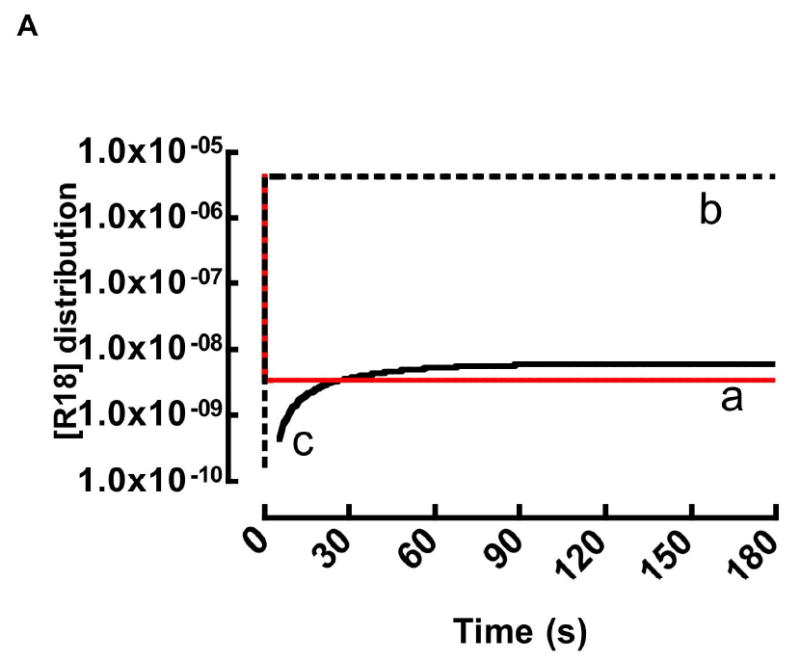
Realtime distribution kinetics of 4.4 μm R18 among a) aqueous phase b) HSA and c) DOPC beads derived from Eqn. 6 using the high estimates of rate parameters: k1 = 1.0 ×107 M-1s-1, k-1 = 0.73 s-1, k2 = 1.2 ×106 M-1s-1, k-2 = 1.2×10-5s-1. Here, the addition of a 2μL aliquot of 4.4μM DMSO-solubilized R18 to 0.1% HSA buffer yields all but ≈ 3 nM (curve a) of HSA•R18 complexes (curve b) in ≪0.1sec during which time equilibrium is established (Eqn. 6a). At equilibrium, the residual (≈3 nM) R18 binds to beads (curve c). The steady state concentration of free R18 is replenished by fresh monomers dissociating from b to maintain equilibrium. It is later shown using a more accurate set rate parameters that residual [R18]eq is ≈10nM (see Section F text for details).
Under these conditions, a quasi-steady-state model78 can be used to derive a single rate parameter, such as an effective rate constant (keff in Eqn. 13 and derived in Appendix A), to describe the association of monomeric R18 and lipobeads. keff is constant for the data set, because the variability of the individual parameters is self correcting within the confines of parameter space that yields a good fit to the experimental data.
| (13a) |
| (13b) |
It can be shown that a simultaneous fit of experimental data to Eqns. 12 and 13 yields the same result. Thus, it is instructive to evaluate keff over a range of ki parameter space defined by fixing one of the given ki's while varying the other two rate parameters. Adjustment to [HSA]0 lead to a predictable change in keff, for example a tenfold increase in [HSA] effects a 10-fold decrease in keff (data not shown). The model analysis also yielded the following site occupancies at the end of each time course for DOPC; DSC respectively, (0.44 μM) 2.4×106; 1.56×106 (1.76 μM) 3.5×106; 2.15×106 and (4.4 μM) 3.7×106; 2.34×106. To summarize Fig. 5 data, a singular keff ≈ 1×104 M-1s-1, represents a robust overall rate at which R18 partitions into DOPC and DSC membranes where the significant finding of these experiments is the 37% difference in the absolute numbers of saturable binding sites associated with DOPC and DSC membranes. As shown in Fig. 3 the maximum site occupancies fall in a range where the differences in the self-quenching of R18 in DOPC and DSC membranes are minimal and within experimental error. Thus the observed quantitative differences in R18 occupied DOPC and DSC lipobeads are less susceptible to confounding effects that are likely at higher mol% (see discussion).
F. Estimates of the critical aggregation concentration of R18
In water, the 18-carbon chain of R18 confers surfactant-like properties to the probe. It has been shown that surfactants whose aliphatic chains are longer than 12 carbons are likely to form aggregates at concentrations that are much lower than their CAC.61 To the best of our knowledge, the CAC of R18 in water is thus far unknown. The difficulty in its determination can be attributed to its tendency to form self-quenching dimers,2 at very low concentrations.27 As previously discussed with respect to Eqn. 6, a large stoichiometric excess of HSA was used in order to ensure that the equilibrium concentration of free amphiphile was kept below its heretofore, unknown CAC. The good correlation between experiment and theory suggests that under our experimental conditions the equilibrium concentration of monomeric R18 was maintained below the CAC. It has been over thirty years since Aniansson, Wall and coworkers80 developed a theoretical formalism for describing the aggregation of amphiphiles, in terms of a stepwise process as given in Eqn. 14, in our nomenclature. Where R181 denotes monomeric R18, and R18a denotes an aggregate of a R18 molecules, k±a represent the respective association and dissociation rate constants. ka may vary according to the coefficient due to cooperativity effects. 81
| (14) |
If k2 (in Eqn. 6) ≫ ka then, one might expect subtle differences between theory and experiment, whereas if k2 ≤ ka then the applicability of Eqn. 6 is expected to fall off very badly. To establish some baseline expectations about the perturbative effects of aggregation on the applicability of the Eqn. 6 we excluded serum albumin from some measurements. The results shown in Figure 7A for the 0.25μM R18 suggest that ka > k2,. The fluorescence intensity of the serum-free sample is significantly lower than, the 0.1% HSA containing sample. This suggests that amphiphile aggregates transfer poorly, if at all, to membranes.
Figure 7.
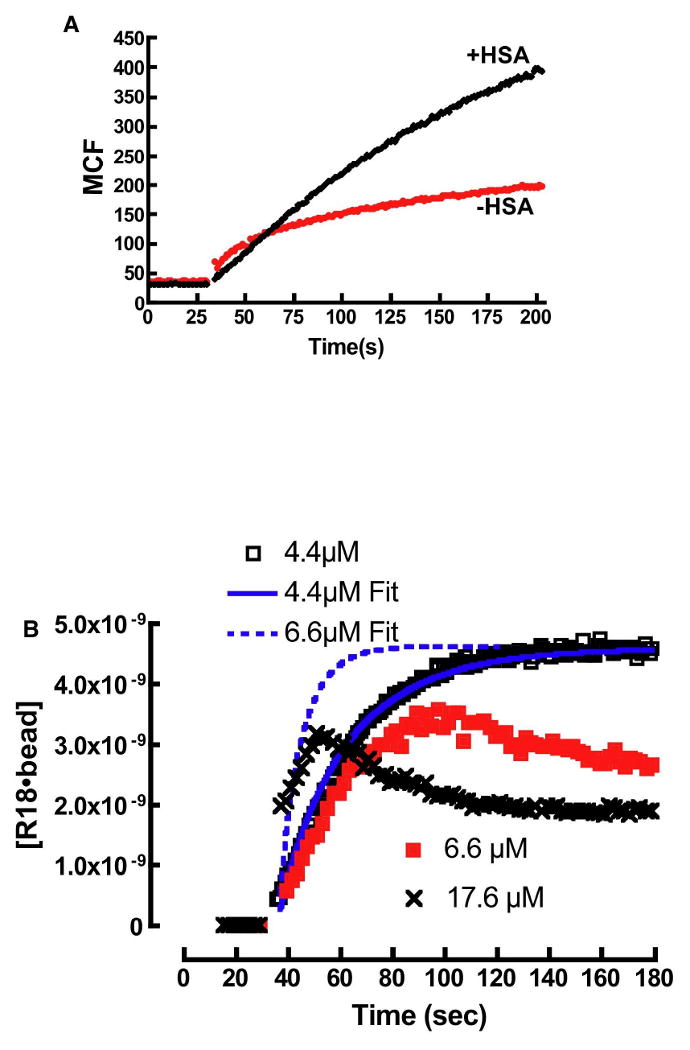
A. Plot of R18 binding to DOPC membranes in buffer containing 0.1% HSA and no HSA. In the absence of HSA the intensity of R18 is much lower than HSA containing media. B. Probe aggregation leads to anomalous binding kinetics of R18 to beads. At 4.4μM the equilibrium concentration of R18, [R18]eq is below the CAC and the binding curve shows agreement with a model (4.4μM Fit) that ignores the effects of aggregation (Eqn. 14). At 6.6μM the binding time-course for the binding of R18 to beads is shown to deviate from model predictions (6.6μM Fit). This is attributed to probe aggregation when the equilibrium concentration of free R18 exceeds CAC. The anomalous binding characteristics increase at 17.6μM.
We then examined the transfer kinetics of R18 to lipobeads, suspended in 0.1% HSA buffer over a concentration range of 0.25μM to 17.6μM. As demonstrated above, the correlation between model simulations and experiments was reasonable up to 4.4μM R18. When [R18]0 was raised to 6.6μM, the differences between theoretical expectations and experiment became significant as shown in Figure 7B. The early binding rate is slower than expected, and the probe intensity turns over and decreases without reaching a plateau. The behavior is similar to the positive control experiment shown in Figure 7A. At 17.6μM R18, increased aggregation produces a complex kinetic trace. The decrease in intensity is likely due to the association of beads with highly self-quenched aggregates or due to detergent-like solubilization of membranes by R18 micelle aggregates. 82
The inferred onset of aggregation at [R18]0 = 6.6μM implies that the equilibrium concentration of free R18 at this level is equal or greater than the CAC. [R18]eq was evaluated from the equilibrium constant, (see Fig. 6). As discussed in Section E, the uncertainties in the derived rate parameters are within a factor of 10. Fig. 8A shows a plot of [R18]eq. versus [R18]0 for each concentration of R18 used herein. The lower and upper limiting values of Ka represent the range of uncertainty in [R18]eq.. The initial estimate of CAC was assumed to fall within the range of values of [R18]eq for [R18]0 = 6.6 μM –i.e. 3nM to 42 nM. The CAC was subsequently resolved in an assay designed to measure the onset of aggregation.83 The intensity of R18-solubilized in Triton X-100 was measured using a spectrofluorometer, and compared to the intensity of the same concentration of R18 dissolved in water over a 1-100 nM concentration range. In Triton X-100, the intensity of R18 increased linearly with concentration whereas in water the intensity of R18 emission was not proportional to concentration due to probe aggregation. Below 10 nM, the relative intensities of R18 in water and Triton X-100 were comparable or within a factor of 2. The differences at low concentration were attributed to dimerization of R18 in water.27 Fig. 8B shows a plot of the intensity ratio of 1%Triton X-100 and water-solubilized R18 versus the logarithm of [R18]0. With increasing concentration, an acute change in the slope of the ratiometric intensity measurements is shown to have an inflection point at 14 nM. The inflection point was determined to be the CAC.83 It is worth noting that the experimental determination of CAC enables an improvement in the accuracy of the derived rate parameters, as one imagines that the experimental value of CAC is much closer to the correct value of [R18]eq than a factor 10. In this way the rate parameters rescaled to CAC are: k1 = 3.2×106M-1s-1, k-1 = 0.73s-1, k2 = 3.6 × 106M-1s-1. The values of [R18]eq. derived from the CAC corrected rate parameters are shown as the middle line in Fig. 8A.
G. FRET assay for Quantitation of bound R18 acceptors on beads
The RET data (y-axis, QDA/QD in Figure 4B) were converted to an assay of C, the number of acceptors per R02 on beads (see Eqn. 4) and plotted as shown in Figure 8A. The Forster based formalism of RET21 is accurate within a narrow range of acceptor density of 0 to 0.5Acceptors/R02. The approach assumes random and uniform distribution of molecules over the defined 4πr2 surface area of the 5μm beads. This assumption is accurate in DOPC membranes at the limiting acceptor density of 0.5 Acceptors/R02. Because of the phase segregated domains in DSC membranes, the degree of random and uniform distribution of acceptors over the total surface area of the bead is uncertain. Accordingly, only the results of the FRET quantification assay on DOPC beads are appropriate for comparison to fluorescence calibration beads. The data in Figure 8A were converted to an absolute number of R18 acceptors on each bead by multiplying the derived values of C by 2.1×106, the total number of R02-sized (R0 =61Å) unit areas on a 5μm bead. The converted data were superimposed over the fluorescence calibration bead-derived data from Figure 5, as shown in Figure 8B. It is also worth noting that the onset of significant probe aggregation (see Fig. 3) on beads occurs at site occupancies that are much greater than the upper limit for accuracy of Wolber & Hudson21 approach - 0.5 acceptors/R02 (≈1×106R18/bead). Therefore, the data are not confounded by self-quenching in this regime. We took the close agreement between the two data sets as validation of the FRET scheme, as we have previously authenticated the applicability of these beads in comparison to commercial standards.36 The accuracy of FRET depends on the derived value of R0, where probe aggregation is expected to effect perturbations in JDA and κ2 (cf. Results Section B). Our analysis of the spectral overlap between the donor F18 and dimeric R18 has shown that the change in JDA is minimal (Table 1). The close correlation between the calibration bead and FRET data, suggests that the assumed value of κ2 = 2/3 is valid for this system. This is consistent with the argument presented by Fayer and coworkers2 that a Poisson distribution and random orientation is accurate to describe R18 acceptors in micelles as long as the mole fraction is less that 0.1 (or 10mole%).
Discussion
This study establishes a quantitative approach for examining membrane structure and lateral heterogeneity attributed to coexisting lipid domains in live cell membranes. The assay is based upon the differential dynamics of partitioning of an exogenous fluorescent lipid probe into supported lipid bilayer membranes of different composition. We examined the association kinetics of R18 with lipid bilayers presented as liquid disordered, Ld, phase prepared from DOPC and liquid ordered, Lo, phases prepared from a ternary mixture of DOPC, SM, and Cholesterol (DSC) where DSC membranes are modeled after canonical lipid rafts.84
In lipid bilayer membranes, free volume or area refers to the overall, randomly distributed void space not occupied by lipids and water in the membrane.85,86 Lateral diffusion of lipids in membranes has been analyzed in terms of “free area” models that posit that diffusive mobility is facilitated by random density fluctuations, where the redistribution of free area creates voids greater than some critical area next to a diffusing molecule, which then fills the void by lateral transalation.50 85,86 In this way the rate of lateral diffusion has been shown to decrease as a function of cholesterol content or other membrane condensing acyl chain saturated lipids such as SM87 due in part to a decrease in free area.88 Free volume or area properties are important to the permeation of amphiphiles, and in our application provide a direct measure of free space that is accessible to penetrant molecules.50 Accordingly, the partitioning of R18 into lipid membranes is regulated by the frequency of the density fluctuations that open up voids that are equal to or greater than the cross-sectional area of the probe.50
With its two unsaturated acyl chains, DOPC occupies a relatively large molecular area (71Å2) whereas saturated chains of SM occupy less volume (62Å2).38 The ‘condensing effect’ of cholesterol is driven by the mutual orientation of cholesterol's planar sterol ring and the hydrophobic tail, which enables hydrogen bonding interactions with saturated acyl chains of SM.33 32 Previous studies have shown that a membrane mixture equivalent to the 1:1:1 DSC mixture herein is expected to present a molecular area per lipid of 40-47Å2.38 DSC is accordingly expected to present less free volume capacity for exogenous probes.50
We have relied on the substantial body of literature of the photophysical properties of rhodamine B2,30,54,58 to establish a quantitative assay, that directly measures free volume properties of lipid membranes. In a polar environment, aggregation brings the rhodamine xanthene rings into mutual proximity as coplanar non-fluorescing “H-dimers”57 that are characterized by a blue shift in their absorption spectrum (Figure 2C) relative to the monomer.57 Titration of R18 in membranes of different composition has yielded differential levels of self-quenching that are sensitive to molecular area.8 While the process by which concentration dependent self-quenching propagates in membranes has been attributed to energy transfer 2,3,8,58 or molecular interactions89 it has been difficult to establish a clear basis for it. We have therefore taken a phenomenological approach to developing an analytical method of describing the proliferation of self-quenching of R18 as a function of its mole fraction in membranes supported on mono-disperse sized beads (see Eqn. 8 & 9). In earlier studies, others8,12,58 have shown that the onset of self-quenching that is manifested by self-quenching of R18 solubilized in single component vesicle membranes was linear over the 1-9mol% fraction range,12,58 but exhibited exponential characteristics8 in cholesterol containing membranes. On DOPC lipobeads we show that the onset of quenching occurs at χ≥0.3%mol and linearly increases on the logarithmic scale up to χ≈5mol%. On DSC lipobeads the onset of quenching (at 37°C) occurs at χ ≤ 0.1mol%. These data are best represented in terms of a fit to an nth order polynomial and exponential function respectively. Eqns. 8 & 9 allow for the parametric treatment of surface concentration dependent quenching as a function time, which enables the real-time kinetic analysis of the association of R18 and lipobeads.
Elsewhere, Vaz and coworkers have recently used stopped flow measurements to examine the kinetics and thermodynamics of association of a two-acyl chain probe, NBD-dimyristoylphosphatidyl-ethanolamine (NBD-DMPE)83 and a single acyl chain NBD-lysomyristoyl phosphatidylethanolamine (NBD-lysoMPE)72 with large unilamellar vesicles in Ld (POPC) and Lo (1:1 POPC/Chol) and 6:4 SM/Chol) phases. These studies have shown that the association kinetics of two-footed NBD-DMPE with all membranes is 4 orders of magnitude slower than those measured for NBD-lysoMPE where the forward rate constants were close to the diffusion limit. The study also found small differences in the forward binding rates to POPC and POPC/Chol while SM/Chol membranes kinetics were smaller by an order of magnitude for both probes. It is therefore not surprising that we do not observe a significant difference between the kinetics of R18's association with DOPC and DSC. Nevertheless, unlike the earlier studies,83 our assay allows us to evaluate the free area differences in DSC and DOPC membranes, based on their saturable capacity to hold exogenous R18 (Fig. 4-6). The 37% fewer sites in DSC membranes are well correlated to the expected drop in molecular area due to the condensing effects of cholesterol and SM, as previously discussed.33,38
When the mol% fraction of “endogenous” R18 is extended to 10 mol% in bulk membranes, DSC membranes display a >2 fold enhancement of quenching (Fig. 3) relative to DOPC at 37°C. This measurement represents an interesting way in which the structural differences between DSC and DOPC are amplified over 500 fold. When the probe is reconstituted as an endogenous part of the model membrane, its homotypic interactions are regulated by its equilibrium distribution in the bulk membrane in which it is an integral part (Fig. 3). It is reasonable to expect that as its mol% fraction increases, the probe and the membrane will redistribute to an equilibrium. Accordingly, it has been shown that probes such as N-(lissamine Rhodamine B sulfonyl)dipamitoylphosphapatidylcholine form aggregates in membranes above some threshold in a manner which depends on the membrane composition, temperature and pH.8,89 Elsewhere, it has also been argued that the surface distribution and orientations of membrane probes are no longer randomized at mol% fractions exceeding 10 in DOPC-like membranes or Triton X-100 micelles.2 The introduction of exogenous probes to preassembled membrane structures is governed by the equilibrium distribution of free volume. 50,72,86 It is therefore gratifying that in our real time experiments the exogenous R18 probes that are accepted into the pure DOPC and DOPC bulk membranes are limited to surface occupancies that are up to ≈3mol% of the bulk membrane. At this concentration, the perturbation of the membrane structures of DOPC and DSC by “endogenous” R18 impurities (fig. 3) is minimized, in such a way that the calibration concentration quenching curves (Eqns. 8&9) are more likely to accurately represent the quenching conditions of real-time kinetics. We consider the good correlation between the differential free volumes capacity of the two model membranes and their molecular area-differences to be a good indicator of the applicability our parametric kinetic model.
One of our goals in undertaking this study was to establish a quantitative and intuitive framework in which to estimate the surface density of probes on membranes using a known set of thermodynamic and kinetic parameters. The equilibrium distribution of [R18]0 among 3 phases is given in Eqn. 15 where, [R18]eq, is the free probe in the aqueous phase, [R18]lb is the surface concentration on lipobeads in units of moles/dm2, is the ratio of the membrane surface area supported by n =1×109 beads to the 1dm3 volume of water (Vw) used in our experiment and [HSA•R18]eq is the serum bound protein.
| (15) |
The formal relationship between Eqn. 15 and model kinetic and equilibrium parameters is described in Appendix A. From Figure 6 we estimate that the distribution of [R18]0 = 4.4 μM among the aqueous phase, serum albumin and beads is according to the following proportions: [R18]eq ≈ 10.0 nM, [HSA•R18]eq ≈ 4.384 μM, and [R18]lbAlb ≈ 6.0 nM. It is desirable to maintain [R18]t at levels below the CAC value, and this condition is assured by using [HSA]0 in high excess. As keff (0221D)[HSA]0-1, increasingly high concentrations of the serum albumin limit the steady state concentration of monomeric R18 and thus reduce the rate at which the probe is transferred to membranes, but not the equilibirum concentration of [R18]lb. These results are consistent with the earlier finding of Vaz et al28,29 that serum-bound amphiphiles are not directly exchangeable with membranes. In the present application, a bulk concentration of [R18]0 = 4.4 μM represents an approximate upper limit concentration of R18 that can be applied to membranes in 0.1% (97μM) HSA buffer without concern of exceeding the CAC. Therefore these experimental conditions optimize the kinetics of delivery to bead membranes, keff is optimized by using a stoichiometric ratio of [HSA]0 and [R18]0 that yields a concentration of monomeric R18 that is just below the aggregation threshold.
Summary and Conclusions
We began this work in order to better understand the process by which R18 distributes between water, serum albumin and membranes in a model system. We intend to bridge past14-17 and current work related to the real-time transfer of R18 from a water/HSA environment into a heterogeneous environment of living cells as outlined in Figure 1. To recapitulate our original goals: In our previous work, on cells we have encountered some difficulty in the quantitative analysis of the transfer of monomeric R18 from the aqueous phase to membranes due to the confounding effects of: a) Changes to the spectroscopic characteristics (absorption cross-section and emission quantum yield) of R18 due to concentration dependent aggregation in membranes. A specific problem related with this issue, concerns the elucidation of how the spectroscopic changes in the acceptor probes can affect the analysis of FRET data. b) Probe aggregation at very low concentrations and an undefined critical aggregation constant. To address these issues, we have used monodisperse-sized lipobeads that can support a well-defined number of lipids in a reproducible manner. A titration of increasing mol% R18 into membrane vesicles has enabled the reconstitution of probes whose concentration-depended quenching is well defined between 0 and 10 mol%. A novel set of fluorescence calibration beads has proven to be useful in establishing a quantitative basis for analyzing the fluorescence readout of membrane-associated probes by flow cytometry. Addition of exogenous R18 to DOPC and DSC lipobeads has been analyzed according to mass action kinetics in which the transfer of R18 to beads is mediated by serum albumin, and defined by phenomenological kinetics. The finding that the site occupancy of exogenous R18 in DOPC and DSC membranes is limited to a few mole% has important implications for FRET in cell membranes. Our analysis of the spectra of R18 monomers and dimers suggest that there is little variation in the spectral overlap integral of either monomeric or dimerized acceptors and FRET donor molecules of interest to our studies (Table1). We imagine that the limited free-volume capacity of membranes to hold exogenous R18, suggests that differences in κ2 for monomeric and dimeric acceptor conditions are likely to be small at the lower mol% of exogenous R18 due to the notion that probes are expected to be randomly distributed and oriented below a much higher threshold of 10 mol% at least in Ld phases.2,3
To conclude, this study has examined two limiting models of cell membranes on beads, and demonstrated by quantitative measurement, the structural differences in Ld, DOPC and Lo, DSC membranes. In cells, these limiting forms of membrane structure coexist laterally in the plasma membranes. In view of that, the bead assay is conceptually useful, in demonstrating, (spectroscopically and quantitatively) how R18 can be used to report the presence of heterogeneous domains. It is then possible to dissect the coexistence of membrane domains in living cells, by using FRET to report on the differential kinetics of the localized accumulation of R18 acceptors at two receptor sites as defined in Fig. 1. To recapitulate earlier statements, it is believed that the α4β1 integrin, is confined to liquid disordered domains17 and that the formyl peptide receptor (FPR) is localized in liquid ordered domains in the plasma membranes of the same population of U937 cells.26 However these findings emerged from disparate experimental conditions. Our present study has shown that R18 accumulates differentially in membranes that are modeled after liquid disordered domains (DOPC) and ordered domains (DSC). In this regard, we have observed that R18 acceptors differentially accumulate at the sites of α4β1 and FPR expression in living cells (see supplementary Fig. S1). The model system developed here is applicable to the analysis of these results. A detailed analysis of local FRET at these sites will be published elsewhere.
Supplementary Material
Figure 9.
A. Analysis of FRET in DOPC beads. Plot of R18 surface concentration in terms of acceptors/R02 versus time for three concentrations of R18 as listed in the legend. B. Correlation of FRET derived values of absolute R18 acceptors on DOPC beads and R18/bead derived from calibration beads for three titers of [R18]0 shown in the legend.
Acknowledgments
This work was supported by NIH K25AI60036, U54MH074425, HL081062, NSF CTS0332315, Dedicated Health Research Funds of the University of New Mexico School of Medicine (C-2294-T). Images in this paper were generated in the University of New Mexico Cancer Center Fluorescence Microscopy Facility, supported as detailed on the webpage: http://hsc.unm.edu/crtc/microscopy/Facility.html. We thank Drs Ralph Young (Eastman Kodak, Rochester, NY) and Eva Chi (UNM) for stimulating discussions and critical review of our manuscript.
Appendix A
Application of the steady state approximation to the association of R18 with lipobeads.
From Equation 6:
| (A1) |
| (A2) |
substituting A2 into Equation 12
| (A3) |
since independently-measured k-2 is small (1.2×10-5s-1) and [HSA]0≫ [lipids]0 A3 simplifies to:
| (A4) |
Appendix B
Concerning equilibrium distribution of [R18]0 among water, membrane, and serum albumin. From Equation 6a:
| (B1) |
at equilibrium
| (B2) |
| (B3) |
substituting Equation B2 into B3 and simplifying:
| (B4) |
The degree of labeling ([R18]lbAlb in Eqn. 15) is governed by a partition coefficient, Kp, which at low concentration of the probe is usually expressed in terms of an equilibrium ratio of the surface concentration of bound probes and free probe in the aqueous phase and has units of length (Eqn. B5).
| (B5) |
| (B6), |
then,
| (B7) |
At equilibrium, R18 is partitioned according to Equation 15 in the text, and substituting the terms in Equations B6 and B7 into Equation 15 yields Equation B8.
| (B8) |
Footnotes
Supporting information: Fig. S1 is included as a supplementary data. This information is available free of charge at http://pubs.acs.org
References
- 1.Yamazaki I, Tamai N, Yamazaki T. J Phys Chem. 1990;94:516–525. [Google Scholar]
- 2.Ediger MD, Domingue RP, Fayer MD. Journal Of Chemical Physics. 1984;80:1246–1253. [Google Scholar]
- 3.Baumann J, Fayer MD. Journal Of Chemical Physics. 1986;1:4087–4107. [Google Scholar]
- 4.Nakashima K, Duhamel J, Winnik MA. Journal Of Physical Chemistry. 1993;14:10702–10707. [Google Scholar]
- 5.Leenhouts JM, Dekruijff B. Biochimica Et Biophysica Acta Biomembranes. 1995;26:121–126. doi: 10.1016/0005-2736(95)00093-i. [DOI] [PubMed] [Google Scholar]
- 6.Wunderliallenspach H, Gunthert M, Ott S. Biochemistry. 1993;26:900–907. doi: 10.1021/bi00054a022. [DOI] [PubMed] [Google Scholar]
- 7.Stegmann T, Schoen P, Bron R, Wey J, Bartoldus I, Ortiz A, Nieva JL, Wilschut J. Biochemistry. 1993;26:11330–11337. doi: 10.1021/bi00093a009. [DOI] [PubMed] [Google Scholar]
- 8.Macdonald RI. Journal Of Biological Chemistry. 1990;15:13533–13539. [PubMed] [Google Scholar]
- 9.Pozzi D, Lisi A, Deros I, Ferroni L, Giuliani A, Ravagnan G, Grimaldi S. Photochemistry And Photobiology. 1993;57:426–430. doi: 10.1111/j.1751-1097.1993.tb02313.x. [DOI] [PubMed] [Google Scholar]
- 10.Melikyan GB, Deriy BN, Ok DC, Cohen FS. Biophys J. 1996;71:2680–91. doi: 10.1016/S0006-3495(96)79459-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Niles WD, Cohen FS. J Gen Physiol. 1991;97:1101–19. doi: 10.1085/jgp.97.6.1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hoekstra D, Deboer T, Klappe K, Wilschut J. Biochemistry. 1984;23:5675–5681. doi: 10.1021/bi00319a002. [DOI] [PubMed] [Google Scholar]
- 13.Stegmann T, Hoekstra D, Scherphof G, Wilschut J. Journal Of Biological Chemistry. 1986;25:10966–10969. [PubMed] [Google Scholar]
- 14.Chigaev A, Waller A, Zwartz GJ, Buranda T, Sklar LA. J Immunol. 2007;178:6828–39. doi: 10.4049/jimmunol.178.11.6828. [DOI] [PubMed] [Google Scholar]
- 15.Larson RS, Davis T, Bologa C, Semenuk G, Vijayan S, Li Y, Oprea T, Chigaev A, Buranda T, Wagner CR, Sklar LA. Biochemistry. 2005;44:4322–31. doi: 10.1021/bi048187k. [DOI] [PubMed] [Google Scholar]
- 16.Chigaev A, Zwartz GJ, Buranda T, Edwards BS, Prossnitz ER, Sklar LA. J Biol Chem. 2004;279:32435–43. doi: 10.1074/jbc.M404387200. [DOI] [PubMed] [Google Scholar]
- 17.Chigaev A, Buranda T, Dwyer DC, Prossnitz ER, Sklar LA. Biophys J. 2003;85:3951–62. doi: 10.1016/S0006-3495(03)74809-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mutucumarana VP, Duffy EJ, Lollar P, Johnson AE. J Biol Chem. 1992;267:17012–21. [PubMed] [Google Scholar]
- 19.Yegneswaran S, Smirnov MD, Safa O, Esmon NL, Esmon CT, Johnson AE. J Biol Chem. 1999;274:5462–8. doi: 10.1074/jbc.274.9.5462. [DOI] [PubMed] [Google Scholar]
- 20.Yegneswaran S, Wood GM, Esmon CT, Johnson AE. J Biol Chem. 1997;272:25013–21. doi: 10.1074/jbc.272.40.25013. [DOI] [PubMed] [Google Scholar]
- 21.Wolber PK, Hudson BS. Biophys J. 1979;28:197–210. doi: 10.1016/S0006-3495(79)85171-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jacobson K, Mouritsen OG, Anderson RG. Nat Cell Biol. 2007;9:7–14. doi: 10.1038/ncb0107-7. [DOI] [PubMed] [Google Scholar]
- 23.Anderson RG, Jacobson K. Science. 2002;296:1821–5. doi: 10.1126/science.1068886. [DOI] [PubMed] [Google Scholar]
- 24.Edidin M. Annual Review Of Biophysics And Biomolecular Structure. 2003;32:257–283. doi: 10.1146/annurev.biophys.32.110601.142439. [DOI] [PubMed] [Google Scholar]
- 25.Simons K, Vaz WLC. Annual Review Of Biophysics And Biomolecular Structure. 2004;33:269–295. doi: 10.1146/annurev.biophys.32.110601.141803. [DOI] [PubMed] [Google Scholar]
- 26.Xue M, Vines CM, Buranda T, Cimino DF, Bennett TA, Prossnitz ER. J Biol Chem. 2004;279:45175–84. doi: 10.1074/jbc.M407053200. [DOI] [PubMed] [Google Scholar]
- 27.Nakashima K, Fujimoto Y. Photochemistry And Photobiology. 1994;60:563–566. [Google Scholar]
- 28.Abreu MSC, Estronca L, Moreno MJ, Vaz WLC. Biophysical Journal. 2003;84:386–399. doi: 10.1016/S0006-3495(03)74859-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Estronca L, Moreno MJ, Laranjinha JAN, Almeida LM, Vaz WLC. Biophysical Journal. 2005;88:557–565. doi: 10.1529/biophysj.104.047050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Selwyn JE, Steinfeld JI. J Phys Chem. 1972;76:762–774. [Google Scholar]
- 31.McConnell HM, Radhakrishnan A. Biochimica Et Biophysica Acta Biomembranes. 2003;10:159–173. doi: 10.1016/s0005-2736(03)00015-4. [DOI] [PubMed] [Google Scholar]
- 32.Radhakrishnan A, McConnell H. Proc Natl Acad Sci U S A. 2005;102:12662–6. doi: 10.1073/pnas.0506043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Demel RA, Vandeene* LL, Bruckdor* KR. Biochimica Et Biophysica Acta. 1972;255:311. doi: 10.1016/0005-2736(72)90030-2. [DOI] [PubMed] [Google Scholar]
- 34.Dietrich C, Bagatolli LA, Volovyk ZN, Thompson NL, Levi M, Jacobson K, Gratton E. Biophysical Journal. 2001;80:1417–1428. doi: 10.1016/S0006-3495(01)76114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Buranda T, Huang J, Rama Rao GV, Ista LK, Larson RS, Ward TL, Sklar LA, Lopez GP. Langmuir. 2003;19:1654–1663. [Google Scholar]
- 36.Wu Y, Campos SK, Lopez GP, Ozbun MA, Sklar LA, Buranda T. Anal Biochem. 2007;364:180–92. doi: 10.1016/j.ab.2007.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wu Y, Lopez GP, Sklar LA, Buranda T. Anal Biochem. 2007;364:193–203. doi: 10.1016/j.ab.2007.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stottrup BL, Stevens DS, Keller SL. Biophys J. 2005;88:269–76. doi: 10.1529/biophysj.104.048439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Parker CA. Photoluminescence of solutions. Elsevier; Amsterdam: 1968. [Google Scholar]
- 40.Bhattacharya AA, Grune T, Curry S. Journal Of Molecular Biology. 2000;10:721–732. doi: 10.1006/jmbi.2000.4158. [DOI] [PubMed] [Google Scholar]
- 41.Sklar LA, Hudson BS, Simoni RD. Biochemistry. 1977;16:5100–5108. doi: 10.1021/bi00642a024. [DOI] [PubMed] [Google Scholar]
- 42.Demant EJ, Richieri GV, Kleinfeld AM. Biochem J. 2002;363:809–15. doi: 10.1042/0264-6021:3630809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Spector AA. Journal Of Lipid Research. 1975;16:165–179. [PubMed] [Google Scholar]
- 44.Pownall HJ. Journal Of Molecular Neuroscience. 2001;16:2–3. doi: 10.1385/JMN:16:2-3:109. [DOI] [PubMed] [Google Scholar]
- 45.Zakim D. Journal Of Membrane Biology. 2000;15:101–109. doi: 10.1007/s00232001080. [DOI] [PubMed] [Google Scholar]
- 46.Kleinfeld AM. Journal Of Membrane Biology. 2000;15:79–86. doi: 10.1007/s002320001056. [DOI] [PubMed] [Google Scholar]
- 47.Vaz WLC, Melo E. Journal Of Fluorescence. 2001;11:255–271. [Google Scholar]
- 48.Tanford C. The hydrophobic effect: Formation of micelles and biological membranes. Wiley-Interscience; New York: 1980. [Google Scholar]
- 49.Almeida PFF, Vaz WLC, Thompson TE. Biochemistry. 1992;31:6739–6747. doi: 10.1021/bi00144a013. [DOI] [PubMed] [Google Scholar]
- 50.Marrink SJ, Sok RM, Berendsen HJC. J Chem Phys. 1996;104:9090–9099. [Google Scholar]
- 51.Gennis RB. Biomembranes -Molecular Structure and Functions. Springer-Verlag; New York: 1989. [Google Scholar]
- 52.Ramette RW, Sandell EB. J Am Chem Soc. 1956;78:4872–4878. [Google Scholar]
- 53.McRae EG, Kasha M. J Chem Phys. 1961;11:38. [Google Scholar]
- 54.Valdes-Aguilera O, Neckers DC. Acc Chem Res. 1989;22:171–177. [Google Scholar]
- 55.Rohatgi KK, Singal GS. J Phys Chem. 1966;70:1695–1701. [Google Scholar]
- 56.Drexhage . In: Dye Lasers. Schafer F, editor. Vol. 1. Springer-Verlag; Heidelberg: 1989. pp. 155–189. [Google Scholar]
- 57.Kasha M. Radiation Res. 1963;20:55–71. [PubMed] [Google Scholar]
- 58.Johansson LBA, Niemi A. Journal Of Physical Chemistry. 1987;21:3020–3023. [Google Scholar]
- 59.Cerione RA, McCarty RE, Hammes GG. Biochemistry. 1983;22:769–76. doi: 10.1021/bi00273a010. [DOI] [PubMed] [Google Scholar]
- 60.Birks JB. Photophysics of aromatic molecules. Wiley-Interscience; NY: 1970. [Google Scholar]
- 61.Mukerjee P. J Phys Chem. 1965;69:2821–2827. [Google Scholar]
- 62.Lakowicz JR. Principles of Fluorescence Spectroscopy. 2. Plenum Press; New York: 1999. [Google Scholar]
- 63.Dale R, Eisinger J, Blumberg W. Biophys J. 1979;26:161–194. doi: 10.1016/S0006-3495(79)85243-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Dale RE. Orientational averaging in long-range excitation energy transfer ensembles of various dimensionalities. Conference Digest; 3rd Conference on Luminescence; Szeged, Hungary. 1979. [Google Scholar]
- 65.Baksh MM, Jaros M, Groves JT. Nature. 2004;427:139–41. doi: 10.1038/nature02209. [DOI] [PubMed] [Google Scholar]
- 66.Boxer SG. Current Opinion in Chemical Biology. 2000;4:704–709. doi: 10.1016/s1367-5931(00)00139-3. [DOI] [PubMed] [Google Scholar]
- 67.Sackmann E. Science. 1996;271:43–48. doi: 10.1126/science.271.5245.43. [DOI] [PubMed] [Google Scholar]
- 68.Salafsky J, Groves JT, Boxer SG. Biochemistry. 1996;35:14773–14781. doi: 10.1021/bi961432i. [DOI] [PubMed] [Google Scholar]
- 69.Veatch SL, Keller SL. Phys Rev Lett. 2005;94:148101. doi: 10.1103/PhysRevLett.94.148101. [DOI] [PubMed] [Google Scholar]
- 70.Nolan JP, Sklar LA. Nature Biotech. 1998;16:633–638. doi: 10.1038/nbt0798-633. [DOI] [PubMed] [Google Scholar]
- 71.Nichols JW, Pagano RE. Biochemistry. 1982;21:1720–1726. doi: 10.1021/bi00537a003. [DOI] [PubMed] [Google Scholar]
- 72.Sampaio JL, Moreno MJ, Vaz WL. Biophys J. 2005;88:4064–71. doi: 10.1529/biophysj.104.054007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Abreu MS, Moreno MJ, Vaz WL. Biophys J. 2004;87:353–65. doi: 10.1529/biophysj.104.040576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Nichols JW, Pagano RE. J Biol Chem. 1983;258:5368–71. [PubMed] [Google Scholar]
- 75.Nichols JW. Biochemistry. 1985;24:6390–6398. doi: 10.1021/bi00344a011. [DOI] [PubMed] [Google Scholar]
- 76.Richieri GV, Ogata RT, Kleinfeld AM. Journal Of Biological Chemistry. 1996;10:11291–11300. doi: 10.1074/jbc.271.19.11291. [DOI] [PubMed] [Google Scholar]
- 77.Wu Y, Zwartz G, Lopez GP, Sklar LA, Buranda T. Cytometry A. 2005;67:37–44. doi: 10.1002/cyto.a.20171. [DOI] [PubMed] [Google Scholar]
- 78.Benson SW. Foundations of Chemical Kinetics. McGraw-Hill; New York: 1960. [Google Scholar]
- 79.Motulsky HJ, Mahan LC. Mol Pharmacol. 1984;25:1–9. [PubMed] [Google Scholar]
- 80.Aniansson EAG, Wall SN, Almgren M, Hoffmann H, Kielmann I, Ulbricht W, Zana R, Lang J, Tondre C. Journal Of Physical Chemistry. 1976;80:905–922. [Google Scholar]
- 81.Nagarajan R, Ruckenstein E. Langmuir. 1991;7:2934–2969. [Google Scholar]
- 82.Maher P, Singer SJ. Biochemistry. 1984;23:232–40. doi: 10.1021/bi00297a010. [DOI] [PubMed] [Google Scholar]
- 83.Abreu MSC, Moreno MJ, Vaz WLC. Biophysical Journal. 2004;87:353–365. doi: 10.1529/biophysj.104.040576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Dietrich C, Volovyk ZN, Levi M, Thompson NL, Jacobson K. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2001;11:10642–10647. doi: 10.1073/pnas.191168698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Falck E, Patra M, Karttunen M, Hyvonen MT, Vattulainen I. Biophys J. 2005;89:745–52. doi: 10.1529/biophysj.105.065714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Falck E, Patra M, Karttunen M, Hyvonen MT, Vattulainen I. Biophys J. 2004;87:1076–91. doi: 10.1529/biophysj.104.041368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Burns AR, Frankel DJ, Buranda T. Biophys J. 2005;89:1081–93. doi: 10.1529/biophysj.105.060327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Almeida PF, Vaz WL, Thompson TE. Biophys J. 2005;88:4434–8. doi: 10.1529/biophysj.105.059766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Massari S, Colonna R, Folena E. Biochimica Et Biophysica Acta. 1988;9:149–157. doi: 10.1016/0005-2736(88)90019-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


