Boundary Stiffness Regulates Fibroblast Behavior in Collagen Gels

Abstract

Recent studies have illustrated the profound dependence of cellular behavior on the stiffness of 2D culture substrates. The goal of this study was to develop a method to alter the stiffness cells experience in a standard 3D collagen gel model without affecting the physiochemical properties of the extracellular matrix. A device was developed utilizing compliant anchors (0.048–0.64 N m⁻¹) to tune the boundary stiffness of suspended collagen gels in between the commonly utilized free and fixed conditions (zero and infinite stiffness boundary stiffness). We demonstrate the principle of operation with finite element analyses and a wide range of experimental studies. In all cases, boundary stiffness has a strong influence on cell behavior, most notably eliciting higher basal tension and activated force (in response to KCl) and more pronounced remodeling of the collagen matrix at higher boundary stiffness levels. Measured equibiaxial forces for gels seeded with 3 million human foreskin fibroblasts range from 0.05 to 1 mN increasing monotonically with boundary stiffness. Estimated force per cell ranges from 17 to 100 nN utilizing representative volume element analysis. This device provides a valuable tool to independently study the effect of the mechanical environment of the cell in a 3D collagen matrix.

INTRODUCTION

Recent studies have illustrated the profound dependence of cellular behavior and functions such as matrix adhesions, migration and contractile force generation on the stiffness of the cell surroundings.¹⁴ These observations have significant implications in researching numerous in vivo disease state conditions which exhibit changes in the tissue mechanical properties. For example, the stiffness of the extracellular matrix (ECM) has been shown to “actively influence” the development of tumors^28,57 and differentiation of human mesenchymal stem cells.^18,50

A phenomenon particularly sensitive to the mechanical stiffness of the ECM is differentiation of fibroblast cells into the myofibroblast phenotype. Myofibroblasts are modified fibroblasts which exhibit smooth-muscle like features such as heightened contractile force and expression of α-smooth muscle actin (α-SMA).²¹ This cell phenotype is present in granulation tissue during wound healing and plays an important role in wound closure and ECM synthesis.^21,26,54 Previous studies have clearly illustrated—both in vivo and in vitro—that ECM stiffness and presence of transforming growth factor-β1 (TGF-β1) cytokine are critical for myofibroblast differentiation and sustenance. ^{13,21,25–27,52} Irregular changes to these primary regulating factors results in dysregulation of myofibroblast activity which could lead to abnormal pathological states such as tissue fibrosis,^12,42,54 thus quantitative controlled studies of the combined effects of stiffness and cytokines on fibroblast behavior are needed.

Initial in vitro investigations into the role of stiffness on cell behavior were carried out on 2D polymer substrates by changing the polymer chemistry to alter the substrate stiffness. Commonly employed polymer substrates include polyacrylamide (PA), polyethylene glycol (PEG) and polydimethyl siloxane (PDMS). Polymer gels provided the advantage of an “easily tunable” and “stable” stiffness substrate.⁴⁸ Additional advantages include the ability to study and quantify traction forces generated by cells using time lapse microscopy due to the transparency of the polymer substrates.¹⁴ However, these systems fail to accurately recreate the interstitial conditions experienced by the cells in vivo. Fibroblasts cultured on 2D substrates tend to be “pancake” shaped—spread with cellular extensions —as compared to spindle or stellate shaped as observed for cells cultured in 3D matrices.⁴⁷ Other differences include the formation of an “artificial polarity” between upper and lower surfaces of the non-polar cells (fibroblasts and leukocyte cells) on 2D substrates.^10,17 Cell migration, another crucial cellular function, differs greatly in cells cultured in 3D gels compared to on 2D substrates.⁴⁷ Further, for cells to adhere to these inert polymers, collagen or other ECM proteins must be attached to the surface or mixed throughout the hydrogel. The homogeneity and presentation of the proteins to the cells is difficult to control and quantify.

The need to overcome the drawbacks of 2D gels and to create conditions more closely resembling those experienced by cells in vivo led to the development of several synthetic and natural polymers for the 3D matrix structures.⁴⁸ Synthetic polymer gels such as PA and PDMS were selected due to their prior use in 2D studies and the ease to “tune” the mechanical properties of the gels,⁴⁸ but the fact that these gels are not biodegradable and their inherent toxicity makes it impossible to carry out long-term studies in these gels. A synthetic substitute for these gels is PEG-based hydrogels.^45,48,51 PEG gels formed by photo-polymerization (exposure to UV)⁴⁵ have been used for 2D and 3D studies and offer controllable mechanical properties (by controlling the cross-linking and the amount of PEG monomers) and controlled cell–ECM interaction (by employing specific adhesion peptides into the gels).^45,48 However, synthetic polymers do not recapitulate the tissue biochemical environment or dynamic reciprocity between cells and the native ECM. Further, increased peptide density alters cell behavior ^48,58 and chemical cross-linking can be cytotoxic and alter the matrix biochemistry.

Natural biopolymer-based 3D gels offer an advantageous representation of in vivo conditions since they include the native functionalities of the tissues hence providing support for nearly every cell type. Type I collagen is the most commonly used biopolymer gel for cell experimentation as it is the primary constituent in connective tissues. Also collagen-based gels provide advantages including weak immunogenic nature, biodegradability, and, most importantly, dynamic reciprocity for cell–matrix interactions.^23,52 For mechanobiology studies, the intrinsic mechanical properties of the gels can be modified by changing the collagen concentration in the gel⁵⁸ or by adjusting the cross-linking in collagen gels.^{9,22,29,49,55} The drawback of these techniques is that they affect the biochemistry of the gel, inadvertently affecting the cell behavior and making it impossible to isolate the effects of the mechanical environment. Alternatively, the resistance to deformation by the cells, i.e., effective stiffness of the gels, can be altered mechanically by changing the external boundaries. The profound effect of the boundary condition is clearly illustrated by observing cell behavior in the two most common configurations for culturing cell-populated collagen gels: fixed and free. Cells cultured in gels rigidly attached (fixed) to the boundary exhibit substantially different morphology and behavior compared to cells cultured in gels freely floating in media.^1,24 Further, loading the edges of floating collagen gels (i.e., isotonic loading) leads to decreasing extent of compaction of collagen gels by the resident cells in a dose-dependent manner with increasing weight applied to the edges.^39,53 In addition, stretching the edges of a cell-populated collagen gel to a constant displacement (i.e., applying a static prestrain) alters the contractile forces and ECM gene regulation in the resident cells.^35,36 Hence, it is evident that cells in the interior of the gels can sense and respond to changes in the boundary condition, even though they are not near the boundary.

The goal of this study is to develop a system to alter the effective stiffness of cell-populated collagen gels using a purely mechanical strategy. In the system described herein, modulation of the effective stiffness surrounding the cells is attained by employing cantilevered beams as springs attached to the boundary of cell-populated collagen gels. This configuration modulates the boundary stiffness of the gel over a broad range in a graded manner and bridges the gap between the two extreme boundary stiffness cases of infinitely stiff (rigidly attached gels) and infinitely compliant (free floating gels). Finite element simulations and experimental validation studies using fibroblast and valvular interstitial cells were employed to test the proof of concept for the system. This system provides a new tool for studying the role of stiffness-dependent biology in 3D matrices for understanding the etiology of fibrocontractive diseases and cancer progression with possible applications in tissue engineering and stem cell differentiation.

RESEARCH DESIGN AND METHODS

Device Development

Device Principle

In the present system, a standard cell-populated collagen gel is held along its edges by porous anchors, and the stiffness of the boundary is set to precise values utilizing thin vertical cantilever beams as compliant springs (Fig. 1). This configuration modulates the boundary stiffness over a broad range in a graded manner by using a series of stainless steel cantilever beams (Small Parts, Inc.) of different diameters. The rest of the apparatus was made from high density polyethylene (HDPE) (McMaster Carr Inc.). The materials were chosen due to their easy availability, low cost, ability to withstand autoclave temperatures and inertness to long incubation periods.

FIGURE 1.

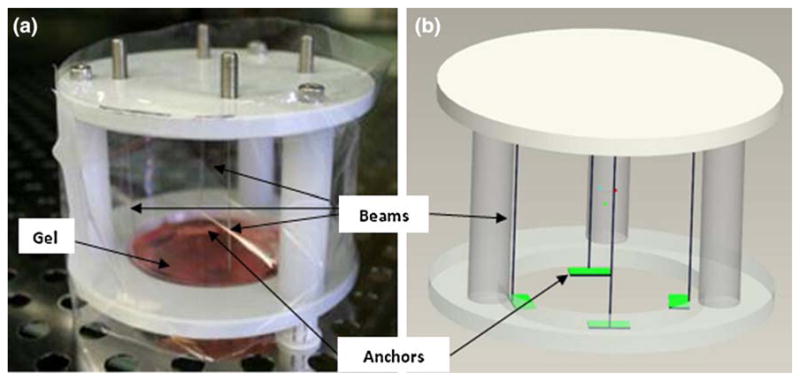
(a) Photograph and (b) computer aided drawing of the controlled boundary stiffness device showing the four stainless steel beams that act as compliant springs and the porous anchors that attach to the gel.

The stiffness of the boundary is dependent on the spring stiffness which can be calculated from the equation for bending of a cantilever beam:

$$K=3\frac{EI}{L^3}$$ (1)

where K is the spring constant (N m⁻¹), E is the Young’s modulus of the beam material (Pa), L is length of the cantilever beam (m), and I is the moment of inertia (m⁴) given by πr⁴/4 for a beam of circular cross section, where r is the radius of the beam (m). As the stiffness of the beam is a fourth-order function of its radius, spring stiffness can be modulated by changing the beam diameter.

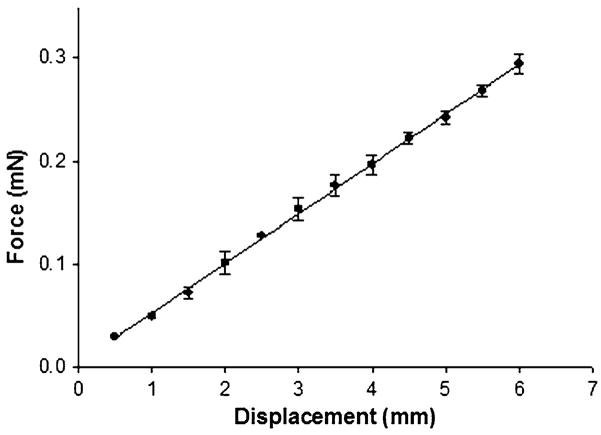
The stainless steel beams are calibrated by measuring the force in response to displacements ranging from 0.5 to 6.0 mm in increments of 0.5 mm using a micrometer (Mittituyo) and an electronic balance (±0.01 mN, Mettler Inc.). From these measurements, the K values were calculated from the slope of the force–displacement curve using linear regression (Fig. 2). All beams were loaded within their linear region as verified by the linearity of the force–displacement curves.

FIGURE 2.

Force–displacement calibration curve for the stainless steel cantilever beams with a diameter of 139 μm (0.0055 in.) in bending (mean ± SD, n = 3 repeated measures).

Device Operation

The cell-populated collagen gels are cast with four porous anchors (Vyon, Porvair Co.) along the edges and attached to the device by the four thin beams. The gels are submerged in culture media and free from any other attachments in a 60 mm untreated tissue culture dish top. A thin polypropylene sheet is wrapped around the device to ensure sterility over the culture period.

Compaction and contraction of the gel by the cells causes deflection of the pads and the beams. This deflection is measured by digital image analysis using a Cannon Rebel XT 6.5 megapixel digital camera and a macro lens (fixed 60 mm focal length). The images are obtained from underneath and are taken perpendicular to the gel to minimize parallax. The digital images taken of the base of the culture dish are analyzed using Image J (NIH) to monitor the compaction of the gel. The cell-generated forces are calculated along each axis as

$$F=K\frac{\mathrm{\Delta }x}{2}.$$ (2)

K is the spring stiffness from Eq. (1) and Δx is the change in distance between the two beams along one axis (each beam contributes half of the change in distance between the pads) (Fig. 3). The spatial resolution of 12 μm at the fixed focal length corresponds to 7.2 μN and 0.48 μN theoretical resolutions for the stiffest and the most compliant boundaries, respectively. When calibration errors (micrometer and balance) and movement due to jostling upon removal from the incubator are taken into account (~40 μm possible shift for the stiff beams and 500 μm for the compliant beams), the repeatability is approximately 25 μN for all beams regardless of stiffness.

FIGURE 3.

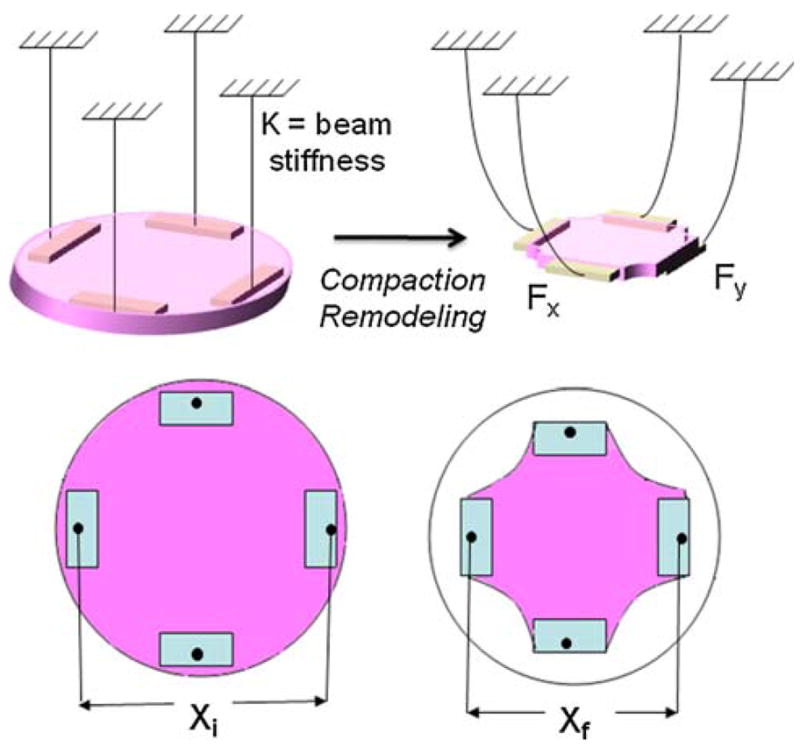
Schematic of method to measure cell force by measuring the displacement of the pads; F_x = 1/2K(X_i − X_f) where F_x is the force in the ‘x’ direction and K is the stiffness of the beams.

The optical method allows for sterile, non-contact measurements that are very inexpensive and reproducible. However, the accuracy of the displacement measurements is limited at the high stiffness level and with low cell densities since the minute displacements are at the lower bounds of sensitivity. Other methods of measurements may be needed to obtain forces from extremely small displacements. Instrumented beams employed by the culture force monitors were considered but are difficult to keep sterile and are costly and cumbersome, especially for large long-term experiments. With the current configuration, we are able to run up to 20 samples in parallel.

Demonstration Using Finite Element Modeling

To more clearly demonstrate the principle underlying this new methodology, finite element (FE) simulations were carried out. For the first simulation, an FE model was constructed to study the change in the effective stiffness of the system due to changes in the boundary stiffness. Second, to demonstrate how the stiffness of the boundaries modulates the balance between cell-generated matrix compaction and cell-generated forces, cell contraction was simulated by thermal contraction of an elastic solid disc supported by springs. Neither simulation corresponds exactly to the controlled boundary stiffness system; however, each illustrates the strong influence that the boundary condition has on the cells far from the boundary itself. For both analyses, a solid 3D circular model of the gel was created in FE analysis software (LS-Dyna, ver. 971, LSTC) subdivided into 1200 elements with 2490 nodes. The material properties were set to values representative of collagen gels in the low strain regime (E = 25–50 kPa, υ = 0.33),⁴⁷ and dimensions were representative of the collagen gels used in the device (60 mm diameter, 1 mm thickness).

The first study involved using transverse deflection to study the effective stiffness due to addition of springs at the boundary of the gel. Transverse deflection is a commonly employed method to measure the in-plane stiffness of membranes such as thin soft tissue samples. ³² The concept of the simulation can be explained using the analogy of a trampoline. A basic trampoline is composed of a bed of stiff material attached to a steel frame by coiled springs. The elasticity of the trampoline structure is a function of bed material stiffness and also the elasticity of the coiled springs. By changing the stiffness of the coiled springs at the boundary, the overall stiffness measured by transverse deflection changes, even though the bed material remains the same. This resultant deflection of the structure can also be attained by changing the material properties of the bed of the trampoline, but keeping the spring stiffness unchanged. Transverse deflection of an elastic material under boundary conditions varying from infinitely stiff boundary (fixed gel) to a compliant boundary was simulated. Three levels of spring stiffness were chosen for the intermediate stiffness levels in the range of beam stiffness used in the experimental studies (0.06, 0.08, and 0.1 N m⁻¹). Three levels of stiffness for the gel material were also selected (25, 40, and 50 kPa) for simulations where the spring stiffness was kept constant (0.1 N m⁻¹). The gels were transversely deflected by the point load at the center of the gel and force vs. deflection calculations were carried out.

For the second simulation, a finite element thermal analysis was carried out as an analog to the cell-mediated contraction of the gels. Heating of most materials results in expansion and cooling results in contraction (shrinking). Dimensional changes are generally in proportion to the change in temperature, the relationship expressed by the coefficient of thermal expansion. However, a change in temperature can also result in a change in the stresses within a material depending upon the boundary constraint. For example, for given temperature decrease, an unconstrained metal pipe will decrease in diameter without generating stresses, whereas a pipe embedded in concrete will not change in shape but will generate considerable stresses at the boundary and within the materials. Quantitatively, the amount of deformation of the material is determined by the change in temperature and coefficient of thermal expansion (α). The temperature of the solid model (using MAT_ELASTIC_PLASTIC_ THERMAL “card”) was studied over a range of 60 °C with 10 °C steps with α = 20 × 10⁻⁷ °C⁻¹. These values are simply chosen out of convenience and do not have any physical relevance in terms of the actual thermal properties of the gels or the culture conditions since no change in temperature is applied to the gel in the actual experiments.

Experimental Methods

Cell Culture

Human dermal fibroblasts from neonatal foreskin were obtained from the American Type Culture Collection (ATCC, Manassas, VA). The cells were expanded in T-150 flasks (BD Biosciences, Bedford, MA) at 37 °C in humidified 10% CO₂ conditions with Dulbecco’s modified Eagle medium (DMEM, Mediatech Inc., Herndon, VA) supplemented with 10% bovine calf serum (Hyclone, Logan, UT) and 1% penicillin/streptomycin/ampothericin B (Invitrogen, Carlsbad, CA). Fibroblasts used for the experiments were passage 8 or 9. Valvular interstitial cells (VICs), used for subset of experiments, were obtained from primary isolations of adult porcine aortic valves and cultured as described above with 15% fetal calf serum (Hyclone). VICs used for the experiments were passage 3–5.

Collagen Gel Fabrication

Fibroblast- and VIC-populated collagen gels were prepared by the method outlined by Bell et al.³ Acid-soluble Type 1 rat tail tendon collagen was dissolved in 5.0 mM HCl.¹⁷ Six milliliter samples for the gels were cast in the 60 mm tissue culture dish tops (Corning Costar) by mixing 2.64 mL of 5 mg mL⁻¹ collagen; 1.32 mL 5× DMEM; 0.26 mL of NaOH and 1.91 mL of concentrated cell solution within media made from 1× DMEM, 10% or 15% fetal bovine serum for fibroblast and VIC gels, respectively and 1% penicillin and streptomycin. Each gel had an initial collagen gel concentration of 2 mg mL⁻¹ and cell concentration of 0.5 × 10⁶ cells mL⁻¹ at seeding. The cell-seeded gels were incubated at 37 °C in humidified 10% CO₂ conditions.

Pilot Studies

A preliminary experiment was conducted to validate the principle of the device using fibroblast-populated collagen gels. Collagen gels were cultured in the controlled boundary stiffness device with two different boundary stiffness levels, low (0.048 N m⁻¹) and high (0.409 N m⁻¹) with and without TGF-β1 (10 ng mL⁻¹). The gels were cultured for 72 h at 37 °C in humidified 10% CO₂ incubation condition. Cell-generated forces were measured, mechanical tests were carried out, and immunohistochemistry was performed on the gels as described in subsequent sections to assess the response of cells to the changes in the boundary stiffness.

Measurement of Cell-Generated Forces

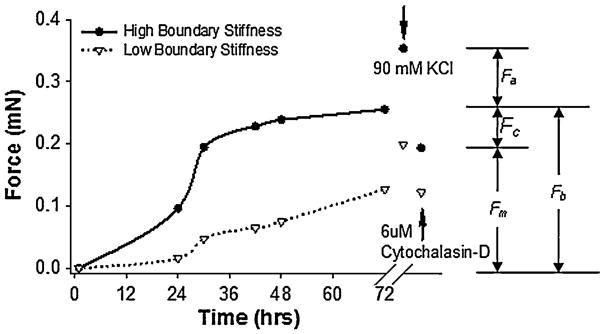
The contractile force generated by the cells within the gel was measured by monitoring the deflection of the cantilever beams as described under the Device Operation section. The gels were cultured in the device for 72 h to allow for complete compaction and changes in phenotype in response to the altered boundary conditions.^1,53 The force during compaction (basal tension, F_b) along each axis was quantified every 12 h. In the terminology of Brown and colleagues¹⁵ and shown in Fig. 4, this basal tension is the “apparent total force output” which comprises of two major components: an active “cell-generated force, F_c” and passive residual “matrix tension, F_m” (fixed tension in the matrix from collagen remodeling by fibroblasts). In a subset of experiments, following the 72-h incubation period the gels were treated with 90 mM potassium chloride (KCl) and the activated force, F_a, was measured. KCl activates contraction in muscle and muscle-like cells by depolarization of the cell membrane. Since myofibroblasts exhibit muscle-like behavior, excitation with KCl is effective for quantifying the extent of fibroblast-to-myofibroblast differentiation. ³⁷ To determine the residual matrix tension as a general metric of cell-mediated remodeling, the gels were rinsed in PBS following the KCl treatment and then treated with cytochalasin D (6 μM, Sigma) for 4 h to disrupt the actin cytoskeleton and thus eliminate active cell tension.^30,52

FIGURE 4.

Representative time-course of generation of basal tension by human foreskin fibroblasts in collagen gels anchored with low (0.041 N m⁻¹, bottom curve) and high (0.48 N m⁻¹, top curve) stiffness beams. Data points indicate average between the two forces measured on orthogonal axes. The cells can be stimulated by 90 mM KCl to contract to a higher activated force, F_a, above the basal tension, F_b. The basal tension is composed of an active cell-generated force, F_c, and a passive residual matrix tension, F_m, which remains after treatment with cytochalasin-D.

Mechanical Testing

In a subset of the samples, uniaxial mechanical tests were performed on VIC-seeded collagen gels to quantify the effect of boundary conditions on the intrinsic stiffness of the gels. Following the incubation of the gels in the controlled boundary stiffness device, the thickness of each gel was measured using a laser displacement system (LDS, LK-081, Keyence Corporation, Woodcliff Lake, NJ) as previously described.⁴ A small reflective disc is placed onto the sample, allowing the sample to reach equilibrium (2 min). The laser system then records the thickness (±10 μm accuracy).² A 12.5 mm wide strip was then cut from the center of the specimen, placed in an isotonic saline bath, and mounted on a magnetic drive uniaxial testing machine (ElectroPuls 1000, Instron Corp.) custom fitted with a low force transducer (±0.001 N, Interface, Inc.) and optical marker tracking (SVE, Instron). A tare load of 1 mN was applied and the gauge length measured, then the sample was cyclically stretched for eight cycles between stretch ratios of 1.0 to 1.1. The deformations in the center of the sample were measured using two small metal markers with barbs placed on the surface of the sample. The Lagrangian stress–stretch ratio (σ−λ) data were fit to an exponential model

$$\sigma =A\left(e^{B(\lambda -1)}-1\right)+{\sigma }_0$$ (3)

where A and B are material parameters and σ₀ is the initial (tare) stress. The maximum tangent modulus, MTM, was computed (MATLAB, Mathworks) as a metric of the maximum intrinsic stiffness of the gel. The structural stiffness, K, at 0.1 mN was calculated as a functional measure of the matrix stiffness at a level corresponding to the force generated by a population of cells.

Immunohistochemistry

The location and organization of α-SMA-positive cells present in a subset of samples was assessed using immunohistochemistry. As α-SMA is the most accepted marker of the myofibroblast phenotype, this technique provided a measure of fibroblast-to-myofibroblast differentiation. Following removal of the strip for mechanical testing, the remaining portion of the specimen pinned down to a PDMS filled dish was fixed with 10% buffered neutral formalin for 7 h and transferred to 70% ethanol. A small rectangular sample was removed for histological preparation. Following dehydration in graded ethanol solutions and paraffin embedding, the sample was cut in 5 μm sections and stained with α-SMA antibody (Clone 1A4, Dakocytomation) followed by biotinylated goat antimouse IgG2A (Vector Laboratories). Harris hematoxylin counterstain (Richard-Allan Scientific) was used to identify the nuclei in the tissue. The sections were viewed on an upright microscope (Eclipse E600, Nikon) and images acquired with a RT Color Spot camera (Diagnostic Instruments, Inc.).

Dose-Dependent Studies

To measure trends in forces produced by fibroblasts with level of boundary stiffness, multiple spring values were utilized. Fibroblast-populated collagen gels were cultured as described in the section “Collagen gel fabrication.” The gels were incubated in the controlled boundary stiffness device with the boundary beams’ stiffness levels ranging over an order of magnitude of stiffness (~0.05 to 0.6 N m⁻¹, Table 1, one gel per test condition) for 72 h.

TABLE 1.

Diameters of the stainless steel beams along with the measured effective spring stiffness in (cantilevered) bending, K(N = 3).

Beam diameter (mm)	K(N m−1) (±SD)
0.127	0.048 ± 0.007
0.152	0.090 ± 0.009
0.178	0.141 ± 0.016
0.229	0.305 ± 0.026
0.241	0.409 ± 0.012
0.267	0.641 ± 0.024

To assess the response of the cells to TGF-β1, three concentrations of TGF-β1 (0, 5, and 10 ng mL⁻¹)⁵ were used in conjunction with the low (0.048 N m⁻¹) and high (0.409 N m⁻¹) stiffness beams. Cell-seeded collagen gels (one gel per test condition) were prepared with as described in the section “Collagen gel fabrication” and cultured for 72 h.

Statistics

The purposes of this study were to develop a new method and to demonstrate the broad range of experiments and measurements made possible with the device. No hypotheses were formally tested in this work, thus statistical comparisons were not made. In most experiments only one or two samples of each experimental condition were cultured; however, the majority of experiments were repeated to demonstrate the reliability of the method. Trends in force with the experimental variables (boundary stiffness and TGF-β1 concentration) were determined using linear regression (SigmaPlot, Systat Software, Inc.). As this method is biaxial and force is calculated independently along each axis, the average force along the axes is reported.

RESULTS

Simulations

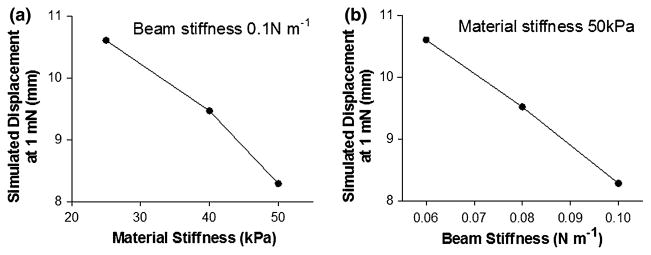
Finite element simulations demonstrate that both the material stiffness and the boundary stiffness affect the overall transverse deflection of the system. The predicted deflection of the center of the material under an arbitrary small load of 1 mN for materials of increasing intrinsic stiffness (Fig. 5a) and boundary beam stiffness (Fig. 5b) show monotonically decreasing trends.

FIGURE 5.

Results from the transverse deflection simulations of the finite element model under varying boundary conditions. (a) The displacement of the central node of the finite element model decreases with increasing intrinsic stiffness of membrane attached to spring boundary (0.1 N m⁻¹) during transverse deflection. (b) The displacement of central node also decreases with increasing stiffness of the boundary springs with membrane stiffness constant at 50 kPa.

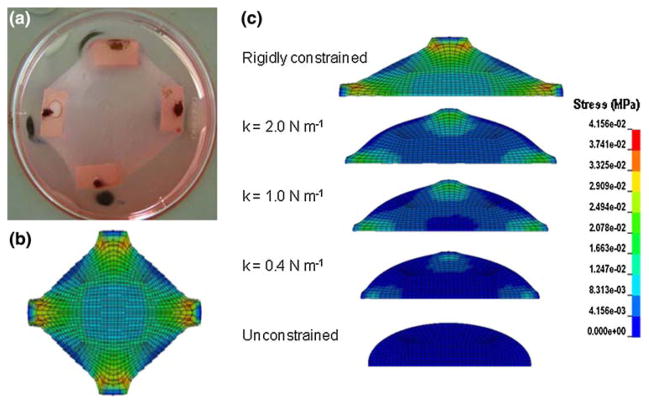
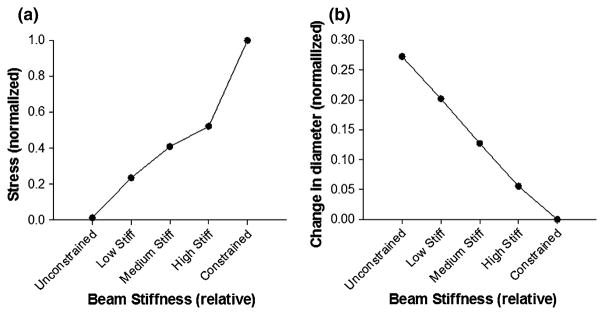
The contracted shape of the circular FE model due to the simulated drop in temperature is qualitatively similar to that of the remodeled collagen gel attached to a highly stiff boundary (cf. Figs. 6a and 6b). The gel rigidly constrained to the boundary along the two perpendicular axes shows highest stress near the attachment pads, whereas the unconstrained model exhibits a negligible increase in stresses but contracts inward considerably (Fig. 6c). The stress in the center of the model increases (Fig. 7a) and the deformation decreases (Fig. 7b) monotonically with increasing boundary stiffness.

FIGURE 6.

(a) Digital image of a fibroblast-seeded collagen gel following 72 h of compaction (well diameter is 60 mm). (b) Von Mises stresses in the finite element model following the analysis for thermal compaction. (c) Von Mises stress in a mid-line crosssection of the finite element model as a result of the simulated change in temperature. The gels are arranged as per the boundary conditions. The top image represents a gel rigidly constrained at the boundary along the four axes, followed by gels constrained by springs of decreasing stiffness. The bottom image represents an unconstrained gel.

FIGURE 7.

(a) Von Mises stress in the center of the finite element model (normalized to the stresses in the constrained gels) in response to the change in the temperature under different boundary conditions. (b) Change in the diameter of the finite element model due to change in temperature under different boundary conditions (normalized to the change in diameter for the constrained gel).

Pilot Studies

Time-course of Contraction

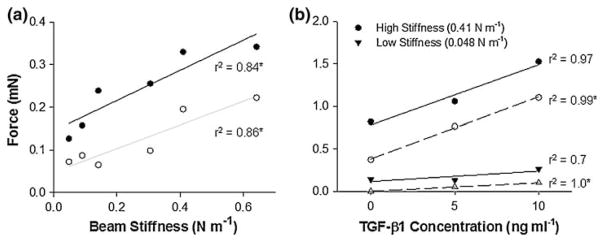
Figure 4 shows the force generated by two fibroblast-seeded collagen gels cultured in the controlled boundary stiffness device; one with stiff beams (0.409 N m⁻¹) and one with compliant beams (0.048 N m⁻¹). As observed from the graph, the basal tension generally levels off after 72 h in culture, and the cells in gels with higher boundary stiffness generate higher traction forces. The basal tension generated against the stiff spring boundary (~0.25 mN) is more that twice that generated by cells in gels under compliant spring boundary condition (~0.1 mN). Addition of KCl activates contraction of the cells resulting in an increase in force generation: the force rises an additional ~0.1 mN for stiff spring boundary and ~0.06 mN for compliant spring boundary. Addition of cytochalasin-D disrupts the actin cytoskeleton, thereby eliminating the active contraction of the cells. The force measured following cytochalasin-D deactivation (0.09 mN for the compliant spring boundary and 0.18 mN for the stiff spring boundary) represents the residual tension present in the gel due to the remodeling and reorganization of the collagen gel matrix by the cells in response to the boundary condition over the three days in culture.

Changes in Mechanical Properties Due to Remodeling

The stiffness of the gels appears to be dependent on the boundary stiffness that the VIC-populated gels were exposed to and the presence of TGF-β1 as illustrated by Table 2. Increasing the boundary stiffness of the gels results in an increased MTM of the gels. This stiffening is indicative of greater remodeling of the gels by the cells as compared to gels with compliant or free boundary. The addition of TGF-β1 leads to further stiffening of the matrix, indicating that TGF-β1 enhances cellular remodeling activity. The structural stiffness (calculated from the model parameters at 0.1 mN force applied by the testing machine) was low for all groups (<1 N m⁻¹) and did not correlate with the boundary condition or the presence of TGF-β1.

TABLE 2.

Pilot results from uniaxial tensile testing on strips of VIC-populated collagen gels after 72 h cultured free floating (“Free”) or anchored to compliant (0.048 N m⁻¹) or stiff (0.41 N m⁻¹) springs in the absence or presence of 5 ng mL⁻¹ TGF-β1.

Boundary condition	TGF-β1(+/−)	Width (mm)	Thickness (mm)	L0 (mm)	σ0 (kPa)	A (kPa)	B (−)	K (N m−1)	MTM (kPa)	RMS (kPa)	r2 (−)
Free	−	6.86	0.30	16.92	0.156	0.115	26.5	0.52	43.5	0.12	0.93
Free	+	5.67	0.31	21.14	0.000	0.286	15.5	0.44	20.9	0.15	0.81
Compliant	−	12.19	0.11	22.49	0.160	0.248	26.2	0.51	86.9	0.20	0.95
Compliant	+	11.73	0.13	24.5	0.220	0.306	25.2	0.57	96.0	0.13	0.98
Stiff	−	10.08	0.17	18.74	0.084	0.280	29.1	0.90	149.1	0.15	0.99
Stiff	+	10.82	0.14	21.5	0.068	0.029	57.4	0.39	530.8	0.20	0.99

The low root mean square error (RMS) and the high coefficient of determination (r²) indicate that the exponential model fit the data well. One sample from each group was tested.

Gel Thickness and α-SMA Expression by Fibroblasts

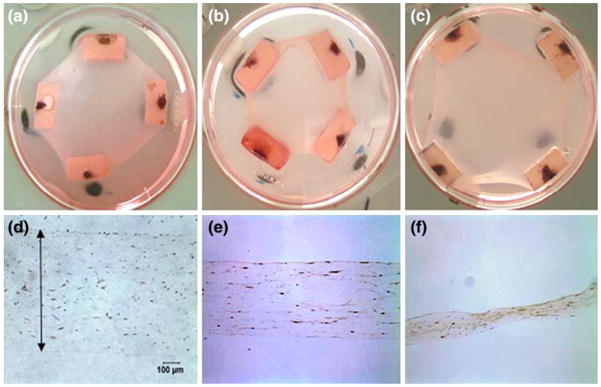
Figure 8 shows representative images of compacted gels after culturing for 3 days with compliant beams without TGF-β1, compliant beams with TGF-β1, and stiff beams with TGF-β1. The gels are more compacted in the plane with the compliant springs but more compacted in thickness with the stiff beams. Qualitatively, there was little staining for α-SMA in the compliant gels without TGF-β1, slightly more with TGFβ1, and substantial staining with stiff boundaries in the presence of TGF-β1.

FIGURE 8.

Compaction of the gels after culturing for 3 days with (a, d) compliant beams (K = 0.048 N m⁻¹) without 10 ng mL⁻¹ TGF-β1 (b, e) compliant beam with TGF-β1 and (c, f) in presence of stiff beam (K = 0.57 N m⁻¹) and TGF-β1. The diameter of the dish is 60 mm and original magnification is 200× (d, e, and f).

Dose-Dependent Studies

The basal tension and activated force generated by fibroblasts in the gels exhibited positive trends with boundary stiffness over the broad range studied (Fig. 9a). After 72 h of culture, the forces generated by the cells in the gels ranged from ~0.12 mN to 0.36 mN, increasing monotonically with beam stiffness. Upon addition of KCl, the active force generated by the cells increased over the basal tension by 0.6–2.2 mN with an increasing trend with beam stiffness. Both the basal tension and activated force trended upwards with TGF-β1 concentration for both compliant and stiff beams (Fig. 9b).

FIGURE 9.

The basal tension (closed symbols) and activated force upon 90 mM KCl stimulation (open symbols) generated by human foreskin fibroblasts (0.5 million cells mL⁻¹) trends upward with (a) increasing boundary stiffness and (b) TGF-β1 concentration. The “*” next to r² values indicates significant slope, p <0.05; each data point represents one gel.

DISCUSSION

This article describes a new tool for investigating the role of the mechanical environment on the behavior of cells within a 3D extracellular matrix. The method utilizes external springs which are purely mechanical elements, thus large ranges of effective stiffness at the cell level can be studied without directly altering the composition or the mechanical and biochemical properties of the extracellular matrix. In a recent review by Peyton et al.,⁴⁸ the authors highlight evidence from 2D in vitro model systems that clearly shows the profound influence of substrate stiffness on cell shape, migration, proliferation, and differentiation, but note that it remains to be seen whether or not these same effects translate to 3D systems. Here we demonstrate, for the first time, pronounced effects on cell behavior of altered boundary stiffness, most notably cell compaction of ECM, contractile force, and expression of α-SMA, in a biofidelic 3D system.

This system of constraining tissue boundaries is analogous to the application of splints in wound healing.^7,26 Wound splints do not directly attach to the provisional matrix within healing tissue; rather they are applied to tissue surrounding the wound. Despite the lack of local attachment, splints exhibit strong effects on the phenotype and function of cells within the center of the wound, most notably the increased rate of myofibroblast activation.²⁶ Springs have also been used to apply “constant force” to human burn scar biopsies, and those under spring loading had increased number of myofibroblasts.³³ The increased presence of the α-SMA positive cells observed by immunohistochemistry in our study with higher boundary stiffness (Fig. 8) is consistent with this phenotypic shift, yet further quantification of α-SMA protein levels by immunoblotting and additional immunohistological markers for the myofibroblast phenotype are needed for confirmation of these results. In vivo and in vitro, high levels of myofibroblast activation in rigidly attached gels relative to free gels has also been observed, although this effect has previously been attributed to elevated intrinsic collagen gel stiffness rather than the higher stiffness of the boundary constraint. ^1,20,26 Our data suggest that it is the boundary stiffness, and not the local properties, that dominates the effective stiffness at the cell level in these soft collagen gels. We provide finite element analysis to help explain how the effects of the mechanical constraints are propagated into the interior of the gels.

Cell-Mediated Gel Compaction

Preliminary results from the fibroblast-populated collagen gels cultured in the controlled boundary stiffness device show a monotonic increase in the compaction and cell-generated forces over time which eventually levels out at about 72 h. This behavior has been observed previously for uniaxially constrained gels using isometric force transducers in “culture force monitors”.^16,54 In the first phase of compaction (initial 12 h), there is a rapid increase in force. This force is generally attributed to initial spreading and migration of the cells within the matrix resulting in the rearrangement of the collagen fibrils and compaction of the gel.²⁴ The second phase at longer time points is dominated by the active contraction of the cells and their ability to exert prolonged traction on the collagen fibers. This phase is highly dependent upon the stiffness of the boundary conditions as clearly demonstrated by comparing cell behavior in free and fixed gels. In fixed gels, the cells are able to generate substantial tension in the matrix and remain actively contractile, whereas in free-floating gels the cells become quiescent and a considerable proportion of cells undergo apoptosis.^24,52 Further, in the presence of TFG-β1, the phenotypic shift between fibroblast and myofibroblast appears to only happen in fixed and highly stiff boundary gels as indicated by α-SMA positive staining in these groups but not in the compliant or free groups (Fig. 8). This behavior has been qualitatively shown previously in comparisons between free and fixed gels for a variety of fibroblastic cell types.^1,56 In our experiments, there is also a trend toward higher activated force in response to KCl with increasing boundary spring stiffness (Fig. 9a). This finding further indicates a phenotypic shift to more muscle-like cell behavior.

Utilizing cross-linked collagen-GAG sponges, Gibson and colleagues²⁰ found that the contractile forces generated by fibroblasts during attachment and spreading are not altered by the effective stiffness of their surroundings. In these tests, the effective stiffness was modulated by both altering the crosslinking of the sponge and tethering uniaxially to beams of a range of compliance values. Discrepancies between these results and our findings of strong stiffness-dependent force generation are most likely due to differences between how cells interact with relatively stiff sponges compared to very soft collagen gels. Our simulations indicate that the cells in soft collagen gels should “feel” the change in boundary stiffness. More recently, Chen and colleagues⁴¹ reported on an analogous method at the micro-scale utilizing micropatterned polymer pillars as cantilevered beams of adjustable stiffness (by varying length or diameter). Similar to our findings, they report that cellular forces are higher when cultured against “high” boundary stiffness compared to “low” boundary stiffness. Further, they report a slight increase in cell-generated forces with a 2.5-fold increase in initial collagen concentration, presumably due to higher intrinsic stiffness of the matrix.

The use of a non-crosslinked collagen gel as a tissue model allows for the cells to interact with the matrix and remodel it, a dynamic reciprocity similar to that occurring in vivo.^23,52 Changes in gel properties due to remodeling can be assessed as a powerful metric of stiffness-dependent cell activity, a functional measure not possible in inert polymer gel systems. However, this dynamic reciprocity can also confound the analysis of stiffness-dependent behavior since the material stiffness is dynamically changing as a function of boundary stiffness. A positive feedback loop could potentially arise where increased local stiffness of the gel due to cell-mediated remodeling in turn stimulates cells to increase remodeling of the matrix. Regulation (and dysregulation) of matrix remodeling warrants further study in this system.

Finite Element Simulations

The simulations of transverse loading indicate that the effective stiffness of the system increases substantially due to either an increase in the intrinsic stiffness of the material or by an increase in stiffness of the springs at the boundary. For example, increasing the stiffness of the membrane 2-fold from 25 to 50 kPa has a similar impact on the displacement (at a given force) as increasing the spring stiffness approximately 2-fold from 0.06 to 0.1 N m⁻¹. Although the deformations and loads in the actual culture system are all co-planar, this transverse (trampoline-like) loading simulation demonstrates the concept that changes in the boundary conditions can be “felt” by the cells without altering the local properties of the material itself.

Despite the simplicity of the thermal simulations, the contraction of the circular FE model due to the simulated drop in temperature is strikingly similar in appearance to the cell-mediated compaction of a collagen gel attached to a highly stiff boundary (cf. Figs. 6a and 6b). The simulations also indicate that uniform contraction of the cells within the gels results in graded compaction and generated force as a function of the stiffness of the boundary. These findings are in agreement with the trends in our experimental data (cf. Figs. 7a and 9a). For a given temperature change, peak stresses at the constrained edges are 20-fold higher in the fixed case compared to the free case, and the stresses in the central homogeneous region in the central 20% of the sample increase monotonically with boundary stiffness. These results highlight the fact that, even though all of the elements are “stimulated” equally by the change in temperature, each element may decrease in size and generate stresses to a different extent depending upon the constraints on that individual element by adjacent elements. Such thermal analyses have been utilized to simulate how uniform cellular contraction (each “cell” contracts equally) produces non-uniform stress distributions in a cell layer depending upon the boundary constraints.⁴⁴ As with previous thermal analyses, these simulations represent an analog to cell contraction assuming homogeneous activity, thus the temperature, thermal coefficient, and material properties do not correspond to actual physical entities. Quantitatively, the deformation of the simulated collagen gel is inversely dependent on the temperature change and the thermal coefficient of the material chosen for the simulation. Nonetheless, the behavior of populations of cells in a collagen gel after limited time in culture appears to be captured well by the thermal analysis. At long culture times (>2 days), however, the phenotype of the cells may be altered to a more or less contractile state depending upon the global mechanical conditions and thus would no longer exert homogeneous contraction.

Biaxial vs. Uniaxial Stiffness Modulation

The biaxial configuration is advantageous as it enables the study of cell response to boundary anisotropy which can be achieved by attaching springs of different stiffness along the two axes. This anisotropy of stiffness is not easily attained with PA, PEG, or other polymer substrates. Such anisotropic studies could provide a picture of the alignment and orientation of the cells and corresponding re-organization of the collagen fibers due to cell migration and orientation. Holmes and colleagues^39,53 have shown that anisotropic stress boundary conditions (obtained by hanging different weights on each axis) lead to anisotropic properties in fibroblast-remodeled collagen gels after only 72 h of culture. In the present system, compliance of the beams can be customized to match the anisotropic stiffness of specific tissues in the body and simulate the response of cells in tissues without uniform boundaries e.g., valvular interstitial cells in heart valves. Further, unlike isotonic boundary conditions applied using weights and pulleys which have an estimated 31% frictional losses,³⁹ there are no connections between the springs and the gels that could impede deflection in any direction in the plane of the tissue. A limitation of this biaxial format is that a relatively large gel is needed to obtain a central homogenous region large enough to perform functional tests on the gel. In the biaxial configuration, only the center has homogeneous equibiaxial compaction as seen by the FE simulations (Fig. 6). If bulk mechanical and biochemical assays were replaced with methods applicable to smaller tissue samples, the device could be scaled down allowing higher throughput. Uniaxial versions could also be utilized; however, massive realignment of the cells and collagen would be expected along with compaction of the gel into a string-like shape.

The forces measured in our studies are the same order of magnitude as measured with isometric (rigid) force transducers attached uniaxially to collagen gels.^6,11,15,40 However, as our measurements are the first biaxial measurements of forces of compaction in collagen gels, the magnitudes of forces cannot be directly compared. In uniaxially constrained systems, the cells profoundly align the collagen fibers and align themselves along the axis between the constraints, thus the cell contractile forces are generally assumed to be predominantly along the measured axis. In our system with equal stiffness along orthogonal axes, the cells are assumed to be randomly oriented within the plane of the tissue in the central area. Along the edges between the attachment pads the cells are likely to aligned parallel to the edge.

Force Per Cell Estimation

One of the key differences between the myofibroblast phenotype and the quiescent fibroblast phenotype is the exertion of higher traction forces.⁸ Therefore analysis of force generated on a per cell basis would serve as a crucial non-immunochemical method for assessing myofibroblast differentiation. In the majority of studies attempting to quantify the contractile force generated by a population of cells within a matrix, the force per cell is calculated by dividing the total (uniaxial) force by the number of cells.^11,15 Using this calculation, fibroblasts generate 0.1 mN per million cells (i.e., 0.1 nN per cell) for high stiffness beams after 72 h of culture in our study; this value is in the low end of the range reported for fibroblasts in uniaxial isometric culture monitors (0.1–10 mN per million cells)^11,15 and cardiac fibroblasts cultured under biaxial isotonic conditions (1.4 mN per million cells).³⁹ This calculation is straightforward but assumes all cells act in parallel (see schematic, Fig. 10a) which is clearly not an accurate representation. Alternatively, if one assumes that all cells act in series, the force measured would be the force generated by a single cell (Fig. 10b) which is also not physically possible. In reality, the cells are distributed approximately uniformly throughout a cell-populated collagen gel (at least initially) and thus some groups of cells act in parallel and others in series (Fig. 10c). To account for this distribution, researchers have divided the force by cell crosssectional area in a given histological cross-section.⁴⁰ This approach is an improvement, but only valid for a uniaxially constrained gel. Ideally, a computational model such as the anisotropic biphasic theory³⁸ could be utilized to simulate compaction and cell contraction, yet even sophisticated models rely on assumptions of cell–ECM interactions that are not valid for long culture times (>5 h culture).

FIGURE 10.

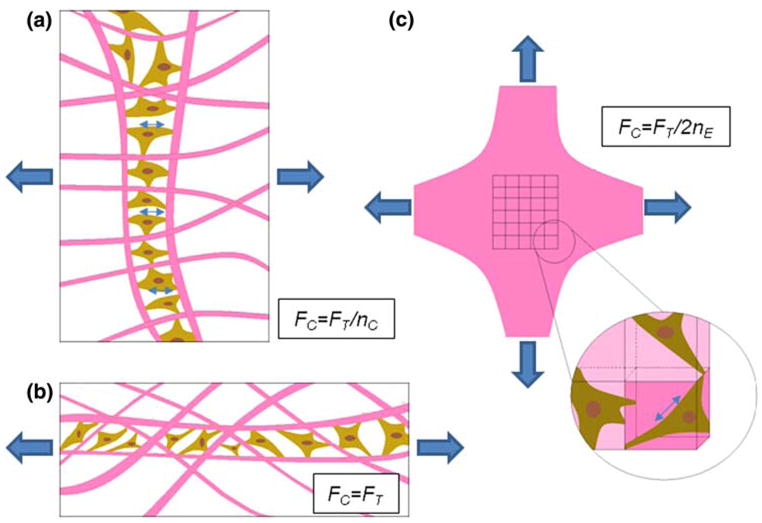
Schematic represents idealized arrangements of cells in (a) parallel and (b) series formations in a collagen gels for the purpose of estimating the force per cell, F_c, assuming uniaxial restraint. (c) Shows a biaxial configuration subdivided into representative volume elements (RVEs) with each RVE containing a single fibroblast in random orientation. F_c is lowest in (a), highest in (b), and in between in (c) (n_c = number of cells, n_E = number of RVEs in parallel in a given cross section).

In our system, the cells generate roughly equal forces on the two constrained axes. Here a relatively straightforward approach would be to utilize a representative volume element (RVE) containing one cell and the surrounding volume of ECM (Fig. 10c, inset). The number of RVEs can be determined simply by dividing the final volume of the gel by the number of cells (here we use initial cell number assuming no net change in cell number). In the uniaxial case, the force per cell can be calculated by dividing the total force along one axis by the number of RVEs in a cross-section assuming that all of the cell force is directed along the axis of constraint. In the equibiaxial case, we assume that the cells are oriented randomly in the plane of the tissue and that each cell pulls predominantly in one direction (i.e., bipolar cells) thus, on average, half of the total force exerted by the cells is directed along each axis (see Appendix for derivation). The total force along an axis (measured by beam displacement) can be found by integrating over the RVEs in the perpendicular cross-section taking into account the uniform angular distribution of cell orientations. As a first approximation, the shape of each RVE is assumed to be a cube. As the shape of the contracted gel is roughly cruciform, only the central area (region of interest-approximately half of the maximum dimension) is considered in this calculation. Using this method, the force per cell for fibroblasts cultured for 72 h in the basal medium is approximately 17 nN per cell for low stiffness beams and 100 nN per cell for high stiffness beams. These values compare favorably to estimated individual fibroblast contractile forces generated in collagen-GAG sponges (26 nN per cell average, maximum 450 nN) obtained by analyzing bending of ECM “struts”²⁵ and to recent values for NIH 3T3 cells calculated using micro-pillars as bending beams (14 nN per cell with low boundary stiffness (0.098 N m⁻¹) and 24 nN with high boundary stiffness (0.397 N m⁻¹)).⁴¹ These values are substantially higher than values estimated for fibroblasts in the same system calculated by dividing force by total cell number (~3 nN/cell).²⁰

Although this RVE method appears to provide a better estimate for the order of magnitude of forces generated by the cells than assuming the cells act in parallel, the values should be interpreted with caution. These calculations assume that the contractile forces are relatively homogeneously distributed in the gel, whereas our FE thermal analysis indicates that the “cell-generated” stresses near the attachment pads are greater than in the central region of interest (Fig. 6). Further, the calculations are based on initial cell number and estimated volume. With longer term culture (>1 day) cells proliferate and undergo apoptosis, and these processes are likely to be strongly dependent upon boundary condition as shown by comparing free and fixed gels.¹⁹ Although live/dead staining was performed periodically to assess cell viability which was high (data not shown), additional measurements are needed. In future studies the cell number and gel volume will be quantified at various time points throughout the culture period; as these are destructive measurements, a large number of gels will be needed for this quantification.

Effects of Cell Type, Cell Density, Collagen Concentration, Serum, and TGF-beta

To demonstrate the versatility of this method, pilot studies were completed with a variety of beam stiffness levels, TGF-β1 concentrations, cell seeding densities, and cell types. Although all cell types that we have utilized generated higher forces with high stiffness boundaries than with low stiffness boundaries, our preliminary data indicate that there is a large variation of the magnitude of forces between stromal cells from lungs, heart valves, and the dermis (data not shown). In particular, human fetal lung fibroblasts generated much higher forces (~1.0 mN) than valvular interstitial cells (~0.41 mN) and dermal fibroblasts (~0.35 mN) (beam stiffness of 0.41 N m⁻¹ and 0.5 million cells per mL in all cases).

The goal of the device is to alter the mechanical environment of the cells without altering the matrix properties; hence studies using different collagen densities were not carried out. The concentration of 2 mg mL⁻¹ selected for our study is consistent with most cell-seeded collagen gel model systems.^16,39 Higher levels of apoptosis have been observed with lower initial collagen densities.⁵⁸ Further, high collagen concentration has been shown to adversely affect the extent of fibroblast-mediated compaction of the matrix.⁵⁸ Cell density is also clearly an important parameter in collagen gel remodeling and may confound analysis of stiffness-dependent cell behavior utilizing this system. Preliminary results from our device (data not shown) indicate greater compaction and higher force generation with higher initial seeding density, consistent with previous findings utilizing culture force monitors.^3,11,49 The measured force is monotonic with cell number but does not appear to be proportional to the cell number as recently reported for microtissues⁴¹; relationships between seeding density and metrics of gel compaction are complex because of the change in dynamics of cell–cell and cell–matrix interactions due to compaction of gels over time.^46,49 In terms of practical considerations, we found that initial seeding densities less than 0.5 million cells per mL did not produce force to bend the bars sufficiently for accurate measurements.

Components in serum are generally considered necessary for cells to adhere to the matrix, actively generate forces, and remodel the collagen as shown quantitatively using culture force monitoring.^11,34,35 Nevertheless, in experiments utilizing collagen gels, the use of serum is variable. For example Germain and colleagues⁴³ utilize 10% serum in their study of TGFβ isoforms (β1, β2, and β3) and myofibroblast activation, yet Arora et al.¹ and Jiang et al.³¹ measure free compaction of gels by fibroblasts in the absence of serum. In our experience, 10% FBS is sufficient for expansion of fibroblastic cells in standard (2D) culture and for robust compaction and force generation in collagen matrices, thus 10% FBS was used in the present studies.

Cytokines, many of which are present in serum, have also been identified as important regulators of the cell behavior in vitro and in vivo. Profibrotic cytokines, most notably TGF-β1, induce differentiation of fibroblasts into the highly contractile myofibroblast phenotype. ²¹ Addition of TGF-β1 to the gels cultured in the controlled boundary stiffness device results in greater basal tension and activated force generation with both low and high beam stiffness levels. The cytokine appears to have a much more potent action with the high beam stiffness beams eliciting approximately 10 times the active force of contraction observed with the low stiffness beams (Fig. 9b). Although these data are preliminary and are meant to demonstrate the utility of the system rather than test a hypothesis as to the action of TGF-β1, in previous work a similar increase in the extent and rate of contraction of free gels has been attributed to addition of TGF-β1 to the media.¹

CONCLUSION

In conclusion, we have presented a simple yet powerful new method for modulating the mechanical environment of cells within standard 3D collagen gels without exogenously altering the biochemical composition of the gel. Isolating mechanical effects on the cells is critical for studying mechanobiology and for determining interactions between stiffness and other stimuli such as electrical, chemical and biochemical signals known to profoundly affect cell behavior. For the first time, cell contractility measurements can be made within gels in between the standard “fixed” and “free” configurations. As standard cell-populated gels are utilized in this system, cell-mediated remodeling and cell phenotype can be evaluated by the extensive array of mechanical, biochemical, imaging, and immunohistochemical characterization methods previously developed for studying these model systems. Further, the changes in response to alterations in the global mechanical environment can be directly compared to a large body of literature of the effects of other stimuli on cells in these gels. We expect this device and principle will be valuable for understanding the role of the external mechanical environment in the development of various pathologies in the body, in particular the progression of the fibrocontractive diseases. Other applications for this model would be in functional tissue engineering, angiogenesis, cancer research, and also understanding mechanical determinants of stem cell differentiation.

APPENDIX

Estimation of the Force Per Cell Using the RVE Method

To estimate the average force per cell, we assume that the cells are oriented randomly in the plane of the tissue, and that each cell pulls predominantly in one direction (i.e., bipolar cells). Using the RVE method, the total force measured along one axis, F_T, can be computed from the average force per cell, F_C, by integration:

$$F_{\text{T}}={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{n}_{\text{E}}R(\theta )F_{\text{C}}cos(\theta )d\theta$$ (A.1)

where n_E is the number of cells in parallel (RVEs a cross-section), and R(θ) is the angular distribution of cells. If the distribution of cells orientations is assumed uniform (constant with θ), and we note that the integral of R(θ) = 1 by definition, then:

$$F_{\text{T}}=n_{\text{E}}\left[sin\frac{\pi }{2}-sin\frac{-\pi }{2}\right]F_{\text{C}}=2n_{\text{E}}{F}_{\text{C}}.$$ (A.2)

Thus, F_C = F_T/2n_E in our system.

To determine the size of an RVE, the final volume of the gel is calculated by multiplying the projected area (from digital images, e.g., Fig. 8a) by the thickness (from histological sections, e.g., Fig. 8d) and is divided by the total number of cells in the gel. The number of cells (RVEs) contributing to the total force is estimated by dividing the cross-sectional area in the central region of interest perpendicular to the axis on which force is measured by the cross-sectional area of the RVE which is assumed to be a cube. As the shape of the contracted gel is roughly cruciform, the width of the region of interest is approximately half of the maximum dimension of the gel.