Efficient Nonbonded Interactions for Molecular Dynamics on a Graphics Processing Unit

Abstract

We describe an algorithm for computing nonbonded interactions with cutoffs on a graphics processing unit (GPU). We have incorporated it into OpenMM, a library for performing molecular simulations on high performance computer architectures. We benchmark it on a variety of systems including boxes of water molecules, proteins in explicit solvent, a lipid bilayer, and proteins with implicit solvent. The results demonstrate that its performance scales linearly with the number of atoms over a wide range of system sizes, while being significantly faster than other published algorithms.

Introduction

Significant work has been done recently to implement molecular dynamics algorithms on graphics processing units (GPUs).^1–3 Given the very large computing power of GPUs when compared to CPUs, this has the potential to greatly extend the time scale accessible to molecular simulations.

In typical MD simulations, the calculation of nonbonded interactions account for most of the processing time. This is therefore the most important part of the calculation to optimize. Several different approaches have been tried for implementing nonbonded interactions on GPUs, but none have been entirely satisfactory. All of them have either scaled poorly to large system sizes, or else have achieved only a small fraction of the maximum theoretically possible performance.

In this paper we present a new method for implementing nonbonded interactions on a GPU. It displays linear scaling over a wide range of system sizes while having significantly higher performance for a complete MD simulation (not just non-bonded interactions) than previously published O(N) methods.

Background

In principle, finding all interactions between a set of N atoms requires O(N²) time. In practice, it is usually acceptable to ignore interactions beyond a cutoff distance, or to treat them with an approximation such as reaction field, particle mesh Ewald, or fast multipole method.⁴ This reduces the complexity to O(N), since the number of atoms within the cutoff distance of a given atom is independent of system size. It is typically implemented using a voxel based method.⁵ Each atom is assigned to a voxel, and then interactions are calculated only between atoms in nearby voxels. This is often combined with a neighbor list to avoid performing the voxel calculation on every time step.

Unfortunately, these algorithms adapt poorly to GPUs due to the different memory architecture. CPUs include large amounts of fast cache memory to optimize random memory access. In contrast, GPUs have very little cache memory, and instead are optimized for in-order memory access.⁶ For example, performing a computation on a series of atoms can be very fast:

for i = 1 to (# of atoms)

perform computation on atom i

In contrast, using a neighbor list involves accessing atoms out of order:

for i = 1 to (# of neighbor list entries)

perform computation on the two atoms in entry i

In practice, this usually means that indirect memory access (of the form array[index[i]]) is slow, while direct memory access (of the form array[i]) is fast.

To implement nonbonded interactions efficiently on a GPU, it is therefore essential to avoid indirect memory access whenever possible. Several approaches have been tried to this problem.

Friedrichs et al.¹ recently reported a GPU based MD code that provided up to 700 times speedup for Generalized Born implicit solvent simulations in comparison to a widely used CPU based code. Indirect memory access was avoided through the simple expedient of using an O(N²) algorithm for the nonbonded interactions. Unfortunately, this means that their method scales poorly with system size. That makes it suitable for small or medium sized proteins with implicit solvent, but not for larger systems including explicit solvent.

Anderson et al.² implemented a Lennard-Jones force using a voxel based algorithm to generate neighbor lists. They relied on the GPU's small texture cache to reduce memory access times, sorting the atoms spatially to increase the number of cache hits. The resulting algorithm gave excellent linear scaling, but achieved a much smaller speedup relative to a CPU than the method of Friedrichs et al., reflecting the poor match of this method to the GPU architecture. They reported performance for a simple polymer model as being similar to a CPU cluster with 32 cores, indicating a speedup of something less than 32 times relative to a single core. Also, their benchmark simulations were much simpler than typical MD simulations: there were no Coulomb interactions, and identical Lennard-Jones parameters were used for all atoms. This avoided the need to look up per-atom force field parameters during the force calculations. As discussed above, accessing per-atom data is the primary bottleneck for algorithms of this type, so real molecular simulations using this algorithm would likely be much slower than suggested by the benchmark simulations. Their polymer model also lacked many of the bonded interactions found in most molecular force fields, and including these would likely further decrease the performance.

Stone et al.³ implemented Coulomb and Lennard-Jones forces using a voxel based method directly, rather than first generating a neighbor list. Compared to Anderson et al., Stone et al. reported a smaller speedup relative to CPUs: approximately 9 times speedup for the nonbonded force calculation, and 5 times speedup for the whole simulation.

Algorithm

Basic algorithm

We used the O(N²) algorithm of Friedrichs et al. as the starting point for our method. Rather than starting from an O(N) algorithm designed for CPUs and attempting to port it to GPUs, we instead decided to begin with an algorithm that was already optimized for GPUs and look for ways to reduce its computational complexity.

This algorithm begins by dividing atoms into blocks of 32. This block size is chosen to match the size of a warp on Nvidia GPUs, allowing maximum use of shared memory while avoiding the need for explicit thread synchronization. The N² interactions between atoms then divide into (N/32)² tiles, with each tile involving 32² interactions (Figure 1). Due to symmetry, only half of the tiles actually need to be calculated. A group of threads is assigned to evaluate the interactions within each tile. Since a tile involves interactions between 64 atoms (32 atoms for tiles along the diagonal which calculate the interactions within a single block), the positions and force field parameters for those atoms are first loaded into shared memory, where the threads can then access them very quickly. This greatly decreases the amount of data transferred from main memory: only one atom for each 16 interactions evaluated, compared to two atoms for each interaction when using a neighbor list.

Figure 1.

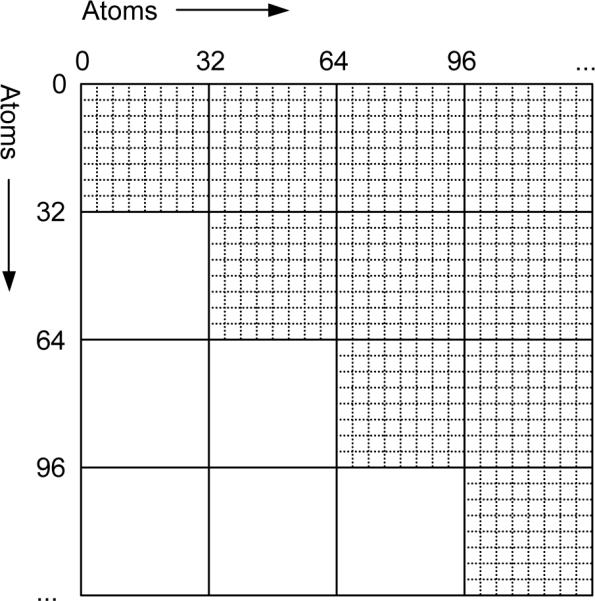
Atoms are divided into blocks of 32, which divides the full set of N² interactions into (N/32)² tiles, each containing 32² interactions. Tiles below the diagonal do not need to be calculated, since they can be determined from symmetry.

Identification of interacting blocks

A problem with this algorithm is that it evaluates all interactions, even for atoms that are far apart. We therefore make the following modification: instead of calculating forces for all tiles, we first identify tiles for which all atoms are sufficiently far apart to guarantee there are no interactions. We then perform the detailed force calculation only for those tiles that might have interactions, omitting those which can be easily excluded. In essence, this is exactly equivalent to a neighbor list; but instead of listing atoms that might interact, it lists blocks of 32 atoms that might interact.

The identification of interacting blocks involves two steps:

1. Calculate an axis aligned bounding box for the 32 atoms in each block.

2. Calculate the distance between bounding boxes for each pair of blocks. If this is above the cutoff distance, the corresponding tile is guaranteed to have no interactions and can be skipped.

Step 1 is a trivial O(N) operation. Step 2 can be done using a variety of algorithms similar to those used for building ordinary neighbor lists. For the work described in this paper, we simply compared every bounding box to every other. This means that, strictly speaking, the computational complexity is O(N²), but in practice the computation is still dominated by the force calculations which scale as O(N). For very large systems, step 2 could be replaced with a different algorithm whose computational complexity was lower, such as a voxel based method or a sort and sweep algorithm.⁷ As with standard neighbor lists, the identification of interacting blocks may be performed each time step, or only once every several time steps. The latter choice reduces the cost of building the neighbor list, but requires some padding to be added to the cutoff so that blocks will be included even if they do not currently interact, but might interact within the next few time steps.

Reordering of atoms to optimize coherence

If the above algorithm is to be efficient, it is essential that atoms be ordered in a spatially coherent way. That is, all the atoms in a block must be close to each other. Otherwise, the bounding boxes will be very large and few tiles will be excluded from the force calculation.

For proteins and other biological macromolecules, this is easily achieved. Atoms are simply assigned to blocks in order along the polymer chain, so sequential atoms will always remain spatially close to each other. For water molecules, it is more of a problem. A single block of 32 atoms will span many molecules, and each of those molecules is free to move independently of the others. To solve this, we periodically reorder water molecules to ensure spatial coherency. This is done as follows:

1. Divide space into square voxels of width w, where w should be similar to (or possibly smaller than) the cutoff distance.

2. Calculate the centroid of each water molecule, and assign it to the corresponding voxel.

3. Trace through the voxels in a spatially contiguous order⁸ to generate a new order for the water molecules. That is, we first take all of the molecules from the first voxel, then all the molecules from the second voxel, etc.

The method described above is found to give linear scaling over a large range of system sizes, but it still has room for improvement. If a tile contains even a single pair of interacting atoms, all 1024 interactions in that tile must be computed. There are even some tiles that contain no interactions at all, yet still get computed because the bounding boxes are within the cutoff distance. The efficiency can be improved with the following change.

For each tile that has been identified as interacting, we compute the distance of the bounding box of the first block from each atom in the second block. If it is greater than the cutoff distance, we set a flag indicating that no interactions need be calculated for that atom. We have effectively increased the granularity of the neighbor list: each element corresponds to 32 interactions instead of 1024.

When a thread is computing interactions for this tile, it checks the flags:

for i = 1 to 32

if atom i has interactions

compute interaction

There are 32 such threads for each tile, each one computing the interactions of one atom in the first block with all atoms in the second block. To avoid thread divergence, all 32 threads must loop over atoms in the same order, in contrast to the original algorithm where each thread loops over atoms in a different order. This means that all threads compute forces on the same atom at the same time, and a reduction is needed to sum those forces. As a result, the cost of computing each interaction is increased. When only a few atoms in a block have interactions, this is still much faster than computing the full set of 1024 interactions, but when many atoms have interactions, it is better to ignore the flags and use the standard method, even though this involves computing more interactions.

In practice, we find that when 12 or fewer out of the 32 atoms in a block have interactions, it is best to use the flags and compute interactions for only those atoms. When more than 12 atoms have interactions, it is best to ignore the flags and compute all interactions.

Performance

To measure the performance of our algorithm, we incorporated it into OpenMM¹ and performed a series of simulations of different sized systems. All simulations were run on a 3 GHz Intel Core 2 Duo CPU and an Nvidia GeForce GTX280 GPU. Nonbonded interactions were cut off at 1 nm, and interactions beyond the cutoff were approximated with the reaction field method, which is similar in form to a shifting function. The integration time step was set to 2 fs. Covalent bonds involving hydrogen atoms were constrained with the SHAKE algorithm⁹ at a tolerance of 10⁻⁵, while water molecules were kept fully rigid with the SETTLE algorithm.¹⁰ A Langevin integrator was used to maintain the temperature at 300K.¹¹ All parts of the computation other than nonbonded interactions (bonded interactions, integration, etc.) were done as described by Friedrichs et al. Except when otherwise stated, all simulations were 100 ps (50,000 time steps) long.

Water molecules were reordered every 100 time steps as described above to maintain spatial coherency. The reordering was done on the CPU rather than the GPU. There is no reason it could not be done on the GPU, but because it only happens every 100 time steps, it makes a negligible contribution to the total processing time, and we therefore saw no need to further accelerate it.

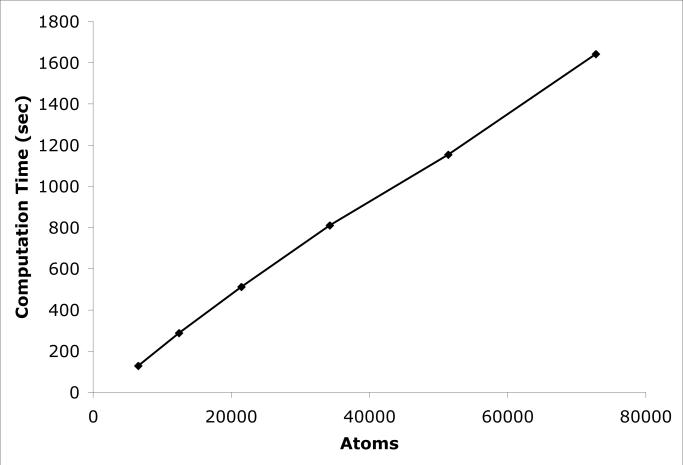
We first simulated cubic boxes of SPC water molecules¹² of various sizes. This provides a simple test of how performance scales with the number of atoms, independent of all other factors. The results are shown in Table 1 and Figure 2. The performance is almost perfectly linear over the whole range of system sizes.

Table 1.

Performance of simulating cubic boxes of water of varying sizes. All simulations were 100 ps (50,000 time steps) long.

Box Size (nm)	Atoms	Computation Time (sec)	ns/day
4	6540	127	68
5	12426	285	30
6	21483	510	17
7	34251	808	11
8	51393	1154	7.5
9	72768	1642	5.3

Figure 2.

Computation time for a 100 ps simulation of a cubic box of water as a function of the number of atoms in the system.

We next simulated a set of proteins of widely varying sizes in explicit water: the villin headpiece subdomain,¹³ the D14A variant of the lambda repressor monomer,^14,15 and one chain of the α-spectrin subunits R15, R16, and R17 from chicken brain.¹⁶ We also simulated a trimer of influenza virus fusion peptide embedded in a lipid bilayer.¹⁷ This last simulation was significant in that it contained several different classes of small, interchangeable molecules: 16,812 waters, 500 POPC lipids, 56 Cl⁻ ions, and 46 Na⁺ ions. The reordering procedure described above was applied independently to each of these classes of molecules every 100 time steps.

The results are shown in Table 2. For the three solvated proteins, the performance is again linear in the total number of atoms. The membrane system, on the other hand, runs about 18% slower than would be expected for a box of water with the same number of atoms. This is because the long, flexible lipid molecules are not bounded as tightly by axis aligned bounding boxes, leading to slightly larger boxes and more interactions that must be calculated.

Table 2.

Performance of simulating proteins in explicit solvent. All simulations were 100 ps (50,000 time steps) long. See the text for descriptions of the systems.

Protein	Total Atoms	Protein Atoms	Computation Time (sec)	ns/day
villin	8867	582	216	40
lambda	16437	1254	418	21
α-spectrin	73886	5078	1733	5.0
peptide in membrane	77373	834 (+26000 lipid atoms)	2145	4.0

Our algorithm can also be used for simulations with implicit solvent. Table 3 shows the performance of simulating villin, lambda repressor, and α-spectrin with the Onufriev-Bashford-Case (OBC) generalized Born model for implicit solvent.¹⁸ These simulations were 400 ps (200,000 time steps) long. For villin and lambda repressor, the performance is actually worse with cutoffs than when using the simple O(N²) algorithm.¹ For such small systems, the cost of constructing a neighbor list outweighs the small gain from calculating fewer interactions. For α-spectrin, on the other hand, using a cutoff speeds up the computation by more than a factor of 3. The break-even point at which a cutoff becomes beneficial appears to be approximately 1500 atoms.

Table 3.

Performance of simulating proteins with OBC implicit solvent.

Protein	Atoms	Computation Time (sec)	ns/day
villin	582	86	402
lambda	1254	176	196
α-spectrin	5078	617	56

To compare the performance of our GPU code to an optimized CPU implementation, we repeated the simulation of lambda repressor in explicit solvent with three different widely used molecular dynamics packages: NAMD 2.6,¹⁹ AMBER 9,²⁰ and Gromacs 4.²¹ As far as possible, we tried to make the simulations identical to the GPU simulation described above. NAMD and AMBER do not support the reaction field approximation for long range interactions, so they used a switching function and a simple cutoff, respectively. To reduce the cost of neighbor list generation in NAMD and Gromacs, the neighbor list was only regenerated once every 8 time steps, but it was constructed based on a cutoff of 1.1 nm to ensure that most interactions within 1 nm would still be found. All simulations were run on a single CPU core. All three packages were compiled from source using the GCC 4.3 compiler and the default compilation options selected by their respective configuration scripts.

The results are shown in Table 4. On the hardware tested, Gromacs was the fastest, taking 19 times as long as the GPU implementation, while AMBER was the slowest, taking 59 times as long as the GPU. Stated differently, a single GPU is as fast as a 19 core cluster running Gromacs or a 59 core cluster running AMBER, assuming negligible communication overhead and linear scaling of performance with cluster size. In practice, neither of those assumptions is likely to be valid, which means the single GPU is as fast as an even larger cluster. For example, when simulating a large membrane/protein system, Gromacs is reported to be only about 12 times as fast running on a 64 core cluster as when running on 4 cores of a single node, not 16 times as fast as would be the case if performance scaled linearly.²¹ Similarly, a large collection of benchmarks for AMBER show that its performance typically increases by a factor of between 6 and 10 when scaling from 4 cores to 64 cores.²²

Table 4.

Performance of simulating lambda repressor with explicit solvent using three different CPU based molecular simulation packages.

Program	Computation Time (sec)	ns/day	GPU Speed Advantage
NAMD 2.6	11682	0.74	28
AMBER 9	24653	0.35	59
Gromacs 4	8058	1.07	19

Our GPU code was 28 times faster than NAMD, in contrast to the method of Stone et al. which was reported to be 5 times faster than NAMD. One must be conservative in comparing these numbers, since they were produced by simulating different systems on different hardware. Also, they implemented only the nonbonded forces on the GPU, while calculating bonded forces and doing integration on the CPU. Even so, it is clear that our method is significantly faster than theirs.

It is more difficult to compare our performance to the method of Anderson et al., since they only reported cluster performance rather than single core performance, but it appears to be at least similar to what they reported. Furthermore, their implementation did not support standard molecular force fields, only a highly simplified polymer model, and their method's performance would likely be much slower with any realistic molecular force field.

For any system larger than a few thousand atoms, our method is dramatically faster than the O(N²) algorithm used by Friedrichs et al. Its performance scales linearly over a wide range of system sizes, making it suitable for simulating large molecules in explicit solvent.

Conclusions

We have developed a new algorithm for computing nonbonded interactions with cutoffs on a GPU. Its performance scales linearly with the number of atoms over a wide range of system sizes, while being significantly faster than previously published algorithms for computing accurate molecular force fields on GPUs.

With this method, a single GPU can now deliver performance comparable to that of a small to medium sized CPU cluster with high speed interconnects. An obvious next step is to parallelize the algorithm so that computations can be split between multiple GPUs. A small GPU cluster could potentially offer performance rivaling that of the largest CPU clusters currently available, bringing very long simulation time scales within the reach of a much larger set of researchers.