Determination of side-chain-rotamer and side-chain and backbone virtual-bond-stretching potentials of mean force from AM1 energy surfaces of terminally-blocked amino-acid residues, for coarse-grained simulations of protein structure and folding. 1. The Method

Abstract

In this and the accompanying paper, we report the development of new physics-based side-chain-rotamer and virtual-bond-deformation potentials which now replace the respective statistical potentials used so far in our physics-based united-reside UNRES force field for large-scale simulations of protein structure and dynamics. In this paper, we describe the methodology for determining the corresponding potentials of mean force (PMF’s) from the energy surfaces of terminally-blocked amino-acid residues calculated with the AM1 quantum-mechanical semiempirical method. The approach is based on minimization of the AM1 energy for fixed values of the angles λ for rotation of the peptide groups about the C^α ⋯ C^α virtual bonds, and for fixed values of the side-chain dihedral angles χ, which formed a multi-dimensional grid. A harmonic-approximation approach was developed to extrapolate from the energy at a given grid point to other points of the conformational space in order to compute the respective contributions to the PMF. To test the applicability of the harmonic approximation, the rotamer PMF’s of alanine and valine obtained with this approach have been compared with those obtained by using a Metropolis Monte Carlo method. The PMF surfaces computed with the harmonic approximation are more rugged and have more pronounced minima than the MC-calculated surfaces but the harmonic-approximation- and MC-calculated PMF values are linearly correlated. The potentials derived with the harmonic approximation are, therefore, appropriate for UNRES for which the weights (scaling factors) of the energy terms are determined by force-field optimization for foldability.

1 Introduction

Nowadays, all-atom simulations of protein structure and dynamics are very expensive, and can be applied successfully only to small proteins even when the solvent is treated implicitly.^1–4 Recent advancements in all-atom molecular dynamics by porting molecular dynamics codes to Graphical Processor Units (GPUs),⁵ which has provided a 700-fold speed-up compared to single-processor runs, as well as construction of computers dedicated to molecular dynamics,⁶ will shift the available time scale of all-atom simulations; however, it is not likely that the millisecond simulation scale will be available soon with the all-atom approach. Coarse-grained approaches to the simulation of protein structure and dynamics, as well as to protein-structure prediction, in which each amino-acid residue is represented by a few interaction sites are, therefore, of great interest in the field.^7–10 Defining a coarse-grained model implies averaging over those degrees of freedom which are not considered in the model. The partition function of a coarse-grained system and all ensemble averages should correspond to those of the pertinent all-atom system; consequently, a logical choice for the effective energy function of a coarse-grained system is the potential of mean force (PMF), which is a function of the coarse-grained degrees of freedom;^11–13 we also term this PMF the restricted free energy (RFE) function.^{14, 15} The statistical or knowledge-based potentials,^7–10 which are commonly applied in predicting protein structure and even simulations of protein folding^{16, 17} are obtained by converting the distributions of geometrical variables (such as, e.g., the distances between side-chain or residue centers) into potentials of mean force by applying the Boltzmann principle.¹⁸ Each such component is determined in the context of an “average” protein environment and, consequently, the sum of such components, which constitutes the total statistical potential-energy function, does not have a connection to the partition function, of the respective all-atom system. In particular, different component potentials might include the same interactions, which could, therefore, be included more than once in the effective energy function. Moreover, the distribution functions are derived from protein conformations at minimum free energy, mostly in crystal state. The physical meaning of statistical potentials is, therefore, obscure.^{19, 20}

During the last decade, we have been developing a coarse-grained physics-based force field termed UNRES (UNited RESidue).^{14, 15, 21–29} By contrast to most united-residue force fields, UNRES was carefully derived, based on the physics of interactions, as a cluster-cumulant expansion³⁰ of the RFE function of a protein plus the surrounding solvent, in which the secondary degrees of freedom had been averaged out.^{14, 15, 25} The cluster-cumulant expansion expresses the many-body PMF as a sum of factors, each of which pertains to a smaller part of the system, taking into account only those parts of the total many-body PMF which are not present in the other factors. This feature of the cluster-cumulant expansion prevents us from multiple counting of the same interactions in more than one term. Each group of related factors constitutes given terms in the effective energy function (such as, e.g., virtual-bond stretching, virtual-bond-angle bending, virtual-bond torsional, side-chain side-chain interaction, etc.); if a factor pertains to more than two interaction sites, it corresponds to effective multibody interactions. This approach to derive the effective energy function provides a clear physical meaning of its constituents and enables us to consider small systems while parameterizing the factors; consequently, even highly accurate methods of molecular quantum mechanics have been used in parameterizing UNRES energy components.^{24, 25, 27} Moreover, approximate analytical expressions can be derived for the energy terms,¹⁵ based on Kubo’s³⁰ generalized-cumulant expansion, which is especially important for multibody terms, for which conventional formulas (such as, e.g., the Lennard-Jones functional form for non-bonded interactions) are not applicable. Furthermore, the factor expansion of the total PMF and the expansion of the factors into Kubo’s cumulant series enabled us to introduce the temperature dependence of the correlation terms.²⁸ An alternative approach to treat the many-body PMF of coarse-grained systems, termed multi-scale coarse-graining (MS-CG) was proposed recently by Voth and coworkers;^11–13 in this approach, the coarse-grained forces are fitted to the average forces obtained from all-atom simulations of a given system.

For practical reasons, the cluster-cumulant expansion has to be truncated; in the present UNRES we keep up to fourth-order factors. Because of this truncation and because it is not possible to determine the factors in an absolutely accurate manner, the UNRES force field has been calibrated to reproduce structural and folding-thermodynamics data of training proteins; for this purpose, we designed a hierarchical-optimization method^{23, 26, 28, 31, 32} in which the force field is optimized so that the free energy decreases with increasing native-likeliness below the folding-transition temperature. The multibody terms were not present in the first version of UNRES,^{21, 22} and the force field was applicable to recognize protein folds only in threading-with-energy-minimization calculations.²² Ab initio structure calculations with UNRES became possible after the correlation terms were introduced. At first, only the terms accounting for the correlation between backbone-electrostatic (hydrogen-bonding) interactions were introduced,¹⁴ which enabled us to calculate the structures of α-helical proteins,^{33, 34} while later introduction of the correlation terms pertaining to the coupling between backbone-local and backbone-electrostatic interactions¹⁵ enabled us to extend the application of UNRES to the β and α + β proteins. The UNRES force field is outlined in section 2.1.

Initially,^33–36 UNRES was applied to predict protein structure by global optimization of the effective potential-energy function. We implemented the Conformational Space Annealing (CSA) method^{33, 37–39} to carry out global optimization with UNRES. The UNRES/CSA approach was found to be capable of ab initio prediction of the structures of proteins of different structural classes with good accuracy, as demonstrated in the CASP blind-prediction experiments; ^{33, 35, 36} these results were obtained by predicting the native structure of a protein as the global minimum in the UNRES energy surface.

Later,^40–42 by developing the Langevin-dynamics formalism for UNRES, we extended its application to simulating protein-folding pathways. We found⁴² that ab initio folding of real-size proteins can be simulated with this approach, and that UNRES provides a 4000-fold speed-up compared to all-atom simulations with explicit water and about a 200-fold speed-up compared to all-atom simulations with implicit water. We have pursued this approach further by introducing replica-exchange molecular dynamics,^{43, 44} which enabled us to revise the force field to calculate thermodynamic characteristics of protein folding.²⁸ We have also extended the UN-RES/MD approach to multichain proteins⁴⁵ and to simulate dynamic formation and breaking of disulfide bonds during protein folding and unfolding,⁴⁶ and implemented principal-component analysis to investigate protein-folding pathways with UNRES.^{47, 48} Recently, by fine-graining the UNRES code for calculations on massively-parallel machines,⁴⁹ we extended the time and size scale of simulations to microsecond simulations of about 800-residue proteins, making it possible to accomplish such simulations in days. Given the fact that the UNRES time scale is about 3 orders of magnitude larger than the all-atom time scale, the UNRES time scale is equivalent to an all-atom millisecond time scale and comparable to the biological time scale.

In its intial form,^{21, 22} UNRES was parameterized mainly by using distribution functions determined from protein-crystal data except for those corresponding to backbone-electrostatic interactions parameterized earlier, by using free-energy surfaces derived from all-atom calculations, ⁵⁰ based on our dipole model of peptide-group interactions.⁵¹ Most of these knowledge-based potentials have subsequently been replaced in UNRES by those derived from all-atom energy surfaces obtained by ab initio^{24, 25, 27} quantum-mechanical calculations. Nevertheless, two types of local knowledge-based terms, both in functional form and parameterization, determined in our earlier work²² from the statistics of the Protein Data Bank (PDB)⁵² remained until recently; these were the virtual-bond-angle bending potentials and the potentials determining the energetics of side-chain rotamers. These terms did not determine the fold of the chain and, therefore, did not impair the overall characterization of UNRES as a physics-based force field. Nevertheless, these short-range terms determine the details of the geometry of the polypeptide chains particularly in the loop regions. It should be noted that the PDB statistics used to derive them is biased by long-range interactions which certainly impairs the accuracy of these local potentials and, consequently, the accuracy of the calculated structures. Moreover, we found that the functional forms that best fit the PDB statistics²² may result in unstable forces in UNRES/MD simulations.⁴⁰ In our recent paper,²⁷ we reported the determination of physics-based virtual-bond-angle bending potentials [U_b(θ_i) in eq. 1] for UNRES by using our general approach¹⁵ of factoring the RFE of the polypeptide chains into contributions coming from specific types of interactions together with the energy maps of terminally-blocked glycine, alanine, and proline calculated in our earlier work.²⁴ In this and the accompanying paper,⁵³ using the AM1 semiempirical method⁵⁴ to compute energy surfaces, we determined the side-chain-rotamer and side-chain and backbone virtual-bond-stretching potentials. In this paper, we present the methodology and illustrate it with examples of terminally-blocked alanine and valine. In the accompanying paper, we discuss in detail the semiempirical side-chain-rotamer and side-chain and backbone virtual-bond-stretching energy surfaces, compare them with the surfaces determined from PDB statistics, fit analytical expressions to them, and present the performance of the updated force field (which also includes the new physics-based virtual-bond-angle-bending potentials determined in our recent work²⁷) in simulations of the folding of small proteins.

The last remaining statistical terms of UNRES are the potentials for side-chain side-chain interactions. We are now replacing these original terms²¹ by determining them from all-atom molecular-dynamics simulations of pairs of molecules modeling amino-acid side chains in explicit water.^55–58 We are also working on introducing temperature dependence into the side-chain side-chain interaction potentials,⁵⁹ which is very important in view of the significant dependence of hydrophobic association on temperature.

2 Methods

2.1 The UNRES force field

In the UNRES model,^{14, 15, 21–29} a polypeptide chain is represented by a sequence of α-carbon (C^α) atoms linked by virtual bonds with attached united side chains (SC) and united peptide groups (p). Each united peptide group is located in the middle between two consecutive α-carbons. Only these united peptide groups and the united side chains serve as interaction sites, the α-carbons serving only to define the chain geometry, as shown in Figure 1. The UNRES force field has been derived as an RFE function^{14, 15} of an all-atom polypeptide chain plus the surrounding solvent, where the all-atom energy function is averaged over the degrees of freedom that are lost when passing from the all-atom to the simplified system (viz. the degrees of freedom of the solvent, the dihedral angles χ for rotation about the bonds in the side chains, and the torsional angles λ for rotation (Figure 2a) of the peptide groups about the C^α ⋯ C^α virtual bonds).⁶⁰ The RFE is further decomposed into factors coming from interactions within and between a given number of united interaction sites.¹⁵ Expansion of the factors into generalized Kubo cumulants³⁰ enabled us to derive approximate analytical expressions for the respective terms,^{14, 15} including the multibody or correlation terms, which are derived in other force fields from structural databases or on a heuristic basis.⁶¹ The theoretical basis of the force field is described in detail in our earlier paper.¹⁵

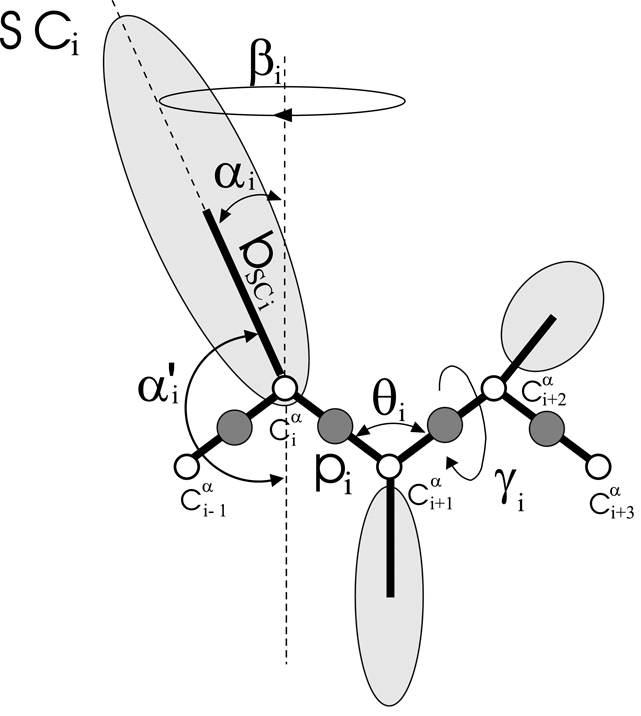
Fig. 1.

The UNRES model of the polypeptide chain. Dark circles represent united peptide groups (p), open circles represent the C^α atoms, which serve as geometric points. Ellipsoids represent side chains, SC′_s, with their centers of mass attached at the b_SC to the corresponding C^α′s. The p’s are located half-way between two consecutive C^α atoms. The virtual-bond angles θ, the virtual-bond dihedral angles γ, and the angles α_SC and β_SC that define the location of a side chain with respect to the backbone are also indicated. In addition, the angle α′ (which is the supplement of α) implemented in the construction of side-chain polar coordinate system (Figure 2 and Figure 5) is shown.

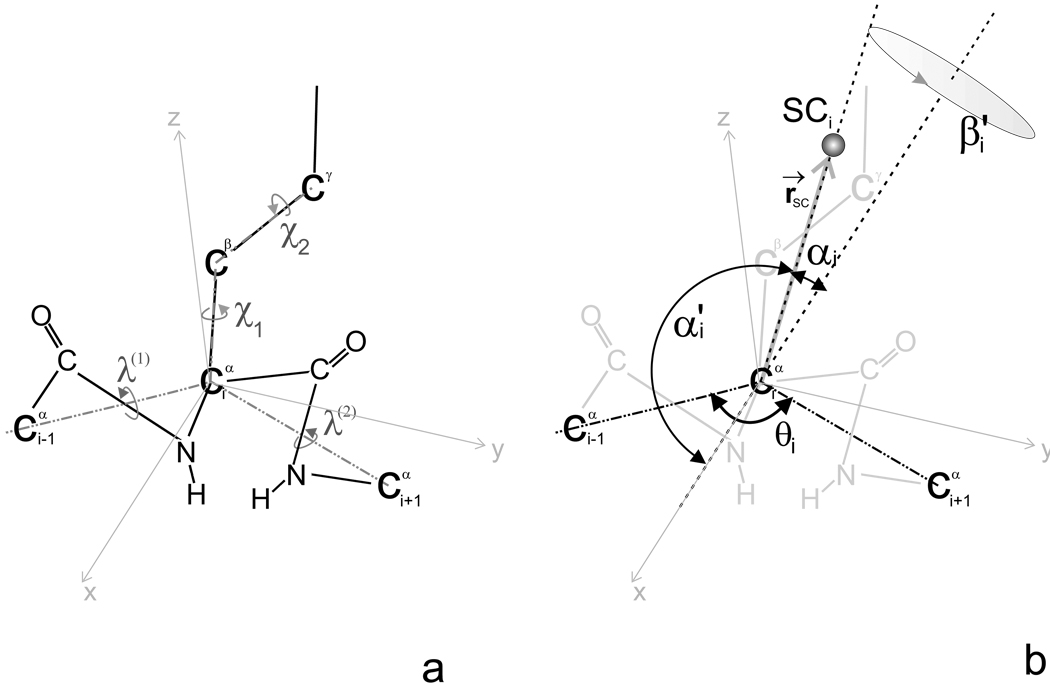
Fig. 2.

Illustration of an all-atom representation (a), and the united-residue representation with atoms and chemical bonds colored light grey (b), of the model systems for the calculation of the potentials of mean force of the rotamers of united side chains and side-chain virtual-bond-stretching potentials of mean force. In both pictures, the dashed lines indicate the virtual bonds and solid lines chemical bonds. The ${\mathrm{C}}_i^{\alpha }$ atom is at the origin of the reference system, the x axis of the reference system is the bisector of the virtual-bond angle θ, the y axis lies in the plane of the three C^α atoms, is perpendicular to the x axis and directed from ${\mathrm{C}}_{i-1}^{\alpha }\text{to}{\mathrm{C}}_{i+1}^{\alpha }$ and all three axes (x, y, and z) form a right-handed reference system. r_SC is the vector pointing from ${\mathrm{C}}_i^{\alpha }$ to the geometric center of the side chain, λ⁽¹⁾ and λ⁽²⁾ are the dihedral angles for the rotation of the peptide groups about the C^α ⋯ C^α virtual-bond axes⁶⁰ and χ¹, χ² … are the dihedral angles for the rotations about the bonds of the side chain. The angles α′ (which is the supplement to the α_SC angle of Figure 1) and β′ (which is the negative of the β_SC angle of Figure 1) are the polar coordinates of the side-chain unit vector, r̂_SC. The polar angle β′ corresponds to clockwise rotation of the SC center about the x axis from the xy plane, starting from the positive side of the y axis. For small side chains (e.g,. Ala, Pro, Ser, Thr), β′ has the same sign as the C^β − C^α − ⋯ C′ dihedral angle (which is ≈ −120° for the L- and ≈ 120° for the D-amino-acid residues).

The energy of the virtual-bond chain is expressed by eq. (1).

$$\begin{array}{cc}U\hfill & =w_{\mathit{\text{SC}}}{\displaystyle \sum _{i<j}{U}_{{\mathit{\text{SC}}}_i{\mathit{\text{SC}}}_j}+w_{{\mathit{\text{SC}}}_p}}{\displaystyle \sum _{i\ne j}{U}_{{\mathit{\text{SC}}}_i{p}_j}+w_{\mathit{\text{pp}}}^{V\mathit{\text{DW}}}}{\displaystyle \sum _{i<j-1}{U}_{p_i{p}_j}^{V\mathit{\text{DW}}}+w_{\mathit{\text{pp}}}^{\mathit{\text{el}}}{f}_2(T)}{\displaystyle \sum _{i<j-1}{U}_{p_i{p}_j}^{\mathit{\text{el}}}}\hfill \\ \hfill & + w_{\mathit{\text{tor}}}{f}_2(T){\displaystyle \sum _i{U}_{\mathit{\text{tor}}}({\gamma }_i)+w_{\mathit{\text{tord}}}{f}_3(T)}{\displaystyle \sum _i{U}_{\mathit{\text{tord}}}({\gamma }_i,{\gamma }_{i+1})}\hfill \\ \hfill & + w_b{\displaystyle \sum _i{U}_b({\theta }_i)+w_{\mathit{\text{rot}}}}{\displaystyle \sum _i{U}_{\mathit{\text{rot}}}({\alpha }_{{\mathit{\text{SC}}}_i},{\beta }_{{\mathit{\text{SC}}}_i})+w_{\mathit{\text{bond}}}}{\displaystyle \sum _i{U}_{\mathit{\text{bond}}}(d_i)}\hfill \\ \hfill & + w_{\mathit{\text{corr}}}^{(3)}{f}_3(T)U_{\mathit{\text{corr}}}^{(3)}+w_{\mathit{\text{corr}}}^{(4)}{f}_4(T)U_{\mathit{\text{corr}}}^{(4)}+w_{\mathit{\text{corr}}}^{(5)}{f}_5(T)U_{\mathit{\text{corr}}}^{(5)}+w_{\mathit{\text{corr}}}^{(6)}{f}_6(T)U_{\mathit{\text{corr}}}^{(6)}\hfill \\ \hfill & + w_{\mathit{\text{turn}}}^{(3)}{f}_3(T)U_{\mathit{\text{turn}}}^{(3)}+w_{\mathit{\text{turn}}}^{(4)}{f}_4(T)U_{\mathit{\text{turn}}}^{(4)}+w_{\mathit{\text{turn}}}^{(6)}{f}_6(T)U_{\mathit{\text{turn}}}^{(6)}\hfill \end{array}$$ (1)

Each term is multiplied by an appropriate weight, w_x and the terms corresponding to factors of order higher than 1 are additionally multiplied by the respective temperature factors which were introduced in our recent work²⁸ and which reflect the dependence of the first generalized-cumulant term in those factors on temperature, as discussed in ref. 28. The factors f_n are defined by eq. (2).

$$f_n(T)=\frac{\text{ln}[\text{exp}(1)+\text{exp}(-1)]}{\text{ln}\{\text{exp}[{(T/T_o)}^{n-1}]+\text{exp}[-{(T/T_o)}^{n-1}]\}}$$ (2)

where T_o = 300K.

The term U_SCiSCj represents the mean free energy of the hydrophobic (hydrophilic) interactions between the side chains, which implicitly contains the contributions from the interactions of the side chain with the solvent. The term U_SCipj denotes the excluded-volume potential of the side-chain – peptide-group interactions. The peptide-group interaction potential is split into two parts: the Lennard-Jones interaction energy between peptide-group centers $\left(U_{p_i{p}_j}^{V\mathit{\text{DW}}}\right)$ and the average electrostatic energy between peptide-group dipoles $\left(U_{p_i{p}_j}^{\mathit{\text{el}}}\right)$; the second of these terms accounts for the tendency to form backbone hydrogen bonds between peptide groups p_i and p_j. The terms U_tor, U_tord, U_b, and U_rot are the virtual-bond-dihedral angle torsional terms, virtual-bond dihedral angle double-torsional terms, virtual-bond angle bending terms, and side-chain rotamer terms; these terms account for the local propensities of the polypeptide chain. The terms $U_{\mathit{\text{corr}}}^{(m)}$ represent correlation or multibody contributions from the coupling between backbone-local and backbone-electrostatic interactions, and the terms $U_{\mathit{\text{turn}}}^{(m)}$ are correlation contributions involving m consecutive peptide groups; they are, therefore, termed turn contributions. The multibody terms are indispensable for reproduction of regular α-helical and β-sheet structures.^{14, 15, 61} The terms U_bond(d_i), where d_i is the length of the ith virtual bond and nbond is the number of virtual bonds, are simple harmonic potentials of virtual-bond distortions; they have been introduced recently⁴⁰ for molecular-dynamics implementation.

The internal parameters of $U_{p_i{p}_j}^{V\mathit{\text{DW}}},U_{p_i{p}_j}^{\mathit{\text{el}}},U_{\mathit{\text{tor}}},U_{\mathit{\text{tord}}},U_b,U_{\mathit{\text{corr}}}^{(m)},\text{and}{U}_{\mathit{\text{turn}}}^{(m)}$ were derived by fitting the analytical expressions to the RFE surfaces of model systems computed at the MP2/6-31G** ab initio level,^{24, 25, 27} while the parameters of U_SCiSCj , U_SCipj , U_bond, and U_rot were derived by fitting the calculated distribution functions to those determined from the PDB.²² The equilibrium values of the virtual-bond lengths were taken from the PDB statistics as mean values corresponding to the C^α ⋯ SC or C^α ⋯ C^α virtual bonds,²² while the force constants were assigned an arbitrary value of 500 kcal/(mol × Å²).⁴⁰ The purpose of the present work is to determine physics-based U_rot and U_bond terms for the side chains, as well as the U_bond terms for the backbone. The w′s are the weights of the energy terms, and they can be determined only by optimization of the potential-energy function, as described in our earlier work.^{23, 26, 28}

2.2 Determination of physics-based U_rot and U_bond potentials

2.2.1 Formulation of the problem

In this work, in order to determine physics-based U_rot and U_bond terms for the side chains, we have implemented our earlier-developed formalism¹⁵ in which the RFE of a polypeptide chain is factored into components, each of which corresponds only to interactions involved in a particular RFE term. We used terminally-blocked amino-acid residues as model systems (Figure 2a) and calculated the potential of mean force for each residue type⁵³ as a function of the components of the unit vector of the C^α ⋯SC vector (r̂_SC) expressed in a local coordinate system with the x axis being the bisector of the virtual-bond angle θ, the y axis lying in the plane of the three C^α atoms, ${\mathrm{C}}_{i-1}^{\alpha },{\mathrm{C}}_i^{\alpha },{\mathrm{C}}_{i+1}^{\alpha }$, and the z axis making a right-handed coordinate system with those two axes, as shown in Figure 2b. The dependence of the energy on the b_SC virtual-bond length is included in the side-chain U_bond term of eq. (1). The most important variables to be averaged out (i.e., those which have a wide range of variation) are the angles λ⁽¹⁾ and λ⁽²⁾ for rotation of the peptide groups about the C^α ⋯ C^α virtual-bond axes⁶⁰ (Figure 2a) and the internal angles of rotations of the side chains (χ, Figure 2a); we will group the variable χ′s into a vector χ = (χ¹, χ², ⋯, χⁿ)^T where n is the number of the χ angles and “T” in the superscript denotes the transpose of a matrix or a vector. The remaining variables to be averaged out are the angles for the rotation of the methyl groups (these are ignored because the energy depends only weakly on them), the distortions of the chemical bond lengths and bond angles of the all-atom chain, and the out-of-plane distortions of the peptide groups; additionally, we require that the space spanned by these variables is orthogonal to that spanned by the angle θ and the coordinates of r̂_SC; in other words, their variation does not change these geometric parameters. We will denote these other variables by y′. Thus, the potential of mean force F_X of a terminally-blocked residue of type X can be expressed as a function of θ and r_SC by eq. (3).

$$\begin{array}{c}\hfill F_X(\theta ,{\widehat{\mathbf{r}}}_{\mathbf{\text{SC}}})=-{\beta }^{-1}\text{ln}\{{(2\pi )}^{-(n+2)}{(V_{\mathbf{y}\prime })}^{-1}\hfill \\ {\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cdots }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{{\mathrm{\Omega }}_{\mathbf{y}}^{\prime }}{\int }\text{exp}[-\beta e_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },\mathbf{y}\prime )]d{\lambda }^{(1)}d{\lambda }^{(2)}d{\chi }^{1}d{\chi }^2\dots d{\chi }^{n}d{V}_{\mathbf{y}\prime }}\}\end{array}$$ (3)

where β = (RT)⁻¹, T being the absolute temperature and R the universal gas constant, Ω_y′ denotes the region of space corresponding to y′, whereas dV_y′ denotes the respective volume elements, e_X denotes the energy surface of terminally-blocked residue of type X. To compute the U_rot(θ, r̂_SC) term, we must subtract from F_X(θ, r̂_SC) the contribution already considered²⁷ in the virtual-bond angle potential; we will denote it by F̄_X′(θ) where X′ is terminally-blocked alanine, proline, or glycine, alanine representing all residue types except for proline and glycine. The quantities, U_rot(θ, r̂_SC) and F̄_X′(θ) are defined by eq. (7) and eq. (8), respectively. The coordinates of the geometric center of a side chain and the components of the corresponding unit vector r̂_SC are defined by eq. (4) and eq. (5), respectively (it should be noted that these equations refer to the coordinate system of Figure 2, where the central C^α atom is placed at the origin of the coordinate system).

$${\mathbf{r}}_{\mathit{\text{SC}}}=N_{\mathit{\text{SC}}}^{-1}{\displaystyle \sum _{i=1}^{N_{\mathit{\text{SC}}}}{\mathbf{r}}_{l_i}}$$ (4)

$${\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}=\frac{1}{b_{\mathit{\text{SC}}}}{\mathbf{r}}_{\mathit{\text{SC}}}$$ (5)

with

$$b_{\mathit{\text{SC}}}=\Vert {\mathbf{r}}_{\mathit{\text{SC}}}\Vert ={(x_{\mathit{\text{SC}}}^2+y_{\mathit{\text{SC}}}^2+z_{\mathit{\text{SC}}}^2)}^{1/2}$$ (6)

where N_SC is the number of non-hydrogen atoms in a side chain except C^α which is part of a side chain in the UNRES representation but is located at the origin of the coordinate system defined in Figure 2b and l_i is the number of the ith non-hydrogen side-chain atom (excluding C^α).

$$U_{\mathit{\text{rot}}}(\theta ,{\widehat{\mathbf{r}}}_{\mathbf{\text{SC}}})=F_X(\theta ,{\widehat{\mathbf{r}}}_{\mathbf{\text{SC}}})-{\overline{F}}_{X\prime }(\theta )$$ (7)

$${\overline{F}}_{X\prime }(\theta )=-{\beta }^{-1}\text{ln}\left\{{(2\pi )}^{-2}{(V_{\mathbf{y}}^{\prime })}^{-1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{{\mathrm{\Omega }}_{\mathbf{y}\prime }}{\int }\text{exp}\{-\beta [e_{X\prime }({\lambda }^{(1)},{\lambda }^{(2)},\mathbf{y}\prime )]\}d{\lambda }^{(1)}d{\lambda }^{(2)}d{V}_{\mathbf{y}\prime }}\right\}$$ (8)

The virtual-bond-stretching potentials of the side chains, U_bond(b_SC), are defined by eq. (9) as the potential of mean force for the deformation of a virtual C^α ⋯ SC bond in a terminally-blocked amino-acid residue.

$$\begin{array}{c}\hfill U_{\mathit{\text{bond}}}(b_{\mathit{\text{SC}}})=-{\beta }^{-1}\text{ln}\{{(2\pi )}^{-(n+2)}{(V_{\mathbf{y}″})}^{-1}\hfill \\ \hfill {\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cdots {\displaystyle \underset{-\pi }{\overset{\pi }{\int }}}{\displaystyle \underset{{\mathrm{\Omega }}_{\mathbf{y}″}}{\int }\text{exp}[-\beta e_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },\mathbf{y}″)]d{\lambda }^{(1)}d{\lambda }^{(2)}d{\chi }^{1}d{\chi }^2\dots d{\chi }^{n}d{V}_{\mathbf{y}″}}}\}\hfill \end{array}$$ (9)

where y″ denotes the subspace of variables, of a terminally-blocked amino-acid residue that conserve a given value of b_SC given the values of λ⁽¹⁾, λ⁽²⁾, and χ¹, χ², … χⁿ, Ω_y″ is a shorthand for the space spanned by these variables, and dV_y″ is the respective volume element.

2.2.2 Use of harmonic approximation to evaluate U_rot and U_bond from AM1 energy surfaces

To evaluate F_X(θ, r̂_SC) for calculating U_rot from eq. (7) and to calculate U_bond, we first computed the energy maps of all natural terminally-blocked L-amino-acid residues as functions of λ⁽¹⁾, λ⁽²⁾, and the χ angles involving non-hydrogen atoms (thus, no χ angle was defined for the alanine residue) by using the AM1 semiempirical method.⁵⁴ Use of the ab initio approach was prohibitively expensive and it was found in earlier works^{24, 62} that the AM1 method gives energy surfaces of terminally-blocked glycine, alanine, and proline qualitatively similar to those computed with the ab initio method. Glycine was not considered because it does not have a side chain. For Ala, only the grid in λ⁽¹⁾ and λ⁽²⁾, and for Pro only the grid in λ⁽²⁾ angles was defined. For each grid point, a starting conformation was constructed based on the standard valence geometry; the conformation was subsequently energy-minimized in all internal coordinates except for the grid variables. We used the MOPAC’93⁶³ program to carry out the calculations.

To evaluate the integral in eq. (3), we need to express e_X as a function of λ⁽¹⁾, λ⁽²⁾, θ, r_SC, and y′. To simplify further notation, we define z, the vector composed of θ and the three coordinates of r_SC, as given by eq. (10). (We will switch to the unit vector, r̂_SC in eq. (29) which expresses the final potentials of mean force for side-chain rotamers.)

$$\mathbf{z}=\left(\begin{array}{c}\theta \\ x_{\mathit{\text{SC}}}\\ y_{\mathit{\text{SC}}}\\ z_{\mathit{\text{SC}}}\end{array}\right)=\left(\begin{array}{c}\theta \\ {\mathbf{r}}_{\mathit{\text{SC}}}\end{array}\right)$$ (10)

As in our earlier work,²⁷ in which we determined physics-based potentials for virtual-bond-angle bending, we used the harmonic expansion of the energy at each point of the grid to explore the energy surface in the space orthogonal to that spanned by the grid variables, as given by eq. (11).

$$e_X({\lambda }^{(1)},{\lambda }^{(2)},\mathbf{z},\mathbf{y}\prime )\approx e_X^{*}+\frac{1}{2}\mathbf{\Delta }{\mathbf{z}}_{\perp }^{*T}{\mathbf{H}}_{{\mathbf{z}}_{\perp }{\mathbf{z}}_{\perp }}^{*}\mathbf{\Delta }{\mathbf{z}}_{\perp }^{*}+\mathbf{\Delta }{\mathbf{z}}_{\perp }^{*T}{\mathbf{H}}_{{\mathbf{z}}_{\perp }\mathbf{y}\prime }^{*}\mathrm{\Delta }{\mathbf{y}\prime }^{*}+\frac{1}{2}\mathbf{\Delta }{\mathbf{y}\prime }^{*T}{\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }^{*}\mathbf{\Delta }{\mathbf{y}\prime }^{*}$$ (11)

with

$$e_X^{*}\equiv e_X^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })=e_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },{{\mathbf{z}}_{\perp }}^{*},{\mathbf{y}\prime }^{*})$$ (12)

$$H_{z_{\perp i}{z}_{\perp j}}^{*}\equiv H_{z_{\perp i}{z}_{\perp j}}^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })=\frac{{\partial }^2{e}_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },{{\mathbf{z}}_{\perp }}^{*},{\mathbf{y}\prime }^{*})}{\partial z_{\perp i}\partial z_{\perp j}}$$ (13)

$$H_{z_{\perp i}{y}_k^{\prime }}^{*}\equiv H_{z_{\perp i}{y}_k^{\prime }}^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })=\frac{{\partial }^2{e}_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },{{\mathbf{z}}_{\perp }}^{*},{\mathbf{y}\prime }^{*})}{\partial z_{\perp i}\partial y_k^{\prime }}$$ (14)

$$H_{y_k^{\prime }{y}_l^{\prime }}^{*}\equiv H_{y_k^{\prime }{y}_l^{\prime }}^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })=\frac{{\partial }^2{e}_X({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi },{\mathbf{z}}_{\perp }^{*},{\mathbf{y}\prime }^{*})}{\partial y_k^{\prime }\partial y_l^{\prime }}$$ (15)

$$\mathbf{\Delta }{\mathbf{z}}_{\perp }^{*}\equiv \mathbf{\Delta }{\mathbf{z}}_{\perp }^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })={[\mathbf{z}-{\mathbf{z}}^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })]}_{\perp }$$ (16)

$$\mathbf{\Delta }{\mathbf{y}\prime }^{*}\equiv \mathbf{\Delta }{\mathbf{y}\prime }^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })=\mathbf{y}\prime -{\mathbf{y}\prime }^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })$$ (17)

where H denotes a Hessian matrix, and the asterisks indicate the values corresponding to the points on the non-adiabatic energy maps. The terms with the first derivatives of e_X are not present in eq. (11) because $e_X^{*}({\lambda }^{(1)},{\lambda }^{(2)},\mathit{\chi })$ has been minimized with respect to all variables except for λ⁽¹⁾, λ⁽²⁾, and χ, which are held constant. The symbol Δz_⊥ = (Δθ, Δr_SC⊥) denotes the distortion of z from the value corresponding to the relaxed geometry at a given grid point, subject to the condition that the values of χ dihedral angles are the same as those at the grid point. In the linear approximation, the vector Δr_SC⊥ can be defined as a linear combination of the columns of an N × 3-dimensional matrix v_SC⊥ , which is calculated from the matrix v_SC defined by eq. (18) by applying a projection operator, P_χ, to remove the components that belong to the space spanned by dihedral angles χ in the neighborhood of a grid point, as given by eq. (19) and eq. (20).

$${\mathbf{v}}_{\mathit{\text{SC}}}=\left(\begin{array}{c}{\mathbf{0}}_{3\times 3}\\ ⋮\\ {\mathbf{0}}_{3\times 3}\\ {\mathbf{I}}_{3\times 3}\\ ⋮\\ {\mathbf{I}}_{3\times 3}\end{array}\right)$$ (18)

$${\mathbf{v}}_{{\mathit{\text{SC}}}_{\perp }}={\mathbf{P}}_{\chi }{\mathbf{v}}_{\mathit{\text{SC}}}$$ (19)

$${\mathbf{P}}_{\chi }=\mathbf{I}-{\mathbf{\nabla }}_{\mathit{\chi }}\mathbf{R}{({\mathbf{\nabla }}_{\mathit{\chi }}{\mathbf{R}}^T{\mathbf{\nabla }}_{\mathit{\chi }}\mathbf{R})}^{-1}{\mathbf{\nabla }}_{\mathit{\chi }}{\mathbf{R}}^T$$ (20)

with

$${\mathbf{\nabla }}_{\mathit{\chi }}\mathbf{R}=(\begin{array}{cccc}\frac{\partial \mathbf{R}}{\partial {\chi }^1}& \frac{\partial \mathbf{R}}{\partial {\chi }^2}& \cdots & \frac{\partial \mathbf{R}}{\partial {\chi }^m}\end{array})$$ (21)

where R denotes the vector of Cartesian coordinates of all the atoms of terminally-blocked residue X and I_{m × m} is an m-dimensional identity matrix [where m = 3 in eq. (18) and m = 3N in eq. (20)], while 0_{3 × 3} denotes a 3 × 3 matrix of zeros. The matrices of zeros in eq. (18) correspond to the positions of the coordinates of non-side-chain atoms and C^α in the vector v_SC, while the unit matrices in eq. (18) correspond to those of side-chain atoms excluding C^α; for clarity these are the last entries in the v_SC matrix.

Likewise, the subspace corresponding to Δy′ is defined, in the linear approximation, by the set of 3N − 6 − n − 4 eigenvectors (with n fixed χ angles, 3 fixed coordinates of r_SC and fixed angle θ) corresponding to non-zero eigenvalues of the projection operator, P_y′ which removes the contributions corresponding to the variation of λ⁽¹⁾, λ⁽²⁾, χ, and z_⊥, as well as net translations and rotations of the molecule, from the space spanned by the Cartesian coordinates of all atoms.

$${\mathbf{P}}_{\mathbf{y}\prime }=\mathbf{I}-\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T$$ (22)

$$\mathbf{Y}=(\begin{array}{cccccc}{\nabla }_{{\lambda }^{(\mathbf{1})}}\mathbf{R}& {\nabla }_{{\lambda }^{(\mathbf{2})}}\mathbf{R}& {\nabla }_{\mathit{\chi }}\mathbf{R}& {\mathbf{v}}_{\mathit{\text{SC}}}& \mathbf{T}& \mathbf{\Omega }\end{array})$$ (23)

where T_{3N × 3} and Ω_{3N × 3} are the matrices of the basis vectors of translations and of the increments of the coordinates of the atoms of the system resulting from infinitesimal rotations of the molecule about the axes of the reference system, respectively [eq. (24)].

$$\mathbf{T}=\left(\begin{array}{c}{\mathbf{I}}_{3\times 3}\\ {\mathbf{I}}_{3\times 3}\\ ⋮\\ {\mathbf{I}}_{3\times 3}\\ ⋮\\ {\mathbf{I}}_{3\times 3}\end{array}\right) \mathbf{\Omega }=\left(\begin{array}{c}{\mathbf{\omega }}_1\\ {\mathbf{\omega }}_2\\ ⋮\\ {\mathbf{\omega }}_k\\ ⋮\\ {\mathbf{\omega }}_N\end{array}\right)$$ (24)

with

$${\mathbf{\omega }}_k=\left(\begin{array}{ccc}-y_k& x_k& 0\\ -z_k& 0& x_k\\ 0& -z_k& y_k\end{array}\right)$$ (25)

Thus, the parts of the Hessian matrix can be computed from (eq. 26 – eq. 28).

$${\mathbf{H}}_{{\mathbf{z}}_{\perp }{\mathbf{z}}_{\perp }}={\mathbf{v}}_{\perp }^T{\mathbf{H}}_{\mathbf{\text{RR}}}{\mathbf{v}}_{\perp }$$ (26)

$${\mathbf{H}}_{\mathbf{y}\prime {\mathbf{z}}_{\perp }}={{\mathbf{\Pi }}_{\mathbf{y}\prime }}^T{\mathbf{H}}_{\mathbf{\text{RR}}}{\mathbf{v}}_{\perp }$$ (27)

$${\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }={{\mathbf{\Pi }}_{\mathbf{y}\prime }}^T{\mathbf{H}}_{\mathbf{\text{RR}}}{\mathbf{\Pi }}_{\mathbf{y}\prime }$$ (28)

where H_RR denotes the Hessian matrix in Cartesian coordinates expressed in the local coordinate system of Figure 2a, and Π_y′ denotes the matrix of the eigenvectors of P_y′ of eq. (22) corresponding to non-zero eigenvalues; the columns of this matrix define the space orthogonal to that spanned by the columns of Y.

Inserting eq. (11) into eq. (3) and integrating over y′ results in eq. (29) for the potential of mean force.

$$\begin{array}{c}{F}_X(\theta ,{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}})\approx -{\beta }^{-1}\text{ln}\{2^{-(n+2)}{\pi }^{-(n-N/2+2)}{V}_{\mathbf{y}\prime }^{-1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cdots {\displaystyle \underset{-\pi }{\overset{\pi }{\int }}{(\text{det}{\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }^{*})}^{-\frac{1}{2}}\times }}}\\ \text{exp}\{-\beta [e_X^{*}+\frac{1}{2}\mathbf{\Delta }{\mathbf{z}}^{*T}({\mathbf{H}}_{{\mathbf{z}}_{\perp }{\mathbf{z}}_{\perp }}^{*}-\frac{1}{4}{\mathbf{H}}_{{\mathbf{z}}_{\perp }\mathbf{y}\prime }^{*}{\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }^{*-1}{\mathbf{H}}_{{\mathbf{z}}_{\perp }\mathbf{y}\prime }^{*T})\mathbf{\Delta }{\mathbf{z}}^{*}]\}d{\lambda }^{(1)}d{\lambda }^{(2)}d{\chi }^{1}d{\chi }^2\cdots d{\chi }^n\}\end{array}$$ (29)

with

$$\mathbf{\Delta }{\mathbf{z}}^{*}=\left[\begin{array}{c}\hfill \theta -{\theta }^{*}\hfill \\ \hfill b_{\mathit{\text{SC}}}^{*}({\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}-{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}^{*})\hfill \end{array}\right]$$ (30)

where $b_{\mathit{\text{SC}}}^{*}$ is the value of the virtual-bond length corresponding to a given grid point.

By slight modification of eq. (29), we obtain an approximate expression for the virtual-bond-stretching potential, U_bond [eq. (31)].

$$\begin{array}{c}\hfill U_{\mathit{\text{bond}}}(b_{\mathit{\text{SC}}})\approx -{\beta }^{-1}\text{ln}\{2^{-(n+2)}{\pi }^{-(n+N/2+2)}{V}_{\mathbf{y}\prime }^{-1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cdots {\displaystyle \underset{-\pi }{\overset{\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\displaystyle \underset{{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}}{\int }{(\text{det}{\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }^{*})}^{-\frac{1}{2}}\times }}}}}\hfill \\ \hfill \text{exp}\{-\beta [e_X^{*}+\frac{1}{2}\mathbf{\Delta }{\mathbf{z}\prime }^{*T}({\mathbf{H}}_{{\mathbf{z}}_{\perp }{\mathbf{z}}_{\perp }}^{*}-\frac{1}{4}{\mathbf{H}}_{{\mathbf{z}}_{\perp }\mathbf{y}\prime }^{*}{\mathbf{H}}_{\mathbf{y}\prime \mathbf{y}\prime }^{*-1}{\mathbf{H}}_{{\mathbf{z}}_{\perp }\mathbf{y}\prime }^{*T})\mathbf{\Delta }{\mathbf{z}\prime }^{*}]\}d{\lambda }^{(1)}d{\lambda }^{(2)}d{\chi }^{1}d{\chi }^2\cdots d{\chi }^{n}d\theta d^3{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}\}\hfill \end{array}$$ (31)

with

$$\mathbf{\Delta }{\mathbf{z}\prime }^{*}=\left[\begin{array}{c}\hfill \theta -{\theta }^{*}\hfill \\ \hfill b_{\mathit{\text{SC}}}{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}-b_{\mathit{\text{SC}}}^{*}{\widehat{\mathbf{r}}}_{\mathit{\text{SC}}}^{*}\hfill \end{array}\right]$$ (32)

To determine the backbone virtual-bond-stretching potentials, we have to provide a formula for the force constant of the trans peptide group, k_pept. Following the procedure of ref 27, and using N-acetyl-N′-methyl amide, we can express it by eq. (33).

$$k_{\mathit{\text{pept}}}={\mathbf{h}}_{d_p{d}_p}-\frac{1}{4}{\mathbf{h}}_{d_p\mathbf{y}}^T{\mathbf{H}}_{\mathbf{\text{yy}}}^{-1}{\mathbf{h}}_{d_p\mathbf{y}}$$ (33)

where d_p is the C^α ⋯ C^α virtual-bond length, h_dpdp is the second derivative of the energy of the model system in d_p (the Hessian element), h_dpy is the vector of mixed derivatives of the energy in d_p and other variables orthogonal to it (contained in the vector y), and H_yy is the matrix of the second derivatives of the energy in the orthogonal variables. We leave the determination of the virtual-bond potentials to the accompanying paper.⁵³

As in our earlier work,^{24, 27} we evaluate F_X, defined by eq. (29), by numerical quadrature on an (n + 2)-dimensional grid in λ⁽¹⁾, λ⁽²⁾, χ¹, χ², …, χⁿ. The grid size in the λ⁽¹⁾, λ⁽²⁾, and χ angles for the Ac-Ala-NHMe and Ac-Val-NHMe test cases considered in this work was 30°. This resulted in 144 grid points for Ac-Ala-NHMe, where only λ⁽¹⁾ and λ⁽²⁾ formed a grid (the only χ angle corresponds to methyl group rotation and is not significant) and 1728 points for Ac-Val-NHMe. All potentials of mean force were computed at T = 298°K.

2.2.3 Use of canonical Monte Carlo method to compute PMF

In order to obtain insight about the possible inaccuracy in, and artifacts introduced by, using the harmonic approximation in this work, we have also calculated the PMF’s of terminally-blocked alanine and valine by using a canonical Monte Carlo approach.⁶⁴ The procedure was as follows: for a current conformation of Ac-Ala-NHMe or Ac-Val-NHMe, an atom and a Cartesian coordinate (x, y, or z) were selected at random and the coordinate perturbed by adding a random number drawn from a uniform probability distribution from the interval [−δ, δ], where δ is a perturbation amplitude (0.1 Å in this work). Then the energy was evaluated by using the AM1 semiempirical method of molecular quantum mechanics with the MOPAC’93 program.⁶³ The Metropolis test⁶⁴ was applied to accept or reject the new conformation. Three-dimensional histograms in the angles α′, β′, and θ were constructed “on the fly”. The MC algorithm was merged into the MOPAC’93 program.

For Ac-Ala-NMe and Ac-Val-NHMe, we ran 144 and 216 independent trajectories, respectively. The starting conformations were taken from non-adiabatic energy maps of these peptides, defined on a grid with 30° size in λ⁽¹⁾ and λ⁽²⁾ for Ac-Ala-NHMe (144 points) and 60° size in λ⁽¹⁾, λ⁽²⁾, and χ¹ for Ac-Val-NHMe (216 points); each of the dihedral angles ranged from −180° to 180°. Each trajectory consisted of 14 million MC steps for Ac-Ala-NHMe and 15 million MC steps for Ac-Val-NHMe, respectively. The acceptance rate was about 55%.

In order to check whether the sampling procedure did not introduce artifacts and the number of steps was sufficient, we calculated the autocorrelation function for the virtual-bond angles θ. The autocorrelation function is defined by eq. (34).

$$C(t)=\langle \theta (0)\theta (t)\rangle$$ (34)

where t is the number of MC steps (the “time”) and 〈⋯〉 denotes direct average. The autocor-relation functions for both Ac-Ala-NHMe and Ac-Val-NHMe are shown in Figure 3. It can be seen that they exhibit a uniformly decaying behavior and become effectively zero after about 50,000 MC steps, which is a more than four orders of magnitude smaller number compared to the total simulation length.

Fig. 3.

Decay of the autocorrelation function C(t) [eq. (34)] of the angle θ in Metropolis Monte Carlo simulations for alanine (solid line) and valine (dashed line)

3 Results and Discussion

The contour plots of the PMF surfaces of Ac-Ala-NHMe and Ac-Val-NHMe calculated with the direct MC approach and with the use of the harmonic approximation, respectively, for two selected values of θ (90° and 140°) are shown in Figure 4. The plots have been drawn in cylindrical projection with the parallels and meridians of the energy maps corresponding to the β′ and α′ angles, respectively. For better visualization, the center of the projection has been shifted to α′ = 180°. The construction of this projection is outlined in Figure 5. It can be seen that the low-PMF regions of both residues are in the region of 90° < α′ < 180° and β′ < 0°, fitting the geometry of L-amino-acid residues. For θ = 90°, the low-PMF region extends to lower values of α′ and the PMF’s calculated with the use of the harmonic approximation even have two minima: one for large values of α′ (about 165°) and another one for α′ ≈ 105°; for both minima β′ ≈ −90°. Only the first minimum appears for θ = 140°. The first minimum corresponds to positioning of the SC site almost along the bisector of the corresponding θ angles, pointing away from the C^α ⋯ C^α ⋯ C^α frame as found in the β-strands. The second minimum corresponds to the perpendicular orientation of the C^α ⋯SC axis with respect to the C^α ⋯ C^α ⋯ C^α plane with the SC center located above the plane. A closer inspection of conformations with the most significant statistical weight showed that the dominant conformations contributing to this minimum are those from the ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ region, which is almost absent in proteins. On the other hand, with the AM1 energy function, the ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ conformation is only 1.67 kcal/mol above the global minimum (the ${\mathrm{C}}_{\mathit{\text{eq}}}^7$ conformation). Ab initio calculations carried out in our earlier work²⁴ have also shown than the ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ conformation of L-alanine is not as disfavored by energy as would appear from the analysis of PDB statistics. It should be noted that the free-energy map of rotamer potentials of valine (Figure 4e and f) has no low-energy region (for α′ close to 105°) corresponding to the ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ conformation. Therefore, the absence of ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ conformations of alanine might be the effect of protein context. This problem, along with comparison of all AM1-derived potentials with statistical potentials, will be discussed in the accompanying paper.⁵³

Fig. 4.

Side-chain-rotamer PMF surfaces of Ac-Ala-NHMe (a – d) and Ac-Val-NHMe (e – h) obtained by Metropolis MC (a, c, e, g) and harmonic approximation approaches (b, d, f, h) for θ = 90° (a, b, e, f) and θ = 140° (c, d, g, h), respectively. See Figure 5 for explanation of the applied cylindrical projection of the polar coordinates of r̂_SC on the rectangle. The parallels (lines of constant α′) are the distorted circles centered about the “South Pole” (except the parallel corresponding to α′ = 90°, which is a square centered at the “South Pole”) and semicircles centered about the “North Pole” (except those corresponding to α = 90° which constitute two half-squares). The meridians are the lines intersecting the parallels and running between the “North Pole” and the “South Pole”. The parallels and the meridians are each spaced 15°. The PMF color scale (in kcal/mol) is shown above the contour plots and the PMF’s on each plot are relative to the lowest PMF in the corresponding section of the PMF surface.

Fig. 5.

Illustration of the cylindrical projection of the unit sphere spanned by the end of the r̂_SC vector in the local side-chain coordinate system of Figure 2 on the rectangle representing the polar coordinates implemented to draw the PMF maps in Figure 4 and Figure 6 as well as in Figure 2 and 3 of the accompanying paper.⁵³ The “South Pole” (α′ = 180°) is the point in the center of the rectangle, and the “North Pole” (α′ = 0°) is in the middle of the left and of the right vertical side of the rectangle. The axis x runs through the poles with α′ = 180° corresponding to negative and α′ = 0° to positive x, the axis y runs through the “Equator” (α′ = 90°) at β′ = 180° (negative y) and β′ = 0° (positive y), and the axis z runs through the “Equator” at β′ = 90° (positive y) and β′ = −90° (negative y). The “Equator” and its projection on the rectangle are marked by a dashed circle and dashed lines, respectively, and the meridians running through the axes x and y or x and z and their projections are marked with solid circles and lines. Other parallels (radial lines running through the poles) and meridians (distorted circles or distorted semicircles centered in the poles) are not shown to keep the picture readable; they are shown in the PMF maps in Figure 4 and Figure 6.

To determine if the presence of a minimum with dominant contributions from the ${\mathrm{C}}_{\mathit{\text{ax}}}^7$ region is not caused by not including solvation, we carried out additional AM1 calculations for the terminally-blocked Ala residue with the COSMO mean-field solvation model.⁶⁵ As shown in Figure 6, the minimum still appears.

Fig. 6.

Side-chain-rotamer PMF surface of Ac-Ala-NHMe obtained by including the solvation COSMO model⁶⁵ in AM1 calculations. The free-energy scale is shown in the small top panel.

It can be observed that the low-energy regions in the PMF plots obtained by direct MC simulation are wider and nearly flat, compared to those obtained by using the harmonic approximation, which show steeper variation of the PMF and are more featured. For example, for Ac-Ala-NHMe, the second minimum in the section of the PMF at θ = 90° (with α′ ≈ 105°, β′ ≈ −90°), which is clearly observed in the PMF obtained with the use of the harmonic approximation (Figure 4b), is very shallow in the PMF obtained by direct MC simulations (Figure 4a). This observation suggests that the harmonic approximation overestimates the increase of the PMF between grid points and, consequently, the ruggedness of the PMF surfaces.

Despite the overemphasized ruggedness of the harmonic-approximation PMF’s, they are quite well related by linear regression to those determined by using the Metropolis MC approach. When the PMF values within 20 kcal/mol above the global PMF minimum are taken into account, these regression lines are given by eq. (35) and eq. (36) for alanine and valine, respectively.

$$F_{X,\mathit{\text{Ala}}}^{\mathit{\text{MC}}}=0.281\times F_{X,\mathit{\text{Ala}}}^{\mathit{\text{harm}}}+1.924,{\sigma }_{\mathit{\text{PMF}}}=1.5\text{kcal}/\text{mol},R=0.6540$$ (35)

$$F_{X,\mathit{\text{Val}}}^{\mathit{\text{MC}}}=0.285\times F_{X,\mathit{\text{Val}}}^{\mathit{\text{harm}}}+0.178,{\sigma }_{\mathit{\text{PMF}}}=1.2\text{kcal}/\text{mol},R=0.7877$$ (36)

where $F_{X,\mathit{\text{Ala}}}^{\mathit{\text{MC}}}\text{and}{F}_{X,\mathit{\text{Val}}}^{\mathit{\text{MC}}}$ are the PMF’s of Ala and Val obtained with the Metropolis MC method, $F_{X,\mathit{\text{Ala}}}^{\mathit{\text{harm}}}\text{and}{F}_{X,\mathit{\text{Val}}}^{\mathit{\text{harm}}}$ are those obtained with the use of the harmonic approximation, σ_PMF is the standard deviation of $F_X^{\mathit{\text{MC}}}$, from the regression line, and R is the correlation coefficient. The corresponding plots are shown in Figure 7.

Fig. 7.

Scatter plots of the harmonic-approximation (abscissae) and MC-determined (ordinates) side-chain-rotamer PMF’s of Ac-Ala-NHMe (a) and Ac-Val-NHMe (b) with regression lines.

4 Conclusions

As a follow-up to our recent work on the determination of the potential of mean force corresponding to the C^α ⋯ C^α ⋯ C^α virtual-bond-angle bending in polypeptide chains,²⁷ we have proposed an approach to calculate the potentials of mean force corresponding to the energetics of the side-chain-rotamer states, U_rot, as well as virtual-bond deformation, U_bond, in the UNRES model of polypeptide chains. This approach is based on constructing non-adiabatic energy maps of terminally-blocked amino-acid residues on a grid in the angles λ⁽¹⁾ and λ⁽²⁾ for rotation of the peptide group about the C^α ⋯ C^α virtual bonds (where energy is minimized in all variables except those forming the grid), and then integrating over the space of all variables except those defining the local geometry of a side chain and the adjacent C^α ⋯ C^α ⋯ C^α frame (θ, α′, and β′) or the length of a C^α ⋯SC virtual bond (b_SC) by using the energy calculated at grid points and the harmonic approximation outside the grid points. The approach requires local energy minimization for several hundreds to several tens of thousands conformations, depending on the kind of amino-acid residue (compared to tens of millions energy evaluations when using Monte Carlo methods to determine the PMF), which enables us to use the methods of molecular quantum mechanics to compute the energy. Comparison of the PMF’s calculated with this approach and those obtained with the use of a direct approach based on canonical Monte-Carlo sampling has shown that use of the harmonic approximation results in too-steep an increase of the PMF outside the regions of minima and, thereby, too-rugged PMF landscapes with more minima or more pronounced minima than for the PMF surfaces in the MC-determined PMF’s. This suggests that fitting the PMF’s with an analytical expression should not be aimed at reproducing all fine details of the PMF surfaces but, instead, should be directed at smoothing them. Nevertheless, the PMF values determined by using the harmonic approximation and by using canonical MC are related by linear regression with a slope of about 0.3, which is not a problem because every UNRES energy term is multiplied by a weight factor [eq. (1)], which is determined only by optimization of the complete force field.^{23, 26, 28} Because the MC approach is an option to determine the PMF with the use of QM methods only for small amino-acid residues such as alanine and valine, while it is prohibitively expensive for larger amino-acid residues, we consequently use the harmonic-approximation-based method to determine U_rot and U_bond for all 19 side chains in the accompanying paper.