Abstract
Objective:
This study examined the influence of on-premise alcohol-outlet densities and of drinking-driver densities on rates of alcohol-related motor vehicle crashes. A traffic-flow model is developed to represent geographic relationships between residential locations of drinking drivers, alcohol outlets, and alcohol-related motor vehicle crashes.
Method:
Cross-sectional and time-series cross-sectional spatial analyses were performed using data collected from 144 geographic units over 4 years. Data were obtained from archival and survey sources in six communities. Archival data were obtained within community areas and measured activities of either the resident population or persons visiting these communities. These data included local and highway traffic flow, locations of alcohol outlets, population density, network density of the local roadway system, and single-vehicle nighttime (SVN) crashes. Telephone-survey data obtained from residents of the communities were used to estimate the size of the resident drinking and driving population.
Results:
Cross-sectional analyses showed that effects relating on-premise densities to alcohol-related crashes were moderated by highway traffic flow. Depending on levels of highway traffic flow, 10% greater densities were related to 0% to 150% greater rates of SVN crashes. Time-series cross-sectional analyses showed that changes in the population pool of drinking drivers and on-premise densities interacted to increase SVN crash rates.
Conclusions:
A simple traffic-flow model can assess the effects of on-premise alcohol-outlet densities and of drinking-driver densities as they vary across communities to produce alcohol-related crashes. Analyses based on these models can usefully guide policy decisions on the siting of on-premise alcohol outlets.
Studies of the relationship between alcohol outlets and alcohol-related crashes have shown that greater numbers of alcohol outlets are related to higher motor vehicle crash rates across large geographic units such as provinces and cities (e.g., Rush et al., 1986; Watts and Rabow, 1983); within states over time (e.g., Escobedo and Ortiz, 2002; Holder and Blose, 1987); and within smaller geographic units, such as smaller cities within a dense urban region (e.g., Los Angeles; Scribner et al., 1994). Although studies have shown that at the neighborhood level outlet densities are related to crashes independently of local patterns of alcohol use (e.g., Van Oers and Garretsen, 1993), studies also have shown that greater travel distance between outlets is unrelated to greater crash (Gruenewald and Ponicki, 1995; Jewell and Brown, 1995) and arrest rates (Lapham et al., 1998). Finally, these studies have shown in addition that the geographic patterning of alcohol outlets and alcohol-related crash and arrest rates are related, with neighborhoods with greater outlet densities having more crashes and adjacent areas (even those with no alcohol outlets) also experiencing higher crash rates (Gruenewald et al., 1996; Lapham et al., 1998).
Regarding drinking and driving, which must precede drinking and crashing, Colon and Cutter (1983) and Smart and Docerty (1976) found that increased outlet densities were associated with lower drinking and driving rates. Gruenewald et al. (2002), however, found that both driving after drinking and driving while intoxicated were related to venue preference (e.g., restaurants over bars) and that the strongest influence on both driving after drinking and driving while intoxicated was preferred drinking location, considered together with (i.e., interacted with) drinking patterns, particularly drinking frequency. All of these ecological studies have been cross-sectional, but a recent panel study done at the ZIP-code level (Treno et al., 2006) showed that greater alcohol-outlet densities were related to higher alcohol-related crash rates over a 6-year time frame just as in the cross-sectional studies.
As this brief review suggests, more recent studies have focused on smaller geographic areas—for example, neighborhoods rather than entire states—and more specific issues. Because the concentration of outlets plays a central role in the production of alcohol-related traffic crashes, residential areas that have the largest numbers of drinking drivers do not necessarily exhibit greater rates of alcohol-related crashes (Gruenewald et al., 1996). It is residential areas with greater numbers of alcohol outlets (or neighborhood areas adjacent to them) that exhibit higher rates of alcohol-related crashes (Gruenewald et al., 1996). These are often poor minority areas with communities housing residents who are less likely to drink and drive (Gruenewald et al., 2000). Thus, members of low-income minority neighborhoods are more likely to experience crashes related to drinking and driving even though they are less likely to be the party that produces them.
Community systems and community geography
A number of community systems and associated subsystems influence drinking and driving behavior. Subsystems affecting drinking and driving are (a) vehicular traffic, (b) alcohol availability, (c) alcohol consumption, (d) formal controls, (e) informal controls, (f) social and economic consequences, and (g) mortality and morbidity (Holder, 1998; Holder et al., 2005). The above observation that minority communities bear an undeserved and disproportionate share of the ill consequences of drinking and driving suggests that the community systems that support drinking, driving, and crashing are not uniform across the geography of neighborhoods.
Studies of the relationships between alcohol availability, use, and problems are just beginning to address the spatial relationships between these components of community systems. Since the mid-1990s, researchers have begun to apply geographic-information-system technologies to map the geographic distribution of drinking patterns and problems in community settings (Wieczorek and Hansen, 1997; Wieczorek and Coyle, 1996). Their work provides the essential basis for the current change in perspective with regard to understanding community-based alcohol problems. It also serves as the foundation on which geostatistical systems foster analyses of geographic data. Coupled with spatial-analysis methods (Ponicki and Gruenewald, 2005), the combination of spatial data and analysis provides a firm statistical basis for insights into the local ecology of alcohol problems (e.g., alcohol-related pedestrian injuries; LaScala et al., 2000, 2001, 2004) and the targeted delivery of preventive health services (Wieczorek and Hansen, 1997). Coupled with models of the spatial dynamics of community systems, these technologies may more clearly reveal the community-based nature of many alcohol problems, providing needed opportunities for the development of well-informed local alcohol policies and planning. One goal of this article is to show one way in which these developments can take place.
Traffic flow and the geography of traffic crashes
To produce a mathematical model that is suitable for planning purposes and that takes into account related issues of traffic flow, it is necessary to address the contingent nature of drinking, driving, and crashing. The approach taken in this study was to view motor vehicle crashes in general, and alcohol-related crashes in particular, as functions of traffic flow. In the absence of traffic, crashes do not occur. In the presence of traffic, it is expected that crashes occur at some rate, r, a rate proportional to traffic flow itself. If 1,800 cars per day flow along a roadway and r = .0005, then an average of about one crash per day is expected. The value of r, of course, is not constant but varies according to other conditions of the driving environment and the drivers themselves. Thus, greater numbers of alcohol outlets are expected to increase the value of r by contributing to the flow of impaired drivers on the roadway system. Larger pools of resident drinking drivers are expected to increase the value of r by contributing to the flow of consumers through alcohol outlets.
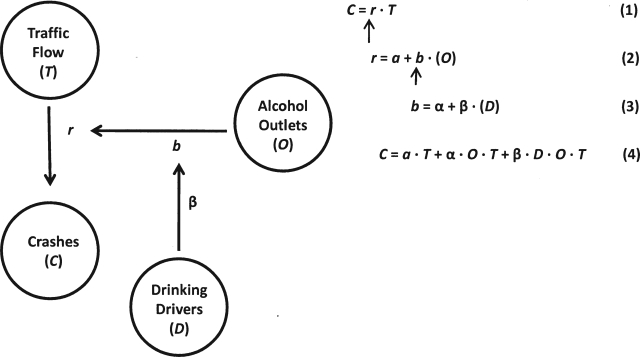
With these points in mind, Figure 1 shows in graphic form the theoretical representation of the relationships sequences of drinking drivers, alcohol outlets, and traffic crashes (left), together with its associated mathematical model (right). The model is based on a formulation of the relationships between drinking drivers, alcohol outlets, and traffic crashes in terms of discrete flow theory (Roberts, 1976), informed by the results of the analyses presented below. The approach provides an explicit representation of system relationships and clear statements of system components in terms of priority of action. Applied here, the graphic representation shows that (a) the effects of drinking drivers and alcohol outlets are contingent on the presence of traffic flow and (b) the effects of drinking drivers are contingent on traffic flow and the availability of outlets in which to consume alcohol. (This simplification overlooks drinking and driving related to consumption in other drinking venues, a number of which were tested as noted below.)
Figure 1.
Digraph (left) and algebraic representations (right) of relationships of alcohol outlets to traffic crashes
The equations to the right of the figure express the relationship of crashes, C, to traffic flow, T (Equation 1), the absence of a constant term recognizing that no crashes will occur in the absence of traffic flow; the relationship of outlets, O, to the production of crashes from traffic flow, r (Equation 2); and the relationship of drinking drivers, D, to the production of drunken driving from alcohol outlets, b (Equation 3). This multilevel model is summarized in reduced form in Equation 4. Note that Equation 4 predicts that crashes will result from traffic flow independent of outlets (coefficient a > 0). Equation 4 also states that outlets are expected to affect the production of crashes from traffic flow independent of the size of the local pool of drinking drivers (coefficient α > 0) but that larger pools of drinking drivers are expected to place upward pressure on the production of drinking drivers from outlets (coefficient β > 0).
All effects in the final model (Equation 4) are contingent on the main effect, traffic flow, T. The double and triple interactions for outlets and the drinking-driving population indicate that, in units with a given level of traffic flow, the likelihood of alcohol-related crashes is greater within geographic units with greater outlet densities and larger populations of drinking drivers and lower in units with lower outlet densities and smaller populations of drinking drivers.
The following analyses include “lagged effects,” to assess the extent to which crash rates in given neighborhood areas (termed local units) are affected by alcohol outlets and drinking drivers in adjacent geographic units (termed lagged units). This finding is particularly likely when events in small units such as those in this study are analyzed (Chou, 1991) and when processes such as drunk driving that have a strong spatial component are examined (Gruenewald et al., 1996).
Beginning with the conceptual model shown in Figure 1, the current study used cross-sectional and time-series spatial-panel analysis methods to relate traffic flow, alcohol availability, the size of the drinking-driving population, and features of the driving environment to rates of alcohol-involved crashes. Rather than testing particular hypotheses regarding potential linear statistical relationships between these measures, the analyses presented here tested an overall model of these relationships; a means of conceptualizing as a whole some aspects of community systems related to drinking and driving and alcohol-related crashes. In doing so, the current study used data from individual and archival sources aggregated at the level of geographic units within multiple communities over a 4-year time span.
Method
Data were obtained as part of the Community Trials Project evaluation (Holder et al., 1995). This evaluation implemented a series of environmental preventive interventions intended to reduce alcohol-related traffic and nontraffic injuries and deaths in three experimental communities. The Community Trials Project tested the efficacy of these interventions against data obtained from three matched comparison communities (documented in Holder et al., 2000). Archival and telephone-survey data from all six sites, four in California and two in South Carolina, were used from 4 of the 5 years in which data were collected, April 1992 through March 1996. The data were “geocoded” into neighborhood areas specifically designed to reflect the population distribution within each site (see Gruenewald et al., 1996). The archival data measured rates of alcohol-related traffic crashes, densities of retail alcohol outlets, rates of local and highway traffic flow, road-network densities, and local population. The telephone-survey data were from residents age 18 or older. For purposes of the current article, only one measure from this source was of interest: the estimated size of the local drinking-and-driving population.
The outcome variable for these analyses was single-vehicle nighttime (SVN) crashes, accidents involving one motor vehicle occurring between 8:00 pm and 4:00 am. Although not all such crashes are alcohol related, the rate of alcohol involvement in these crashes is sufficiently high that SVN crashes are used as a valid surrogate for all crashes that result from drinking and driving (Heeren et al., 1985; Mounce et al., 1988; Richman, 1985). The time, date, and cross-street location of each crash was obtained in California from the State Wide Integrated Traffic Reporting System and in South Carolina from the Department of Public Safety. Using a geographic information system (MapInfo, 1998), each of the 4,912 SVN crashes that occurred during the 4-year study period was located, or “geocoded,” onto an electronic map, with a 98% “hit rate,” placing each crash within a neighborhood area used as a unit of analysis (see below). Annual rates of SVN crashes were expressed in terms of kilometers of local and highway roadway length.
The addresses of all licensed active retail alcohol outlets were obtained from the California State Department of Beverage Control and the South Carolina Department of Revenue. Outlets were categorized as on-premise (bars, restaurants) and off-premise (supermarkets, convenience stores, liquor stores) establishments and were geocoded onto the same electronic maps as the SVN crashes, with a hit rate of 90%. The outlets were aggregated into the geographic units used for analysis and scaled like the SVN crashes, by kilometers of local and roadway length.
Traffic-flow data from the four California communities were obtained from summaries of measured traffic flow by street segments collected for the 5 years before and including 1992. They were averaged within geographic units to summarize cross-sectional differences in these measures (further discussed in Gruenewald et al., 1996). Highway traffic flow and local traffic flow were measured separately and represent the average number of vehicles per day passing along selected roadway segments. Traffic-flow data were unavailable for the two South Carolina communities. Estimates were made based on a set of environmental (road-network density, miles of local and highway roadway) and sociodemographic (residential population density, age distribution, and income) characteristics. Separate spatial regression models were used to estimate local and highway traffic-flow rates for areas of communities in California (accounting for R2 = .83 and R2 = .61, respectively). Coefficients from these models were used to estimate local and highway traffic flow across all areas of all six communities. These latter estimates were used in the analyses presented here.
The number of intersections (cross streets) and the total roadway length for each geographic unit was obtained from TIGER file (Topographically Integrated, Geographically Encoded Reference files) maps, electronic maps that can be uploaded into geographic-information-system software such as MapInfo (1998). Road-network density was defined as the number of intersections within a geographic unit divided by the total roadway length within the unit. Road-network density is an important component of the driving environment, because, as it increases, the complexity of the driving task (and therefore the likelihood of crashing) should also increase.
For this population-based model, the growth in the population of each geographic unit over the 4 years studied was estimated from 1990 Census Bureau figures, census growth estimates for the years 1990 through 1997, and geographic distributions of random-digit-dial household respondents over the years of the general population survey study (see below). Using 1990 census data as the base, census growth estimates were used to establish the average rate of population increase over the time of the study for each community. Relative distributions of household-survey respondents (weighted by enumerated household size) were used to distribute estimated population values by geographic areas. Population density within geographic units was then calculated by dividing the estimated population in each geographic unit by total kilometers of roadway within the unit.
As in earlier work (Gruenewald et al., 1996), roadway length was chosen to scale outlet density rather than population or units of geographic area, because drinkers access alcohol outlets by means of roads, and roadway length gives more sensible density measures. For example, urban areas of high population density with a large number of outlets might have low outlet density based on population but high outlet density based on roadway length. Similarly, an urban area that includes a body of water near a street with many outlets would have low outlet density based on geographic units but high outlet density based on roadway length. For these reasons, all density measures in the study were scaled by roadway miles.
The telephone survey from which the information was obtained to determine the size of local drinking-driver populations was conducted throughout the year to avoid seasonal biases (Lemmens and Knibbe, 1993). Households, defined as single-family dwellings (houses or apartments) in which one or more adults lived as their primary residence, were contacted on a random-digit-dial basis, all adult household members age 18 or older were enumerated, and respondents were selected randomly for the interview. The response rate was 65% and the completion rate 80%. Respondents were considered drinking drivers if they answered “yes” to an item asking whether, during the 5 months preceding the interview, they had driven within 4 hours of consuming one or more alcoholic drinks. Respondents also were asked the major cross streets nearest their residences to enable geo-coding, for which there was a 78.5% hit rate. Drinking-driver density was estimated by multiplying the population of each geographic unit by the proportion of survey respondents who reported driving after drinking and dividing the result by the total kilometers of roadway in the geographic unit.
Geographic units
One hundred forty-four geographic units were defined as the areal bases for the study. These units were constructed to (a) provide a reasonable number of survey observations per area, (b) follow population gradients across community areas (small in densely populated areas and large in sparsely populated areas), (c) cut across political and geographical boundaries (e.g., census blocks and main road arterials), and (d) permit accurate geocoding of the variables in the study. Other existing units, such as census tracts and blocks, were not used because, for a number of reasons, they are problematic. A complete discussion of these issues and unit definitions can be found in Gruenewald et al. (1996, 2000).
Modeling spatial relationships
Within each community, all of the geographic units were contiguous with at least one other unit. Events occurring in areas arrayed contiguously in space are unlikely to be independent, and errors of estimate when statistically modeling these events are likely to be correlated (spatial autocorrelation). Generalized least-squares estimators provide unbiased estimates of effects when spatial autocorrelation is present and provide diagnostics for correlated measurement error (Cliff and Ord, 1981; Griffith, 1988). These procedures have been applied to cross-sectional and time-series cross-sectional spatial-panel data in previous studies (Gruenewald et al., 1996, 2000) and will not be discussed further here. It should be noted, however, that the same procedures that permit diagnosis of spatial autocorrelation also permit tests of spatially lagged regressors on endogenous measures (e.g., the effects of independent variables measured in lagged geographic units on dependent variables in local units). Procedures for the construction and testing of spatial lags have been implemented in spatial-analysis systems (Ponicki and Gruenewald, 2005) and were applied in the current study (see also Gruenewald et al., 1996).
Two sets of cross-sectional models and one set of time-series models were finally selected for presentation below following a number of diagnostic runs to test different model specifications. In both sets of cross-sectional models, measures of traffic flow, road-network complexity, alcohol availability, drinking-driver populations, and spatial lagged effects of outlets and drinking-driving populations were stepped in, increasing model complexity at each step and enabling assessment of variants of the model shown in Figure 1. The first set of cross-sectional analyses began by modeling the simple effects of traffic flow on crash rates (estimating r for highway and local traffic flow separately). To this model were added, successively, measures of road-network complexity (expected to put upward pressure on r), measures of outlet density (expected to put upward pressure on r), and drinking-driver densities (expected to put upward pressure on b). This procedure provided the simplest test of the model presented in Figure 1. First-order spatial lagged effects for outlet densities and available pools of drinking drivers were added to the final model. The constant term was excluded from the first set of analyses under the assumptions that both local traffic flow and highway traffic flow were measured without error and that crashes would go to zero under conditions of no traffic flow.
The second set of cross-sectional analyses was more comprehensive than the first set and included a constant term and additional main effects. The essential mathematical form of this model was derived from the assumption that highway and local traffic-flow measures were each biased downward. The consequence of this assumption is to require the addition of a nonzero constant and main-effects terms to the model. These analyses also include tests of main-effects terms for cross-street density and lagged on-premise outlet density that would be included in a full multilevel model of these effects (Johnson et al., 1998).
The time-series spatial-panel analyses make somewhat different, and simplifying, assumptions. First, they assume that every unit has its own unique level of effect on the outcome (a unique effect term is included for each of the 144 geographic units under study, a least-squares dummy variable model; Hsiao, 1986). Under the assumption of unit independence, this approach guarantees an unbiased estimate of the unique effects of independent on dependent measures. Second, because no data were available regarding changes in traffic-flow rates over time, these analyses assumed that local and highway traffic flow are constants and are absorbed into these unit effects. Third, the unit independence assumption was further diagnosed and controlled using generalized least squares corrections for spatial and Cochrane-Orcutt corrections for temporal autocorrelation (Greene, 1993; Ponicki and Gruenewald, 2005).
Results
Table 1 presents descriptive statistics for the measures used in the cross-sectional analyses based on data from the 144 geographic units averaged across the 4 survey years. SVN crash density was multiplied by 100 to simplify reporting of coefficient estimates. Although minimums of zero do appear in the table, these observations were infrequent, and the range of variation of dependent and independent measures was sufficient to avoid problems related to censoring. The distribution of SVN crash rates was approximately normal, with conditional normality of this dependent measure assured by tests conducted in the context of each analysis model (reported below). It should be noted that the average roadway length across the geographic units was 50.542 kilometers. Thus, the range of variation in the measures reported in Table 1, when considered in terms of counts rather than densities, was considerable. For example, the estimated numbers of drinking drivers within geographic units varied from 25 to 14,690, a nearly 588-fold difference.
Table 1.
Descriptive statistics
| Variable | Dimension | Min. | Max. | M | (SD) |
| SVN crash density | Crashes per kilometer of roadway (×100) | 0.000 | 46.296 | 17.293 | 9.169 |
| Local flow | Motor vehicles per day | 0.205 | 4.347 | 2.523 | 0.752 |
| Highway flow | Motor vehicles per day | 0.000 | 1,946.541 | 87.922 | 232.984 |
| On-premise outlet density | Outlets per kilometer of roadway | 0.000 | 2.467 | 0.258 | 0.348 |
| Drinking-driver density | Drinking drivers per kilometer of roadway | 0.487 | 291.164 | 30.777 | 37.661 |
| Road-network density | Intersections per kilometer of roadway | 0.705 | 6.647 | 3.365 | 1.419 |
| Total roadway length | Combined local and highway kilometers | 3.851 | 269.748 | 50.542 | 52.472 |
Notes: Min. = minimum; max. = maximum; SVN = single-vehicle nighttime.
Table 2 shows the results for the first series of cross-sectional analyses conducted on these data, presenting b coefficients with associated asymptotic t statistics; rho; a measure of spatial autocorrelation among model residuals, its t value; and fit statistics with p values for successive models. The first numerical column of the table shows the results of regressing SVN crash densities over measures of local and highway traffic flow (as stated above, the constant is fixed at zero for all these models). Absent all other independent measures, both local traffic flow and highway traffic flow were significantly related to crash rates, and spatial autocorrelation among the residuals was strong and positive (ρs = .5032; 25.3% of the variance in the residuals accounted for by correlation among adjacent disturbance terms). The addition of interaction terms representing the effects of road network density on the production of crashes from traffic flow significantly improved model fit (G2 statistic near bottom of table). Greater road-network density reduced crash rates related to local flow but increased crash rates related to highway flow. Crashes were more likely to happen in areas with greater road-network density and highway flow.
Table 2.
Cross-sectional traffic-flow model (no constant; bs appear above, asymptotic ts below)
| Variable | Model I | Model II | Model III | Model IV | Model V |
| Constant | — | — | — | — | — |
| Local flow | 6.0187 | 9.1644 | 9.2127 | 9.3176 | 9.2671 |
| 12.0699*** | 9.5178*** | 9.6617*** | 9.6271*** | 8.9748*** | |
| Highway flow | 0.0080 | −0.0189 | −0.0362 | −0.0363 | −0.0536 |
| 2.2561* | −2.4824** | −4.0848*** | −3.4584*** | −3.8666*** | |
| Road-Network Densitya × Local Flow | −1.0802 | −1.1121 | −1.1704 | −0.6084 | |
| −4.2821*** | −4.5789*** | −4.5844*** | −2.2579** | ||
| Road-Network Density × Highway Flow | 0.0248 | 0.0214 | 0.0214 | −0.0009 | |
| 3.8215*** | 3.3906*** | 3.3676*** | −0.1103 | ||
| On-Premise Outlet Density × Local Flow | −1.4960 | −0.8863 | −3.0179 | ||
| −1.7591* | −0.5312 | −1.3589 | |||
| On-Premise Outlet Density × Highway Flow | 0.2009 | 0.2014 | 0.2190 | ||
| 3.5115** | 2.4895** | 2.1278* | |||
| Drinking-Driver Density × On-Premise Outlet Density × Local Flow | −0.0019 | 0.0010 | |||
| −0.2680 | 0.1053 | ||||
| Drinking-Driver Density × On-Premise Outlet Density × Highway Flow | −0.0002 | −0.0007 | |||
| −0.4304 | −0.9457 | ||||
| Lagged Drinking-Driver Density × On-Premise Outlet Density × Local Flow | 0.0164 | ||||
| 0.2346 | |||||
| Lagged Drinking-Driver Density × On-Premise Outlet Density × Highway Flow | 0.0037 | ||||
| 0.7693 | |||||
| Lagged On-Premise Outlet Density × Local Flow | −6.7389 | ||||
| −3.1891*** | |||||
| Lagged On-Premise Outlet Density × Highway Flow | 0.2868 | ||||
| 3.7572*** | |||||
| Spatial autocorrelation | |||||
| ρs | .5032 | .4019 | .4043 | .4027 | .5318 |
| t | 5.5275*** | 3.9253*** | 3.9295*** | 3.3783*** | 5.8449*** |
| Model test | |||||
| ΔG2 | 21.9468 | 13.2840 | .7215 | 21.3610 | |
| p | <.001** | .0013** | .6972 | .0003*** | |
All densities are for local geographic units unless specified otherwise.
p < .05, one tailed;
p < .01, one tailed;
p < .001, one tailed.
The third model introduces on-premise outlet densities, again accounting for a significant improvement in model fit. Greater on-premise densities further reduced the production of crashes from local flow and further increased the production of crashes from highway flow. Crashes were more likely to happen in areas with greater on-premise density and highway flow. As noted above, diagnostic runs for these models were performed but, in the interest of brevity, are not presented here; this is also true of the models presented in Tables 3 and 4.
Table 3.
Cross-sectional traffic-flow model (with constants and main effects; bs appear above, asymptotic ts below)
| Variable | Model I | Model II | Model III | Model IV | Model V |
| Constant | 10.9366 | 9.0257 | 10.6103 | 12.0071 | 4.8590 |
| 3.8798*** | 1.7499* | 2.1774** | 2.3904** | 0.8796 | |
| Local flow | 2.7701 | 6.1156 | 5.4198 | 5.1555 | 7.5519 |
| 2.6865** | 2.9652** | 2.7513** | 2.5582** | 3.4410*** | |
| Highway flow | 0.0008 | −0.0220 | −0.0318 | −0.0387 | −0.0554 |
| 0.2277 | −2.7695** | −3.3002*** | −3.2499*** | −3.7125*** | |
| Road-network densitya | −0.2176 | −1.6134 | −2.5161 | −0.9075 | |
| −0.1142 | −0.8213 | −1.1688 | −0.3877 | ||
| Road-Network Density × Local Flow | −0.8813 | −0.4691 | −0.2182 | −0.4693 | |
| −1.2506 | −0.6544 | −0.2727 | −0.5632 | ||
| Road-Network Density × Highway Flow | 0.0207 | 0.0171 | 0.0174 | 0.0019 | |
| 2.9758** | 2.5766** | 2.5732** | 0.2285 | ||
| On-premise outlet density | 26.1311 | 33.6790 | 35.4976 | ||
| 2.0039* | 1.4231 | 1.1493 | |||
| On-Premise Outlet Density × Local Flow | −8.2619 | −11.1505 | −13.3290 | ||
| −2.2941* | −1.5502 | −1.3256 | |||
| On-Premise Outlet Density × Highway Flow | 0.1241 | 0.1829 | 0.2134 | ||
| 1.7869* | 1.9942* | 1.9911* | |||
| Drinking-Driver Density × On-Premise Outlet Density | 0.0323 | 0.4440 | |||
| 0.0777 | 0.8691 | ||||
| Drinking-Driver Density × On-Premise Outlet Density × Local Flow | −0.0021 | −0.1194 | |||
| −0.0186 | −0.8840 | ||||
| Drinking-Driver Density × On-Premise Outlet Density × Highway Flow | −0.0010 | −0.0028 | |||
| −0.5737 | −1.1275 | ||||
| Lagged on-premise outlet density | 15.5132 | ||||
| 0.7617 | |||||
| Lagged Drinking-Driver Density × On-Premise Outlet Density | −1.0669 | ||||
| −1.2749 | |||||
| Lagged On-Premise Outlet Density × Local Flow | −9.6066 | ||||
| −1.3176 | |||||
| Lagged On-Premise Outlet Density × Highway Flow | 0.2389 | ||||
| 2.7030** | |||||
| Lagged Drinking Driver Density × On-Premise Outlet Density × Local Flow | 0.3580 | ||||
| 1.2224 | |||||
| Lagged Drinking Driver Density × On-Premise Outlet Density × Highway Flow | 0.0042 | ||||
| 0.7040 | |||||
| Spatial autocorrelation | |||||
| ρs | .1223 | .0445 | .0359 | −.0071 | .0758 |
| t | .9699 | .3377 | .2683 | −.0520 | .5556 |
| Model test | |||||
| ΔG2 | 17.6503 | 20.7591 | 3.0901 | 15.6540 | |
| p | .0005*** | .0001*** | .3779 | .0157* | |
All densities are for local geographic units unless specified otherwise.
p < .05, one tailed;
p < .01, one tailed;
p < .001, one tailed.
Table 4.
Time-series cross-sectional traffic-flow model
| Variable | Model I | Model II | Model III |
| On-premise outlet density | 13.0136 | 7.8177 | −17.3806 |
| 1.6363 | 0.9712 | −1.6277 | |
| Drinking-Driver Density × On-Premise Outlet Density | 0.0906 | 0.1187 | |
| 2.8476** | 3.6990*** | ||
| Lagged on-premise outlet density | −21.7577 | ||
| −1.3703 | |||
| Lagged Drinking-Driver Density × On-Premise Outlet Density | 0.6082 | ||
| 3.9292*** | |||
| Spatial autocorrelation | |||
| ρs | .1102 | .0787 | .0611 |
| t | 1.5422 | 1.0845 | .8336 |
| Temporal autocorrelation | |||
| ρt | −.2439 | −.2324 | −.2174 |
| z | −5.0696*** | −4.8306*** | −4.5186*** |
| Model test | |||
| ΔG2 | 10.5935 | 23.3614 | |
| p | .0011** | .0000*** | |
p < .01, one tailed;
p < .001, one tailed.
Introducing the effects of local drinking-driver populations on local crash rates in Model IV failed to improve model fit. However, in the final model, the addition of spatial lag terms for on-premise outlets significantly improved model fit. The coefficients estimated in this model showed that greater outlet densities in adjacent (not local) areas placed further downward pressure on the production of crashes from local flow and upward pressure on the production of crashes from highway flow. In no models were there significant effects related to the size of drinking-driver populations local or lagged. Importantly, significant lagged effects were obtained in a model (Model V) in which overall greater levels of local flow were related to greater crash rates, overall greater levels of highway flow were related to lesser crash rates, greater road-network densities were related to lowered production of crashes from local flow, and greater on-premise outlet densities were related to greater production of crashes from highway flow.
Table 3 presents the results obtained when a free constant and additional main effect and interaction terms are introduced into the basic models of Table 2. There was a dramatic reduction in the level of spatial autocorrelation across all models, suggesting that much correlated error was the result of model misspecification. There remains, however, considerable agreement between the models presented in the two tables. Overall, local traffic flow continues to be related to greater crash rates and highway traffic flow to lower crash rates. Road-network density continues to be related to greater production of crashes from highway traffic flow. On-premise outlet densities similarly continue to be related to greater production of crashes from highway traffic flow, as do lagged on-premise outlet densities. The similarities between Tables 2 and 3 are striking, as is the finding that drinking-driver population densities, both local and lagged, appear unrelated to crash rates in community areas.
Table 4 displays the results for the time-series analyses of data from the 144 geographic units over 4 years. A single constant term is absent, replaced in the estimation procedure by unit effects, providing a constant term for each geographic unit. Both spatial and temporal autocorrelation can arise in time-series cross-sectional spatial panels. Here, spatial autocorrelation was nonsignificant, but temporal autocorrelation was significant in all three models. With suitable controls for these effects included in the analyses, on-premise outlet density was marginally nonsignificant in the first, simplest model predicting SVN crash rates. The addition of the interaction term for drinking-driver and outlet densities was significant in Model II. Growth and decline in the available pool of drinking drivers was related to greater and lesser effects of outlet densities on crash rates. Examining the spatially lagged effects of both outlet density and drinking-driver density in the final model, significant improvement in the prediction of SVN crashes was again obtained. In this case, greater pools of drinking drivers in lagged areas jointly contributed to rates of crashes related to density of outlets in local areas.
Additional models also were tested to determine whether two other outlet densities—off-premise outlets (from archival data) and residential outlets (from survey data)—were related to SVN crashes. Survey data were used to obtain measures of population densities for drinkers who prefer to drink at home and drinkers who prefer to drink at friends' and relatives' homes. Spatial lags for the two additional outlet densities and the two population densities also were created. The models tested using these additional outlet and population density measures, both local and lagged, indicated that they were unrelated to SVN crashes.
Discussion
What do the results of these complex models reveal about the relationships between alcohol outlets and alcohol-related crashes? And what do they contribute toward an understanding of the community systems underlying drinking and driving? To provide answers to these two questions, it is perhaps best to stand back from the analyses and view them from the perspective of the systems being analyzed. As suggested in the introduction, community systems that underlie drinking and driving include, among other factors, relationships between traffic-flow patterns, alcohol outlets, and the use of these outlets by drinking drivers. Models that are used to analyze these data are mathematical representations of the theoretical relationships between these measures and may be less (e.g., linear statistical models) or more (e.g., discrete flow models) appropriate to the task of analyzing data from these systems. Presumably, more appropriate models will produce more appropriate, and more informative, answers to the questions we pose about the performance and behavior of the systems under study.
In the case of the first question posed about these results, there are three central issues these analyses illustrate about the relationships between outlets and crashes. First, the relationships between outlets and crashes are fully mediated by traffic flow; outlets act through traffic flow to produce crashes (Tables 2 and 3). Second, alcohol outlets and, specifically, highway traffic flow interact to affect rates of traffic crashes (Tables 2 and 3). Third, growth in available pools of drinking drivers place upward pressure on these interactive relationships, further accelerating the effects of outlets on crash rates (Table 4). Thus, the results of the current analyses suggest that the effects of alcohol outlets on crashes are highly context dependent, linked to local patterns of traffic flow, sources of drinking drivers, and the geographic patterning of neighborhood characteristics (spatial lag effects) in community settings.
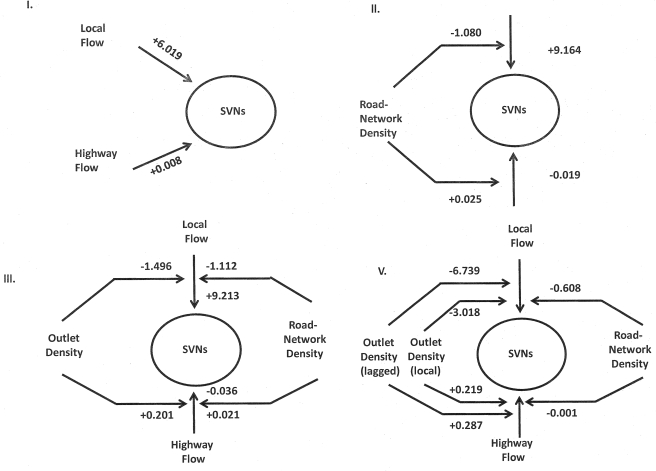
The digraphs presented in Figure 2 outline the effects observed in the current study. Considering only the primary effects of significance from the analyses presented in Table 2, a sequence of drawings display, first, the direct effects of greater local and highway traffic flow on rates of SVN crashes (Model I, Table 2). Measured in comparable metrics (Table 1), crash rates are much more substantively related to local (b = +6.019) than to highway (b = +0.008) flow. The second model derived from the table (Model II, Table 2) shows how the measure of road-network density moderates the effects of local and highway flow. Greater road-network density is related to lesser production of crashes from local traffic flow (b = −1.080), but greater road-network density is related to greater production of crashes from highway traffic flow (b = +0.025). Road-network density moderates the production of crashes from local and highway traffic flows, altering the crash rate related to each traffic source.
Figure 2.
Digraph representations of single-vehicle nighttime (SVN) crashes
The third model presented in Figure 2 (Model III, Table 2) presents a further elaboration of the previous model with the inclusion of on-premise alcohol outlets as additional moderating factors in the production of SVN crashes from local and highway traffic flow. Here greater on-premise outlet densities are shown related to lesser effects of local flow on crashes (b = −1.496) and greater effects of highway flow on crashes (b = +0.201). Finally, the fifth model (Model V, Table 2) presents an elaboration of the previous models that includes the effects of spatially lagged on-premise densities as further moderators of traffic-flow effects. Greater lagged on-premise densities are shown to be related to lesser effects of local flow on crashes (b = −6.739) and greater effects of highway flow on crashes (b = +0.287). The key point, made clear in these figures, is that the effects of an ecological measure such as outlet densities alter the nature of the relationships between both local and highway traffic flow and crashes, either aggravating or mitigating the degree to which crashes are produced from these sources. Importantly, as the study shows, these moderating effects are not restricted to local areas but spread across adjacent (lagged) areas of communities, providing additional information about the ecological contexts of crash rates.
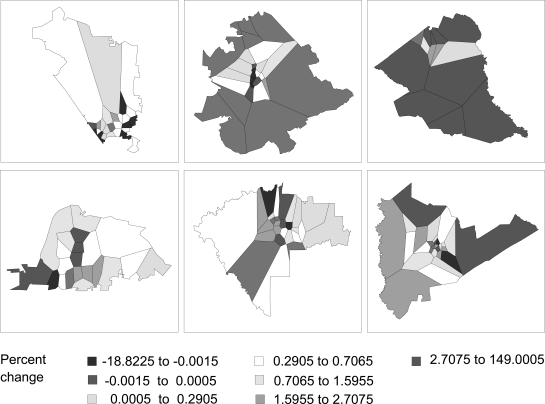
Regarding the second question, the results contribute both to the way the generation of alcohol-related crashes from alcohol outlets in community settings is viewed and, more importantly, the way policy regarding the local distribution of alcohol is viewed. To see how this is the case, consider Figure 3, which graphically displays the expected relationships between a 10% increase in on-premise outlet densities and the corresponding percentage increases in rates of SVN crashes for each of the 144 areas under study (based on Table 2, Model V). Taking into account the local cross-sectional features of each of the 144 areas, the impact of a 10% increase in outlet densities can be either negligibly or substantially related to increases in SVN crash rates, ranging from −19% to 149%. These different outcomes for these different geographic areas of the communities suggest that overall measures of the impact of on-premise outlet densities on crash rates mask substantial local variation. Thus, in the current study across all areas, a 10% increase in on-premise outlet densities is related to a modest overall 2.4% increase in SVN crashes. However, in dense downtown areas with great amounts of local traffic flow or rural areas with little highway traffic, the impact of more on-premise outlets on crash rates appears negligible (or slightly negative). In both downtown and rural areas threaded with highway traffic, the impact of more on-premise outlets on crash rates is dramatic. The figure shows these areas as dark gray units.
Figure 3.
Percentage change in single-vehicle nighttime crashes with a 10% increase in on-premise outlet density
Clearly, the impact of alcohol outlets on harmful outcomes such as alcohol-related crashes is highly context dependent. It was expected that there would be an overall increase in alcohol-involved crashes related to overall increases in outlet densities. Any particular outlet location may or may not contribute to such increases, but it is certainly unlikely that the location of any single on-premise outlet will substantially contribute to overall increases in SVN crash rates. This supposition suggests that it may be possible to locate alcohol outlets in community settings that are, more or less, related to harmful outcomes. Planning and zoning departments may use this information to develop plans that restrict locations of outlets to ‘safe’ environments, and public planners may begin to consider the possibility of rationally planning locations of outlets in community settings.
Limitations
There are two reasons the present study calls for additional research. First, the study has numerous limitations that prohibit generalizing the results to multiple community settings. These limitations include not only the limited sample of communities under current study but also the limitations of the measures taken into consideration. Thus, the traffic-flow measures, to take one example, are not well developed, do not take into account the most salient features of flow related to crashing (e.g., density vs. speed), and had to be crudely generalized to two communities for which these data were simply unavailable. Similarly, although there is a well-replicated relationship between densities of alcohol outlets and crashes, the current study does not permit distinguishing between the effects of bars versus restaurants, the effects of large versus small retail establishments, or alcohol-outlet densities versus the densities of other retail establishments.
Second, studies of a similar kind have the potential to contribute substantially to community-based alcohol policies regarding the distributions of alcohol outlets, policies that could foster healthier communities and safer drinking. In this regard, one could look forward to engineering, in this limited sense, safer communities based on data that are both relatively widely available and directly applicable to the problem of drinking and driving. With suitable development of data-acquisition technologies, spatial-analysis models, and spatial models of the dynamics of community systems supporting drinking and driving, this engineered approach to drinking and driving may be moved from research to application.
Footnotes
This research was supported by the Center for Substance Abuse Prevention, National Institute on Alcohol Abuse and Alcoholism (NIAAA) grant AA09146, and NIAAA center grant AA06282.
References
- Chou Y-H. Map resolution and spatial autocorrelation. Geographical Analysis. 1991;23:228–246. [Google Scholar]
- Cliff AD, Ord JK. Spatial processes: Models and applications. London, England: Pion Limited; 1981. [Google Scholar]
- Colon I, Cutter HS. The relationship between beer consumption and state alcohol and motor vehicle policies to fatal accidents. Journal of Safety Research. 1983;14(2):83–89. [Google Scholar]
- Escobedo LG, Ortiz M. The relationship between liquor outlet density and injury and violence in New Mexico. Accident Analysis & Prevention. 2002;34:689–694. doi: 10.1016/s0001-4575(01)00068-9. [DOI] [PubMed] [Google Scholar]
- Greene WH. Econometric analysis. 2nd ed. New York: Macmillan; 1993. [Google Scholar]
- Griffith DA. Advanced spatial statistics. Dordrecht, The Netherlands: Kluwer Academic; 1988. [Google Scholar]
- Gruenewald PJ, Johnson FW, Treno AJ. Outlets, drinking, and driving: A multilevel analysis of availability. Journal of Studies on Alcohol. 2002;63:460–468. doi: 10.15288/jsa.2002.63.460. [DOI] [PubMed] [Google Scholar]
- Gruenewald PJ, Millar A, Ponicki WR, Brinkley G. Physical and economic access to alcohol: The application of geostatistical methods to small area analysis in community settings. In: Wilson RA, Dufour MC, editors. The epidemiology of alcohol problems in small geographic areas. (NIAAA Research Monograph No. 36, NIH Publication No. 00–4357. Bethesda, MD: National Institute on Alcohol Abuse and Alcoholism; 2000. pp. 163–212. [Google Scholar]
- Gruenewald PJ, Millar AB, Treno AJ, Yang Z, Ponicki WR, Roeper P. The geography of availability and driving after drinking. Addiction. 1996;91:967–983. doi: 10.1046/j.1360-0443.1996.9179674.x. [DOI] [PubMed] [Google Scholar]
- Gruenewald PJ, Ponicki WR. The relationship of the retail availability of alcohol and alcohol sales to alcohol-related traffic crashes. Accident Analysis & Prevention. 1995;27:249–259. doi: 10.1016/0001-4575(94)00067-v. [DOI] [PubMed] [Google Scholar]
- Heeren T, Smith R, Morelock S, Hingson R. Surrogate measures of alcohol involvement in fatal crashes: Are conventional indicators adequate? Journal of Safety Research. 1985;16:127–134. [Google Scholar]
- Holder HD. Alcohol and the community: A systems approach to prevention. New York: Cambridge University Press; 1998. [Google Scholar]
- Holder HD, Blose JO. Impact of changes in distilled spirits availability on apparent consumption: A time series analysis of liquor-by-the-drink. British Journal of Addiction. 1987;82:623–631. doi: 10.1111/j.1360-0443.1987.tb01524.x. [DOI] [PubMed] [Google Scholar]
- Holder HD, Grube JW, Gruenewald PJ, Saltz RF, Treno AJ, Voas RB. Community approaches to prevention of alcohol-related accidents. In: Watson RR, editor. Drug and alcohol abuse reviews: Vol. 7. Alcohol, cocaine and accidents. Totowa, NJ: Humana Press; 1995. pp. 175–194. [Google Scholar]
- Holder HD, Gruenewald PJ, Ponicki WR, Treno AJ, Grube JW, Saltz RF, Roeper P. Effect of community-based interventions on high risk drinking and alcohol-related injuries. Journal of the American Medical Association. 2000;284:2341–2347. doi: 10.1001/jama.284.18.2341. [DOI] [PubMed] [Google Scholar]
- Holder HD, Treno AT, Levy D. Community systems and ecologies of drug and alcohol problems. In: Stockwell T, Gruenewald PJ, Toumbourou JW, Loxley W, editors. Preventing harmful substance use: The evidence base for policy andpractice. Hoboken, NJ: John Wiley & Sons; 2005. pp. 149–161. [Google Scholar]
- Hsiao C. Analysis of panel data. New York: Cambridge University Press; 1986. [Google Scholar]
- Jewell RT, Brown RW. Alcohol availability and alcohol-related motor vehicle accidents. Applied Economics. 1995;27:759–765. [Google Scholar]
- Johnson FW, Treno AJ, Taff GA, Gruenewald PJ. Drinking over the life course within gender and ethnic groups: A hyperpara-metric analysis. Journal of Studies on Alcohol. 1998;59:568–580. doi: 10.15288/jsa.1998.59.568. [DOI] [PubMed] [Google Scholar]
- Lapham SC, Skipper BJ, Skipper I, Skipper K, Skipper R. Factors related to miles driven between drinking and arrest locations among convicted drunk drivers. Accident Analysis & Prevention. 1998;30:201–206. doi: 10.1016/s0001-4575(97)00084-5. [DOI] [PubMed] [Google Scholar]
- LaScala EA, Gerber D, Gruenewald PJ. Demographic and environmental correlates of pedestrian injury collisions: A spatial analysis. Accident Analysis & Prevention. 2000;32:651–658. doi: 10.1016/s0001-4575(99)00100-1. [DOI] [PubMed] [Google Scholar]
- LaScala EA, Gruenewald PJ, Johnson FW. An ecological study of the locations of schools and child pedestrian injury collisions. Accident Analysis & Prevention. 2004;36:569–576. doi: 10.1016/S0001-4575(03)00063-0. [DOI] [PubMed] [Google Scholar]
- LaScala EA, Johnson FW, Gruenewald PJ. Neighborhood characteristics of alcohol-related pedestrian injury collisions: A geostatistical analysis. Prevention Science. 2001;2:123–134. doi: 10.1023/a:1011547831475. [DOI] [PubMed] [Google Scholar]
- Lemmens PHHM, Knibbe RA. Seasonal variation in survey and sales estimates of alcohol consumption. Journal of Studies on Alcohol. 1993;54:157–163. doi: 10.15288/jsa.1993.54.157. [DOI] [PubMed] [Google Scholar]
- MapInfo. MapInfo for Windows 3.0: Reference manual. Troy, NY: Author; 1998. [Google Scholar]
- Mounce N, Pendleton O, Gonzales O. Alcohol involvement in Texas driver fatalities. College Station, TX: Texas Transportation Institute, Texas A&M University; 1988. [Google Scholar]
- Ponicki WR, Gruenewald PJ. S3: The Spatial Statistical System users guide, V5.2. (NIAAA Center Grant Number AA06282) Berkeley, CA: Prevention Research Center, Pacific Institute for Research and Evaluation; 2005. [Google Scholar]
- Richman A. Human risk factors in alcohol-related crashes. Journal of Studies on Alcohol. 1985;(Supplement No. 10):21–31. doi: 10.15288/jsas.1985.s10.21. [DOI] [PubMed] [Google Scholar]
- Roberts FS. Discrete mathematical models with applications to social, biological, and environmental problems. Upper Saddle River, NJ: Prentice Hall; 1976. [Google Scholar]
- Rush BR, Gliksman L, Brook R. Alcohol availability, alcohol consumption and alcohol-related damage: I. The distribution of consumption model. Journal of Studies on Alcohol. 1986;47:1–10. doi: 10.15288/jsa.1986.47.1. [DOI] [PubMed] [Google Scholar]
- Scribner RA, MacKinnon DP, Dwyer JH. Alcohol outlet density and motor vehicle crashes in Los Angeles county cities. Journal of Studies on Alcohol. 1994;55:447–453. doi: 10.15288/jsa.1994.55.447. [DOI] [PubMed] [Google Scholar]
- Smart RG, Docerty D. Effects of the introduction of on-premise drinking on alcohol-related accidents and impaired driving. Journal of Studies on Alcohol. 1976;37:683–686. [Google Scholar]
- Treno AJ, Johnson FW, Remer LG, Gruenewald PJ. The impact of outlet densities on alcohol-related crashes: A spatial panel approach. Accident Analysis & Prevention. 2006;39:894–901. doi: 10.1016/j.aap.2006.12.011. [DOI] [PubMed] [Google Scholar]
- Van Oers JAM, Garretsen HFL. The geographic relationship between alcohol use, bars, liquor shops and traffic injuries in Rotterdam. Journal of Studies on Alcohol. 1993;54:739–744. doi: 10.15288/jsa.1993.54.739. [DOI] [PubMed] [Google Scholar]
- Watts RK, Rabow J. Alcohol availability and alcohol-related problems in 213 California cities. Alcoholism: Clinical and Experimental Research. 1983;7:47–58. doi: 10.1111/j.1530-0277.1983.tb05410.x. [DOI] [PubMed] [Google Scholar]
- Wieczorek WF, Hansen CE. New modeling methods: Geographic information systems and spatial analysis. Alcohol Health and Research World. 1997;21:331–339. [PMC free article] [PubMed] [Google Scholar]
- Wieczorek WF, Coyle JJ. Spatial analysis of DWI offenders for alcohol-related services. Paper presented at the Association of American Geographers 92nd Annual Meeting; Charlotte, NC. 1996, April. [Google Scholar]