Abstract
An influential theoretical perspective differentiates in humans an explicit, rule-based system of category learning from an implicit system that slowly associates different regions of perceptual space with different response outputs. This perspective was extended for the first time to the category learning of nonhuman primates. Humans and macaques learned categories composed of sine-wave gratings that varied across trials in bar width and bar orientation. The categories had either a single-dimensional, rule-based solution or a two-dimensional, information-integration solution. Humans strongly dimensionalized the stimuli and learned the rule-based task far more quickly. Six macaques showed the same performance advantage in the rule-based task. In humans, rule-based category learning is linked to explicit cognition, consciousness, and to declarative reports about the contents of cognition. The present results demonstrate an empirical continuity between human and nonhuman primate cognition, suggesting that nonhuman primates may have some structural components of humans’ capacity for explicit cognition.
Keywords: category learning, implicit/explicit cognition, primate cognition, comparative cognition, rhesus monkeys
Learning and using categories is a basic cognitive function for humans and animals. Consequently, categorization is a focus of research involving humans (Ashby & Maddox, 2005; Brooks, 1978; Murphy, 2003; Nosofsky, 1987; Rosch & Mervis, 1975; Smith & Minda, 1998) and animals (Cerella, 1979; Herrnstein, Loveland, & Cable, 1976; Jitsumori, 1994; Lea & Ryan, 1990; Smith, Redford, & Haas, 2008; Vauclair, 2002; Wasserman, Kiedinger, & Bhatt, 1988).
Early categorization theories assumed that organisms apply a single category-learning system to all category problems. Different descriptions were offered for this system (e.g., Medin & Schaffer, 1978; Reed, 1972). In hindsight, it was predictable that categorization would not be so simple and unitary. Categorization is an important enough capacity that it might deserve (and receive) distributed and varied expression in cognition. Fortunately, many researchers transcended the “single system” claim and described the interactions and tradeoffs among different representational systems in categorization. For example, Cook and Smith (2006), Reed (1978), Smith and Minda (1998), and Wasserman et al. (1988) showed that different processes dominate categorization at different stages of category learning. For another example, Ashby and his colleagues showed in numerous studies that different processes dominate category learning depending on whether or not the correct categorization rule is easy to describe verbally (review in Ashby & Maddox, 2005).
Consequently, a multiple-systems theoretical perspective has become an important part of the human categorization literature (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Ell, 2001; Erickson & Kruschke, 1998; Homa, Sterling, & Trepel, 1981; Minda & Smith, 2001; Rosseel, 2002; Smith & Minda, 1998). The idea is that organisms have multiple categorization utilities that learn different statistical features of the repeating and differentiating environment. The multiple-systems perspective has profoundly enriched the human literature, but it has barely been extended to comparative categorization research (see Herbranson, Fremouw, & Shimp, 1999). The overarching goal of the present research is to encourage this extension.
Within the multiple-systems perspective, a crucial distinction is made between explicit and implicit categorization systems (Ashby & Valentin, 2005; Brooks, 1978; Kemler Nelson, 1984; Love, 2002; Smith & Shapiro, 1989; Smith, Tracy, & Murray, 1993). An explicit system is thought to use analytic, rule-based processes and to depend on working memory and executive attention. In contrast, an implicit system is thought to use nonanalytic, multi-dimensional processes and to learn slowly by mapping regions of perceptual space to response outputs.
Illustrating this distinction, Brooks (1978) found that intentional and incidental categorizations by humans were, respectively, analytic and nonanalytic. Similarly, Kemler Nelson (1984) found that intentional and incidental category learners, respectively, solved category problems using single-dimensional rules or multidimensional family resemblance. Waldron and Ashby (2001) found that a cognitive load selectively and strongly disrupted rule-based category learning (also Love, 2002). In a related finding, Smith et al. (1993) showed that depression selectively impaired rule-based category learning (perhaps because individuals with depression lacked the cognitive resources for hypothesis generation and rule evaluation).
The implicit-explicit distinction was placed into a cognitive-neuroscience framework in the COVIS (Competition between Verbal and Implicit Systems) theory of category learning described by Ashby and his colleagues (Ashby et al., 1998; Maddox & Ashby, 2004; Ashby & Waldron, 1999). COVIS places two systems in competition during category learning: an explicit system (based in the anterior cingulate, the prefrontal cortex, the head of the caudate nucleus, and the hippocampus) that learns through hypothesis testing and systematic reasoning, and an implicit system (based largely in the striatum) that learns procedurally through the catalysis of immediate reinforcement signals.
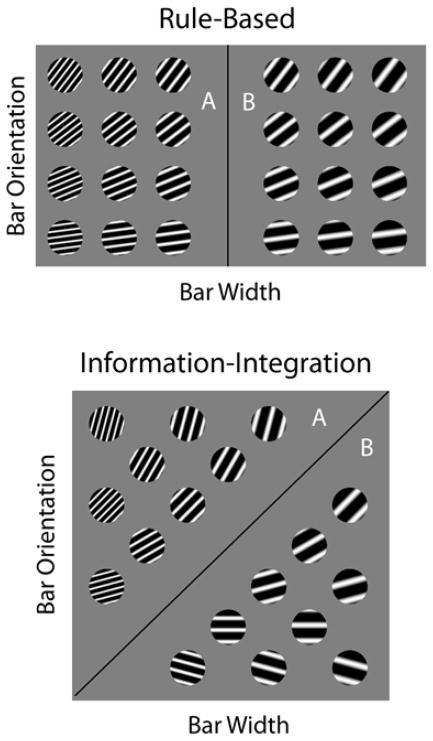
Much of the evidence for these category-learning systems comes from rule-based (RB) and information-integration (II) category tasks, like those illustrated in Figure 1. Each exemplar in both of these categorization tasks is a circular sine-wave grating that varies across trials in bar width and bar orientation. In the experiments described below, there were 300 such exemplars in each category of each task, but only some of these are shown in Figure 1.
Figure 1.
Examples of rule-based and information-integration category structures. The stimuli are sine-wave disks varying in bar width and orientation. In the top panel, the vertical decision bound shows that only variation in bar width carried diagnostic category information, so optimal performance was governed by a one-dimensional (bar-width) rule. In the lower panel, the diagonal decision bound shows that bar width and orientation both carry category information—information from both dimensions must be integrated into a category decision. Each panel illustrates some of the three hundred stimuli that were selected from within the exemplar space of Category A and Category B using methods described in the text.
In the top panel of Figure 1, the vertical category boundary denotes that only X-axis variation (i.e., bar width) carries valid information about category membership, and the participant must discover this dimensional rule from successive presentations of single exemplars, with feedback following each response. This is an example of an RB task because the category bound can be discovered via logical reasoning.
In contrast, in the II categorization task illustrated in the lower panel, the diagonal category boundary indicates that both bar width and orientation carry valid category information, and the participant must learn the dimensional-integration principle that allows correct category assignment, once again based on the successive presentation of single exemplars with feedback. In this case, accuracy is maximized only if information from both stimulus dimensions is integrated into the category decision. Note that there is no simple way to verbally describe this category boundary.
The RB and II tasks are matched for category size, within-category exemplar similarity, between-category exemplar separation, and the a priori perceptual difficulty of the categorization problem. In these senses, the two tasks serve as mutual controls. They differ only in the RB-II aspect that is critical to the present research.
Humans show distinct behavioral differences in learning these two categorization tasks (for a review, see, e.g., Ashby & Maddox, 2005). They strongly dimensionalize these stimuli. They learn RB category tasks quickly through explicit-reasoning and hypothesis-testing processes. They declare verbally their task solution. In contrast, humans learn II category tasks more slowly. They integrate the dimensions poorly because they perceive them so separably, and they have difficulty describing their solution verbally. The empirical goal of the present research is to ask whether similar behavioral differences characterize the approach of nonhuman primates to RB and II category tasks.
Monkeys might rely less than humans on dimensional analysis and category rules, either because of the differential development of prefrontal cortex in the two species or because of the differential availability of language. If so, monkeys might not show an RB advantage because the tasks are otherwise carefully balanced. This would be an important theoretical statement about primate-human differences in categorization, and about the ancestral categorization system from which that of humans emerged.
On the other hand, dimensional analysis and category rules might be a general property of cognition across primates or even mammals. In this case, monkeys would still show a strong RB advantage. This would demonstrate an important continuity across the primate lineage. In fact, the possibility that primates can use rules and hypotheses on-line is an issue with deep empirical roots in comparative psychology (Harlow, 1949; Krechevsky, 1932; Rumbaugh & Pate, 1984). The research would also bear on issues of declarative and explicit cognition in primates, to the extent that they show a performance pattern that is acknowledged to be declarative and conscious in humans. Finally, the possibility of explicit category rules in nonverbal species would focus attention on the presumed link between rule-based cognition and verbalization-language, given a nonverbal species in which that link is necessarily broken.
Experiment 1: Humans
In Experiment 1, we gave humans the two-dimensional RB and II category tasks illustrated in Figure 1. We expected that RB category learning would proceed faster than II category learning, replicating the typical finding and grounding our methodology for subsequent use with nonhuman primates.
Method
Participants
Participants were 60 undergraduates from the University at Buffalo, the State University of New York, who participated to fulfill a course requirement in two experimental sessions lasting about an hour each. Our participant pool was balanced for gender. Participants had apparently normal or corrected-to-normal visual acuity and a mean age of 19.5 years. The racial mix of our participant pool was 41% Caucasian, 45% Asian, 10% African-American, and 4% Other. As a tool to increase performance motivation, the top scorers were awarded cash prizes in the experiment.
Stimuli
Each category exemplar was a circular sine-wave grating that varied on two dimensions: bar width (spatial frequency) and bar orientation (tilt). The disks subtended 4.77 degrees of visual angle, viewed on a 16-inch screen with an 800 × 600 pixel resolution from a distance of about 24 inches. In the present experiments, width varied from 0.366 cycles per degree of visual angle to 1.408 cycles per degree. Tilt varied from 0.307 radians to 1.925 radians. Exemplars were created using the randomization technique developed by Ashby and Gott (1988). In accordance with this method, categories were first defined by bivariate normal distributions along the two stimulus dimensions, within which each stimulus dimension ranged along a normalized 0-to-100 scale. Each stimulus was created by drawing a random sample (x, y) from the Category A or Category B distribution. To control for statistical outliers, the random sample was discarded if its Mahalanobis distance (e.g., Fukunaga, 1972) was greater than 3.0. This process was repeated until 300 Category A and 300 Category B exemplars had been generated.
Category structures
In the vertical RB task shown in the top panel of Figure 1 (in which only the spatial-frequency dimension carried useful information), Category A had these population parameters: Mean X=35.86, Mean Y=50, Variance X=16.33; Variance Y=355.55, Covariance XY=0. Category B had these population parameters: Mean X=64.14, Mean Y=50, Variance X=16.33; Variance Y=355.55, Covariance XY=0. In the major-diagonal II task shown in the bottom panel of Figure 1 (X-Axis, Spatial Frequency; Y-Axis, Orientation), Category A had these population parameters: Mean X=40, Mean Y=60, Variance X=185.94; Variance Y=185.94, Covariance XY=169.61. Category B had these population parameters: Mean X=60, Mean Y=40, Variance X=185.94; Variance Y=185.94, Covariance XY=169.61.
In the end, the 300 chosen Category A and Category B exemplars in the two tasks were slightly adjusted so that their sample means and sample covariance matched the desired population values for the two categories in the task. Finally, a linear transformation was applied to each stimulus coordinate-pair to map its values from the original 0-to-100 scale to a space representing actual values of spatial frequency (cycles per degree) and orientation (radians) used in the experiment. These mappings were: Spatial Frequency = 1.0 + X/30.0; Orientation = y X pi/200 + pi/9.
Categorization trials
Each trial consisted of one Gabor disk presented in the center-top of a computer screen against a gray background. The response icons (A and B) were located on the screen’s lower-left and lower-right. At center-bottom of the screen, a text banner showed participants’ increasing (or decreasing) point total as the task progressed.
Humans responded by pressing the S or L keyboard keys, spatially positioned to correspond to the A or B on the screen, and labeled for the purposes of the experiment as A or B. Humans, when correct, saw a green Correct text banner centered between the two response icons as both response icons disappeared. Their point total incremented, and there was a 1-s, computer-generated reward whoop. Humans, when incorrect, saw a red Incorrect text banner centered between the two response icons as both response icons disappeared. Their point total decremented, and there was a 3-s, computer-generated penalty buzz.
Instructions
Beginning each session, participants were told that they would see striped circles and that they should decide whether each belonged to Category A or B. They were told that they would have to guess at first, but that they should be able to learn how to respond correctly as they went along. The feedback sounds and point consequences were explained to them. For motivation’s sake, they were also told about the $10 prize that would be awarded to the two participants who earned points most efficiently by classifying the circles correctly.
Procedure
Each participant was tested individually in two experimental sessions. They received 600 trials of the RB task and 600 trials of the II task, in a counterbalanced order determined by their sequential participant number. In each session, participants saw the 300 Category A and 300 Category B stimuli in the task exactly once, presented in random order. To accomplish this, the stimuli were presented by sampling without replacement.
Results
Accuracy-based analyses
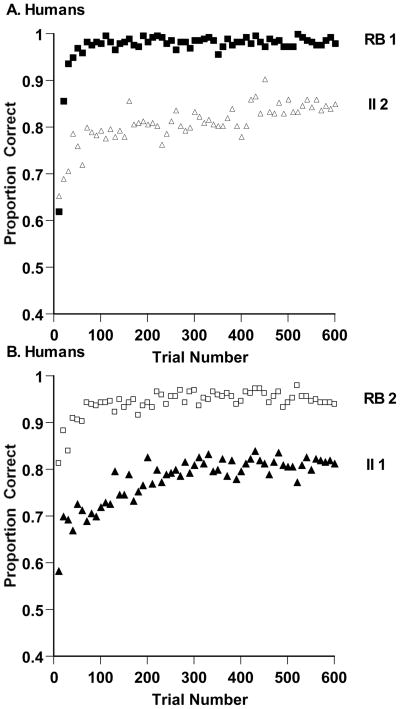
The aggregate proportion correct for all human participants is shown in Figure 2A, B for successive 10-trial blocks in the RB and II tasks. The data were analyzed using a three-way analysis of variance (ANOVA), with task type (RB, II) and trial block (1–60) as within-subject factors, task order as a between-subjects factor, and with task type nested within task order. The analysis found a significant main effect for task, F (2, 58) = 126.20, prep = .999, ηp2 = .539. Participants were .96 and .79 correct overall on the RB and II tasks, respectively. The analysis also found a significant effect for trial block, F (59, 3422) = 14.75, prep = .999,ηp2 = .198. Participants showed substantial learning across their sessions, from .67 correct in the first block to .90 correct in the last block. The interaction between trial block and task type, F (118, 3422) = 1.84, prep = .999, ηp2 = .06, indicated that participants improved differentially on the two tasks, as is shown in the figures. RB performance moved more quickly to a higher asymptote.
Figure 2.
A. Proportion of correct responses in each 10-trial block for thirty humans who performed 600 trials of a rule-based (RB) and information-integration (II) category task in that order. B. Proportion of correct responses in each 10-trial block for thirty humans who performed 600 trials of an II and RB category task in that order.
Model-based analyses
The accuracy-based analyses suggest that participants in both conditions learned the categories effectively. Before concluding this, however, it is important to confirm that participants used a strategy of the optimal type. To answer this question, we fit four different types of decision bound models (e.g., Maddox & Ashby, 1993) to the data from each individual participant. The II model assumed a pre-decisional (linear) integration of information across dimensions, Two RB models were fit. The 1D models assumed the application of a one-dimensional rule (i.e., a vertical or horizontal decision bound), and the CJ model assumed the use of a two-dimensional, conjunctive rule. Finally, the RG model assumed a random-guessing strategy (see the Appendix for details). The II and RB models make no detailed processing assumptions, but they assume that each participant’s responses are compatible with either an II or RB strategy, respectively.
First, we fit the categorization models to each human’s performance taking all 600 trials as a single block. The II, 1D, CJ, and RG models fit best the performance of 52, 7, 1, and 0 participants in the II condition. The accuracy of the participants who used an II strategy was higher than the participants who used an RB strategy (i.e., 0.810 versus 0.696).
The II, 1D, CJ, and RG models, respectively, fit best the performance of 5, 54, 1, and 0 participants in the RB condition. The 5 participants for whom the II model fit best had best-fitting decision bounds that were not strictly vertical. Even so, in each case, these bounds were nearly vertical and the accuracy of the II and RB participants was hardly different (0.940 vs. 0.965). These results confirm that almost all participants effectively learned the categories and did so using something like the optimal decision bound.
We also fit each human’s data taking the categorization trials in 100-, 200-, or 300-trial blocks. In this case, we classified each human according to the best-fitting model in their last block of responding (i.e., their last 100, 200, or 300 trials). In most cases, the last 100, 200, and 300 trials pointed to the same best-fitting model. When they did not, we took the participant to be best fit by the best-fitting model for two out of the three analyses. The results of this analysis were as follows.
The II, 1D, CJ, and RG models fit best the performance of 51, 8, 0, and 1 participants in the II condition. Here, too, the accuracy of the participants who used an II strategy was higher than the participants who used an RB strategy (i.e., 0.815 versus 0.695).
The II, 1D, CJ, and RG models fit best the performance of 3, 57, 0, and 0 participants in the RB condition. The 3 cases in which the II model was best fitting mean that the best-fitting decision bounds for those participants were not strictly vertical. Even so, those bounds were nearly vertical and the accuracy of the II and 1D participants was hardly different (0.959 vs. 0.935). These results further confirm that almost all participants effectively learned the categories and did so using something like the optimal decision bound.
In all respects, the results of Experiment 1 replicated the traditional finding of a strong difference in the speed of acquisition between RB and II tasks for humans. These results grounded our methodology as we evaluated next whether nonhuman primates would produce the same data pattern.
Experiment 2: Monkeys
Experiment 2 generalized the human phenomena to the category learning of nonhuman primates, by examining the behavior of six rhesus monkeys (Macaca mulatta) in the paradigm of Experiment 1.
Method
Participants
Chewie (8 years old), Han (5 years old), Lou (14 years old), Luke (8 years old), Murph (14 years old), and Obi (4 years old) were tested. They had been trained, using procedures described elsewhere (Rumbaugh, Richardson, Washburn, Savage-Rumbaugh, & Hopkins, 1989; Washburn & Rumbaugh, 1992), to respond to computer-graphic stimuli by manipulating a joystick. They had been tested in prior studies on a variety of computer tasks. The monkeys were tested in their home cages at the Language Research Center of Georgia State University, with ad lib access to the test apparatus, working or resting as they chose during long sessions. The animals were neither food deprived nor weight reduced for the purposes of testing and they had continuous access to water.
Apparatus
The monkeys were tested using the Language Research Center’s Computerized Test System—LRC-CTS (described in Rumbaugh et al., 1989; Washburn & Rumbaugh, 1992)—comprising a Compaq DeskPro computer, a digital joystick, a color monitor, and a pellet dispenser. Monkeys manipulated the joystick through the mesh of their home cages, producing isomorphic movements of a computer-graphic cursor on the screen. Contacting appropriate computer-generated stimuli with the cursor brought them a 94-mg fruit-flavored chow pellet (Bio-Serve, Frenchtown, NJ) using a Gerbrands 5120 dispenser interfaced to the computer through a relay box and output board (PIO-12 and ERA-01; Keithley Instruments, Cleveland, OH). Correct responses were accompanied by a computer-generated series of ascending tones that bridged the animals to their reward. On incorrect responses, there was a computer-generated buzzing sound and a 20-s penalty timeout.
Procedure
The stimuli, category structures, and trial displays were those already described in Experiment 1. The monkeys made their categorization decision using a digital joystick to move a cursor (a tiny red ellipse) to touch the response icon of their choice. Each trial began with a black square presented in the same position as the to-be-categorized stimulus. Animals moved the cursor to touch this square as a trial-start response, indicating their readiness. The black square released to the Gabor disk, and the two response icons were illuminated. To avoid any confusion with past response icons used by the animals, the A-response icon was a mirror-imaged TB. The B-response icon was a mirror-imaged QC. These were both novel response stimuli.
The monkeys received 6,000 trials in the RB and II tasks, with the exception of one animal in one task that lost one trial due to computer error. These 6,000 trials were 10 random permutations of the 300 Category A and 300 Category B stimuli available for a task. To allow this succession of permutations, stimuli were sampled without replacement until the supply of 600 stimuli was exhausted, and then the 600 stimuli were re-introduced. The monkeys, as humans, were mainly given the spatial-frequency RB task with a vertical decision bound and the positive II task that were illustrated in Figure 1. The two exceptions to this procedure are described next.
Data analysis
The six macaques completed 6,000 trials of both the RB and II tasks in counterbalanced order (Chewie, Han, Lou: RB-II; Luke, Murph, Obi: II-RB). Four macaques (Han, Lou, Murph, and Obi) completed the vertical RB task shown in the top panel of Figure 1 and the positive II task shown in the bottom panel of Figure 1. Chewie and Luke completed an initial session of 6,000 trials (Chewie: II Positive, Luke: RB Vertical). In both cases, these macaques exhibited a strong and persistent response bias in which they made the same response essentially every trial. In neither case was there any learning. Accordingly, these two sessions were not analyzed. Chewie’s II task was repeated following his RB task, this time using the II Negative task instead of the II Positive task he originally experienced and failed. Luke’s RB task was repeated following his II task, this time using the RB Horizontal task instead of the RB Vertical task he originally experienced.
Results
Accuracy-based analyses
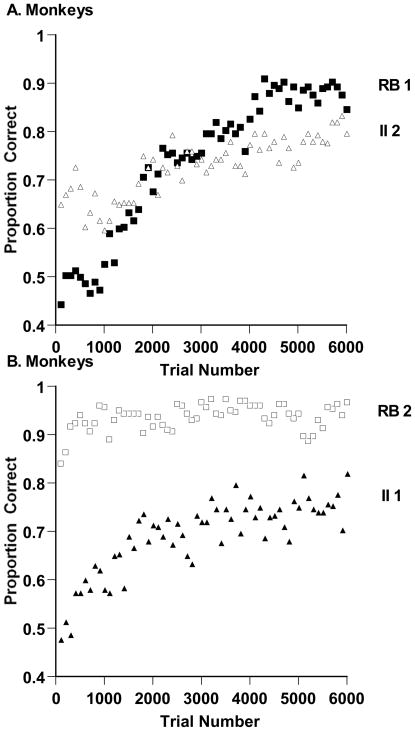
The aggregate proportion correct for all macaque participants is shown in Figures 3A and 3B for successive 100-trial blocks in the RB and II tasks. In comparing the performance of monkeys and humans in Figures 3 and 2, respectively, remember that there was a 10-fold difference in trial-block length and total trials on task. We return momentarily to the relative slowness of monkeys’ category learning. The data were analyzed using a three-way analysis of variance (ANOVA), with task type (RB, II) and trial block (1–60) as within-subject factors, task order as a between-subjects factor, and with task type nested within task order. The analysis found a significant main effect for task, F (2, 4) = 7.40, prep = .884, ηp2 = .826. Macaques were .84 and .71 correct overall on the RB and II tasks, respectively. The analysis also found a significant effect for trial block, F (59, 236) = 8.05, prep = .999, ηp2 = .746. Macaques showed substantial learning across their sessions, from .60 correct in the first block to .86 correct in the last block. The interaction between trial block and task type, F (118, 236) = 2.27, prep = .999, ηp2 = .532, indicated that participants improved differentially on the two tasks, as is shown in the figure. In the RB-II task order (Figure 3A), macaques improved from a very low RB performance level (as they initially acclimated to the task) to a very high level late in the experiment. In the II-RB task order (Figure 3B) they were sharp and sensitive RB categorizers from that task’s outset, having earlier accomplished their task acclimation.
Figure 3.
A. Proportion of correct responses in each 100-trial block for three monkeys who performed 6,000 trials of a rule-based (RB) and information-integration (II) category task in that order. B. Proportion of correct responses in each 100-trial block for three monkeys who performed 6,000 trials of an II and RB category task in that order.
Monkeys’ and humans’ relative speeds of learning
These data provide one of the closest existing comparisons between the categorization of humans and nonhuman primates. Clearly, monkeys’ speed of acquisition was slower overall than was that of humans. For example, over their 600 trials, the human accuracies were .974 (RB first), .943 (RB second), .780 (II first), and .810 (II second). In contrast, in their first 600 trials, the monkey accuracies were .492 (RB first), .901 (RB second), .537 (II first), and .670 (II second). It is interesting that even in these 600-trial performance levels, one sees the crucial result of the experiment foreshadowed. Both of the monkeys’ first-task performances began at near-chance levels as task-acclimation occurred. II-second performance was slightly better than this, after acclimation had been accomplished in the first task. But RB-second performance was dramatically better. RB acquisition in the second task epoch was extremely rapid, showing in another way its privilege within the primate category-learning system.
The species differences in overall learning rate accords well with other cross-species estimates of the speed of learning (Smith, Minda, & Washburn, 2004; also compare Medin & Dewey, 1984, Medin, Altom, & Murphy, 1984). It should be borne in mind that some of the difference arose because humans were given explicit instructions about the structure of the category-learning task and about their goals within it. Monkeys had to learn the task’s grammar and goals procedurally from their experience within it. In addition, humans received all their trials in one day instead of on successive days—there might have been forgetting across days by the monkeys. Thus one should take the learning-rate difference seriously but not over-interpret it.
Model-based analyses
We fit the categorization models to the monkeys’ data in much the same way we did with the humans. First, we fit the models to the first 600 trials of each monkey’s performance. The II, 1D, CJ, and RG models fit best for 0, 4, 0, and 2 participants, respectively in the II condition. The II, 1D, CJ, and RG models fit best for 1, 2, 0, and 3 participants, respectively in the RB condition. Across the two task conditions, all 5 of the best fits by the RG model were in the animals’ first task, demonstrating again that monkeys can have fairly slow time-courses of category learning.
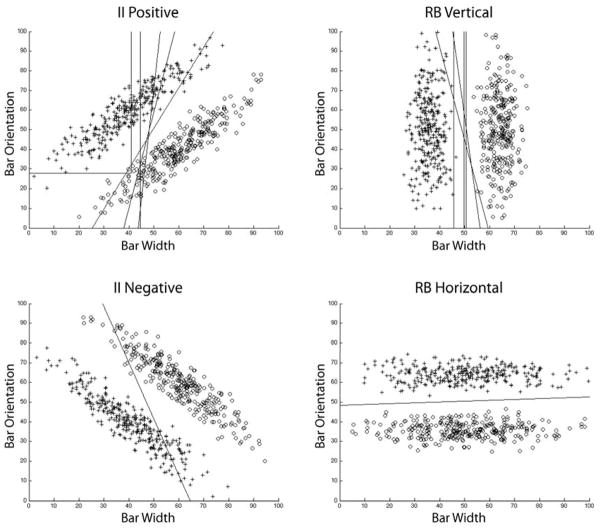
In addition, we fit the last 1000 trials of each monkey’s data and classified each monkey according to which model provided the best fit. We also repeated this classification for fits to the last 2000 trials and to the last 3000 trials. The results were essentially identical to those reported here. Figure 4 shows the best fitting decision bounds overlaid on the categorization stimuli for all animals in both conditions. The results of the modeling analyses are described now.
Figure 4.
The stimuli used in the information-integration (II) and rule-based (RB) conditions of Experiments 1 and 2 and the decision bounds that provided the best fits to the last 1,000 responses of the macaques in Experiment 2. Five macaques received the positive information-integration task (top-left panel) and the vertical rule-based condition (top-right panel. One macaque received the negative information-integration task (bottom-left panel) and one received the horizontal rule-based condition (bottom-right panel).
The II, 1D, CJ, and RG models fit best for 4, 1, 1, and 0 participants, respectively in the II condition. This is a difference from the proportions of model fits seen in Experiment 1—85% of humans performing an II task were best fit by the II model, but only 66% of monkeys were. For reasons that we describe now, this difference should not be over-interpreted, and indeed the monkeys’ pattern of model fits strengthens the overall interpretation of the article.
The four participants for which the II model fit best had best-fitting decision bounds that were not strictly vertical and that assumed information integration. One sees in Figure 4, however, that except for two cases, these bounds were substantially vertical. Table 1 explores this issue in more detail. There, goodness-of-fit (i.e., BIC) scores are given for the best-fitting II and RB models, along with the percentage of responses accounted for by the decision bounds assumed by these models. The fit score for the best-fitting model is given in bold. Note that for participant 3, the II model fits much better and accounts for many more responses. This is the bound in Figure 4 with the shallowest slope. For the other 5 participants, the differences in fit between the II and RB models are more modest and there are almost no differences in the ability of the two models to account for the monkey’s responses. Thus, although the behavior of 4 of the 6 monkeys was best described by an II model, only one monkey effectively integrated the bar width and orientation information. The other animals all showed a strong dimensional focus. If anything, the animals dimensionalized the stimulus space more strongly than the humans did, not less strongly.
Table 1.
Model-fitting results for the last 1,000 trials of II task performance by each monkey participant. The BIC score for the best-fitting model is given in bold.
| II Participant | II Model | RB Model | ||
|---|---|---|---|---|
| BIC | % Accounted | BIC | % Accounted | |
| 1 | 634.4 | 88.0 | 640.9 (1D) | 88.1 (1D) |
| 2 | 479.8 | 89.7 | 570.4 (1D) | 88.7 (1D) |
| 3 | 291.1 | 95.8 | 822.6 (1D) | 82.1 (1D) |
| 4 | 1216.9 | 70.5 | 1210.5 (1D) | 70.5 (1D) |
| 5 | 982.6 | 73.8 | 958.8 (CJ) | 75.9 (CJ) |
| 6 | 793.1 | 81.0 | 890.2 (1D) | 83.6 (1D) |
In the RB condition, the II, 1D, CJ, and RG models fit best for 2, 4, 0, and 0 participants, respectively. The 2 participants for which the II model fit best had best-fitting decision bounds that were not strictly vertical. However, Figure 4 shows that in both cases, these bounds were nearly vertical. Table 2 confirms that in these two cases, the 1D model accounted for at least as many responses as the better fitting II model. Thus, all 6 participants effectively showed substantial dimensional learning.
Table 2.
Model-fitting results for the last 1,000 trials of RB task performance by each monkey participant. The BIC score for the best-fitting model is given in bold.
| RB Participant | II Model | 1D Model | ||
|---|---|---|---|---|
| BIC | % Accounted | BIC | % Accounted | |
| 1 | 550.6 | 92.3 | 558.7 | 92.3 |
| 2 | 811.4 | 86.2 | 800.4 | 86.2 |
| 3 | 766.6 | 86.0 | 798.6 | 86.2 |
| 4 | 441.1 | 94.2 | 434.3 | 94.2 |
| 5 | 551.2 | 91.7 | 545.6 | 91.9 |
| 6 | 256.1 | 97.4 | 251.6 | 97.4 |
In summary, the model fitting shows that most of the macaques used a decision bound of the same type as the optimal bound. Even so, it is also clear that the animals showed a strong tendency to analyze and dimensionalize the stimuli, even when this was not the optimal strategy. The results demonstrated, in monkey category learners, too, a strong difference in the speed and level of acquisition between RB and II tasks.
General Discussion
We gave humans and macaques RB and II category-learning tasks using an established human methodology. Both species strongly dimensionalized the perceptual space, sharply attended to single dimensions, and learned RB category tasks easily. In contrast, in II tasks that require perceptual integration, learning in both species was slower and less effective. Many researchers have granted rules an important role in human categorization (Ahn & Medin, 1992; Ashby & Ell, 2001; Erickson & Kruschke, 1998; Medin, Wattenmaker, & Hampson, 1987; Nosofsky, Palmeri, & McKinley, 1994; Regehr & Brooks, 1995). Here, macaques showed a similar pattern. To some extent, macaques demonstrated their use of rule-based categorization processes that are deemed in humans to be explicit, conscious, declarative, and reasoning/language-based. The results represent a new continuity between primate and human cognition.
It was not pre-ordained that the cognitive systems of macaques would be organized in a dimensionalized, rule-preferring format. For example, other species might perceive these stimuli more integrally and less separably than humans (Foard & Kemler Nelson, 1984; Garner, 1974; Garner & Felfoldy, 1970; Handel & Imai, 1972; Lockhead, 1972), just as young humans sometimes perceive multidimensional stimulus combinations more integrally than adult humans (Shepp & Swartz, 1976; Shepp, Burns, & McDonough, 1980; L. Smith & Kemler 1977, 1978; Smith & Kemler Nelson, 1984; Ward, 1983). Given a non-dimensionalized perceptual space, the RB and II tasks used in the present experiments would be identical in within-category coherence, between-category separation, stimulus distance/similarity relationships, and inherent task difficulty, and thus no difference in the speed of acquisition would be predicted.
RB and II tasks would also be equally learnable given a mechanism based on configural representations (Pearce, 1987, 1994). Configural theory presumes that multidimensional stimulus compounds—in their entirety—enter into associations with outcomes and responses. Our RB and II tasks were exact structural rotations of one another through 45o of perceptual space, and therefore would equally support the use of configural representations in building adaptive response strategies.
RB and II category learning might also be equivalent given an elemental theory of discrimination. In II tasks, every trial presents task-relevant information along both dimensions. As long as neither dimension is totally ignored, there is no way for attention to be wrong-footed so that relevant information is missed on some trials. Important models of attention and discrimination learning (e.g., Sutherland & Mackintosh, 1971; Mackintosh, 1975) left ample room for the parallel gain of associative strength to occur for multiple relevant cues in a way that could support equivalent RB and II learning. Indeed, some elemental approaches to discrimination learning might predict an II learning advantage. After all, animals trained with multiple relevant cues available usually acquire a discriminatory habit faster than animals trained with only one cue (e.g., Eninger, 1952). Sutherland and Mackintosh (1971, p. 141) showed that the combined strengths of two relevant cues would often be greater than the strength of the relevant cue in single-cue learning. At worst, when there is a weak and strong cue (in salience or reinforcement predictiveness), the multiple-cue case produces performance equal to (not worse than) the single-cue case (Sutherland & Mackintosh, 1971, ch. 4, p. 131; Warren, 1953; Harlow, 1945). These additivity effects were analyzed and modeled in work by Restle (1955, 1957) and by Sutherland and Macintosh, (1971, ch. 5). Note that these early studies generally focused on the inclusion of two cues that were highly correlated with trial outcomes, whereas in the present studies the cues were only partially correlated with outcomes. Therefore, one cannot automatically extrapolate from those studies to the present case. Nonetheless, those studies do not lead one to expect the strong RB (single-cue) preference shown by monkeys here. In a sense, the present data furthers those studies by studying the case in which partially predictive information is presented along two dimensions.
Remember also that there is evidence that II learning is managed in humans (and perhaps in monkeys) by an implicit-striatal system that uses a form of procedural learning. If humans and monkeys learned II and RB tasks using this system, then again one would not predict a strong RB performance advantage. The implicit system relies on nonanalytic, multi-dimensional processes that slowly learn to map response outputs to regions of perceptual space, and it, too, would be indifferent to the rotation of the task in perceptual space and to the dimensional alignment of the task’s axes.
Yet humans and monkeys showed a strong RB performance advantage when the axes of the task’s solution were aligned with dimensionalized perception. This clearly suggests that both groups used some attentional/cognitive category-learning process that emphasized single-cue solutions, rather than multiple-cue associations. There is no rationale for suggesting that this rule- or hypothesis-like system was striatally based. To the contrary, the natural interpretation of our results is that monkeys showed for the first time here a version of the RB-II implicit-explicit dissociation that has been a dominant feature of recent work in the cognitive neuroscience of category learning.
This continuity across humans and nonhuman primates raises additional questions. First, when in evolutionary time—given that a commitment was not necessary—was the commitment made by the mammal-primate lineage to place special emphasis on the dimensional organization of tasks and on single-dimensional solutions to multidimensional category tasks. This question has a distinguished pedigree in comparative psychology. Lashley (1929) found that rats often made cue-response associations quite suddenly (e.g., Sutherland & Mackintosh, 1971, Figure 4.1). With equal notoriety, Krechevsky (1932) reported that rats appeared to adopt the same response strategy for a series of trials, as though they were testing single-cue behavioral hypotheses and discarding them until finding one strongly correlated with reward. These observations were the controversial basis for the Noncontinuity Theory of animal discrimination learning, and they are consonant with the present results that reveal a preferential, single-cue system in category learning. However, those observations were not strongly grounded in systematic experiments, and other theoretical perspectives have been taken toward them (Sutherland & Mackintosh, 1971). The present RB-II paradigm offers a constructive convergent paradigm for exploring—comparatively and systematically—these attentional phenomena.
Second, it is interesting to consider why—given that the commitment was not necessary—the mammal/primate lineage made the commitment to dimensional task organizations and unidimensional task solutions. What was the benefit to single-dimensional foci and category rules? What was the character or quality of real-world, ecological categories for mammals/primates that helped engender this commitment? Even without knowing these answers, clearly this commitment opened extraordinary possibilities for analysis, hypotheses, rules, inferences, symbolic representations, and linguistic labels that reached their full development in the hominids.
Third, short of that full development, it is interesting to evaluate the elements of humans’ rule-based system that macaques do or do not share. The human system is analytic, dimensionalizing, verbal, explicit, and conscious. The results show that macaques share with humans the analytic and dimensional framework within which they grasped RB tasks with substantial privilege. However, macaques are not verbal as humans are, and this has an important implication for theories of human categorization. The original formulation of COVIS (Ashby et al., 1998) conflated explicit reasoning and verbalization (the acronym’s V is for Verbal), even though little evidence suggested the necessity of verbalization and language for rule-based, explicit categorization. The macaques are a sharp reminder that this is an unnecessary conflation. Recent discussions of implicit-explicit theory have avoided this error (Ashby & Valentin, 2005). There could be explicit forms of rule use that are not verbally grounded, though they could be grounded in some dimensional, symbolic, nonverbal proxy or precursor. Lea and Wills (2008) also pointed out that animals may show single-cue solutions in tasks that are different in character from those of humans, and that the construct of rule-use needs careful definition when used to compare performances across species.
Macaques were also slower dimensional focusers and rule learners than humans. This difference is consistent with existing knowledge about monkeys’ general prefrontal development. They should be “explicitly challenged” given what is known about human-primate differences in neuroanatomy. We believe there is constructive theoretical work to be done in considering the evolutionary and cognitive waypoints from monkeys’ gradual abstraction of category rules to humans’ rapid appreciation of them. One possible attentional-dimensional accelerant would be an increasingly sharp rivalry between cues in a task, so that zero-sumness came more quickly to crowd out all but one cue. Theories of selective attention and discrimination have incorporated such a rivalry, inverse, or zero-sum principle to different degrees (Sutherland & Mackintosh, 1971; Mackintosh, 1975). Another possible attentional-dimensional accelerant would be a growing capacity for symbolic/dimensional/propositional representations that let humans think logically about hypotheses and rules. An emerging explicit consciousness of rules and hypotheses could also be an underlying factor that accelerated rule-based category learning along the hominid line.
On this last point, while the present results may reveal in macaques a system of rule-based reasoning that is in some respects continuous with that of humans, they certainly do not force the conclusion that macaques hold their rules declaratively, explicitly, or in conscious awareness. Clearly, more research should be forthcoming to explore this possibility and ground it empirically, by further dissociating explicit from implicit category learning in macaques.
For example, because the explicit system uses working memory and executive attention, it should be relatively resilient to changes in the timing and nature of the feedback signal. Maddox, Ashby, and Bohil (2003) showed that II category learning in humans, but not RB category learning, is impaired if the feedback signal is delayed even by 2.5 seconds after response. Showing this dissociation in macaques would provide further evidence that explicit and implicit category-learning systems in humans and macaques are similar.
For another example, Maddox, Ashby, Ing, and Pickering (2004) showed that RB category learning in humans, but not II learning, was impaired if the amount of time to process the feedback signal is limited. Showing this dissociation in macaques would suggest that they also deliberately process the feedback given on training trials, as part of a suite of processes that may include hypothesis memory and evaluation.
In the end, we hope that the present research will foster a dialog among comparative, cognitive, and neuroscience researchers of category learning. It will be fruitful to compare humans’ and animals’ categorization competencies and limitations and to correlate these with the differential development of the brain systems that serve category learning. Currently, few cognitive-neuroscience articles directly address issues and findings relating to animal categorization (Ashby & Maddox, 2005).
We also hope that our research will draw theoretical connections from the contemporary systems study of cognitive neuroscience (e.g., Ashby et al., 1998) to Harlow (1949) on learning sets, Krechevsky (1932) on animal hypotheses, Lashley (1942) on discontinuity theory, Rumbaugh and Pate (1984) on mediational learning, and to Mackintosh (1975), Restle (1955, 1957), Sutherland and Mackintosh (1971), Trabasso and Bower (1968), and Zeaman and House (1963) on animals’ processes of selective attention and discrimination learning. For we believe that earlier insights and debates, paired with complementary empirical techniques and theoretical perspectives, still have great potential to illuminate comparative psychology.
Acknowledgments
The preparation of this article was supported by Grant HD-38051 from NICHD, Grant BCS-0634662 from NSF, Grant R01 MH3760-2 from NIMH, and by support from the U.S. Army Research Office through the Institute for Collaborative Biotechnologies under grant W911NF-07-1-0072. The authors thank Ted Evans for assistance with data collection from the monkeys.
APPENDIX
This appendix describes the models that were fit to each participant’s data and the model fitting procedure. For more details, see Maddox and Ashby (1993).
Rule-Based Models
The One-Dimensional Classifier (1D) assumes the participant sets a decision criterion on one stimulus dimension (either bar width or orientation). The model has two parameters (a criterion on the relevant dimension, and perceptual noise variance).
The Conjunction Rule Classifier (CJ) assumes that the rule used by participants is a conjunction of the type: “Respond A if the bar width is small AND the orientation is > 45°, otherwise respond B.” Although several different versions of the model could be fit to the present data, only the version that seemed plausible based on a visual inspection of the response data was fit. The GCC has 3 parameters: one for the single decision criterion placed along each stimulus dimension (one for orientation and one for bar width) and a perceptual noise variance.
Information-Integration Models
The Information-Integration Model (II) assumes a general linear classifier strategy in which participants divide the stimulus space using a linear decision bound. The II model has 3 parameters: the slope and intercept of the linear decision bound and a perceptual noise variance.
Random Response Models
Two models assumed random responding – one with unbiased guessing (zero parameters) and one with biased guessing (one parameter).
Model Selection
Parameters were estimated using the method of maximum likelihood, and the Bayesian Information Criterion (BIC; Schwarz, 1978) was used for model selection:
where r is the number of free parameters, N is the sample size, and L is the likelihood of the model given the data.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xan.
Contributor Information
J. David Smith, Department of Psychology and Center for Cognitive Science, SUNY Buffalo.
Michael J. Beran, Language Research Center, Georgia State University
Matthew J. Crossley, Department of Psychology, University of California Santa Barbara
Joseph. T. Boomer, Department of Psychology, SUNY Buffalo
F. Gregory Ashby, Department of Psychology, University of California Santa Barbara.
References
- Ahn W, Medin DL. A two-stage model of category construction. Cognitive Science. 1992;16:81–121. [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ell SW. The neurobiology of human category learning. Trends in Cognitive Science. 2001;5:204–210. doi: 10.1016/s1364-6613(00)01624-7. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Gott RE. Decision rules in the perception and categorization of multidimensional stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1988;14:33–53. doi: 10.1037//0278-7393.14.1.33. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT. Human category learning. Annual Review of Psychology. 2005;56:149–178. doi: 10.1146/annurev.psych.56.091103.070217. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Valentin VV. Multiple systems of perceptual category learning: Theory and cognitive tests. In: Cohen H, Lefebvre C, editors. Handbook of categorization in cognitive science. New York USA: Elsevier; 2005. pp. 547–572. [Google Scholar]
- Ashby FG, Waldron EM. The nature of implicit categorization. Psychonomic Bulletin & Review. 1999;6:363–378. doi: 10.3758/bf03210826. [DOI] [PubMed] [Google Scholar]
- Brooks LR. Nonanalytic concept formation and memory for instances. In: Rosch E, Lloyd BB, editors. Cognition and categorization. Hillsdale, NJ USA: Erlbaum; 1978. pp. 169–211. [Google Scholar]
- Cerella J. Visual classes and natural categories in the pigeon. Journal of Experimental Psychology: Human Perception and Performance. 1979;5:68–77. doi: 10.1037//0096-1523.5.1.68. [DOI] [PubMed] [Google Scholar]
- Cook RG, Smith JD. Stages of abstraction and exemplar memorization in pigeons’ category learning. Psychological Science. 2006;17:1059–1067. doi: 10.1111/j.1467-9280.2006.01833.x. [DOI] [PubMed] [Google Scholar]
- Eninger MU. The role of generalised approach and avoidance tendencies in brightness discrimination. Journal of Comparative and Physiological Psychology. 1953;45:604–608. doi: 10.1037/h0053833. [DOI] [PubMed] [Google Scholar]
- Erickson MA, Kruschke JK. Rules and exemplars in category learning. Journal of Experimental Psychology: General. 1998;127:107–140. doi: 10.1037//0096-3445.127.2.107. [DOI] [PubMed] [Google Scholar]
- Foard CF, Kemler Nelson DG. Holistic and analytic modes of processing: The multiple determinants of perceptual analysis. Journal of Experimental Psychology: General. 1984;113:94–111. doi: 10.1037//0096-3445.113.1.94. [DOI] [PubMed] [Google Scholar]
- Fukunaga K. Introduction to statistical pattern recognition. New York: Academic Press; 1972. [Google Scholar]
- Garner WR. The processing of information and structure. Potomac, MD USA: Erlbaum; 1974. [Google Scholar]
- Garner WR, Felfoldy FL. Integrality of stimulus dimensions in various types of information processing. Cognitive Psychology. 1970;1:225–241. [Google Scholar]
- Handel S, Imai S. The free classification of analyzable and unanalysable stimuli. Perception and Psychophysics. 1972;12:108–116. [Google Scholar]
- Harlow HF. The formation of learning sets. Psychological Review. 1949;56:51–65. doi: 10.1037/h0062474. [DOI] [PubMed] [Google Scholar]
- Harlow HF. Studies in discrimination learning by monkeys: VI. Discrimination between stimuli differing in both colour and form, only in color, and only in form. Journal of General Psychology. 1945;33:225–235. doi: 10.1080/00221309.1945.10544507. [DOI] [PubMed] [Google Scholar]
- Herbranson WT, Fremouw T, Shimp CP. The randomization procedure in the study of categorization of multidimensional stimuli by pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 1999;25:113–135. [PubMed] [Google Scholar]
- Herrnstein RJ, Loveland DH, Cable C. Natural concepts in pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 1976;2:285–301. doi: 10.1037//0097-7403.2.4.285. [DOI] [PubMed] [Google Scholar]
- Homa D, Sterling S, Trepel L. Limitations of exemplar-based generalization and the abstraction of categorical information. Journal of Experimental Psychology: Human Learning and Memory. 1981;7:418–439. doi: 10.1037//0278-7393.10.4.638. [DOI] [PubMed] [Google Scholar]
- Jitsumori M. Discrimination of artificial polymorphous categories in humans and nonhumans. In: Hayes SC, Hayes LJ, Sato M, Ono K, editors. Behavior analysis of language and cognition. Washington, DC USA: APA; 1994. pp. 91–106. [Google Scholar]
- Kemler Nelson DG. The effect of intention on what concepts are acquired. Journal of Verbal Learning and Verbal Behavior. 1984;23:734–759. [Google Scholar]
- Krechevsky L. “Hypotheses” in rats. Psychological Review. 1932;39:516–532. [Google Scholar]
- Lashley KS. Brain mechanisms and intelligence: A quantitative study of injuries to the brain. Chicago: University of Chicago Press; 1929. [Google Scholar]
- Lashley KS. An examination of the “continuity theory” as applied to discriminative learning. Journal of General Psychology. 1942;26:241–265. [Google Scholar]
- Lea SEG, Ryan CME. Unnatural concepts and the theory of concept discrimination in birds. In: Commons ML, Herrnstein RJ, Kosslyn SM, Mumford DB, editors. Quantitative analyses of behavior. VIII. Hillsdale, NJ USA: Erlbaum; 1990. pp. 165–185. [Google Scholar]
- Lea SEG, Wills AJ. Use of multiple dimensions in learned discriminations. Comparative Cognition and Behavior Reviews. 2008;3:115–133. [Google Scholar]
- Lockhead GR. Processing dimensional stimuli: A note. Psychological Review. 1972;79:410–419. doi: 10.1037/h0033129. [DOI] [PubMed] [Google Scholar]
- Love BC. Comparing supervised and unsupervised category learning. Psychonomic Bulletin and Review. 2002;9:829–835. doi: 10.3758/bf03196342. [DOI] [PubMed] [Google Scholar]
- Mackintosh NJ. A theory of attention: Variations in the associability of stimuli with reinforcement. Psychological Review. 1975;82:276–298. [Google Scholar]
- Maddox WT, Ashby FG. Comparing decision bound and exemplar models of categorization. Perception and Psychophysics. 1993;53:49–70. doi: 10.3758/bf03211715. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG. Dissociating explicit and procedural-learning based systems of perceptual category learning. Behavioural Processes. 2004;66:309–332. doi: 10.1016/j.beproc.2004.03.011. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Bohil CJ. Delayed feedback effects on rule-based and information-integration category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:650–662. doi: 10.1037/0278-7393.29.4.650. [DOI] [PubMed] [Google Scholar]
- Medin DL, Altom MW, Murphy TD. Given versus induced category representations: Use of prototype and exemplar information in classification. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10:333–352. doi: 10.1037//0278-7393.10.3.333. [DOI] [PubMed] [Google Scholar]
- Medin DL, Dewey GI. Learning of ill-defined categories by monkeys. Canadian Journal of Psychology. 1984;38:285–303. [Google Scholar]
- Medin DL, Schaffer MM. Context theory of classification learning. Psychological Review. 1978;85:207–238. [Google Scholar]
- Medin DL, Wattenmaker WD, Hampson SE. Family resemblance, conceptual cohesiveness, and category construction. Cognitive Psychology. 1987;19:242–279. doi: 10.1016/0010-0285(87)90012-0. [DOI] [PubMed] [Google Scholar]
- Minda JP, Smith JD. Prototypes in category learning: The effects of category size, category structure, and stimulus complexity. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:775–799. [PubMed] [Google Scholar]
- Murphy GL. The big book of concepts. Cambridge, MA USA: MIT Press; 2003. [Google Scholar]
- Nosofsky RM. Attention and learning processes in the identification and categorization of integral stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1987;13:87–108. doi: 10.1037//0278-7393.13.1.87. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Palmeri TJ, McKinley SK. Rule-plus exception model of classification learning. Psychological Review. 1994;101:53–79. doi: 10.1037/0033-295x.101.1.53. [DOI] [PubMed] [Google Scholar]
- Pearce JM. A model of stimulus generalization for Pavlovian conditioning. Psychological Review. 1987;94:61–73. [PubMed] [Google Scholar]
- Pearce JM. Similarity and discrimination: A selective review and a connectionist model. Psychological Review. 1994;101:587–607. doi: 10.1037/0033-295x.101.4.587. [DOI] [PubMed] [Google Scholar]
- Reed SK. Pattern recognition and categorization. Cognitive Psychology. 1972;3:382–407. [Google Scholar]
- Reed SK. Category vs. item learning: implications for categorization models. Memory & Cognition. 1978;6:612–621. doi: 10.3758/bf03198251. [DOI] [PubMed] [Google Scholar]
- Regehr G, Brooks LR. Category organization in free classification: The organizing effect of an array of stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:347–363. [Google Scholar]
- Restle FA. A theory of discrimination learning. Psychological Review. 1955;62:11–19. doi: 10.1037/h0046642. [DOI] [PubMed] [Google Scholar]
- Restle FA. Discrimination of cues in mazes: a resolution of the “place-vs-response” question. Psychological Review. 1957;64:217–228. doi: 10.1037/h0040678. [DOI] [PubMed] [Google Scholar]
- Rosch E, Mervis CB. Family resemblances: Studies in the internal structure of categories. Cognitive Psychology. 1975;7:573–605. [Google Scholar]
- Rosseel Y. Mixture models of categorization. Journal of Mathematical Psychology. 2002;46:178–210. [Google Scholar]
- Rumbaugh DM, Pate JL. The evolution of cognition in primates: A comparative perspective. In: Roitblat HL, Bever TG, Terrace HS, editors. Animal cognition. Hillsdale, NJ USA: Erlbaum; 1984. pp. 569–589. [Google Scholar]
- Rumbaugh DM, Richardson WK, Washburn DA, Savage-Rumbaugh ES, Hopkins WD. Rhesus monkeys (Macaca mulatta), video tasks, and implications for stimulus-response spatial contiguity. Journal of Comparative Psychology. 1989;103:32–38. doi: 10.1037/0735-7036.103.1.32. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shepp BE, Swartz K. Selective attention and the processing of integral and nonintegral dimensions. A developmental study. Journal of Experimental Child Psychology. 1976;22:73–85. doi: 10.1016/0022-0965(76)90091-6. [DOI] [PubMed] [Google Scholar]
- Shepp BE, Burns B, McDonough D. The relation of stimulus structure to perceptual and cognitive development: Further tests of a separability hypothesis. In: Becker J, Wilkening F, editors. The integration of information by children. Hillsdale, NJ USA: Erlbaum; 1980. pp. 113–145. [Google Scholar]
- Smith JD, Kemler Nelson DG. Overall similarity in adults’ classification: The child in all of us. Journal of Experimental Psychology: General. 1984;113:137–159. [Google Scholar]
- Smith JD, Minda JP. Prototypes in the mist: the early epochs of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;24:1411–1436. [Google Scholar]
- Smith JD, Minda JP, Washburn DA. Category learning in rhesus monkeys: A study of the Shepard, Hovland, and Jenkins tasks. Journal of Experimental Psychology: General. 2004;133:398–414. doi: 10.1037/0096-3445.133.3.398. [DOI] [PubMed] [Google Scholar]
- Smith JD, Redford JS, Haas SM. Prototype abstraction by monkeys (Macaca mulatta) Journal of Experimental Psychology: General. 2008;137:390–401. doi: 10.1037/0096-3445.137.2.390. [DOI] [PubMed] [Google Scholar]
- Smith JD, Shapiro JH. The occurrence of holistic categorization. Journal of Memory and Language. 1989;28:386–399. [Google Scholar]
- Smith JD, Tracy J, Murray MJ. Depression and categorization. Journal of Experimental Psychology: General. 1993;122:331–346. doi: 10.1037//0096-3445.122.3.331. [DOI] [PubMed] [Google Scholar]
- Smith LB, Kemler DG. Developmental trends in free classification: Evidence for a new conceptualization. Journal of Experimental Child Psychology. 1977;24:279–298. [Google Scholar]
- Smith LB, Kemler DG. Levels of experienced dimensionality in children and adults. Cognitive Psychology. 1978;10:502–532. doi: 10.1016/0010-0285(78)90009-9. [DOI] [PubMed] [Google Scholar]
- Sutherland NS, Mackintosh NJ. Mechanisms of animal discrimination learning. New York: Academic Press; 1971. [Google Scholar]
- Trabasso TR, Bower GH. Attention in learning: Theory and research. New York: Wiley; 1968. [Google Scholar]
- Vauclair J. Categorization and conceptional behavior in nonhuman primates. In: Bekoff M, Allen C, editors. The cognitive animal: Empirical and theoretical perspectives on animal cognition. Cambridge, MA: MIT Press; 2002. pp. 239–245. [Google Scholar]
- Waldron EM, Ashby FG. The effects of concurrent task interference on category learning: Evidence for multiple category learning systems. Psychonomic Bulletin & Review. 2001;8:168–176. doi: 10.3758/bf03196154. [DOI] [PubMed] [Google Scholar]
- Ward TB. Response tempo and separable-integral responding: Evidence for an integral-to-separable processing sequence in visual perception. Journal of Experimental Psychology: Human Perception and Performance. 1983;9:103–112. doi: 10.1037//0096-1523.9.1.103. [DOI] [PubMed] [Google Scholar]
- Warren JM. Additivity of cues in visual pattern discrimination by monkeys. Journal of Comparative and Physiological Psychology. 1953;46:484–486. doi: 10.1037/h0055613. [DOI] [PubMed] [Google Scholar]
- Washburn DA, Rumbaugh DM. Testing primates with joystick-based automated apparatus: Lessons from the Language Research Center’s Computerized Test System. Behavior Research Methods, Instruments, and Computers. 1992;24:157–164. doi: 10.3758/bf03203490. [DOI] [PubMed] [Google Scholar]
- Wasserman EA, Kiedinger RE, Bhatt RS. Conceptual behavior in pigeons: categories, subcategories, and pseudocategories. Journal of Experimental Psychology: Animal Behavior Processes. 1988;14:235–246. [Google Scholar]
- Zeaman D, House BJ. The role of attention in retardate discrimination learning. In: Ellis NR, editor. Handbook of mental deficiency: Psychological theory and research. New York: McGraw-Hill; 1963. [Google Scholar]