The dimensionality of discourse

Abstract

The paragraph spaces of five text corpora, of different genres and intended audiences, in four different languages, all show the same two-scale structure, with the dimension at short distances being lower than at long distances. In all five cases the short-distance dimension is approximately eight. Control simulations with randomly permuted word instances do not exhibit a low dimensional structure. The observed topology places important constraints on the way in which authors construct prose, which may be universal.

As we transition from paragraph to paragraph in written discourse, one can think of the path through which one passes as a trajectory through a semantic space. Understanding the discourse is, in some sense, a matter of understanding this trajectory. Although it is difficult to predict exactly what will follow from a given discourse context, we can ask a broader question. Does the cognitive system impose any fundamental constraints on the way in which the discourse evolves?

To investigate this issue, we constructed semantic spaces for five corpora, of different genres and intended audiences, in four different languages and then calculated the intrinsic dimensionality of the paragraph trajectories through these corpora. Each trajectory can be embedded in an arbitrary number of dimensions, but it has an intrinsic dimensionality, independent of the embedding space. For instance, in latent semantic analysis (LSA) applications, it is typical to use a 300-dimensional space (1). However, the points that represent the paragraphs in this 300-dimensional space do not fill the embedding space; rather they lie on a subspace with a dimension lower than the embedding dimension. The fact that a low-dimensional structure can be embedded in a higher dimensional space is routinely used in the study of nonlinear dynamic systems, in which the embedding theorem (2) relates the dimensionality of the dataset under study to the dimensionality of the dynamics that describes it.

Historically, the dimensionality of the discourse trajectory has been implicitly assumed to be very large, but it has never been calculated. Here we show that the dimensionality of the trajectory is surprisingly low (approximately eight at short distances) and that its structure is probably universal across human languages. Although the question of dimensionality has not generally been considered before, it can be used to guide the development of new models of prose, which are constrained to reproduce the observed dimensional structure.

Modeling Semantics

The first step toward being able to calculate the dimensionality of text is to create a vector representation of the semantics conveyed by each paragraph. Recent years have seen increasing interest in automated methods for the construction of semantic representations of paragraphs [e.g., LSA (3), the topics model (4, 5), nonnegative matrix factorization (6), and the constructed semantics model (7)]. These methods were originally developed for use in information retrieval applications (8) but are now widely applied in both pure and applied settings (3). For example, LSA measures correlate with human judgments of paragraph similarity; correlate highly with humans’ scores on standard vocabulary and subject matter tests; mimic human word sorting and category judgements; simulate word–word and passage–word lexical priming data; and accurately estimate passage coherence. In addition, LSA has found application in many areas, including selecting educational materials for individual students, guiding on-line discussion groups, providing feedback to pilots on landing technique, diagnosing mental disorders from prose, matching jobs with candidates, and facilitating automated tutors (3).

By far the most surprising application of LSA is its ability to grade student essay scripts. Foltz et al. (9) summarize the remarkable reliability with which it is able to do this, especially when compared against the benchmark of expert human graders. In a set of 188 essays written on the functioning of the human heart, the average correlation between two graders was 0.83, whereas the correlation of LSA’s scores with the graders was 0.80. A summary of the performance of LSA’s scoring compared with the grader-to-grader performance across a diverse set of 1,205 essays on 12 topics showed an interrater reliability of 0.7 and a rater-to-LSA reliability of 0.7. LSA has also been used to grade two questions from the standardized Graduate Management Admission Test. The performance was compared against two trained graders from Educational Testing Services (ETS). For one question, a set of 695 opinion essays, the correlation between the two graders was 0.86, and LSA’s correlation with the ETS grades was also 0.86. For the second question, a set of 668 analyses of argument essays, the correlation between the two graders was 0.87, whereas LSA’s correlation to the ETS grades was 0.86.

In the research outlined above, LSA was conducted on paragraphs. However, it is known to degrade rapidly if applied at the sentence level, where capturing semantics requires one to establish the fillers of thematic roles and extract other logical relationships between constituents. Nevertheless, to achieve the results outlined above, LSA must be capturing an important component of what we would typically think of as the semantics or meaning of texts. In this study, we investigate the geometric structure of this kind of semantics.

The Correlation Dimension

There are many different dimensions that can be defined for a given dataset. They include the Hausdorff dimension, the family of fractal dimensions, D_n (capacity, D₀; information, D₁; correlation, D₂, etc), the Kaplan-Yoke dimension, etc. (10). A usual choice for small datasets is the correlation dimension (11) because it is more efficient and less noisy when only a small number of points is available. It can be shown that D_capacity ≥ D_information ≥ D_correlation, but in practice almost all attractors have values of the various dimensions that are very close to each other (10, 12).

The correlation dimension is derived by considering the correlation function

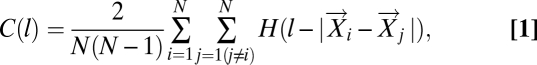where 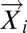is an M dimensional vector pointing to the location of the ith point in the dataset in the embedding space, M is the number of dimensions within which the data are embedded, N is the total number of data points, and H is the Heaviside function. The correlation function is therefore the normalized count of the number of distances between points in the dataset that are less than the length l. The correlation dimension, ν, is then given by

In other words, the correlation dimension is given by the slope of the ln[C(l)] vs. ln(l) graph.

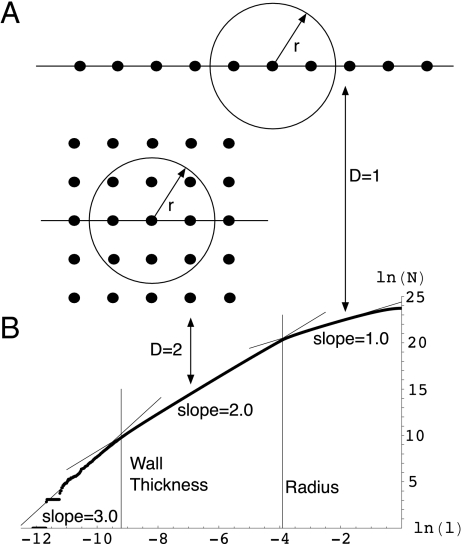
The correlation dimension captures the way that the number of points within a distance l scales with that distance. For points on a line, doubling the distance l would double the number of points that can be found within that distance. For points on a plane, the number of points within a distance l quadruples as l doubles. In general, the number of points within distance l will scale as l^ν, where ν is the correlation dimension (Fig. 1A).

Fig. 1.

The measured dimensionality of a long pipe. (A) Schematic representation of the scaling of the correlation function with distance; the number of points within a distance r scales as r^D. (B) Correlation function for 100,000 points randomly distributed so as to define a hollow tube of length unity. The radius of the tube is 10⁻² and the thickness of the tube wall 10⁻⁴. The slopes give dimensions of 3.0, 2.0, and 1.0, respectively, at length scales that are smaller than the thickness of the wall, between the thickness of the wall and the diameter of the tube, and longer than the diameter of the tube.

The correlation dimension, as well as all other dimensions, are strictly defined only at the limit 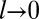(with 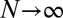). In practice, the limit essentially means a length scale that is much smaller than any other length scale of the system. With that definition in mind, one can envision geometric structures that exhibit different well-defined dimensions at different length scales, as long as those length scales are well separated. A typical example is a long hollow pipe. At length scales longer than its diameter, the pipe is one-dimensional. At intermediate scales, between the diameter of the tube and the thickness of the wall, the pipe is two-dimensional. At scales shorter than the wall thickness, the pipe looks three-dimensional. Fig. 1B shows a plot of the correlation function for such a structure. We see that the three scales are clearly distinguishable, with narrow transition regions around the length scales of the wall thickness and diameter, as expected. A similar example in the reverse order is a large piece of woven cloth. It looks two-dimensional at long scales, but at short scales it is composed of one-dimensional threads. This is the picture that the five language corpora that we have studied present; they look low-dimensional at short scales and higher-dimensional at long scales.

Description of the Corpora

We have calculated the correlation dimension of five corpora, in English, French, modern and Homeric Greek, and German. The English corpus includes text written for children as well as adults, representing the range of texts that a typical US college freshman will have encountered. The French corpus includes excerpts from articles in the newspaper Le Monde, as well as excerpts from novels written for adults. The modern Greek corpus comprises articles in the political, cultural, economic, and sports pages of the newspaper Eleftherotypia, as well as articles from the political pages of the newspaper Ta Nea. The German corpus includes articles from German textbooks and text extracted from Internet sites and is intended to represent the general knowledge of an adult native speaker of German. The Homeric corpus consists of the complete Iliad and Odyssey. The Homeric corpus also contains large bodies of contiguous text, whereas the other four corpora are made up of fragments that are at most eight paragraphs long. The paragraphs (stanzas for Homer) in all five corpora are mostly 80–500 words long. The English corpus includes 37,651 paragraphs, the French 36,126, the German 51,027, the modern Greek 4,032, and the Homeric 2,241 paragraphs.

Calculating Paragraph Vectors

For the majority of the results presented in this article, we used the method of LSA (3) to construct paragraph vectors. For each corpus, we construct a matrix whose elements, M_ij, are given by

where m_ij is the number of times that the jth word type is found in the ith paragraph. j ranges from one to the size of the vocabulary and i ranges from one to the number of paragraphs. Further,

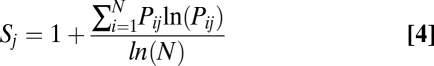is the weight given to each word, which depends on the information entropy of the word across paragraphs (13). In the above expression

is the probability density of the jth word in the ith paragraph, and N is the total number of paragraphs in the corpus (13).

Given the matrix M, we then construct a reduced representation by performing singular value decomposition and keeping only the singular vectors that correspond to the n largest singular values. This step relies on a linear algebra theorem, which states that any M × N matrix A with M > N can be written as A = USV^T, where U is an M × N matrix with orthonormal columns, V^T is an N × N matrix with orthonormal rows, and S is an N × N diagonal matrix (14). By writing the matrix equation as

it is clear that for a spectrum of singular values S_l that decays in some well-behaved way, the matrix A can be approximated by the n highest singular values and corresponding singular vectors. LSA applications achieve best results by keeping typically 300 values at this step (1). The number of singular values that we keep in the five corpora ranges from 300 to 420.

Measurements of the Correlation Dimension

In calculating the correlation dimension of the corpora, we use the normalized, rather than the full, paragraph vectors. The choice is motivated by the observation that the measure of similarity between paragraphs used in LSA applications is the cosine of the angle between the two vectors. By using the cosine as the similarity measure, the method deemphasizes the importance of vector length to the measure of semantic distance. Vector length is associated with the length of the paragraph the vector represents; two paragraphs can be semantically very similar, though being of significantly different length. However, the cosine is not a metric, so we use the usual Cartesian distance, 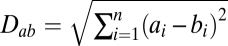, for the dimension calculations, but we will use it with the normalized vectors. This is equivalent to defining the dimensionality of the Norwegian coast, for example, by using the straight-line distances between points on the coast instead of the usual surface distances. The two are equivalent over short scales but can be expected to diverge somewhat over distance scales comparable to the radius of the Earth. Because angular distances in language corpora are seldom greater than π/2, both the arc length and the Cartesian metrics give similar results for all but the longest scales.

There are several ways one can calculate the correlation dimension (e.g., ref. 15; see also an extensive review in ref. 16). One of the earliest methods is the maximum likelihood estimate (17), which is known in the dynamics literature as the Takens estimate (18, 19); the estimate was proposed independently by Ellner (20) and again recently by Levina and Bickel (21). However, although the Takens estimate is rigorously a maximum likelihood estimate, in practice, if we need to calculate the correlation dimension of a structure over an intermediate range of distances we need to specify the end points of each linear region of interest, and that choice influences the estimate. To avoid this problem, we chose to estimate the slopes with a “bent-cable” regressive method (22). The bent-cable model assumes a linear regime, followed by a quadratic transition component, followed by another linear regime, described by the equation:

where

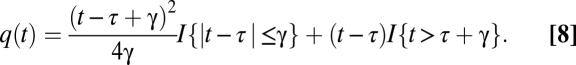It is commonly used in describing ecological phase transitions and is particularly useful in our case, because it allows us to capture the quadratic transition between the low and upper scales and avoid contamination of the slope estimates from this region (note that the lower slope estimate is given by b₁ and the upper slope estimate by b₁ + b₂).

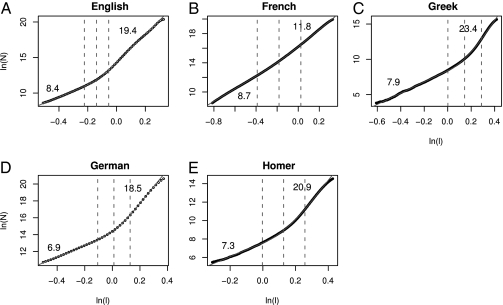
Fig. 2A shows the log of the number of distances, N, that are less than l plotted against the log of l for the English corpus, as well as the bent-cable fit and slope estimates. The Takens estimates are also provided in the caption for comparison purposes. Fig. 2 B–E shows the same plot for the French, Greek, German, and Homeric corpora, respectively. The bent-cable estimates for the dimensionality of the short and long distances, respectively, are 8.4 and 19.4 for the English corpus, 6.9 and 18.5 for German, 8.7 and 11.8 for French, 7.9 and 23.4 for Greek, and 7.3 and 20.9 for Homer. All five corpora clearly show a “weave-like” structure, in which the dimensionality at short distances is smaller than the dimensionality at long distances. Furthermore, the value of the low dimension is approximately eight for all five corpora, suggesting that this may be a universal property of languages.

Fig. 2.

The measured dimensionality of the five corpora. (A) the English corpus, (B) the French corpus, (C) the modern Greek corpus, (D) the German corpus, (E) Homer. All corpora exhibit a low-dimensional structure, with the dimensionality at long scales being higher than at short scales. The Takens estimates are 7.4 and 19.8 for the English corpus, 9.1 and 13.1 for the French, 8.6 and 28.3 for the Greek, 7.4 and 22.2 for the German, and 8.2 and 25.3 for Homer. The solid lines show the best-fitting bent-cable regression.

We carried out K-fold cross-validation for the bent-cable model and several alternative models to make sure that the estimates of dimension were based on models that fit the data well without being overly complex (see, e.g., ref. 23 for a discussion of K-fold cross-validation). Four models were cross-validated: the bent-cable regression model and polynomial regression models of degree 1 (linear), 2, and 3. We were especially interested in showing that the bent-cable model is superior to the quadratic polynomial, so as to justify the assertion that there are two linear regions of the correlation dimension function. To carry out cross-validation, the data for each correlation dimension plot were randomly divided equally into 10 samples or folds. For each fold, a predictive model was developed from the nine remaining folds. The predictive model was then applied to the held-out fold, and the residual sum of squares for the predictions of that model was calculated (CV RSS). The mean CV RSS across the 10 folds served as a measure of predictive validity—models with lower values are better models than those with higher values. Table 1 displays the CV RSS for each corpus and model. The bent-cable regression model had the lowest CV RSS for each row of the table, which confirms the impression that it is a good descriptive model for the correlation dimension functions.

Table 1.

CV RSS for each corpus and model

Corpus	Linear	Poly. 2	Poly. 3	Bent-cable
English	3.24 (0.95)	0.30 (0.20)	0.21 (0.09)	0.05 (0.04)
English topics	29.04 (4.99)	1.27 (0.14)	0.39 (0.15)	0.10 (0.05)
English NMF	22.38 (2.68)	2.72 (0.31)	0.21 (0.05)	0.11 (0.04)
German	2.53 (1.32)	0.17 (0.04)	0.14 (0.17)	0.03 (0.06)
French	0.68 (0.15)	0.04 (0.01)	0.03 (0.02)	0.01 (0.01)
Greek	24.41 (4.02)	4.31 (0.38)	0.67 (0.15)	0.26 (0.06)
Homer	7.30 (2.87)	0.35 (0.06)	0.25 (0.15)	0.11 (0.03)

Values are mean (SD). The models include polynomial regression (Poly.) with degree 1 through 3 and the bent-cable regression model.

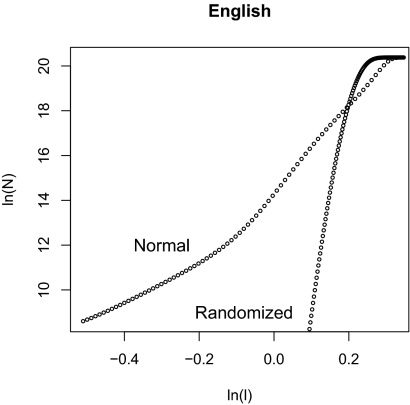
As a control test, we also calculated the correlation dimension for a space constructed by randomly combining words from the English space. To construct the randomized English corpus, we build each paragraph in turn by taking at random, and without replacement, a word from the corpus until we reach the length of the original paragraph, and we repeat the process for all of the paragraphs. It is thus clear that the randomized corpus contains the exact number of paragraphs and words as the original, and that all word frequencies are also exactly the same; however, the word choice for each paragraph has been permuted. Fig. 3 shows a plot of the correlation function for that corpus. The number of paragraphs, the length of each paragraph, and the numbers of occurrences of each word are the same in the two corpora, but the random corpus does not have a low-dimensional structure. Instead the points are space-filling within the limitations of the sample size. This implies that the observed low-dimensional structure is a property of the word choice in the paragraphs and not a property of the word frequency or paragraph length distributions of the corpus.

Fig. 3.

The measured dimensionality of the randomized English corpus. The randomized corpus does not show the low-dimensional structure of the English corpus, and it is space-filling within the limitations of the number of points used. This implies that the low-dimensional structure is a property of the word choice in the paragraphs and not of paragraph length or word frequency in the corpus.

In addition to LSA, several methods for modeling the semantic relationships between paragraphs have been developed in recent years. We replicated the results for the English corpus with two of these methods: the topics model (4, 5) and the nonnegative matrix factorization (NMF) (6). Unlike LSA, both of these methods yield semantic space-like representations of paragraphs with interpretable components. For example, a given topic from a topics model or NMF component might code “finances”, so that paragraphs to do with “money” or “financial institutions” are associated with that topic or component.

The topics model focuses on the probability of assigning words from a fixed vocabulary to word tokens in a paragraph. For a given token, words related to the gist of a paragraph should have high probability, even when they do not appear in the paragraph. For example, for a paragraph about finances, the probability of the word “currency” should be significantly higher than the probability of a random word, such as “frog,” even if neither word appeared in the paragraph. To accomplish this type of generalization, the model includes latent random variables called topics. For each topic, z, there is a separate distribution over words, P(w|z). The latent variables allow for a compressed representation of paragraphs as a distribution over topics, P(z). The number of topics is arbitrary and is typically set to several hundred. The words that appear in paragraphs are related to topics through a generative process, which assumes that each word in a paragraph is selected by first sampling a topic from P(z) and then sampling a word from P(w|z). The probability of words within paragraphs is given by

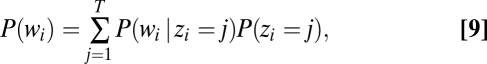where i indexes the word tokens within a paragraph, and j indexes the topics.

The generative process can be inverted with Bayesian methods to identify topics that are most probable given the corpus and reasonable priors. Additional assumptions need to be made to estimate the parameters of the model. For example, Steyvers and Griffiths (5, 24) assume that P(z) and P(w|z) are distributed as multinomials with Dirichlet priors. Once topics distributions over all paragraphs are estimated, the similarity of pairs of paragraphs can in turn be estimated by calculating the divergence of their distributions.

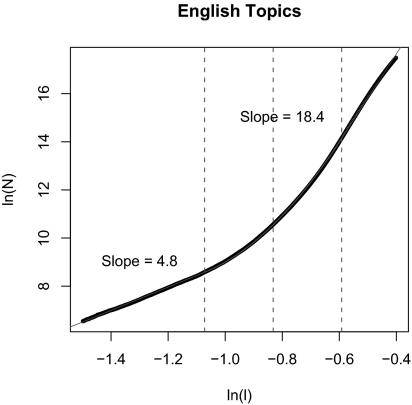
Fig. 4 displays the correlation function for the topic distributions for the English corpus that were estimated with the method of Steyvers and Griffiths (5, 24). The number of topics was set to 600 on the basis of previous research (4), and a stop-list was used. A stop-list is a set of high-frequency function words that are excluded to prevent them from dominating the solution. Stop-listing was not necessary for LSA, because its weighting procedure reduces the impact of high-frequency words. The distance between pairs of paragraphs was calculated with the square root of the Jensen-Shannon divergence. Because this measure has been shown to meet metric criteria (25, 26), it is more appropriate for the correlation dimension analysis than other measures of divergence that do not meet these criteria, such as the Kullback-Leibler divergence. Note that the two-level structure is clearly replicated, although the dimension estimates are lower. We did not expect to obtain the same estimates, given that the spatial assumptions of the correlation dimension analysis are not met (the axes of the space are not orthogonal). Nevertheless, the weave structure remains.

Fig. 4.

The English corpus using the topics model. Paragraph distances are calculated using the square root of the Jensen-Shannon divergence, which is a metric. Although the dimensions are not orthogonal, and therefore one would not expect the correlation dimension to give interpretable results, we can still discern a two-scale dimensional structure.

To obtain a converging estimate of dimensionality using a different dimensionality reduction algorithm, we chose to implement NMF (6). NMF has also been applied to calculate paragraph similarity, and, like the topics model, has been found to produce interpretable dimensions (6). Unlike the topics model, however, the version of NMF that we used is predicated on the minimization of squared Euclidean metric and so is more directly comparable to the LSA case. Furthermore, although the dimensions that NMF extracts are not constrained to be orthogonal as in LSA, in practice, the factors that are commonly produced in text processing domains tend to be approximately orthogonal, and so it is reasonable to think that dimensionality estimates based on NMF and LSA should be similar.

To carry out NMF, standard LSA preprocessing was carried out on the term–paragraph counts for the English corpus (see above). The resulting nonnegative matrix M was then approximated by the product of two nonnegative matrices, W and H. Recall that the rows of M hold the n transformed counts for each of the p paragraphs. Hence,

where M is p × n, W is p × r, and H is r × n. The value of r was set to 420, which is the same number of dimensions for the LSA model. A multiplicative update rule of Lee and Seung (6) was applied to find values of W and H that minimize the reconstruction error (D) between M and WH, as measured by the Euclidean objective function,

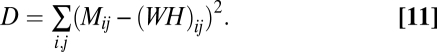The Lee and Seung method requires that the columns of W are normalized to unit length after each training iteration, so that the solution is unique. The Euclidean distance between normalized rows of the final W estimates the similarity between the corresponding paragraphs in the NMF space.

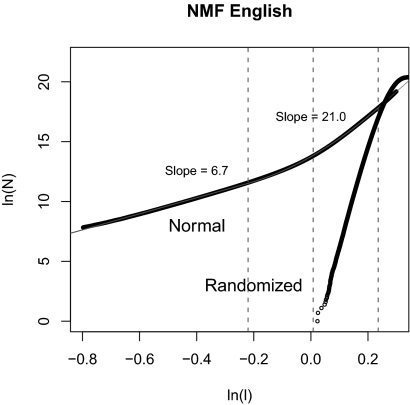
Fig. 5 displays the correlation function for the NMF space based on the distances between all pairs of paragraphs (i.e., rows of W) for the English corpus. Note that the two-level structure that appears in Fig. 2A is replicated once again. As in the case of the topics model, this replication is remarkable when we consider that not all of the assumptions of the correlation dimension analysis are met. Note also that the dimension estimates are much closer to those obtained with LSA, perhaps because the assumptions are better met.

Fig. 5.

The English corpus using the NMF model. Paragraph distances are calculated using Euclidean distance. Although the dimensions are not constrained to be orthogonal, and therefore one would not expect the correlation dimension to give interpretable results, a weave-like two-scale dimensional structure is again evident. The randomized corpus is again space-filling to the limit of the dataset, suggesting that the observed dimensional structure is a property of the word choice in the paragraphs and not of paragraph length or word frequency in the corpus.

Discussion

The results reported above place strong constraints on the topology of the space through which authors move as they construct prose and correspondingly the space through which readers move as they read prose. In all five corpora there are two distinct length scales. At the shorter length scale the dimensionality is ≈8 in each case, whereas at the longer scale the dimensionality varies from ≈12 to ≈23. Furthermore, the control simulations imply that these dimensionality are directly related to word choice and not to other properties of the corpora, such as the distribution of word frequencies or the distribution of paragraph lengths.

The above results can guide the development of models of language. Perhaps the simplest way one could attempt to characterize the paragraph trajectory would be as a random walk model in an unbounded Euclidean space. In such a model, each paragraph would be generated by drawing a multivariate Gaussian sample and adding that to the location of the previous paragraph. Such a model is implicitly assumed in applications of LSA to the testing of textual coherence (8) and to textual assessment of patients for mental illnesses such as schizophrenia (27). However, such models cannot reproduce the observed weave-like dimensional structure.

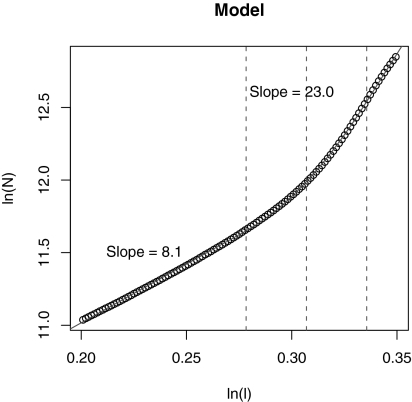
So what could produce the observed structure? To investigate this question, we implemented a version of the topics model (as discussed above). Rather than train the model on a corpus, however, we used the model to generate paragraphs on the basis of its priors. We set the number of topics to eight and generated 1,000 paragraphs, each 100 words long. The Dirichlet parameter was set to 0.08, and each topic was associated with 500 equiprobable and unique words. That is, there was no overlap in the words generated from different topics. This later assumption is a simplification of the original model that was used to avoid having to parameterize the amount of overlap. Fig. 6 shows the correlation plot derived from this corpus by applying LSA with 100 dimensions. It displays the two-scale structure with a lower dimensionality of 8.1 and an upper dimensionality of 23.0, approximating the pattern seen in the data.

Fig. 6.

Measured dimensionality from the corpus generated from a version of the topics model.

To understand how the model captures the two-scale structure, consider the topic distributions generated from the Dirichlet prior. With a parameter of 0.08, most samples from the Dirichlet distribution have a single topic that has a much higher probability than the other topics. Paragraphs generated from these samples have words drawn from just one pool. However, there is a subset of samples that have two topics with substantive probability. Paragraphs generated from these samples have words drawn from two of the pools. The paragraph pairs that appear in the upper region involve comparisons between paragraphs that are dominated by topics that are different from each other. The paragraph pairs that appear in the lower region involve comparisons between one paragraph that is dominated by a single topic and one paragraph that has a substantive probability for the same topic but also includes another topic with reasonable probability. The common topic brings the representations of these paragraphs closer together. Because there are eight topics, there are eight dimensions in which these comparisons can vary. The model demonstrates that it is not necessary to posit a hierarchically organized model to account for the two-scale structure.

Conclusions

The correlation dimensions of five corpora composed of texts from different genres, intended for different audiences, and in different languages—English, French, Greek, Homeric Greek, and German—were calculated. All five corpora exhibit two distinct regimes, with short distances exhibiting a lower dimensionality than long distances. In each case, the dimensionality of the lower regime is approximately eight. This pattern is not observed if words are permuted to disrupt word cooccurrence. The observed structure places important constraints on models of constructing prose, which may be universal.