Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics

Abstract

We show how to apply the method of temperature-accelerated molecular dynamics (TAMD) in collective variables [Maragliano L, Vanden-Eijnden E (2006) Chem Phys Lett 426:168–175] to sample the conformational space of multidomain proteins in all-atom, explicitly solvated molecular dynamics simulations. The method allows the system to hyperthermally explore the free-energy surface in a set of collective variables computed at the physical temperature. As collective variables, we pick Cartesian coordinates of centers of contiguous subdomains. The method is applied to the GroEL subunit, a 55-kDa, three-domain protein, and HIV-1 gp120. For GroEL, the method induces in about 40 ns conformational changes that recapitulate the t → r^′′ transition and are not observed in unaccelerated molecular dynamics: The apical domain is displaced by 30 Å, with a twist of 90° relative to the equatorial domain, and the root-mean-squared deviation relative to the r^′′ conformer is reduced from 13 to 5 Å, representing fairly high predictive capability. For gp120, the method predicts both counterrotation of inner and outer domains and disruption of the so-called bridging sheet. In particular, TAMD on gp120 initially in the CD4-bound conformation visits conformations that deviate by 3.6 Å from the gp120 conformer in complex with antibody F105, again reflecting good predictive capability. TAMD generates plausible all-atom models of the so-far structurally uncharacterized unliganded conformation of HIV-1 gp120, which may prove useful in the development of inhibitors and immunogens. The fictitious temperature employed also gives a rough estimate of 10 kcal/mol for the free-energy barrier between conformers in both cases.

Since Koshland’s introduction of the concept of “induced fit” (1), it is well accepted that conformational changes upon ligand binding underlie a substantial fraction of protein functionality (2, 3). Crystal structures of hundreds of proteins in both apo and liganded states often display evidence for motion of domains relative to one another over length scales characteristic of the domains themselves (4). Crystallographic conformers of the same protein, however, cannot provide much insight into the detailed mechanism of conformational change, especially if more than one hinge or other flexible element is involved. Even worse, there are many multidomain proteins for which only a single crystallographic conformer exists despite functional requirements for multiple conformers. On top of obscuring the structural biology of many multidomain proteins, often a single crystallographic conformer is too narrow a basis upon which to design molecules that act as allosteric effectors: agents that stabilize either active or inhibitory conformations by binding to sites other than those used by the primary ligands. It has therefore become attractive to probe the details of protein conformational dynamics using simulation methods, such as molecular dynamics (MD) and related techniques.

Domain-level conformation is characterized using a few collective variables (CVs; e.g., interdomain hinge angles or low-frequency normal modes), denoted here by 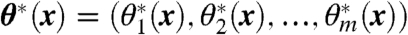, which are functions of atom Cartesian coordinates, the fundamental variables of crystallography and classical MD simulations (5, 6). Generally, any set θ^∗(x) defines a space in which equilibrium probabilities at constant temperature are proportional to the Boltzmann factor of the associated restricted free energy F(θ):

[1]

Here, 〈·〉 denotes the canonical (Boltzmann-weighted) average at temperature T and β = 1/k_BT where k_B is Boltzmann’s constant. Because constant-temperature MD can generate configurations at their correct Boltzmann-weighted probabilities, it can in principle be harnessed to compute free energy over any set of CVs via sampling of p(θ). However, the time scales required for dynamical simulations to push systems over free-energy barriers in CV space scale exponentially with the product of the inverse thermal energy β and barrier height. As a result, traditional all-atom MD simulation has difficulty surmounting even relatively small barriers of a few kcal/mol in computationally accessible times.

Approaches to overcome this limitation generally involve biasing techniques to focus sampling in relevant regions of CV space, often combined with coarse-graining schemes (e.g., united-atom, C_α Gaussian networks) to reduce computational expense. Probably the most popular among these techniques is the so-called targeted MD (7), which samples conformation by “attracting” a system to a target structure using a biased potential containing target information. Other methods such as thermodynamic integration (8), umbrella sampling/histogram reweighting (9), and nonequilibrium work methods (10, 11), among others, have been applied to protein simulations to compute restricted free energy along one or two CVs and thereby explore the conformational space projected in these variables. A major limitation of these techniques is that they are only applicable if the number of CVs is small. This requires the user to make an a priori choice based on intuition of which variables are important and which are not, which is often unsatisfactory because it can introduce an unrealistic bias on how the event(s) of interest will occur.

Except perhaps for metadynamics (12), there currently does not seem to be a method by which one can perform accelerated sampling of a relatively large CV space via an all-atom, explicit solvent MD simulation with no target bias. Here, we propose a method that meets the following criteria:

1. Retains atomistic details and explicit solvent

2. Uses no target bias

3. Is flexible in determining type and number of conformational CVs

4. Ensures that the free-energy surface of those variables is sampled correctly at the physical temperature

5. Provides means to tune the degree of acceleration for rough characterization of the free-energy landscape

6. Is easily implemented on top of existing MD packages.

This method uses the temperature-accelerated MD (TAMD) (13) technique in which the free-energy landscape at the physical temperature of a large set of suitably chosen CVs is explored fast using an artificially high fictitious temperature. TAMD is similar to adiabatic molecular dynamics methods (14, 15) except it does not require reformulation of system equations of motion. We report results of application of this method to enhance the rate at which two particular all-atom, explicitly solvated proteins, the Escherichia coli GroEL chaperonin subunit and the HIV-1 envelope gp120, sample distinct conformational states defined by relative orientations of their domains. Here, the CVs are Cartesian coordinates of centers of mass of carefully selected subdomains; in particular, we treat 27 CVs for GroEL and 69 for HIV-1 gp120. For both cases, we demonstrate reasonably accurate prediction of target conformations as well as unanticipated conformations that may be physiologically relevant.

Model

We provide here a brief sketch of the TAMD method; theoretical details have appeared elsewhere (13, 16, 17) and are presented again in SI Text. One should first envision a standard, all-atom MD simulation evolving fundamental variables (i.e., atomic coordinates) x(t) using a thermostat (such as Langevin dynamics) at the physical thermal energy β^-1. Consider now a set of m CVs θ^∗(x) each of which is a function of x. One could conduct an MD simulation in which forces are applied to restrain each CV 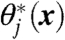to a particular value θ_j. In such a case, the dynamics of fundamental variable x_i would be

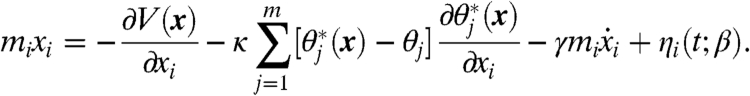[2]

Here, m_i is the mass of x_i, V(x) is the interatomic potential, κ is the “spring constant” in the restraining force, γ is the Langevin friction coefficient, and η is white noise satisfying the fluctuation-dissipation theorem at physical temperature β^-1:

[3]

Like any restrained constant-temperature dynamics, such simulations can serve as the kernels of thermodynamic integration, because the ensemble average of the restraining force calculated via time average along the MD trajectory,

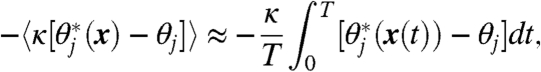[4]

gives an estimate of the negative gradient of the free energy associated with the set of CVs at the local point defined by the restraint values θ.

In TAMD, instead of fixing restraint values, they are treated as slow variables that evolve according to their own equations of motion, which here we take as diffusive [though other choices are possible (13)]:

[5]

Here, 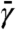is a fictitious friction, 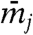is a mass, the first term on the right-hand side represents the instantaneous force on variable θ_j, and the second term represents thermal noise at the fictitious thermal energy :

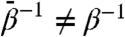[6]

The advantage of TAMD, as shown in detail elsewhere (13) and recounted in SI Text, is that if (i) 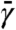is chosen sufficiently large so as to guarantee that the slow variables indeed evolve slowly relative to the fundamental variables, and (ii) κ is sufficiently large such that θ^∗(x(t)) ≈ θ(t) at any given time, then the force acting on θ is approximately equal to minus the gradient of the free energy. In other words, the dynamics of θ(t) is effectively

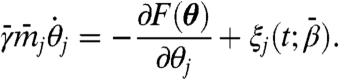[7]

This yields an important implication: The slow variable dynamics conforms to an equilibrium constant-temperature ensemble at fictitious temperature 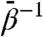subject to the restricted free energy F(θ) evaluated at the physical temperature β^-1. The MD simulation (at β) simply serves as a tool for on-the-fly approximation of the local gradients of F(θ). Hence, points in CV space are sampled according to fictitious Boltzmann factor 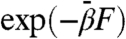which is tuned to be more uniform than the assocated physical Boltzmann factor exp(-βF) by taking 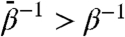. TAMD therefore can accelerate a trajectory θ(t) through CV space by increasing the likelihood of visiting points with relatively low physical Boltzmann factors.

We stress that we use TAMD here as a method for exploring the free energy in a set of CVs without actually reconstructing it explicitly using histogram methods or thermodynamic integration. In the latter case, one would perform a series of restrained MD simulations at different values of the CVs visited in a TAMD trajectory and then use the resulting free-energy gradients to interpolate globally the free energy. As shown in ref. 16, this can be done efficiently for moderately high dimensional CV spaces even if the points at which the mean force are evaluated do not lie on a regular grid. In the present study, however, the dimensionality of the CV space is probably too high to perform such a reconstruction. This is not an issue, however, if one only wishes to perform conformational sampling of the CV space, as we do here. In addition, we will show later how the artificial temperature used in TAMD can be used to get a rough estimate of the main free-energy barrier on this landscape (SI Text).

TAMD requires identifying CVs beforehand. It is important to note that TAMD puts no intrinsic limitation on the type or number of CVs. In particular, there is no reason with TAMD to restrict onself to only a few CVs; we consider 27 CVs simultaneously in GroEL and 69 CVs in gp120, as discussed below. The conformational transitions we wish to accelerate involve both relative rotational and translation motion of domains, so a minimal requirement of our choice of CVs is that they allow for the activation of such motion. Here, we use Cartesian coordinates of centers of mass of subdomains; i.e., spatially contiguous residue groups smaller than domains.

Specifically, for GroEL, we predefine a 10-Å-radius subdomain for each interdomain hinge. We then clustered residues in the apical and equatorial domains into three additional subdomains each, and reserved a final subdomain to include all intermediate domain residues not included in the two hinge subdomains, for a total of nine subdomains and therefore 27 CVs. For gp120, we clustered the inner domain into 9 subdomains and the outer domain into 14 subdomains, for a total of 69 CVs. Subdomain memberships and details regarding how they were determined are reported in SI Text.

Results

All simulations reported here were of all-atom, explicitly solvated/neutralized models of the GroEL subunit and unliganded gp120 using NAMD version 2.7 (18) and the CHARMM force field (19, 20) with TIP3P waters (21) with temperature controlled at 310 K using a conventional Langevin thermostat. A TAMD friction 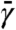of 50 ps^-1 and a spring constant κ of 100 kcal/mol·Å² were used uniformly. All TAMD trajectories were launched from MD-equilibrated configurations. Details regarding system preparation and parameter values appear in SI Text.

The GroEL Subunit.

GroEL is a homotetradecameric complex comprised of a back-to-back stacking of two seven-membered rings of 60-kDa, three-domain protomers (Fig. 1A) (22). GroEL catalyzes folding of substrate proteins by harnessing the energy of ATP binding and hydrolysis to drive large conformational rearrangements thought to cycle the complex into alternating states of protein binding and release. Based on crystal structures in apo and ligand-bound states, the conformational changes displayed by GroEL protomers in the complex are remarkably large: The so-called apical domain (the site of substrate binding) translates by 30 Å as the interdomain hinges open by a collective 60°. It also twists along its own axis by about 90° to position its main binding surface to bind the essential cochaperonin GroES.

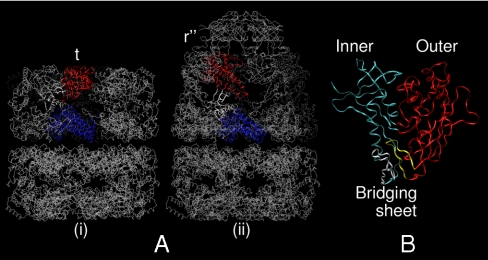
Fig. 1.

Crystallographic backbone renderings of (A) the GroEL homotetradecamer in (i) apo (41) and (ii) nucleotide/cochaperonin (GroES)-bound (42) states, and (B) HIV-1 gp120 in the CD4/17b bound state (29). In each panel of A, one protomer is rendered depicting the equatorial (blue), intermediate (white), and apical (red) domains. In B, inner domain is blue, outer is red, and the components of the bridging sheet, β2/3 and β20/21, are white and yellow, respectively.

Conformational changes in GroEL have been considered using normal mode analysis (23) and simulated by means of several target-bias methods (24, 25) and unbiased all-atom MD (26). Because of its large domain motions, GroEL is a particularly strong predictive challenge for conformational sampling. Also, an important unresolved question about the structural dynamics of GroEL is whether directionality of the apical domain twist is intrinsic to the subunit fold or depends upon protomer–protomer interactions in the GroES-bound tetradecamer.

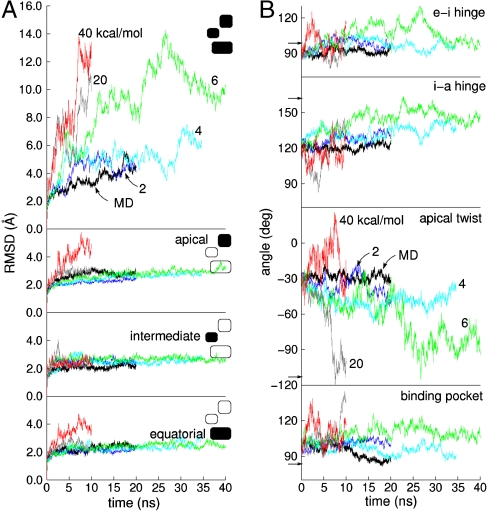
In Fig. 2A, we show root-mean-squared deviations (rmsds) of atom positions computed for the 20-ns MD and each of the TAMD simulations for 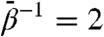, 4, 6, 20, and 40 kcal/mol. The uppermost panel shows rmsds for the entire subunit, and each of the remaining panels show domain-aligned rmsds. The whole-subunit rmsd for 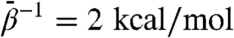is quantitatively similar to that computed from standard MD, indicating that this low fictitious temperature is insufficient to accelerate large-scale conformational changes on 20-ns time scales. However, for all other 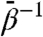, we observe rapid increases in rmsd, and generally the degree to which the rmsd increase is accelerated and the maximum values it samples increase with increasing . By itself, increased whole-subunit rmsd does not prove that domains are moving relative to one another; similar behavior of rmsd is expected when a globular protein unfolds. The domain-aligned rmsds, however, make clear that domain folds are preserved in almost all cases for which , for which domain rmsds do not exceed 3 Å. Domain unfolding becomes substantial for 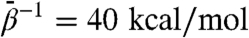. Therefore, the large rmsds displayed for intermediate values of 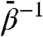are due to relative rigid-body motion of domains.

Fig. 2.

(A) All-atom rmsd from MD and TAMD simulations of the GroEL subunit. Uppermost panel depicts whole-subunit rmsd, and subsequent panels depict domain-aligned rmsds for apical, intermediate, and equatorial domains, respectively. Black traces correspond to traditional MD simulation; other traces colored according to fictitious temperature 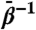as labeled in the Uppermost panel. (B) ICs used to measure conformation derived from the CVs vs. simulation time. From Top to Bottom are shown the hinge angle between the equatorial and intermediate domains, the hinge angle between intermediate and apical domains, the dihedral describing the twist of the apical domain, and the angle defining the disposition of the nucleotide binding pocket. Color scheme is same as in A. Arrows along the y axis denote IC values in the crystallographic r^′′ state (42).

Having established the bounds on 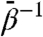for which accelerated domain-domain motion is observed while maintaining domain folds, we now consider the nature of this motion. Based on a comparison of the crystallographic t and r^′′ states, we defined four internal coordinates (ICs) based on the subdomain-center CVs: (i) the equatorial-intermediate and (ii) intermediate-apical interdomain hinge angles, (iii) the twist angle of the apical domain, and (iv) an angle characterizing the nucleotide binding pocket formed by the equatorial and intermediate domains. Precise definitions of these ICs appear in SI Text. In Fig. 2B, we show traces of each of these ICs for each of the MD and TAMD simulations. With the exception of the binding pocket angle, the ICs show essentially no change in the standard (unaccelerated) MD simulation. Arrows on the y axis in Fig. 2B indicate values of IC’s in the crystallographic r^′′ state. Of the two hinges, the hinge between the intermediate and apical domains experiences the larger change, responding to some degree in almost all TAMD simulations. The 6 kcal/mol TAMD simulation resulted in a combined 60° of opening of these two hinges, exactly what is inferred by comparison of the two crystallographic states. The apical domain twists by 90° in both the 6 and 20 kcal/mol TAMD simulations. Compared to the standard (unaccelerated) MD simulation, the intermediate temperature TAMD simulations sample a wider range of values of the ICs, and no one IC significantly goes beyond the value displayed by the r^′′ structure. These data demonstrate that the kinds of motion one expects based on the known crystallographic conformations are displayed by TAMD simulation.

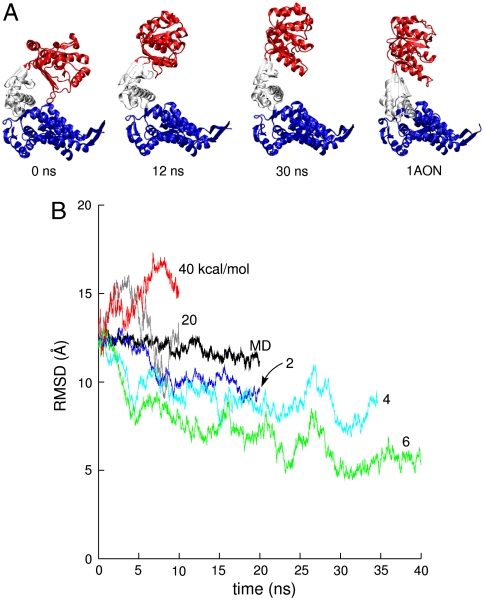
We examined the degree to which the TAMD-based “blind search” succeeds at generating conformations close to the r^′′ state. In Fig. 3A, we show representative snapshots from the simulation along with the static r^′′ crystal structure. As can be seen, the blind search does a remarkably good job recapitulating the target structure. At approximately 30 ns of run time, the 6 kcal/mol TAMD conformation is almost a perfect match for the r^′′ with the only major difference being a slight “outward” tilt of the intermediate and apical domains (relative to the location of the hypothetical sevenfold axis), resulting in an open nucleotide pocket. A measure of the degree to which the target structure is realized is the whole-subunit rmsd computed using the target structure as the reference, shown in Fig. 3B. These data indicate that the runs at 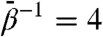and 6 kcal/mol generate conformational samples closest to the target structure, with a minimum deviation of about 5 Å.

Fig. 3.

(A) Snapshots of the GroEL subunit from TAMD simulation at 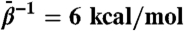. Rightmost panel shows the crystallographic r^′′ state from the same viewpoint. (B) Whole-subunit rmsd relative to the crystallographic r^′′ state (42) for traditional MD simulation and various TAMD simulations. Color scheme follows that of Fig. 2.

We point out that both the t and r^′′ conformers have only been shown crystallographically stable in tetradecameric complexes in which each subunit shares substantial buried interfacial area with four neighboring subunits (two intraring and two interring). These interactions stabilize the conformers to an unknown degree. Although the t conformer remains relatively stable over long times in MD simulations as a free subunit (24), it is unknown to what extent an uncomplexed r^′′ conformer is stable. We therefore conducted a separate TAMD simulation with 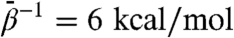beginning from the r^′′ conformer with ADP bound. We present detailed results in SI Text; important for this discussion is that the major conformational change displayed by an initially r^′′ conformer is an outward tilt of the intermediate and apical domains (relative to the hypothetical sevenfold axis). We observe conformations in this simulation that approach to within 2.3 Å rmsd relative to the most r^′′-like conformations generated in the original, t-state–initiated TAMD. It is remarkable that, starting from two very different conformers, namely t and r^′′, TAMD-based accelerated sampling converges upon a single conformation that differs slightly from the r^′′ state in a way consistent with the absence of neighboring protein–protein interactions in a heptameric ring.

HIV-1 gp120.

The product of the HIV-1 env gene, when trimerized and cleaved into fragments known as gp41 and gp120, forms the “spike” complex on the viral surface responsible for viral tropism and mediation of fusion of virus with a target cell (27, 28). The gp120 fragment possesses specific binding sites for the cell-surface CD4 and CCR5/CXCR4 coreceptors, the latter of which is “induced” by a poorly understood conformational change initiated by CD4 binding. As depicted based on crystallographic data in Fig. 1B, gp120 is comprised of an “inner” and “outer” domain, and the coreceptor binding site is structurally associated with a “bridging” four-strand β-sheet with a hairpin contributed by each domain (β2/3 from the inner, and β20/21 from the outer). Molecules that bind specifically to the unliganded form of gp120 could inhibit infection by blocking gp120’s ability to form the required coreceptor binding site. Unfortunately, all available crystal structures of HIV-1 gp120 include CD4 binding-site ligands; there is as yet no structural information on unliganded HIV-1 gp120, severely hampering the design of such allosteric inhibitors.

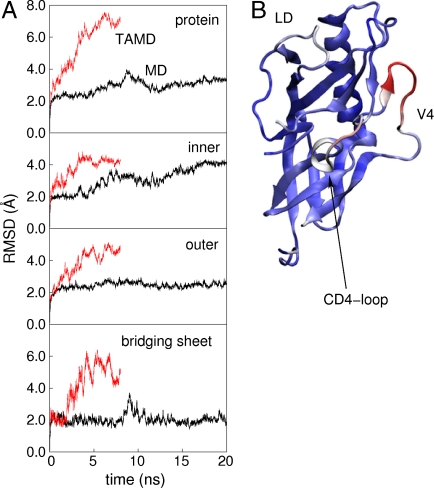
We generated four 4-ns TAMD trajectories at a fictitious temperature of 6 kcal/mol on an explicitly solvated, all-atom model of gp120 based on the 1g9n crystal structure (29). As with GroEL, we observed in gp120 that TAMD induced accelerated motion as measured by whole-protein rmsd, whereas domain-specific rmsds indicated predominantly rigid domain-level folds, as shown in Fig. 4A. The outer domain conformation was more flexible under TAMD predominantly due to enhanced flexibility of the already-flexible D, V4, and CD4-binding loops, as depicted in Fig. 4B, rather than any unfolding of secondary or tertiary structure.

Fig. 4.

(A) All-atom rmsd from MD and TAMD simulations of HIV-1 gp120. Uppermost panel depicts the whole-protein rmsd, and subsequent panels depict domain-aligned rmsds for the inner and outer domains, and bridging sheet, respectively. Black traces correspond to the traditional MD simulation and red traces to 4 ns of TAMD at 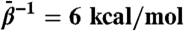, followed by 4 ns of unaccelerated MD. (B) Cartoon rendering of the HIV-1 gp120 outer domain colorized according to the difference in per-residue rms fluctuation in TAMD vs MD, with warmer colors signifying larger differences. The D-loop (“LD”), V4 loop, and CD4-binding loop are indicated.

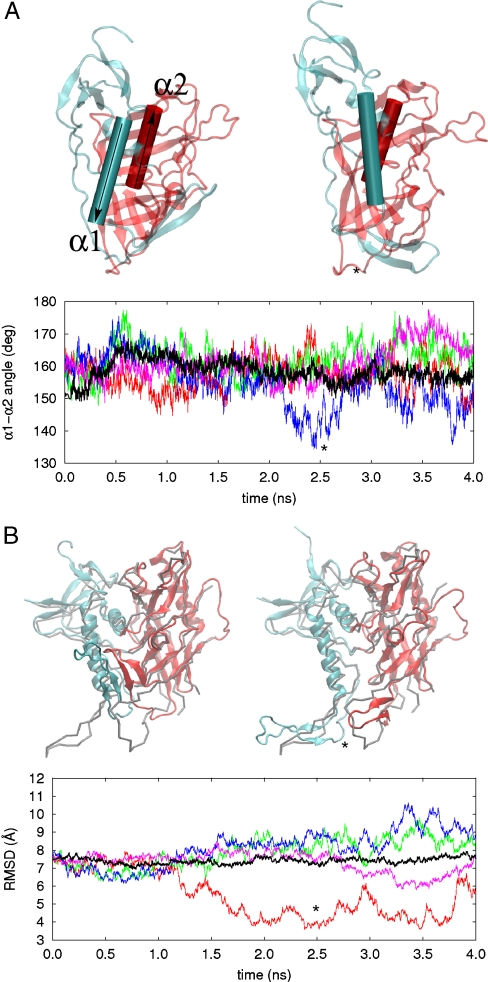
Two predominant types of large-scale conformational changes were observed in the four TAMD simulations: (i) disengagement and counterrotation of inner and outer domains about an axis approximately joining their centers of mass, and (ii) dissociation of bridging sheet elements β2/3 and β20/21 from each other and from the rest of the protein. We show in Fig. 5A traces of the angle between helices α1 of the inner domain and α2 of the outer domain as a proxy for relative domain orientation, for standard MD and the four TAMD replicas. All TAMD runs showed significantly more counterrotation than did MD, and in one case domains are counterrotated by almost 30°, which exposes nearly 1,000 Å² of previously buried surface area. In Fig. 5B we show the rmsd from our standard MD and the four TAMD replicas relative to the gp120 conformation in the crystal structure including bound antibody F105 (30), an HIV-1 gp120 structure unique in that the bridging sheet is not formed yet no stabilizing disulfides were required for crystallization. One of the replicas is observed to converge upon the F105-bound crystallographic conformer to within 3.6 Å rmsd from an initial difference of about 8 Å.

Fig. 5.

(A) Counterrotation of inner and outer domains of HIV-1 gp120 in MD (black) and four TAMD replicas vs. simulation time. The Left-hand structure shows the initial orientation of helices α1 and α5. The Right-hand structure corresponds to the conformation at the time indicated by an asterisk. Inner domain is cyan and outer domain is red. Arrows indicate N-to-C direction of each helix. (B) rmsd relative to the F105-bound conformation of HIV-1 gp120 (30) vs. simulation time for standard MD (black) and four TAMD replicas. Left-hand structure shows an alignment of the CD4-bound conformer (inner domain cyan, outer red) and the F105 bound conformer (gray trace). Right-hand structure shows an alignment of a TAMD-generated conformational with minimal rmsd relative to the F105 conformer.

Discussion

We are unaware of any other examples of blind-search conformational sampling algorithms capable of the level of predictive accuracy we observe for TAMD on GroEL and gp120 for any all-atom multidomain proteins. TAMD does not require the coarse-graining employed in Gaussian network models that have been used recently in Monte Carlo–based rigid-body interdomain conformational search in hinge-bending proteins (31) where domain motions on scales smaller than domain size are predicted. TAMD permits observation of larger-scale conformational changes than in the so-called “self-guided Langevin dynamics” simulations (32) that have recently been employed to explore both secondary and tertiary structure in the three-domain nitrogen regulatory protein C (NrtC) upon phosphorylation but only lead to sub-5-Å-scale changes (33). This suggests that all-atom TAMD using subdomain CVs is a uniquely promising method of performing large-scale conformational sampling of multidomain proteins.

TAMD can be tuned to enhance the sampling frequency of conformations low in free energy and accessible to one another by pathways through CV space with modest barriers by identifying an appropriate range of values for the fictitious temperature 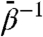(see SI Text for details). This is well-suited for interdomain conformational search when one makes the reasonable assumption that barriers to interdomain motion are somewhat larger than thermal energy but much smaller than barriers associated with disruption of secondary and tertiary protein structure. We have shown here that for GroEL and gp120 with these CVs, 6 kcal/mol of acceleration is sufficient to “activate” the CVs to overcome barriers to functionally relevant large-scale interdomain motion on computationally accessible time scales. In the case of GroEL, more than 20 kcal/mol induced the melting of tertiary (and some secondary) structures, and less than 4 kcal/mol induced no real accelerated interdomain motion. This indicates that the free-energy barrier between the conformers is of the order of 10 kcal/mol.

Specifically in regard to GroEL, although the t and r^′′ states have been observed crystallographically only in complexes, it is striking that the nature of the motion required of the GroEL subunit as inferred by the complex-bound crystallographic conformers is clearly intrinsic to the subunit, particularly in regard to the twist direction of the apical domain. Also, many conformations sampled in both 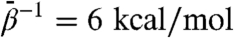TAMD simulations differ from the r^′′ state by a rigid inward tilt of the intermediate and apical domains to close the ATP binding pocket. It is plausible that such inward tilting is not favorable in isolated subunit but can be induced in protomers in the ring by GroES binding and/or apical–apical interdomain interactions between neighboring protomers. In order to test this notion it is necessary to perform TAMD on minimal chaperonin models consisting of a heptameric GroEL ring and a hepatmeric GroES cap.

With regard to HIV-1 gp120, because atomic-level information on an unliganded conformer is lacking, we used TAMD to explore the protein’s conformational repertoire from an initially stable, ligand-bound conformation. Our data suggest that the unliganded form of gp120 is characterized by counterrotation of inner and outer domains. Because we accelerated using a modest fictitious temperature of 6 kcal/mol, it is fairly likely that such conformations are physiologically accessible and may easily transition back to crystallographic conformations upon binding of CD4, which releases some 10 kcal/mol of free energy (34). Our data also suggest that there are likely relatively many conformations that satisfy the basic criteria of an unliganded gp120 compared to ligand-bound, which may partially explain the unusually large -TΔS associated with CD4 binding to gp120 [approximately 40 kcal/mol (34)]. Significantly, we observe that TAMD produces gp120 conformations very close to that displayed by gp120 bound to antibody F105, indicating as with the GroEL subunit that TAMD is a potentially useful method for predicting functionally relevant domain-level conformational changes. Perhaps most significant, however, is the implication that transition to the liganded conformation could be interrupted by ligands that bind to residues buried in the CD4-bound conformation but exposed in our unliganded model, including residues on α5 distal to α1, or outer-domain-facing residues on the N-terminal end of α1. There are several ligands known to bind near/at the CD4 site on gp120 that do not induce bridging sheet formation, such as the 12p1/HNG peptides (35) and monoclonal antibodies b12 (36, 37), b13 (30), and m18 (38, 39). Our unliganded model provides some basis upon which to speculate about how these and other noninducing ligands bind to gp120 and inhibit its function. We caution, however, that there is as yet little basis for supposing that the accuracy of our TAMD-generated conformations, especially regarding side chains, is sufficently high to warrant detailed ligand-docking calculations. It is therefore hoped that future mutagenesis studies focused on buried α1 and α5 residues may support the conformational predictions made here and shed some new light on allosteric inhibition of gp120’s ability to bind coreceptor. Also, recent publication of the crystal structure of the HIV-1 gp120 core with a more completely resolved inner domain including the gp41-interactive region (40) (though it is a stabilized mutant) provides an important opportunity for further exploration of gp120 conformational variability using TAMD.