Origins of catalysis by computationally designed retroaldolase enzymes

Abstract

We have investigated recently reported computationally designed retroaldolase enzymes with the goal of understanding the extent and the origins of their catalytic power. Direct comparison of the designed enzymes to primary amine catalysts in solution revealed a rate acceleration of 10⁵-fold for the most active of the designed retroaldolases. Through pH-rate studies of the designed retroaldolases and evaluation of a Brønsted correlation for a series of amine catalysts, we found that lysine pK_a values are shifted by 3–4 units in the enzymes but that the catalytic contributions from the shifted pK_a values are estimated to be modest, about 10-fold. For the most active of the reported enzymes, we evaluated the catalytic contribution of two other design components: a motif intended to stabilize a bound water molecule and hydrophobic substrate binding interactions. Mutational analysis suggested that the bound water motif does not contribute to the rate acceleration. Comparison of the rate acceleration of the designed substrate relative to a minimal substrate suggested that hydrophobic substrate binding interactions contribute around 10³-fold to the enzymatic rate acceleration. Altogether, these results suggest that substrate binding interactions and shifting the pK_a of the catalytic lysine can account for much of the enzyme’s rate acceleration. Additional observations suggest that these interactions are limited in the specificity of placement of substrate and active site catalytic groups. Thus, future design efforts may benefit from a focus on achieving precision in binding interactions and placement of catalytic groups.

Because natural enzymes catalyze reactions with tremendous rate accelerations and specificities, a long-standing goal in enzymology and protein engineering has been to reliably design new enzyme catalysts for chemical reactions of interest. Computational protein design offers a promising tool for achieving this goal. Computational protein design methods use specialized potential energy functions in combination with search algorithms to optimize an amino acid sequence for a given protein structure and function (1–3). These methods have been adapted to the challenge of designing enzyme active sites (4–8).

Although new enzymatic activities have been designed computationally, the resulting catalysts have catalytic efficiencies (k_cat/K_M values) of about 1–100 M^-1 s^-1 (4,7,8), considerably less than values of 10⁵–10⁹ M^-1 s^-1 typical of natural enzymes, and similar to those of early catalytic antibodies. In contrast to catalytic antibody methods and other stochastic processes, however, the potential for success of computational enzyme design is tied to the predictive power of the computational model. Thus, future improvement of our ability to computationally design enzymatic activity will require ongoing rigorous assessment of the successes and failures of the design process.

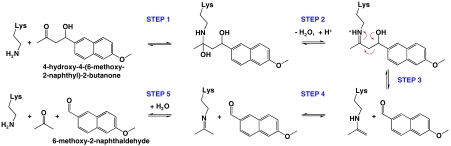
We therefore sought to investigate the origins of the catalytic power of recently reported computationally designed retroaldolases (7). One of few examples of catalytic activities designed using computational modeling alone, these enzymes were developed to catalyze the retroaldol cleavage of 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone (Fig. 1), a fluorogenic substrate developed for catalytic antibody studies (9). This retroaldol reaction is catalyzed by amines through the formation of an iminium (or Schiff base) intermediate. Analogous to the strategy used by type I aldolases (10), formation of the iminium intermediate with the enzymatic lysine side chain provides an electron sink, facilitating the retroaldol cleavage. Several catalytic antibodies and peptide systems have been developed that utilize this lysine iminium strategy (11–16).

Fig. 1.

Major steps in amine-catalyzed retroaldol reaction. Proton transfers, binding events, and some intermediate steps are omitted for clarity.

The lysine side chain provides a key catalytic element in the enzymatic reaction, yet the free lysine side chain in solution can also catalyze the retroaldol reaction. Thus, to evaluate the contribution of the computationally designed active sites to catalysis, we first determined the rate acceleration of the enzymes beyond that of the lysine side chain alone. Next, we asked how the computational design procedure facilitates additional catalysis beyond that of the lysine side chain alone. We investigated the catalytic contribution of each of three elements used in designing the enzymes: a hydrophobic pocket intended to lower the pK_a of the catalytic lysine, a stabilized, positioned water molecule for facilitation of proton transfer, and binding interactions with the substrate (Fig. 2) (7). We provide an accounting for much of the catalysis by the most active of the computationally designed retroaldolases and use these results to evaluate strengths and limitations of current enzyme design methodology.

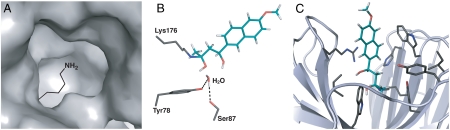
Fig. 2.

Three elements comprise the catalytic motif used for the retroaldolases investigated in this paper (7), illustrated here with the designed model for the most active enzyme, RA61. The experimental crystal structure for RA61 did not contain ligand, and the binding orientation of the substrate is not known. (A) A hydrophobic pocket was intended to lower the pK_a of the catalytic lysine side chain. (B) Hydrogen-bonding interactions to a bound water molecule were incorporated into the design models. In RA61, the side chains modeled in contact with the bound water are Tyr78 and Ser87. (C) Hydrophobic side chains line the active site cavity, providing a binding surface for the hydrophobic substrate.

Results and Discussion

Conditions for Kinetic Studies.

To investigate mechanisms of catalysis in an enzymatic system, it is necessary to identify assay conditions in which the enzyme is stable and the substrate is soluble. We found that substrate solubility was exceeded in previously used conditions for the designed enzymes (7,17). Thus, we tested buffers and cosolvents and identified conditions that provided improved solubility while protein stability was maintained (see Materials and Methods). For the variants tested herein, the enzymes could not be saturated with substrate under conditions where the substrate remained soluble. We therefore focused exclusively on second-order rate constants (k_cat/K_M), measured under subsaturating conditions where initial rates increased linearly with both enzyme and substrate concentration (ν_o = k_cat/K_M[E][S]). The resulting values of k_cat/K_M are within 2-fold of those from the original report for the variants tested (Table 1) (7).

Table 1.

Second-order rate constants at pH 7.5 and rate acceleration relative to lysine in solution

Catalyst	(kcat/KM)obs, (M-1 s-1) *	Rate acceleration
RA61	0.49	2.0 × 105
RA60	0.16	6.7 × 104
RA45	0.11	4.6 × 104
RA34	0.22	9.2 × 104
Lysine in solution	2.4 × 10-6	(1)

^* Observed second-order rate constants at 25 °C, in 50 mM sodium phosphate, 300 mM NaCl, and 5% DMSO, pH 7.5. Standard deviations were less than 20% over multiple assays and protein preparations.

The second-order rate constant k_cat/K_M reports on the difference in energy between the free enzyme and substrate in solution and the rate-limiting transition state in the steps up to and including formation of the 6-methoxy-2-naphthaldehyde product that is monitored by fluorescence (steps 1–3, Fig. 1). These rate constants are especially useful for our purposes because they can be directly compared to the second-order rate constants for the corresponding nonenzymatic reactions of primary amines in solution. This comparison provides a direct evaluation of the transition state stabilization provided by the designed enzyme active sites.

For practical reasons described below, we obtained k_cat/K_M values from initial rates under presteady-state conditions, before the first turnover. Under subsaturating conditions, k_cat/K_M values obtained before the first turnover are the same as those obtained under multiple-turnover conditions. For the designed retroaldolases, however, tight binding of the fluorescent product creates a special complication that can make multiple-turnover conditions difficult to achieve. This complication is described in the following paragraphs because it results in unexpected assay behavior that could be misinterpreted as a kinetic burst, and because it has interesting implications for the specificity of the active site. However, the present studies used initial rates measured under conditions where only low concentrations of product were formed, so the complication described below does not affect the kinetic results reported herein.

As the 6-methoxy-2-naphthaldehyde product begins to build up, it can return to the active site to form a covalent Schiff base species with the active site lysine (SI Appendix). This covalent enzyme-product species is not a part of the reaction pathway, and its stability and rate of formation may be enhanced by the aldehyde functionality of the product relative to the ketone of the substrate (18).

Formation of the covalent enzyme-product species reduces the reaction rate in the fluorescence-based assay in two ways. First, the concentration of free enzyme available to react is reduced; this reduces the actual rate of the reaction. Second, the measured rate is reduced because the fluorescent signal of the product is lost upon binding to the enzyme. For all of the retroaldolase variants tested, an exponential loss of fluorescent signal was evident when 6-methoxy-2-naphthaldehyde was incubated with enzyme in the absence of substrate (SI Appendix).

During a reaction time course beginning with substrate, this rebinding of product can manifest as an apparent burst of fluorescence (SI Appendix). Although the reductions in the rate of fluorescence development arising from this mechanism can appear burst-like, they need not follow normal expectations for burst kinetics. Reductions in apparent rate arising from this mechanism can occur under second-order conditions where the enzyme is almost entirely unsaturated by substrate, when the enzyme is in excess, and well after or before a full turnover of the enzyme.

Thus, there are two sources of burst-like kinetics to consider in this system. First, traditional burst kinetics may arise under saturating conditions due to the occurrence of a rate-limiting step subsequent to product formation, such as proton transfer or release of acetone in steps 4 and 5 (Fig. 1). Second, the apparent burst described above relates to product rebinding to the enzyme in an off-pathway state and does not provide kinetic information about steps 4 and 5. For example, RA61 shows continuous reaction progress curves over multiple turnovers at low enzyme concentration but curvature in the fluorescence time course at higher enzyme concentration where product rebinding is more pronounced (SI Appendix). We estimate a K_d for product dissociation from RA61 of about 10–30 μM, considerably lower than the K_M, which is greater than 500 μM (SI Appendix).

Because the present studies were performed under conditions where little product builds up during the reactions and with enzyme concentrations below the K_d for product rebinding, the fluorescence loss due to product binding does not complicate our efforts to investigate contributions to catalysis of the retroaldol reaction (steps 1–3). Nevertheless, this unexpected and tight product inhibition illustrates how one hallmark of natural enzymes, their exquisite specificity, remains a challenge for enzyme engineering.

Rate Acceleration Relative to Lysine Side Chain in Solution.

In the protein engineering literature, rate acceleration is frequently reported as k_cat/k_uncat, where k_uncat often represents the first-order, nonenzymatic water-mediated reaction. However, mechanistically appropriate small-molecule catalysts in solution can provide another useful comparison (19–21). In the case of the retroaldolases, the enzymatic reaction is catalyzed by a lysine side chain that is required for activity (7), whereas the reaction in water is specific-base catalyzed through a different chemical mechanism. Thus, for understanding the catalytic contribution of the designed active sites, a more direct measure of rate acceleration is provided by comparing the second-order rate constant for the enzymatic active site lysine with that of the lysine side chain alone, free in solution.

For comparison to the retroaldolase rate constants, Table 1 includes a value for the nonenzymatic, second-order rate constant of the lysine side chain in solution at pH 7.5, taken from the value for a primary alkylamine of pK_a 10.6, as described in a later section. The most active of the reported retroaldolases has a rate acceleration of 2 × 10⁵ relative to the lysine side chain in solution, and the other enzyme rate constants range from 10⁴- to 10⁵-fold above lysine in solution._†

How do the designed enzymes achieve these rate accelerations beyond those of the catalytic lysine side chains within their active sites? The computational design strategy included three elements intended to contribute to catalysis: a hydrophobic pocket to lower the pK_a of the catalytic lysine, a bound water motif designed to facilitate proton transfers, and binding interactions with the substrate (Fig. 2) (7). We investigated the contributions provided by each of these elements to the rate acceleration of the designed retroaldolases, with a focus on the most active of these enzymes, RA61.

Catalytic Contribution of Shifted Lysine pKa.

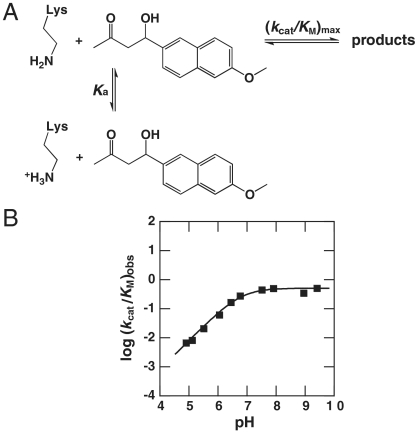
One of the strategies employed in the computational design process was to attempt to lower the pK_a of the catalytic lysine residue by placing it within a hydrophobic pocket (Fig. 2A). Because the deprotonated, neutral form of lysine is required to form the iminium intermediate and progress to products, lowering the pK_a of the catalytic lysine effectively increases the concentration of active enzyme available to react, thereby increasing the observed second-order rate constant for reaction of free enzyme and substrate (Fig. 3A).

Fig. 3.

Dependence of second-order rate constant on pH. (A) Scheme for pH dependence. The deprotonated, neutral form of lysine is required for reaction, whereas protonated, charged lysine cannot form the iminium and progress to products. Thus, in this model, the concentration of active enzyme is controlled by the pK_a of the catalytic lysine. (B) pH dependence for the RA61-catalyzed reaction. The fit to a single titratable group gives a pK_a of 6.8. Plots for the other variants are included in the SI Appendix.

To determine whether the computational design process was successful in lowering the pK_a of the catalytic lysine, we measured pH-rate profiles for several of the retroaldolases (Fig. 3B and Table 2). The assignment of the observed pK_a values to the catalytic lysine is discussed further in SI Appendix and is supported by a pH-binding study for RA61. Relative to the solution pK_a of the lysine side chain of 10.6, observed pK_a values are considerably shifted in the retroaldolases, with measured values from 6.8–7.5. These perturbed pK_a values are consistent with prior observations of lysine pK_a shifts in similar enzymes, including acetoacetate decarboxylase and catalytic antibodies and helical peptides that catalyze the same or related reactions (11, 22–24).

Table 2.

pK_a values for the designed retroaldolases obtained from pH-rate profiles and estimated catalytic contribution calculated with a Brønsted value of +0.54

Retroaldolase	pKa	Estimated catalytic contribution
RA34	> 7	≤ 14-fold
RA45	7.5	14-fold
RA60	7.2	13-fold
RA61	6.8	10-fold

Our goal was to estimate the catalytic contribution of these observed pK_a shifts, and for this we needed more information. Lowering the pK_a by one unit can increase the reactivity by raising the concentration of active, neutral lysine by up to 10-fold. However, lowering the pK_a also reduces the reactivity of the neutral amine species, as the amine becomes less nucleophilic. To determine how much the reactivity decreases, we determined the relationship between pK_a and reactivity for a series of nonenzymatic amines in solution. This information, combined with the measured enzymatic pK_a values, allowed us to estimate the catalytic contribution from lowering the pK_a of the enzymatic lysine side chains.

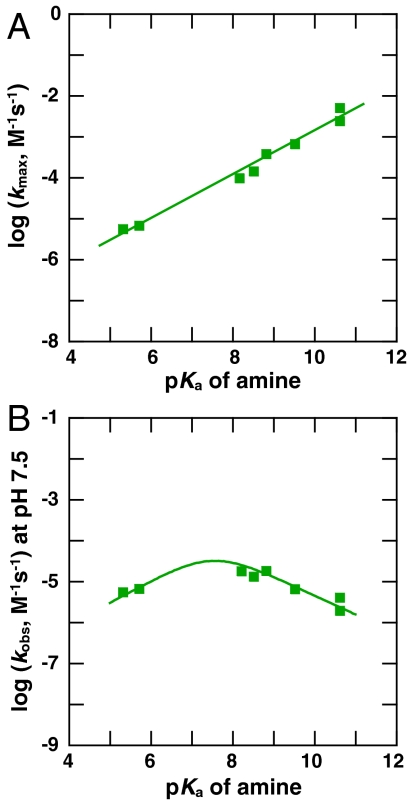
We measured rate constants for the retroaldol reaction of 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone catalyzed by a series of primary amines of the structure RCH₂NH₂ across a broad range of pK_a values (Table 3). Plotting the log of the maximal rate constants for the amines against their pK_a values yields the linear relationship with slope of +0.54 ± 0.03 (Fig. 4A). This slope represents a Brønsted value, a quantity related to changes in charge distribution between the ground state and transition state of the reaction (25, 26). The Brønsted slope provides an empirical relationship between reactivity and pK_a for the amine-catalyzed retroaldol reaction. The relationship can be replotted, as in Fig. 4B, to account for the concentration of neutral amine present at the pH value of the reaction conditions, here pH 7.5. The plot in Fig. 4B relates the observed rate constant (k_obs) at pH 7.5 to the pK_a of the amine and illustrates that the optimal amine catalysts have pK_a values similar to the pH of the reaction conditions.

Table 3.

pH-independent second-order rate constants for amine-catalyzed retroaldol reactions of 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone

Amine	pKa	kmax (M-1 s-1) *
Cyanomethylamine	5.3	5.8 × 10-6
Trifluoroethylamine	5.7	7.1 × 10-6
Propargylamine	8.2	1.0 × 10-4
Bromoethylamine	8.5	1.5 × 10-4
Chloroethylamine	8.8	4.0 × 10-4
Ethanolamine	9.5	6.9 × 10-4
Butylamine	10.6	5.3 × 10-3
Methylamine	10.6	2.6 × 10-3

^*k_max refers to the rate constant for the fully deprotonated, neutral species, whereas k_obs is used elsewhere for the observed rate constant for an amine at a given pH.

Fig. 4.

(A) Relationship between the pH-independent second-order rate constant of the fully deprotonated, neutral amine (k_max) and pK_a for the retroaldol reactions of 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone catalyzed by amines listed in Table 3. The slope obtained by linear fit is 0.54 ± 0.03, where the error is the standard error of the slope. (B) Relationship between the observed second-order rate constant at pH 7.5 (k_obs) and pK_a for the same reactions.

The relationship in Fig. 4B shows that the dependence of k_obs on pK_a is not steep, and the difference in observed rate constant between an amine of pK_a 10.6 and 6.8, as in RA61, is modest, about 10-fold. Thus, an enhancement of ∼10-fold is estimated for RA61, assuming that the enzymatic and nonenzymatic Brønsted values are similar, and similar rate enhancements are estimated for the other designed retroaldolases (Table 2).

Several observations suggest that the nonenzymatic Brønsted value provides a reasonable estimate of the relationship between reactivity and pK_a in the enzyme. First, studies of nucleophilic substitution reactions have suggested that changes in pK_a values arising from changes in substituent groups (as used to obtain the nonenzymatic Brønsted value here) have similar effects on reactivity to changes in pK_a values arising from different solvation environments (as the enzymatic pK_a shift presumably entails), and equivalent Brønsted values have been measured for solvation and substituent pK_a perturbations (27, 28). Second, although differences in the rate-limiting step between nonenzymatic and enzymatic reactions are possible, a Brønsted value of +0.8 reported for iminium formation with primary amines (29) suggests that if iminium formation rather than the retroaldol step limited either the enzymatic or nonenzymatic reactions, a value larger than +0.54 might be expected. A larger Brønsted value, whether arising from a different rate-limiting step, or as is sometimes observed, from placement in a low dielectric environment, would result in smaller catalytic contributions from the pK_a shifts (see SI Appendix for catalytic contributions calculated using different Brønsted values). Finally, because the crystallographic structure of RA61 shows a relatively open, partially solvent-exposed active site (Fig. 2C), dramatic changes in mechanism for the enzymatic retroaldol cleavage relative to the solution amine-catalyzed reaction are not anticipated. Altogether, it seems likely that the catalytic contribution of shifting the pK_a of the active site lysine in the retroaldolases is around 10-fold and does not account for the majority of their rate acceleration.

What other elements of the designed retroaldolase active sites provide their rate acceleration above that of the lysine side chain in solution? In RA61, the shifted pK_a appears to contribute about 10-fold out of a total of 10⁵-fold rate acceleration relative to the lysine side chain in solution. To understand the remaining rate acceleration of this most active variant, we investigated the other design elements in RA61.

Catalytic Contribution of Designed Water Interactions.

A hydrogen bond network was included in the design calculations used to develop the retroaldolases. This network was intended to stabilize a water molecule that in turn would facilitate proton transfer in multiple steps. In RA61, the computational design model included hydrogen-bonding interactions between a water molecule and Tyr78 and Ser87 (Fig. 2B). To evaluate whether the modeled water motif contributes to the rate acceleration by RA61, we mutated these residues and assessed the effects on catalysis.

In contrast to expectations for catalytic residues, mutation of Tyr78 and Ser87 increased activity by 2- to 3-fold, and a double mutation led to a 5-fold increase in activity over wild type (Table 4). No significant change was seen in the pH-rate profile of the double mutant relative to RA61.

Table 4.

Second-order rate constants for RA61 mutants at pH 7.5

Variant	(kcat/KM)obs (M-1 s-1)	Mutant/WT
Wild type RA61	0.49	(1)
Tyr78Phe	1.56	3.2
Tyr78Ala	0.98	2.0
Ser87Ala	0.79	1.6
Ser87Gly	1.8	3.7
Tyr78Phe/Ser87Ala	2.6	5.3

The increase in activity upon loss of these designed interactions indicates that either these interactions do not facilitate reaction at the active site or that the predicted interactions are not made. The crystal structure determined for this enzyme does not contain bound ligand and therefore cannot be used to evaluate the presence of the predicted water molecule. The active site of RA61 is relatively open and solvent-exposed, so bulk solvent may act to facilitate proton transfers. It is possible that mutations of Tyr78 and Ser87 increase activity slightly by allowing greater access to bulk solvent, although this model remains to be tested. Regardless, we can conclude that the designed water motif does not contribute to catalysis by RA61.

Catalytic Contribution of Hydrophobic Binding Interactions.

A third and final element included in the design calculations was binding interactions with the hydrophobic surface of the substrate molecule. While specific binding interactions were not explicitly required in the design calculations, hydrophobic binding interactions with substrate are favored by van der Waals and solvation terms in the energy function (7). The design model of RA61 shows close proximity of the hydrophobic naphthyl rings with hydrophobic side chains (Fig. 2C). These types of interactions are expected to stabilize the transition state bound within the active site and would thus contribute to catalysis. In particular, binding interactions with the transition state would be expected to increase the enzymatic second-order rate constant examined here, which corresponds to the difference in energy between the transition state and the free enzyme and substrate in solution.

To estimate the catalytic contribution of binding interactions to the rate acceleration of RA61, we compared the reactions of the full substrate to those of an alternative substrate that lacks the hydrophobic naphthyl side chain, 4-hydroxy-4-methyl-2-pentanone (Table 5). The second-order rate constants for the nonenzymatic reactions differ by 4- to 5-fold from those of the full substrate, suggesting that intrinsic differences in reactivity are small. In contrast, the rate constants for enzyme-catalyzed reactions of the larger and smaller substrates differ by more than 10³-fold. The differential reactivity between large and small substrates in RA61 compared to the amine-catalyzed reactions provides an estimate of around 500-fold for the contribution of the enzyme’s interaction with the naphthyl side chain. As the smaller substrate has two additional methyl groups that could make hydrophobic interactions in the active site and both substrates retain the hydroxybutanone scaffold, the full catalytic contribution from binding interactions is expected to be somewhat larger.

Table 5.

Observed second-order rate constants at pH 7.5 for retroaldol cleavage of 4-hydroxy-4-methyl-2-pentanone and full substrate

Catalyst	kobs (M-1 s-1)	kobs (M-1 s-1)	Ratio*
Propargylamine	1.7 × 10-5	3.3 × 10-6	5
Trifluoroethylamine	7.0 × 10-6	1.8 × 10-6	4
RA61	0.49	2.3 × 10-4	2,100

^*k_obs for the full substrate divided by k_obs for the smaller substrate.

Conclusions and Implications.

Computational enzyme design methods represent a promising tool for engineering new enzymes. Yet the success of these methods depends on their predictive power, so it remains crucial to experimentally evaluate computationally designed enzymes and to determine the strengths and limitations of computational design procedures.

The results presented here illustrate that the computationally designed retroaldolases provide around 10⁵-fold rate acceleration beyond catalysis by the lysine side chain alone in solution. Studies of pH-rate profiles and a Brønsted analysis of nonenzymatic reactions suggest that about 10-fold of this rate acceleration arises from shifted pK_a values for the catalytic lysines in the enzymes. For RA61, the most active of the retroaldolases, comparison of reactivities with a smaller aldol substrate provides an estimate of around 500-fold for the catalytic contribution of enzymatic binding interactions with the hydrophobic naphthyl side chain of the substrate. A designed water hydrogen-bonding network did not appear to make any catalytic contribution in RA61.

Thus, our results suggest that around 5,000-fold of the rate acceleration of RA61 can arise through a combination of binding the substrate into the active site and increasing the amount of reactive primary amine available to catalyze the reaction. The 40-fold remaining rate acceleration may arise through additional binding energy with the hydroxybutanone scaffold or the 4-hydroxy-4-methyl-2-pentanone substrate used for comparison herein. Other elements of catalysis not directly tested herein such as desolvation of the substrate and the reactive amine as well as entropic effects of localizing the substrate and the amine can also be linked to binding energies (30).

Binding substrate and providing reactive chemical groups represent fundamental strategies of natural enzymes. However, natural enzymes offer highly specific interactions that provide optimal stabilization in the transition state of the reaction. Two observations suggest that the designed retroladolases lack the precision and specificity in their interactions with substrate that are seen in natural enzymes. The observed tight inhibition by the naphthaldehyde product indicates that the enzymes favorably accommodate the naphthyl rings in a position that is translated toward the enzyme by 2–3 Å (SI Appendix). Furthermore, the substrate 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone has a chiral center but we see no evidence of significant stereospecificity in RA61 (SI Appendix), suggesting that this enzyme has little preference for specific orientations of the naphthyl rings with respect to iminium bond. These results suggest that RA61 achieves its rate acceleration without taking advantage of the precise positioning and specific interactions that help natural enzymes to achieve selective stabilization of transition states.^‡ Thus, an important next step in the development of computational enzyme design methodology may be a careful assessment of the extent to which computational design can yield precise placement of side chains and ligands on an atomic level.

Our results demonstrate that the retroaldolases utilize fundamental elements of catalysis—binding interactions and stabilization of charge through reactive chemical groups—in achieving rate acceleration. The observed lack of a catalytic contribution from the designed water interaction with Tyr78 and Ser87 illustrates how designed elements may not always work as anticipated based on structural models. Thus, quantitative, experimental dissection of the catalytic contributions of designed enzymes provides necessary feedback for future improvement. By critically evaluating catalytic contributions in designed enzymes, we stand to gain a deeper insight into both catalytic mechanisms and future possibilities for engineering practical and beneficial enzymes.

Materials and Methods

Materials.

The compounds 4-hydroxy-4-methyl-2-pentanone, 6-methoxy-2-naphthaldehyde, 2-aminoacetonitrile, 2,2,2-trifluoroethylamine, propargylamine, 2-bromoethylamine, 2-chloroethylamine, ethanolamine, methylamine, and butylamine were obtained from Sigma-Aldrich/Fluka at the highest available purity.

The fluorogenic substrate 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone was synthesized from acetone and 6-methoxy-2-naphthaldehyde as previously described (9) and further purified by silica gel chromatography in hexanes/ethyl acetate. Substrate quantitation was checked by comparison of ¹H NMR signal to an internal standard.

Proteins were obtained using the previously described procedures (7), including an autoinduction expression protocol followed by purification by His₆-tag affinity to Ni-NTA resin (QIAGEN). Proteins were extensively dialyzed into a storage buffer of 25 mM sodium phosphate, pH 7.5, 100 mM NaCl or 50 mM sodium phosphate pH 7.5, 300 mM NaCl. Protein concentration was determined by absorbance at 280 nm in 6 M guanidinium HCl. Mutants of RA61 were constructed using inverse PCR mutagenesis.

Cosolvent and Buffer Conditions.

The low solubility of substrate 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone in water dictates that cosolvents be included in kinetic assays. Initial investigations of the designed proteins used 2.7% acetonitrile in assays (7). However, under these conditions, we observed substantial departure from linearity in plots of nonenzymatic rate versus substrate concentration suggestive of a loss of substrate through insolubility. We therefore tested other cosolvent conditions. Several prior studies of antibody and peptide catalysis of the retroaldol reaction of the same substrate used 5% cosolvent (15). In 5% DMSO, substrate concentrations of ∼500 μM could be reached before significant curvature in nonenzymatic rates was evident.

In testing conditions for pH-rate profiles, we found that many organic buffers either inhibited the enzymatic reaction or accelerated the nonenzymatic reactions. Enzymatic and nonenzymatic reactions were not affected by varying the concentration of acetate, phosphate, and carbonate, so these buffers were used in all assays. Reaction pH values were checked by tests of mock reactions with a pH meter.

Kinetic Assays.

Second-order rate constants were determined under conditions in which rates remained linear with enzyme and substrate concentration over at least 10-fold ranges. Standard assay conditions were 25 °C, 50 mM sodium phosphate, 300 mM NaCl, and 5% DMSO at pH 7.5. Stocks of the 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone substrate were made in DMSO and stored at -20 °C. Reaction kinetics were monitored by following fluorescence of the product 6-methoxy-2-naphthaldehyde on a FluoroLog 3 spectrofluorometer (HORIBA Jobin Yvon) with excitation at 330 nm and emission at 452 nm. Product concentration was calibrated by measurement of a standard curve of 6-methoxy-2-naphthaldehyde fluorescence. Quartz cuvettes were used for all assays, and evaporation was controlled by use of excess reaction volume and tight-sealing caps.

Reactions of 4-hydroxy-4-methyl-2-pentanone were monitored by proton NMR on a 600 MHz system with PRESAT water suppression. Reaction conditions were 25 °C, 50 mM sodium phosphate, pH 7.5, 300 mM NaCl, and 5–8% D₂O for lock signal. Reactions were kept in a temperature-controlled water bath between data collection time points. The acetone peak was integrated and compared to an internal standard, sodium 2,2,3,3-tetradeutero-3-trimethylsilylpropionate and a standard curve of acetone integration under identical buffer conditions and delay times. All reactions were first-order with respect to both enzyme or amine and substrate.

pH-Rate Profiles.

Second-order rate constants were measured at different pH values using the buffer conditions described above (50 mM sodium carbonate, phosphate, or acetate, 300 mM NaCl, and 5% DMSO). Control experiments with enzyme incubated at pH extremes and subsequently assayed at pH 7.5 indicated that the protein was not irreversibly denatured during the course of the experiments. Data were fit to the following relationship, derived from the kinetic scheme shown in Fig. 3:

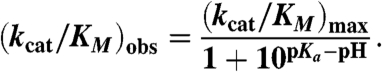Nonenzymatic, Amine-Catalyzed Reactions.

Second-order rate constants for amine-catalyzed reactions were measured under conditions in which rates remained linear with both substrate and amine concentration over at least 10-fold ranges. Spot checks were performed to ensure that no significant third-order effects were observed with buffer components. pH values of aqueous amine stock solutions were adjusted to match the reaction pH before addition to buffer solutions, and pH values of the final reaction conditions were tested in mock reactions. Amine-catalyzed rate constants were measured at several different pH values and average values for maximal rate constants were determined using the above equation. While the presence of DMSO cosolvent in reaction conditions has effects on both pH and pK_a values, at 5% DMSO, these effects will be small (< 0.5 units) and will not significantly affect the correlation (31–34).