Use of Integrated SPECT/CT Imaging for Tumor Dosimetry in I-131 Radioimmunotherapy: A Pilot Patient Study

Abstract

Integrated systems combining functional (single-photon emission computed tomography; SPECT) imaging with anatomic (computed tomography; CT) imaging have the potential to greatly improve the accuracy of dose estimation in radionuclide therapy. In this article, we present the methodology for highly patient-specific tumor dosimetry by utilizing such a system and apply it to a pilot study of 4 follicular lymphoma patients treated with I-131 tositumomab. SPECT quantification included three-dimensional ordered-subset expectation-maximization reconstruction and CT-defined tumor outlines at each time point. SPECT/CT images from multiple time points were coupled to a Monte Carlo algorithm to calculate a mean tumor dose that incorporated measured changes in tumor volume. The tumor shrinkage, defined as the difference between volumes drawn on the first and last CT scan (a typical time period of 15 days) was in the range 5%–49%. The therapy-delivered mean tumor-absorbed dose was in the range 146–334 cGy. For comparison, the therapy dose was also calculated by assuming a static volume from the initial CT and was found to underestimate this dose by up to 47%. The agreement between tracer-predicted and therapy-delivered tumor-absorbed dose was in the range 7%–21%. In summary, malignant lymphomas can have dramatic tumor regression within days of treatment, and advanced imaging methods allow for a highly patient-specific tumor-dosimetry calculation that accounts for this regression.

Introduction

Some of the best response rates with radionuclide therapy have been achieved in non-Hodgkin's lymphoma (NHL), which is considered to be a relatively radiosensitive malignancy that may be effectively treated with low-dose-rate radiation.¹ Tositumomab is a monoclonal antibody that selectively binds to CD20 on the surface of normal and malignant B-cells and can be labeled with I-131 to yield I-131-labeled tositumomab (the Bexxar therapeutic regimen, GlaxoSmithKline, Research Triangle Park, NC). At our university, I-131 tositumomab radioimmunotherapy (RIT) was evaluated as initial treatment for advanced follicular lymphoma and resulted in a 95% response and a 75% complete response.² In patients previously treated with chemotherapy, the reported overall response ranged from 47% to 68%, and the complete response ranged from 20% to 38%. While these results are promising, there is much room for improving efficacy with individualized treatment planning.

For effective individualized treatment planning, it is imperative that methods are developed for accurate dosimetry and that correlations are established between tumor-dose response and normal organ-dose toxicity, as well as between absorbed doses predicted by the tracer study and those delivered by the therapy. Limited previous I-131 RIT patient studies investigating the tracer-predicted and the therapy-delivered tumor doses report good agreement,³ as well as considerable variation.⁴ It is anticipated that concord between tracer and therapy studies will improve with the availability of more accurate imaging/quantification techniques. It is, however, possible that changes in biodistribution occur for reasons such as altered clearance of therapy administration due to the radiobiologic damage delivered to malignant tumor cells.⁴ In the majority of clinical radionuclide therapy studies, statistically significant tumor-dose-response correlations have not been established,^1,5–7 possibly due to inaccuracies in dose estimation. In these past studies investigating tracer-therapy and dose-response correlations, pharmacokinetics from planar imaging or methods combining single-photon emission computed tomography (SPECT) with planar imaging were used to determine cumulated tumor activities. Quantitative planar-imaging methods are suboptimal due to interference from activity in overlying and underlying tissue and, unlike SPECT, require careful background subtraction. In past RIT patient studies, the model-based Medical Internal Radiation Dose (MIRD) Committee “S-factor” approach has been used for the dosimetry calculation, except in one study where patient-specific three-dimensional (3D) calculations were carried out.⁷ A review article discusses the significant improvement that can be achieved with image-based patient-specific dosimetry, which couples patient anatomy and activity distribution with Monte Carlo radiation transport.⁸

The recent availability of integrated SPECT/CT, where patient anatomy and radionuclide distribution can be imaged sequentially in a single session, is a turning point for SPECT-activity quantification and patient-specific dosimetry. The computed tomography (CT) spatial resolution of such systems is typically on the order of 1 mm, while the SPECT resolution is around 5–10 mm. The higher resolution coregistered CT can be used to improve the SPECT reconstruction, to delineate tumor and organ volumes of interest, and to define the patient anatomy for Monte Carlo–based dose estimation. When CT anatomic information is available from integrated imaging at multiple time points, changes in tumor volume can be measured and included in the dosimetry calculation. This is especially important with malignant lymphomas, which can be highly sensitive to radiation and can have dramatic tumor regression within days of treatment.⁹ However, in most studies thus far, a fixed tumor mass typically determined from a single baseline CT has been used for the dosimetry calculation. The assumption of a constant mass for a tumor that is actually regressing results in an underestimation of the absorbed dose because of the inverse relationship between dose and mass for a given uptake. Two previous studies discuss the significance of tumor regression in dosimetry for I-131 RIT and include a time-varying tumor mass in their MIRD-based dosimetry approach.^10,11

In two recent studies, integrated SPECT/CT-imaging-based tumor-organ dosimetry was demonstrated in a patient with thyroid cancer,¹² and bone marrow dosimetry was demonstrated in NHL patients undergoing RIT.¹³ In the present study, we present methodology for highly patient-specific tumor dosimetry, which accounts for changes in tumor volume measured with an integrated system. The dosimetry was carried out by coupling functional (SPECT) and anatomic (CT) images from multiple time points with a Monte Carlo algorithm previously developed at our institution.¹⁴ The methodology was applied to a pilot study of 4 follicular lymphoma patients treated with I-131 tositumomab and pharmacokinetics, and tumor dosimetry results from tracer and therapy imaging are presented. The focus of the present work was on using advanced imaging methods to carry out an accurate patient-specific calculation of mean tumor dose, rather than on 3D dose-distribution calculations. For 3D dose-distribution computations to be meaningful, tumor voxels from multiple time points need to be accurately registered, and in the case of deforming/regressing tumors (such as those seen in the present patient study), this problem is nontrivial and is the focus of a different study.¹⁵ Normal organ dosimetry was not carried out because, in this pilot study, the focus was on tumor dosimetry, and the imaging field of view (FOV) in the axial direction was selected such that the tumor was in the center, and as a result, normal organs of interest in RIT (such as the kidney, liver, and spleen) were not included or only partially included in the FOV.

Materials and Methods

Patients

Four (4) refractory follicular NHL patients undergoing I-131 radioimmunotherapy at our clinic volunteered for this research study involving multiple scans on the integrated SPECT/CT system. (The clinical protocol only involves planar imaging.) The clinical protocol for drug administration consisted of two steps.¹⁶ In step 1 (tracer administration), on day 0, patients received an infusion of unlabeled (cold) tositumomab, followed by an infusion of tositumomab labeled with 185 MBq (5 mCi) of I-131. In step 2 (therapy administration), which was 8 days after step 1, patients received an infusion of the same amount of unlabeled tositumomab, followed by an infusion of tositumomab labeled with an amount of I-131 (Table 1) calculated to deliver a nominal whole-body absorbed dose of 75 cGy, based on clinical post-tracer planar imaging computations.

Table 1.

Administered Activity and Summary of Tracer and Therapy Pharmacokinetics for the Whole Body Within the SPECT FOV

	Patient 1	Patient 2	Patient 3	Patient 4
Administered therapy activity	2.82 GBq	3.50 GBq	3.92 GBq	3.77 GBq
Effective half-life (tracer)	68 hours	67 hours	75 hours	69 hours
Effective half-life (therapy)	59 hours	68 hours	61 hours	64 hours
Residence time (tracer)	30 hours	21 hours	22 hours	28 hours
Residence time (therapy)	28 hours	18 hours	22 hours	26 hours

SPECT, single-photon emission computed tomography; FOV, field of view.

SPECT/CT acquisition and reconstruction

Patients were imaged on a Siemens Symbia TruePoint SPECT/CT scanner (Hoffman Esta, IL) with a six-slice CT capability. Each patient was imaged at three time points within 6 days after the tracer administration and at three time points within the first 10 days following therapy administration. The first tracer-imaging time point was within 1–2 hours after the administration, but due to dead time and radiation exposure considerations, the earliest therapy imaging time point was limited to 1–2 days after the administration. The SPECT data were acquired by using a high-energy parallel-hole collimator and the following specifications: 180 degrees and 30 stops per head; 40 seconds per stop; body contouring; 20% photopeak at 364 keV; two adjacent 6% scatter-correction windows; and a 128 × 128 matrix with a pixel size of 4.8 mm. The CT component of acquisition used full-circle rotation, 130 kV, 35 mAs, and 5-mm slices. The CT scan time was less than 20 seconds and was obtained without contrast and without a breath hold. The X-ray exposure each patient received due to each low-dose CT scan was 0.28 rem.¹⁷ The CT data were reconstructed with a 512 × 512 × 196 matrix and 0.98 × 0.98 × 2 mm voxel size, using commercial ESOFT (Siemens) software.

SPECT reconstruction was carried out by using a 3D ordered-subset expectation-maximization (3D OSEM) algorithm developed at our institution,¹⁸ instead of the commercial software of the integrated system. This allowed for dead-time correction of the post-therapy projection data, based on a paralyzable model and the measured dead-time constant of the SPECT system.^19,20 Data were reconstructed by using 15 iterations and 6 subsets and included 3D depth-dependent detector-response compensation, attenuation correction, and scatter correction. The detector response was determined from point-source measurements in air and was modeled by a rotationally symmetric single exponential added to a Gaussian.¹⁸ Effect of the noncircular orbit was accounted for in the depth-dependent detector-response functions by retrieving the radial position information from the header of the SPECT-projection data. For nonuniform attenuation correction, the CT-based attenuation map from the commercial software was used. For scatter correction, a triple-energy-window scatter estimate was included in the OSEM algorithm in a manner appropriate for Poisson statistics.²¹ The reconstructed SPECT counts were converted to activity by using a calibration factor determined from a measurement with a known amount of I-131 activity in a 100-mL plastic sphere centered in a water-filled elliptical phantom. Recovery coefficients for partial volume compensation in small volumes²² were not utilized in this study because the tumors analyzed were large (39–408 mL).

Tumor definition and time-activity data

Independent of SPECT, tumors were outlined on CT at each time point, slice by slice, by a nuclear medicine specialist with radiology CT training, utilizing visualization tools to enhance contrast and magnification. All tumors of significant size that were within the camera FOV were outlined (2 tumors in patient 1, 2 in patient 2, 1 in patient 3, and 1 in patient 4). The tumor volume of interest at each time point was applied to the corresponding coregistered quantitative SPECT image to generate the tumor time-activity data. For tumor, where the uptake is noninstantaneous, a biexponential fit was carried out, including the (0.0) point. When fitting the post-therapy data, the first post-tracer time point (measured within 1–2 hours after administration) was included in the fit because of the lack of an early post-therapy imaging time point. Although, in past studies, tumor time-activity data has been typically fitted with monoexponentials, we used a biexponential to better model both the noninstantaneous uptake and clearance phases. The residence time estimates derived from using mono- and biexponential fitting have been compared in previous studies.^3,23

SPECT-based time-activity data were also generated for the “whole body.” Because of the limited FOV of the SPECT camera in the axial direction (39 cm), the whole body is defined in this study as the total body section that is within the SPECT camera FOV. For the whole body, there is instantaneous uptake, and so, a monoexponential was used to fit the time–activity data.

Tumor dosimetry

The DPM (dose planning method) Monte Carlo electron and photon transport program²⁴ designed for radiation absorbed-dose computations in external beam radiotherapy was adapted and validated for our present application in internal emitter therapy.¹⁴ In the present study, for each time point, the inputs to DPM were the coregistered SPECT image, CT-derived density map, and the CT-defined tumor outlines. To obtain the density map, the previously described CT-based attenuation map was converted to a map of densities (ρ(x,y,z)) by dividing each attenuation coefficient voxel value (μ₃₆₄(x,y,z)) by the mass attenuation coefficient (μ/ρ) at 364 keV. This method is based on the observation that at the energy of interest, μ/ρ shows little variation between tissue.²⁵ The output from DPM at a given time point was the 3D absorbed-dose-rate map and summary tables computed for that time point. For the 512 × 512 × 196 matrix, the time to generate low-uncertainty DPM dose-rate distributions simulating 1 billion decays was 2.8 hours on a 3-GHz Power Mac system (Apples). The photon cut-off was set at 4 keV and the electron cut-off was set at 200 keV, since the range in water of an electron of this energy (approximately 0.5 mm) is much less than the voxel dimensions.

At each time point, the DPM output summary tables for each predefined tumor provide the absorbed-dose-rate averaged over the volume, 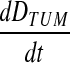, in units of mGy/MBq.s, as well as the fraction of that dose rate that is due to self-irradiation, f_TUM, and the fraction due to irradiation from the rest of the body, f_RB. These quantities from DPM can then be combined with the SPECT-derived values for the relative source strength for the tumor (r_TUM) and rest of the body (r_RB) at the given time point and the time-integrated cumulated activity in the tumor (Ã_TUM) and the rest of the body (Ã_RB) to determine the mean absorbed dose to the tumor, D_TUM, as shown in Equation 1:

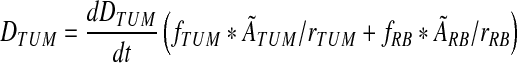(1)

The scaling by the relative source strength factors is necessary to account for differences between the relative cumulated activities in the tumor and rest-of-the-body and the relative activities in tumor and rest of the body at the specific time point for which the DPM results were derived.

To incorporate the changing tumor mass, the calculation of mean absorbed dose, using Equation 1, was carried out over three time periods. (The three time periods were: zero to T₁, T₁ to T₂, and T₂ to infinity. Here, T₁ is the midpoint of the first and second imaging time point and T₂ is the midpoint of the second and third time points.) The time-activity curves were divided into the three time periods, and the cumulated activity for each period was determined. For each period, the DPM absorbed-dose rate and other parameters of Equation 1 were also determined by using SPECT/CT images and tumor outlines corresponding to each of the three imaging time points. The doses computed by using Equation 1 for each of the three time intervals were then summed to obtain the total mean absorbed dose to the tumor. The therapy-delivered absorbed dose to the tumor was calculated based on data from the three post-therapy imaging points, while the tracer-predicted absorbed dose to the tumor was calculated by scaling the results based on data from the three post-tracer imaging points by the ratio of therapy to tracer administered activity.

In SPECT-based patient-specific dosimetry, the contribution to mean tumor dose from activity outside the camera FOV is ignored because the activity map on which the calculation is based is only available for the FOV. Because the rest-of-the-body contribution to tumor dose falls off rapidly with distance from the tumor, ignoring activity outside the FOV is not a significant source of error when the tumor is away from the edges of the FOV,²⁶ which was the case in the present study.

Results

SPECT/CT images

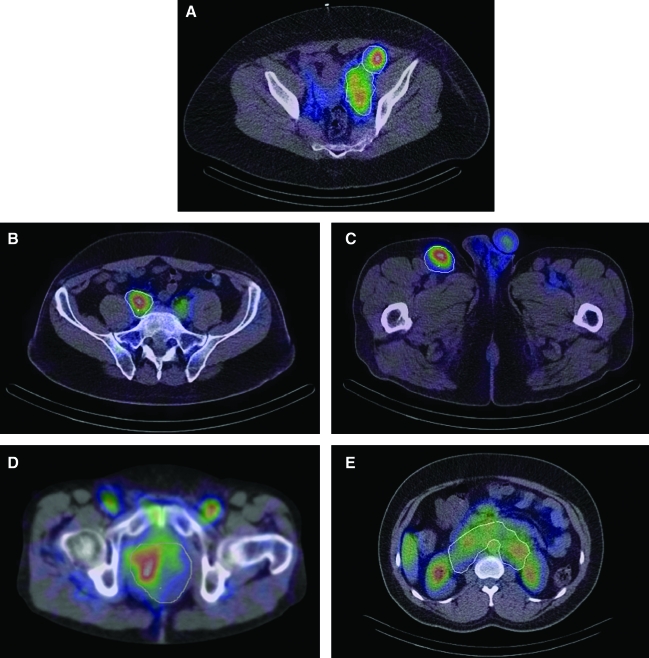
Figure 1 shows typical slices with tumor outlines displayed on fused post-therapy SPECT/CT images. Figure 1A depicts uptake in massive left pelvic lymphadenopathy surrounding the external and internal iliac vascular bundle in patient 1. Figure 1B depicts increased activity in tumor along the right common iliac lymph nodal chain in patient 2. Fainter activity is seen contralaterally, reflecting intravascular blood pool activity of 131-I tositumomab. Figure 1C shows intensely focal activity in the right inguinal lymphadenopathy in patient 2 and fainter activity in the testicles. Figure 1D shows uptake in a large pelvic tumor surrounding and encasing multiple small-bowel loops in patient 3. Significant activity is also seen in the femoral artery and vein. Figure 1E shows activity distribution in a massive retroperitoneal lymphadenopathy in the para-aortic and aortocaval space in patient 4. The image also shows significant uptake in the liver and normal organs in close proximity to the tumor, such as kidneys, aorta, and bowel.

FIG. 1.

Fused single-photon emission computed tomography (SPECT) and computed tomography (CT) images from the integrated system showing (A) pelvic tumors of patient 1, (B) iliac tumor of patient 2, (C) inguinal tumor of patient 2, (D) pelvic tumor of patient 3, and (E) abdominal tumor of patient 4. Tumor outlines were defined on CT independent of SPECT.

While there is intense focal activity uptake within the CT-defined tumor boundary in Figure 1A, 1B, and 1C, there is less concord between the anatomic tumor outline and SPECT uptake in Figure 1D and 1E. This is because of the nonuniform activity distribution within the tumor outline and because these tumors encase and compress or are adjacent to normal anatomic structures that have substantial background activity. In Figure 1D, the nonuniformity likely reflects 131-I tositumomab pooling in the mesenterial vasculature associated with the bowel loops, which are encased by the tumor. In Figure 1E, the tumor outlined as a single volume is a conglomeration of multiple enlarged lymph nodes, hence the uptake is nonuniform within the outline. In addition, the uptake can be nonuniform due to differences in the tumor biology.

Tumor shrinkage

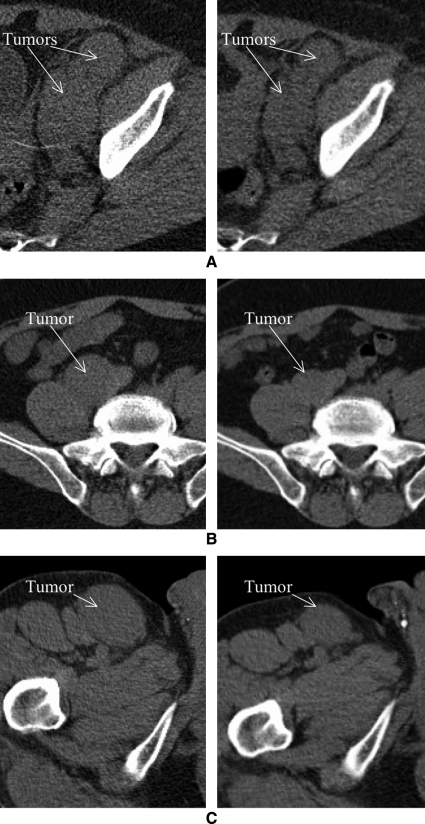
The initial tumor volume defined on the first scan is given in Table 2. The measured tumor shrinkage during tracer imaging and during therapy imaging, and the total tumor shrinkage, defined as the percent difference between the volumes drawn on the first post-tracer SPECT/CT scan and on the last post-therapy SPECT/CT scan (a typical time period of 15 days), is also given in Table 2. Shrinkage was most significant (up to 49%) for the tumors of patients 1 and 2 and these reductions in tumor volumes were clearly evident on CT (Figure 2). In patient 1, the reduction in tumor volume was significant only after the therapy administration, while in patient 2, significant volume reduction (up to 23%) was measured after just the tracer administration.

Table 2.

Summary of Tumor Shrinkage and Mean Tumor-Absorbed Dose from Tracer and Therapy Imaging

	Patient 1		Patient 2		Patient 3	Patient 4
	Large pelvic tumor	Small pelvic tumor	Iliac tumor	Inguinal tumor	Pelvic tumor	Abdominal tumor
Initial tumor volume	313 mL	39 mL	234 mL	140 mL	400 mL	408 mL
Shrinkage (during tracer imaging)	1%	−10%	23%	18%	4%	−2%
Shrinkage (during therapy imaging)	26%	31%	17%	31%	3%	17%
Total shrinkage	31%	27%	45%	49%	5%	15%
Residence time (using tracer imaging)	2.70 hours	0.41 hours	0.71 hours	0.44 hours	1.11 hours	1.89 hours
Residence time (using therapy imaging)	2.16 hours	0.25 hours	0.59 hours	0.37 hours	0.85 hours	1.55 hours
Predicted dose (using tracer imaging)	359 cGy	360 cGy	192 cGy	181 cGy	183 cGy	281 cGy
Delivered dose (using therapy imaging)	334 cGy (7%)a	283 cGy (21%)	211 cGy (−10%)	207 cGy (−14%)	146 cGy (20%)	241 cGy (14%)
Delivered dose (assuming static   tumor volume)	278 cGy (−20%)b	243 cGy (−17%)	147 cGy (−43%)	141 cGy (−47%)	148 cGy (1%)	239 cGy (−1%)

^aDifference between tracer-predicted and therapy-delivered doses.

^bDifference between therapy dose estimated by assuming a static tumor volume from the initial computed tomography scan and the result in the row above, where the tumor regression measured over multiple scans was included in the calculation.

FIG. 2.

Comparison of the computed tomography scans from the first post-tracer (left) and last post-therapy (right) imaging time points that demonstrate the regression in (A) the pelvic tumors of patient 1 (shrinkage 31% and 21% for the 2 tumors), (B) the iliac tumor of patient 2 (shrinkage 45%), and (C) the inguinal tumor of patient 2 (shrinkage 49%).

Independent of the regression measured by the present SPECT/CT research study the clinical response classification for these patients was also available from the clinical protocol. As part of their standard clinical care, based on post-therapy clinical CT, patient response was categorized as complete response (CR), partial response (PR) or progressive disease (PD) as defined in reference 2. The clinical response for the patients were: patient 1, CR at 6 months; patient 2, CR at 6 months; patient 3, PD at 6 weeks; patient 4, PD at 10 weeks.

Time-activity data

Whole body

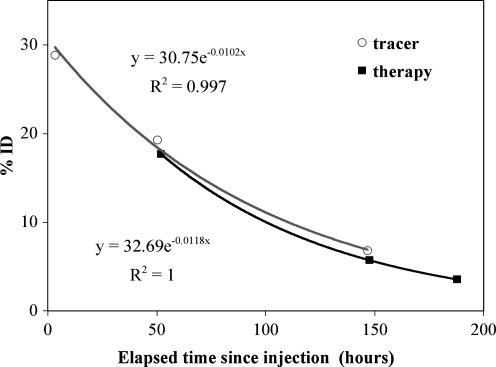
At the first post-therapy time point, the main window count rate was up to 18,000 counts per second and dead-time correction increased the counts by up to 8%, but by less than 2% at subsequent post-therapy time points. The tracer and therapy whole-body time-activity curves with monoexponential fitting are compared in Figure 3 for a typical patient. Here, %ID is the measured activity normalized by the injected activity; hence, if tracer and therapy pharmacokinetics are similar, we expect concord between the two curves. The effective half-lives and residence times (obtained by integrating the fitted curves) are compared in Table 1. On average, the agreement between tracer and therapy data for the whole body is within 10% for the effective half-life and within 8% for the residence time.

FIG. 3.

Whole-body (within field of view) time–activity data for patient 1 with a monoexponential fit.

Based on the fit to the time-activity data, the remaining activity from the tracer injection at the time of the therapy administration (8 days later) was calculated. In all cases, the remaining tracer activity was <1 mCi, which was less than 1% of the therapy administration; hence, it is not expected to affect the therapy data.

Tumor

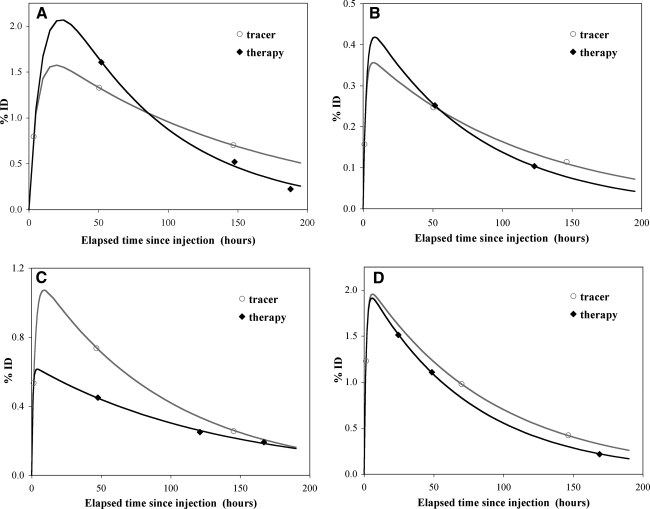
Figure 4 shows representative biexponential fitted curves of tumor time activity for each patient. Note that the last post-therapy data point for patient 2 was not available due to camera malfunction. For tumor, unlike for the whole body, the concord between tracer and therapy time-activity data varied significantly from patient to patient and from time point to time point, as evident in Figure 3. The tumor residence times determined from tracer and therapy imaging are compared in Table 2 and agree to within 22%, on average.

FIG. 4.

Tumor time-activity data with biexponential fitting. (A) Patient 1: Large pelvic tumor. (B) Patient 2: Inguinal tumor. (C) Patient 3: Pelvic tumor. (D) Patient 4: Abdominal tumor.

Tumor dosimetry

The therapy delivered mean tumor-absorbed dose is given in Table 2 and ranged from 146 to 334 cGy. As discussed previously, this dose was determined over three time periods, hence accounting for any changes in the tumor volume measured over the multiple post-therapy time points. For comparison, the therapy-delivered dose was also calculated by assuming a static tumor volume from the initial post-tracer CT for the DPM dose-rate calculation (last row of Table 2). In both cases, the same therapy residence time was used for the dose calculation, and only the tumor volumes and dose rates differed. For the tumors of patients 1 and 2, where regression was most significant, the assumption of a static tumor volume leads to a 20–47% underestimation of the therapy-delivered dose because of the inverse relationship between absorbed dose and mass at a given activity uptake.

In Table 2, the therapy-delivered mean tumor-absorbed dose determined using the three post-therapy time points is compared with the tracer-predicted mean tumor-absorbed dose determined from using the three post-tracer time points. The agreement between the predicted and delivered doses ranged from 7% to 21% and was within 15%, on average. The estimated Pearson's correlation between the predicted and delivered doses was 0.90 and the p-value for testing whether the correlation was different from zero was 0.013. The tumor regression affects both the uptake and the dose, and for this limited sample size, reasonable agreement was achieved between the tracer-predicted and the therapy-delivered doses when the change in tumor volume was included in the calculations of both residence time and dose.

The contribution to mean tumor-absorbed dose from activity in the rest of the body within the SPECT FOV ranged from 14% to 24% for the 6 tumors. The rest-of-the-body contribution was lowest for the inguinal tumor (Fig. 1C) with intense focal uptake and was highest for the abdominal tumor (Fig. 1E), which was in close proximity to normal organs with significant uptake. This result for patients is consistent with a previous I-131 phantom study, which showed that neglecting the photon contribution from the rest of the body underestimates the tumor dose by 10%–25%.²⁷

Discussion

The rapid regression of some of the tumors in the present study (up to 49% within a period of 15 days) is consistent with previous RIT studies showing dramatic shrinkage of malignant lymphomas within days of the therapeutic administration.^10,11 In patient 2, significant (up to 23%) regression was measured in post-tracer imaging prior to therapy administration. In this case, because the tracer administration was only 185 MBq, it can be inferred that the initial tumor shrinkage was in response to the unlabeled (cold) antibody, which is coadministered with I-131 tositumomab and has been shown to have some therapeutic effect.²⁸ Stunning effects associated with the radioactivity in the diagnostic dose have been reported in I-131 therapy of thyroid carcinoma²⁹ but have not been documented in radioimmunotherapy.

Despite tumor regression, most dosimetry calculations in radionuclide therapy, patient specific or otherwise, have been carried out by assuming a constant tumor mass from a baseline CT (typically obtained a few weeks before start of treatment). In the present dose calculation, we accounted for tumor regression by utilizing integrated imaging data from multiple time points. For comparison, the therapy-delivered dose, assuming a static CT volume from the initial scan, was also calculated and was found to underestimate the dose by up to 47% because of the inverse relationship between dose and mass at a given uptake. In the present study, reasonable agreement (within 15%, on average) and correlation (Pearson's correlation = 0.9) were achieved between the predicted and delivered doses when the tumor regression was included in the calculations. A larger study with more patients is needed to establish the trends observed in the present study. Agreement between tracer-predicted and therapy-delivered tumor dose would validate the use of a tracer study in treatment planning, to predict the radiation doses that would be received from therapy.

The mean tumor-absorbed doses reported in this article (ranging from 146 to 334 cGy) are within the range reported in previous studies on dose response in I-131 tositumomab therapy of NHL patients.^6,7 Estimation of the error in patient dosimetry results is difficult. However, patient-specific Monte Carlo–based methods, such as those used in this study, are known to provide the most accurate dose calculation, being limited only by the accuracy of their inputs, which in the present case, were the coregistered quantitative SPECT image, CT image, and CT-defined tumor outlines. SPECT-activity quantification of I-131 is particularly challenging because of spatial-resolution and septal-penetration effects. Using 3D OSEM reconstruction methods, such as those used in the present work, in previous phantom studies, we have demonstrated quantitative accuracy better than 10% for “tumor” volumes down to 16 mL without partial volume correction.³⁰ In patient studies, SPECT-CT misregistration is another source of error but is minimized with integrated imaging systems. We have carried out simulation studies to investigate the sensitivity of SPECT/CT-imaging-based dosimetry to misregistration.²⁶ These studies showed that good accuracy (<3% error for relatively large tumors, such as those of the present study) can be achieved when concurrent offsets in three dimensions are <2 mm, which is feasible with an integrated system. Even with integrated imaging, breathing introduces misregistration, but is less significant when imaging the pelvis and abdomen region, as in the present study. In the present study, much emphasis was placed on careful definition of the tumor at each time point. For 4 of the 6 tumors, the boundaries were clearly visible on CT (Fig. 4), but for the other 2, where the tumor was encasing and compressing normal anatomic structure or was a conglomeration of multiple enlarged nodes, accurate definition on the low-dose CT acquired without contrast was challenging. In such cases, the uncertainty in tumor definition may be a main source of error in the dosimetry calculation.

In the present study, because of the small sample size, no statistical analysis was carried out to determine the correlation between the absorbed dose to the tumor and response. This pilot study was the basis for initiating a larger, ongoing study for evaluating dose response from 50 NHL patients to be imaged on the integrated system. Apart from the calculations of mean tumor dose presented in this article, we are also investigating 3D, time-dependent dosimetry in deforming tumor volumes to compute quantities such as effective uniform dose,¹⁵ which may correlate better with response than mean dose.

Conclusions

This work demonstrates the utility of integrated SPECT/CT imaging in carrying out highly patient-specific tumor dosimetry following radioimmunotherapy. Integrated imaging and advanced SPECT reconstruction methods were used to determine the pharmacokinetics and the dosimetry, incorporating changes in tumor volume in the calculation. In 4 of the 6 tumors analyzed, highly significant regression was measured within days of the treatment; hence, the comparison calculation assuming a static tumor volume significantly underestimated the dose. There was reasonable agreement and correlation between tracer-predicted and therapy-delivered tumor doses when regression was included in the calculations, but a larger patient study is needed to establish these trends.

Acknowledgments

This work was supported by grant 2R01 EB001994 awarded by the National Institutes of Health, United States Department of Health and Human Services (Bethesda, MD). The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the funding agencies. The authors thank Hans Vija, Ph.D., and James Chapman, Ph.D., of Siemens Medical Solutions for helpful discussions about the SPECT/CT system.

Disclosure Statement

Dr. Kaminski receives research support from GlaxoSmithKline and royalties from Bexxar.