EXPERIMENTAL VERIFICATION OF THE ROLE OF INTERSTITIAL FLUID PRESSURIZATION IN CARTILAGE LUBRICATION

Summary

The objective of the current study was to measure the friction coefficient simultaneously with the interstitial fluid load support in bovine articular cartilage, while sliding against glass under a constant load. Ten visually normal 6 mm diameter cartilage plugs harvested from the humeral head of four bovine shoulder joints (ages 2-4 months) were tested in a custom friction device under reciprocating linear motion (range of translation ±2mm; sliding velocity 1mm/s), subjected to a 4.5N constant load. The frictional coefficient was found to increase with time from a minimum value of μ_min = 0.010±0.007 (mean±standard deviation) to a maximum value of 0.243±0.044 over a duration ranging from 920s to 19,870s (median: 4,560 s). The corresponding interstitial fluid load support decreased from a maximum of 88.8±3.8% to 8.6±8.6%. A linear correlation was observed between the friction coefficient and interstitial fluid load support (r²=0.96±0.03). These results support the hypothesis that the temporal variation of the friction coefficient correlates negatively with the interstitial fluid load support, and that consequently interstitial fluid load support is a primary mechanism regulating the frictional response in articular cartilage. Fitting the experimental data to a previously proposed biphasic boundary lubrication model for cartilage yielded an equilibrium friction coefficient of μ_eq =0.284±0.044. The fraction of the apparent contact area over which the solid matrix of cartilage is in contact with the glass slide was predicted at φ =1.7%±6.3%, significantly smaller than the solid volume fraction of the tissue, φ^s =13.8%±1.8%. The model predictions suggest that mixed lubrication prevailed at the contact interface under the loading conditions employed in this study.

Introduction

The main function of articular cartilage is to serve as the bearing material of diarthrodial joints, transmitting large loads with minimum friction and wear. Its frictional properties have been of keen interest to biotribologists since the 1930′s. Several mechanisms for joint lubrication have been proposed including hydrodynamic lubrication [26], boundary lubrication [7,15,36,43], weeping lubrication [29,30], boosted lubrication [46], biphasic self-generating lubrication mechanism [32], elastohydrodynamic and micro-elastohydrodynamic lubrication [9,10], and biphasic boundary lubrication [3,5,13].

An important and useful measure in the study of joint lubrication is the frictional coefficient. Experimental studies have found that articular cartilage can have very low friction coefficients upon loading (0.002 to 0.02) [6-8,13,17,18,23,24,28,29,45], which may be favorable for maintaining the high wear resistance of the tissue. But if the load is maintained constant for durations of several hours, this coefficient becomes quite elevated (0.2-0.4) [13,25,28,29,46].

Any proposed mechanism for joint lubrication should be able to quantify this transient response. It has been proposed that this behavior is related to the pressurization of fluid in the tissue during loading [3,13,27-30]. Under this hypothesis, the fluid load support significantly reduces the frictional coefficient due to load transfer between the solid and fluid phases. When the interstitial fluid pressure within the tissue subsides to zero, the frictional coefficient reaches an equilibrium value.

Based on these observations, we previously proposed a boundary friction model for articular cartilage which formulates the dependence of the transient, or effective, frictional coefficient (μ_eff ) on the interstitial fluid pressurization and an equilibrium frictional coefficient [3,5]. In our earlier experimental study [5], the effective friction coefficient was correlated against the interstitial fluid load support predicted theoretically from the biphasic theory [31]. More recently, we have developed techniques to measure the interstitial fluid pressure and fluid load support directly [34,40,41].

The objective of the current study was to measure the friction coefficient simultaneously with the interstitial fluid load support in bovine articular cartilage while sliding against glass under a constant load. The hypothesis is that the variation of the effective friction coefficient correlates negatively with the interstitial fluid load support, and that consequently interstitial fluid load support is a primary mechanism regulating the frictional response in articular cartilage.

Material and Methods

Biphasic Boundary Friction Model

The biphasic boundary friction model proposed previously [5] quantifies the load sharing between the solid and fluid phases of the porous-permeable cartilage at the contact interface. The model takes into account the interstitial fluid pressurization and the fraction of the area over which the solid phases of opposing surfaces are in contact. In a biphasic material the total stress is given by σ = −pI + σ^e , where p is the interstitial fluid pressure, σ ^e is the effective stress resulting from solid matrix strains, and I is the identity tensor. The normal contact force at the interface is given by $W={\int }_A\mathbf{n}\cdot \sigma \mathbf{n}dA$, where n is the unit outward normal at the interface and A is the apparent contact area. Integrating the fluid pressure over the contact interface produces $W^p=-{\int }_{A}pdA$, and the ratio W^p/W is called the interstitial fluid load support [4,19,40,41]. Because of the porous nature of the contact interface, the actual load supported by the interstitial fluid pressure at the contact interface depends on the surface porosities. If φ denotes the fraction of the contact area over which solid-to-solid contact occurs, then the component of the load supported by interstitial fluid pressure is (1–φ)W^p . It follows that the component of the contact force which is supported by the contacting solid phases is W^ss = W – (1–φ)W^p . These load components may all vary over time.

According to our friction model, the frictional force F at the contact interface results primarily from the solid-to-solid friction, and is thus proportional only to W^ss,

$$F={\mu }_{\mathit{eq}}{W}^{\mathit{ss}}={\mu }_{\mathit{eq}}\left[W-(1-\phi )W^p\right],$$ (1)

where μ_eq is the equilibrium frictional coefficient achieved when the interstitial fluid pressure subsides, i.e., when W^P = 0. For idealized smooth porous surfaces, φ is given by the product of the solid area fractions of the opposing surfaces. (For example, in the limiting case of smooth non-porous surfaces, φ=1.) For non-smooth surfaces contacting at asperities, or equivalently under mixed lubrication conditions, φ will be smaller than this idealized value. Thus, for cartilage sliding against an impermeable surface such as glass, the upper bound on φ is the solid volumetric content of the cartilage sample (the volumetric and area fractions being the same according to Delesse’s law).

Given the relation of Eq.(1), the effective friction coefficient reduces to

$${\mu }_{\mathit{eff}}=F∕W={\mu }_{\mathit{eq}}\left[1-(1-\phi )\left(W^p∕W\right)\right].$$ (2)

It can be noted from Eq.(2) that the effective friction coefficient μ_eff varies as a linear function of the interstitial fluid load support W^p/W , with a negative slope. According to this model the minimum value of μ_eff is achieved when the fluid load support is greatest; under certain loading configurations the maximum value of W^p/W can be unity [40], yielding a minimum value as low as φμ_eq for μ_eff. This model neglects the interfacial viscous shear contribution of the lubricant in comparison to the solid-to-solid friction. Therefore, in the limit of fluid-film lubrication, when a full-thickness film separates the contacting surfaces (W^p/W = 1, φ = 0), the predicted friction coefficient is μ_eff = 0.

Experimental Methods

Ten visually normal cartilage plugs, 8mm in diameter, were harvested from the humeral head of bovine shoulder joints obtained from a local abattoir (4 joints, ages 2-4 months). Samples were stored at −20°C in physiological buffered saline (PBS) solution. On the day of testing samples were thawed to room temperature for half an hour. Using a sledge microtome (Leica Instruments GmbH, Nussloch, Germany, Model SM2400) all the underlying bone and about 2 mm of tissue was removed from the deep zone to produce thin samples with parallel surfaces (final average thickness = 0.68±0.13 mm); the articular surface was left intact. In order to obtain a uniform cylindrical cross section 6mm plugs were further cored out from the microtomed samples using a biopsy punch. Samples were equilibrated at room temperature in PBS solution mixed with protease inhibitors (Complete protease inhibitor cocktail tablets, Roche Applied Science, IN) for an additional half hour prior to testing.

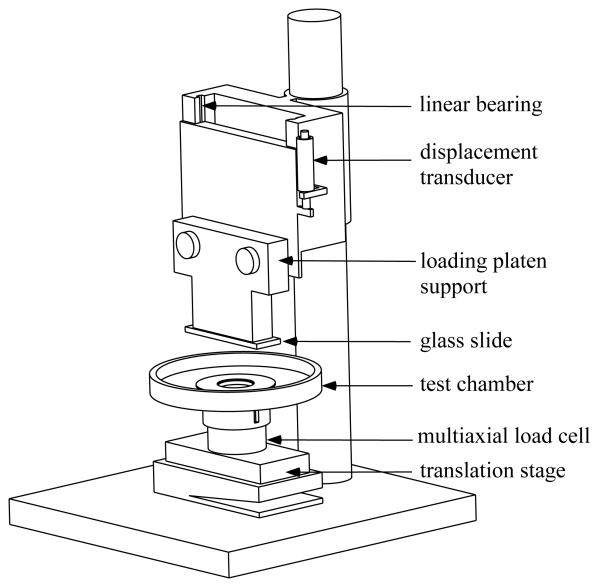
Normal loads were prescribed by a dead weight mounted on linear bearings above the loading-platen support and applied onto the articular surface via a 1mm glass slide (Figure 1). Sliding motion was provided by a computer controlled translation stage (Model PM500-1L, Newport Corporation, CA). All loads were measured with a multi axial load cell mounted on the translation stage (Model 20E12A-M25B,JR3 Inc., CA). Displacements were monitored with a linear variable differential transformer (HR100, Shaevitz sensors, VA) connected in parallel with the indenter. Fluid pressure measurements were made on the face opposite the articular surface [34,40,41] using a microchip piezoresistive pressure transducer (NPC 1210 series; Lucas NovaSensor, CA). Data acquisition and control was performed using a personal computer equipped with a data acquisition card (PCI-MIO-16XE, National Instruments, Austin, TX) and running the Labview data acquisition software (National Instruments, Austin, TX). All experiments were performed at room temperature, with the specimen and loading glass surface immersed in PBS solution mixed with protease inhibitors.

Figure 1.

Schematic of friction device.

Frictional measurements of glass on cartilage were made under the configuration of unconfined compression creep with a prescribed load of 4.5N and intermittent sliding over logarithmic time increments (range of translation ±2mm; sliding velocity 1mm/s). The normal force (W), frictional force ( F), interstitial fluid pressure load (W^p ), and creep displacement were monitored throughout the test. The frictional coefficient (μ_eff = F/W ) and fluid load support (W^p/W ) were calculated from the average values of W , F , and W^p over each sliding cycle. The test was terminated when the interstitial fluid load support (W^p/W ) reduced to approximately 10%. Following the tests, samples were allowed to recover in PBS for a duration equal to or greater than the test duration, before being frozen at −20°C.

Following completion of all the tests, samples were thawed and equilibrated in PBS for two hours and their wet weights were measured (M220, Denver Instrument, Denver, CO). The samples were then lyophilized overnight and reweighed dry. The solid content φ^s was calculated from the ratio of the dry and wet weights.

For statistical analysis, a linear regression was performed between the experimentally measured μ_eff and W^p/W . The regression parameters were used to evaluate μ_eq and φ according to Eq.(2). A paired Student t-test was performed to determine statistical differences between the parameter φ determined from the regression, and the experimentally measured solid content φ^s .

Results

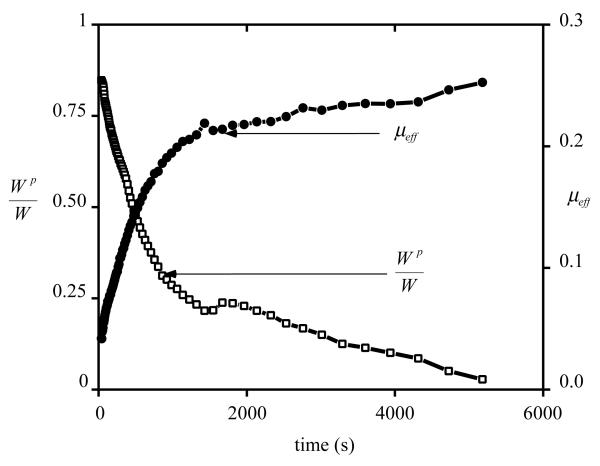
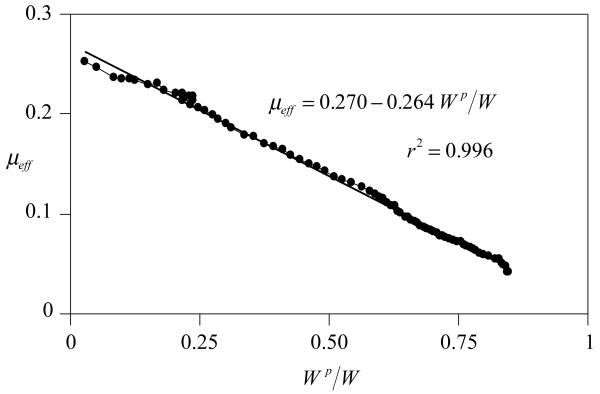
A representative plot for the transient variation of the frictional coefficient and the corresponding fluid load support is shown in Figure 2. For all samples, the effective frictional coefficient μ_eff was found to increase with time from a minimum value of μ_min = 0.01±0.007 (mean±standard deviation) to a maximum value of 0.243±0.044 over a duration ranging from 920s to 19,870s (median: 4,560 s). The corresponding fluid load support decreased from a maximum of 88.8±3.8% to 8.7±8.6%. Plotting the fluid load support against the frictional coefficient yielded a nearly linear response as shown in Figure 3, with an average coefficient of determination of r²=0.96±0.03 over all the samples. From this linear regression analysis of μ_eff versus W^p/W , average values of μ_eq =0.283±0.044 and φ=0.017±0.063 were obtained. φ was statistically smaller than the solid fraction of cartilage obtained from direct measurements, φ^s =0.139±0.017 (p=0.0002).

Figure 2.

Effective friction coefficient, μ_eff, and interstitial fluid load support, W^p/W , versus time, for a representative sample.

Figure 3.

μ_eff versus W^p/W for the representative sample of Figure 2.

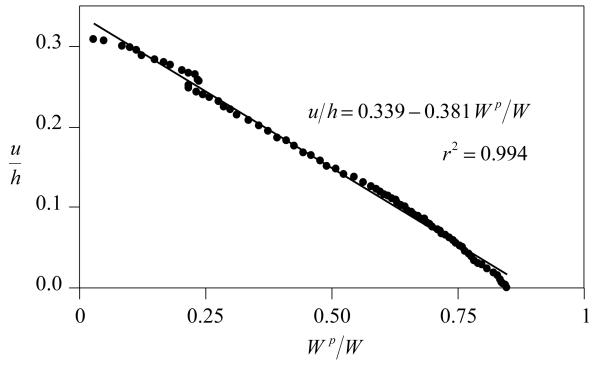
For all samples the percentage decrease in thickness at equilibrium was 35.4%±8.9%. A near-unity linear correlation was observed between creep displacement u (normalized by the sample thickness h) and interstitial fluid load support, with r²=0.98±0.01 (Figure 4).

Figure 4.

Creep displacement versus interstitial fluid load support, for the representative sample of Figure 2.

Discussion

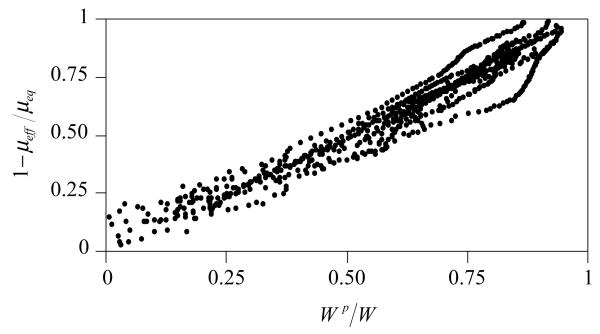
The objective of the current study was to test the hypothesis that a linear correlation exists between the frictional coefficient and interstitial fluid pressurization in articular cartilage. In contrast to our earlier experimental friction study [5] where the fluid pressurization in cartilage was predicted from a theoretical analysis, the current study relies exclusively on experimental measurements, making it independent of any modeling assumptions. The near-unity coefficient of determination observed between μ_eff and W^p/W (shown for a representative sample in Figure 3 and for all samples in Figure 5) unequivocally establishes that the temporal variation in the friction coefficient is tied to the concomitant variation in interstitial fluid load support. These results strongly suggest that interstitial fluid pressurization is a primary mechanism in the regulation of the frictional response of articular cartilage [3,13,27-30]. By supporting the majority of the load transmitted across the contact interface the interstitial fluid pressurization reduces the load supported by the contacting collagen-proteoglycan matrix and glass surface, considerably reducing the frictional force relative to the total contact force. As long as the interstitial pressure remains elevated, the effective friction coefficient is small (Figure 2 & Figure 3). As the fluid pressure reduces to zero the contact force increasingly shifts to the solid matrix, consequently increasing the friction coefficient.

Figure 5.

Combined plot of 1-μ_eff/μ_eq versus W^p/W for all the specimens of this study, showing a nearly linear response between the friction coefficient and interstitial fluid load support.

The correlation observed between the creep displacement and interstitial fluid pressurization (Figure 4) is consistent with predictions from theoretical biphasic analyses of articular cartilage in unconfined compression [2,39]. This result implies that the creep displacement correlates with the friction coefficient, which confirms the earlier experimental observation by McCutchen [29]. The creep response of cartilage in unconfined compression is well understood. Upon step loading, the cylindrical cartilage sample is axially compressed while expanding laterally. Initially, because of its low permeability and the great resistance to fluid exudation, the sample maintains its original volume while its interstitial fluid pressurizes [2,48]. Over time, the interstitial fluid exudes from the tissue while the pressure slowly subsides, reducing the tissue volume and increasing its axial compression. This mechanism explains why the creep deformation varies at the same rate as interstitial fluid pressurization.

A limitation of the current study is that the measurement of interstitial fluid pressurization cannot be performed directly at the articular surface, where the sliding friction occurs, but on the opposite face of the sample. Since cartilage mechanical properties are inhomogeneous through the depth [1,20,37,47] the interstitial fluid pressurization will be depth-dependent as confirmed both experimentally [34] and theoretically [21,22]. To help overcome this limitation the cartilage specimens used in this study were microtomed as thinly as practical to reduce the degree of inhomogeneity between the articular surface and the sample bottom. Another limitation of direct measurements of interstitial fluid pressurization is that a delay in pressurization is observed in the initial response [33,40], which can be explained by the pressure transducer impedance [34]. As a consequence of both of these factors, the peak interstitial fluid load support measured in the current study (~89%) may underestimate the actual value at the articular surface.

Because of the limitation in measuring the exact value of interstitial fluid load support, the value of the solid-to-solid contact area fraction, φ, determined from the linear regression analysis may not be accurate; indeed, in three of ten samples which showed among the lowest values of μ_min (0.003-0.006) the value of φ predicted from the analysis was negative. Nevertheless, based on the measured minimum friction coefficient, and its theoretical lower bound of φμ_eq, the results of this study do indicate that the solid-to-solid contact area fraction is smaller than its theoretical upper bound given by the solid content of cartilage (φ<φ^s). According to the friction model, this result implies that a mixed lubrication mode is likely to prevail at the contact interface, at least under the load magnitude applied in the current study. This indirect observation remains to be confirmed from more direct measurements. Future studies may also determine the influence of factors such as sliding velocity, load magnitude and testing configuration on this mixed lubrication mode.

One of the enduring paradoxes of the studies of cartilage lubrication has been the observation that the friction coefficient can vary from a very small value to a large value [12,13,29,35], as confirmed in the current study. A small friction coefficient, as observed in the early time response under creep loading (averaging 0.01 in this study), is consistent with the functional role of articular cartilage as a bearing material. However, the elevated friction coefficient achieved under equilibrium conditions (0.24 in this study) would likely be highly detrimental to load transmission across articular surfaces, potentially leading to rapid wear and degeneration [12]. It is important to note that the increase in friction coefficient over time is not permanent, as shown in previous studies [12]. Allowing the tissue to recover and loading it again reproduces the same transient increase from a small minimum value to an elevated equilibrium value. Thus, the change in μ_eff cannot be attributed to wear or the removal of a putative boundary lubricant at the articular surface.

The answer to this conundrum is that under physiological loading conditions the interstitial fluid pressure in healthy cartilage is unlikely to ever reduce to zero, as can be deduced from a variety of experimental and theoretical analyses. For example, in a study of rolling and sliding contact of cylindrical biphasic cartilage layers [4], it was found from theory that interstitial fluid load support may exceed 95% for rolling or sliding velocities as low as ~3 μ m/s. From experimental measurements of interstitial fluid pressurization in confined compression [41], fluid load support was found to exceed 60% at loading frequencies as low as 0.0001 Hz (one loading cycle over 2 hrs 45 min). Thus, even minute reciprocal motions in a joint will maintain elevated fluid pressurization in cartilage. It is therefore important to distinguish physiological loading conditions from a creep experiment conducted under laboratory conditions, where a static load can be maintained for several hours until equilibrium is reached. When the results of these previous studies are combined with the current one, it may be concluded that the friction coefficient will always remain low in vivo, in healthy joints.

In recent years there has been a revived interest in the role of articular cartilage boundary lubricants such as phospholipids [14] or lubricin [43,44] and related glycoproteins such as superficial zone protein [11,16,38,42]. Many of the studies that have investigated the influence of these boundary lubricants on cartilage friction have not accounted for the role of interstitial fluid pressurization, perhaps attributing the low frictional coefficient of cartilage entirely to these lubricants. We believe that boundary lubricants complement the role of interstitial fluid pressurization, because studies which have compared the frictional response of articular cartilage using synovial fluid versus saline have generally demonstrated a lower minimum friction coefficient with synovial fluid [12,29]. This finding is consistent with the prevailing hypothesis that the boundary lubricant is present in significant amounts in synovial fluid (in addition to its potential presence in the superficial zone of cartilage). Forster and Fisher [12] found a minimum friction coefficient of μ_min ≈0.006 and equilibrium friction coefficient of μ_eq ≈0.49 with synovial fluid, versus μ_min ≈0.0075 and μ_eq ≈0.56 with Ringer’s solution. It may be concluded that boundary lubricants supplement the primary role of interstitial fluid pressurization to help further reduce the friction coefficient of cartilage. One potential mechanism in the framework of Eq.(2) is that boundary lubricants may reduce the value of μ_eq (which will influence μ_min as well), a hypothesis which remains to be tested directly.

In summary this study provides direct experimental evidence in support of the primary role of interstitial fluid pressurization in the frictional response of articular cartilage. The framework of the biphasic boundary friction model helps in the interpretation of these experimental data and can account for the role of boundary lubricants and mixed lubrication conditions at the contact interface. Future studies may investigate the precise role of boundary lubricants in the context of this framework and explore methods for measuring the solid-to-solid contact area fraction more directly.