DYNAMIC RESPONSE OF IMMATURE BOVINE ARTICULAR CARTILAGE IN TENSION AND COMPRESSION, AND NONLINEAR VISCOELASTIC MODELING OF THE TENSILE RESPONSE

Abstract

Objectives

Very limited information is currently available on the constitutive modeling of the tensile response of articular cartilage and its dynamic modulus at various loading frequencies. The objectives of this study were to 1) formulate and experimentally validate a constitutive model for the intrinsic viscoelasticity of cartilage in tension, 2) confirm the hypothesis that energy dissipation in tension is less than in compression at various loading frequencies, and 3) test the hypothesis that the dynamic modulus of cartilage in unconfined compression is dependent upon the dynamic tensile modulus.

Methods

Experiment 1: Immature bovine articular cartilage samples were tested in tensile stress relaxation and cyclical loading. A proposed reduced relaxation function was fitted to the stress-relaxation response and the resulting material coefficients were used to predict the response to cyclical loading. Adjoining tissue samples were tested in unconfined compression stress relaxation and cyclical loading. Experiment 2: Tensile stress relaxation experiments were performed at varying strains to explore the strain-dependence of the viscoelastic response.

Results

The proposed relaxation function successfully fit the experimental tensile stress-relaxation response, with R² =0.970±0.019 at 1 % strain and R² =0.992±0.007 at 2 % strain. The predicted cyclical response agreed well with experimental measurements, particularly for the dynamic modulus at various frequencies. The relaxation function, measured from 2% to 10% strain, was found to be strain-dependent, indicating that cartilage is nonlinearly viscoelastic in tension. Under dynamic loading, the tensile modulus at 10 Hz was ~2.3 times the value of the equilibrium modulus. In contrast, the dynamic stiffening ratio in unconfined compression was ~24. The energy dissipation in tension was found to be significantly smaller than in compression (dynamic phase angle of 16.2±7.4° versus 53.5±12.8° at 10⁻³ Hz). A very strong linear correlation was observed between the dynamic tensile and dynamic compressive moduli at various frequencies ( R² =0.908±0.100).

Conclusion

The tensile response of cartilage is nonlinearly viscoelastic, with the relaxation response varying with strain. A proposed constitutive relation for the tensile response was successfully validated. The frequency-response of the tensile modulus of cartilage was reported for the first time. Results emphasize that fluid-flow dependent viscoelasticity dominates the compressive response of cartilage, whereas intrinsic solid matrix viscoelasticity dominates the tensile response. Yet the dynamic compressive modulus of cartilage is critically dependent upon elevated values of the dynamic tensile modulus.

Introduction

The response of articular cartilage under tensile loading has been shown to be viscoelastic, exhibiting stress-relaxation under a prescribed strain [1, 2], creep under a prescribed stress [3], and a strain-rate dependent modulus [1, 4]. The cartilage tensile modulus has also been observed to be one to two orders of magnitude greater than the compressive modulus, as evident from studies which have independently reported tensile [1, 4] and compressive [5] measurements, and from more recent studies where both properties were measured on the same or adjoining tissue samples [6–8].

The viscoelasticity of cartilage in compression results primarily from the pressurization and flow of its interstitial fluid under loading, whereby energy is dissipated as a result of frictional drag between the solid collagen-proteoglycan matrix and the fluid [9–11]. This flow-dependent response in compression has been successfully modeled by the biphasic theory of Mow et al. [10] and verified experimentally from direct measurements of interstitial fluid pressure in creep, stress-relaxation and dynamic loading [12–14]. In tension however, when accounting for the disparity between the tensile and compressive moduli of cartilage, theoretical predictions from the biphasic theory ascribe negligible viscoelasticity to flow-dependent effects in tension [15]. These results suggests that the viscoelastic response of cartilage in tension may be attributed almost exclusively to flow-independent mechanisms of energy dissipation which are intrinsic to the solid collagen-proteoglycan matrix of the tissue. Thus, tensile measurements of the viscoelastic response of cartilage can yield its flow-independent tensile properties, while the flow-dependent viscoelastic response can be investigated under dynamic compression.

Very limited information is currently available on the constitutive modeling of the tensile response of articular cartilage [16] and its dynamic modulus at various loading frequencies. Consequently, the first objective of this study was to formulate and validate a constitutive model for the intrinsic viscoelasticity of cartilage in tension. Specifically, it was of interest to identify a suitable relaxation function which can accurately describe the response of cartilage under tensile stress-relaxation and cyclical loading; and to determine whether the viscoelastic behavior of cartilage in tension is linear, quasilinear, or nonlinear. The second objective was to confirm the hypothesis that energy dissipation under dynamic compression is greater than in tension, because of the additional flow-dependent dissipative mechanism in compression. The third objective was to test the hypothesis that the dynamic modulus of cartilage in unconfined compression is dependent upon the dynamic tensile modulus.

To achieve these objective, immature bovine articular cartilage samples were tested under tensile stress-relaxation, at strain magnitudes ranging from 1% to 10%, to characterize the relaxation function of the tissue. A subset of specimens were also tested under sinusoidal stresses at frequencies ranging from 10⁻³ to 10¹ Hz to determine the tensile dynamic modulus and phase angle experimentally. The relaxation response was fitted to a proposed constitutive relation and the resulting fitted material parameters were used to predict the dynamic tensile modulus and phase angle at various frequencies. These theoretical predictions were subsequently compared to the corresponding experimental measurements for the purpose of validating the model. In addition, tissue samples harvested from adjoining sites were tested under dynamic unconfined compression loading to determine the dynamic compressive modulus and phase angle. The phase angle data were then compared to the corresponding tensile response to determine the extend of energy dissipation in tension versus compression. The dynamic moduli were compared to determine whether a correlation existed between the tensile and compressive responses.

Materials and Methods

Sample Preparation

In Experiment 1, twelve sets of cartilage samples (12 cylindrical disks and 24 rectangular strips) were harvested from the humeral head and glenoid of five fresh bovine shoulder joints (2–4 months old) obtained from a local abattoir. Each set consisted of two adjacent rectangular samples harvested parallel (//) and perpendicular (⊥) to the local split line direction, used for both tensile stress-relaxation and dynamic loading along both directions, and one cylindrical sample harvested between the tensile specimens, and used for static and dynamic unconfined compression. In Experiment 2, 12 additional rectangular samples were harvested, six parallel (//) and six perpendicular (⊥) to the local split line direction, though not necessarily from adjacent locations, and used for tensile stress-relaxation. Using a sledge microtome (Model 1400; Leiz, Rockleigh, NJ), approximately 0.5–1 mm of tissue was removed from the deep zone to remove remnants of subchondral bone and microvasculature, leaving the articular surface intact. For tensile testing, dumbbell-shaped specimens (width=1.27±0.07 mm, thickness=1.50±0.16 mm, length=4.49±0.55 mm) were further cut out from the rectangular bars using a custom die cutter; for unconfined compression, cylindrical plugs (h=1.98±0.05 mm, Ø=4 mm) were cored out using a biopsy punch. The harvested samples were stored in phosphate buffered saline (PBS) at −20°C until ready for use.

Testing Apparatus

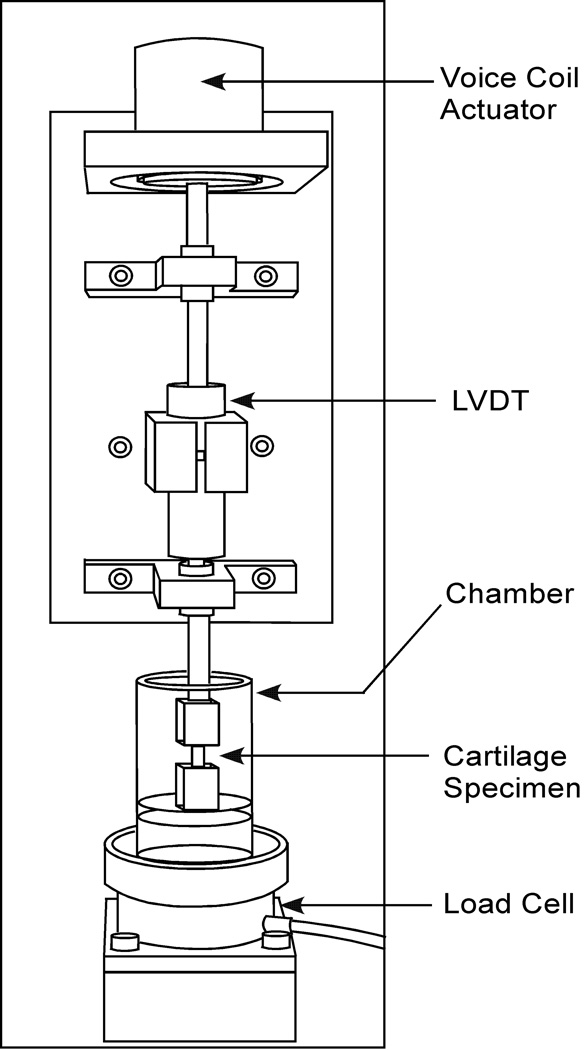
The custom-designed tensile testing apparatus (Figure 1) consisted of a voice-coil force actuator (Model LA17-28-000A; BEI Kimco Magnetics Division, San Marcos, CA, 71N peak force), connected in series with a linear variable differential transformer (LVDT) for displacement measurements (Model PR812-200, Schaeviz Sensors, Hamptons, VA, ±5 mm), the tissue sample mounted within custom grips (modeled after those used in [1]) in a PBS-filled testing chamber, and a load cell (Model 8523, Burster, Sterling Heights, MI, ±200N). The force actuator, connected to a power supply (Model PST-040-13-DP, Copley Controls Corp., Canton, MA, +40VDC at 13A continuous) and controller box (Model TA115, Trust Automation INC., San Luis Obispo, CA, 150W continous/325W peak) was controlled via a force feedback loop using a desktop computer with a data input and output board (Model PCI-MIO-16XE-10, National Instruments, Austin, TX) running the LabView software package (Version 6.1, National Instruments, Austin, TX). The same loading device was used for compressive loading, by replacing the specimen grips with impermeable frictionless loading platens [17].

Figure 1.

Schematic of the custom-designed testing apparatus.

Tensile Strain Compensation

Both tensile and compressive displacements were measured with the LVDT, and strain was calculated from the change in displacement relative to the initial specimen grip to grip length for tensile loading, and the initial specimen thickness for compressive loading. In the tensile specimens, the strain in the gauge section was estimated from the grip-to-grip strain using a correction factor determined in preliminary studies, from the slope of a linear regression between grip-to-grip strain and optical strain measurements of the gauge section. Optical strain measurements could only be conducted at frequencies of 10⁻¹ Hz or lower, due to blurring of the images at higher frequencies, thus necessitating the use of grip-to-grip strain. From preliminary measurements performed at three loading frequencies between 10⁻³ and 10⁻¹ Hz, the conversion factor between gauge strain and grip-to-grip strain was 0.980±0.096 (n=3), with a linear regression coefficient R² =0.916±0.024. Because this conversion factor is very close to unity, the gauge strain was taken to be equal to the grip-to-grip strain. It was assumed that this conversion factor remained the same at the higher tested frequencies.

Loading Protocol

On the day of testing, specimens were thawed at room temperature in PBS solution for one hour, and the specimen dimensions were measured with a custom micrometer device. All subsequent tests were performed in PBS containing protease inhibitors (Complete Cocktail Tablet, Roche Applied Science, Indianapolis, IN). An initial tare load of 0.3 N (equivalent to 157 kPa for tensile studies, and 24 kPa for compressive studies) was then applied onto each sample, to prevent tensile specimens from being curved and to maintain proper platen contact for compressive loading, while keeping the tare strains in a low range. The specimen was allowed to equilibrate under this tare load (0.5 hour) for both tensile and compressive loading.

For dynamic tensile and compressive loading in Experiment 1, cyclical loads were applied onto the specimen using a sinusoidal profile of the form F = F₀ (1 − cos 2πft)/2 ( f =loading frequency, ranging from 10⁻³ to 10 Hz), varying in amplitude from 0 to F₀ above the tare load. Cyclical loads consisted of 7 cycles at 10 Hz, 5 cycles at 5 Hz, 4 cycles at 2 Hz, 3 cycles at 1 Hz, and 1 cycle at 10⁻¹, 10⁻², 10⁻³ Hz, applied in that given order. At the end of each test at a given frequency, the specimen was allowed to recover under the tare load for a duration equal to twice that of the cyclical test. In principle, any of the loading cycles could be used for the analysis of results; the 5^th cycle at 10 Hz, 4^th cycle at 5 Hz, 3^rd cycle at 2 Hz, 2^nd cycle at 1 Hz, and 1^st cycle at 10⁻¹ to 10⁻³ Hz were selected to measure the dynamic modulus and phase angle for both tension and compression. For dynamic tensile loading, F₀ was 0.5 N (262 kPa when calculated with the initial gauge cross-sectional area of the dumbbell-shaped specimen) from 10⁻¹ to 10 Hz. Since the dynamic modulus of cartilage decreases with decreasing frequency, it was necessary to reduce F₀ at the lower frequencies to maintain the strains in a small range; 0.44 N (231 kPa) was applied at 10⁻² Hz and 0.38 N (199 kPa) at 10⁻³ Hz. For dynamic unconfined compression, F₀ was 2 N (159 kPa) through 10⁻¹ to 10 Hz, 1.1 N (88 kPa) at 10⁻² Hz, and 0.6 N (48 kPa) at 10⁻³ Hz. The magnitude of F₀ in unconfined compression was selected to produce a comparable amount of tensile strain along the radial and circumferential directions of the cylindrical disks as in the uniaxial tensile loading experiments of the dumbbell-shaped specimens. This was estimated by assuming that cartilage behaves as an incompressible solid (a reasonable approximation at higher loading frequencies [18]), from which it can be deduced that the radial and circumferential tensile strains are equal in magnitude to one-half of the axial compressive strain. For both tensile and compressive cyclical loading experiments, the magnitude | G* | and phase angle ∠G* of the dynamic modulus were determined from Fourier analysis of the measured stress and strain responses. (This type of analysis implicitly assumes that the response is linear viscoelastic, which is reasonable under the small strains applied in Experiment 1.)

At the completion of dynamic tensile loading, following a 2000 s recovery period, the specimen was pre-conditioned with a cyclical load of 0.5 N (262 kPa) at 1 Hz, applied for 100 s, then allowed to recover for 200 s. This pre-conditioning was followed by a series of four stress relaxation tests. In each test, the strain was ramped up in 0.8 s to its final value; the tissue sample was allowed to relax for 1000 s; the sample was unloaded and allowed to recover for 2000 s under a tare load of 0.3 N (172 kPa). Two consecutive tests were performed up to 1% strain (to investigate repeatability), followed by two additional tests to 2% strain.

In addition to the dynamic unconfined compressions tests on the cylindrical disks, the equilibrium Young’s modulus in compression ( E_−Y ) was measured from unconfined compression stress-relaxation tests: Following equilibration under a tare load of 0.3 N (24 kPa), three consecutive strain increments (to 2%, 4%, and 6 % strain) were applied with a ramp velocity of 1 µm/s, each followed by a stress-relaxation lasting 1500 s to 2000 s. E_−Y was determined from the slope of the linear regression of equilibrium stresses vs. applied strains.

In Experiment 2, twelve additional dumbbell-shaped specimens (width=1.29±0.08 mm, thickness=1.35±0.17 mm, length=3.98±0.59 mm) harvested parallel and perpendicular to the local split line direction were each tested in stress-relaxation following a similar protocol as in Experiment 1: Pre-conditioning with a cyclical load (1 Hz for 100 s) followed by recovery (200 s); consecutive stress-relaxation tests (twice each at 2 %, 4 %, 6 %, 8 %, and 10 % strain), each lasting lasting 1000 s, followed by a 2000 s recovery.

Analysis of Viscoelastic Response in Tension

Under uniaxial tension the viscoelastic response of cartilage may be described by the modified superposition method [19–21],

$$\sigma [\epsilon (t),t]=g[\epsilon (0),0]{\sigma }^e[\epsilon (t)]+{\displaystyle {\int }_0^t{\sigma }^e[\epsilon (t-\tau )]\frac{\partial g[\epsilon (\tau ),\tau ]}{\partial \tau }}d\tau$$ (1)

where σ[ε,t] is the stress applied to the tissue sample, ε(t) is the strain, σ^e [ε] is the equilibrium elastic stress-strain response, and g[ε,t] is the reduced relaxation function. This formulation is sufficiently general to describe a category of nonlinear viscoelasticity when g[ε(t),t] is an explicit function of strain. When g = g(t), the viscoelastic behavior is linear and the material may be described either as quasi-linear viscoelastic (if σ^e [ε] is a nonlinear function of ε ) or linear viscoelastic (if σ^e [ε]=E_+Yε , where the tensile Young’s modulus E_+Y is constant).

In the current study, after investigating several candidate functions, we use the following reduced relaxation function [22]:

$$g[\epsilon ,t]=1+\frac{\alpha [\epsilon ]}{1+{\left(\frac{t}{\tau [\epsilon ]}\right)}^{\beta [\epsilon ]}}$$ (2)

In the more general case of nonlinear viscoelasticity the material functions α and β (both unitless and positive) and τ (units of time) may vary with strain. Note that g[ε, 0]=1+α[ε] and g[ε,t → ∞] = 1 . The equilibrium stress-strain response is modeled generically as

$${\sigma }^e[\epsilon ]=E_{+Y}[\epsilon ]\epsilon$$ (3)

where E_+Y is a function of the strain for a nonlinear equilibrium elastic response.

The parameters E_+Y, α, β, τ appearing in the above constitutive equations were determined by curve-fitting the tensile stress-relaxation responses in Experiments 1 and 2, using a quasi-Newton optimization method. In Experiment 1, where strains remained below 2%, the material parameters were assumed to be strain-independent for the purpose of predicting the dynamic response under sinusoidal loading. In Experiment 2, the strain-dependence of these parameters was investigated.

Statistical Analyses

Two-way ANOVA with repeated measures was performed to investigate the effects of loading type (unconfined compression, tensile loading //, and tensile loading ⊥), and loading frequency on | G* | and ∠G* in the cyclical loading tests of Experiment 1 (SAS Institute Inc., NC). Similarly, two-way ANOVA with repeated measures was used to investigate the effects of strain and test repeatability (first and second test at each strain level) on the material parameters E_+Y,α, β, τ in the tensile stress-relaxation tests of Experiments 1 and 2. In all cases, α was set at 0.05 and the significance was set at p<0.05; post-hoc testing of the means was performed with Bonferroni adjustment.

Results

Tensile Measurements

Experiment 1

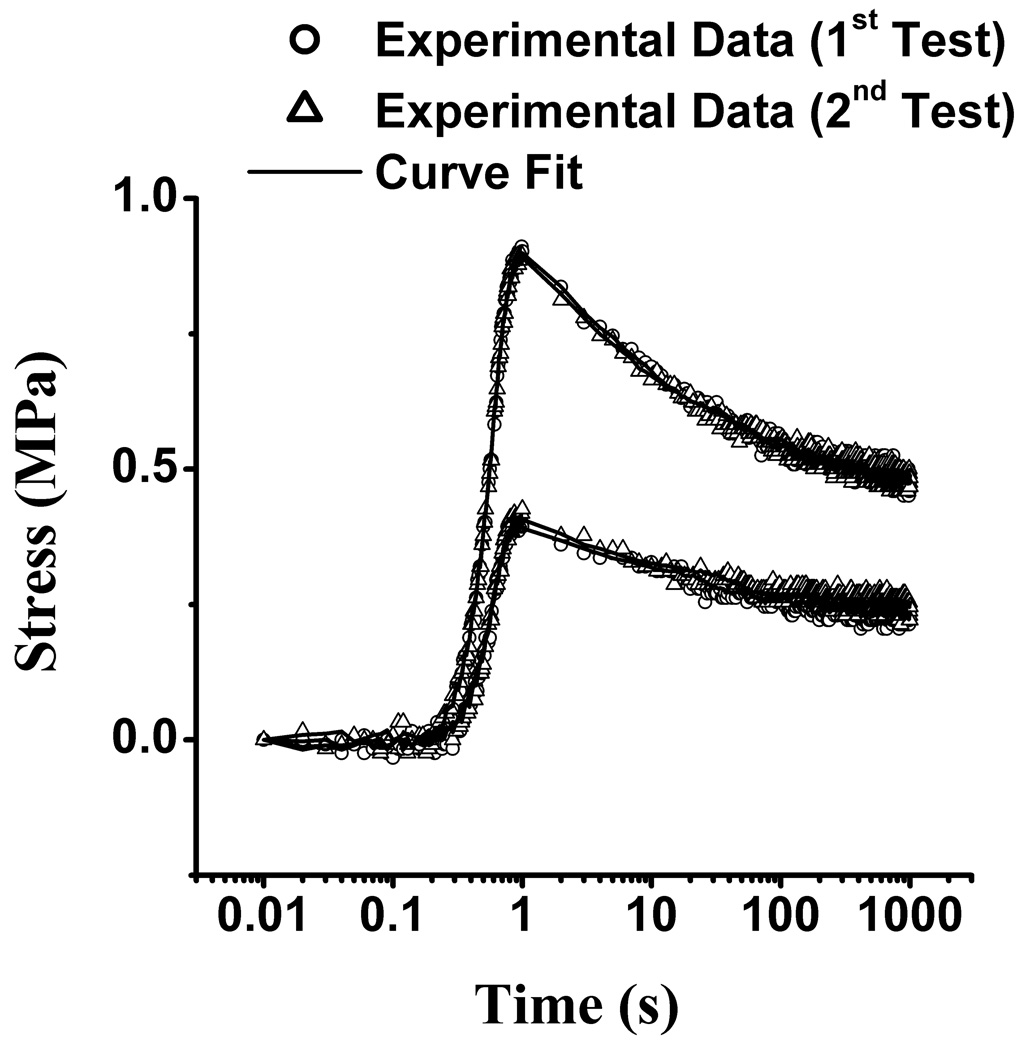
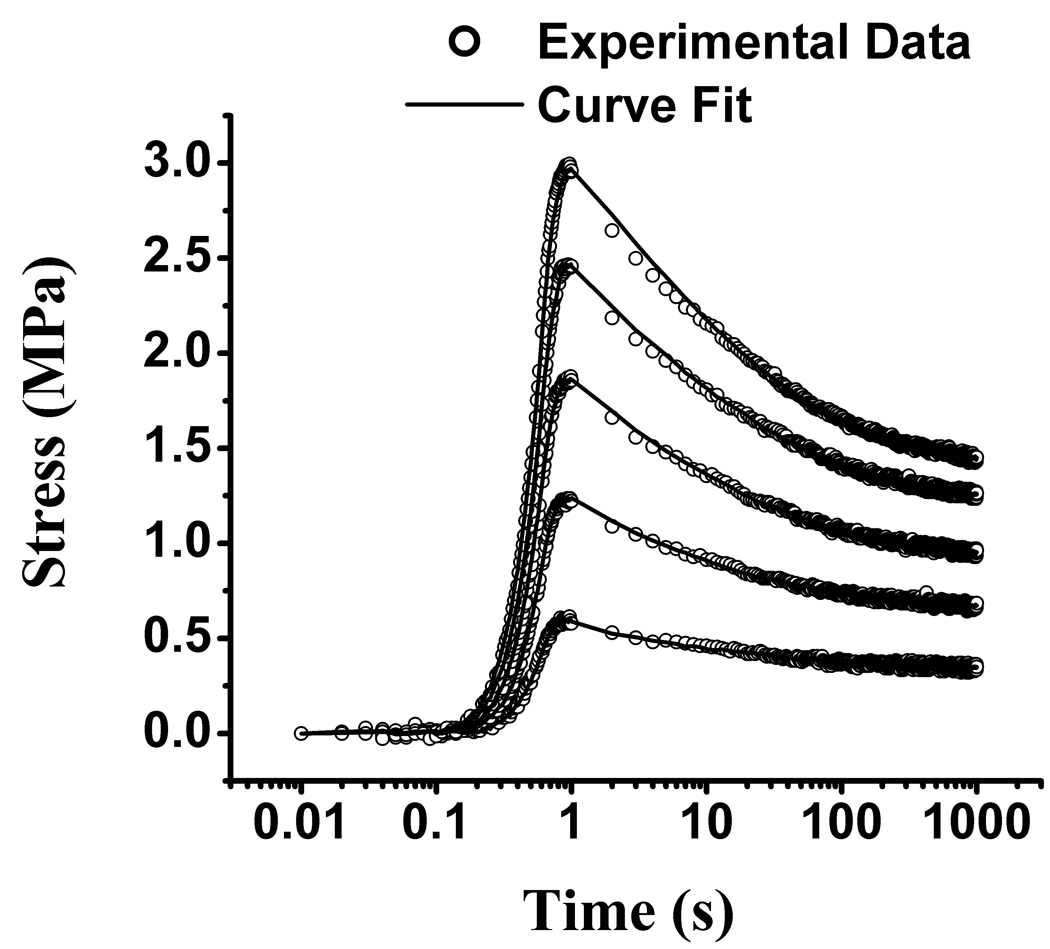
The experimental tensile stress-relaxation data at 1% and 2% strain (n=12 for //, and n=12 for ⊥) were curve-fitted successfully with Eqs.(1)–(3) (Figure 2). The average and standard deviation of the coefficient of determination for these curve-fits was R² =0.970±0.019 at 1 % strain and R² =0.992±0.007 at 2 % strain. E_+Y, α, β, τ showed no statistical differences between the first and second tests (p>0.3); consequently, the results reported in Figure 3 (triangular symbols) represent the average of both tests. No statistical differences were observed between 1 % and 2 % strain levels (p=1.0), and between parallel (//) and perpendicular (⊥) directions (p=1.0). Average values of the tensile modulus at 1 % and 2 % strain were E_+Y =17.4±5.1 MPa for // and E_+Y =16.6±4.6 MPa for ⊥.

Figure 2.

Representative tensile stress-relaxation responses for a typical specimen from Experiment 1, showing the first and second tests at 1% and 2% strain. The solid curves represent the curve-fitted theoretical stress responses.

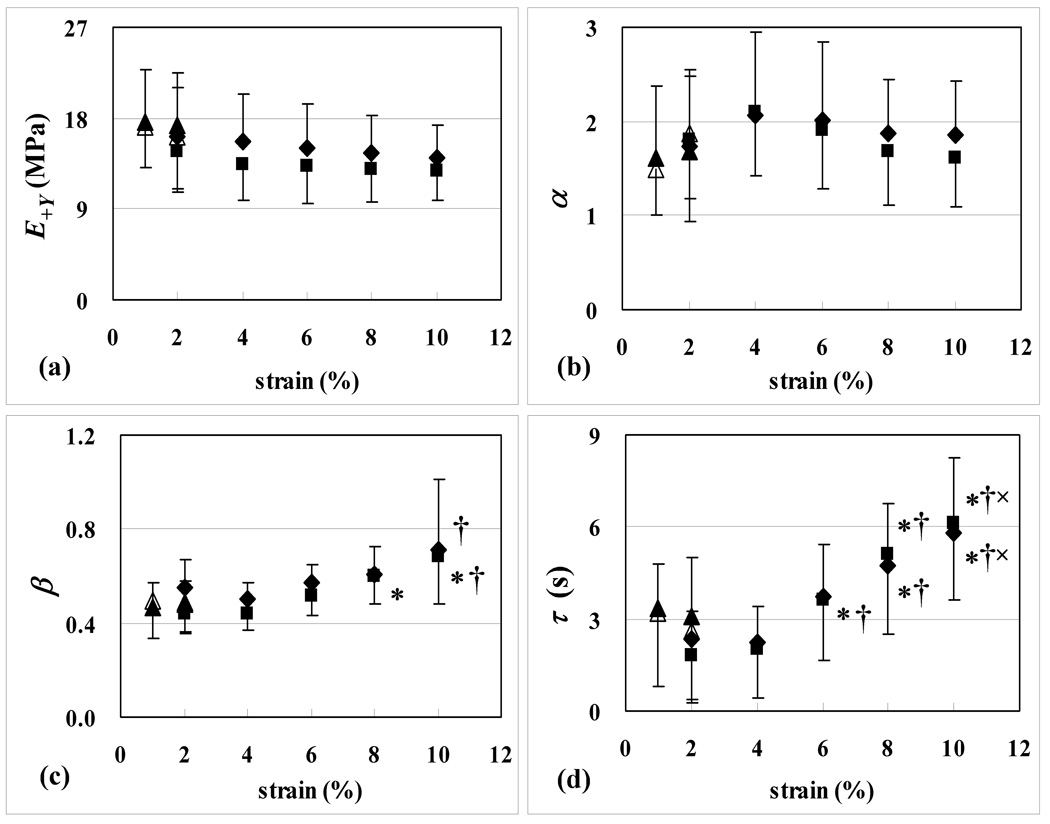
Figure 3.

Mean and standard deviation of (a) E_+Y, (b) α , (c) β, and (d) τ from tensile stress-relaxation tests at various applied strains. Experiment 1: ▲ for // samples, Δ for ⊥ samples. Experiment 2: ◆ for // samples, ■ for ⊥ samples. Additional symbols denote significant statistical differences against corresponding values at 2 % (*), 4 % (†), and 6 % (×) strain levels (p<0.05).

Typical stress-strain responses from the cyclical tensile loading tests are presented in Figure 4 for frequencies ranging from 10⁻³ to 10¹ Hz. The measured strain ranged from 0.005±0.001 at 10 Hz to 0.010±0.003 at 10⁻³ Hz. The applied load was very nearly a pure sinusoid as assessed by its total harmonic distortion ranging from 4.7±1.1 % at 10⁻³ Hz to 4.3±3.5 % at 10 Hz . The experimental dynamic modulus | G^* | and phase angle ∠G^* , determined from Fourier analyses of stress and strain responses (Figure 5), varied with loading frequency, exhibiting characteristic viscoelastic responses. The tensile | G^* | ranged from 21.7±4.8 MPa at 10⁻³ Hz to 38.6±6.6 MPa at 10 Hz for // specimens (n=12), and from 20.5±4.5 MPa at 10⁻³ Hz to 38.5±5.0 MPa at 10 Hz with ⊥ specimens (n=12). No statistical differences were observed between // and ⊥ specimens at any frequencies ( | G^* | : p=1.0, ∠G^* : p=1.0). Neither | G^* | nor ∠G^* exhibited statistical differences between 1 Hz and 10 Hz (p>0.06).

Figure 4.

Tensile stress-strain response for a typical specimen at various loading frequencies (Experiment 1). Symbols represent the experimental response and solid curves represent the theoretical prediction, using material properties curve-fitted from the corresponding stress-relaxation experiment for this specimen.

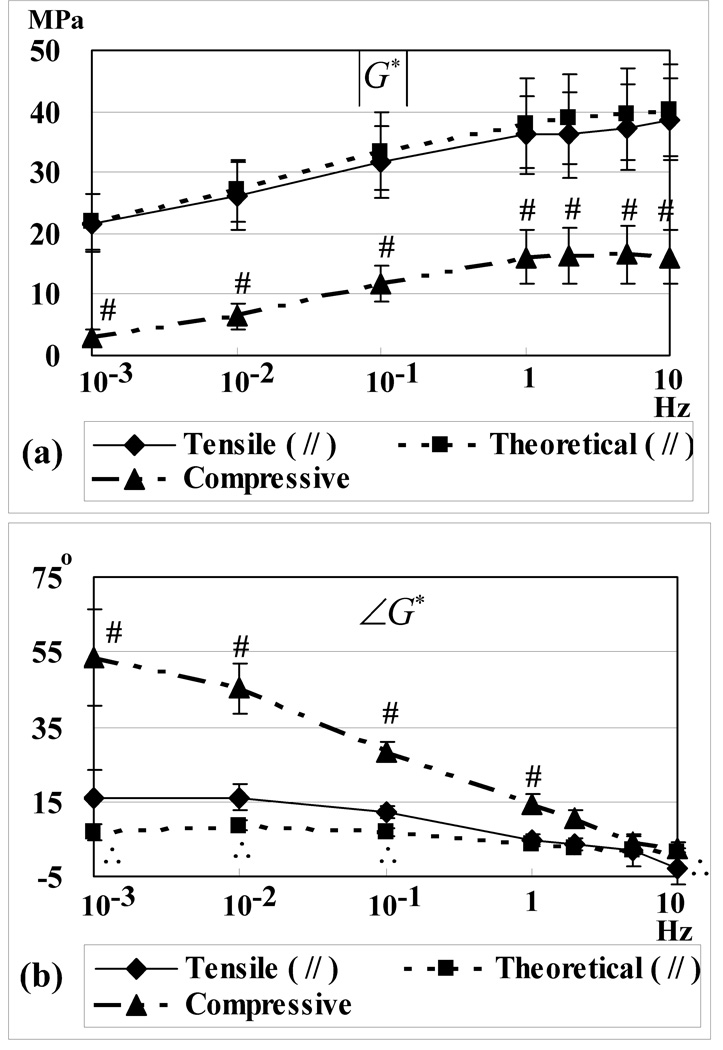
Figure 5.

Experimental dynamic moduli | G^* | (a) and phase angles ∠G^* (b) in tension and compression, and corresponding theoretical predictions (tensile case), as a function of loading frequency. Tensile results are presented for // samples only, as ⊥ samples exhibit a virtually identical response. Symbols denote significant statistical differences between dynamic tension and compression (#), and between experimental results and theoretical predictions (∴) (p<0.05).

Specimen-specific values of the material parameters E_+Y , α, β, τ determined from stress-relaxation tests at 1% strain (averaged from the first and second test) were used in Eqs.(1)–(3) to predict the cyclical response from theory (Figure 4). The theoretical dynamic modulus and phase angle were evaluated from a numerical Laplace transform of the relaxation function, using the numerical scheme described by Huang et al. [23] (since the Laplace transform of Eq.(2), with constant material coefficients, is not available in closed form). Predicted tensile values of | G^* | and ∠G^* are presented in Figure 5. Good agreement was observed between experimental and theoretical values of | G^* | , for both // and ⊥ samples, with no statistical differences observed at any of the frequencies (p≥0.40). However, the theoretical ∠G^* was statistically smaller than the experimental ∠G^* in the range from 10⁻³ to 1 Hz (p<0.04).

Experiment 2

The experimental tensile stress-relaxation data from 2% to 10% strain (n=6 for //, and n=6 for ⊥) were curve-fitted successfully with Eqs.(1)–(3), with R² ranging from 0.989±0.006 at 2 % to 0.998±0.001 at 10 % (Figure 6). No statistical differences were observed in E_+Y, α, β, τ between the first and second test at any strain level, either for // or ⊥ specimens (p=1.0). Consequently, the material coefficients reported in Figure 3 represent averages of the first and second test results. No statistical differences were observed in E_+Y, α, β, τ between // and ⊥ specimens, at any strain level (p=1.0). E_+Y and α showed no statistically significant strain-dependence in either // or ⊥ samples, while β and τ showed strain-dependent increases in both // and ⊥ samples (Figure 3). The average value of E_+Y over 2 % to 10 % strain was 15.1±4.2 MPa for // and 13.4±3.5 MPa for ⊥ specimens.

Figure 6.

Representative tensile stress-relaxation responses for a typical specimen from Experiment 2, showing the first of two tests at each of 2%, 4%, 6%, 8% and 10% strain. The solid curves represent the curve-fitted theoretical stress responses.

Compressive Measurements

Experiment 1

The compressive equilibrium Young’s Modulus obtained from the slope of the linear regression to the equilibrium stress versus strain response (Figure 7, R² =0.996±0.004) was E_−Y =0.663±0.229 MPa. The measured strain ranged from 0.012±0.003 at 10 Hz to 0.022±0.009 at 10⁻³ Hz for unconfined compressive dynamic loading. The applied load was very nearly a pure sinusoid as assessed by its total harmonic distortion ranging from 1.8±0.8 % at 10⁻³ Hz to 5.2±1.2 % at 5 Hz and 9.4±1.4 % at 10 Hz. The experimental dynamic modulus | G^* | and phase angle ∠G^* , determined from Fourier analyses of stress and strain responses in compression are also reported in Figure 5. In unconfined compression | G^* | ranged from 3.0±1.3 MPa at 10⁻³ Hz to 16.2±4.4 MPa at 10 Hz (n=12). The compressive | G^* | was significantly smaller than the corresponding tensile | G^* | (p<0.001) and the compressive ∠G^* was significantly larger than the corresponding tensile ∠G^* (p<0.006) at nearly all frequencies (Figure 5). In compression, neither | G^* | nor ∠G^* exhibited statistical differences between 1 Hz and 10 Hz (p=1.00). In a parametric plot of compressive versus tensile | G^* | at various frequencies, a very high correlation was observed (compressive versus //, R² =0.908±0.100; compressive versus ⊥, R² =0.949±0.019) (Figure 8).

Figure 7.

Linear regression of unconfined compression equilibrium stress versus strain responses (mean and standard deviation over all cylindrical disks in Experiment 1). The slope represents the compressive equilibrium Young’s modulus, E_−Y.

Figure 8.

Parametric plot of compressive | G^* | versus tensile | G^* | for // samples, at various frequencies (closed symbols). Open symbol represents the equilibrium response. A very similar correlation is observed with ⊥ samples. Means and standard deviations of the correlation coefficients are reported in the text.

Discussion

The first objective of this study was to formulate and validate a constitutive model for the intrinsic viscoelasticity of cartilage in tension. Using the modified superposition principle of Eq.(1), it was found that the stress-relaxation responses under small strains can be curve-fitted successfully with the constitutive models of Eqs.(2) and (3), using constant material parameters, as attested by the near-unity coefficients of determination (Figure 2). A satisfactory curvefit of the relaxation response represented the first step in the validation of the constitutive model. The next step was to demonstrate the predictive ability of the model in an independent set of experiments. The results shown in Figure 4 and Figure 5 demonstrate that the model adopted in this study was very successful at predicting the dynamic tensile modulus | G^* | from independent cyclical loading experiments on the same tissue samples, though it underestimated the phase angle ∠G^* . The implication from the latter finding is that the energy dissipation characterized during tensile stress-relaxation underestimated the energy dissipation during tensile cyclical loading.

The third step was to investigate whether the viscoelastic response was nonlinear. Interestingly, the tensile modulus E_+Y was observed to be statistically independent of strain (Figure 3a), suggesting that the equilibrium stress-strain response of immature bovine cartilage is linear in the range of strains used in this study. For comparison purposes, Woo et al. [24] and Roth and Mow [25] reported a nonlinear tensile equilibrium stress-strain response in bovine articular cartilage, whereas Akizuki et al. [1] reported a linear tensile equilibrium stress-strain response for human knee cartilage. Interestingly, Charlebois et al. [26] reported that immature bovine cartilage relaxes to zero load when conducting tests for 5 to 10 hours, thus predicting an equilibrium modulus of zero; they warned that tests conducted for shorter times would overestimate the equilibrium modulus. This finding is discussed in further details below. These variable literature findings suggest that the source of cartilage and its age have a significant influence on its equilibrium response. In the current study, the parameter α was also observed to be statistically independent of strain (Figure 3b). Note that 1 + α represents the ratio of peak to equilibrium tensile stress under a step increase in tensile strain; it also represents the ratio of the peak dynamic modulus to equilibrium modulus in tension, |G^*|_max = (1+α)E_+Y . A constant value of α implies that the dynamic stiffening of cartilage in tension is not a function of the applied strain.

In contrast, the exponent β and ‘time constant’ τ were both observed to increase with strain, in a nearly quadratic manner. The physical meaning of the material coefficient β is best understood when looking at the frequency response of |G^*|. At low frequencies |G^*| approaches the value of the equilibrium tensile modulus E_+Y ; at high frequencies it approaches the value of the instantaneous tensile modulus (1 + α)E_+Y. β controls the width of the frequency range over which |G^*| transitions between these two extreme values, with increasing values of β implying a narrower range. This range also spans the frequencies which exhibit the greatest viscoelastic energy dissipation. An increase in τ implies a rightward shift in the frequency responses of |G^*| and ∠G^* , or equivalently, a slower stress-relaxation response. Within the context of Eq.(1), these strain-dependent material coefficients imply a nonlinear viscoelastic response.

The second objective of this study was to confirm the hypothesis that energy dissipation under dynamic compression is greater than in tension. Indeed, the phase angle ∠G^* observed in Experiment 1 was statistically greater in unconfined compression than in tension, with a peak value of 53.6°±12.8° in unconfined compression at 0.001 Hz, and 16.2°±7.4° in tension (//) at 0.001 Hz (Figure 5). This result supports the hypothesis that fluid flow-dependent energy dissipation is much less significant in tension than in compression. This hypothesis is also supported by the observation that the ratio of peak dynamic modulus to equilibrium modulus is much greater in unconfined compression than in tension: In compression the peak value of |G^*| (~16 MPa) is 24 times greater than E_−Y ; in tension, the peak value of |G^*| (~39 MPa) is only ~2.3 times greater than E_+Y. Thus, interstitial fluid pressurization under dynamic unconfined compression loading contributes very significantly to the dynamic stiffening of the tissue, whereas fluid pressurization appears to be much less significant (and probably negligible, as suggested from theory [15]) in tension.

The third objective of this study was to test the hypothesis that the dynamic modulus of cartilage in unconfined compression is dependent upon the dynamic tensile modulus. This hypothesis derives from the recognition that unconfined compression of a cylindrical disk subjects cartilage to tensile strains in the radial and circumferential directions. The lateral expansion of the tissue under axial compressive loading is resisted by its tensile properties. (In contrast, confined compression subjects cartilage exclusively to compressive strains and the tensile properties of the tissue play no role in such a loading configuration.) The observation that the dynamic unconfined compression modulus correlates linearly with the dynamic tensile modulus in the range 10⁻³ to 10¹ Hz (Figure 8) supports this hypothesis, but does not prove it. The proof is available from theory [15, 27]. These results explain the counter-intuitive observation that the tensile modulus of cartilage is much greater than its compressive modulus, even though the primary loading mode of the articular layers of diarthrodial joints is in compression.

In addition to addressing these specific objectives, a number of additional observations can be made based on the results of this study. The reason for performing two stress-relaxations tests at each strain increment was to determine whether the tissue response was repeatable, or whether permanent tissue microdamage might be occurring, particularly at the higher strain levels. The finding that statistical differences could not be detected between the first and second test, neither in Experiment 1 (Figure 2) nor in Experiment 2, confirms that the responses were indeed repeatable and truly viscoelastic, not viscoplastic. This observation was particularly relevant considering the duration of testing for each tensile specimen (~17,500 s = 4.9 hr in Experiment 1 and ~31,800 s = 8.8 hr in Experiment 2).

The equilibrium value of the tensile modulus, E_+Y , was determined by curve-fitting the transient stress-relaxation responses; in effect, it was obtained by extrapolation since none of the experimental responses actually reached equilibrium. Based on representative mean values of the material coefficients of the relaxation function (for example, α = 1.81, β = 0.54 , and τ = 3.55, Figure 3), it can be estimated from Eq.(2) that the stress response would have relaxed to within 10% of its equilibrium value ( g = 1.1) in ~680 s, and to within 1% of its equilibrium value ( g = 1.01) in ~53,300 s or 14.8 hr. The stress value at 1,000 s (the duration used in this study) is estimated to be within ~8% of its equilibrium value.

A potential limitation of our study is that the true equilibrium response of the tissue was not measured directly but implied from extrapolation. Our decision to limit the duration of stress-relaxation to 1000 s per test was motivated in part by preliminary measurements where we conducted experiments for up to 48 hours. The main finding of these preliminary experiments was that cartilage would continue to relax in tension for as long as it was tested, which would suggest that the equilibrium modulus might indeed eventually approach zero. However, we were concerned about tissue degradation over such long testing durations and compared tests performed with and without protease inhibitors. Results with protease inhibitors showed that the load did not relax down as fast as without them, implying that the relaxation observed without protease inhibitors was indeed influenced by tissue degradation. Unfortunately, protease inhibitors loose their effectiveness with time. Thus, despite all efforts, it is not possible to prevent tissue degradation for a test lasting 48 hours, unless the testing solution is refreshed during the experiment, which can significantly disturb the measurements of the load relaxation response. Consequently we concluded that, in practical terms, it is not possible to determine conclusively whether the continuous relaxation observed after several hours of loading is a purely viscoelastic behavior, or whether it is compounded significantly by tissue degradation. Instead, this study focused on performing measurements of the repeatability of the load response for shorter duration tests, on the basis that repeatability is the best way to determine whether mechanically measurable degradation occurred. Based on our preliminary studies, we did not reproduce Charlebois et al’s finding of zero modulus in immature tissue after 5–10 hours of testing [26], as our tissue samples exhibited non-zero load values for testing periods up to 48 hours, when using protease inhibitors.

The tensile moduli measured parallel and perpendicular to the split line direction were not statistically different in this study. This result is in contrast to studies of human adult cartilage [4, 6] and bovine mature and immature cartilage [7, 24, 25] which show that the modulus is generally stiffer along the parallel direction. This outcome may be attributed to the very young age of the tissue samples used in the current study, as we have observed that the characterization of split line directions is less evident in immature than mature tissue, often requiring optical magnification to visualize the direction.

In summary, this study proposes and validates a constitutive model for the intrinsic viscoelasticity of cartilage in tension, bridging a significant gap in the cartilage literature which had not addressed this topic since the earlier work of Woo and co-workers [16]. The equilibrium stress-strain response of immature bovine cartilage is observed to be linear, though the viscoelastic response is nonlinear due to the strain-dependence of the relaxation function. This finding of nonlinear viscoelasticity sheds new light into the transient response of cartilage in tension, demonstrating a level of complexity not previously anticipated in the cartilage literature, and perhaps explaining the limited reports on constitutive modeling of the tensile response of cartilage. To the best of our knowledge, this study is the first to report experimental measurements of the tensile modulus of articular cartilage over a frequency spectrum. A most interesting finding is that intrinsic viscoelasticity of the collagen-proteoglycan matrix (in this immature bovine cartilage) leads to a dynamic stiffening of the tensile modulus by a factor of ~2.3 at 10 Hz, compared to the equilibrium tensile modulus. In the limit of very high loading frequencies, this dynamic tensile stiffening is predicted to be 1 + α ~ 2.8. In contrast, the dynamic stiffening in unconfined compression is ~24. According to our earlier theoretical models, this observed difference between the tensile and compressive responses can be attributed to the much more significant interstitial fluid pressurization and flow-dependent viscoelasticity occurring under compressive loading. The results of this study support the hypothesis that fluid flow-dependent viscoelasticity is much less significant in tension than in compression, and that the dynamic response of cartilage in unconfined compression is also a function of its dynamic tensile properties. These results emphasize that fluid-flow dependent viscoelasticity dominates the compressive response of cartilage, whereas intrinsic solid matrix viscoelasticity dominates the tensile response. Yet the dynamic compressive modulus of cartilage is critically dependent upon elevated values of the dynamic tensile modulus. These results help us elucidate the complex response of articular cartilage to dynamic loading in compression and tension. They provide new insight on how to select material properties in finite element analyses of diarthrodial joint contact, particularly with regard to the response at physiological loading rates.