Charge regularization in phase separating polyelectrolyte solutions

Abstract

Theoretical investigations of phase separation in polyelectrolyte solutions have so far assumed that the effective charge of the polyelectrolyte chains is fixed. The ability of the polyelectrolyte chains to self-regulate their effective charge due to the self-consistent coupling between ionization equilibrium and polymer conformations, depending on the dielectric constant, temperature, and polymer concentration, affects the critical phenomena and phase transitions drastically. By considering salt-free polyelectrolyte solutions, we show that the daughter phases have different polymer charges from that of the mother phase. The critical point is also altered significantly by the charge self-regularization of the polymer chains. This work extends the progress made so far in the theory of phase separation of strong polyelectrolyte solutions to a higher level of understanding by considering chains which can self-regulate their charge.

INTRODUCTION

Theoretical formulation of phase behavior of polyelectrolyte solutions has been a difficult challenge, primarily due to the long-ranged nature of chain connectivity and electrostatic interaction, and the nonlinear coupling between the polymer charge and counterions. All of the theories^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} of coexistence of polyelectrolyte phases, formulated so far, with varying levels of approximations, have the common key assumption that each polyelectrolyte chain maintains the same constant effective charge for all coexisting phases at all allowed ranges of temperature, polyelectrolyte concentration, and salt concentration. This assumption cannot be correct in view of the large body of literature, based on theoretical arguments,^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30} computer simulations,^{31, 32, 33, 34, 35, 36, 37, 38} and experiments,^{39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56} on the effective charge of polyelectrolyte chains even in homogeneous systems (with one thermodynamic phase).

Basically, the polyelectrolyte conformations are altered by counterion condensation, which in turn is a balance between the electrostatic attraction between the counterion and ionized polymer segments and the translational entropy of counterions in the volume surrounding the polymer. The extent of counterion condensation is affected by many factors including the nature of the counterion (size and valency), concentration of added salt, polymer concentration, solvent dielectric constant, and temperature. This effect has been addressed abundantly in the literature by considering isolated chains,¹⁶ polyelectrolyte brushes,¹⁹ and gels.²⁰ The response of the polyelectrolyte to differing degree of counterion condensation, as the experimental conditions such as the temperature and ionic strength are varied, has been addressed in the contexts of phase transitions of brush heights, volume transitions of gels, and coil-globule transitions of single chains. In general, this response can be highly nonlinear. In particular, theoretical considerations by Khokhlov and Kramarenko²⁰ for the volume transitions of gels have shown that the counterion condensation can lead to a cascade of gel collapse. As the counterions condense, the gel volume decreases with a consequent decrease in the effective dielectric constant of the gel, which in turn allows more binding of counterions inside the gel. This cascade results in a sharp volume transition from a swollen gel into essentially a dry gel. There have also been manifestations of the same effect in several other situations involving brushes^{24, 25} and single chains.^{23, 26, 27, 28, 29, 30} In addition to these theoretical arguments, computer simulations^{31, 32, 33, 34, 35, 36, 37, 38} and experiments^{39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56} have shown clearly that the effective charge of the polymer varies as the experimental variables change.

In light of the recognition that the polymer charge can vary when polymer concentration, temperature and other experimental parameters are changed, the assumption of a constant polymer charge throughout the phase diagram is erroneous. The polymer charge must be allowed to regulate itself in computing the phase diagram. To the best of our knowledge, self-regularization of polymer charge during phase separation is not yet addressed, in spite of the crowded literature on polyelectrolyte solutions. The primary goal of the present paper is a construction of polyelectrolyte phase behavior by accounting for the charge regularization of the chains as the temperature and composition of the solution are changed. The simplest situation of salt-free polyelectrolyte solutions is considered in this paper. It turns out that charge regularization plays a significant role and drastically modifies the phase behavior computed with fixed polymer charge.

The phase behavior of polyelectrolyte solutions has encountered several theoretical attempts with varying approximations. The notable theories are from Khokhlov and Nyrkova,¹ Warren,⁵ Gottschalk et al.,⁶ Mahdi and de la Cruz,⁷ and Muthukumar.¹² The translational entropy of dissociated counterions was recognized by Khokhlov and Nyrkova¹ to contribute significantly to the phase behavior and an effective reduction in the apparent degree of polymerization (N) of the polymer. By adopting the same approach, coexistence and spinodal curves were calculated by Warren.⁵ In these theories, volume of counterions and their electrostatic correlations, and conformational fluctuations of the chains were ignored. The volume of counterions was included in the work of Gottschalk et al.,⁶ but still ignoring fluctuations in charge density and polymer density. The effect of polymer fluctuations was partially addressed by Mahdi and de la Cruz⁷ within the random phase approximation (RPA) for salt-free polyelectrolyte solutions. This work led to rather strange predictions such as liquid-liquid coexistence for N≤30 and liquid-gel coexistence for N≥30. This surprise can be traced¹² to the inadequacy of RPA for salt-free solutions. By recognizing that a reasonable candidate for the free energy of polyelectrolyte solutions should reduce, in the least, to the Flory–Huggins theory⁵⁷ for uncharged polymers and to the Debye–Hückel theory⁵⁸ of the restricted primitive model^{59, 60} for simple electrolyte solutions without any polymer chains, a theory¹² of polyelectrolyte phase behavior was derived by Muthukumar. In this work, contributions from conformational fluctuations of polymers were also included. We build on the latter theory to address the polymer charge regularization.

The essential elements of the model used in the present study are as follows. The polyelectrolyte solution is taken as an incompressible system consisting of the polyelectrolyte, its counterions, and the solvent. The concentrations of the counterions and the polymer are connected by the condition of electroneutrality. The counterions, polymer segments and the solvent molecules are assumed to have comparable volumes. The charged entities interact with the extended Debye–Hückel potential and the polymer-solvent interactions are prescribed by the Flory–Huggins χ parameter. In addition, fluctuations associated with counterion distributions and polymer conformations are included. This model is the same as in Ref. 12, for a fixed degree of ionization. As pointed out above, this model recovers the Flory–Huggins theory when charges and fluctuations are suppressed and the Debye–Hückel-Restricted-Primitive-Model for simple electrolytes when the degree of polymerization is unity. On top of our previous model, we now allow the degree of ionization to be a variable. Here, the free energy of the model of Ref. 12 is modified by adopting another model for counterion adsorption equilibrium introduced earlier by Muthukumar in Ref. 29. In this model, the counterion adsorption is controlled self-consistently by adsorption energy associated with each ion-pair, translational entropy of unadsorbed counterions, the entropy associated with different ways of forming ion-pairs among all potential charged polymer segments, and polymer conformations. It has been recognized⁶¹ for some time that the dielectric constant in the neighborhood of the polymer backbone can be significantly different from that in the bulk solution. In view of this, we take the energy of the ion-pair formed by the counterion and a polymer segment to be stronger by a factor of the dielectric mismatch between the polymer backbone and the bulk, instead of the uniform Bjerrum energy for ion-pairs in the bulk. Another way of accounting for the local variations of the dielectric constant is to assume an average bulk dielectric constant which is the concentration-weighted average of dielectric constants of the solvent and polymer, as was done in Ref. 20. In our model, as the counterion adsorption is local, the local dielectric constant appears in the adsorption energy. Another feature of the present theory is that both the electrostatic interaction strength (defined through the Bjerrum length ℓ_B) and the Flory–Huggins χ parameter change together as the temperature is varied instead of independent changes in ℓ_B and χ.

We show below that the allowance of charge regularization significantly alters the critical point and the phase diagram, in comparison with those computed in all other previous works where the polymer charges are assumed to be the same throughout the phase separation. There occurs a feedback mechanism between charge regularization and thermodynamic immiscibility between the polymer and solvent. In fact, the daughter phases have different polymer charges from that of the mother phase after phase separation.

THEORY

The present theory is an extension of our earlier work on polyelectrolyte solutions,²² phase behavior with fixed polymer charge,^{12, 14} and counterion adsorption²⁹ on flexible polyelectrolyte chains. The theoretical basis for the underlying assumptions in the model is discussed in Refs. ^{12, 14, 22, 29} and only a brief description is given below.

We consider a solution of n polyelectrolyte chains, each with N segments of length ℓ, and n_s uncharged solvent molecules, with the total volume Ω. Each of the polymer segments is assumed to carry one negative charge and the corresponding counterions are monovalent positive charges. The degree of ionization α of the chain is a variable and there are αnN counterions in the solution, satisfying the electroneutrality condition. We assume that the solvent molecules, segments, and counterions have the same molar volume ℓ³ and that the solution is incompressible.

The total free energy density of the solution, defined as the total Helmholtz free energy per unit volume in units of k_BT (Boltzmann’s constant times the temperature), has the following contributions: (i) translational entropy of polymer chains, dissociated counterions, and solvent molecules (f_s), (ii) entropy of adsorbed counterions (f_sa), (iii) hydrophobic interaction between the polymer backbone and solvent (f_χ), (iv) electrostatic interaction between polymer segments (f_el), (v) gain in energy due to the formation of ion-pairs accompanying counterion adsorption (f_ad), (vi) fluctuations of dissociated counterions (f_fl,i), and (vii) conformational fluctuations of the polymer chains (f_fl,p).

The free energy density due to the entropy of mixing of the polymer, solvent, and counterions is given by the familiar form,

$$f_s=\frac{\varphi }{N}\text{log}\varphi +{\varphi }_c\text{\hspace{0.17em}log}{\varphi }_c+{\varphi }_s\text{\hspace{0.17em}log}{\varphi }_s,$$ (1)

where ϕ,ϕ_c, and ϕ_s are the volume fractions of the polymer (ϕ=nNℓ³∕Ω), counterions (ϕ_c=αnNℓ³∕Ω), and solvent (ϕ_s=n_sℓ³∕Ω). These volume fractions are related by the incompressibility constraint,

$$\varphi +{\varphi }_c+{\varphi }_s=1,$$ (2)

and along with the electroneutrality constraint,

$${\varphi }_c=\alpha \varphi ,$$ (3)

there is only one independent variable for defining the composition of the solution.

Since (1−α)N counterions are adsorbed to each chain on an average and there are N!∕[((1−α)N)!][(αN)!] ways of formation of ion-pairs, the free energy density associated with the entropy of adsorbed counterions, with the Stirling approximation, is

$$f_{sa}=\left[\alpha \text{\hspace{0.17em}log}\alpha +\left(1-\alpha \right)\text{log}\left(1-\alpha \right)\right]\varphi .$$ (4)

All nonlinear effects resulting from possible cooperative features associated with placement of counterions along the polymer contour are ignored in the present model.

The hydrophobic interaction energy between the polymer backbone and solvent is taken from the Flory–Huggins theory as

$$f_{\chi }=\chi \varphi {\varphi }_s,$$ (5)

where χ is the usual chemical mismatch parameter representing the mutual local interaction energies among solvent molecules and polymer segments (if they were to be uncharged). Since most of the polyelectrolyte backbones are immiscible with the polar solvents typically used in polyelectrolyte solutions, χ is about 0.5 or higher.⁵⁷ We further assume that there are no enthalpic contributions from counterion-solvent interactions.

The electrostatic interaction energy among all polymer segments is obtained by the following mean field argument. For a single chain of contour length L=Nℓ, the intrachain electrostatic energy is

$$\frac{F_{el}}{k_{B}T}=\frac{{\alpha }^2}{2}{\int }_0^L\frac{ds}{\ell }{\int }_0^L\frac{d{s}^{\prime }}{\ell }V\left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right],$$ (6)

where V[R(s)−R(s^′)] is the pairwise electrostatic energy between the segments s and s^′ located at R(s) and R(s^′), respectively. Assuming the Debye–Hückel approximation for V, with the screening due to the counterions,

$$V\left(\mathbf{r}\right)=\frac{{\ell }_B\text{\hspace{0.17em}exp}\left(-\kappa r\right)}{r},$$ (7)

where the strength of the interaction is the Bjerrum length ℓ_B,

$${\ell }_B=\frac{e^2}{4\pi {ϵ}_0ϵk_{B}T},$$ (8)

where e, ϵ₀, and ϵ are the electronic charge, permittivity of the vacuum, and the dielectric constant of the solvent, respectively. The range of the interaction is given by the Debye length κ⁻¹, where

$${\tilde{\kappa }}^2=4\pi {\tilde{\ell }}_B\alpha \varphi ,$$ (9)

with $\tilde{\kappa }\equiv \kappa \ell$ and ${\tilde{\ell }}_B\equiv {\ell }_B∕\ell$. Combining Eqs. 6, 7, 8 and representing V(r) as its Fourier transform, we get

$$\frac{F_{el}}{k_{B}T}=2\pi {\alpha }^2{\ell }_B{\int }_0^L\frac{ds}{\ell }{\int }_0^L\frac{d{s}^{\prime }}{\ell }\int \frac{d^{3}k}{{\left(2\pi \right)}^3}\frac{e^{i\mathbf{k}\cdot \left[\mathbf{R}\left(\mathbf{s}\right)-\mathbf{R}\left({\mathbf{s}}^{\prime }\right)\right]}}{\left(k^2+{\kappa }^2\right)}.$$ (10)

The two limits of κ=0 and κR⪢1 (where R is the average radius of gyration of the chain) can be readily identified from Eq. 10. For κ² large, the k-integral becomes a delta function in [R(s)−R(s^′)] and for κ=0, it is 1∕4π|R(s)−R(s^′)|,

$$\frac{F_{el}}{k_{B}T}=\{\begin{array}{cc}\frac{2\pi {\alpha }^2{\ell }_B}{{\kappa }^2}{\int }_0^L\frac{ds}{\ell }{\int }_0^L\frac{d{s}^{\prime }}{\ell }\delta \left[\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right],& \kappa R⪢1\\ \frac{{\alpha }^2{\ell }_B}{2}{\int }_0^L\frac{ds}{\ell }{\int }_0^L\frac{d{s}^{\prime }}{\ell }\frac{1}{\left|\mathbf{R}\left(s\right)-\mathbf{R}\left(s^{\prime }\right)\right|},& \kappa =0.\end{array}\phantom{\}}$$ (11)

Thus, for κR⪢1, the electrostatic interaction is short-ranged, analogous to the two-body excluded volume interaction, with the strength ∼α²ℓ_B∕κ². In this limit, by assuming that the monomer density is uniform, we get

$$\frac{F_{el}}{k_{B}T}=\frac{2\pi {\alpha }^2{\ell }_B}{{\kappa }^2}\frac{N^2}{\Omega },$$ (12)

and the free energy density f_el=F_elℓ³∕(k_BTΩ) is

$$f_{el}=\frac{2\pi {\alpha }^2{\tilde{\ell }}_B}{{\tilde{\kappa }}^2}{\varphi }^2.$$ (13)

In experimental systems relevant to the study of phase behavior, there are large enough numbers of counterions in the system so that f_el given by Eq. 13 would be adequate. This expression has been used in our previous studies of polyelectrolyte phase behavior. However, one can be more careful by using a crossover formula between the limits given in Eq. 11. Such a formula was derived in Ref. 22. From our numerical work with this formula, it turns out that the corrections from the crossover to the result of Eq. 13 are only minor. The transparency of this conclusion may be seen from the following argument. By averaging 1∕|R(s)−R(s^′)| in Eq. 11 over the Gaussian chain statistics and performing the s-integrals, we get

$$\frac{F_{el}}{k_{B}T}=\frac{4}{3\sqrt{\pi }}{\alpha }^2{\ell }_B\frac{N^2}{R},\kappa =0.$$ (14)

The dependence of α²ℓ_BN²∕R is obvious even from a dimensional analysis¹⁵ of Eqs. 6, 7. Rewriting the above expression in terms of uniform monomer density,

$$f_{el}=\frac{{\ell }^3{F}_{el}}{\Omega k_{B}T}=\frac{4}{3\sqrt{\pi }}{\left(\frac{4\pi }{3}\right)}^{1∕3}{\alpha }^2{\tilde{\ell }}_B{\varphi }^2{\left(\frac{N}{\varphi }\right)}^{2∕3}.$$ (15)

We combine the limits of Eqs. 13, 15 by the interpolation formula,

$$f_{el}=2\pi {\alpha }^2{\ell }_B{\varphi }^2\frac{N^{2∕3}}{\left[\frac{3^{4∕3}{\pi }^{7∕6}}{2^{5∕3}}{\varphi }^{2∕3}+{\tilde{\kappa }}^2{N}^{2∕3}\right]}.$$ (16)

As is evident for large values of N of interest to polyelectrolytes, the corrections to Eq. 13 are only minimal. Nevertheless, we use Eq. 16 for the free energy density from polymer-polymer electrostatic interactions in the present calculation of phase diagrams.

The gain in free energy due to the formation of an ion-pair associated with the adsorption of one counterion to a charged segment is −e²∕(4πϵ₀ϵ_ℓd), where ϵ_ℓ is the local dielectric constant and d is the dipole length between the charge of the monomer and the counterion. In this prescription, the dielectric constant varies rapidly from a low value near the chain backbone to the high bulk value, as recognized in the literature.⁶¹ We imagine a worm around the chain backbone with radius d within which the dielectric constant is ϵ_ℓ and outside it is ϵ. We write this ion-pair energy in terms of ℓ_B, by defining a parameter δ, called the dielectric mismatch parameter,

$$\delta \equiv \frac{ϵ}{{ϵ}_{\ell }}\frac{\ell }{d}.$$ (17)

The local dielectric constant in the region of counterion binding to the pendant charged groups of the polymer in aqueous solutions is somewhat in the range⁶¹ of 5–10. Furthermore, the distance d between the charged monomer and the counterion in an ion-pair, can be larger than the distance between two consecutive charges on the chain backbone. As a result, the value of the parameter δ is expected to be of order unity. In view of the lack of adequate understanding of the polarization forces at short distances, we take δ only as a parameter. The total energy associated with ion-pairs from all adsorbed counterions is

$$\frac{F_{ad}}{k_{B}T}=-nN\left(1-\alpha \right)\frac{e^2}{4\pi {ϵ}_0{ϵ}_{\ell }d{k}_{B}T}=-nN\left(1-\alpha \right){\tilde{\ell }}_B\delta ,$$ (18)

so that the adsorption energy density is

$$f_{ad}=-\left(1-\alpha \right)\varphi {\tilde{\ell }}_B\delta .$$ (19)

The free energy density due to fluctuations in the density of dissociated counterions, f_fl,i, has already been derived¹² by solving the linearized Poisson–Boltzmann equation for non-neutral charged plasma, as in the Debye–Hückel theory. The result (details given in Ref. 12) is

$$f_{fl,i}=-\frac{1}{4\pi }\left[\text{log}\left(1+\tilde{\kappa }\right)-\tilde{\kappa }+\frac{1}{2}{\tilde{\kappa }}^2\right].$$ (20)

This contribution is due to the Coulomb interactions between the counterions in the cloud around the polymer chains. Note that the above expression depends on the concentration of only the dissociated counterions [through Eq. 9], in spite of its identical appearance to the Debye–Hückel expression for symmetric electrolytes, with finite ion sizes and overall electroneutrality. Also, Eq. 20 reduces to the Debye–Hückel limiting law expression in the limit of ℓ→0,f_fl,i→−(κℓ)³∕(12π), as was derived in Ref. 22 by considering only the counterion cloud around polymer chains.

Finally, the free energy density due to fluctuations in polymer density is expressed as follows. It is known from scaling arguments¹⁵ that the free energy density of semidilute polyelectrolyte solutions is proportional to ϕ^3∕2 and ϕ^9∕4, respectively, in salt-free and highly salty solutions. A crossover formula between these two limits, along with the numerical prefactors, was derived in Ref. 22. This crossover description is rather elaborate and it turns out from our numerical work that polymer fluctuations play only a minor role in locating the phase boundary. In view of this, we have used the following interpolation formula, as in Ref. 14:

$$f_{fl,p}=\frac{\frac{2^{3∕4}}{9}\sqrt{\frac{\pi }{3}}{\left(\frac{3}{2}\right)}^{-9∕4}{\left(4\pi {\alpha }^2{\tilde{\ell }}_B\right)}^{3∕4}{\varphi }^{9∕4}}{{\tilde{\kappa }}^{3∕2}+2^{5∕4}\sqrt{\frac{\pi }{3}}{\left(\frac{3}{2}\right)}^{-3∕4}{\left(4\pi {\alpha }^2{\tilde{\ell }}_B\right)}^{1∕4}{\varphi }^{3∕4}}.$$ (21)

The total free energy density f (in units of k_BT) is the sum of the above seven contributions,

$$f=f_s+f_{sa}+f_{\chi }+f_{el}+f_{ad}+f_{fl,i}+f_{fl,p}.$$ (22)

In addition to the above contributions, there can be effects arising from the dipole nature of the ion-pairs formed by counterion adsorption. In general, these dipoles can interact with other such dipoles and monopoles, which in turn can make a hierarchy of multipole clusters. In the present study dealing with polymer solutions, we assume that such higher order interactions are sufficiently weak unlike in situations pertinent to neat polyelectrolyte salts (such as crystalline states, molten salts, and collapsed states).

The parameters in the present model are the Bjerrum length ℓ_B, Flory–Huggins parameter χ, and the dielectric mismatch parameter δ, in addition to the experimental variables of temperature and polymer concentration. It is to be noted that both ℓ_B and χ are temperature dependent. As the temperature is changed in an experiment, both ℓ_B and χ change simultaneously and not independently. Therefore, we define a reduced temperature variable t using which both ℓ_B and χ can be expressed. We choose the inverse of ℓ_B to identify the reduced temperature variable. Alternatively, the inverse of χ can be equally chosen to identify t. Furthermore, in general, the dielectric constants of solutions depend on temperature. In view of this, we combine all temperature effects appearing in the definition of ℓ_B and define the reduced temperature t as

$$t\equiv \frac{\ell }{4\pi {\ell }_B}.$$ (23)

The temperature dependence of χ is chosen in the present study as

$$\chi \equiv \frac{\theta }{2T},$$ (24)

where θ is the Flory theta temperature. Rewriting this equation in terms of the reduced temperature,

$$\chi \equiv \frac{a_{\chi }}{20\pi t},$$ (25)

where

$$a_{\chi }=\frac{10\pi ϵk_B\theta }{e^2}.$$ (26)

The parameter a_χ reflects the value of the θ temperature and is taken as a measure of the hydrophobic interaction between the polymer and solvent. In general, a_χ is temperature dependent due to the appearance of ϵ in Eq. 26 and deviations from the simple inverse temperature dependence of χ as given in Eq. 24. The value of a_χ is of order unity. For example, a_χ=1 for aqueous systems corresponding to χ=0.6. In the present study, we have explored the range of 0.5≤a_χ≤1.0.

If the dielectric constant is uniform throughout the solution with the value ϵ and if the length of the dipole in the ion-pair is identical to the chemical distance between the consecutive charges on chain backbone (defined as ℓ here), then the dielectric mismatch parameter δ is unity. Since the local effective dielectric constant in the neighborhood of ion-pair formation can be smaller than in the bulk and the length of the dipole can be larger than monomer separation distance, δ is expected to be larger than unity. In this study, we have considered the range of 1≤δ≤2. Finally, for the degree of polymerization N, we have considered only one typical case with N=1000.

We have computed the coexistence curves by minimizing the free energy density. In the present system, there are three components, viz., polyelectrolyte, counterion, and solvent. The chemical potential of each of these components must be equal in the coexisting phases. If a point (ϕ,ϕ_c,ϕ_s) lies inside the phase boundary, it will demix into two phases with composition $({\varphi }^a,{\varphi }_c^a,{\varphi }_s^a)$ of the a-phase and composition $({\varphi }^b,{\varphi }_c^b,{\varphi }_s^b)$ of the b-phase. If x is the fraction of the solution separating into the a-phase, then according to the lever rule,

$$\varphi =x{\varphi }^a+\left(1-x\right){\varphi }^b,$$ (27)

and there are two other similar lever rules for ϕ_c and ϕ_s. Additionally, we take the degree of ionization in the a- and b-phases as α^a and α^b, respectively. Thus, there are nine variables ($x,{\varphi }^a,{\varphi }_c^a,{\varphi }_s^a,{\varphi }^b,{\varphi }_c^b,{\varphi }_s^b,{\alpha }^a$, and α^b) and five independent constraints [incompressibility constraints: ${\varphi }^a+{\varphi }_c^a+{\varphi }_s^a=1={\varphi }^b+{\varphi }_c^b+{\varphi }_s^b$; electroneutrality constraints: ${\varphi }^a={\alpha }^a{\varphi }_c^a,{\varphi }^b={\alpha }^b{\varphi }_c^b$; and the lever rule from Eq. 27]. Therefore, there are four independent variables. By performing the four-dimensional minimization of free energy density of Eq. 22, for a set of values of t,a_χ, and δ, we have constructed the phase diagram. The numerical procedure is carried out with the downhill simplex algorithm.⁶²

RESULTS AND DISCUSSION

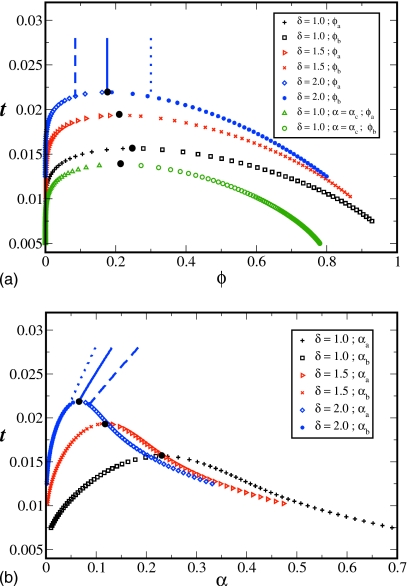
We have computed the phase diagrams as plots of the reduced temperature versus volume fraction of the polyelectrolyte for different values of the parameters a_χ and δ. We have allowed the degree of ionization of the polyelectrolyte to self-regulate during the phase separation. Thus, for every choice of a_χ,δ, and N, there are unique values of α,ϕ, and t corresponding to the global free energy minimum of the system. In contrast to the uncharged two-component polymer solutions, the self-regulating degree of ionization acts effectively as another order parameter for the system in addition to the usual order parameter of polyelectrolyte concentration. In view of this, our results of composition variation and the variation in the degree of ionization are presented in terms of two panels, as the reduced temperature is varied. The typical results are given in Fig. 1 for a_χ=1 and N=1000, and three values of δ (1.0, 1.5, and 2.0). Figure 1a is the usual depiction of the phase diagram as t versus ϕ plots, whereas Fig. 1b gives the accompanying variations in α.

Figure 1.

Temperature-concentration (a) and temperature-charge (b) phase diagrams for a polymer solution with variable degree of ionization. Parameters are the following: N=1000, a_χ=1.0, and δ=1.0, 1.5, and 2.0. Vertical lines correspond to the homogeneous phase for δ=2.0: ϕ=0.085 (dashed), ϕ=ϕ_c=0.176 (solid), and ϕ=0.300 (dotted). Higher concentration corresponds to lower degree of ionization. Critical points are given by black dots. The lowest curve in (a) is for fixed charge α_c=0.23 (chosen to be the value at the critical point with variable charge) at δ=1.0.

Let us first consider the results for δ=2. The critical point is at t^⋆=0.022,ϕ^⋆=0.176 and α^⋆=0.065. For reduced temperatures below t^⋆, two phases, viz., polymer-poor a-phase (represented by blue diamonds) and polymer-rich b-phase (represented by blue filled circles) coexist. Above t^⋆, the solution is homogeneous. The three vertical lines (solid, dashed, and dotted) joining the coexistence curve in Fig. 1a denote the temperature quenches in the homogeneous phase until the coexistence curve is reached. The solid line is the quench at the critical composition. The dashed and dotted lines are for polyelectrolyte concentrations below and above, respectively, the critical volume fraction. Naturally, the volume fraction of the polymer does not change as the temperature is reduced in the homogeneous phase. However, as the adsorption energy associated with the adsorption of counterions to polymer segments becomes more attractive as the temperature is lowered, more and more ion-pairs will form with a consequent effect of reducing the degree of ionization of the polymer. This is clearly seen in Fig. 1b. Based on our model, the calculated value of α is 0.131 for ϕ=0.176 (critical volume fraction) at the initial temperature of the quench, t=0.028. As the temperature is decreased, the value of α decreases progressively as given by the solid blue line in Fig. 1b until it reaches the critical point with α^⋆=0.065. Furthermore, as the polyelectrolyte concentration increases, the effect of dielectric mismatch from lowered local dielectric constant around polymer backbone becomes more pronounced with a consequent result of enhanced ion-pair formation (i.e., lowered degree of ionization). This is clearly evident from Fig. 1b by comparing the values of α for ϕ=0.085, 0.176, and 0.3 at the initial temperature of the quench (t=0.028). The corresponding values of α are 0.183, 0.131, and 0.098. Thus, in our model, the degree of ionization decreases with polymer concentration in the homogeneous phase. In addition, as discussed above, α decreases with t for each of these concentrations in the homogeneous phase. Please note the switch in the ordering of the dashed and dotted lines in Figs. 1a, 1b.

For temperatures below t^⋆, two phases with volume fractions ϕ^a (dilute phase) and ϕ^b (concentrated phase) coexist. As seen in Fig. 1b, the value of α is not uniform. The values of α in the daughter phases are different from the value in the mother phase. As shown in Fig. 1b, α is higher in the dilute phase (blue diamonds) and lower in the concentrated phase (blue filled circles). This is fully expected in view of the dependence of α on ϕ in the homogeneous phase. Furthermore, the temperature dependence of α in the dilute phase turns out to be quite rich. As the temperature is lowered, the degree of ionization in the dilute phase increases unlike in the homogeneous phase. This is due to faster decrease in polymer concentration in the dilute coexisting phase which in turn leads to an increase in α and overcompensating the expected decrease with lowering temperature. The cooperative (antagonistic) dependence of α on t in the dilute phase [blue diamonds in Fig. 1b] is reflected by the opposite curvature to that of ϕ on t [blue diamonds in Fig. 1a]. Also, if we were to consider extremely low temperatures where the polymer concentration of the coexisting dilute phase is below the overlap concentration, then α in this phase decreases with temperature. For such low temperatures, our calculations give that the α-t curves for the dilute branches in Fig. 1b turn around with the opposite slope [not shown in Fig. 1b]. For the coexisting concentrated phase, the polymer concentration increases [blue filled circles in Fig. 1a] with a reduction in temperature. Both a reduction in temperature and an increase in concentration lead synergistically to a decrease in α, as is seen with the blue filled circles in Fig. 1b. The curvature of this branch of the coexistence curve has the same sign as the corresponding branch (concentrated phase) in Fig. 1a. As a reminder, the dense phase of the coexistence curve is the right hand side branch in Fig. 1a and the left hand side branch in Fig. 1b and vice versa for the dilute phase.

The role of the dielectric mismatch parameter is illustrated by the blue (δ=2.0), red (δ=1.5), and black (δ=1.0) curves in Figs. 1a, 1b. The above discussed features are the same for each of these sets. The critical point depends on δ. The values of t, ϕ, and α at the critical point are t^⋆=0.022, ϕ^⋆=0.1736, and α^⋆=0.0658 for δ=2.0; t^⋆=0.019, ϕ^⋆=0.209, and α^⋆=0.118 for δ=1.5; and t^⋆=0.015, ϕ^⋆=0.246, and α^⋆=0.233 for δ=1.0. As the value of the dielectric mismatch parameter δ increases, the counterion adsorption is favored more with a resultant decrease in α. This then leads to reduced entropy of free counterions and intersegment electrostatic repulsion. As a result, the region in the parameter space for the existence of stable homogeneous phase is reduced.

We now compare the results with charge regularization against the hypothetical situation of assuming constant polymer charge at all concentrations and temperatures during phase separation. The lowest curve in Fig. 1a (green triangles denoting the dilute phase and green circles denoting the concentrated phase) is the coexistence curve if α were fixed at the value of 0.233 for a_χ=1, δ=1, and N=1000. For this case, the critical values of t and ϕ are 0.014 and 0.213, respectively. This value of α was chosen to be the critical value of α with charge regularization for the same values of other parameters [black curves in Figs. 1a, 1b]. It is clear from a comparison between the black and green curves in Fig. 1a that the coexistence curve with fixed charge is significantly different from that with charge regularization. Of course, the analog of the black curve in Fig. 1b, for fixed charge, is a vertical line at α=0.233 (not shown). In fact, almost any coexistence curve can be arbitrarily made up for fixed α, depending on the choice of α.

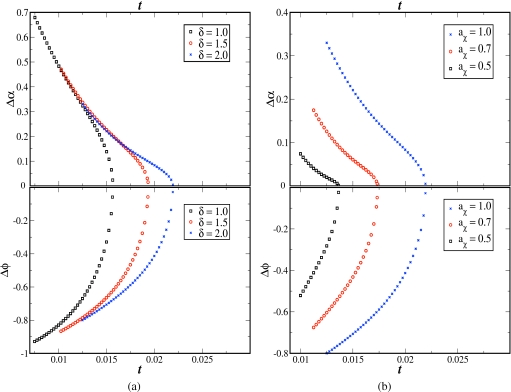
As discussed above, the shape of the coexistence curve for the α variable is different from that for the ϕ variable, due to the interdependence of counterion adsorption on temperature and polymer concentration. By defining Δϕ and Δα as the differences in ϕ and α between the coexisting phases, their dependencies on temperature are plotted in Fig. 2a, where the role of δ is shown. The same data of Figs. 1a, 1b are combined for δ=1.0, 1.5, and 2.0, a_χ=1.0, and N=1000. The opposite curvatures of the curves for Δα and Δϕ are evident, as already discussed above. As the dielectric mismatch parameter δ increases, the instability of the homogeneous phase is enhanced due to the increased counterion adsorption. Based on the numerical data presented in Fig. 2a, the order parameter Δϕ vanishes as the reduced temperature approaches the critical temperature t^⋆, approximately according to the expected mean-field law, Δϕ∼(t^⋆−t)^1∕2. Similar analysis of the numerical data for Δα versus (t^⋆−t) has not been successful in obtaining a critical exponent, due to insufficient numerical accuracy near the critical point, although this exponent appears to be less than 0.5.

Figure 2.

Gaps between daughter phases in degrees of ionization (Δα=α_A−α_B) [top] and concentration (Δϕ=ϕ_A−ϕ_B) [bottom] vs reduced temperature (t) for two cases: (a) a_χ=1.0 and δ=1.0,1.5,2.0 and (b) δ=2.0 and a_χ=1.0,0.7,0.5. N=1000.

We have also investigated the role of the Flory–Huggins parameter on the phase diagram by computing the coexistence curves for a_χ=1.0, 0.7, and 0.5 and keeping δ=2.0 and N=1000. Instead of presenting all computed coexistence curves, we present only the critical points and the temperature dependencies of Δα and Δϕ. The critical points for a_χ=1.0, 0.7, and 0.5 are, respectively (t^⋆=0.022,ϕ^⋆=0.1736,α^⋆=0.0658), (t^⋆=0.0173,ϕ^⋆=0.1286,α^⋆=0.03), and (t^⋆=0.0136,ϕ^⋆=0.0825,α^⋆=0.0101). Not surprisingly, phase separation is promoted as the chemical mismatch parameter a_χ increases. The cooperative nature of the various contributions from the hydrophobic effect, local dielectric constant mismatch, polymer concentration, and temperature to the extent of counterion adsorption is reflected in the shapes of Δα versus t curves in Fig. 2.

CONCLUSIONS

We have computed the phase behavior of salt-free solutions of flexible polyelectrolytes using a model that allows the polymer charge to self-regulate during phase separation. In the present model, counterion adsorption to polymer segments is mediated self-consistently by local dielectric constant near the polymer backbone being different from the bulk value, translational entropy of free counterions, and polymer conformations. The consequences of the combined effects from the electrostatic and hydrophobic interactions are included.

The key results are as follows:

• (1)In the homogeneous phase, the polymer charge decreases with a reduction in temperature and an increase in polymer concentration.
• (2)The region of stable homogeneous phase decreases as the dielectric mismatch parameter [δ, Eq. 17] or the Flory–Huggins chemical mismatch parameter (χ) increases.
• (3)The daughter phases have different degrees of ionization, the higher concentration having the lower polymer charge.
• (4)In the dilute coexisting phase, the net increase in polymer charge with lowering temperature is due to the opposing forces for counterion adsorption from the decreasing polymer concentration and decreasing temperature. In the concentrated coexisting phase, the decrease in polymer charge with lowering temperature is dictated by the synergistic effects from increasing polymer concentration and decreasing temperature.
• (5)The allowance of charge regularization significantly affects the critical point and the coexistence curve calculated with fixed polymer charge.
• (6)Although polymer charge is not a conserved quantity such as the polymer concentration, it behaves like an additional order parameter. The critical exponent for the disappearance of the discontinuity in the degree of ionization as the temperature is increased toward the critical temperature is different from that for the discontinuity in the polymer concentration.

There are several avenues where the present model needs to be extended and its predictions critically validated. The foremost is the experimental relevance. For the salt-free polyelectrolyte solutions discussed in the present study, the critical value of the reduced temperature t is in the range of 0.015–0.023 for 1.0≤δ≤2.0 and 0.5≤a_χ≤1.0. Given the definition of the reduced temperature in Eq. 23, for aqueous solutions of flexible polyelectrolytes of the type sodium polystyrene sulfonate at room temperature (ℓ_B∕ℓ∼3.0), t is about 0.0265. This means that for such salt-free aqueous solutions, there is no phase separation, which is indeed consistent with experiments. Therefore, in order to verify the predicted phase behavior, it is necessary to either choose a different solvent with smaller dielectric constant (say with half the value for water), or polymers with more hydrophobic backbones.

Another alternative is to generalize the present theory to experimental situations where phase separation is known to occur.^{39, 40, 41, 42, 44, 45, 46, 47, 49, 50, 51, 53, 54, 55, 56} A particular example is the case of aqueous solutions of sodium polystyrene sulfonate containing some divalent salts such as barium chloride.^{39, 40, 47, 51, 55} The system now becomes more complex with many components: polymer, counterion, cation, and anion of the added salt and solvent. The chemical potentials of each of these components need to be equated in the coexisting phases. By fixing the polymer charge, we have recently computed the phase diagram¹⁴ for this multicomponent system by satisfying the Donnan equilibrium. However, in view of the implications of the present study, the polymer charge should be allowed to self-regulate in constructing the phase diagrams. This exercise is planned for the future as an extension of our earlier work¹⁴ for salty polyelectrolyte solutions with fixed charge to charge regularization. This would allow a comparison between our model and existing data on the five-component systems. Furthermore, it would also be of interest to explore the role of the ionic radii of counterions (from the polymer and added salt), representing the specificity of the ions, on the phase diagrams. There is an opportunity to address the ion specificity in our model, because the ionic radius appears as the dipole length in the definition of the local dielectric mismatch parameter δ [Eq. 17].

On the theoretical side, the present model is only a mean field theory despite the inclusion of fluctuations of counterion density and polymer conformations. It suffers from all of the weaknesses present in the Flory–Huggins theory of polymer mixtures and the Debye–Hückel Restricted Primitive Model of simple electrolytes. The consequences of composition fluctuations beyond the saddle point approximation must be accounted for in order to capture the Ising critical behavior, which is apparently seen in experiments.^{47, 51} As the polymer charge is an additional order parameter in phase separating solutions, a new critical index corresponding to the degree of ionization, might be needed in describing the critical phenomena of polyelectrolyte solutions.

As a final remark, it might be necessary to include multipole electrostatic interactions in the free energy of the system, particularly at very low temperatures where one of the coexisting phases approaches the limit of molten polyelectrolyte salts.