Effects of visual gain on force control at the elbow and ankle

Abstract

Visual feedback is essential when minimizing force fluctuations. Varying degrees of somatotopic organization have been shown in different regions of the brain for the upper and lower extremities, and visual feedback may be processed differently based on the body effector where feedback-based corrections are used. This study compared the effect of changes in visual gain on the control of steady-state force at the elbow and ankle. Ten subjects produced steady-state isometric force to targets at 5 and 40% of their maximum voluntary contraction at seven visual gain levels. Visual gain was used effectively at both joints to reduce variability of the force signal and to improve accuracy, with a greater effect of visual gain at the elbow than the ankle. Visual gain significantly decreased the regularity of force output, and this effect was more pronounced at the elbow than the ankle. There were accompanying changes in the proportion of power in the 0–4, 4–8, and 8–12 Hz frequency bins of the force signal across visual gain at the elbow. Changes in visual gain were accompanied by changes in both agonist and antagonist electromyographic (EMG) activation at the elbow. At the ankle joint, there were only changes in agonist EMG. The results suggest better use of visual information in the control of elbow force than ankle force and this improved control may be related to the changes in the pattern of agonist and antagonist activation.

Introduction

Minimizing fluctuations in force is desirable during most everyday motor tasks. This is most readily appreciated by considering tasks that require a steady motor output such as threading a needle or pushing on the gas pedal of a car to maintain a consistent speed. Visual feedback is essential when attempting to minimize force fluctuations to hold force steady. Indeed, removing visual feedback during a steady-state force contraction to a target leads to an exponential decrease in force output, 0.5–1.5 s following the withdrawal of visual feedback (Vaillancourt and Russell 2002). This is because peripheral receptors alone do not provide sufficient information on force output to allow force to be maintained at the target force level in the absence of visual information (Slifkin et al. 2000). During visuomotor control, visual feedback is transferred from the visual cortex to the parietal and premotor areas of the cortex, and subcortical areas of the basal ganglia and cerebellum (Milner and Goodale 1993; Caminiti et al. 1996; Johnson et al. 1996; Glickstein 2000; Vaillancourt et al. 2003, 2006b). Varying degrees of somatotopic organization have been shown in each of these regions of the brain (Grodd et al. 2001; Alkadhi et al. 2002; Flanders 2005; Miyachi et al. 2006; Nelson and Chen 2008) and thus visual feedback may be processed differently based on the body effector where the feedback-based correction is used.

In addition to centrally based differences in somatotopic organization, peripheral factors may also affect the ability to hold force steady. It has previously been shown that the amplitude of force fluctuations is inversely related to the maximal force and number of motor units in the upper extremity muscles such that stronger muscles with higher numbers of motor units have the lowest normalized force variability (Hamilton et al. 2004). In other words, normalized index finger force fluctuations are greater than normalized wrist or elbow force fluctuations (Hamilton et al. 2004). Across upper and lower extremity muscles, however, this may not be true. Tracy et al. (2007) compared the relative force variability across elbow flexors, knee extensors and the first dorsal interosseus muscle of the hand. Although the two strongest muscle groups (elbow flexors and knee extensors) had reduced force fluctuations compared to the finger muscle, the stronger knee extensor muscle had a higher coefficient of variation than the elbow flexor muscle. Variability in force output across the upper and lower extremity joints may not therefore simply be a function of maximum strength and number of motor units. It is possible that the control of force fluctuations, and hence steadiness, is not as finely tuned in the control of lower extremity muscles when compared to upper extremity muscles, especially when one considers the functional specificity of the upper versus lower extremities. For example, the upper extremity is suited for precise manipulation of the digits and tool use (Arbib et al. 2009), and the lower extremity is suited to produce locomotion and maintain postural stability (Jacobs and Horak 2007). An effective way of manipulating force control (steadiness) is by changing the gain of visual feedback. If force control is inherently different between the upper and lower extremity, then visual feedback may have different effects on the activation of muscles that control force output at the elbow and ankle joints.

The gain of visual feedback (i.e., the amount of visual information provided) has been shown to have a significant impact on both the magnitude and time-dependent properties of variability in upper extremity precision grip force output (Jagacinski and Flach 2003; Sosnoff and Newell 2005; Sosnoff et al. 2006; Vaillancourt et al. 2006a; Lee Hong and Newell 2008). It is not clear, however, whether a parametric change in visual gain affects the control of steady-state force of larger body effectors beyond precision grip force control. It is also not clear whether a parametric change in visual gain affects the control of upper and lower limb muscles similarly. The purpose of this study was to compare the effect of visual gain on the control of steady-state force at the elbow and ankle joints. The hypothesis tested was that, given the functional specificity of upper versus lower extremities, changes in visual gain would have a greater effect on force control at the elbow than the ankle. We also examined the effect of visual gain on agonist and antagonist muscle activation at the elbow and ankle joints. Given that the ankle joint is not usually associated with changes in the fine control of force output in response to visual feedback, we hypothesized that, in contrast to the elbow, the ankle would show a cocontraction pattern of activation that would not be affected by changing visual gain. A cocontraction pattern of muscle activation is commonly seen early in motor learning and declines as learning progresses under both static (Darainy et al. 2004; Darainy and Ostry 2008) and dynamic (Burdet et al. 2001) conditions.

Materials and methods

Subjects

Ten neurologically healthy subjects of average physical activity level participated in this study (five males, five females, mean age 28.4 years, range 23–38 years). Informed consent was obtained from each subject prior to testing, and the Institutional Review Board of the University of Illinois at Chicago approved the protocol.

Apparatus and procedures

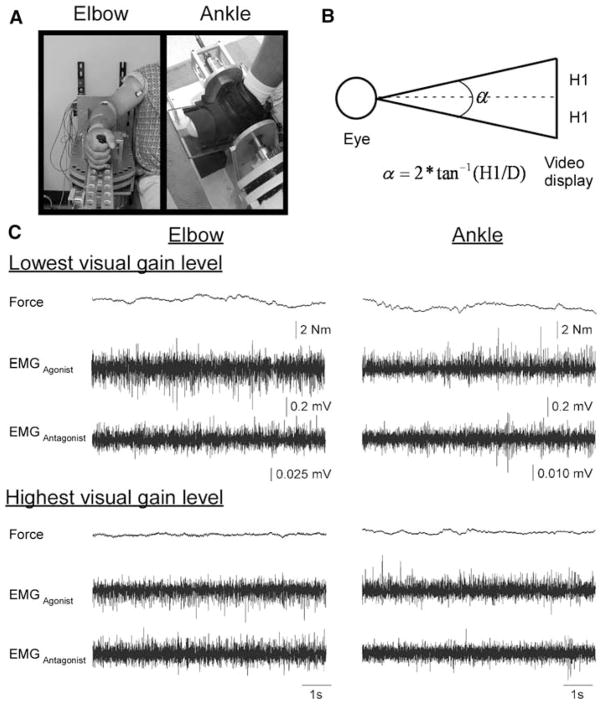
Elbow and ankle manipulanda devices were used for testing (Fig. 1a). For testing at the elbow, the subject was seated with the arm abducted between 75° and 90° depending on the comfort of each subject. The arm examined in this study was always the dominant limb, defined as the hand preferentially used for writing. The forearm rested on a rigid, lightweight manipulandum that was locked in place, but when unlocked could freely rotate only in the horizontal plane. The axis of rotation was aligned with the elbow joint. Full extension of the elbow was defined as 0°. For testing at the ankle, the subject was seated with the knee and hip flexed to 90°. The same side of the body was tested for the ankle as for the elbow. The foot rested in a ski boot manipulandum that when unlocked could rotate in the sagittal plane. The axis of rotation was aligned with the ankle joint, and the manipulandum was locked in place with the ankle joint at 90°.

Fig. 1.

a The elbow and ankle manipulanda used for testing. b The calculation for visual gain where α is the visual gain (degrees), H1 is half the height of the force fluctuations viewed on the computer visual display (mm), and D is the distance from the eye to the video display monitor (held constant at 762 mm). c Force and EMG records from one trial at the lowest visual gain level (0.008°) and the highest visual gain level (1.95°) at the elbow (left panels) and the ankle (right panels) for one subject

Joint force was measured by a torque transducer mounted on a shaft at the axis of rotation of each manipulandum. Joint torque was used as the measure of force. The force signal was digitized at 1,000 samples per second and stored on a computer for offline analysis. Surface electromyographic (EMG) electrodes were placed on the biceps brachii (elbow agonist), triceps brachii (elbow antagonist), tibialis anterior (ankle agonist) and soleus (ankle antagonist) muscles. The EMG signals were amplified (gain = 1,000) and bandpass filtered between 20 and 450 Hz (Delsys Inc., Boston, MA, USA).

Maximum voluntary contraction (MVC) was established for each subject separately at the elbow and ankle joints. MVC was taken as the average peak force in three 6 s trials of maximum effort of isometric elbow flexion or ankle dorsiflexion. Following this, 5% of MVC and 40% of MVC were calculated for each subject at each joint and these were the low and high force targets set for each subject. Force output to these targets was examined at the elbow and ankle under seven visual gain levels. Across all visual gain levels, force was displayed on a computer screen in front of the subject as a vertical marker. A second stationary marker bar on the screen represented target location. The width of the target always corresponded to 0.1 N m of force. A computer-generated preparatory beep alerted the subject to prepare for a trial. A second “go” beep was generated 1 s after the preparatory beep as a signal to the subject to begin the trial. At the go beep, subjects were instructed to isometrically move the force marker to the target and to hold it there as steady as possible until they heard the third beep. The third beep signaled the subject to end the trial after 17 s. Subjects were instructed to try to keep the force as steady as possible at the target regardless of the visual gain. Three trials at each visual gain level and target level were collected. All subjects remained naïve to the expected effect of visual gain on the ability to hold force steady at the target.

Seven visual gain levels were examined through a visual gain manipulation that held distance constant. Visual gain was manipulated by changing the visual angle. Visual angle is an informational property that has been shown to be important in the veridical perception of objects (Levin and Haber 1993; Gogel and Eby 1997) and has also been shown to be the critical variable in mediating gain-related changes in force control (Vaillancourt et al. 2006a). The current study manipulated visual gain relative to total force at each joint rather than optimizing visual gain relative to each joint. The calculation for visual gain is shown in Fig. 1b. Since distance is held constant in this paradigm, visual angle is equivalent to visual gain. In calculating visual gain, the standard deviation of force was assumed to be 0.3 N m (Vaillancourt et al. 2006a). The standard deviation was then multiplied by 6 (0.3 × 6 = 1.8) to approximate the full range of estimated variance (shown as the height, 2 × H1 in Fig. 1b). Since previous work has shown that most of the changes in force variability occur below a 1° visual angle (Vaillancourt et al. 2006a), the majority of visual gain levels were concentrated below 1°. The seven visual gain levels examined in the present study were 0.008°, 0.02°, 0.05°, 0.125°, 0.31°, 0.78° and 1.95°. There was a multiplicative scale factor of 2.5 between each visual gain level.

Data analysis

Prior to calculating the dependent measures for the force and EMG time series, offline processing was performed between 7 and 16.5 s. This time period was chosen to allow subjects ample time to acquire the force target and because subjects have a tendency to release force prematurely near the end of the force trajectory. These time series represent the steady-state phase of the force production task. The force data were low-pass filtered using a Butterworth filter at 30 Hz (fourth-order dual pass). The EMG data were full wave rectified and then low-pass filtered using a Butterworth filter at 60 Hz (fourth-order dual pass).

The following measures were calculated on the force data. First, relative force (% MVC) was quantified by dividing the mean force by the MVC and multiplying by 100. Second, force variability was examined using the standard deviation (SD) of force (N m). Third, the root mean square error (RMSE) was quantified as the average sum of the squared deviations of the participant’s force from the target force. Fourth, approximate entropy (ApEn) was quantified to examine the time-dependent structure of the force output (Pincus 1991; Pincus and Goldberger 1994; Pincus and Singer 1996). ApEn returns a value between 0 and 2 and reflects the predictability of future values in a time series based on previous values. For example, a sine wave has accurate short- and long-term predictability and this corresponds to an ApEn value close to 0. For a completely random signal (viz. white Gaussian noise), each future value in the time series is independent and unpredictable from previous values and the ApEn value tends toward 2. The same algorithm and parameter settings (m = 2; r = 0.2 × standard deviation of the signal) were used here and in previous work (Slifkin et al. 2000; Vaillancourt and Newell 2003). Fifth, power spectral analysis methods were used to quantify the power in specific frequency bins of the force signal. Auto-spectral analysis of the force signal was performed using Welch’s averaged periodogram method, with a window size of 2,000. Since the force signal was sampled at 1,000 Hz, this approximated a 0.5 Hz frequency bin for each power spectral estimate. Because specific neurophysiological processes are related to the frequency structure of force output, the proportion of power was examined in the 0–4, 4–8 and 8–12 Hz bins (Vaillancourt and Newell 2003). In each bin, the sum of power for that bin was divided by the sum of power between 0 and 30 Hz. Physiological tremor is present at higher frequencies between 5 and 12 Hz in the force recording (Elble and Randall 1976; Elble and Koller 1990), and most of the power related to slow sensorimotor (e.g., visuomotor) processing is located in the 0–4 Hz band of the force spectrum (Freund and Hefter 1993; Slifkin et al. 2000; Vaillancourt et al. 2001; Tracy 2007).

For the EMG data analysis, the mean EMG activity was quantified for the agonist and antagonist muscles separately. In addition, cocontraction between the agonist and antagonist muscles at each joint during the force task was examined using the algorithm suggested by Winter (1990). The equation (below) assesses the percentage of overlapping area in the EMG signals from each agonist–antagonist pair by identifying the common area between two signals across a specified time period (from 7 to 16.5 s of steady-state force) and dividing it by the combined area of both signals:

$$\%\text{Concon}=2\frac{\int min[{\mathit{EMG}}_i(t),{\mathit{EMG}}_j(t)]\text{d}t}{\int {\mathit{EMG}}_i(t)\text{d}t+\int {\mathit{EMG}}_j(t)\text{d}t}$$

where min is the minimum between two signals at time t.

This algorithm has been used during movement (Vaillancourt et al. 2004; Prodoehl et al. 2008) and force production tasks (Prodoehl et al. 2006).

Statistical analysis

For each dependent measure, the average across the three trials was calculated. Next, a three-way repeated measures analysis of variance (ANOVA) was performed to detect significant main and interaction effects on each measure, respectively. The first factor was joint (elbow, ankle), the second factor was force level (low: 5% MVC, high: 40% MVC), and the third factor was visual gain level (0.008°, 0.02°, 0.05°, 0.125°, 0.31°, 0.78°, and 1.95°). Significant effects were reported at p < 0.05. While we show all the statistical results from the three-way ANOVAs (Tables 1, 3, 4), we focus the results and discussion on the main purpose of the study by examining the joint by visual gain interactions only. Tukey post hoc tests were used to follow up significant joint by visual gain interactions to identify the locus of the interactions. To examine the visual gain between joints, linear regression was applied to the data from the visual gain levels that showed significant differences across joint in the post hoc joint by visual gain testing. A steeper slope at one joint compared to the other would indicate a stronger effect of visual gain at that joint. Significant three-way interactions were followed up with separate one-way ANOVAs for each joint at each force level.

Table 1.

ANOVA results for force amplitude measures

	Relative force		Standard deviation		Root mean square error
	F	p	F	p	F	p
Joint	0.7	0.410	5.5	0.044*	4.7	0.059
Force	4,319.1	< 0.001*	170.5	< 0.001*	0.7	0.433
Visual gain	28.2	< 0.001*	46.0	< 0.001*	27.1	< 0.001*
Joint × force	1.1	0.315	6.8	0.028*	0.03	0.859
Joint × visual gain	2.4	0.038*	4.1	0.002*	10.7	< 0.001*
Force × visual gain	0.7	0.634	13.2	< 0.001*	1.7	0.131
Joint × force × visual gain	1.2	0.329	1.9	0.095	1.5	0.186

^*A significant result p <0.05

Table 3.

ANOVA results for force structure measures

	ApEn		Proportion power 0–4 Hz		Proportion power 4–8 Hz		Proportion power 8–12 Hz
	F	p	F	p	F	p	F	p
Joint	85.1	< 0.001*	48.8	< 0.001*	3.2	0.107	14.0	0.005*
Force	49.6	< 0.001*	5.9	0.039*	4.4	0.067	0.40	0.545
Visual gain	35.0	< 0.001*	3.6	0.004*	2.3	0.045*	4.9	< 0.001*
Joint × force	15.1	0.004*	13.2	0.005*	10.5	0.010	2.9	0.121
Joint × visual gain	2.9	0.017*	2.93	0.015*	2.5	0.034*	2.5	0.030*
Force × visual gain	0.8	0.569	1.7	0.133	3.0	0.013*	1.7	0.136
Joint × force × visual gain	2.0	0.088	1.8	0.118	2.5	0.031*	2.1	0.062

^*A significant result, p < 0.05

Table 4.

ANOVA results for EMG measures

	Mean agonist EMG		Mean antagonist EMG		Co-contraction
	F	p	F	p	F	p
Joint	1.8	0.211	49.2	< 0.001*	83.0	< 0.001*
Force	85.1	< 0.001*	54.7	< 0.001*	17.9	0.002*
Visual gain	4.9	< 0.001*	7.3	< 0.001*	1.5	0.193
Joint × force	1.3	0.286	39.2	< 0.001*	0.7	0.424
Joint × visual gain	0.7	0.653	6.7	< 0.001*	1.2	0.344
Force × visual gain	0.6	0.695	2.2	0.054	0.3	0.912
Joint × force × visual gain	1.9	0.102	2.1	0.070	1.9	0.098

^*A significant result, p < 0.05

Results

Force amplitude

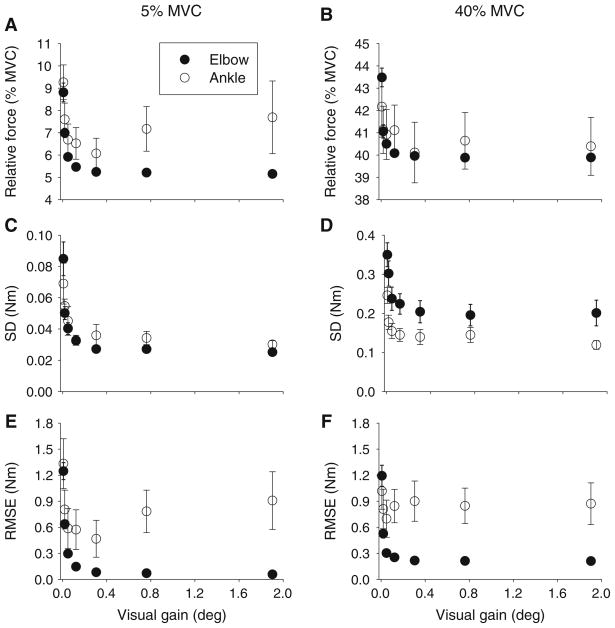
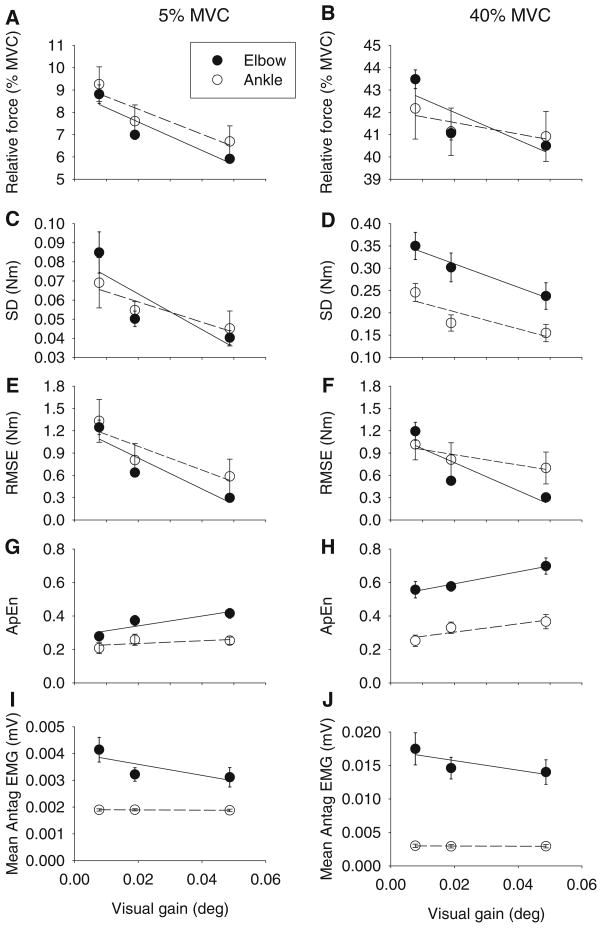
There was no significant difference between MVC at the elbow and ankle joints (t(1,9) = 1.45, p = 0.181). Increasing the visual gain led to reductions in relative force closer to both the 5% MVC and 40% MVC target force levels (Fig. 2a, b). While these reductions in force were low in terms of absolute force (averaging across both joint and force level, mean absolute force changed less than 2 N m across all visual gain levels), there was a significant interaction between joint and visual gain on relative force output (Table 1). Tukey post hoc tests for the joint by visual gain interaction showed that all of the visual gain effects occurred at the three lowest visual gain levels for both joints. To further examine this effect of visual gain on relative force, linear regression was applied to the mean data from the three lowest visual gain levels that showed significant differences in the post hoc testing. Equation parameters from the linear regression are provided in Table 2. Inspection of the data in Table 2 shows that at each force level, the slope of the regression line was steeper for the elbow than the ankle (Table 2; Fig. 3a, b), supporting a stronger effect of visual gain on reducing relative force to better approximate the target at the elbow than at the ankle.

Fig. 2.

Mean relative force (a, b), standard deviation (c, d), and root mean square error (e, f) across the seven visual gain levels for the 5% MVC condition (left panels) and the 40% MVC condition (right panels). Data shown are the mean and standard error for the elbow (filled circles) and ankle (open circles)

Table 2.

Slope, intercept and coefficient of determination (r²) from the linear regression analysis used to follow up significant joint by visual gain interactions

	5% MVC						40%MVC
	Elbow			Ankle			Elbow			Ankle
	Slope	Intercept	r2	Slope	Intercept	r2	Slope	Intercept	r2	Slope	Intercept	r2
Relative force	−63.65	8.84	0.85	−56.09	9.26	0.83	−61.63	43.23	0.68	−25.68	42.05	0.66
SD	−0.93	0.08	0.71	−0.53	0.07	0.87	−2.62	0.36	0.97	−1.92	0.24	0.74
RMSE	−20.76	1.25	0.84	−15.97	1.31	0.78	−18.79	1.15	0.74	−6.92	1.02	0.83
ApEn	2.96	0.28	0.79	0.83	0.22	0.41	3.57	0.52	0.98	2.47	0.25	0.80
Power 0–4 Hz	−0.20	0.92	0.41	0.37	0.92	0.20	−0.76	0.88	0.97	−0.28	0.94	0.48
Power 4–8 Hz	−0.06	0.04	0.27	−0.19	0.06	0.14	0.50	0.05	0.94	0.09	0.05	0.10
Power 8–12 Hz	0.15	0.02	0.74	−0.13	0.02	0.27	0.18	0.02	0.99	0.12	0.01	0.85
Mean antagonist EMG	−0.02	0.004	0.60	−0.001	0.002	0.82	−0.07	0.02	0.67	−0.001	0.003	0.44

Fig. 3.

Linear regression applied to mean relative force (a, b), standard deviation of force (c, d), root mean square error of force output (e, f), approximate entropy (g, h) and mean antagonist EMG (i, j) across the three lowest visual gain levels (0.008°, 0.02°, and 0.05°), which showed significant results for the 5% MVC condition (left panels) and the 40% MVC condition (right panels). Data shown are the mean and standard error for the elbow (filled circles) and ankle (open circles). Parameters of the linear regression are provided in Table 2

Variability in force output

Visual inspection of single subject force records from one trial (Fig. 1c) shows reduced force fluctuations as a function of increasing gain at the elbow compared to the ankle. At the group level, as expected, the standard deviation (SD) of force decreased as visual gain increased (Fig. 2c, d). There was, however, a significant joint by visual gain interaction (Table 1). Tukey post hoc testing of this interaction showed that all of the visual gain effects occurred at the three lowest visual gain levels in each joint. To examine whether the effect of visual gain on SD was stronger at the elbow than at the ankle, linear regression was used to examine the rate of change of SD across these first three significant visual gain levels at each joint and force level (Fig. 3c, d). A steeper slope would indicate a stronger effect of visual gain on variability. The linear regression equation parameters are shown in Table 2. The slope was consistently steeper at the elbow than the ankle across both force levels, supporting a stronger effect of visual gain on force variability at the elbow than at the ankle.

For root mean square error (RMSE), the error decreased as visual gain increased (Fig. 2e, f). However, this was qualified by a significant joint by visual gain interaction (Table 1). The error decreased more at the elbow joint than at the ankle joint as visual gain increased. Post hoc testing results showed that all of the changes in RMSE due to visual gain occurred at the three lowest visual gain levels. Linear regression was used to examine the rate of change of RMSE across the first three visual gain levels at each joint and force level (Fig. 3). There was a stronger effect of visual gain on reducing RMSE at the elbow than at the ankle, as evidenced by steeper slopes of the regression lines at the elbow than the ankle (Table 2).

Structure of force variability

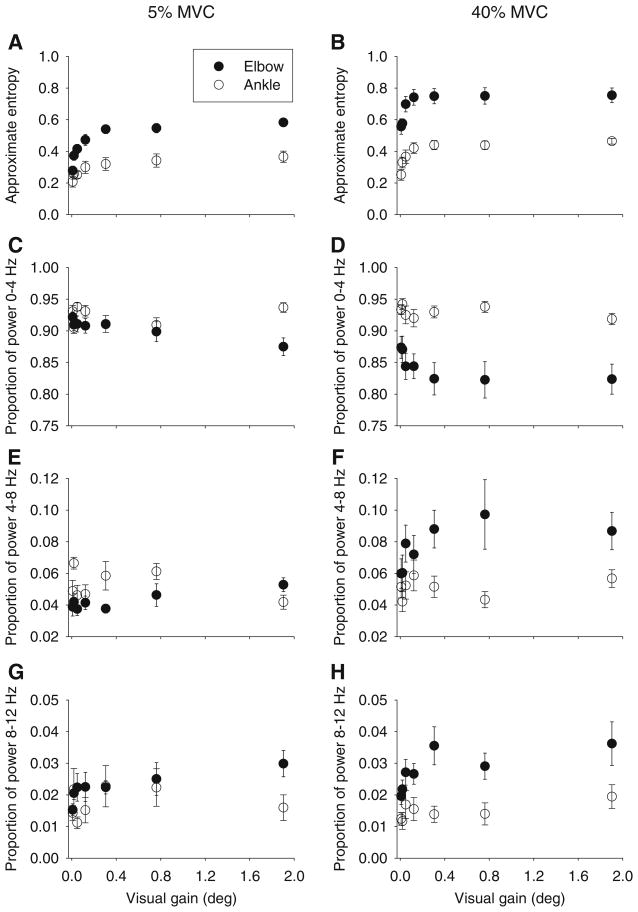
To examine changes in the time structure of the force signal across visual gain, the approximate entropy (ApEn) was examined (Fig. 4a, b). Higher ApEn values indicate increased complexity in the signal. ApEn values changed significantly as a function of joint and visual gain (Table 3). For this interaction, ApEn increased as visual gain increased when averaged across both force levels, although visual gain had a bigger effect on ApEn at the elbow than the ankle. Tukey post hoc follow-up testing for the joint by visual gain interaction showed that all of the visual gain effects on ApEn occurred at the three lowest visual gain levels for both joints. Linear regression across the ApEn data from the first three visual gain levels at each joint and force level (Fig. 3g, h) showed a stronger effect of visual gain on increasing ApEn at the elbow than at the ankle as evidenced by steeper slopes of the regression lines at the elbow than the ankle (Table 2).

Fig. 4.

Mean approximate entropy (a, b), proportion of power in the force signal between 0 and 4 Hz (c, d), proportion of power in the force signal between 4 and 8 Hz (e, f), and proportion of power in the force signal between 8 and 12 Hz (g, h) across the seven visual gains for the 5% MVC condition (left panels) and the 40% MVC condition (right panels). Data shown are the mean and standard error for the elbow (filled circles) and ankle (open circles)

To examine changes in the frequency structure of the force signal across visual gain, the proportion of power in the 0–4, 4–8 and 8–12 Hz frequency bins was examined. Comparison of the scale of the y-axis in Fig. 4c, h demonstrates that the majority of power in the force signal was located in the 0–4 Hz frequency bin. Table 3 shows the results of the ANOVA. There were significant joint by visual gain interactions at each frequency bin. For the 0–4 and 8–12 Hz frequency bins, there were no significant effects of visual gain on the proportion of power at the ankle joint. At the elbow joint, the proportion of power in the 0–4 and 8–12 Hz frequency bins changed as a function of visual gain with all of the changes occurring within the first two visual gains. For the 4–8 Hz power bin, there was a significant three-way interaction (Table 3) that was examined using separate one-way ANOVAs for each joint at each force level to examine the effect of visual gain on changing the proportion of power in the force signal in the 4–8 Hz range. For the low force level, there was no significant effect of visual gain on proportion of power in the 4–8 Hz bin at the elbow (F(6,54) = 1.51, p = 0.19), but there was a significant effect of visual gain at the ankle (F(6,54) = 3.61, p = 0.004). At the higher force level, there was a significant effect of visual gain on the proportion of power in the 4–8 Hz bin at the elbow (F(6,54) = 3.79, p = 0.003), but not at the ankle (F(6,54) = 0.93, p = 0.48).

In summary, visual gain was used effectively at both joints to reduce variability (SD) of the force signal and to improve accuracy (relative force and RMSE), and there was a bigger effect of visual gain at the elbow compared to the ankle for each of these measures. Accompanying these changes in the amount of variability and error were changes in the structure of the force signal. The force signal was more complex (less regular) at the elbow than the ankle. Visual gain significantly affected the regularity of force output with the signal becoming more complex as visual gain increased. This effect was more pronounced at the elbow than the ankle. This change in regularity was accompanied by changes in the proportion of power of the force signal across visual gain at the elbow.

EMG results

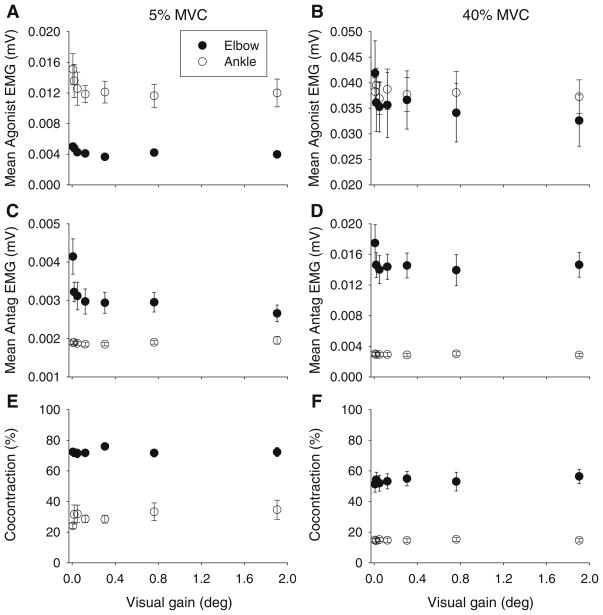
For mean agonist EMG (Fig. 5a, b), there was no significant joint by visual gain interaction (Table 4).

Fig. 5.

Mean agonist EMG (a, b), mean antagonist EMG (c, d) and the percentage of cocontraction between agonist and antagonist EMG signals (e, f) across the seven visual gain levels for the 5% MVC condition (left panels) and the 40% MVC condition (right panels). Data shown are the mean and standard error for the elbow (filled circles) and ankle (open circles)

For mean EMG of the antagonists (Fig. 5c, d), there was a significant joint by visual gain interaction (Table 4). Tukey post hoc follow-up testing of the joint by visual gain interaction showed that mean EMG antagonist was significantly higher for the first visual gain compared to the other visual gain levels at the elbow, but there was no effect of visual gain on mean antagonist EMG at the ankle (Fig. 3). Linear regression analysis (Fig. 3i, j) confirmed steeper slopes for mean antagonist EMG at the elbow across both force levels compared to the ankle (Table 2). A bivariate correlation analysis was performed to assess the relationship between SD of force and both agonist and antagonist EMG activity at each joint (Table 5). At the elbow, both agonist and antagonist muscle activity were significantly correlated with SD at both force levels. At the ankle, however, only agonist EMG at the 5% force level was significantly correlated with SD. There was no significant correlation between force variability and antagonist EMG at the ankle.

Table 5.

Bivariate correlations between SD and agonist and antagonist EMG across joint

Force level	Elbow				Ankle
	Agonist		Antagonist		Agonist		Antagonist
	r2	p	r2	p	r2	p	r2	p
5%	0.77	0.009*	0.96	< 0.001*	0.96	< 0.001*	0.002	0.928
40%	0.69	0.020*	0.64	0.029*	0.13	0.430	0.35	0.161

^*A significant result, p < 0.05

Cocontraction was essentially unchanged by visual gain at either joint (Fig. 5e, f). There was no significant joint by visual gain interaction (Table 4).

Discussion

This study examined the effects of changing visual gain on the control of steady-state force at the elbow and ankle. There were three novel findings. First, increases in visual gain led to improvements in the steadiness of force output at both the elbow and the ankle. Second, visual gain affected the variability and structure of force output more at the elbow than the ankle. Third, improved control at the elbow with increased visual gain was related to changes in the pattern of agonist and antagonist muscle activation.

Previous studies, on the effects of visual gain on the variability and structure of force output, have examined precision force control at the finger, a region of the body expected to be able to finely manipulate force in response to changes in visual feedback (Sosnoff et al. 2006; Vaillancourt et al. 2006a; Hong et al. 2008; Lee Hong and Newell 2008). At the finger, the amount and structure of force fluctuations has been shown to change considerably from 0.05° visual gain up to a 1° visual gain level with little change beyond 1° (Vaillancourt et al. 2006a). In the present study, the changes in force variability and the structure of force output at the elbow and ankle occurred within this range, with significant effects seen at visual gain levels of 0.008°, 0.02° and 0.05°. This extends previous findings at the finger to show that changes in visual gain can be effectively used in the control of large joints, such as the elbow and ankle, to improve the steadiness of isometric force output.

In dynamic force control studies, which have examined differences across upper and lower extremity joints, the variability of peak force for isometric aiming contractions has been shown to be higher for the lower extremity muscles than the upper extremity ones (Christou et al. 2003; Christou and Rodriguez 2008). The results of the present study extend these findings to include differences between the elbow and ankle in error control when maintaining steady-state force as a function of visual gain. Thus, while overall variability may be different across joints, visual gain affected the variability and structure of force output more at the elbow than the ankle.

Despite a very small absolute change in force across visual gain levels, it is possible that the change in force across visual gain levels could underlie the change in force variability across gain levels seen here. However, it has previously been shown that when the mean force remains constant across visual gain levels, changes in visual gain still lead to significant changes in the standard deviation of force (Vaillancourt et al. 2006a). This suggests that while small changes in mean force output may affect the standard deviation of force, the changes in mean force are unlikely to fully explain the changes observed in force variability and the structure of force output.

Consistent with the changes in error control, the second main finding of this study was that visual gain affected the variability and structure of force output more at the elbow than the ankle. There are several central and peripheral mechanisms, which might underlie better use of visual information in the control of elbow force than ankle force, although these mechanisms are not mutually exclusive. Centrally, one mechanism may be differences in the cortical area devoted to different regions of the body (Foerster 1936; Penfield and Boldry 1937). It has been suggested based on EMG studies examining hand muscle synergies during grasping (Santello et al. 1998; Weiss and Flanders 2004) that in addition to an anatomically based homunculus, general functional somatotopy may also exist within the motor cortex (Flanders 2005). Flanders (2005) suggests that, as found in auditory and visual areas, sensory and motor cortical areas have repeated two-dimensional representations of behaviorally important or commonly experienced features or functions. Given that the upper extremity is involved in dexterous and functionally specific tasks more often than the lower extremity, the functional somatotopy might be more clearly defined and integrated with the visual cortex for cortical regions devoted to the upper extremity than for cortical regions devoted to the lower extremity.

Another central mechanism to explain better use of visual feedback to improve control at the elbow than the ankle may be differences in the specific brain regions controlling the upper and lower extremity joints (Miyai et al. 2001; Luft et al. 2002; Kapreli et al. 2006). It has been suggested that differences in cortical activation profiles during upper and lower extremity movement may reflect the movement’s underlying behavioral context (Luft et al. 2002). Related to the current study, the behavioral context of using visual feedback to minimize force fluctuations in the upper extremity (e.g., holding a cup full of liquid steady) is likely to be different from the behavioral context of using visual feedback to minimize force fluctuations in the lower extremity (e.g., maintaining pressure on a gas pedal to hold an odometer constant). As such, the different effects of visual feedback on upper versus lower limb control might be a consequence of the functional specificity of the upper and lower limbs.

Attentional demands are another central mechanism by which changes in visual gain may affect force control. Kotb et al. (2005) used transcranial magnetic stimulation to probe the effect of spatial attention on sensorimotor integration. They showed that requiring spatial attention to a stimulated hand could induce stronger afferent inhibition of a motor-evoked potential. Increased attention has also been shown to affect cortical activation patterns during visual tracking of moving targets. Using fMRI, Culham et al. (1998) showed that brain activation related to moving visual stimuli in parietal and frontal areas could be more than doubled when items were tracked attentively. In the present study, it is possible that high visual gain forced an increased spatial attentiveness which likely contributed to improved force control seen at the higher gain levels.

Peripheral mechanisms, which might contribute to changes in force fluctuations in the upper and lower extremity visuomotor control include differences in the force-generating capacity of the muscles involved and the patterns of motor unit activity. Previous estimates of force capacity for the elbow flexors compared to the ankle dorsiflexors have found the ankle dorsiflexors to be approximately 34% stronger than the elbow flexors (Christou and Rodriguez 2008). In the present study, however, there was no significant difference between maximal isometric strength at the elbow and ankle joints. This discrepancy in results may be related to the position of the limbs during testing. Christou and Rodriguez (2008) tested elbow strength with the shoulder held horizontally at 90° and the elbow flexed to 90°, a position which would be expected to produce lower maximal isometric force than the position used in the current study (see Fig. 1a). Given the similarity of force output between the biceps brachii and the tibialis anterior found in the present study, it seems unlikely that force capability could explain the differences in control observed in this study. Also, subjects produced force that was a percentage of their maximum rather than an absolute force, which further minimized the likelihood of force-generating differences, explaining the differences found here. With regard to the pattern of motor unit activity, motor unit recruitment has been found to play a large part in controlling force output in limb muscles (Adrian and Bronk 1929). It has been suggested that, while increased motor unit synchronization may contribute to larger force fluctuations, a more likely functional role of motor unit synchronization may be to facilitate the rate of force development during rapid contractions or to promote skilled muscle synergies (Semmler 2002). The recruitment of motor units has been shown to occur through a very similar range of forces for the elbow and ankle. Both the biceps brachii (Kukula and Clamann 1981) and the tibialis anterior (Van Cutsem et al. 1997) have shown recruitment of motor units through at least 90% of the contractile force range. This suggests that motor unit recruitment differences in the muscles may not easily explain the differences in control with the visual feedback manipulation.

The third main finding in the present study was that improved control at the elbow with increased visual gain may be due to changes in the pattern of agonist and antagonist muscle activation. In the present study, the standard deviation of force decreased and approximate entropy increased with increased visual gain, more so at the elbow than the ankle. Approximate entropy is a measure of complexity of the force signal. Thus, as more visual information is provided about the force output (i.e., increased visual gain), the neuromuscular system is able to use that information to promote reduced variability in a more complex, less regular manner. Increased visual feedback information allows for more precise updating of the feedback processes that make up the visual control loop of isometric force output (Sosnoff and Newell 2005). In force control, redundancy exists in the muscle activation patterns that can be used to maintain a given force output (Latash et al. 2001). In other words, there are many combinations of muscle activation patterns around a joint that can be utilized to maintain a given force output. Fluctuations in force have been shown to be directly influenced by alterations in synergistic muscle activation (Shinohara et al. 2006, 2009). Also, improved performance in an isometric force production task has been suggested to be due to adaptation of the pattern of muscle activation in a manner that exploits the mechanical and functional attributes of each muscle group (Shemmell et al. 2006). The results of this study are compatible with the idea that the pattern of muscle activation can be altered in response to enhanced visual information, and that these patterns are different depending on the body effector where the feedback corrections are used.

Increasing complexity in force output at the elbow resulted from changes in both the agonist and antagonist muscles, rather than from a change in the cocontraction pattern between the agonist and antagonist. We had hypothesized that the ankle would show a cocontraction pattern that would scale with changes in visual gain, but the results do not support this hypothesis. It should be noted, however, that only the primary agonist and antagonist muscles at each joint were studied here. Further examination of other synergistic agonist and antagonist muscle pairs is warranted to determine whether they altered their recruitment pattern in response to changes in visual information differently at the elbow than the ankle joint and to better isolate the source of the changes in variability.

Understanding how visual information can be used to improve force control at different joints is important when one considers the increased use of robotic-assisted rehabilitation devices (Shadmehr and Mussa-Ivaldi 1994; Reinkensmeyer et al. 2000; Lum et al. 2002). What is required, however, to make full use of this technology is a greater understanding of how robotic training can best promote adaptation and lasting improvements in physical performance and behavior. The results of the present study suggest that while visual feedback can be used effectively to improve steadiness of force output at both the elbow and the ankle, the elbow may be better suited to take advantage of enhanced visual information.