Abstract
Rorqual whales (Balaenopteridae) represent not only some of the largest animals of all time, but also exhibit a wide range in intraspecific and interspecific body size. Balaenopterids are characterized by their extreme lunge-feeding behaviour, a dynamic process that involves the engulfment of a large volume of prey-laden water at a high energetic cost. To investigate the consequences of scale and morphology on lunge-feeding performance, we determined allometric equations for fin whale body dimensions and engulfment capacity. Our analysis demonstrates that larger fin whales have larger skulls and larger buccal cavities relative to body size. Together, these data suggest that engulfment volume is also allometric, increasing with body length as 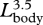 . The positive allometry of the skull is accompanied by negative allometry in the tail region. The relative shortening of the tail may represent a trade-off for investing all growth-related resources in the anterior region of the body. Although enhanced engulfment volume will increase foraging efficiency, the work (energy) required to accelerate the engulfed water mass during engulfment will be relatively higher in larger rorquals. If the mass-specific energetic cost of a lunge increases with body size, it will have major consequences for rorqual foraging ecology and evolution.
. The positive allometry of the skull is accompanied by negative allometry in the tail region. The relative shortening of the tail may represent a trade-off for investing all growth-related resources in the anterior region of the body. Although enhanced engulfment volume will increase foraging efficiency, the work (energy) required to accelerate the engulfed water mass during engulfment will be relatively higher in larger rorquals. If the mass-specific energetic cost of a lunge increases with body size, it will have major consequences for rorqual foraging ecology and evolution.
Keywords: allometry, morphology, foraging
1. Introduction
The fossil record is replete with examples of gigantism in a wide range of marine and terrestrial taxa; however, the large body size of extant rorqual whales (Balaenopteridae) is unprecedented (Alexander 1998). Some balaenopterids, such as blue (Balaenoptera musculus) and fin whales (Balaenoptera physalus), represent an extreme in body size among all vertebrates, both past and present. Despite a general trend for some lineages to increase in body size over time (Hone & Benton 2005), it is unknown why rorquals do not exhibit even larger body sizes. Furthermore, theories and mechanisms regarding limits to large body size in whales are rare (Alexander 1998), probably because of our general lack of knowledge about the physiology of these animals. Recent advances in digital tag technology have revolutionized the study of rorquals in their natural environment, especially with respect to foraging mechanics and energetics (Acevedo-Gutierrez et al. 2002; Croll et al. 2005; Goldbogen et al. 2007, 2008; Bailey et al. in press). Integrating these data provides novel opportunities to examine how animals function at the outlying limits of body mass and also to explore the physiological limits to body size.
The extreme body size of rorquals, reaching up to 28 m long in blue whales (Mackintosh & Wheeler 1929), necessitates high absolute energetic requirements. Rorquals meet this energetic demand using a bulk-filter-feeding strategy, lunge feeding, which involves the engulfment and filtering of a large volume of prey-laden sea water that is commensurate of their body size (Goldbogen et al. 2007). This tremendous engulfment capacity, however, does not come without a cost. The engulfment process generates large amounts of drag and therefore incurs a high energetic cost that consequently limits foraging time (Acevedo-Gutierrez et al. 2002; Goldbogen et al. 2007). Physical principles indicate that unsteady manoeuvres and locomotor performance, such as lunge feeding, will decrease with body size (Webb & Debuffrenil 1990; Domenici 2001). Larger rorquals may be subject to these detrimental scaling effects and therefore suffer relatively higher energetic costs for lunge feeding. However, even though the basic mechanics of lunge feeding are now relatively well understood (Goldbogen et al. 2006, 2007; Potvin et al. 2009), little is known about how this process scales with body size.
The most important morphological parameter that determines the mechanics and energetics of lunge feeding is mouth area. The area of the mouth exposed to flow controls the flux of water into the buccal cavity and also the amount of drag that is sustained (Goldbogen et al. 2007). The magnitude of both the engulfed water and the drag generated during engulfment contributes to the overall energetic cost of a lunge (Potvin et al. 2009). Mouth area is defined by dimensions of the skull and mandibles, and together they constitute the mouth region which encompasses approximately 25 per cent of the whale's total body length. Such a large proportion of the body devoted to mouth area undoubtedly enables tremendous engulfment capacity, thereby increasing the energetic efficiency of a lunge. Because engulfment volume and drag are functionally linked to the dimensions of the skull, an allometric analysis of these structures will provide an indication as to how lunge-feeding performance scales with body size.
During a morphometric study of blue (B. musculus) and fin whales from the Southern Hemisphere, Mackintosh & Wheeler (1929) discovered that larger individual whales had larger skulls, and also shorter tails, relative to body size. These data were derived from an intense period of shore-based whaling in the Southern Ocean, and it is unlikely that such a sample could ever be replicated, making their record unique and invaluable. In the end, they provided no explanation for these patterns of relative growth, but recommended further analyses. Additionally, their measurements were taken before Huxley (1932) developed the modern concept of allometry and before researchers fully understood how lunge feeding works.
Here, we provide a complete allometric analysis of Mackintosh & Wheeler's (1929) morphometric dataset for fin whales, and also incorporate relevant data from other published sources of body mass, girth and fluke span. We then assess the functional implications for the relative growth of the structures that determine lunge-feeding performance, particularly with respect to the engulfment apparatus. Our analysis demonstrates that the allometry of fin whale skulls indeed increases mass-specific engulfment capacity, but at a potentially higher energetic cost because more energy is probably required to accelerate more engulfed water. Within an ecological context, relatively higher costs in larger rorquals could decrease diving capacity and have major impacts on rorqual foraging ecology.
2. Material and methods
(a). Allometry of fin whale body dimensions
We built a comprehensive dataset of fin whale morphology by synthesizing data from several studies associated with strandings and the whaling industry. All morphological measurements were taken by the same researchers using the same methods (Mackintosh & Wheeler 1929), with the exception of body mass (Mackintosh 1942; Quiring 1943; Nishiwaki & Oye 1951; Ash 1953; Lockyer 1976; Lockyer & Waters 1986; Víkingsson et al. 1988), maximum body girth (Mackintosh 1942; Lockyer & Waters 1986; Víkingsson et al. 1988; Bose & Lien 1989) and fluke span (True 1904; Bose & Lien 1989).
The complete dataset from each source was digitized by hand and then entered into spreadsheet formats. Log-transformed data were analysed using reduced major axis regression (Bohonak & Van der Linde 2004) to derive allometric equations and 95% confidence intervals (CI). Allometric equations were determined for each body dimension (figure 1) as a function of overall body length Lbody (table 1). Using these 95% CI, the null hypothesis of geometric similarity was rejected if the slope of the allometric relationship (to the tenths decimal place) was significantly different than 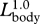 for linear dimensions,
for linear dimensions, 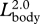 for mouth area and projected area of the body and
for mouth area and projected area of the body and 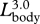 for body mass and engulfed water mass.
for body mass and engulfed water mass.
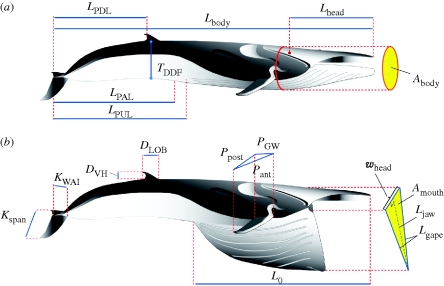
Figure 1.
Fin whale body dimensions. Each body dimension (blue lines) is represented by a symbol (see table 1 for details); images modified from Goldbogen et al. (2007). (a,b) The allometric equations for these body dimensions were determined with respect to the length of the body (table 1).
Table 1.
Allometric equations for fin whale body dimensions as a function of total body length (Lbody).
| symbol | parameter | reference number from Mackintosh & Wheeler (1929) | n | slope | 95% CI |
r2 | |
|---|---|---|---|---|---|---|---|
| general body dimensions | |||||||
| Mc | body mass | n.a.a | 96 | 2.60 | 2.42 | 2.78 | 0.90 |
| Abody | frontal body area (greatest maximum projection) | n.a.b | 41 | 2.25 | 1.76 | 2.74 | 0.69 |
| Lhead | severed head length (occipital condyle to tip of snout) | 20 | 519 | 1.21 | 1.19 | 1.24 | 0.93 |
| LPUL | post-umbilical length (umbilicus to notch of flukes) | 11 | 707 | 0.85 | 0.83 | 0.86 | 0.94 |
| LPAL | post-anal length (anus to notch of flukes) | 10 | 750 | 0.78 | 0.76 | 0.80 | 0.80 |
| LPDL | post-dorsal fin length (dorsal fin to notch of flukes) | 8 | 562 | 0.83 | 0.81 | 0.86 | 0.84 |
| TDDF | tail depth at dorsal fin (dorsal–ventral) | 24 | 455 | 1.19 | 1.13 | 1.24 | 0.79 |
| engulfment apparatus | |||||||
| Lgape | length of gape (tip of snout to angle of gape) | 4 | 296 | 1.24 | 1.20 | 1.28 | 0.93 |
| whead | greatest width of the head (bizygomatic width) | 21 | 296 | 1.15 | 1.10 | 1.19 | 0.90 |
| Ljaw | lateral projected length of mandibles (palate to tip of mandibles) | √(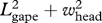 ) ) |
296 | 1.25 | 1.21 | 1.29 | 0.93 |
| Amouth | mouth area (planar or maximum) | Lgape × whead | 296 | 2.39 | 2.33 | 2.46 | 0.95 |
| LVGB | length of ventral groove blubber (snout to posterior end of grooves) | 1–12 | 457 | 1.14 | 1.12 | 1.16 | 0.97 |
| propulsion and control surfaces | |||||||
| Pant | leading edge length of flipper (tip to anterior insertion) | 17 | 476 | 1.02 | 0.98 | 1.06 | 0.86 |
| Ppost | trailing edge length of flipper (tip to axilla) | 16 | 668 | 1.07 | 1.03 | 1.11 | 0.78 |
| PGW | greatest width of flipper (near medial insertion) | 19 | 487 | 1.05 | 1.01 | 1.09 | 0.85 |
| DVH | dorsal fin, vertical height (dorsal–ventral) | 14 | 579 | 0.86 | 0.78 | 0.93 | 0.46 |
| DLOB | dorsal fin, length at base (anterior–posterior) | 15 | 558 | 0.97 | 0.87 | 1.06 | 0.42 |
| Kspan | fluke span (lateral, tip to tip) | n.a.c | 30 | 1.07 | 0.89 | 1.25 | 0.84 |
| KWAI | flukes, width at insertion (notch of fluke to medial insertion) | 9 | 681 | 0.84 | 0.81 | 0.88 | 0.80 |
aData from Lockyer (1976), Lockyer et al. (1985), Lockyer & Waters (1986), Víkingsson et al. (1988), Nishiwaki & Oye (1951), Ash (1953), Mackintosh (1942) and Quiring (1943).
bDerived from maximum girth measurements from Lockyer & Waters (1986), Víkingsson et al. (1988) and Mackintosh (1942).
cData from True (1904) and Bose & Lien (1989).
(b). Volumetric capacity of the buccal cavity
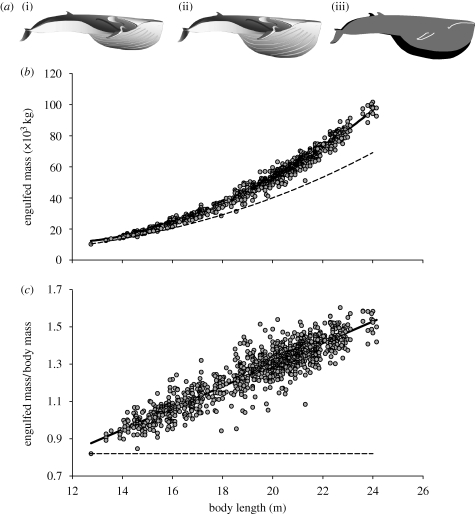
Engulfment capacity is limited morphologically by dimensions of the skull (mouth area) and buccal cavity (Goldbogen et al. 2007). Mouth area is directly determined by the projected length of the mandibles (Ljaw) and the width of the skull (whead). Given that the walls of the buccal cavity (ventral groove blubber) are highly distensible up to four times its resting length in the circumferential direction (Orton & Brodie 1987), its maximum capacity is ultimately determined by the overall length of the ventral groove system (L0). Observations of subsurface lunges (i.e. Bryde's whale in BBC Blue Planet: Open Ocean Chapter; blue whale in History Channel's Evolve: Size) show that the expansion of the buccal cavity never exceeds the area of the mouth within the transverse plane, whereby each slug of water that enters the mouth largely maintains its shape after engulfment (Potvin et al. 2009). This justifies the simple approximation of maximum buccal cavity volume as the sum of two-quarter ellipsoids, one anterior to and the other posterior to the temporomandibular joint (TMJ), both of which are constrained geometrically by these specific morphological dimensions (Ljaw, whead, L0).
The volume of each quarter ellipsoid is calculated as (4/3)π abc (full ellipsoid) where a,b and c represent the major and minor radii of each ellipse (figure 2). Length a runs along the main longitudinal axis of the whale's body (i.e. from snout to fluke); length b along the dorsoventral axis (in the direction of the mandibles at maximum gape) and length c along the body's transverse axis from one flipper to the other. For example, the section of the buccal cavity that is posterior to the TMJ consists of one-fourth of that ellipsoidal volume, where a = L0 − Ljaw, b = Ljaw 1.2 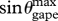
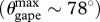 and c = whead/2. Here, the factor of 1.2 arises from the disarticulation and rotation of the jaw during a lunge, which slightly increases mouth area (Lambertsen et al. 1995; Goldbogen et al. 2007), and therefore the size of the ellipsoid. Thus, the engulfed mass ratio, engulfed water mass divided by the whale's body mass (Mw/Mc), posterior to the TMJ is given by:
and c = whead/2. Here, the factor of 1.2 arises from the disarticulation and rotation of the jaw during a lunge, which slightly increases mouth area (Lambertsen et al. 1995; Goldbogen et al. 2007), and therefore the size of the ellipsoid. Thus, the engulfed mass ratio, engulfed water mass divided by the whale's body mass (Mw/Mc), posterior to the TMJ is given by:
| 2.1 |
where ρw corresponds to the density of sea water. Assuming a similar one-quarter, three-dimensional ellipsoid shape for the buccal cavity anterior to the TMJ, we can again define the following engulfed mass ratio:
| 2.2 |
where a = Lpalate ∼ Ljaw, b = Ljaw 1.2 sin78° and c = whead/2. The sum of two engulfed mass ratios yields the total engulfed mass (mass-specific). Although this approximation does not account for the space occupied by the thoracic cavity, the magnitude of that volume is relatively small when compared with the engulfed volume. Furthermore, the elevation of the skull that occurs during mouth opening (Koolstra & Van Eijden 2004; Calambokidis et al. 2007) suggests that the influx of engulfed water is not hindered by the position of the thoracic cavity.
Figure 2.
Pro-E renderings of a buccal cavity filled to maximum capacity. (a) The engulfed water mass was represented by two quarter-ellipsoids: one posterior to (b) and the other anterior to (c) the temporomandibular joint (TMJ), where the magnitude of each was calculated by equations (2.1) and (2.2), respectively. The dimensions of each quarter ellipsoid were determined by specific morphological dimensions. The red line is perpendicular to the long axis of the body and the ends of the red line represent the estimated location of the mandibular condyles at maximum gape. The length of the jaws (Ljaw) from the location of the TMJ to the mandibular symphysis is represented by the solid yellow line. The dashed yellow line shows the position of Ljaw at maximum gape. Each quarter ellipsoid was rotated differently in three-dimensional space to aid visualization. The green line is the length from the TMJ to the end of the ventral groove system (L0−Ljaw).
We explored the effects of morphological variation on engulfment capacity by incorporating the data for each morphological parameter separately into the allometric equations that evaluate the engulfed mass ratio. Most of the morphological data were not always collected from the same individual; thus, each data point shown in figure 3 corresponds to single measurement for one of these four body dimensions (Mc, L0, Ljaw and whead) folded within the other three embodied in the ‘averages’ predicted by our allometric equations. The scatter of these data represents an estimate of the variation in engulfment capacity owing solely to morphological variation.
Figure 3.
Allometry of maximum engulfment capacity. (a) Schematics of maximally filled buccal cavities for (i) the smallest (12 m), (ii) the largest (24 m) fin whale in the dataset are scaled to one another, and (iii) the outlines of each are superimposed in order to show the relative changes in the tail and buccal cavity. Images modified from Goldbogen et al. (2007). (b) Engulfed mass is proportional to  (r2 = 0.99). If engulfed mass were isometric, it would follow the dashed line. (c) Engulfed mass relative to body mass increased with body length as
(r2 = 0.99). If engulfed mass were isometric, it would follow the dashed line. (c) Engulfed mass relative to body mass increased with body length as  (r2 = 0.85). The dashed line represents isometry.
(r2 = 0.85). The dashed line represents isometry.
3. Results and discussion
(a). Scaling of the engulfment apparatus
Our analysis demonstrates that all fin whale body dimensions, except those associated with propulsion and control surfaces, exhibit significant allometry (table 1). The relative length and width of the skull increased with body size 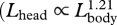 ,
, 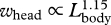 ), thereby increasing the area of the mouth that is dedicated to engulfment (
), thereby increasing the area of the mouth that is dedicated to engulfment (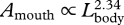 ). Enhanced mouth area will increase the flux of water into the mouth during a lunge, which is accommodated by relatively larger buccal cavities in larger whales (
). Enhanced mouth area will increase the flux of water into the mouth during a lunge, which is accommodated by relatively larger buccal cavities in larger whales (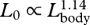 ). Given these allometric patterns, our calculations suggest that engulfment capacity (Mw) is proportional to
). Given these allometric patterns, our calculations suggest that engulfment capacity (Mw) is proportional to 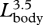 (figure 3b). The ratio of engulfed mass relative to body mass emphasizes this increase in capacity, scaling as
(figure 3b). The ratio of engulfed mass relative to body mass emphasizes this increase in capacity, scaling as 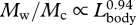 . Thus, the largest fin whales (Lbody = 24 m) realize a 70 per cent increase in mass-specific engulfment capacity over recently weaned juveniles (Lbody = 12 m) (figure 3c). The engulfment capacity calculated for fin whales larger than 14 m was equal in magnitude to, or larger than, their own body size. Increased engulfment capacity should also increase the energetic cost of lunge feeding, given that at least half of the energy used during a lunge is because of the active process of engulfment, whereby the engulfed water mass is accelerated up to the instantaneous speed of the whale's body (Potvin et al. 2009). Because the force required to accelerate the engulfed water inside the buccal cavity is proportional to the magnitude of that engulfed water mass (Potvin et al. 2009), it follows that the corresponding work (energy) is also proportional to the engulfed water mass. The increase in mass-specific engulfment capacity with body size (figure 3) therefore suggests that the mass-specific work required for engulfment must not only increase with size but also does so allometrically.
. Thus, the largest fin whales (Lbody = 24 m) realize a 70 per cent increase in mass-specific engulfment capacity over recently weaned juveniles (Lbody = 12 m) (figure 3c). The engulfment capacity calculated for fin whales larger than 14 m was equal in magnitude to, or larger than, their own body size. Increased engulfment capacity should also increase the energetic cost of lunge feeding, given that at least half of the energy used during a lunge is because of the active process of engulfment, whereby the engulfed water mass is accelerated up to the instantaneous speed of the whale's body (Potvin et al. 2009). Because the force required to accelerate the engulfed water inside the buccal cavity is proportional to the magnitude of that engulfed water mass (Potvin et al. 2009), it follows that the corresponding work (energy) is also proportional to the engulfed water mass. The increase in mass-specific engulfment capacity with body size (figure 3) therefore suggests that the mass-specific work required for engulfment must not only increase with size but also does so allometrically.
The relative expansion of the head in larger fin whales was accompanied by a concomitant decrease in the relative size of the posterior region (caudal peduncle) of the body (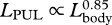 ,
, 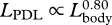 ,
, 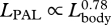 ). This trend occurs despite a general elongation of the entire body, as indicated by the negative allometric relationship between mass and body length (
). This trend occurs despite a general elongation of the entire body, as indicated by the negative allometric relationship between mass and body length (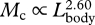 ). We speculate that the decreased growth rate in the posterior region of the body could represent a trade-off for investing all growth-related resources in the anterior region. Despite a predicted decrease in mass-specific metabolic rate, Lockyer (1981) suggested that these patterns of relative growth were required to meet the increased energetic demands of a larger body. A relatively smaller tail could reduce metabolic costs related to the maintenance (i.e. resting metabolic rate) and use of the primary locomotor muscles that are located within that body region. In this way, the relative growth of the head and tail could be a putative adaptation for saving energy if relatively smaller tails are still capable of producing sufficient thrust during locomotion; although the tail region was negatively allometric, the fluke itself is isometric (table 1) and therefore implies that the mechanical energy used during locomotion is relatively the same. Conversely, most of the expanded head region is devoted to an enlarged, but weakly muscularized tongue that is composed largely of adipose tissue (Slijper 1979), which will require relatively less energy to sustain than muscle.
). We speculate that the decreased growth rate in the posterior region of the body could represent a trade-off for investing all growth-related resources in the anterior region. Despite a predicted decrease in mass-specific metabolic rate, Lockyer (1981) suggested that these patterns of relative growth were required to meet the increased energetic demands of a larger body. A relatively smaller tail could reduce metabolic costs related to the maintenance (i.e. resting metabolic rate) and use of the primary locomotor muscles that are located within that body region. In this way, the relative growth of the head and tail could be a putative adaptation for saving energy if relatively smaller tails are still capable of producing sufficient thrust during locomotion; although the tail region was negatively allometric, the fluke itself is isometric (table 1) and therefore implies that the mechanical energy used during locomotion is relatively the same. Conversely, most of the expanded head region is devoted to an enlarged, but weakly muscularized tongue that is composed largely of adipose tissue (Slijper 1979), which will require relatively less energy to sustain than muscle.
The same type of allometry (relatively larger heads and smaller tails with increasing body size) apparently occurs in other large rorqual species as well, including blue (Mackintosh & Wheeler 1929), sei (Balaenoptera borealis) (Matthews 1938) and humpback whales (Megaptera novaeangliae) (Matthews 1937). However, these datasets have not been subjected to a formal allometric analysis. Moreover, it is unclear whether smaller rorqual species, such as Bryde's (Balaenoptera edeni) and minke whale (Balaenoptera acutorostrata), also exhibit significant allometry of the skull (Lockyer 1981). By comparing morphometric data among rorquals of different body sizes within a phylogenetic context, we will be able to test, in forthcoming work, whether these allometric patterns represent an adaptation specifically for lunge feeding or an exaptation associated with large body size. Other large baleen whales, including balaenids (bowhead and right whales) and eschrichtiids (grey whales), also have relatively large heads but are not lunge feeders (Werth 2000, 2004). This simple comparison suggests that big heads are not strict adaptations for lunge feeding, but they may be exaptive in rorquals because they facilitate an increase in mass-specific engulfment capacity.
By having a large head, baleen whales have increased baleen area and mouth area relative to body size. These attributes should enhance filter-feeding performance, not only in rorquals as we have shown here (figure 3), but also in continuous ram-feeding balaenids (bowhead and right whales). For example, bowhead whales (Balaena mysticetus) swim at very low, steady speeds with mouth agape to continuously filter zooplankton suspended in the water column, and the rate at which water is filtered (volume per unit time) is the product of swim speed and projected mouth area (Simon et al. 2009). Hydrodynamic analyses indicate that bowhead whales must feed at slow speeds in order to reduce drag (Werth 2004), so the only way to increase filter rate is to increase mouth area via an increase in overall skull size. Given these general arguments, we suggest that large heads in baleen whales function to increase the overall efficiency of filter feeding. If mass-specific metabolic rate decreases with body size, then bulk-filter feeding may represent a mechanism that not only supports large body size (Goldbogen et al. 2007), but also allows for the deposition of substantial lipid stores that are required for fasting and long-distance migration (Brodie 1975). Because large amounts of submucosal adipose tissue are present within the tongue in several baleen whale species, the tremendous size of the head may also serve as a compartment for nutritional storage (Werth 2007).
(b). Scaling of propulsion and control surfaces
In contrast to the allometry of the head and tail, nearly all dimensions of the fluke, dorsal fin and flippers were scaled isometrically. One exception was the width of the flukes at insertion, which was negatively allometric (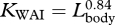 ). Because fluke span scaled isometrically with body size (
). Because fluke span scaled isometrically with body size (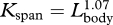 ), fluke aspect ratio may have increased in larger fin whales. High aspect ratio flukes should increase the efficiency of steady swimming at high speeds (Bose & Lien 1989; Woodward et al. 2006), but it will not be very effective in producing lift during the high amplitude swimming strokes that are observed during lunge feeding. An increased span coupled with an increase in aspect ratio will eventually cause excessive bending of the flukes and ultimately decrease hydrodynamic performance (Fish & Rohr 1999). Such an effect may represent a structural limitation to the morphological design of the fluke (Daniel 1988; Bose et al. 1990; Fish & Rohr 1999) and thus preclude fin whales from adopting larger flukes with increasing body size.
), fluke aspect ratio may have increased in larger fin whales. High aspect ratio flukes should increase the efficiency of steady swimming at high speeds (Bose & Lien 1989; Woodward et al. 2006), but it will not be very effective in producing lift during the high amplitude swimming strokes that are observed during lunge feeding. An increased span coupled with an increase in aspect ratio will eventually cause excessive bending of the flukes and ultimately decrease hydrodynamic performance (Fish & Rohr 1999). Such an effect may represent a structural limitation to the morphological design of the fluke (Daniel 1988; Bose et al. 1990; Fish & Rohr 1999) and thus preclude fin whales from adopting larger flukes with increasing body size.
Unlike the fluke, the flippers possess bony reinforcement, but they too were geometrically similar. The lift generated by the flippers, which is proportional to the planform area of the flippers, is thought to balance a negative pitching moment on the body that results from the drag generated during engulfment (Cooper et al. 2008). The positive allometry of mouth area (table 1) suggests that engulfment drag, and therefore drag moments, will increase relative to body size; however, if larger rorquals can distribute engulfment drag forces over longer time scales (given dynamic similarity), they may experience relatively lower peak drag forces. Within this scenario, the isometric scaling of the flippers should be able to provide enough lift torques to counteract head-down pitch caused by engulfment drag and maintain body trim during a lunge.
The general isometric scaling of propulsion and control surfaces suggests that manoeuvrability and unsteady locomotor performance, such as the ability to accelerate the body during a lunge (Goldbogen et al. 2006), will decrease with body size (Webb & Debuffrenil 1990; Domenici 2001). This phenomenon occurs because body mass increases with body size much more rapidly than fluke area or flipper area, both of which are proportional to lift. These mechanical scaling effects may explain why the largest rorqual, the blue whale, feeds almost exclusively on krill because it lacks the manoeuvrability and acceleration needed to adequately exploit fish aggregations, which have higher escape velocities. However, the next two largest rorqual species (fin and sei whales) do eat fish, although the bulk of their diet consists of small crustaceans (Flinn et al. 2002). Some of the larger rorquals clearly have the ability to capture fast fish, but foraging on krill may simply be energetically more efficient with increasing body size. By contrast, some populations of the two smallest rorqual species, Bryde's (B. brydei) and minke whales (B. acutorostrata) feed only on fish (Gaskin 1982) or tend to select fish over krill (Murase et al. 2007). The general inverse relationship between prey size and rorqual body size can be attributed to physiological constraints that have a strong influence on foraging ecology, behaviour and energetics (Tershy 1992). The enhanced engulfment capacity associated with skull allometry in larger rorquals probably increases the efficiency of bulk-filter feeding on smaller prey, whereas relatively smaller skulls and mouths will facilitate capture of larger, more agile prey.
(c). Implications for foraging ecology
Given the increase in mass-specific engulfment capacity with body size (figure 3), we have argued that the mass-specific work required for engulfment—a major component of the energy budget during lunge feeding—must also increase with size. Thus, if the energetic cost of a lunge is positively allometric in this way, and if oxygen storage (Lasiewski & Calder 1971; Hudson & Jones 1986) and maximum metabolic rate (Glazier 2008) scale isometrically, then diving capacity (i.e. dive duration and depth) could be decreased in larger rorquals. In general, diving capacity increases with body size among all air-breathing diving vertebrates because of the differential scaling between metabolic rate (allometric) and blood oxygen stores (isometric) (Halsey et al. 2006). However, despite being some of the largest divers, rorquals are limited to extremely short dive times because of the high metabolic demands of lunge feeding (Acevedo-Gutierrez et al. 2002; Goldbogen et al. 2007). Thus, relatively higher lunge-feeding costs in larger rorquals could diminish the typical advantages associated with large body size and increasingly limit dive time. This hypothesis is corroborated by limited tag data (Croll et al. 2001; Goldbogen et al. 2008); even though blue whales are nearly twice as large as humpback whales, both of them exhibited the same average dive duration (7.8 min) when foraging at approximately the same average depth (blue whales = 140 m, n = 7; humpback whales = 148 m, n = 2).
Limited dive duration would be especially problematic for larger rorquals because they require more time (i.e. dynamic similarity) to (i) accelerate to maximum lunge speed, (ii) perform the lunge and engulf the targeted prey patch and (iii) filter relatively larger engulfed water volumes. If prey patches are very deep, low in density or spatially far apart, then these scaling effects will be increasingly detrimental and make lunge feeding less efficient. Because lunge feeding involves the intermittent engulfment of discrete volumes of prey-laden water at depth, decreased efficiency will necessitate more foraging time to meet energetic demands (Goldbogen et al. 2007). Dense krill patches that are deep during the day typically migrate towards the sea surface at night and disperse into lower density (Zhou & Dorland 2004). Rorquals that target deep, dense krill aggregations will track their diel migration; lunge-feeding effort at depth gradually decreases at dusk and then progressively increases at dawn (Oleson et al. 2007). Such a behavioural switch highlights the importance of dense prey aggregations to the efficiency of rorqual lunge feeding.
Because dense prey patches are generally deep, limited dive time may limit the maximum number of lunges that can be performed per dive in larger rorquals. The number of lunges executed per dive appears to be an indication of prey patch quality (Goldbogen et al. 2008), so the maximum number of lunges that are recorded may be representative of maximum dive capacity. Although the available tag data (Croll et al. 2001; Goldbogen et al. 2006, 2008) do indeed show a decrease in the maximum number of lunges executed per dive with body size (humpback whale = 15, fin whale = 8, blue whale = 6), more tag studies are clearly needed to adequately test this hypothesis. If possible, larger rorquals could lunge at a shallower depth to increase lunge-feeding time relative to transit time, thereby increasing foraging efficiency. A recent study of sympatric Antarctic rorquals revealed that minke whales were foraging on significantly deeper krill patches than humpback whales (Friedlaender et al. 2009). Although there are many possible explanations for this pattern (Friedlaender et al. 2009), we propose an additional hypothesis which suggests that this type of vertical resource partitioning is because of the scaling of lunge-feeding energetics. However, other tag studies have shown the opposite pattern with respect to body size, where humpback whales foraged at a much shallower depth than fin whales (Goldbogen et al. 2006, 2008), albeit at different locations. Again, it is clear that more studies are needed to fully understand the effects of lunge-feeding energetics on diving behaviour.
Positively allometric feeding costs may increasingly limit access to prey patches at depth and, even if larger rorquals are morphologically optimized to increase engulfment capacity for each lunge (figure 3), the overall rate of energy expenditure will eventually increase more rapidly with body size than net energy gain. As a result, larger rorquals will have to devote a greater proportion of their energy intake to power lunge feeding, making them competitively inferior (Alexander 1998). Increasing energetic costs (relative to prey capture) have been shown to limit indeterminate growth in passive suspension feeders (Sebens 1982), and the balance between food supply and energetics may have determined maximum body size in dinosaurs (McNab 2009). Accordingly, the larger size of whales relative to terrestrial mammals is attributed to greater resource abundance in marine environments (McNab 2009). Therefore, if prey abundance is not a limiting factor, allometric foraging costs in baleen whales may ultimately limit maximum body size. Ironically, the bulk-filter-feeding mechanism that is thought to enable large body size in baleen whales could also limit maximum body size because of mechanical scaling effects.
Acknowledgements
We thank N. D. Pyenson and two anonymous reviewers for their comments on this manuscript. Funding was provided by NSERC to R.E.S. and a UBC-UGF to J.A.G. We also thank M. McQuilling for his assistance in figure 2.
References
- Acevedo-Gutierrez A., Croll D. A., Tershy B. R.2002High feeding costs limit dive time in the largest whales. J. Exp. Biol. 205, 1747–1753 [DOI] [PubMed] [Google Scholar]
- Alexander R. M.1998All-time giants: the largest animals and their problems. Palaeontology 41, 1231–1245 [Google Scholar]
- Ash C. E.1953Weights of Antarctic humpback whales. Nor. Hvalfangsttid. 42, 387–391 [Google Scholar]
- Bailey H., Mate B., Irvine L., Palacios D. M., Bograd S. J., Costa D. P.In press Blue whale behavior in the eastern North Pacific inferred from state-space model analysis of satellite tracks. Endangered Species Res. [Google Scholar]
- Bohonak A. J., Van der Linde K.2004RMA: software for reduced major axis regression for Java. v. 1.18. See http://www.kimvdlinde.com/professional/rma.html [Google Scholar]
- Bose N., Lien J.1989Propulsion of a fin whale (Balaenoptera physalus): why the fin whale is a fast swimmer. Proc R. Soc. Lond. B 237, 175–200 (doi:10.1098/rspb.1989.0043) [DOI] [PubMed] [Google Scholar]
- Bose N., Lien J., Ahia J.1990Measurements of the bodies and flukes of several cetacean species. Proc. R. Soc. Lond. B 242, 163–173 (doi:10.1098/rspb.1990.0120) [Google Scholar]
- Brodie P. F.1975Cetacean energetics, an overview of intraspecific size variation. Ecology 56, 152–161 (doi:10.2307/1935307) [Google Scholar]
- Calambokidis J., Schorr G. S., Steiger G. H., Francis J., Bakhtiari M., Marshal G., Oleson E. M., Gendron D., Robertson K.2007Insights into the underwater diving, feeding, and calling behavior of blue whales from a suction-cup-attached video-imaging tag (CRITTERCAM). Mar. Tech. Soc. J. 41, 19–29 (doi:10.4031/002533207787441980) [Google Scholar]
- Cooper L. N., Sedano N., Johansson S., May B., Brown J. D., Holliday C. M., Kot B. W., Fish F. E.2008Hydrodynamic performance of the minke whale (Balaenoptera acutorostrata) flipper. J. Exp. Biol. 211, 1859–1867 (doi:10.1242/jeb.014134) [DOI] [PubMed] [Google Scholar]
- Croll D. A., Acevedo-Gutierrez A., Tershy B. R., Urban-Ramirez J.2001The diving behavior of blue and fin whales: is dive duration shorter than expected based on oxygen stores? Comp. Biochem. Physiol. A Mol. Integr. Physiol. 129, 797–809 (doi:10.1016/S1095-6433(01)00348-8) [DOI] [PubMed] [Google Scholar]
- Croll D. A., Marinovic B., Benson S., Chavez F. P., Black N., Ternullo R., Tershy B. R.2005From wind to whales: trophic links in a coastal upwelling system. Mar. Ecol. Progr. Ser. 289, 117–130 (doi:10.3354/meps289117) [Google Scholar]
- Daniel T. L.1988Forward flapping flight from flexible fins. Can. J. Zool. 66, 630–638 (doi:10.1139/z88-094) [Google Scholar]
- Domenici P.2001The scaling of locomotor performance in predator-prey encounters: from fish to killer whales. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 131, 169–182 (doi:10.1016/S1095-6433(01)00465-2) [DOI] [PubMed] [Google Scholar]
- Fish F. E., Rohr J. J.1999Review of dolphin hydrodynamics and swimming performance. SPAWARS System Center Technical Report, San Diego, CA [Google Scholar]
- Flinn R. D., Trites A. W., Gregr E. J., Perry R. I.2002Diets of fin, sei, and sperm whales in British Columbia: an analysis of commercial whaling records, 1963–1967. Mar. Mamm. Sci. 18, 663–679 (doi:10.1111/j.1748-7692.2002.tb01065.x) [Google Scholar]
- Friedlaender A. S., Lawson G. L., Halpin P. N.2009Evidence of resource partitioning between humpback and minke whales around the western Antarctic Peninsula. Mar. Mamm. Sci. 25, 402–415 (doi:10.1111/j.1748-7692.2008.00263.x) [Google Scholar]
- Gaskin D. E.1982The ecology of whales and dolphins London, UK: Heinemann [Google Scholar]
- Glazier D. S.2008Effects of metabolic level on the body size scaling of metabolic rate in birds and mammals. Proc. R. Soc. B 275, 1405–1410 (doi:10.1098/rspb.2008.0118) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbogen J. A., Calambokidis J., Shadwick R. E., Oleson E. M., McDonald M. A., Hildebrand J. A.2006Kinematics of foraging dives and lunge-feeding in fin whales. J. Exp. Biol. 209, 1231–1244 (doi:10.1242/jeb.02135) [DOI] [PubMed] [Google Scholar]
- Goldbogen J. A., Pyenson N. D., Shadwick R. E.2007Big gulps require high drag for fin whale lunge feeding. Mar. Ecol. Progr. Ser. 349, 289–301 (doi:10.3354/meps07066) [Google Scholar]
- Goldbogen J. A., Calambokidis J., Croll D., Harvey J., Newton K., Oleson E., Schorr G., Shadwick R. E.2008Foraging behavior of humpback whales: kinematic and respiratory patterns suggest a high cost for a lunge. J. Exp. Biol. 211, 3712–3719 (doi:10.1242/jeb.023366) [DOI] [PubMed] [Google Scholar]
- Halsey L. G., Butler P. J., Blackburn T. M.2006A phylogenetic analysis of the allometry of diving. Am. Nat. 167, 276–287 [DOI] [PubMed] [Google Scholar]
- Hone D. W. E., Benton M. J.2005The evolution of large size: how does Cope's rule work? Trends Ecol. Evol. 20, 4–6 (doi:10.1016/j.tree.2004.10.012) [DOI] [PubMed] [Google Scholar]
- Hudson D. M., Jones D. R.1986The influence of body mass on the endurance to restrained submergence in the Pekin duck. J. Exp. Biol. 120, 351–367 [Google Scholar]
- Huxley J.1932Problems of relative growth New York, NY: The Dial Press [Google Scholar]
- Koolstra J. H., Van Eijden T.2004Functional significance of the coupling between head and jaw movements. J. Biomech. 37, 1387–1392 (doi:10.1016/j.jbiomech.2003.12.021) [DOI] [PubMed] [Google Scholar]
- Lambertsen R., Ulrich N., Straley J.1995Frontomandibular stay of Balaenopteridae: a mechanism for momentum recapture during feeding. J. Mammal. 76, 877–899 (doi:10.2307/1382758) [Google Scholar]
- Lasiewski R. C., Calder W. A.1971Preliminary allometric analysis of respiratory variables in resting birds. Resp. Physiol. 11, 152–166 (doi:10.1016/0034-5687(71)90020-X) [DOI] [PubMed] [Google Scholar]
- Lockyer C.1976Body weights of some species of large whales. Ices J. Mar. Sci. 36, 259–273 (doi:10.1093/icesjms/36.3.259) [Google Scholar]
- Lockyer C. H.1981Growth and energy budgets of large baleen whales from the Southern Hemisphere. In Mammals in the seas, vol. 3, pp. 379–487 Rome, Italy: FAO Fish [Google Scholar]
- Lockyer C., Waters T.1986Weights and anatomical measurements of northeastern Atlantic fin (Balaneoptera physalus, Linnaeus) and sei (B. borealis, Lesson) whales. Mar. Mamm. Sci. 2, 169–185 (doi:10.1111/j.1748-7692.1986.tb00039.x) [Google Scholar]
- Lockyer C. H., McConnell C., Waters T. D.1985Body condition in terms of anatomical and biochemical assessment of body fat in North Atlantic fin and sei whales. Can. J. Zool. 63, 2328–2338 [Google Scholar]
- Mackintosh N. A.1942The southern stocks of whalebone whales. Discov. Rep. 22, 197–300 [Google Scholar]
- Mackintosh N. A., Wheeler J. F. G.1929Southern blue and fin whales. Discov. Rep. 1, 257–540 [Google Scholar]
- Matthews L. H.1937The humpback whale, Megaptera nodosa. Discov. Rep. 22, 197–300 [Google Scholar]
- Matthews L. H.1938The sei whale, Balaenoptera borealis. Discov. Rep. 17, 183–290 [Google Scholar]
- McNab B. K.2009Resources and energetics determined dinosaur maximal size. Proc. Natl Acad. Sci. USA 106, 12 184–12 188 (doi:10.1073/pnas.0904000106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murase H., Tamura T., Kiwada H., Fujise Y., Watanabe H., Ohizumi H., Yonezaki S., Okamura H., Kawahara S.2007Prey selection of common minke (Balaenoptera acutorostrata) and Bryde's (Balaenoptera edeni) whales in the western North Pacific in 2000 and 2001. Fish. Oceanogr. 16, 186–201 (doi:10.1111/j.1365-2419.2006.00426.x) [Google Scholar]
- Nishiwaki M., Oye T.1951Biological investigation on blue whales (Balaenoptera musculus) and fin whales (Balaenoptera physalus) caught by the Japanese Antarctic whaling fleets. Sci. Rep. Whales Res. Inst. 5, 91–167 [Google Scholar]
- Oleson E. M., Calambokidis J., Burgess W. C., McDonald M. A., LeDuc C. A., Hildebrand J. A.2007Behavioral context of call production by eastern North Pacific blue whales. Mar. Ecol. Progr. Ser. 330, 269–284 (doi:10.3354/meps330269) [Google Scholar]
- Orton L. S., Brodie P. F.1987Engulfing mechanics of fin whales. Can. J. Zool. 65, 2898–2907 (doi:10.1139/z87-440) [Google Scholar]
- Potvin J., Goldbogen J. A., Shadwick R. E.2009Passive versus active engulfment: verdict from trajectory simulations of lunge-feeding fin whales Balaenoptera physalus. J. R. Soc. Interface 6, 1005–1025 (doi:10.1098/rsif.2008.0492) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiring D. P.1943Weight data on five whales. J. Mammal. 24, 39–45 (doi:10.2307/1374778) [Google Scholar]
- Sebens K. P.1982The limits to indeterminate growth: an optimal size model applied to passive suspension feeders. Ecology 63, 209–222 (doi:10.2307/1937045) [Google Scholar]
- Simon M., Johnson M., Tyack P., Madsen P. T.2009Behaviour and kinematics of continuous ram filtration in bowhead whales (Balaena mysticetus). Proc. R. Soc. B 276, 3819–3828 (doi:10.1098/rspb.2009.1135) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slijper E. J.1979Whales London, UK: Cornell University Press [Google Scholar]
- Tershy B. R.1992Body size, diet, habitat use, and social-behavior of Balaenoptera whales in the Gulf of California. J. Mammal. 73, 477–486 (doi:10.2307/1382013) [Google Scholar]
- True F. W.1904Whalebone whales of the western North Atlantic. Smithson. Contrib. Knowl. 33, 1–332 [Google Scholar]
- Víkingsson G. A., Sigurjónsson J., Gunnlaugsson T.1988On the relationship between weight, length and girth dimensions in fin and sei whales caught off Iceland. Rep. Int. Whaling Comm. 38, 323–326 [Google Scholar]
- Webb P. W., Debuffrenil V.1990Locomotion in the biology of large aquatic vertebrates. Trans. Am. Fish. Soc. 119, 629–641 (doi:10.1577/1548-8659(1990)119<0629:LITBOL>2.3.CO;2) [Google Scholar]
- Werth A. J.2000Feeding in marine mammals. In Feeding: form, function and evolution in tetrapod vertebrates (ed. Schwenk K.), pp. 475–514 New York, NY: Academic Press [Google Scholar]
- Werth A. J.2004Models of hydrodynamic flow in the bowhead whale filter feeding apparatus. J. Exp. Biol. 207, 3569–3580 (doi:10.1242/jeb.01202) [DOI] [PubMed] [Google Scholar]
- Werth A. J.2007Adaptations of the cetacean hyolingual apparatus for aquatic feeding and thermoregulation. Anat. Rec. Adv. Integr. Anat. Evol. Biol. 290, 546–568 (doi:10.1002/ar.20538) [DOI] [PubMed] [Google Scholar]
- Woodward B. L., Winn J. P., Fish F. E.2006Morphological specializations of baleen whales associated with hydrodynamic performance and ecological niche. J. Morphol. 267, 1284–1294 (doi:10.1002/jmor.10474) [DOI] [PubMed] [Google Scholar]
- Zhou M., Dorland R. D.2004Aggregation and vertical migration behavior of Euphausia superba. Deep-Sea Res. Part II Topic. Stud. Oceanogr. 51, 2119–2137 (doi:10.1016/j.dsr2.2004.07.009) [Google Scholar]