Preventable H5N1 avian influenza epidemics in the British poultry industry network exhibit characteristic scales

Abstract

Epidemics are frequently simulated on redundantly wired contact networks, which have many more links between sites than are minimally required to connect all. Consequently, the modelled pathogen can travel numerous alternative routes, complicating effective containment strategies. These networks have moreover been found to exhibit ‘scale-free’ properties and percolation, suggesting resilience to damage. However, realistic H5N1 avian influenza transmission probabilities and containment strategies, here modelled on the British poultry industry network, show that infection dynamics can additionally express characteristic scales. These system-preferred scales constitute small areas within an observed power law distribution that exhibit a lesser slope than the power law itself, indicating a slightly increased relative likelihood. These characteristic scales are here produced by a network-pervading intranet of so-called hotspot sites that propagate large epidemics below the percolation threshold. This intranet is, however, extremely vulnerable; targeted inoculation of a mere 3–6% (depending on incorporated biosecurity measures) of the British poultry industry network prevents large and moderate H5N1 outbreaks completely, offering an order of magnitude improvement over previously advocated strategies affecting the most highly connected ‘hub’ sites. In other words, hotspots and hubs are separate functional entities that do not necessarily coincide, and hotspots can make more effective inoculation targets. Given the ubiquity and relevance of networks (epidemics, Internet, power grids, protein interaction), recognition of this spreading regime elsewhere would suggest a similar disproportionate sensitivity to such surgical interventions.

1. Introduction

The past decade has witnessed a sharp rise in outbreaks of the highly pathogenic H5N1 strain of avian influenza, instigating substantial culling operations, economic damage, human fatalities and fears of a global pandemic. Moreover, disturbing recent field studies have shown that both pre-emptive and reactive large-scale culling of susceptibles produces mixed results at best (Capua & Marangon 2003; Keeling et al. 2003; Stegeman et al. 2004; Capua & Alexander 2006; Menach et al. 2006; Webster et al. 2006); mass vaccination is in some cases impractical (broiler chickens; Truscott et al. 2007) or may exacerbate silent spreading (already a problem in ducks) (Keeling et al. 2003; Kishida et al. 2005; Sturm-Ramirez et al. 2005; Savill et al. 2006); and biosecurity measures (e.g. exclusion, containment, serological monitoring) cannot ensure full protection either (Elbers et al. 2004; Capua & Alexander 2006; Savill et al. 2006). A more fundamental shortcoming of the empirical record is its incompleteness, both in terms of the number of recorded outbreaks (for likelihood estimates) and the specific transmission circumstances for each susceptible. This is where numerical simulation of outbreaks can provide new insights and robust statistics.

In earlier work, Moore & Newman (2000) derived exact solutions for the percolation threshold in simple networks, and stressed the bimodal outbreak response that typifies percolation (ca 5% of susceptibles infected below the threshold, and a giant component of infected sites appearing above it, analogous to a spreading forest fire) (Rhodes & Anderson 1996; Grenfell et al. 2002). Such epidemiological models are part of the larger class of heterogeneous, redundantly wired networks that feature many possible routes between most network nodes, e.g. Internet, social and ecological systems, protein interaction networks, and which exhibit power law statistics (Rhodes & Anderson 1996; Albert et al. 2000; Albert & Barabasi 2002; May 2006). This latter property has led many to conclude that these ‘scale-free’ systems lack characteristic scales altogether, which has important ramifications for prevention and containment. Dybiec et al. (2004) claim that it is impossible to stop epidemics on scale-free networks unless a large proportion of the population is treated. Others offer hope in identifying the most highly connected sites (hubs) as the most vulnerable part of such systems (Albert et al. 2000; Callaway et al. 2000; May & Lloyd 2001; Song et al. 2005; Jeger et al. 2007).

But as simulations mimic complex reality ever more closely, new properties are coming to light. Scale-free networks with non-random mixing (e.g. clustering, degree correlations) have been found to exhibit a phase transition to percolation (Eguíluz & Klemm 2002). Moreover, heterogeneous transmissibility (in the number of links, their distances and their infection probabilities) can broaden this transition from sharp threshold to a separate regime (in our opinion, a highly relevant one) with emergent patchy islands of linked sites, outbreaks of all sizes and intermittent dynamics that invalidate traditional analytical solutions (Bolker & Grenfell 1995; Sander et al. 2002). In addition, past emphasis has frequently been placed on network-architectural properties (e.g. degree distribution, size of the giant component). However, our current study of the dynamics predicated upon a highly realistic network reveals additional features that also merit attention (Kao et al. 2006). This report shows that almost imperceptibly small, but targeted changes in structure may radically alter observed network behaviour (Kao et al. 2007). It also challenges the notion that these systems are scale-free and that targeting hubs is our best defence.

2. Network and simulation properties

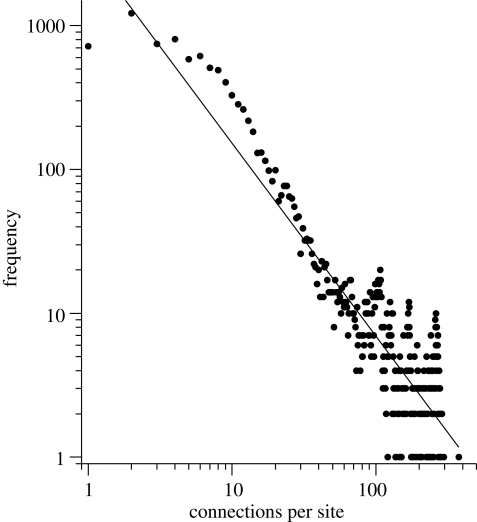
We investigated a suite of six H5N1 avian influenza outbreak models in the British poultry industry (table 1), comprising meat, eggs and game for all eight relevant species on 11 754 premises, 174 slaughter houses and 86 feed mills, based on recent surveys. All models incorporate four different types of transmission: local spread, feed deliveries, abattoir transports and within-company movements (Sharkey et al. 2008). The poultry farms constitute the network nodes; the simulated local spreading plus transport movements of feed, slaughter and company lorries that serve multiple farms comprise about one quarter million (undirected) links between nodes, with specific transmission strengths (table 1). The resulting network is to first order scale-free and highly heterogeneous in connectivity (figure 1). The average number of links is ca 21, but two-thirds of the network has fewer than 10, whereas the top 6 per cent has over 100.

Table 1.

The six types of H5N1 outbreak simulations.

	site-to-site transmissibility
	standard	high	extreme
local spreading rate/day	0.5000	1.000	1.000
slaughter	0.2500	0.500	0.500
feed	0.0625	0.250	0.500
intra-company	0.0156	0.125	0.500
Basic controls	BC	BCHI	BCXT
EU controls	EU	EUHI	EUXT

Figure 1.

Network connectivity. The log–log frequency plot of the number of links per site shows that connectivity is highly heterogeneous and approximates a scale-free distribution.

In addition to standard transmissibilities, simulations with high (HI) and extreme (XT) infection probabilities produced worst-case scenarios (table 1). Although the true likelihoods are still mooted, they likely do not exceed the parameter ranges explored. We furthermore compared a basic control (BC) policy of increased biosecurity, bans on livestock movements and culling upon detection (the latter with species-dependent delays) to the more stringent European Union (EU) controls, which add 3 km protection and 10 km surveillance zones plus dangerous contact-tracing (all sites directly connected to an infected one are treated as if within a protection zone); see electronic supplementary material (Eames & Keeling 2003; Dybiec et al. 2004; Kiss et al. 2005, 2006; Capua & Alexander 2006; Truscott et al. 2007; Sharkey et al. 2008).

Some 50 simulations produced over 40 million individual outbreaks in total. Each outbreak consisted of infecting a randomly selected premise (‘seeding’, probability 1), and recording all subsequent transmissions and status changes of each site, until (i) all sites were virus-free again or (ii) an endemic infection was stopped by timeout (when the maximum allotted time per seeding was reached). The latter situation occurred mostly in high- and extreme-transmissibility simulations, forcing a lower number of seedings (10 000 per simulation, instead of one million for the standard cases). Thus, in BC and EU simulations, each site was seeded about 85 times per simulation; in HI and XT simulations, about once on average. As sites could be reinfected multiple times (becoming susceptible again after each restocking), the outbreak size represents the number of distinct sites that were ever infected during one outbreak.

3. Discrete scale invariance quantifies characteristic scales

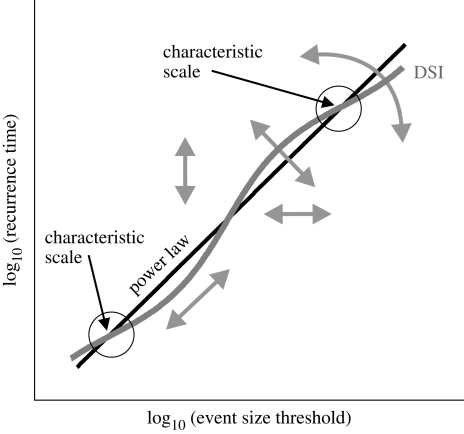
The six main models were analysed in terms of discrete scale invariance (DSI), a feature of many complex systems (Saleur et al. 1996; Johansen & Sornette 1998; Sornette 1998). This statistically stationary signature of preferred scales expresses itself as a log-periodic modulation superposed on a power law probability distribution function (figure 2). In sufficiently large networks, spatial heterogeneity (e.g. in connective topology or transmission probabilities) may create a weak threshold response function (cf. May & Lloyd 2001), causing some small range of outbreak sizes to have a marginally higher likelihood than predicted by a ‘pure’ power law describing all outbreaks. Any such local adjustment to scaling implies that other scales become less likely, yielding an oscillatory pattern along the power law slope; see electronic supplementary material, Sornette (1998) and Jonkers (2007) for the mathematical underpinnings.

Figure 2.

DSI (grey line) modulates a power law probability distribution (black straight line, log–log scale); intersections of the modulation with lesser slope than the power law (circled) identify characteristic scales. Changes in DSI parameter values comprise power law intercept and slope, and phase, amplitude and frequency of the superposed modulation (arrows).

Unless one is aware of DSI's features, it is easy to misinterpret it as a ‘noisy’ power law distribution. Thus, whenever scale-free systems are studied (as in epidemiology), it may be useful to test for the presence of DSI. For an empirical example of apparent (but unacknowledged) DSI in the context of network structure, see Palla et al. (2005, fig. 4b), and in the more relevant context of real epidemics, see Rhodes & Anderson (1996, fig. 1). Apart from providing a new measure with which to compare networks statistically, the presence of DSI in networks implies three relevant epidemiological properties: (i) spreading dynamics operate below the percolation threshold, yet (ii) produce a full spectrum of outbreak sizes, and (iii) large epidemics are extremely vulnerable to targeted inoculation (see below).

We applied a bootstrap technique (Jonkers 2007) to the model-generated sequences of outbreak sizes to quantify their associated recurrence times. This latter quantity expresses the number of outbreaks that on average pass before an epidemic of selected size (or larger) occurs. For example, a recurrence time of 500 implies a likelihood of 0.2 per cent. It is a stationary statistic, affected by network and simulation parameters, but unrelated to seasonality and simulation duration.

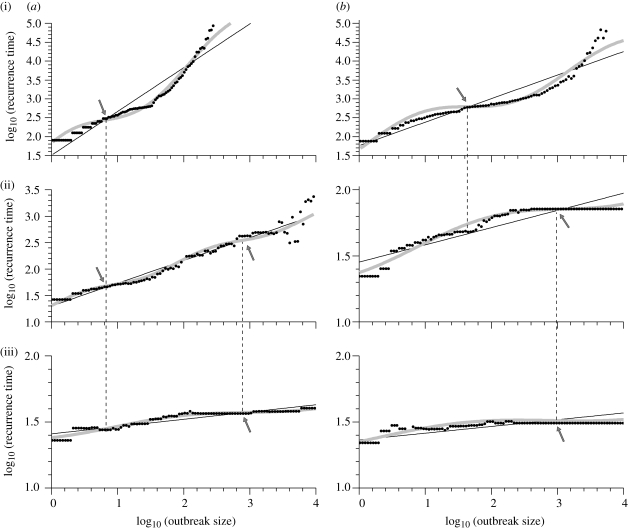
Our H5N1 simulations provide suitable datasets for DSI analysis as their sample size is large, and recorded outbreak sizes and recurrence times each span several orders of magnitude. Figure 3 depicts the resulting log–log plots of minimum outbreak size versus recurrence time, for the six studied models. In all but the most extreme cases, the data not only exhibit a power law but additionally display a clear residual modulation. Characteristic scales are here defined as the coordinates (arrows) where this modulation intersects the power law with a lesser slope than the power law.

Figure 3.

DSI profiles for the British poultry industry network on a log–log scale of minimum outbreak size (initial seeding excluded) versus its typical recurrence time. The best-fitting DSI modulation (grey) is superposed on the pure power law (straight line); black dots represent imposed thresholds in outbreak size; arrows mark characteristic scales for (a) EU and (b) BC controls with (i) normal, (ii) HI and (iii) XT transmissibilities. (a(iii),b(iii)) Smaller power law slopes greatly increase the likelihood of large outbreaks. Dashed vertical lines highlight the continuity of characteristic scales between the three panels of each control strategy. Aspect ratios adjusted for clarity.

By definition, these characteristic scales form a pair; it is the joint profile of a characteristic outbreak size coupled with its characteristic recurrence time that typifies the system. For example, in the EU model, a characteristic outbreak size of ca 10 sites is associated with a typical recurrence time of one in 456 outbreaks, i.e. about 0.2 per cent chance of at least 10 premises becoming infected. This implies that in EU-type models, the range around this particular outbreak size has a slightly higher probability than the first-order approximation of the power law probability distribution of outbreak sizes predicts.

These DSI-derived characteristic scale pairs quantify the severity of the typical outbreaks in each of the different models. For example, the aforementioned EU policy (figure 3a(i)) compares favourably with the equivalent BC strategy (figure 3b(i)), which produces a typical outbreak size of ca 53 sites (over five times larger than EU) coupled with an only slightly longer recurrence time (once per 686 outbreaks). In the worst-case scenario (BCXT), a characteristic outbreak size of 769 premises (nearly 80 times larger than in EU) is associated with a likelihood of about 3 per cent (about 14 times worse than in EU). Overall, these values indicate that increased transmissibility (moving down panels) has a greater effect on aggravating outbreaks than does a weakened biosecurity imposed (moving right from EU to BC).

Moving vertically between panels in either the EU or the BC column of figure 3, the effect of increasing transmissibility can be studied. These comparisons evince how large outbreaks emerge as a new pair of more severe characteristic scales, which gain predominance at the expense of the smaller variety (still vaguely discernable in figure 3a(iii),b(ii)). Thus, the most serious epidemics (figure 3a(iii),b(iii)) do not arise out of a gradual up-scaling of the least harmful ones (figure 3a(i),b(i)), but are a distinct phenomenon that even coexists with the original outbreak distribution in the transitional middle panel (dashed vertical lines between panels mark the continuity of the two distinct statistical signatures). This suggests that containing large epidemics may require a different strategy from one that mitigates small ones.

A final feature of figure 3 is the captured transition to percolation. A related shift is observed in the total distribution of outbreak sizes, which transforms from a power law (in the standard EU and BC models) to a bimodal one for XT simulations (see electronic supplementary material. Thus, in a percolating network like BCXT, viral spread either remains local or becomes network-wide. This state can be reached by reducing biosecurity, increasing transmissibility or both. Another observed shift concerns whether a site likely partakes in many or few outbreaks. These likelihoods become about equal for all sites in the extreme models, whereas the standard cases recover a power law profile (few sites partake in many outbreaks and vice versa). Bootstrap DSI profiles express the network's distance to the percolating state in the power law slope, which decreases from 1.16 in EU and 0.62 in BC (figure 3a(i),b(i)) to below 0.1 in both XT simulations (figure 3a(iii),b(iii)), rendering the concept of characteristic scales less meaningful there. DSI is thus also of potential benefit for determining whether such systems reside in the transitional regime below percolation (Sander et al. 2002). This dangerous regime exhibits a full spectrum of outbreak sizes, but unlike a percolating network, it is acutely vulnerable to targeted countermeasures.

4. Targeted inoculation of specific sites

We explored the effect of inoculating various subsets of sites, i.e. preventing specific sites to pass on infections to others, to determine (i) their role in viral spreading, (ii) necessary and sufficient conditions for large epidemics, and (iii) the most effective countermeasures. Inoculation is here meant in the literal sense of ‘being rendered harmless’. Through which means (vaccination, increased biosecurity or otherwise) this should be achieved is outside the scope of our models and this paper. Furthermore, targeted inoculation was here applied not as a replacement for, but as an addition to, the BC or EU policy, as detection and eradication are deemed indispensable for effective outbreak containment (Lee & Suarez 2005).

Following existing advice (Albert et al. 2000; Song et al. 2005; Jeger et al. 2007; Dent et al. 2008), we focused first on hubs; all other sites we call peripherals. We define hubs here as having at least 40 links to other sites, thereby selecting the top 10.2 per cent of sites when ordered by connectivity. Figure 4a shows the profile of one million outbreak sizes shifting proportionally leftward when all 1195 hubs are inoculated, under BC and EU controls, respectively. Although this strategy works moderately well, we can do far better, as figure 4b demonstrates. Here, we target network hotspots, which we defined as those sites participating in the greatest number of (i) outbreaks, or (ii) viral transmissions or (iii) that have largest characteristic outbreak scales; all three definitions yield largely overlapping subsets and similar results.

Figure 4.

The number of H5N1 avian influenza outbreaks that exceed a given outbreak size in the British poultry industry, for European (EU, grey) and basic containment controls (BC, black), before (solid lines) and after (dotted lines) targeted inoculation. (a) Disabling transmissions from the 1195 network hubs (sites with 40+ connections) yields moderate, proportional improvements. (b) Inoculating network hotspots (325 sites under EU controls, 669 under BC) prevents large and medium-sized outbreaks altogether. Sample size: one million outbreaks per simulation.

Surprisingly, most hotspots are peripherals. Moreover, the reduction under BC in figure 4 is achieved by inoculating 669 hotspots only (5.7% of the network), whereas the target set for EU comprises a mere 325 sites (2.8%). Both subsets are thus considerably smaller than the number of hubs, yet targeting hotspots substantially outperforms hubs in reducing large epidemics. Moreover, the resulting outbreak distribution appears to be an absolute lower bound. Much larger subsets of targets yield a virtually identical profile, suggesting that only massive interventions would prevent these modest outbreaks.

Our ongoing investigations of several different networks focus on discovering what peculiar features distinguish hotspots from ordinary sites, so as to enable practical a priori hotspot recognition in future (unlike the a posteriori methods described above). Interestingly, the presence of long-distance links is neither a necessary nor a sufficient condition for hotspot formation in our models. Instead, hotspots tend to associate spatially (over short distances) to span large areas in thin strands, and, crucially, share many mutual contacts with other hotspots that extend this overlap network-wide (Newman 2003; Palla et al. 2005). This structure provides multiple paths between many local clusters of linked sites that are otherwise poorly connected (compare human-imposed firewalls to prevent percolation, or natural firewalls comprising bands of immune sites as in Sander et al. 2002).

This property of ‘connecting up the network’ has previously been identified by Kao et al. (2007), but in our interpretation, hotspots function as a single collective rather than as numerous individual bridges. To test this assumption, we ran EU and BC simulations in which only local and intra-company transmissions between hotspots were prevented, whereas their feed and abattoir associations were redistributed to minimize intra-hotspot contacts. This rewiring strategy proved just as effective as inhibiting all outward hotspot transmissions. In a second test, we merely rewired feed and abattoir hotspot links without inhibiting any transmission, yet a significant reduction in outbreaks was still achieved (see electronic supplementary material). Contrastingly, targeting up to 100 hotspots has hardly any beneficial effect. This underlines our main conclusions that hotspots are functionally distinct from hubs, constitute a collective network-wide entity and can make more (cost-)effective inoculation targets.