Analysis of a complete DNA–protein affinity landscape

Abstract

Properties of biological fitness landscapes are of interest to a wide sector of the life sciences, from ecology to genetics to synthetic biology. For biomolecular fitness landscapes, the information we currently possess comes primarily from two sources: sparse samples obtained from directed evolution experiments; and more fine-grained but less authentic information from ‘in silico’ models (such as NK-landscapes). Here we present the entire protein-binding profile of all variants of a nucleic acid oligomer 10 bases in length, which we have obtained experimentally by a series of highly parallel on-chip assays. The resulting complete landscape of sequence-binding pairs, comprising more than one million binding measurements in duplicate, has been analysed statistically using a number of metrics commonly applied to synthetic landscapes. These metrics show that the landscape is rugged, with many local optima, and that this arises from a combination of experimental variation and the natural structural properties of the oligonucleotides.

1. Introduction

The concept of the fitness landscape or adaptive landscape was first developed as a metaphor by Wright in 1932 to describe in geographical terms the relationship between genotype and phenotype (Wright 1932). Since then, fitness landscapes have become an integral part of both evolutionary biology and evolutionary computation. Though often overly simplistic in representation (conventionally two- or three-dimensional plots), fitness landscapes have become crucial in terms of our understanding of how an evolving population will behave relative to a static fitness function. The fitness function itself describes a property which will dictate selection; this could plausibly be enzyme activity or specificity in the case of protein evolution, or a measure of drag in the design of airfoils in a ‘real life’ evolutionary optimization problem (Shahrokhi & Jahangirian 2007). Commonly, the evolving population is envisaged as a single hill-climber; an algorithm which crosses the landscape by accepting only genetic modifications (single-point mutations) that result in an improvement in fitness (Kauffman & Levin 1987). How well the hill-climber performs is strongly dictated by the topology of the landscape. If the landscape is rugged it will become trapped at local optima, whereas if the landscape is a ‘Mount Fuji’ type of peak with a smooth ascent, the hill-climber can progress to the global optimum unimpeded.

Despite the origins of fitness landscapes lying in biological evolution and the wealth of literature describing, theoretically, the evolution of biological macromolecules, little is actually known about the properties of real biological fitness landscapes. With the absence of these data, investigations on landscape properties have been based predominantly on model systems such as spin glasses, NK-landscapes (Kauffman & Levin 1987) and perhaps the more biologically pertinent RNA models (Schuster et al. 1994). Less associated (but equally applicable) with biological fitness landscapes are landscape studies considering combinatorial chemical space (Stadler & Stadler 2002), where rules associated with neighbourhood and fitness can be directly applied to guiding chemical synthesis. While mapping the entire sequence space of an average protein is intractable owing to the ‘hyper-astronomical’ number of variants (Voigt et al. 2000), even limited sampling of the sequence space has previously been prohibitive because of the cost of DNA sequencing and (especially) of synthesis. With advances in sequencing technology this is no longer the case, and we can now begin to fully appreciate the diversity displayed by many biological fitness landscapes (Poelwijk et al. 2007).

The sampling of sequences from biological fitness landscapes has often gone hand-in-hand with the family of methods known as directed evolution (Voigt et al. 2000; Poelwijk et al. 2007). The procedure works by iteratively modifying, selecting and amplifying biological macromolecules to induce phenotypic improvements. In this manner the repertoires of existing enzymes have been expanded and de novo biomolecules have been generated. Aptamers are oligonucleotides raised to have high affinity and specificity to both small molecular and large biomolecular targets. Conventionally, aptamers are developed through the technique known as SELEX (Ellington & Szostak 1990; Tuerk & Gold 1990), where sequences with high affinity to a target are enriched iteratively from a vast library of variants (up to 10¹⁶ oligonucleotides). To study the sequence-binding relationships of the aptamers generated, usually only those with the highest affinity (often from each generation of the process) are selected and sequenced. Apart from the expense of the sequencing process, this technique is limited when studying the sequence-fitness landscape as (i) one has no a priori choice of the sequences and (ii) information is generally gained solely on the best aptamers.

In contrast to this, a recent paper by Knight et al. developed aptamers to the fluorescent protein allophycocyanin (APC) on high-density DNA microarrays, by optimizing affinity using an evolutionary algorithm (Knight et al. 2009), the so-called CLADE (closed-loop aptamer-directed evolution) method. As a consequence of using the ‘on-chip’ procedure, the sequence-fitness relationships of over 40 000 aptamers were determined during the optimization process. From these data, the authors were able to construct a detailed structure–activity relationship model, which related aptamer sequence to binding affinity with a high level of accuracy and with considerable predictive power. The microarray platform is particularly suited to the study of DNA–protein interactions because of its ability to perform highly parallelized analyses. Such have been the advances in microarray technology in terms of cost and feature size that it is possible to probe vast regions of the DNA sequence space systematically and impartially. This ethos was exhibited in a study by Warren et al. where the interaction profiles of a transcription factor and a small molecule were determined with every permutation of a duplex DNA sequence 8 bp in length (Warren et al. 2006).

In the CLADE system described above, the binding affinity of the APC aptamer is strongly dictated by the bases furthest away from the microarray chip surface (Knight et al. 2009). If these bases are determinant of protein binding, it is feasible that an attenuated aptamer will be as effective as the longer aptamers. In this study we interrogate the entire sequence recognition profile of a shortened (10 base) APC aptamer. The results from this shortened biomolecule may be just as informative as their longer counterparts; bigger is by no means better in the nucleic acid world, where the specificity afforded by short transcription factor-binding sites governs transcriptional regulation and small hairpins termed ‘tetraloops’ form the essential building blocks of much larger RNA structures (Woese et al. 1990). We study the properties of the fitness landscape generated from every 10-base variant using metrics conventionally applied to artificial fitness landscapes. The implications of these results for the evolution of biomolecules generally and in the case of directed evolution are discussed. To arrive at these predictions we go beyond the raw statistics describing topology and consider how an evolving population will interact with the landscape.

2. Material and methods

Detailed descriptions of chemicals and chip synthesis can be found elsewhere (Knight et al. 2009). Briefly, each microarray chip possessed 93 311 individual spots at each of which a known DNA sequence was synthesized in situ. Initially, 93 311 sequences were chosen at random from the starting population size of 4¹⁰ and synthesized onto two replicate chips. Each replicate chip consisted of the same sequences randomized spatially. The chips were hybridized with the target protein APC, in 1×phosphate-buffered saline (pH 5.5) for 1 h at 37°C, imaged and analysed as described previously (Knight et al. 2009). The mean scores across both chips were taken as the overall binding scores. From these chips, 500 sequences were selected uniformly from the range of binding scores. These 500 sequences were then synthesized onto all remaining chips to permit cross-chip normalization. Each subsequent chip therefore contained 500 controls and 92 811 new sequences, all of which were synthesized and hybridized in duplicate. The entire sequence space required just over 11 pairs of duplicate chips, plus a twelfth pair of chips with 27 655 sequences. The remaining 65 656 spots on the final pair of chips were used to re-synthesize any sequences that had been corrupted, had high standard deviations between chips or scored highly.

Reproducibility between chips was high with a correlation between duplicate sequences of 0.88. Normalization was performed across the whole population using the control sequences present on all chips using JMP software and univariate analysis to match the score distributions. This resulted in all sequences being fitted to the same overall scale to allow direct comparison. These normalized scores serve as direct measures of protein-binding affinity upon which further statistical analysis was based.

3. Results

3.1. Shortening allophycocyanin aptamers

In the study by Knight et al. (2009) into the development of APC aptamers, no form of secondary structure was established to be causal to protein binding (Knight et al. 2009). Binding was believed to be primarily influenced by three bases at the start of the 5′-end of the aptamer sequence in combination with a motif composed principally of cytosine residues further down the chain.

Mapping the complete sequence space of the 30-mer APC aptamer is intractable, as synthesizing 4³⁰ sequences using the Combimatrix technology would take approximately 3.7 billion years (without replicates); a full 10-mer landscape in contrast requires only twenty-four 90K chips (as described in §2). However, simply deleting bases from the 3′-end of the aptamer may have catastrophic unforeseen effects on aptamer binding, due to the complex combinatorial nature of nucleic acid structural interactions. In addition, shortening the aptamer reduces the distance of the binding region from the microarray surface. This has previously been shown to have a negative effect on efficiency in binding assays (Day et al. 1991). To counteract this effect poly-T linkers are commonly used to project the binding sequence away from the chip surface to enhance binding efficiency with minimum effects on binding mechanism (Day et al. 1991).

To ascertain the consequences of attenuating the 30-mer APC aptamers, we used the binding scores of the top 3000 sequences obtained from the penultimate generation of the APC aptamer evolution (Knight et al. 2009) as a benchmark. These scores were compared with the binding scores of the abridged sequences containing only the first 10 bases of each aptamer. In addition, a poly-T linker five bases in length was added to the 3′-end of each aptamer to elevate the shortened sequences from the chip surface. There is a correlation coefficient of 0.73 between the original sequences and their shortened counterparts, indicating that the binding is primarily determined by the first few bases of the aptamer chain. While the abridged sequences do not correlate completely with the 30-mers, the result indicates that these sequences retain most of the binding characteristics of their longer equivalents.

The dissociation constant of the strongest binding 10-mer sequence was measured on an independent platform using surface plasmon resonance (see electronic supplementary material for further details). The observed K_d of 1.88 µM was lower than that of the 30-mer aptamer. Despite this we have seen through the correlation between the 10-mer and 30-mer results that there is strong sequence-dependence on binding. The shortened sequences are not in the strictest sense aptamers (we also present no information on the specificity of these sequences). However, the relationship between sequence and binding and the possible effects of structure warrant further investigation.

3.2. Visualizing the fitness landscape

Simply listing all possible base sequence-affinity combinations in the sequence space of our 10-mer landscape reveals little about its overall or higher level properties. Visualizing the data is hard because, unlike the spatial physical world, nucleic acid sequence space exists in many dimensions and condensing this information into a form that is interpretable by humans is beset with difficulties. Dimensionality reduction techniques such as multidimensional scaling and PCA cannot be usefully applied to the landscape since the points in 10-dimensional aptamer space cannot possibly lie on a hidden, lower-dimensional manifold as the space is completely filled by them, i.e. every point in the 10-dimensional space is represented. Wright himself was aware of the inadequacies of representing high dimensional data using two-dimensional plots and forcing the data to appear as a classic landscape plot can often cause misinterpretations (Wright 1932). In many ways it is better to extract more general features of the landscape than attempting to display the landscape as a whole.

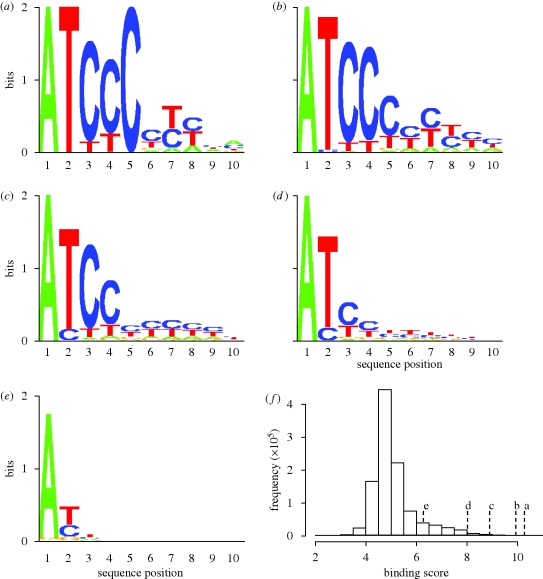
Figure 1 displays the logos of the sequences with the highest binding affinities, indicating the striking dependency of protein binding on the first few residues of the 10-mer. Particularly prevalent is the retention of adenine at the first position of the 5′-end of the sequence, exemplified by its presence within every sequence of the top 10 000 binders. Of note is that in each instance, with the exception of the top 10 binders, there appears to be a general decay in the conservation of bases from the 5′- to 3′-ends, which would seem to suggest that the bases at the 3′-end are less important in their interaction with the protein. This decay is most likely a result of the 3′-bases being closer to the array surface, which will no doubt inhibit interaction with the protein. Clear from the histogram shown in figure 1f is the smooth single distribution in terms of binding affinities, rather than, for instance, partitioning of good and bad binders.

Figure 1.

Sequence logos indicating information content (a measure of statistical entropy) at each of the 10 positions of the aptamer for the (a) top 10, (b) top 100, (c) top 1000, (d) top 10 000 and (e) top 100 000 sequences in terms of binding affinity. (f) Histogram of binding scores and points in the distribution for each of the sequence logos.

3.3. Landscape statistics

In the evolutionary optimization field, fitness landscapes have been studied for many years as a means to understand relationships between optimization problem properties and the success/failure of evolutionary algorithms in finding and maintaining global optima. Epistasis, ruggedness, multimodality and noise all have their effects on an evolutionary algorithm's ability to locate a global optimum. There are now a wealth of metrics to describe these fitness landscape properties (Kallel et al. 2001), though they have usually been applied on artificially generated landscapes, or the landscapes arising from optimization problems defined by mathematical or algorithmic structures. Here, we apply a number of these metrics to a real oligonucleotide landscape. In order to place our findings within the context of earlier research, we compare them with results obtained using the most commonly used class of artificial landscapes for discrete optimization, the NK-landscape.

3.4. The NK-model

The NK-model was first proposed by Kauffman to incorporate interactions between component bits in the binary string (alleles and chromosome in evolutionary computing parlance; Kauffman & Levin 1987; Kauffman 1993) giving rise to landscapes that are tuneable in terms of epistasis and ruggedness. This model can be used to describe the epistatic nature of gene interactions on an individual's fitness, or equally the coupling interactions between amino acids in a protein molecule (Kauffman 1993). The total fitness F of the individual in the NK-model arises from the average fitness of all the positions in the chromosome f_i

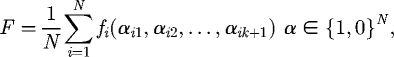3.1

where i is the residue assessed and α_in are the states (1 or 0) of the K+1-coupled residues. When K is zero, the landscape is additive; that is the fitness function is the sum of the independent contributions of each position; this results in a single peak landscape that is easy for a hill-climber to traverse. With increasing values of K, the landscape becomes more rugged resulting in many local optima (Li et al. 2006), making it progressively more difficult to reach the global optimum (Kauffman 1993).

When K reaches its maximum value of N − 1, the landscape is maximally uncorrelated; in fact there is no correlation between neighbouring sequences at all. Here, the NK-model is mimicking a random energy model. The presence of local optima is not an indication of a correlated fitness landscape on its own; even uncorrelated fitness landscapes (where K = N−1), in which fitness is assigned to each individual randomly, are crowded with local optima. Such random energy models have been described by Derrida where the number of local optima is given by the expression 2^N/(N + 1) (Derrida 1981). Generalization to L-ary NK-landscapes yields an expected number of local optima of L^N/[N(L − 1)+1] (Li et al. 2006). These landscapes are far more rugged than those observed in real-world problems, where even landscapes with high levels of noise usually demonstrate an underlying correlation between neighbouring sequences.

The NK-model is useful in the study of fitness landscapes in that its tuneable nature allows practitioners to use NK-landscapes as mimics for more complex systems (Baskaran et al. 1996). The prediction of RNA secondary structure is for instance far more costly in terms of time than the appraisal of fitness in an NK-landscape. Reciprocally, NK-landscapes are systems that have well-established properties that provide a benchmark against which new landscapes can be evaluated (Kauffman & Weinberger 1989). We compare the properties of our 10-mer landscape to those of a series of quaternary NK-landscapes, where α ∈ {3, 2, 1, 0}^N, i.e. there are four alleles at each locus of the chromosome. Quaternary NK-landscapes are employed as they resemble more closely the quaternary nature of the DNA bases within the oligonucleotide sequence, even though they are not commonly applied in the evolutionary literature.

The noise inherent to the experimentally derived data means that direct comparison with noise-free evaluations from the NK-landscapes is not appropriate. Metrics such as autocorrelation will become artificially foreshortened by the presence of experimental variance implying a closer resemblance to NK-landscapes with higher values of K. To provide a more accurate assessment, we attempt to reproduce the level and distribution of noise observed within our experimental landscapes based on the discrepancies observed between replicate chips. Replicating the effect of noise is not necessarily a straightforward task as the NK-landscapes and the oligonucleotide landscape have a differently shaped score distribution. The variation between replicates on different chips has a mean value of 0.38, a median of 0.27 and an s.d. of 0.36, with an apparent double exponential distribution (see electronic supplementary material). The first step is therefore to normalize the score distribution of each of the values observed within the NK-landscapes, so that the mean and the variance are equal to those observed in the experimental evaluations (based on the absolute binding scores). Noise was then added randomly to two instances of each point in the NK-landscape such that the distribution matched that observed in the oligonucleotide landscape (see electronic supplementary material). The mean was then taken for the two points as a measure of absolute score. Evaluations were based on 50 different instances of each NK-landscape.

3.5. Autocorrelation function and correlation length

Fitness landscapes are not defined merely by the fitness function but by the relationship between this function and a neighbourhood defined on the search space. For continuous spaces, the neighbourhood can be defined by the Euclidean metric; for discrete spaces the definition of neighbourhood is often specific to the problem or algorithm under investigation. In sequence analysis, the Hamming distance is a metric describing the minimum number of point mutations required to transform one sequence into another sequence of equal length (Hamming 1950). The Hamming distance is integral to the way in which we perceive fitness landscapes. The relationship between sequence similarity and the fitness associated with each sequence determines the properties of the landscapes.

The correlation length of a fitness landscape is a measure of its ruggedness (Weinberger 1990). In order to infer a fitness landscape from the measured fitness levels, we assume a simple Hamming neighbourhood. Walks on the landscape consist of a series of Hamming point mutations in which one base is selected uniformly at random and changed at random to one of the other three bases.

The autocorrelation function is a measure of the correlation of a function with itself. In the case of a landscape, it is the expected correlation between points on the landscape at a distance of s, during a random walk 〈x⁰, x¹, … 〉 on the landscape, calculated as

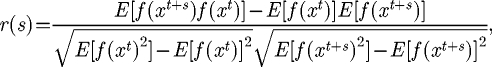3.2

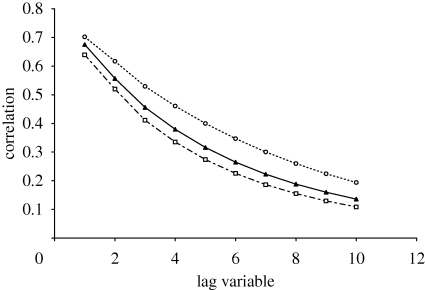
where the expectations E are taken over the random walk. In order to calculate the expectations, 30 independent random walks were performed from each point in the landscape, giving rise to approximately 30 million fitness pairs, f(x^t) and f(x^t+s), for each s. A plot of the autocorrelation for the 10-mer landscape is shown in figure 2. We calculated the autocorrelation function for our oligonucleotide landscape and a series of quaternary NK-models of length N = 10 with varying values of K. For the 10-mer landscape, the correlation falls off approximately as r(s) = exp (−s/τ), where τ is the correlation length. From the plot in figure 2, we can estimate the correlation length for the 10-mer landscape as 4.5. This indicates that the experimentally derived landscape is equivalent to an NK-landscape where K is slightly less than 1 (table 1).

Figure 2.

Displaying level of autocorrelation with increasing step number in a random walk (in terms of Hamming point mutations) for the 10-mer landscape and NK-landscapes where N = 10. Open circles with a broken line denote NK-landscape where K = 0. Filled triangles with a continuous line denote experimental (point mutation). Open squares with a broken line denote NK-landscape where K = 1.

Table 1.

Correlation lengths for NK-landscapes where N = 10.

K	correlation length
0	5.5
1	4
2	3
3	2

There is no consensus as to how to use this information, but there is a common consensus that the more rugged a landscape, the more local optima there are (Kallel et al. 2001). Here, we observe moderately high ruggedness and a small correlation length (roughly equivalent to a noise-free NK-model with K = 1). It has been suggested (Kallel et al. 2001) that mutation rates of an evolutionary algorithm should be set so that mainly points within the correlation length are reached.

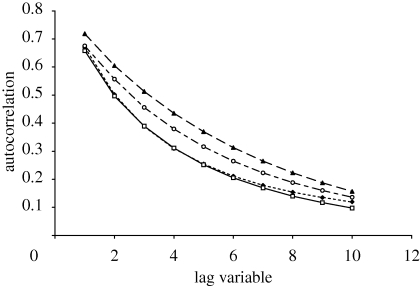
The correlation length is affected by the choice of genetic operator used in evolutionary algorithm optimization. Calculating the correlation length using a Hamming neighbourhood is the appropriate method for point mutation, since each mutation takes a single step within this neighbourhood. Random walks using alternative genetic operators take different types of step and therefore have different neighbourhoods. Figure 3 shows the autocorrelation curves for the point mutation and for three other types of genetic operator: a transposition of any two bases, an insertion of a random base (with all others being shifted right and a deletion at the 3′-end to maintain length), and an insertion–deletion (indel) event. The correlation lengths under these different move sets are estimated as: point mutation = 4.5, transposition = 4.0, insertion = 5.0 and indel = 3.5. The cause of this variation is most likely attributable to the number of base changes caused by each genetic event and the likelihood that these events would disrupt the bases at the 5′-end of the oligonucleotide sequence. For example, indel has the lowest correlation because two or more bases are changed in a single instance; however, insertion has a higher correlation because most alterations are at the 3′-end.

Figure 3.

Displaying level of autocorrelation within the 10-mer landscape with increasing step number in a random walk, for different genetic operators. Filled triangles with a broken line denote insertion. Filled diamonds with a broken line denote transposition. Open squares with a continuous line denote indels.

3.6. Epistasis

In standard population genetics models, each allele is considered to make a contribution to fitness against a background of other alleles, all contributing independently. This model is inadequate when genes interact. Epistasis is a measure of the degree of interaction of the genes: it measures the nonlinearity in a fitness function.

Reeves & Wright (1995) measure the epistasis, η, following Davidor (1991), using the following equation:

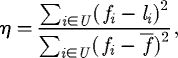3.3

where f_i is the fitness of chromosome i, l_i the sum total contribution to f_i of the chromosome's alleles (their linear effects or contributions) and 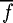the mean fitness over all chromosomes in the chromosome space U (i.e. (A, C, G, T)^L). This gives a value between 0 and 1, which can be interpreted as the amount of variance in fitness that is explained by nonlinear effects. To calculate l_i, the individual effect of an allele is first calculated by measuring the mean fitness of all chromosomes having that allele and subtracting the mean fitness over all chromosomes. The value l_i is then calculated as the sum of these allelic contributions over the alleles in the chromosome i, added to 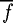. The value of epistasis measured over the 10-mer landscape is 0.532, a value indicating that the genes (i.e. in our case the individual base positions) interact quite strongly. This figure is roughly equivalent to a noisy quaternary NK-landscape where K is slightly less than 1 (table 2).

Table 2.

Relationship between K and the measure of epistasis for an NK-model where N = 10.

K	epistatic variance
0	0.19021
1	0.667056
2	0.890371
3	0.960332

3.7. Optimization on an oligonuleotide landscape

Because of the comprehensive nature of the 10-mer landscape we are not confined to making assumptions about its properties based purely on statistical measures from sampling. It is thus possible to enumerate each of the sequences and determine those that represent local optima. This can be accomplished using a ‘steepest ascent hill-climber’ (Kauffman & Levin 1987) which, starting from a sequence x, considers all the Hamming neighbours of x and moves to the fittest one, repeating this procedure until there is no neighbour fitter than the current sequence. By starting the hill-climber at every sequence, we can not only determine the number of local optima and their properties, but also the points in the landscape that are attracted to each optimum. These so-called ‘basins of attraction’ are useful in characterizing local optima. We are interested in how they will affect genetic algorithm performance and how likely they are to have arisen purely from noise.

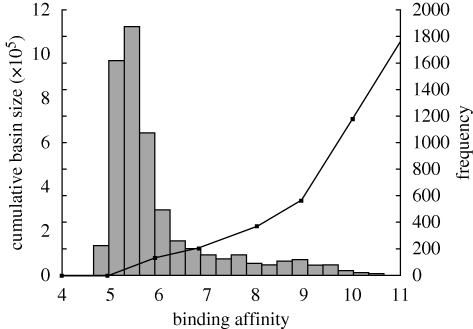
This hill-climber reveals 6805 local optima within the complete sequence landscape. Quantitative assessment of this figure relative to the noisy NK-landscapes is difficult to obtain. However, there is a smooth decline in the mean maximum basin sizes observed with increasing values of K (see electronic supplementary material for a summary of these data). Within the experimental landscape, the size of the basins of attraction varies considerably, from one associated sequence to nearly 30 000. From the histogram shown in figure 4 displaying the distribution of binding affinities of the local optima and the overlaid plot of cumulative basin size, there is a definite (negative) correlation between peak height and basin size. The maximum basin size corresponds most closely to that observed for an NK-landscape where K = 0. Theory dictates that landscapes with many inferior local optima with small basins of attraction will be hard for a genetic algorithm to optimize, especially if the global optimum also has a small basin of attraction. In the 10-mer landscape, the local optima are far from evenly distributed, with the top 1 per cent of local optima (68 sequences) containing 47 per cent of sequences from the landscape within their basins of attraction.

Figure 4.

Histogram of distribution of binding affinities of local optima (frequency), with overlaid plot of cumulative number of individuals associated with these local optima from the total landscape (cumulative basin size).

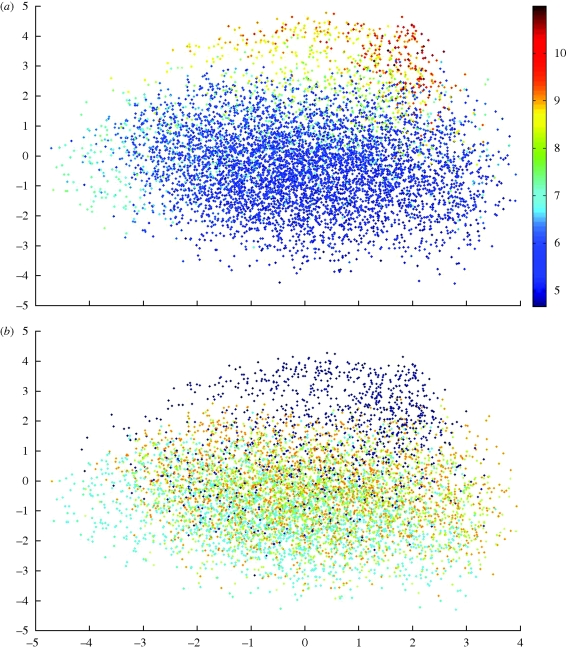
The diameter of the basins of attraction gives an indication of how the local optima are dispersed within the sequence landscape. We take the diameter as the Hamming distance from each local optimum to the most dissimilar sequence within the set of local optima. From table 3, it can be seen that the diameters for all local optima are maximally dissimilar (a Hamming distance of 10). When the set of local optima are reduced to the top 10 and 1 per cent in terms of binding affinity, they become progressively more localized. This localization of high-affinity optima can be visualized in the classical multidimensional scaling plot shown in figure 5a. From the plot in figure 5b it can be seen that these clustered sequences generally possess adenine as the first base at the 5′-end.

Table 3.

Summary of properties of the local optima within the 10-mer landscape.

	min.	first quartile	median	mean	third quartile	max.
individuals associated with each basin	1	10	19	154.1	39	29 974
maximum diameter between each local optimum	10	10	10	10	10	10
maximum diameter between top 10 per cent of local optima	9	9	10	9.54	10	10
maximum diameter between top 1 per cent of local optima	6	7	8	7.559	8	9
distance from every sequence to local optima	0	3	4	4.101	5	10

Figure 5.

Classical multidimensional scaling plot displaying points of local optimum in a two-dimensional projection of sequence space. Plot (a) colours each point by binding affinity; plot (b) is the same with the colour determined by the first base of the sequence. A, dark blue; G, light blue; C, green; T, red.

The landscape presented here represents a static image in terms of noise. In reality, many of these points of optima will shift owing to experimental variance with continued resampling and so will not present permanent fitness barriers to a population evolving on the landscape. If one were wishing to replicate the performance of a hill-climbing algorithm on the real landscape it may be necessary to continually resample each point with added stochastic variance equal to that observed in the real landscape.

3.8. Fitness distance correlation

The fitness distance correlation (FDC) is a measure of search difficulty, which can be used to predict genetic algorithm performance (Jones & Forrest 1995). While there have been criticisms of the FDC from a theoretical point of view (Altenberg 1997), it has practical utility when comparing classes of problems with common features. The FDC is a simple statistic describing the correlation between the fitness function and the distance to the nearest goal of the search. When available, this point is taken as the global optimum and the sequence distance is usually the Hamming distance. For optimization problems where the objective is to maximize the fitness function, easy problems have a negative FDC (approaching −1). With increasing problem difficulty, the FDC rises until it reaches 1 for completely deceptive problems. The FDC for the experimental landscape is −0.32. This equates roughly with our simulations on a quaternary NK-landscape, where N = 10 and K is slightly less than 1 (table 4).

Table 4.

Relationship between K and the fitness distance correlation for an NK-model where N = 10.

K	FDC
0	−0.4444
1	−0.18721
2	−0.05335
3	−0.01497

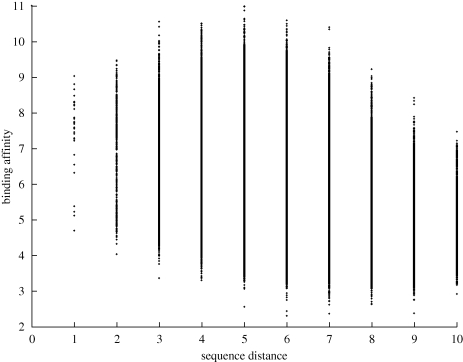
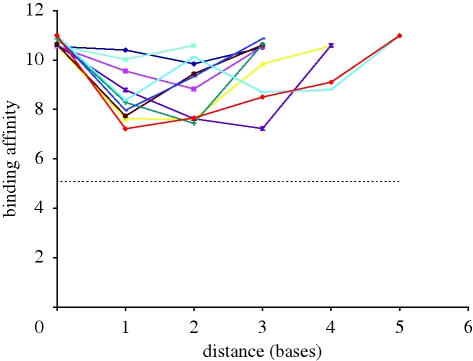
Correlation is used as a simple metric but there is much to be gained by analysing a scatter-plot of sequence and fitness distances. The most striking feature of the scatter-plot shown in figure 6 is the drop in binding affinities exhibited by sequences with a high level of similarity with the global optimum; the sequence with the next highest binding affinity shares only five common bases with the global optimum. To ascertain whether such a feature is indicative of a highly rugged landscape or merely an anomalous global optimum (owing to experimental variance), we studied ‘directed walks’ between the next 10 highest local optima in terms of binding affinity. This entailed iteratively mutating each optimum so that the sequence of the next highest local optimum was produced. (The order in which the non-coincident bases were changed was randomly chosen in each instance.) Figure 7 shows a plot of the paths between each of the 11 highest local optima. It may be noted from this plot that these sequences are more closely related than random. However, there can be as many as five dissimilar bases between sequences. The binding affinities of the intermediate sequences on these ‘walks’ can drop considerably, although they are still much higher than the mean of all the sequences within the landscape.

Figure 6.

Scatter-plot displaying the relationship between Hamming distance from the strongest binder and binding score for the 10-mer landscape.

Figure 7.

Stepwise mutagenesis between local optima. Journeys are from each of the best 11 local optima and the next best local optimum in terms of binding affinity. Violet, point 10→point 11; pink, point 9→point 10; yellow, point 8→point 9; turquoise, point 7→point 8; magenta, point 6→point 7; brown, point 5→point 6; light green, point 4→point 5; dark blue, point 3→point 4; light blue, point 3→point 3; red, point 1→point 2; dotted line denotes mean score.

3.9. Separability

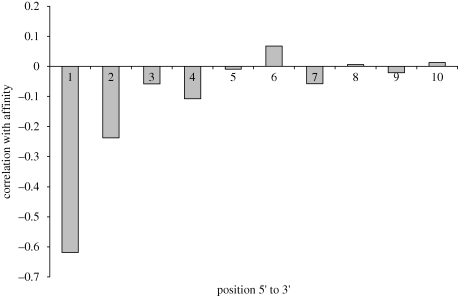
Within a sequence, the identity of bases at a particular position may have a stronger effect on overall fitness than the identity of bases at other positions. Figure 8 shows a plot of the separability of each base, that is how each base within the best sequence correlates with the fitness function. Again this plot demonstrates that the bases at the 5′-end correlate more strongly with fitness than do those at the 3′-end.

Figure 8.

Correlation between sequence position and score.

3.10. The effect of noise

The existence of noise within the measured affinities is a source of ruggedness which affects all of the statistics reported in this section. By using NK-models it is possible to assess the extent to which observed ruggedness arises from noise rather than ‘real’ biochemical interactions. Table 5 shows the correlation lengths, epistatic variances and FDC values for noise-free NK-landscapes. The difference between the values of these statistics for noise-free and noisy landscapes is small. When using noisy models, all three statistics suggest that the measured landscape is equivalent to an NK-landscape with K between 0 and 1. The statistics obtained from noise-free models are very similar, suggesting K values of 1 (autocorrelation), between 0 and 1 (epistatic variance) and just below 2 (FDC). The similarity in the predictions from noisy and noise-free models indicates that the level of noise in the measured data is low and only interferes with the observed interactions to a limited extent.

Table 5.

Landscape statistics for noise-free NK-landscapes with N = 10.

K	correlation length	epistatic variance	fitness distance correlation
0	7	0.0	−0.695058
1	4.5	0.372188	−0.258208
2	3	0.562138	−0.087372
3	2.5	0.746588	−0.036625

Noise is observed to have a strong effect on basins of attraction, by creating a large number of local optima. For example, noisy NK-landscapes with K = 1 have 8662 local optima, on average, while their noise-free equivalents have just 32 local optima, on average. This implies that optimization methods that rely on hill-climbing will be strongly (and adversely) affected by the presence of noise at the level observed here.

3.11. Structure

Underlying each of the metrics that describe the properties of the landscape is the physical interaction between the oligonucleotide and the protein. It was postulated by Knight et al. that the APC aptamers evolved on the array surface adopt structures free from duplex formation (Knight et al. 2009). They found that affinity was highly dependent on the identity of bases at the 5′ sequence end, which would be pointed towards the chip if the chain adopted a hairpin configuration. In addition, no correlation was found between minimum free energy sub-structures and binding affinity.

Mutual information is a measure of the covariance between positions in a sequence and is commonly used to determine the common structure within a group of related DNA motifs. When the level of mutual information was calculated for the top 100 binding sequences, no significant covariance was found (although this may be a result of invariance in many of the positions). Similarly, the DNA folding algorithm hybrid-ss-min (Dimitrov & Zuker 2004) could not predict minimum free energy structures for 82 of these top 100 sequences that began with the bases ‘ATC’. This figure is in contrast to only 14 sequences without predicted structure from the bottom 100 binders that begin with ‘ATC’ (these sequences all had binding affinities within the bottom third of those found within the population). This indicates that duplex formation may in some way be negatively associated with binding affinity.

The absence of a defined structure does not, however, mean a smooth landscape. If folding (i.e. significant secondary structure of the oligonucleotides) is in fact detrimental to protein binding, the landscape will possess many of the features associated with a structured molecule. Such interdependence between bases is demonstrated by the measure of epistasis within the landscape being equal to an NK-model, where K > 0 (mutual information may not be suitable for detecting this relationship).

4. Discussion

In this study we reveal the entire sequence-fitness landscape in terms of binding profile of a 10-mer oligonucleotide. Unlike previous studies into the study of biological fitness landscapes of this magnitude, the data are derived from a real biomolecular system by experimental evaluation. By using a fluorescent protein target, we remove the necessity to label using an additional fluorescent tag, which in previous studies has been shown to lead to spurious interactions (Platt et al. 2009). Therefore, the binding profile is based purely on the interactions between the oligonucleotides and the protein.

Although the sequence landscape has been attenuated to only 10 nucleotides, the dependence of protein binding on the residues furthest away from the chip surface indicates that a shortened sequence is nearly as informative as a much longer one. The abridged chains should still be able to adopt conventional structures such as small hairpins and potentially inter-chain interactions at the chip surface can result in more complex configurations. Although 10-mers are capable of forming hairpins, they are much less likely to than longer sequences. Oligonucleotides that interact strongly with the protein target are most probably in a random unpaired configuration. If the oligonucleotide lacks a defined configuration, structural interactions within the DNA molecule will be of importance to protein binding, as any folding may reduce the interaction with the 5′-end.

Statistical measures on the experimental landscape lead to some interesting results, particularly when compared with those obtained with noisy NK-landscapes. Autocorrelation, FDC and epistatic variance all indicate that the experimental landscape resembles a noisy NK-landscape, where K is between 0 and 1. These measures also indicate that the level of noise in the experimental data is sufficiently low that it does not prevent the identification of epistasis and ruggedness arising from ‘real’ physical interactions. Noise does, however, affect the number and size of attractive basins. This makes it difficult to assess the ‘true’ modality of the landscape.

A simple glance at the binding affinities of the DNA sequences within the dataset indicates that there is no partitioning of good binders and bad binders, but a continuous distribution. This is in marked contrast to a recent study of the protein-binding profile of immunoglobulin E (Katilius et al. 2007). That study found that the sequence was highly immutable within the stem region of the aptamer's hairpin structure, with permutation of the bases causing loss of binding affinity. In this example it would be expected that there would be separate plateaus within the distribution differentiating the strong binding sequences from the general background. The continuous nature of the fitness distribution of the APC landscape, in addition to the large basins of attraction, will no doubt have been conducive to the generation of aptamers to APC through the use of an evolutionary algorithm with a small population. However, it cannot be discounted that within the immunoglobulin E sequence landscape there may be multiple regions that elicit strong interactions with the target protein. For example, it is well documented that aptamers can bind proteins at more than one site (Tasset et al. 1997).

5. Conclusions

We present the entire interaction profile of a real 10-mer oligonucleotide landscape. Advances in microarray in situ synthesis technology have made such a study possible, highlighting the potential to investigate complex biological interactions in a global unbiased manner. Analysis has shown that the landscape is rugged, with epistatic interactions between individual bases. We have indicated here how it is possible to run random and adaptive walks on the landscape to obtain information about the number and distribution of local optima; it would equally be possible to use the data to test and compare population-based genetic algorithms with different parameter settings, e.g. population sizes, mutation rates and cross-over types. This would be valuable equally as a model for prior tuning of algorithms for future-directed evolution experiments or as a model of biomolecular evolution. We suggest that to model the noise in the data in such a simulation, each evaluation of a sequence should be perturbed by adding a random variate from the noise distribution we observed and described above; this would simulate how the genetic algorithm would ‘perceive’ the landscape in an experiment similar to ours.

The data from this experiment are available online at http://dbkgroup.org/direvol.htm, and will provide a valuable resource for researchers in the area. An advantage is that these are real data, not a model system and so offer an interesting alternative to the landscapes previously studied. While artificial fitness landscapes based on RNA secondary structure have proved invaluable to the study of biomolecular evolution, they are by their nature relatively simplistic. Data derived from real evaluations contain information from a much greater range of interactions than purely complementary base pairings. The chips used during this study are not limited to a single use, but can be washed and reused to study the binding profiles of different analytes to provide a catalogue of different landscapes.