Abstract
Recent work on the aerodynamics of flapping flight reveals fundamental differences in the mechanisms of aerodynamic force generation between fixed and flapping wings. When fixed wings translate at high angles of attack, they periodically generate and shed leading and trailing edge vortices as reflected in their fluctuating aerodynamic force traces and associated flow visualization. In contrast, wings flapping at high angles of attack generate stable leading edge vorticity, which persists throughout the duration of the stroke and enhances mean aerodynamic forces. Here, we show that aerodynamic forces can be controlled by altering the trailing edge flexibility of a flapping wing. We used a dynamically scaled mechanical model of flapping flight (Re ≈ 2000) to measure the aerodynamic forces on flapping wings of variable flexural stiffness (EI). For low to medium angles of attack, as flexibility of the wing increases, its ability to generate aerodynamic forces decreases monotonically but its lift-to-drag ratios remain approximately constant. The instantaneous force traces reveal no major differences in the underlying modes of force generation for flexible and rigid wings, but the magnitude of force, the angle of net force vector and centre of pressure all vary systematically with wing flexibility. Even a rudimentary framework of wing veins is sufficient to restore the ability of flexible wings to generate forces at near-rigid values. Thus, the magnitude of force generation can be controlled by modulating the trailing edge flexibility and thereby controlling the magnitude of the leading edge vorticity. To characterize this, we have generated a detailed database of aerodynamic forces as a function of several variables including material properties, kinematics, aerodynamic forces and centre of pressure, which can also be used to help validate computational models of aeroelastic flapping wings. These experiments will also be useful for wing design for small robotic insects and, to a limited extent, in understanding the aerodynamics of flapping insect wings.
Keywords: flexible wings, flapping flight, aerodynamics
1. Introduction
The aerodynamic forces generated by flapping wings depend on several physical factors. These include the kinematics and geometry of the wings, their material architecture and the fluid environment around the wing. Besides these, the solid–fluid interactions between the wing surface and its surrounding air medium also play a key role in aerodynamic force generation. Until recently, it was difficult to numerically model these ‘aeroelastic interactions’, because they involve the mechanics and mutual interactions of both the solid and fluid continua. At every iterative step, it is therefore necessary to ensure that the numerical models provide convergent solutions for both the solid and fluid case, which is computationally very intensive (Kamakoti & Shyy 2004). Because of these complications, most numerical studies (Liu 2002; Ramamurti & Sandberg 2002, 2007; Sun & Tang 2002; Wang 2004; Wang et al. 2004) have focused their attention on rigid wings for which the aeroelastic coupling of solid and fluids can be ignored. Similarly, most experimental studies (Dickinson et al. 1999; Sane & Dickinson 2001; Usherwood & Ellington 2002a,b; Prempraneerach et al. 2003) have also focused on rigid rather than flexible wings. Recently, with the availability of better computational power, there have been some attempts to numerically model aeroelastic interactions to determine the role of wing flexibility in aerodynamic force production (Ho et al. 2003; Shyy et al. 2008). However, these efforts were stymied by the lack of availability of appropriate empirical data required for validation.
The aerodynamics of flapping wings has been most extensively investigated in recent years in the context of insect flight (for reviews see Lehmann 2008; Sane 2003; Wang 2005). However, even here, the role of the solid mechanics of the flapping wings has received surprisingly little attention although wing flexibility has long been recognized as an important factor for insect flight aerodynamics (Wootton 1992, 1993; Wootton et al. 2003; Walker et al. 2009). Combes & Daniel (2003a,b) showed that wing flexural stiffness varies by as many as four orders of magnitude across insect taxa, and wing flexibility is strongly correlated with wing size. Indeed, the absolute wing-span and chord length account for more than 95 per cent of the observed variation in flexural stiffness values for insect wings. The flexible wing surface adapts its shape in response to external fluid forces and thus influences aerodynamic force production during flapping flight (Wootton 1993). Because the patterns of wing flexion are governed primarily by the inertial properties of the wing rather than pressure gradients arising from wing–air aeroelastic interactions, these studies concluded that the aeroelastic feedback was negligible and the wings may be treated as purely inertial, flexible structures in the case of flapping insect wings (Combes & Daniel 2002). Thus, computational simulations of insect wings need only prescribe a pattern of bending that matches the flexibility pattern of actual insect wings. Another important factor to consider when investigating the role of wing flexibility in insects is the presence of wing veins. Like flexibility or wing shape, wing venation patterns are also remarkably diverse across insect taxa, ranging from the extensive venation in the twisting and bending wings of dragonflies (Wootton 1998) to the sparse venation in butterfly forewings. Wing venation may also play a key role in determining the asymmetric dorso-ventral resistance of insect wings in response to aerodynamic forces and therefore also its efficiency in force production (Wootton et al. 2000).
In this paper, we study how wing flexibility influences aerodynamic force generation in flapping flight. Rather than replicate the intricate, anisotropic material and mechanical architecture of insect wings, we approached this problem from purely physical considerations using wings made of isotropic material and systematically varying the values of wing stiffness on a mechanical model of flapping wings. Our approach enables us to change these parameters systematically and thus measure their influence on aerodynamic force generation. Using this model, we generated a database of wing flexibility versus aerodynamic forces to help validate computational models of aeroelastic flapping wings. This study can also inform engineers of robotic flying insects in their choice of materials for artificial wings.
2. Material and methods
2.1. Experimental set-up
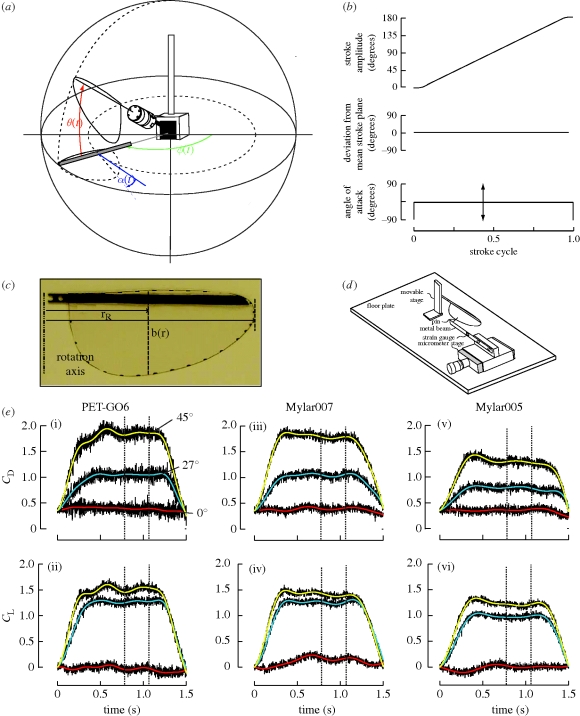
We measured aerodynamic forces on flapping wings using a custom-made dynamically scaled mechanical flapper (figure 1a). This flapper device was built to physically model insect flight and is a slightly modified version of the one described by Dickinson et al. (1999) and Sane & Dickinson (2001). Unless otherwise mentioned, this paper also follows the conventions and nomenclature of Sane & Dickinson (2001). Briefly, the angular motion of wings along three orthogonal Euler angles was actuated via a bevel-geared robotic wrist, which transmitted the motion of coaxial drive motor shafts to a wing holder. Following the terminology of Sane & Dickinson (2001), these angles are termed stroke amplitude (denoted by ϕ), deviation of the wing from the mean stroke plane (θ) and angle of attack (α, figure 1a). The wing could move freely around the translational and rotational axes but its motion around the axis of deviation from mean stroke plane was constrained to ±45° due to the geometry of the gear box. This angle is substantially greater than the typical deviation angles measured in insects (Ellington 1984b), and so this mechanical model can be used to replicate insect wing motion in future studies.
Figure 1.
(a) Experimental set-up. Flapper apparatus for measurement of aerodynamic forces and diagram of the bevel-geared flapper device moving the wing along three orthogonal Euler angles, namely the stroke amplitude ϕ, the deviation from mean stroke plane θ and angle of attack α. The wings were immersed in a tank of oil (46 cm × 41 cm × 152 cm) with walls sufficiently wide to ensure minimal edge effects (data not shown). Instantaneous forces and torques were measured by a sensor attached to the base of the wing model. (b) Sample kinematic plots for each trial. Top panel, angular velocity of the wing is constant throughout the stroke, from 0° to 180°. Middle panel, in all cases, the wing moves along a flat stroke plane with zero deviation from the mean stroke plane. Bottom panel, for each run, the angle of attack is kept at a constant value between −9 and 90° in steps of 4.5°. (c) Test wing: image of the wing attached with rigid carbon fibre leading edge. The wing length is 10 cm, and the maximal chord length 4.5 cm. (d) Measurement of the effective stiffness of the wings (not to scale). The micrometer stage moves the flexible beam along the pin direction and a movable stage adjusts the loading point on the wing. Pre-calibrated foil strain gauges wired in half bridge configuration (350 Ω each) and operating in their linear range measure the forces required to bend the wing through a given distance. Flexural stiffness was then calculated from the bending force and distance using equation (2.2). (e) Sample raw and average plots for three representative angles of attack (0°, 27° and 45°) and at three different stiffness values (PET-G06, Mylar007, Mylar005; see table 1). Top panels show drag coefficients (CD) and bottom panels lift coefficients (CL) as a function of time. In each case, the black line is the actual recorded, inertia-subtracted force and the smooth coloured line as follows: red = 0°, blue = 27°, yellow = 45°. (i,ii) Plots for the most rigid wing (PET-G06; EI ≈ 10−3). (iii,iv) Plots for wings of intermediate stiffness (Mylar007; EI ≈ 10−4). (iv,v) Plots for wings of low stiffness (Mylar005; EI ≈ 10−5).
We used 16 mm, 0.3 Nm torque DC brush motors (Maxon, Sachseln, Switzerland) to power the drive shafts. The motors were equipped with gear heads to reduce speed and with a set of magnetic encoders to provide kinematic feedback and ensure fidelity of the output motion. A custom Matlab (The Mathworks, Natick, MA, USA) Simulink program with WinCon software (Quanser Consulting, Ontario, Canada) was used to drive the motors along pre-programmed kinematic patterns. This software provided commands to the real-time control and data acquisition board (Quanser Consulting) communicating with the hardware. We used proportional–integral–derivative (PID) controllers to run the motors with a precision of 0.1°. To amplify the motion commands from the computer, we used analogue amplifier units (Advanced Motion Control, Camarillo, CA, USA), which provided direct control of the input current received by the motor. The flapper gearbox was affixed with a wing holder to which we attached wings of identical planform but different material properties and flexural stiffness (figure 1a).
The wing–gearbox (2.54 cm × 2.54 cm × 2.54 cm) combination was immersed in a tank (46 cm width × 41 cm × 152 cm length) filled with mineral oil (kinematic viscosity = 3.4 cSt at 20°C, density = 850 kg m−3). This overall set-up enabled us to measure the aerodynamic forces on the wings flapping with pre-programmed kinematic patterns. The Reynolds number for our experiments was calculated to be approximately 2000 using the equation
 |
2.1 |
where b̄ is the mean chord length, Ūt the mean wing tip velocity, AR the aspect ratio, n the wing beat frequency, R the wing length, θ the wing beat amplitude (peak-to-peak in radians) and ν the kinematic viscosity of the fluid (Ellington 1984a).
In each experiment, the wing was started impulsively from rest and moved over a 180° arc in 1.5 s at a constant angle of attack (figure 1b). For each experimental set, the wing moved at 23 different angles of attack from −9 to 90° in 4.5° increments. The wing moved from rest and attained a constant velocity in 0.3 s at an average acceleration of 10 rad s−2. At this acceleration, the transient inertial forces are minimal and the raw force records show a smooth rise to their maximum value. We collected data for 16 wings made of four different materials and systematically varying in their stiffness. The flexural stiffness of the wings was measured using the methods described below.
2.2. Wing material and design
To test the effect of stiffness on lift force and drag force, we used a series of wings with varying values of flexural stiffness EI, where E is Young's modulus and I the area moment of inertia. We generated these wings using four kinds of materials: polyester, polycarbonate, polyethylene and Mylar. Their EI values varied widely, thus enabling us to cover a wide range of stiffnesses (table 1). All wings had identical dimensions. Although these wings are not meant to replicate insect wings, their shape and contour are inspired by insect wings for future applications and ease of comparison with previous literature on this topic. The shape of the wing superficially resembled those of certain Diptera such as Drosophila; however, it was arbitrarily generated using a mathematical equation of the wing contour (see electronic supplementary material, table, for morphological parameters). Because the wing was attached to a holder and a force sensor, the net AR of the wing (15.3) was somewhat higher than for most insects. However, this discrepancy did not influence its aerodynamic characteristics, because the base shaft did not generate any aerodynamic forces of its own. The wing length (without the wing holder) was 100 mm, with maximum and mean chord lengths of 45 mm and 33.7 mm, respectively. The surface area S1 of each wing was equal to 3370 mm2. Each wing was mounted on a carbon rod attached to the drive shaft (figure 1c). The carbon rods were manufactured with holes precisely drilled at the same location to which to attach the wing holder and the length of the beam with rectangular cross-section (1.5 mm × 4.2 mm). The wing sheet and the carbon fibre beam were glued together by an adhesive (Permabond 910) to ensure a firm leading edge. If the process of gluing warped the wing surface, we used the vacuum heater (VWR 1410) to restore flatness after sandwiching the wing between two flat metal plates.
Table 1.
The wings were made of four kinds of polymer materials with known material properties: polyester, polycarbonate, PET-G and Mylar. For each, we used sheets of different thickness denoted by the number (in inches) at the end of each name (e.g. Polyes0.002 represents a wing made of a 0.002 inch thick polyester sheet). In addition to these, we used four sheets of a different polymer called Polymer-(I–IV) to get a sufficient range of flexural stiffness values (EI). We characterized the EI for all models using the bending test described in the Material and Methods section.
| order (low to high) | model name | thickness, t (mm) | EI (nm2) |
|---|---|---|---|
| 1 | Polyes0.002 | 0.05 | 4.39E-6 |
| 2 | Mylar0.003 | 0.075 | 8.62E-6 |
| 3 | Polyes0.003 | 0.075 | 1.01E-5 |
| 4 | Polyes0.005 | 0.125 | 3.24E-5 |
| 5 | Polyes0.004 | 0.1 | 3.92E-5 |
| 6 | Mylar0.005 | 0.125 | 5.44E-5 |
| 7 | Polymer-I | 0.17 | 7.04E-5 |
| 8 | Polymer-III | 0.2 | 8.23E-5 |
| 9 | Polymer-II | 0.2 | 8.91E-5 |
| 10 | Mylar0.007 | 0.175 | 2.15E-4 |
| 11 | Polycarb0.01 | 0.25 | 2.32E-4 |
| 12 | Polymer-IV | 0.36 | 3.50E-4 |
| 13 | Polycarb0.015 | 0.375 | 3.96E-4 |
| 14 | PET-G0.02 | 0.5 | 4.94E-4 |
| 15 | Polycarb0.02 | 0.5 | 5.33E-4 |
| 16 | PET-G0.06 | 1.47 | 8.23E-4 |
2.3. Measurement of wing stiffness
To measure the stiffness E of each wing type used in this study, we used a custom-built wing bending apparatus (figure 1d), similar to the one described by Combes & Daniel (2003a). Note that the wing was flexible only in the chordwise direction and not in the spanwise direction due to the rigid leading edge vein.
Strain gauges (Omega SG-2/350-LY11 in half bridge configuration; 350 Ω) were glued to the surface of a flexible beam. This beam was then mounted on a micrometer stage, which allowed us to finely control the distance through which the stage was moved (figure 1d). This apparatus could measure a maximal force of 0.4 N with a resolution of 1 mN. A pin attached at one end of the beam exerted a point force on the wing model. The force required to bend the wings by a given distance was then reported by the pre-calibrated strain gauges on the micrometer stage. From the values of applied force F, the wing tip displacement δ and chord length of the wing w, we calculated the chordwise flexural stiffness (EIchord) using the following equation (Gordon 1978):
| 2.2 |
In all experiments, the point loads were applied on the wing along the line of maximum chord length. In the chordwise direction, the point of load application was at 70 per cent of the chord length from the rigid leading edge (Combes & Daniel 2003a). Although the range of chordwise stiffness used in these experiments (10−6 to ∼10−3 Nm2, table 1) overlaps with the range measured in real insect wings (10−7 and 10−5; Combes & Daniel 2003a,b), it is important to note that the aerodynamic force generation depends on the solid–fluid coupling between the wing and the fluid, rather than a direct reproduction of any single material characteristic of the wing.
2.4. Force measurement and inertial subtraction
The instantaneous forces and moments on the flapping wings were measured using a six-component force balance (ATI NANO-17, Apex, NC, USA). The cylindrical sensor unit (figure 1a; 17 mm diameter, 14.5 mm length) with a mass of 10 g was calibrated to measure a maximum force of 12 N and a maximum torque of 0.5 Nm along the three orthogonal directions. Here, we report only the force measurements perpendicular and parallel to the wing surface. We filtered the measured forces using a 4 Hz low-pass filter, greater than 10 times the typical frequency of motion (0.33 Hz). The forces were converted to lift and drag components in the inertial coordinates using appropriate trigonometric relations (for details and conventions, see Sane & Dickinson (2001)).
The net force on the wing includes contributions from aerodynamic and inertial forces of the wing–sensor combination, in addition to gravity and buoyancy. To account for the gravitational and buoyancy contributions of the sensor, we measured the forces due to the unloaded sensor for each sensor orientation. To remove the inertial force due to wing motion from the net force measurement, we made a small metal inertial model for each wing with the same mass as the wing. This ‘point mass’ was located at the same distance from the centre of rotation as the centre of mass of the actual wing. We repeated the same motion as the actual wing with the inertial model. The measured force now included contributions from inertial force of the wing–sensor combination and the aerodynamic force on the sensor head. Subtracting this ‘wing-excluded’ record from the total (‘wing-included’) record gave us the net instantaneous aerodynamic force. Because the force coefficients reported here were calculated from force records in the middle of the stroke when the wing was moving at roughly constant velocity, the contribution of added mass is not likely to play a major role in these measurements. The instantaneous aerodynamic forces thus measured were used to calculate the lift and drag force coefficients for the flapping wing (figure 1e(i)–(vi)).
The non-dimensional lift and drag coefficients were derived using the equation (for conventions, see Ellington (1984a) and Sane & Dickinson (2001))
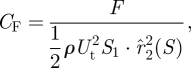 |
2.3 |
where ρ is the density of fluid, Ut the path velocity of the wing tip and F the measured lift (L) or drag (D). In these experiments, the area S1 of each wing was 3370 mm2, and r̂22 (S), the non-dimensional second moment of area, was 0.58, in the range of values reported for real insect wings (Ellington 1984c). When plotted one against the other, these coefficients provided us with aerodynamic polar plots that could be used to quantify the aerodynamic characteristics of the flexible wings.
2.5. Measurement of centre of pressure
To measure the centre of pressure, we used the torque measurements from the force sensor and divided the instantaneous torque value by the instantaneous forces values. The chordwise and spanwise centres of pressure, pchord and pspan, were calculated using the following equations:
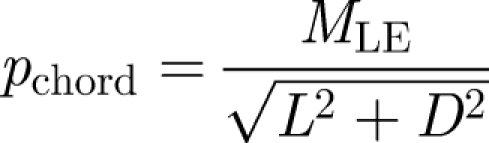 |
2.4a |
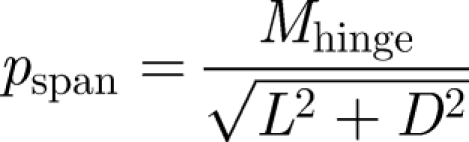 |
2.4b |
where pchord and pspan are the distances of the centre of pressure from the rigid leading edge and wing hinge respectively, MLE and Mhinge are the moments around the leading edge and wing hinge, and L and D are the lift and drag force, respectively. The centre-of-pressure measurements are particularly important to determine the length of the lever arm for calculations of aerodynamic torques and power generated by flapping wings around the wing hinge. In previous literature, this value was assumed to be at 70 per cent along the wing length from base to tip (Fry et al. 2005), based largely on a computational fluid dynamics (CFD) model of the aerodynamic forces and pressure on a flapping wing (Ramamurti & Sandberg 2002). Here we provide, to the best of our knowledge, the first direct measurements of the centre of pressure on flapping wings.
2.6. Measurement of net force angle
For a rigid wing, the net force is oriented perpendicular (normal) to the wing surface profile because the tangential component due to wing surface frictional force is negligible. We measured the deviation of the net force on flexible wings from the normal direction by calculating the ratio of the lift to drag force and using the following inverse trigonometric relationship:
 |
2.5 |
In this equation, β is the angle of deviation of the net force vector from the normal and α is the angle of attack. Because the flexible wing surface realigns with the flow, the actual aerodynamic angle of attack is spatially variable. Thus, the reported value of angle of attack in this paper is the input value, rather than the actual aerodynamic value resulting from solid–fluid interactions. Deviation of the net force vector from the normal provides a convenient measure of how flexibility influences the ability of a wing to generate lift.
3. Results
3.1. Aerodynamic forces are sensitive to wing stiffness
Figure 2a–f shows the plots for measured drag, lift and net force coefficients, respectively, on wing models of various stiffness values as functions of angle of attack. The combined surface and contour plots highlight the changes in drag (figure 2a), lift (figure 2b) and net force coefficients (figure 2c) with changes in angle of attack and flexural stiffness. The same data are represented as projections on the force coefficient (drag, lift, net force) versus angle of attack axis in figure 2d–f, respectively.
Figure 2.
Force coefficients. Parameter maps for (a) drag, (b) lift and (c) net force coefficients as functions of angle of attack and flexural stiffness EI. In each plot, the small filled circles indicate experimentally measured values of lift and drag coefficients with shaded interpolated values in pseudo-colour. Overlying the pseudo-colour plots are the related contour plots (white) for force coefficients. The same data are represented as (d) drag, (e) lift and (f) net force coefficient versus angle of attack. The angle of attack in these experiments varies from −9° to 90° in steps of 4.5°. In (d), (e) and (f), the curves for various materials are displayed in different colours and different symbols for each wing material. (g) The aerodynamic polar plots are represented with various symbols to indicate each wing material. A list of the symbols and corresponding materials is given in the inset in order of increasing rigidity. These symbols are consistent in all subsequent figures.
Drag coefficient rose monotonically with increasing angles of attack (figure 2a,d) for each value of flexural stiffness. However, the magnitude of the drag coefficient became lower as the wings became more compliant. Thus, a flexible wing generates lower drag with increasing flexibility (figure 2d). Similarly, lift coefficients also decreased in magnitude with an increase in wing flexibility, but attained plateau at higher angles of attack (figure 2b,e). At angles of attack greater than 50°, flexible wings generated more lift than rigid wings. Thus, unlike rigid wings, which have a distinct maximum at a 45° angle of attack, the maxima for lift coefficients of flexible wings depend on the flexural stiffness of these wings (figure 2e). The combined effect, in terms of the net force on the wings' surface (figure 2c,f), also showed a monotonic decline as wing flexibility increased.
These data allowed us to construct the CL–CD polar plots for wings with systematically varying EI values (figure 2g). These plots showed a hierarchical structure with the curves nested in order of decreasing stiffness. Thus, the polar curve for the most flexible wing (Polyes0.002, EI = 4.4 × 10−6 Nm2, table 1) was nested within the curve of the wing with the second most flexible wing (Mylar0.003, stiffness = 8.6 × 10−6 Nm2, table 1), and so on, within the estimated experimental error (approx. 5%). All curves of flexible wings were nested within the aerodynamic polar curve of the most rigid wing (PET-G0.06, stiffness = 8.2 × 10−4 Nm2). Within the limits of experimental resolution, these data revealed no intermediate wing stiffness values that could optimize aerodynamic performance. Rather, aerodynamic force generation reduced monotonically as trailing edges of the wings became more flexible.
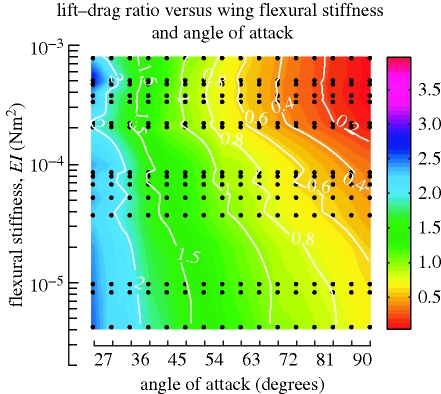
3.2. Lift-to-drag ratios as a function of flexural stiffness
We plotted the effect of wing stiffness on lift-to-drag ratio, which is often used as a measure of aerodynamic performance (figure 3). Because the values of both lift and drag approach zero at low angles of attack, lift-to-drag ratios are not particularly meaningful for angles of attack under 20° and were excluded from the figure. As is evident from the contour plots, which ran approximately parallel to the y-axis, lift-to-drag ratios were relatively insensitive to variation in wing flexibility for angles of attack between 20° and ∼60°. This suggests that the net forces were attenuated, in the process also attenuating lift and drag generation in equal proportion. By this performance measure, at lower angles of attack (20–60°), a flexible wing is neither better nor worse than a rigid wing at generating lift relative to drag.
Figure 3.
Lift-to-drag ratios. Parameter maps of lift-to-drag ratios as functions of flexural stiffness and angle of attack, overlaid with contour plots (white).
The lift-to-drag ratios were more sensitive to wing flexibility ranging from 10−5 to 10−3 Nm2 for a wing moving broadside (i.e. 90° angle of attack). Thus, a very flexible wing moving broadside could generate lift, with lift coefficients of nearly 0.7, while generating less drag than a rigid plate. At very high angles of attack, flexible wings thus outperformed rigid wings.
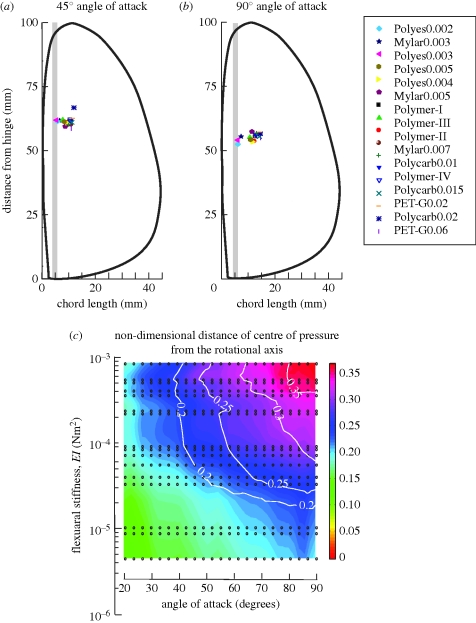
3.3. Changes in centre of pressure with wing flexion
The six-component sensor used in these experiments enabled us to measure torques in addition to absolute forces on the wing. The centre-of-pressure measurements may be used to determine the length of the lever arm for calculations of aerodynamic torques generated by flapping wings around the wing hinge. Because the leading edge vein is rigid in all the experiments reported here, the centre of pressure is unlikely to vary greatly along the span. This was borne out by the data in figure 4a–c, which showed a greater spread along the chordwise axis than along the spanwise axis. Figure 4a,b shows how the measured centre of pressure changed with wing flexibility for two representative angles of attack of 45° (figure 4a) and 90° (figure 4b). As is evident from a visual comparison of these plots, for a wing of any stiffness value, the centre of pressure varies only marginally in spanwise and chordwise directions. However, as the wings became more flexible, the centre of pressure moved towards the rigid leading edge.
Figure 4.
Pressure plots. The location of the centre of pressure for all wing models at angles of attack of (a) 45° and (b) 90°. The symbol list of wing materials is identical to the one in figure 2. The wing shape is represented by the black line contour and the plot is scaled to ensure that the aspect ratio of the wing outline is identical to the actual aspect ratio of the wing. The grey line represents the rigid leading edge. (c) Non-dimensional centre of pressure as a function of angle of attack and flexural stiffness. To non-dimensionalize the centre of pressure, we divided all values by the maximum chord length.
This is further elaborated in figure 4c, which plots the changes in centre of pressure as a function of wing stiffness. The centre of pressure was non-dimensionalized by dividing the values for moment arm by the maximum chord length. For very low angles of attack, the net forces diminished more rapidly than the pressure values, causing the ratio to blow up. Hence, these values have been excluded from figure 4c. The changes in centre of pressure, like their counterparts in forces, also varied systematically with wing stiffness. Importantly, the centre-of-pressure measurements showed a greater variation with increasing angle of attack for rigid wings as compared with compliant wings. For rigid wings, the centre of pressure varied substantially along the chordwise direction as compared with compliant wings. This result contradicts previous models of rigid wings, which have assumed that the centre of pressure remains approximately fixed. Thus, for rigid wing models, it is important to take into account the dynamics of changes in centre of pressure with kinematics. Counterintuitively, as flexibility increased, the centre of pressure was less sensitive to the angle of attack, suggesting that some flexibility in the wing lamina may enable the wing to maintain its centre of pressure. Although this result may be an experimental artefact resulting from the large difference in the structural rigidity of the wing material and the leading edge vein, it is also likely to be important in the case of insect veins, which are known to be substantially more rigid than the wing material.
3.4. Effect of wing stiffness on the angle of net force
Because viscous forces due to shear were negligible compared with pressure-related forces on the wing surface at intermediate to high Reynolds numbers, the net force vector was normal to the wing surface at all times for rigid wings (Dickinson et al. 1999; Usherwood & Ellington 2002a,b; Sane 2003). However, as depicted in the schematics shown in figure 5a,b, this may not be the case for flexible wings.
Figure 5.
Net force angles on rigid and flexible wings. (a,b) Schematic illustrations to indicate the net force vector angle in rigid (a) and flexible (b) wings. In these figures, the cross-section of the wing is depicted as the conventional ball-and-stick figure with the ball indicating the leading edge of the wing and the stick representing the trailing edge. The dotted lines represent tangents to the local curvature in the wing cross-section. (c) Actual force vectors measured on a wing undergoing flapping. The kinematics involve a wing translating from an angle of attack of −9° to an angle of attack of 90°. Data are shown for two wings made of materials of two different flexural stiffness values. The most rigid model (PET-G0.06) is shown in red, and the other, Polymer-II, is shown in green. (d) Pseudo-colour plots show the changes in the orientation of the force vector from the normal direction as a function of angle of attack and flexural stiffness. The values in the plots were obtained by subtracting the net force vector angles of the flexible wings from the corresponding values normal to the wing. At angles of attack below 30°, the changes in angles of the net force are very small and noisy and are hence omitted from the plot.
To test the influence of wing flexibility on the direction of the net force vector in flexible wings, we plotted the angular change Δ in net force vector as the difference between the normal and actual angles in figure 5c, for the illustrative case of a wing starting from −9° to 90° angles of attack. As shown in this figure, the change in the angle of the net force was quite substantial. This is more fully quantified in figure 5d, which shows how the force vector veered from the normal with increasing flexibility. In agreement with previous reports (Dickinson et al. 1999; Sane & Dickinson 2001; Usherwood & Ellington 2002a,b), the net force for rigid wings was normal to the wing surface at all angles of attack. However, as the wings became more flexible, the angular change Δ varied from 0 to greater than 30° for a flexible wing moving broadside. The maximum angular change Δ was measured in the most flexible wing moving at the highest angles of attack and the minimum Δ was measured in the case of rigid wings at all angles of attack.
3.5. The effect of wing veins on aerodynamic performance
Wing veins provide a structural reinforcement to the wing that affects the aerodynamic characteristics of the wings. To investigate the role of wing veins on aerodynamic performance, we added a minimal vein structure to the wings made of the most flexible material (Polyes0.002, table 1). The veins spanned from the hinge to the wing periphery, making angles of 20, 40 or 60° with respect to the rigid leading edge vein (figure 6a). Figure 6b shows the influence of the wing veins on aerodynamic performance via changes in the structural rigidity of the wing. As the veins spanned and reinforced a greater area of the wing, the aerodynamic performance increasingly matched the performance of rigid wings. For wing veins making an angle of 40° and 60° with the leading edge vein, the aerodynamic performance was better than rigid wings, probably because of a positive camber in the wing membrane.
Figure 6.
Force coefficients on models with and without a wing vein framework. The figure shows three models, each with a single vein in addition to the leading edge vein. (a) The veins were glued to a wing with the lowest flexural stiffness (Polyes0.002). The angle between the vein and leading edge was varied from 20° to 40° and 60°, thus enabling us to provide varying rigidity to the wing. (b) Aerodynamic polar plots of flexible wing models with and without wing veins. For comparison, we have also plotted the aerodynamic polars for the most rigid model (PET-G0.06).
4. Discussion
4.1. Aerodynamics of rigid versus flexible wings
The standard airfoil theory was developed specifically for rigid wings and is not easily applicable to flexible wings, as it does not account for solid–fluid interactions. Thus, in models based on standard airfoil theory, the wing is a rigid entity unresponsive to fluid motion. A flexible wing, however, both affects and is affected by changes in its fluid environment. This so-called ‘aeroelastic problem’ is computationally intensive because any numerical treatment that models this phenomenon must provide a convergent solution for two continua—solid and fluid—at each numerical step. The force measurements reported in this paper account for the influence of the wing's material properties and its interaction with the surrounding fluid, thereby incorporating the effects of aeroelasticity on aerodynamic performance. Furthermore, our measurements showed that these aeroelastic effects strongly influenced aerodynamic force generation. Although the importance of wing flexion in aerodynamic force generation has often been acknowledged in past literature, only a few studies have systematically measured the aerodynamic effects of wing flexion, especially in the context of flapping flight (Kamakoti & Shyy 2004; Hamamoto et al. 2007; Heathcote et al. 2008; Song et al. 2008). In the absence of these data, most recent quasi-steady and computational models of flapping wings developed for rigid wings may not readily apply to flexible wings (Sane & Dickinson 2002; Sane 2003; Wang 2005).
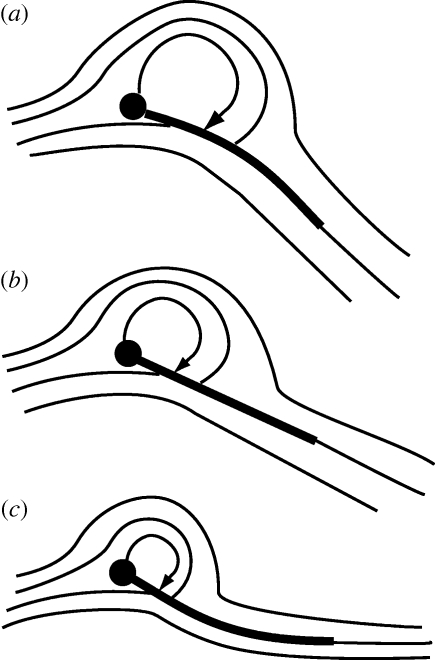
From the force measurements detailed here, it was possible to outline the key features of the flow expected around a flexible flapping wing. It is well documented from several previous studies that a three-dimensional inclined rigid flapping wing generates a smaller but more stable leading edge vortex than its fixed, two-dimensional counterpart (for review, see Sane 2003; Wang 2005). The leading edge vortex is of key importance to the force enhancement in flapping wings and its size is typically proportional to the magnitude of the net aerodynamic force generated by the wing (Ellington et al. 1996). How does flexibility alter this phenomenon? As is evident from the instantaneous force traces in figure 1e, flexibility probably does not fundamentally alter the basic aerodynamic mechanisms during flapping. However, because flexion of the trailing edge generates lower net forces than a rigid wing, the leading edge vortex for a flexible wing is probably smaller than its rigid counterpart, implying that the Kutta condition is established with relative ease when the flexible trailing edge realigns in the direction of the flow. This simple hypothesis, outlined in figure 7, can qualitatively predict the flows to be expected around flexible wings of the kind used in these studies. The nature of flows around flexible wings will be outlined in a future study using flow visualization techniques.
Figure 7.
Qualitative predictions of steady-state flow patterns around a flexible wing. (a,b) A positively cambered flexible wing (a), such as one generated due to wing veins, is predicted to generate greater leading-edge vorticity and hence higher net forces than a rigid wing (b). In contrast, a negatively cambered flexible wing (c) is predicted to generate less leading edge vorticity than the rigid wing.
4.2. Effects on the placement and orientation of forces
For rigid wings, the net force vector is always normal to the wing surface because viscous forces are negligible compared with the pressure forces on the wing (Sane 2003). Because the Reynolds numbers for both the rigid and flexible wings were similar (Re ≈ 2000), it is unlikely that the deviation in the orientation of the net force vector resulted from underlying alterations in values of viscous drag. Rather, they reflected the changes in the shape of the wing surface, which showed increasingly negative camber as the flexibility increased (figure 5b). In comparison, wings with venation were not as negatively cambered and in some cases even assumed positive camber. In this case, the local angles of attack near the trailing edge were closer to or higher than those in the rigid wing. We confirmed this by imaging the wings mid-stroke to show that their profile was indeed negatively cambered in proportion to their flexibility at mid-stroke (data not shown). Thus, changes in orientation of the force vector resulted from the fact that the direction of the normal itself changed as the wing underwent chordwise flexion, as depicted in the simple diagrams of figure 5a,b. If true, this model predicts that greater flexion leads to a greater change in force vector from the normal, as confirmed by the data in figure 5d.
Our data also revealed the centre of pressure to be more sensitive to wing motion than was previously assumed. Furthermore, it also depended on wing flexibility. Even in the case of rigid wings, the non-dimensional centre of pressure moved from approximately 0.2 to 0.35 as the angle of attack increased from 0° to 90°. For flexible wings, the centre of pressure was closer to the rigid leading edge wing vein. Although these values may not be representative of the actual insect wings because they depend on the relative mechanical properties of veins and wing material, these data suggested that it is probably incorrect to assume that the centre of pressure stays fixed even on rigid wings flapping at variable angles of attack.
4.3. The role of wing veins on wing structure and aerodynamics
We tested the hypothesis that wing veins enhance aerodynamic performance by imparting structural rigidity to the wing. Because the wing membrane itself is made of a very thin cuticle, it is structurally not rigid. Although development of thicker wing is sometimes observed, for example in the case of the beetle elytra or sclerotized sections (pterostigma) of dragonfly wings (Norberg 1972), these are substantially heavier and likely to increase the inertial power requirements of the wing muscles. It has therefore been suggested that wing veins enable the insects to generate a structurally rigid wing without compromising its levity. Such inferences about function must be made with some caution, especially as wing veins also have a strong role to play in circulation (Arnold 1964) as well as serving as conduits for wing nerves.
Could wing veins enhance aerodynamic force production by increasing wing stiffness or changing camber? If so, how dense must the vein network be to enhance aerodynamic efficiency? Our results showed that even a very minimal framework of two wing veins, if placed at a sufficiently large angle, could ensure that a flexible wing's aerodynamic characteristics were slightly better than those of a rigid wing (figure 6b). This result may also be easily explained by the hypothesis presented in figure 7a–c. A veined wing enables the membrane between the veins to flex in the direction of the flow, thereby generating a camber. A cambered wing requires greater circulation for establishment of the Kutta condition, and would thus generate a higher net force on the wing. Such a wing is expected to generate leading edge vorticity of greater strength than a rigid airfoil. These results may be useful for engineers seeking to build micro-air vehicles, because they can substantially decrease the load and energy requirement of their robotic flappers with very minimal increase in the wing mass.
4.4. Applications of this study to biological examples of flapping
The measurements reported here show that a uniformly flexible wing generates lower aerodynamic forces than rigid wings under steady-state conditions (figure 2). However, the presence of wing veins can substantially enhance aerodynamic performance to match or even better the rigid airfoil. These observations agree with previous suggestions that flexible wings of insects may generate greater forces due to an enhanced camber in insect flight (Ennos 1989). Although the veins of our model wings do not rigorously match insect wings in their complexity, we were able to generate both positive and negative cambers in these experiments and measure the corresponding forces. The conclusions from these experiments may thus be somewhat applicable to the case of insect wings. Wing flexion is also thought to be important in enhancing aerodynamic forces during rapid stroke reversals (Mountcastle & Daniel 2009). However, our study focused on characterization of the steady-state coefficients in flexible wings and hence an investigation of stroke reversals was beyond the scope of this study. Furthermore, when addressing the biological function of wing flexibility, it is also important to consider other non-aerodynamic advantages to flexible wings in insects, such as assisting the insect during eclosion, ensuring sufficient range of stimuli to wing campaniform strain sensors during flying or grooming, and so on.
Our experiments modelled wings with arbitrary flexibility and variable solid–fluid interactions. Although the geometry and motion of the wings is inspired by insects, these experiments do not readily apply to insect flight because the venation patterns are much simplified and the material anisotropy of the wing membrane is largely ignored. Nevertheless, these studies could provide a few general conclusions applicable to insect flight studies. First, because wing venation provides structural reinforcement to the wing lamina, it is reasonable to conclude that it must also enhance the aerodynamic efficiency of the wings by making them functionally more rigid. Second, although, in some cases, wing veins have been shown to be beneficial in enhancing camber, in several Dipteran insects with sparse venation patterns but a rigid leading edge vein, the concave pattern of flexibility is similar to the one seen in our experiments (S. P. Sane 2007, unpublished). For such cases, we may select artificial wings with a temporal pattern of flexibility matching the actual insect wings, thereby matching solid–fluid interactions. Such cases could then provide examples for which both pattern of flexibility and solid–fluid scaling is insect-like. It must be noted, however, that for appropriate solid–fluid interface scaling, similar studies must be carried out in air rather than oil to ensure that the density ratio of the solid wing and fluid medium is also conserved (Ishihara et al. 2009). Third, the above scheme is especially useful in cases where aeroelastic interactions are important such as in aquatic animals such as fish (Fish et al. 2006; Lauder et al. 2006; Lauder & Madden 2007) and pteropods (Borrell et al. 2005). Our results do not assume any specific aeroelastic model and hence apply to both aerial and aquatic cases, as long as the experimental pattern of flexibility matches the actual pattern of flexibility. An important omission from these studies is torsional flexion along the wing span. Thus, although our study presents some data on how wing flexibility may influence forces during insect flight, it is necessary to keep the above caveats in mind when extending these conclusions to insect flight.
Acknowledgments
A preliminary report of this work was presented at the International Conference of Robotics and Automation held in Kobe, Japan, 2009. This work was supported in part by the National Science Foundation Award no. 0545931 to X.D. and funding from the National Centre for Biological Sciences to S.P.S.
Appendix. List of symbols
- AR
aspect ratio
- b(r)
chord length
- b̄
mean chord length
- CF
dimensionless force coefficient
- CD
dimensionless drag coefficient
- CL
dimensionless lift coefficient
- D
drag
- EI
flexural stiffness
- E
Young's modulus
- F
force
- I
moment of inertia
- L
lift
- MLE
moment around the leading edge
- Mhinge
moment around the hinge
- n
wing beat frequency
- pchord
distance from the centre of pressure to the rigid leading edge
- pspan
distance from the centre of pressure to the wing hinge
- r
radial position along wing length
- R
wing length (spanwise)
- R̄e
mean Reynolds number
- S1
area of a single wing
- r̂2 (S)
non-dimensional second moment of area
- Ut
wing tip velocity
- Ūt
mean wing tip velocity
- w
chord length of the wing
- α
angle of attack
- β
angle of deviation of net force vector from the normal to wing surface
- δ
wing displacement at the point of force application
- ν
kinematic viscosity of fluid
- ϕ
stroke amplitude
- θ
deviation from stroke plane
- ρ
density of fluid
References
- Arnold J. W. 1964. Blood circulation in insect wings. Mem. Entomol. Soc. Can. 38, 3–60. [Google Scholar]
- Borrell B. J., Goldbogen J. A., Dudley R. 2005. Aquatic wing flapping at low Reynolds numbers: swimming kinematics of the Antarctic pteropod, Clione antarctica. J. Exp. Biol. 208, 2939–2949. ( 10.1242/jeb.01733) [DOI] [PubMed] [Google Scholar]
- Combes S. A., Daniel T. L. 2002. Flexible wings and fins: bending by inertial or fluid-dynamic forces? Integr. Comp. Biol. 42, 1044–1026. ( 10.1093/icb/42.5.1044) [DOI] [PubMed] [Google Scholar]
- Combes S. A., Daniel T. L. 2003a. Flexural stiffness in insect wings. I. Scaling and the influence of wing venation. J. Exp. Biol. 206, 2979–2987. ( 10.1242/jeb.00523) [DOI] [PubMed] [Google Scholar]
- Combes S. A., Daniel T. L. 2003b. Flexural stiffness in insect wings. II. Spatial distribution and dynamic wing bending. J. Exp. Biol. 206, 2989–2997. ( 10.1242/jeb.00524) [DOI] [PubMed] [Google Scholar]
- Dickinson M. H., Lehmann F. O., Sane S. P. 1999. Wing rotation and the aerodynamic basis of insect flight. Science 284, 1954–1960. ( 10.1126/science.284.5422.1954) [DOI] [PubMed] [Google Scholar]
- Ellington C. P. 1984a. The aerodynamics of hovering insect flight. VI. Lift and power requirements. Phil. Trans. R. Soc. Lond. B 305, 145–181. ( 10.1098/rstb.1984.0054) [DOI] [Google Scholar]
- Ellington C. P. 1984b. The aerodynamics of hovering insect flight. III. Kinematics. Phil. Trans. R. Soc. Lond. B 305, 41–78. ( 10.1098/rstb.1984.0051) [DOI] [Google Scholar]
- Ellington C. P. 1984c. The aerodynamics of hovering insect flight. II. Morphological parameters. Phil. Trans. R. Soc. Lond. B 305, 17–40. ( 10.1098/rstb.1984.0050) [DOI] [Google Scholar]
- Ellington C. P., Vandenberg C., Willmott A. P., Thomas A. L. R. 1996. Leading-edge vortices in insect flight. Nature 384, 626–630. ( 10.1038/384626a0) [DOI] [Google Scholar]
- Ennos A. R. 1989. Functional wing morphology and aerodynamics of Panorpa germanica (insecta: Mecoptera). J. Exp. Biol. 143, 267–284. [Google Scholar]
- Fish F. E., Nusbaum M. K., Beneski J. T., Ketten D. R. 2006. Passive cambering and flexible propulsors: cetacean flukes. Bioinspir. Biomim. 1, S42–S48. ( 10.1088/1748-3182/1/4/S06) [DOI] [PubMed] [Google Scholar]
- Fry S. N., Sayaman R., Dickinson M. H. 2005. The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 208, 2303–2318. ( 10.1242/jeb.01612) [DOI] [PubMed] [Google Scholar]
- Gordon J. E. 1978. Structures: or why things don't fall down. New York, NY: Penguin Books. [Google Scholar]
- Hamamoto M., Ohta Y., Hara K., Hisada T. 2007. Application of fluid–structure interaction analysis to flapping flight of insects with deformable wings. Adv. Robot. 21, 1–21. ( 10.1163/156855307779293643) [DOI] [Google Scholar]
- Heathcote S., Wang Z., Gursul I. 2008. Effect of spanwise flexibility on flapping wing propulsion, J. Fluids Struct. 24, 183–199. ( 10.1016/j.jfluidstructs.2007.08.003) [DOI] [Google Scholar]
- Ho S., Nassef H., Pornsinsirirak N., Tai Y. C., Ho C. M. 2003. Unsteady aerodynamics and flow control for flapping wing flyers. Progr. Aerospace Sci. 39, 635–681. ( 10.1016/j.paerosci.2003.04.001) [DOI] [Google Scholar]
- Ishihara D., Horie T., Denda M. 2009. A two-dimensional computational study on the fluid–structure interaction cause of wing pitch changes in dipteran flapping flight. J. Exp. Biol. 212, 1–10. ( 10.1242/jeb.020404) [DOI] [PubMed] [Google Scholar]
- Kamakoti R., Shyy W. 2004. Fluid–structure interaction for aeroelastic applications. Progr. Aerospace Sci. 40, 535–558. ( 10.1016/j.paerosci.2005.01.001) [DOI] [Google Scholar]
- Lauder G. V., Madden P. G. A. 2007. Fish locomotion: kinematics and hydrodynamics of flexible foil-like fins. Exp. Fluids 43, 641–653. ( 10.1007/s00348-007-0357-4) [DOI] [Google Scholar]
- Lauder G. V., Madden P. G., Mittal R., Dong H., Bozkurttas M. 2006. Locomotion with flexible propulsors. I. Experimental analysis of pectoral fin swimming in sunfish. Bioinspir. Biomim. 1, S25–S34. ( 10.1088/1748-3182/1/4/S04) [DOI] [PubMed] [Google Scholar]
- Lehmann F. O. 2008. When wings touch wakes: understanding locomotor force control by wake wing interference in insect wings. J. Exp. Biol. 211, 224–233. ( 10.1242/jeb.007575) [DOI] [PubMed] [Google Scholar]
- Liu H. 2002. Computational biological fluid dynamics: digitizing and visualizing animal swimming and flying. Integr. Comp. Biol. 42, 1050 ( 10.1093/icb/42.5.1050) [DOI] [PubMed] [Google Scholar]
- Mountcastle A. M., Daniel T. L. 2009. Aerodynamic and functional consequences of wing compliance. Exp. Fluids 46, 873–882. ( 10.1007/s00348-008-0607-0) [DOI] [Google Scholar]
- Norberg R. A. 1972. Pterostigma of insect wings an inertial regulator of wing pitch. J. Compar. Physiol. 81, 9–22. ( 10.1007/BF00693547) [DOI] [Google Scholar]
- Prempraneerach P., Hover F. S., Triantafyllou M. S. 2003. The effect of chordwise flexibility on the thrust and efficiency of a flapping foil. In Proc. 13th Int. Symp. on Unmanned Untethered Submersible Technology: special session on bioengineering research related to autonomous underwater vehicles, New Hampshire. [Google Scholar]
- Ramamurti R., Sandberg W. C. 2002. A three-dimensional computational study of the aerodynamic mechanisms of insect flight. J. Exp. Biol. 205, 1507–1518. [DOI] [PubMed] [Google Scholar]
- Ramamurti R., Sandberg W. C. 2007. A computational investigation of the three-dimensional unsteady aerodynamics of Drosophila hovering and maneuvering. J. Exp. Biol. 210, 881–896. ( 10.1242/jeb.02704) [DOI] [PubMed] [Google Scholar]
- Sane S. P. 2003. The aerodynamics of insect flight. J. Exp. Biol. 206, 4191–4208. ( 10.1242/jeb.00663) [DOI] [PubMed] [Google Scholar]
- Sane S. P., Dickinson M. H. 2001. The control of flight force by a flapping wing: lift and drag production. J. Exp. Biol. 204, 2607–2626. [DOI] [PubMed] [Google Scholar]
- Sane S. P., Dickinson M. H. 2002. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 205, 1087–1096. [DOI] [PubMed] [Google Scholar]
- Shyy W., et al. 2008. Computational aerodynamics of low Reynolds number plunging, pitching and flexible wings for MAV applications. Acta Mech. Sinica 24, 351–373. ( 10.1007/s10409-008-0164-z) [DOI] [Google Scholar]
- Song A., Tian X. D., Israeli E., Galvao R., Bishop K., Swartz S., Breuer K. 2008. Aeromechanics of membrane wings with implications for animal flight. AIAA J. 46, 2096–2106. ( 10.2514/1.36694) [DOI] [Google Scholar]
- Sun M., Tang J. 2002. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J. Exp. Biol. 205, 55–70. [DOI] [PubMed] [Google Scholar]
- Usherwood J. R., Ellington C. P. 2002a. The aerodynamics of revolving wings. I. Model hawkmoth wings. J. Exp. Biol. 205, 1547–1564. [DOI] [PubMed] [Google Scholar]
- Usherwood J. R., Ellington C. P. 2002b. The aerodynamics of revolving wings. II. Propeller force coefficients from mayfly to quail. J. Exp. Biol. 205, 1565–1576. [DOI] [PubMed] [Google Scholar]
- Walker S. M., Thomas A. L. R., Taylor G. K. 2009. Photogrammetric reconstruction of high-resolution surface topographies and deformable wing kinematics of tethered locusts and free-flying hoverflies. J. R. Soc. Interface 6, 351–366. ( 10.1098/rsif.2008.0245) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z. J. 2004. The role of drag in insect hovering. J. Exp. Biol. 207, 4147–4155. ( 10.1242/jeb.01239) [DOI] [PubMed] [Google Scholar]
- Wang Z. J. 2005. Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210. ( 10.1146/annurev.fluid.36.050802.121940) [DOI] [Google Scholar]
- Wang Z. J., Birch J. M., Dickinson M. H. 2004. Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. J. Exp. Biol. 207, 449–460. ( 10.1242/jeb.00739) [DOI] [PubMed] [Google Scholar]
- Wootton R. J. 1992. Functional morphology of insect wings. Annu. Rev. Entomol 37, 113–140. ( 10.1146/annurev.en.37.010192.000553) [DOI] [Google Scholar]
- Wootton R. J. 1993. Leading edge section and asymmetric twisting in the wings of flying butterflies (Insecta, Papilionoidea). J. Exp. Biol. 180, 105–117. [Google Scholar]
- Wootton R. J. 1998. Smart engineering in the mid-Carboniferous: how well could Palaeozoic dragoflies fly. Science 282, 749–751. ( 10.1126/science.282.5389.749) [DOI] [PubMed] [Google Scholar]
- Wootton R. J., Evans K. E., Herbert R., Smith C. W. 2000. The hind wing of the desert locust (Schistocerca gregaria Forskal). I. Functional morphology and mode of operation. J. Exp. Biol. 203, 2921–2931. [DOI] [PubMed] [Google Scholar]
- Wootton R. J., Herbert R. C., Young P. G., Evans K. E. 2003. Approaches to the structural modelling of insect wings. Phil. Trans. R. Soc. Lond. B 358, 1577–1587. ( 10.1098/rstb.2003.1351) [DOI] [PMC free article] [PubMed] [Google Scholar]