NONINVASIVE MEASUREMENT OF LOCAL THERMAL DIFFUSIVITY USING BACKSCATTERED ULTRASOUND AND FOCUSED ULTRASOUND HEATING

Abstract

Previously, noninvasive methods of estimating local tissue thermal and acoustic properties using backscattered ultrasound have been proposed in the literature. In this article, a noninvasive method of estimating local thermal diffusivity in situ during focused ultrasound heating using beamformed acoustic backscatter data and applying novel signal processing techniques is developed. A high intensity focused ultrasound (HIFU) transducer operating at subablative intensities is employed to create a brief local temperature rise of no more than 10°C. Beamformed radio-frequency (RF) data are collected during heating and cooling using a clinical ultrasound scanner. Measurements of the time-varying “acoustic strain”, that is, spatiotemporal variations in the RF echo shifts induced by the temperature related sound speed changes, are related to a solution of the heat transfer equation to estimate the thermal diffusivity in the heated zone. Numerical simulations and experiments performed in vitro in tissue mimicking phantoms and excised turkey breast muscle tissue demonstrate agreement between the ultrasound derived thermal diffusivity estimates and independent estimates made by a traditional hot-wire technique. The new noninvasive ultrasonic method has potential applications in thermal therapy planning and monitoring, physiological monitoring and as a means of noninvasive tissue characterization.

INTRODUCTION

The delivery of an accurate thermal dose is essential for the success of ablative thermal therapies such as high intensity focused ultrasound (HIFU) (Vaezy et al. 1997; Sanghvi et al. 1999; ter Haar 2001; Wu et al. 2002) and radio-frequency ablation (Mahnken et al. 2004; Frericks et al. 2005; Nour and Lewin 2005) in the clinic. The thermal parameters at the ablation site, namely, thermal diffusivity and perfusion loss, play important roles in the final therapeutic outcome as they influence the evolution of temperature distributions in space and time achieved in the tissue. The thermal diffusivity is an intrinsic tissue thermal property that combines the thermal conductivity and the heat capacity to express the rate at which heat dissipates and, thus, directly influences the time dependence of the temperature distribution in tissue. Perfusion acts as a local sink for excess heat energy by convective transport and depends on the degree of vascularity at the ablation site and proximity to larger blood vessels. In reality, these tissue specific thermal parameters are highly variable between tissue types and also across individuals. Hence, noninvasive methods of measuring these thermal parameters at the treatment location can reduce the uncertainty in therapeutic dose planning and delivery. Development of such technologies could also provide a means of tissue characterization to monitor physiological response to stimulus, or to detect abnormal tissue pathologies, for example (Lagendijk et al. 1988; Cheng and Plewes 2002).

Recently, the use of numerical simulation tools to predict the temperature distribution and thermal dose for therapy dosimetry planning applications has been widely reported in the literature (Meaney et al. 1998; Kolios et al. 1999; Curra 2001). The Pennes bio-heat transfer equation (BHTE) (Pennes 1948) is used to compute the temperature distribution and the thermal dose is computed using the formalism proposed by Sapareto and Dewey (1984). These simulation tools typically use a priori knowledge or assume standard values for tissue thermal parameters, namely, thermal diffusivity and perfusion loss. Uncertainties in the knowledge of these parameters can result in significant errors in the temperature distribution computed using the BHTE and consequently the thermal dose, which is a clinically important indicator of the endpoint of thermal therapy. Providing in situ estimates of the thermal parameters in the treatment region as inputs to the simulation tools would reduce errors in the predicted temperature distributions during planning phases and improve the ability of these tools to effectively adapt to varying local conditions for planning or during treatment.

Imaging techniques based on magnetic resonance imaging (MRI) (Cheng and Plewes 2002) and infrared (IR) imaging (Telenkov et al. 2001) to noninvasively estimate tissue thermal diffusivity and/or perfusion have been previously reported. However, no ultrasound based noninvasive method to estimate these parameters has been developed to the best of the knowledge of the authors. An ultrasound-based estimation technique is a more attractive option for use with therapy delivery systems because MRI requires specialized therapy equipment compatible with high magnetic fields and has lower temporal resolution (frame rate) compared with ultrasound imaging. IR imaging methods are limited to estimation of surface thermal measurements and may not be suitable for deeper ablation sites due to poor penetration.

Ultrasonic methods of estimating tissue thermal and acoustic properties have been recently proposed. Yao and Ebbini (Hui et al. 2004) demonstrated the feasibility of reliably estimating the initial heating rate at a localized heating spot by inducing a temperature change on the order of 1 °C and proposed that the ultrasonically estimated initial heating rate can be used to compute the local tissue absorption. They also demonstrated that the ultrasonically determined initial temperature decay rate after turning off the heating demonstrates excellent agreement with the decay rate obtained from invasive thermocouple readings and conclude that the local perfusion can be estimated from these decay rate measurements. However, no quantitative estimate of the local tissue properties, absorption and perfusion, is obtained in that study. Recently, Sumi and Yanagimura (2005, 2007) proposed a technique for reconstructing the thermal properties such as thermal conductivity and diffusivity provided that quantitative spatial and temporal temperature information of the region-of-interest and reference values of the thermal properties are independently measured a priori. The temperature rise in the sample was induced using a heated waterbath. Simulations and experimental results obtained in a tissue mimicking phantom were presented. Practical application of the methods in noninvasive therapy modalities such as HIFU was not presented in that study.

In this article, a noninvasive ultrasound-based technique for estimating the local thermal diffusivity in situ using focused ultrasound or HIFU heating and application of novel backscattered radio-frequency (RF) signal processing techniques is presented. The technique is designed such that the thermal diffusivity estimation can be performed in the treatment region as part of a therapy planning calibration procedure conducted prior to the therapy delivery session. The theoretical framework underlying the estimation procedure is developed for the in vivo situation using the Green’s function solution for the BHTE including the effect of bulk perfusion as a heat sink. It is shown from the theoretical analysis that the thermal diffusivity can be obtained by tracking the rate of change of the size of the heated region without knowledge of the absolute temperature. The estimated thermal diffusivity can then used as a known quantity to estimate the unknown perfusion term if information about the heat source is available. The effects of heat transport in the presence of a large blood vessel are not considered in this theoretical formulation. Since the current experimental work is limited to in vitro scenarios, the estimation of perfusion is not included in the parameter estimation step. Discussions on extending the parameter estimation step to the in vivo case for measuring perfusion are provided. The parameter estimation technique is based on visualizing the spatiotemporal variation of temperature induced strain (Miller et al. 2002, 2004) estimated from the raw ultrasound backscatter data after a short focused ultrasound heating pulse is applied at subablative intensities. The temperature induced strain is caused by changes in the local sound speed of the medium and thermal expansion (Maass-Moreno et al. 1996; Simon et al. 1998; Varghese et al. 2002). The maximum induced temperature rise is less than 10°C to avoid any permanent changes in tissue. A mathematical analysis of the solution to the heat transfer equation illustrates that the spatiotemporal rate of change of the temperature induced strain profile transverse to the HIFU beam axis of propagation is directly related to the thermal diffusivity. The technique is applied to ultrasound backscatter data collected during in vitro experiments performed in a tissue mimicking phantom and excised turkey breast muscle tissue.

THEORY

The technique adopted in this work for the estimation of the thermal diffusivity is based on determining unknown thermal parameters from the BHTE. For the in vitro case, in the absence of perfusion, the BHTE reduces to the heat transfer equation (HTE). In this analysis, it is assumed that the medium is locally homogenous and isotropic in the local region where the thermal parameters are estimated.

Bio heat transfer equation

The differential equation describing the transient BHTE can be written in axisymmetric cylindrical coordinates as,

$$\frac{\partial T}{\partial t}=K{\nabla }^{2}T-\mathit{\text{bT}}+Q(t)·I(r,z)$$ (1)

where T(r,z,t) is the temperature change in °C, K is the thermal diffusivity (m²/s), Q(t) (°C/s) represents the local in situ heating rate due to ultrasound energy absorption, I(r,z) is the normalized spatial acoustic intensity distribution profile (unitless), r represents the axis perpendicular to beam propagation (transverse) and z represents the beam propagation axis (longitudinal). b is given by w_bρ_bC_b/ρC, where w_b is the blood perfusion rate (ml/s/ml), ρ_b and ρ represent the density of blood and tissue respectively in kg/m³, C_b and C represent the heat capacity of blood and tissue respectively in J/kg/°C. It may be noted that Q is a scalar number and I(r,z) is a two-dimensional (2D) matrix of values between 0 and 1 with the rows representing r and the columns representing z.

The solution of transient BHTE can be expressed in terms of the Green’s function G and the source heating term S(r,z,t) in cylindrical coordinates as (Carslaw and Jaeger 1959; Arfken and Weber 2005),

$$\begin{array}{c}T(r,z,t)\hfill \\ ={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}S(r^{\prime },z^{\prime },t^{\prime })G(r,z,t;r^{\prime },z^{\prime },t^{\prime })\times r^{\prime }{\mathit{\text{dr}}}^{\prime }{\mathit{\text{dz}}}^{\prime }{\mathit{\text{dt}}}^{\prime }}}}\hfill \end{array}$$ (2)

The Green’s function of the transient BHTE is given by (Vyas and Rustgi 1992),

$$\begin{array}{c}G=\frac{r^{\prime }{u}_{t^{\prime }}(t)}{\sqrt{2\mathrm{\pi }}\rho C{[2D(t-t^{\prime })]}^{3/2}}\text{exp}[-b(t-t^{\prime })]\times \text{exp}(-\frac{{(z-z^{\prime })}^2}{4D(t-t^{\prime })})\\ \times \text{exp}(-\frac{(r^2+{r^{\prime }}^2)}{4D(t-t^{\prime })})I_0\left(\frac{r{r}^{\prime }}{2D(t-t^{\prime })}\right)\end{array}$$ (3)

where u_t′(t) is the unit step function,

$$\begin{array}{c}{u}_{{\mathrm{t}}^{\prime }}(\mathrm{t})=1\text{for}\mathrm{t}>{\mathrm{t}}^{\prime }\\ =0\text{for}\mathrm{t}<{\mathrm{t}}^{\prime }\end{array}$$ (4)

I₀(x) is the modified Bessel function of order zero.

The focused ultrasound source is modeled with a Gaussian spatial beam profile along the axial (z) and radial (r) directions as (Parker 1983,1985; Cheng and Roemer 2005),

$$S(r,z,t)=Q_{\mathit{\text{acoustic}}}(t)\times \text{exp}(\frac{-r^2}{{\beta }_r})\times \text{exp}(\frac{-z^2}{{\beta }_z})$$ (5)

where β_r and β_z represent the ultrasound beam width along r and z, respectively and Q_acoustic(t) is the acoustic power deposited per unit volume in W/m³.

Substituting eqn 3 and eqn 5 in eqn 2 and rearranging the terms we get,

$$\begin{array}{c}T(r,z,t)=\frac{1}{\sqrt{2\mathrm{\pi }}\rho C}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{1}{{[2K(t-t^{\prime })]}^{1/2}}{Q}_{\mathit{\text{acoustic}}}(t^{\prime })\text{exp}[-b(t-t^{\prime })]{\mathit{\text{dt}}}^{\prime }}\\ \hfill {\displaystyle \times \underset{-\infty }{\overset{\infty }{\int }}\text{exp}[-(\frac{{z^{\prime }}^2}{{\beta }_z}+\frac{{(z-z^{\prime })}^2}{4K(t-t^{\prime })}\left)\right]{\mathit{\text{dz}}}^{\prime }}\hfill \\ \times {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{{r^{\prime }}^2}{[2K(t-t^{\prime })]}\text{exp}[-(\frac{{r^{\prime }}^2}{{\beta }_r}+\frac{(r^2+{r^{\prime }}^2)}{4K(t-t^{\prime })}\left)\right]I(\frac{r{r}^{\prime }}{2K(t-t^{\prime })})d{r}^{\prime }}\end{array}$$ (6)

Solving the integrals in eqn 6 with respect to r’ and z’ and rearranging the terms,

$$\begin{array}{cc}T(r,z,t)=\hfill & \frac{{\beta }_r\sqrt{{\beta }_z}}{\rho C}{\displaystyle \underset{0}{\overset{t}{\int }}{\mathit{\text{dt}}}^{\prime }{Q}_{\mathit{\text{acoustic}}}({\mathit{\text{t}}}^{\prime })\text{exp}[-b(t-t^{\prime })]}\hfill \\ & \times \frac{\text{exp}[-(\frac{z^2}{4K(t-t^{\prime })+{\beta }_z}\left)\right]}{{(4K(t-t^{\prime })+{\beta }_z)}^{1/2}}\hfill \\ & \times \frac{\text{exp}[-(\frac{r^2}{4K(t-t^{\prime })+{\beta }_r}\left)\right]}{(4K(t-t^{\prime })+{\beta }_r)}\hfill \end{array}$$ (7)

The above equation requires the time integral to be solved numerically. However, by limiting the focused ultrasound heat source to a short burst of energy of duration t₀ applied at t = 0 (Newman and Lele 1985; Parker 1985), the impulse approximation can be used to represent the heat source Q_acoustic(t) as,

$$Q_{\mathit{\text{acoustic}}}(t)=2\alpha I_0{t}_0\delta (t)$$ (8)

where, I₀ is the peak acoustic intensity, α is the acoustic absorption coefficient.

Substituting eqn 8 in 7, we get the temperature profiles during the decay phase as,

$$T(r,z,t)=\underset{A_p(t)}{\underbrace{\frac{2\alpha I_0{t}_0{\beta }_r\sqrt{{\beta }_z}}{\rho C}\text{exp}[-\mathit{\text{bt}}]\frac{\text{exp}[-(\frac{z^2}{4\mathit{\text{Kt}}+{\beta }_z}\left)\right]}{{(4\mathit{\text{Kt}}+{\beta }_z)}^{1/2}(4\mathit{\text{Kt}}+{\beta }_r)}}}\text{exp}[-(\frac{r^2}{4\mathit{\text{Kt}}+{\beta }_r}\left)\right]$$ (9)

If the temperature profiles are observed along the radial direction r for a fixed value of z, the above equation can be expressed as,

$$T(r,z,t)=A_p(t)\text{exp}[-(\frac{r^2}{R(t)}\left)\right]$$ (10)

Equation (10) is the product of A_p(t) and a Gaussian curve with width related parameter R(t) = 4Kt + β_r at time t. The equation demonstrates that it is possible to estimate the thermal diffusivity and the perfusion separately in a sequential manner provided (i) A short duration heating pulse (eqn 8) relative to the times for thermal dissipation is applied to induce the temperature rise, and (ii) Flow is not in large vessels which would result in a directional heat loss but rather through perfusion modeled as a nondirectional heat sink term in the BHTE.

Focused ultrasound beams, such as those employed this article, are particularly well suited to induce temperature rises rapidly and produce a sharp thermal gradient perpendicular to the direction of propagation of the acoustic beam. The focal field of a uniformly excited spherical transducer is not Gaussian but the focal shape can be well approximated by an equivalent Gaussian that is fit by matching average power over the peak. In addition, since the heating effect produced by focused beams is local and the proposed thermal diffusivity estimation technique is also designed to produce a local estimate around that heated location, the use of a nondirectional perfusion term as implemented in the BHTE should be valid. If large blood vessels are present within the parameter estimation region-of-interest that result in a directional heat sink, the parameter estimation method developed based on eqn 1 and the approximate forms that follow would not be valid.

From eqn 10, K is estimated by tracking the rate of change of R(t) i.e.,

$$\frac{d[R(t)]}{\mathit{\text{dt}}}=\frac{d[4\mathit{\text{Kt}}+{\beta }_r]}{\mathit{\text{dt}}}=4K$$ (11)

The estimated thermal diffusivity can then be substituted in A_p(t) to predict the local perfusion b assuming the terms β_r, β_z are known from the characteristics of the HIFU beam profile. As part of the estimation procedure for b, the heat source term 2αI₀t₀/ρC would also have to be determined. This can be performed using an iterative approach such as that proposed by Cheng and Plewes (2002) where the heat source and perfusion terms are alternately computed until the parameter values converge.

The temperature variation at the center of the focal region (r = 0,z = 0) is,

$$\mathrm{T}(\mathrm{r}=0,\mathrm{z}=0,\mathrm{t})=\frac{2\alpha I_0{t}_0{\beta }_r\sqrt{{\beta }_z}}{\rho C{(4\mathit{\text{Kt}}+{\beta }_z)}^{1/2}(4\mathit{\text{Kt}}+{\beta }_r)}\text{exp}[-\mathit{\text{bt}}]$$ (12)

The temperature at the center of the focus will decay as a function of t and is affected by the perfusion constant.

The scope of the experimental results presented in this article was limited to in vitro conditions for which there is no perfusion. Substituting b = 0 in eqn 9, the BHTE reduces to the HTE and we get,

$$T(r,z,t)=\underset{A(t)}{\underbrace{\frac{2\alpha I_0{t}_0{\beta }_r\sqrt{{\beta }_z}}{\rho C}\frac{\text{exp}[-(\frac{z^2}{4\mathit{\text{Kt}}+{\beta }_z}\left)\right]}{{(4\mathit{\text{Kt}}+{\beta }_z)}^{1/2}(4\mathit{\text{Kt}}+{\beta }_r)}}}\text{exp}[-(\frac{r^2}{4\mathit{\text{Kt}}+{\beta }_r}\left)\right]$$ (13)

or equivalent to eqn 10,

$$T(r,z,t)=A(t)\text{exp}[-(\frac{r^2}{R(t)}\left)\right]$$ (14)

where A(t) is equal to A_p(t) with the perfusion constant b set to zero, and R(t) = 4Kt + β_r as before. Thus, the approach to estimating K relies on measuring the rate of change in transverse width of the temperature profile near the HIFU focus.

Estimation of thermal diffusivity using backscattered ultrasound

The estimation of thermal diffusivity using backscattered ultrasound is based on tracking the spatiotemporal evolution of the temperature induced strain profiles. In this approach, a short heating pulse is applied and the resulting temperature induced strain is measured ultrasonically over a period of time sufficient to detect the spatial diffusion of the heat. This section describes how quantitative estimates of the thermal diffusivity can be obtained from time series of the strain profiles.

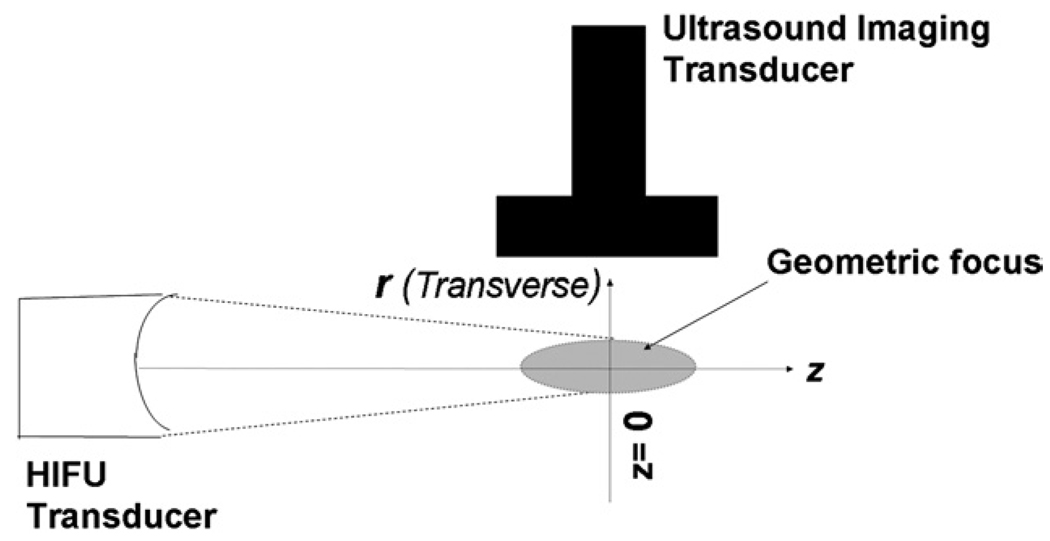
The experimental arrangement, including orientation of the HIFU transducer (used to induce the local temperature rise) and the position of the ultrasound imaging probe and the sample volume being interrogated, is illustrated in Fig. 1. For a short HIFU-induced heating pulse applied at time t = 0, the resulting temperature distribution along the transverse direction r after the HIFU pulse has been turned off is modeled by eqn 14. Previously, it has been demonstrated (Simon et al. 1998; Varghese et al. 2002; Pernot et al. 2004) that the temperature-induced strain (ε) measured from the ultrasound radio-frequency (RF) backscatter signal, for small temperature rises above ambient temperature, is directly proportional to the induced temperature change T(r,t)

$$T(r,t)=k\epsilon (r,t).$$ (15)

where k is a scalar constant.

Fig. 1.

Schematic illustration of the orientation of HIFU therapy transducer, ultrasound imaging transducer and location of the geometric focal spot of the therapy transducer.

The maximum temperature rise that can be induced depends on the range of temperatures for which k is constant to minimize the estimation error resulting from the temperature dependence of this parameter. For example, based on experiments in turkey muscle tissue, it was reported that the strain versus temperature relation is linear for temperature rises up to 10°C (Maass-Moreno et al. 1996; Simon et al. 1998). Miller et. al. (Miller et al. 2002) have reported on the temperature dependence of k and its variability with tissue composition. For example, in normal liver (low fat content) and fatty liver, k remains nearly constant (from 37°C to around 50 °C), whereas for liver with intermediate fat content k is small and may even change sign. For such conditions, the method has fundamental limitations and may not work unless the tissue is heated or cooled to a substantially different operating point.

From eqn 14 and eqn 15, we get,

$$\epsilon (r,t)={\epsilon }_{\text{max}}(t)e^{-r^2/R(t)}$$ (16)

where ε_max = k A(t) (no perfusion) or k A_p(t) (with perfusion).

In this technique, as long as the parameter k is independent of temperature over the range of interest, it is not necessary to know the value of the constant k. The data processing result indicates the degree to which k is constant with temperature. Integrating eqn 16 along r in cylindrical coordinates, the cumulative shift in the ultrasound RF echo locations s(r,t) along the imaging beam has the form of the error function erf(x),

$$s(r,t)={\displaystyle \underset{u=0}{\overset{u=r}{\int }}\mathrm{\epsilon }(u,t)\mathit{\text{du}}=s_{\text{max}}(t)}{\displaystyle \underset{u=0}{\overset{u=r}{\int }}{e}^{-u^2/R(t)}\mathit{\text{du}},}$$ (17)

where s_max(t) is the peak displacement. From eqn 17, it can be seen that the parameter R(t) can be obtained from the s(r,t) profile for measurement time t. It is important to note from eqn 17 that since the integration is performed with respect to r, the perfusion term contained in s_max(t) is separable and allows the thermal diffusivity to be independently estimated.

The above equation does not compensate for the thermal lens effect (decorrelation in the RF signal due to refraction and refocusing of the US beam during heating) (Simon et al. 1998). The thermal “lens” can lead to aberration of the acoustic imaging beam when lateral temperature gradients are large compared with the imaging beam width. As a consequence of this effect, the shape of s(r,t) in the above equation would deviate from the ideal error function erf(x), especially distal to the heated zone. Additional sound propagation modeling, signal processing and filtering would be required to minimize the errors introduced by this effect in the parameter estimation process. Simon and Ebbini (Simon et al. 1998, Fig. 12) have experimentally demonstrated that the effect is dominant at the ends of the HIFU beam and is not present in the central region. Based on this observation, care was taken in the experimental design in this work to ensure that only scanlines towards the center of the focal region were used for analysis to estimate the thermal diffusivity. Placing the HIFU beam in the imaging plane reduces the lateral gradient in the plane at the ends of the HIFU focal zone. Additionally, centering the imaging plane on the HIFU focus minimizes the role of lateral (out of plane) distortion by imposing symmetry.

As indicated in eqn 11, differentiating R(t) with respect to t gives,

$$\frac{d[R(t)]}{\mathit{\text{dt}}}=4K.$$ (18)

Equation (18) shows that by computing the rate of change of R(t) versus t, the thermal diffusivity K can be estimated. The measurement procedure is noninvasive and can use several ultrasound scanlines over a sequence of frames to improve the signal to noise ratio. It may be noted from eqn 17 that errors introduced by the signal processing process in the estimation of s(r,t) will affect the estimated R(t) and consequently the estimated value of thermal diffusivity K. These signal processing related errors are in addition to the underlying model shortcomings such as neglecting thermal lensing, assuming spatial homogeneity in K and neglecting temperature dependence of K (and k). In many cases, we expect these assumptions to hold and we present two experimental examples for which the method is successful.

MATERIALS AND METHODS

Simulations

To validate the ultrasound RF-based estimation technique for the noninvasive estimation of thermal diffusivity, simulations were performed by generating backscattered RF scanlines during a simulated HIFU exposure and applying the estimation algorithm. The procedure outlined by Miller and Bamber (Miller et al. 2002) was followed to simulate the effect of temperature on backscattered RF data. A random scatterer distribution is created with Gaussian distributed amplitudes while the spacing between the scatterers was derived from a uniform distribution. Twenty scatterers per wavelength are generated along each scanline to guarantee fully developed speckle. RF waveforms are synthesized by convolution of a system impulse response with the point scatterer distribution. In this study, the evolution of the temperature field over a 3 cm × 2 cm 2D region around the HIFU focus was computed using an axisymmetric finite element solution of the heat transfer equation implemented in FEMLAB™ (now COMSOL Multiphysics, by COMSOL AB, Stockholm, Sweden). The heat source field was defined using the linear acoustic intensity field for a single element transducer with a geometric focal length of 35 mm and active diameter of 16 mm, operating at 5 MHz; the field of the transducer used in the experiments was mapped using a hydrophone (Golden Lipstick, 200 µm aperture, SEA, Soquel, CA, USA) to confirm that the simulated beam pattern matched the measured transducer field. The HIFU ON-time was 5 s and the cool down phase (OFF-time) was observed for 15 s. The simulation parameters are listed in Table 1. The HIFU exposure intensity was chosen such that the maximum temperature reached at the focus was no greater than 10°C above ambient temperature (37°C). The temperature maps were converted to corresponding sound speed using the mapping reported by Bloch et al. (Bloch et al. 1998) for liver tissue, which is a primary tissue of interest for HIFU treatment applications (in simulations, the acoustic strain coefficient k must be specified but its value is not used in the estimation of diffusivity K). For each scanline, the sound speed depth profile was mapped to apparent displacements of the scatterers and new RF backscattered waveforms were computed for these new scatterer locations. The center frequency of the transmit pulse used in the ultrasound imaging system was 8 MHz with a fractional bandwidth of 60%. The signal-to-noise ratio (SNR) of the simulated RF signals was set to 20 dB by the addition of white noise. Imaging RF waveforms were generated at a frame rate of 1 frame per second for the warming and cooling phases. Fifty realizations of the simulations using different scatterer arrangements were performed to compute first and second order statistics. For the estimation of K, signal analysis was performed along scanlines passing through the HIFU focal zone at z = 0 (Fig. 1). The RF waveform shifts s(r,t) and function R(t) were computed by processing each frame acquired during the cool down phase relative to a reference frame acquired before heating commenced.

Table 1.

Ultrasound and thermal parameter values used in simulation to generate RF data for noninvasive estimation of thermal diffusivity

Center frequency (MHz)	8 MHz, 60% bandwidth
Scatterer density	20 per wavelength
Sound speed (m/s)	1540
Ultrasonic SNR (dB)	20
Sampling rate (MHz)	32
HIFU ON time (s)	5
HIFU frequency (MHz)	5
Initial temperature (°C)	25
Thermal conductivity (W/m/°C)	0.7
Heat capacity (J/kg/°C)	4180
Density (kg/m3)	1000

SNR = signal-to-noise ratio; HIFU = high intensity focused ultrasound; RF = radio-frequency.

RF data analysis

Equation (17) illustrates that the backscatter waveform shifts s(r,t) can be represented by a closed functional form and parameterized in terms of s_max (maximum amplitude) and R (width parameter). In this article, a novel parametric estimation approach is employed to estimate s_max and R in eqn 17 from the RF backscatter data collected during the HIFU experiment. A schematic representation of the estimation technique is presented in Fig. 2. Techniques for estimation of ultrasound echo location shifts s(r,t) between RF data frames acquired from a spatial region-of-interest have been previously used for ultrasound-based temperature estimation (Simon et al. 1998; Miller et al. 2002; Miller et al. 2004). However, such methods first estimate strain and then apply those estimates to temperature estimation. They do not incorporate knowledge of the underlying physical heat diffusion mechanism in the estimation algorithm and result in noisy and often biased estimates for strains that occur over distances that comprise few imaging wavelengths. The approach presented here estimates thermal parameters s_max and R by iterative analysis of the RF data and makes use of thermal diffusion modeling to guide the solution. The processing is cast as a minimization problem and relies on comparing a reference RF waveform (acquired before heating commenced, at time t = t₀) to a post-heating waveform acquired during cool down (t= t_cool). As indicated in eqn 17, the heat transfer model is used to predict the displacement (shift) for a particular choice of parameters (s_max, R) and the predicted shift is applied to the heated waveform. The difference between the shift-corrected and reference waveforms is minimized by searching over the values of (s_max, R). This procedure provides an estimate of strain by relating the measured RF shifts to the underlying heat transfer model for the HIFU heating experiment and is accurate under the assumptions listed above. Furthermore, final degree of correlation, goodness of fit and apparent degree of linearity in the various results of processing provide clear assessment of the validity of several key assumptions.

Fig. 2.

Flowchart of technique to estimate s_max and R in eqn 17.

The steps in the algorithm to find the optimal R(t_cool) for a single scanline passing through the heated region are outlined below:

1. s(r,t) is mathematically modeled using eqn 17 with parameters (s_max, R) set to reasonable initial guess values for a particular time t = t_cool.

2. The RF line acquired at t = t_cool is shifted by function s(r, t_cool). Each data sample of the RF line is shifted by the corresponding value of s(r, t_cool). The shifted data points are then re-sampled onto the same uniform grid as the reference signal acquired at t = t₀. No additional global shift, scaling or any localized corrections other than that specified by s(r,t) is applied to the waveform. The shifting operation is similar in principle to temporal stretching (Alam and Ophir 1997; Varghese and Ophir 1997) and companding (Chaturvedi et al. 1998) earlier proposed in elasticity imaging. However, it must be noted that the phenomenon of thermal lens effect is not an issue in elasticity imaging as in estimating the temperature induced strain from the ultrasound backscatter.

3. The shifted RF line acquired at t = t_cool (step 2) and the reference RF line are both segmented into N nonoverlapping segments and the normalized zero-lag correlation coefficient for each segment i is computed using eqn 19. A fixed value of N is chosen. For a 1 cm scanline segment, a typical value of N is 15. In eqn 19, m is total number of RF samples (typically m = 40) in the segment.

   $${\mathrm{\sigma }}_i=\frac{{\displaystyle \sum _{j=1}^{j=m}{\mathit{\text{RF}}}_{t=t_0}(j,i)*{\mathit{\text{RF}}}_{t=t_{\mathit{\text{cool}}}}(j,i)}}{{\displaystyle \sum _{j=1}^{j=m}{[{\mathit{\text{RF}}}_{t=t_0}(j,i)]}^2*{\displaystyle \sum _{j=1}^{j=m}{[{\mathit{\text{RF}}}_{t=t_{\mathit{\text{cool}}}}(j,i)]}^2}}}$$ (19)

4. The total squared error $\mathit{\text{err}}={\displaystyle {\sum }_{i=1}^{i=N}{(1-{\mathrm{\sigma }}_i)}^2}$ is then computed.

5. The parameters (s_max, R) are updated iteratively until the value of err is less than 0.002.

The values of s_max and R obtained after minimization of err are called the best-fit parameters. Plots of the zero-lag cross-correlation before and after convergence are shown in Fig. 2 (bottom panel). This procedure is repeated for all the RF frames collected during the cool down phase (after HIFU has been turned off) to obtain a set of values of R(t) corresponding to each frame. The optimization algorithm was implemented using the MATLAB (The Mathworks Inc., Natick, MA, USA) function fminsearch, which is based on the Nelder-Mead Simplex search technique (Nelder and Mead 1965).

Phantom experiments

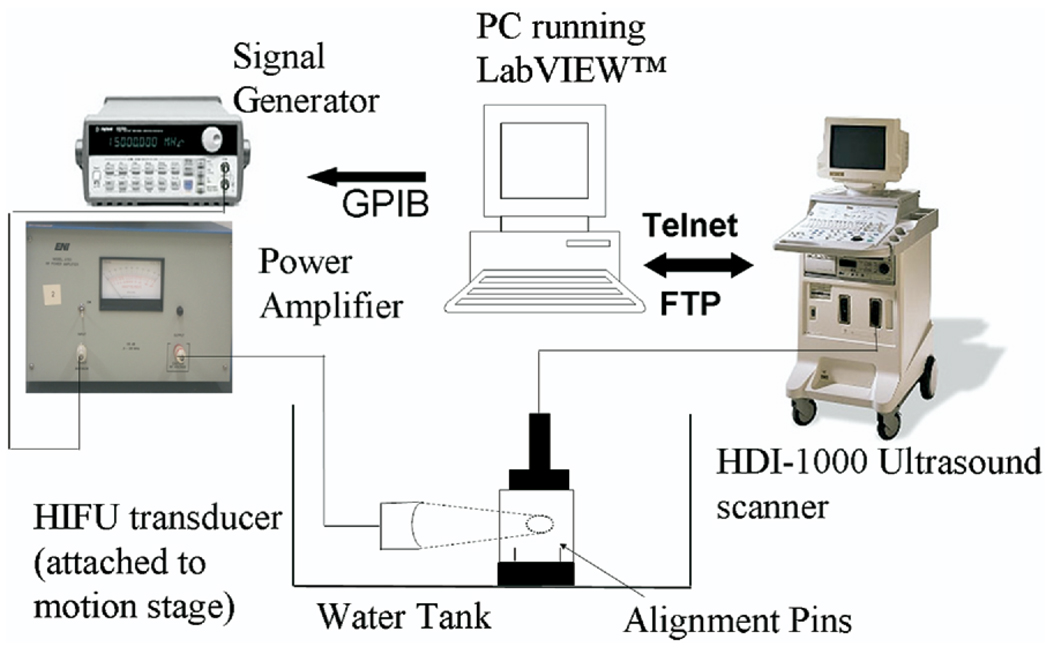
Experiments were performed in a tissue-mimicking phantom made of alginate based hydrogel containing 95% water by weight. The material is simple to prepare, nontoxic, and provides uniform scatterer distributions ideal for speckle tracking studies. The phantom is prepared by dissolving 16 gm of Jeltrate™ dental impression material (Dentsply Caulk Inc., Milford, DE, USA) in 300 ml water while stirring continuously to ensure a homogenous mix. The solution is degassed under vacuum and allowed to settle for 20 min in specially designed sample holders of size 5 × 5 × 6.5 cm³ in which the solution solidifies. The sound speed and the acoustic attenuation of the phantom at 25°C are measured using the sample replacement technique (Bloch et al. 1998; Madsen et al. 1999) with a pair of 7 mm diameter PVDF transducers (Sonic Concepts, Woodinville, WA, USA); measured bulk values for the sample used in this example were c = 1483 m/s and α = 0.35 dB/cm/MHz, respectively. The schematic diagram of the experimental set-up (calipers not shown) is presented in Fig. 3. A 5 MHz HIFU therapy transducer (SU-104, Sonic Concepts, Woodinville, WA, USA) with an aperture diameter of 33 mm and a focal depth of 35 mm was used to deliver the HIFU heating pulse. The HIFU transducer was rigidly attached to a three-dimensional translation stage that allows controlled motion in increments of 1 mm. The driving electronics for the HIFU transducer consisted of a signal generator (HP 33120, Hewlett Packard, Palo Alto, CA, USA) driving a power amplifier (A300, ENI, Rochester, NY, USA). The imaging probe used was the ATL CL10-5 (Philips Medical Systems, Bothell, WA, USA) with a bandwidth of 5 to 10 MHz. Vertical alignment pins affixed to the base of the sample holder were used to co-register the HIFU beam propagation plane with the imaging plane. Specifically, as part of the alignment procedure, the HIFU transducer is operated in pulse-echo mode and translated using the motion stage until the received echo amplitude from the proximal alignment pin is maximized thereby ensuring that the pins are in the HIFU focal plane; the HIFU transducer is then raised to place the focal region above the pins. The imaging transducer is mounted on the sample holder such that alignment pins are visible on B-mode images as straight lines, thus, assuring that the HIFU focal zone lies within the imaging plane.

Fig. 3.

Schematic of experimental set-up for ultrasound thermal diffusivity estimation.

RF data frames time-synchronized with the HIFU delivery were acquired using an ATL HDI-1000 ultrasound scanner (Philips Medical Systems, Bothell, WA, USA) during the HIFU heating phase lasting 5 s and the cool down phase lasting 15 s. The RF data frames were acquired at a frame rate of 1 frame per second. A personal computer running a software program developed in LabVIEW™ (National Instruments, Austin, TX, USA) controlled the operation of the entire system (Anand et al. 2003; Anand and Kaczkowski 2004). The RF data were transferred to the PC at the end of the experiment for offline data analysis. HIFU acoustic intensities were chosen such that the maximum temperature rise induced was approximately 10°C. The RF data sets were analyzed using the algorithm described in the previous section to compute R(t) and a least square fit was performed using eqn 7 to estimate the thermal diffusivity K. The experiment and estimation procedure was repeated on five phantom samples prepared using the same recipe.

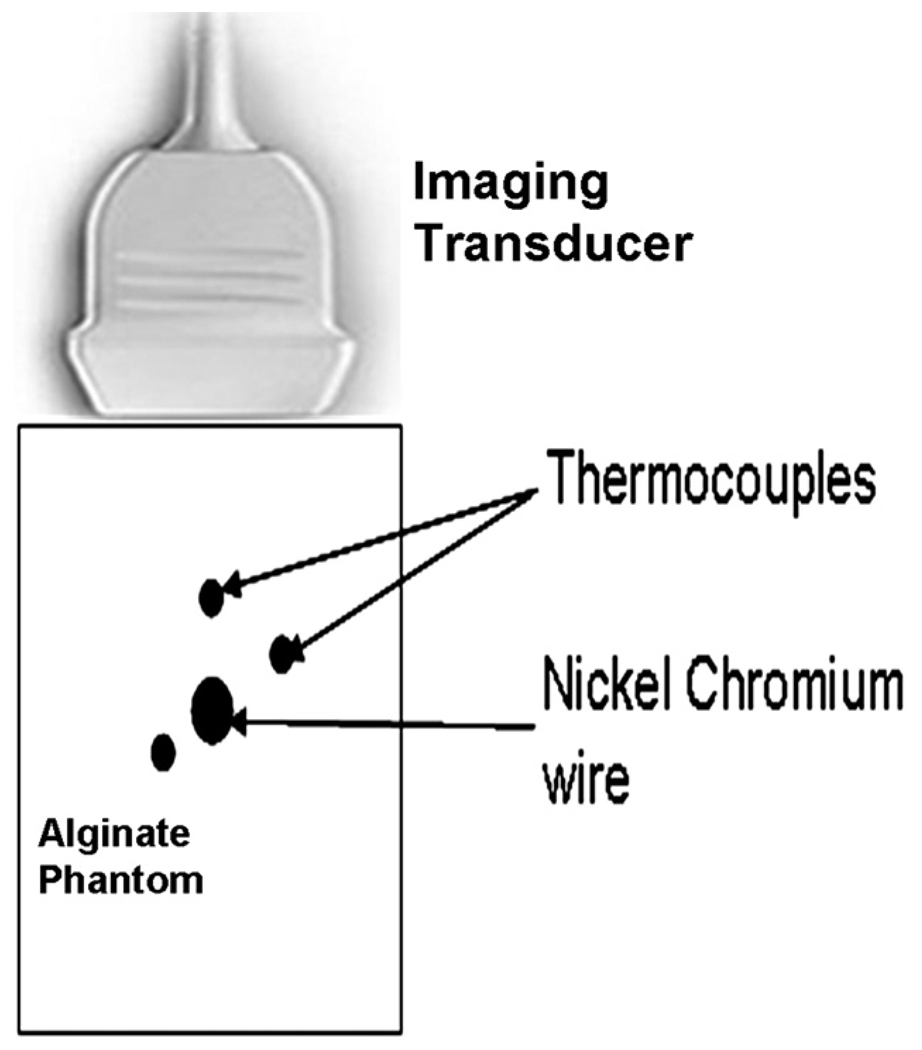
The thermal diffusivity (K) was also independently measured for the phantom samples using the transient hot-wire technique (Carslaw and Jaeger 1959; Prokop et al. 2003), a standard method reported in the heat transfer literature for measuring the thermal properties of solids. The estimates obtained by this method were compared with those obtained using the noninvasive ultrasound-based estimation procedure. A schematic representation of the imaging plane view of the transient hot-wire experiment set-up is shown in Fig. 4. A nickel-chromium (Ni-Cr) heating wire (Omega Engineering Inc., Stamford, CT, USA) was pulled taut through the center of the phantom sample placed in a custom designed aluminum holder. Three 0.2-mm diameter T-type thermocouples with copper-constantan junctions (HYP0-33-1-T-G-60-SMPW-M, Omega Engineering Inc., Stamford, CT, USA) were inserted into the phantom under ultrasound B-mode guidance to ensure that the thermocouple stayed parallel to the heating wire along its length. The thermocouples were placed at different radial distances from the wire, ranging from 2 to 5 mm. The distances from the tip of the thermocouples to the heating wire were measured using the distance measurement feature with L11-5 transducer (Philips Medical Systems, Bothell, WA, USA) on the HDI-1000 clinical ultrasound scanner with a precision of ±0.1 mm. A programmable DC power supply (PSP-2010, Goodwill Instek Ltd, Chino, CA, USA) was connected to the heating element through a series relay switch used to turn the heating circuit on and off remotely. The thermocouple terminals were connected to a data acquisition module (HP 34970, Hewlett Packard Inc., Palo Alto, CA, USA) to store the temperature readings in digitized form. A software-based control program developed in LabVIEW™ (National Instruments, Austin, TX, USA) controlled the delivery of electrical power to the heating wire, and the thermocouple data acquisition. The heating power was obtained using the voltage drop across and current through the wire, monitored with a pair of multimeters throughout the experiment; the measured values were 2 ± 0.01 V and 7 ± 0.01 A, respectively. The total heating time was 90 s and thermocouple data was acquired at 1 Hz throughout this interval. The maximum temperature rise was no greater than 10 to 15°C to prevent irreversible changes to the sample under test and to prevent formation of gas bubbles at the wire-gel interface. The experiments were performed in four samples prepared using the same recipe with three data sets acquired in each sample.

Fig. 4.

Schematic of experimental set-up for transient hot-wire technique

The spatiotemporal temperature distribution radially outward from the heating wire during heating with a constant heat source is approximately described by the following equation in axisymmetric cylindrical coordinates (Carslaw and Jaeger 1959),

$$T(r,t)=-\left(\frac{q}{4\mathrm{\pi }\mathrm{\lambda }}\right)(-{\displaystyle \underset{\frac{r^2}{4\mathit{\text{Kt}}}}{\overset{\infty }{\int }}\frac{e^{-u}}{u}\mathit{\text{du}}})$$ (20)

where the first term, $A=\frac{q}{4\mathrm{\pi }\lambda }$, is a constant and does not vary with time, and the second term is the exponential integral Ei( − r²/4Kt).q represents the power (W) delivered per unit length of the wire, λ represents the thermal conductivity (W/m/°C), K is the thermal diffusivity (m²/s), r represents the radial distance away from the wire (m), and t represents the time (s) after heating commenced. It is important to note that in the transient hot-wire method the thermal diffusivity is measured during the application of a constant heat source (using an embedded hot wire) and using eqn 20, while in the ultrasound based estimation approach the diffusivity is measured during cooling after the application of a short focused ultrasound heating pulse using eqn 17. The thermal diffusivity estimates obtained using the two independent methods are then compared in this article. While eqn 20 and eqn 17 may appear similar in form, 0074hey are derived for very different physical conditions. Equation (20) assumes that the heat source is infinitely long with negligible diameter surrounded by an infinite solid, and these assumptions are reasonable for this experimental arrangement. The exponential integral in eqn 20 is evaluated using the function “expint” included in MATLAB ™ (The Mathworks Inc, Natick, MA, USA). Unknown parameters A and thermal diffusivity K are obtained by finding the best fit to eqn 20 for the thermocouple data. The hot-wire method provides a reference estimate of the thermal diffusivity for the phantom material that is independent of the values obtained using the new backscattered ultrasound technique described in this work, though experimental uncertainty primarily due to thermocouple placement error is actually larger than that for the ultrasonic approach.

In vitro turkey breast muscle experiments

In vitro experiments on turkey breast muscle were performed using the same physical set-up described above for the phantom study. Prior to the experiments, store bought tissue was cut into convenient sizes so that pieces could be placed in the sample holders of dimensions 5 × 5 × 6.5 cm. The cut samples were then immersed in de-ionized water and degassed under vacuum. The degassing process was continued until no visible outgassing from the sample was evident. This process typically lasted 30–40 min. After degassing, the tissue sample was placed near the center of the holder and suspended vertically with the aid of a needle and sewing thread as shown in Fig. 5. Chunks of tissue where the muscle fiber orientation could be visually recognized to be straight were carefully selected for use in the experiment. This orientation is important because of the anisotropy of muscle fibers. In muscle, the attenuation along the fibers exceeds that across the fibers by a factor of 2 or 3 (Duck 1990). The sample was then carefully suspended in the holder ensuring that the direction of propagation of the ultrasound therapy and imaging beam were both perpendicular to the fiber orientation. With the sample held in this position, alginate gel was poured into the holder to encase the tissue sample. This arrangement ensured that the tissue sample was positioned in the center of the holder allowing easy insertion of thermocouples into the tissue. It also ensured that the ultrasound therapy beam enters through a relatively flat front surface. Not doing so may lead to significant refraction and misalignment of the imaging and therapy beams. The propagation distance through the gel was approximately 1 cm. The attenuation and sound speed was measured using the sample replacement technique for each of the samples in the experiment. The average sound speed and attenuation measured over four samples was 1567.8 ± 12.4 m/s and 1.24 ± 0.18 dB/cm/MHz, respectively. These attenuation measurements were performed with the muscle fibers oriented perpendicular to the beam propagation direction. The attenuation values measured with the fibers oriented parallel to the beam propagation direction were 2.1 ± 0.16 dB/cm/MHz. The reported values for attenuation in muscle perpendicular and parallel to the fibers are in the range of 0.9–1.4 dB/cm/MHz and 1.6–2.8 dB/cm/MHz, respectively (Duck 1990). The attenuation of the alginate gel phantom was also independently measured to be 0.34 ± 0.032 dB/cm/MHz. It may be noted that the attenuation and sound speed values are not used in the thermal diffusivity computation, but do affect the heating rate and imaging signal-to-noise ratio.

Fig. 5.

(a) Tissue sample suspended by a sewing thread from a clamp and held in place near the center of the metallic sample holder. (b) Alginate gel is then poured to encase the tissue.

A brief HIFU exposure at an in situ intensity of about 30 W/cm² was applied to estimate the thermal diffusivity (K). The exposures were typically 5 s in duration and the diffusivity was estimated during the cool down period. The actual temperature in the tissue is not needed to measure the spatial diffusion rate of the heat pulse.

RESULTS

Phantom experiment

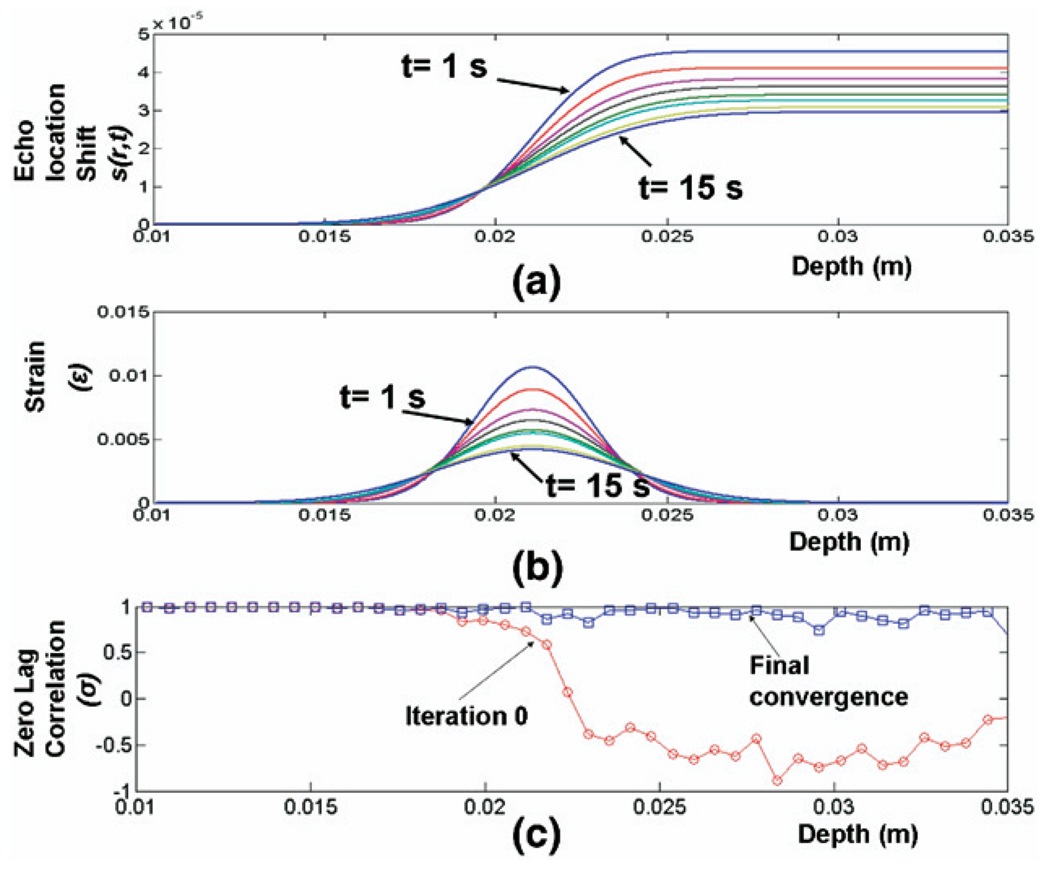
Fig. 6 presents model-derived curves for cumulative acoustic strain s(r,t) (Fig. 6a) and local acoustic strain ε(r,t) (Fig. 6b) at various times after the HIFU heating pulse has been turned off for a RF data set acquired in the alginate phantom. The local strain ε(r,t) is Gaussian as in eqn 16 and s(r,t) has the form of a error function erf(x) as described in eqn 17. It can be clearly seen that the width scale parameter R(t) increases as cooling progresses and the maximum amplitude decreases due to thermal diffusion and conservation of energy. Fig. 6c includes plots of the zero-lag cross-correlation coefficient σ_i at initial iteration 0 and after final convergence of the iterative K-estimation algorithm. At iteration 0 of the algorithm, proximal to the HIFU focal zone, σ_i is close to unity because no shift in the RF signal due to thermal change appears before the heated zone. Correlation reduces sharply approaching the HIFU focal region and stays low beyond the heated zone. This is consistent with the temperature induced echo-shift model represented by eqn 17. After final convergence of the iterative strain estimation procedure, σ_i is close to unity over all depths, illustrating that the model properly accounted for the shifts in the post-heated RF scanline caused by temperature rise. As noted before, s(r,t) does not include the influence of the thermal lens effect, yet the method produces highly correlated results even for regions distal to the HIFU focus. This case illustrates how to evaluate the degree to which the thermal lens effect may interfere with the method.

Fig. 6.

(a) s(r,t) and (b) ε(r,t) from t = 1 s (after start of cool down) to t = 15 s at intervals of 2 s for RF scanline passing through center of HIFU focal region (c) Zero-lag cross-correlation σ_i versus depth at iteration 0 (o) and at final convergence (μ) of the model-based strain estimation algorithm at time t=1 s after start of cooling.

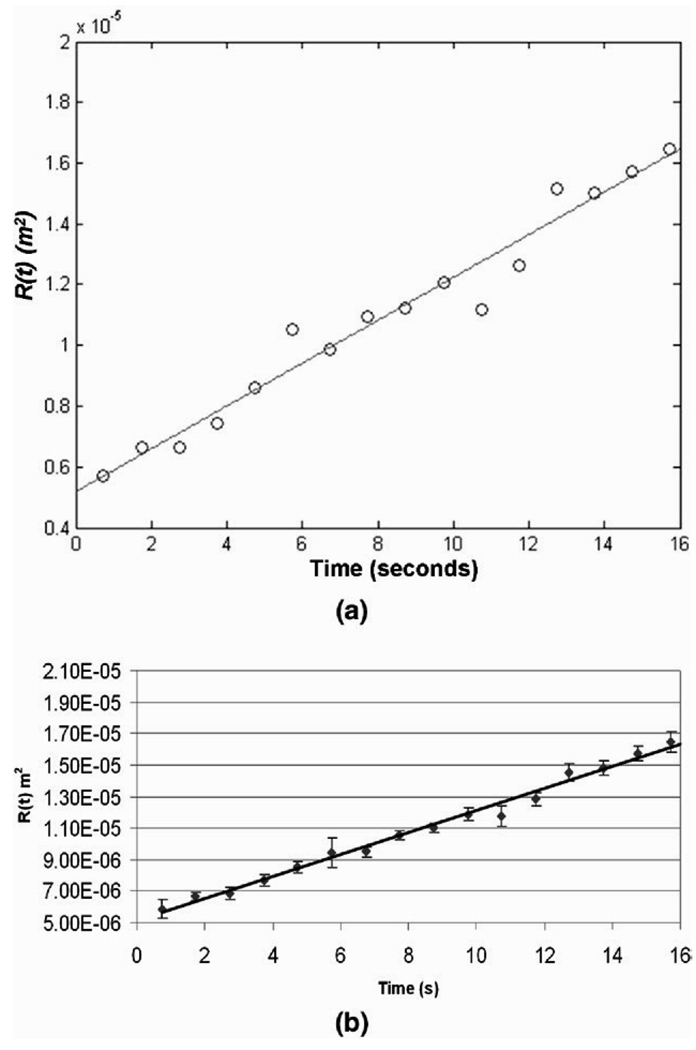
The estimated R(t) values are plotted as a function of time t in Fig. 7a and a least squares linear fit to the data points based on eqn 18 is shown. Note the good agreement (r = 0.96) of the data with the straight line model, indicating a constant value of K for the experiment. The linearity of the model also indicates that the strain coefficient k is constant over this range of temperatures, within experimental accuracy. Thermal diffusivity calculated using eqn 18 is 1.72 × 10⁻⁷ m²/s for this phantom sample. The mean estimate of K obtained noninvasively for the five phantom samples analyzed is 1.7 ± 0.07 × 10⁻⁷ m²/s. Fig. 7b is a plot of the mean value of R(t) for the five different samples as a function of time. The error bars represent the standard deviation in the R(t) estimate at each time instant. The good agreement between the data points and the linear fit demonstrates the robustness of the technique for the experimental conditions in this work.

Fig. 7.

(a) Plot of R(t) versus time t estimated from a RF data set acquired in the alginate phantom. The straight line represents a least squares linear fit to the data points. (b) Plot of the mean value of R(t) versus t from data collected in five independent phantom samples. The error bars represent the standard deviation in R(t).

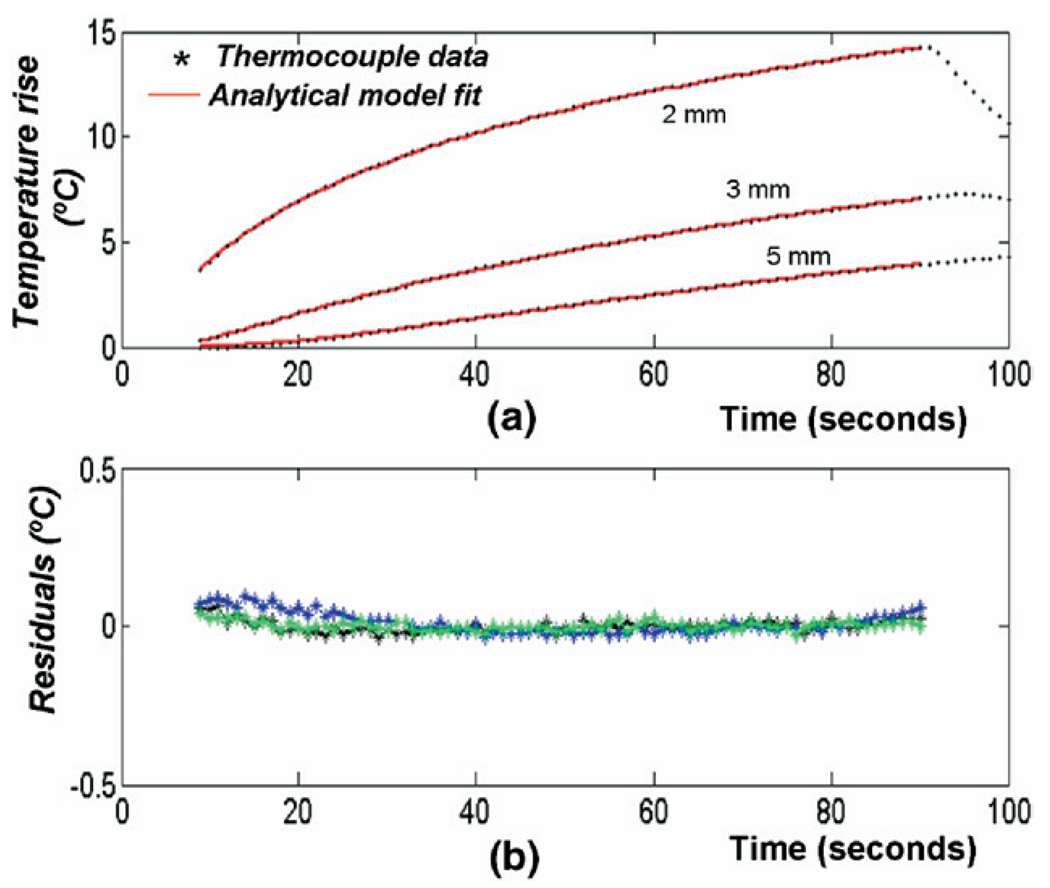
Fig. 8a illustrates the typical temperature profiles obtained during the transient hotwire experiments and the superimposed analytical fit to the temperature data using eqn 20. Fig. 8b shows the residual error in the fit. The mean value of K estimated using this technique in four samples is (1.44 ± 0.2) × 10⁻⁷ m²/s.

Fig. 8.

(a) Temperature profiles measured by thermocouples placed at radial distance of 2, 3 and 5 mm from the nichrome heating wire in the transient hotwire experiment (o) and analytical fit to the data. (b) Error residuals (in degrees Celsius) between the experimental and fitted values. Note the limits along the vertical axis.

Simulations

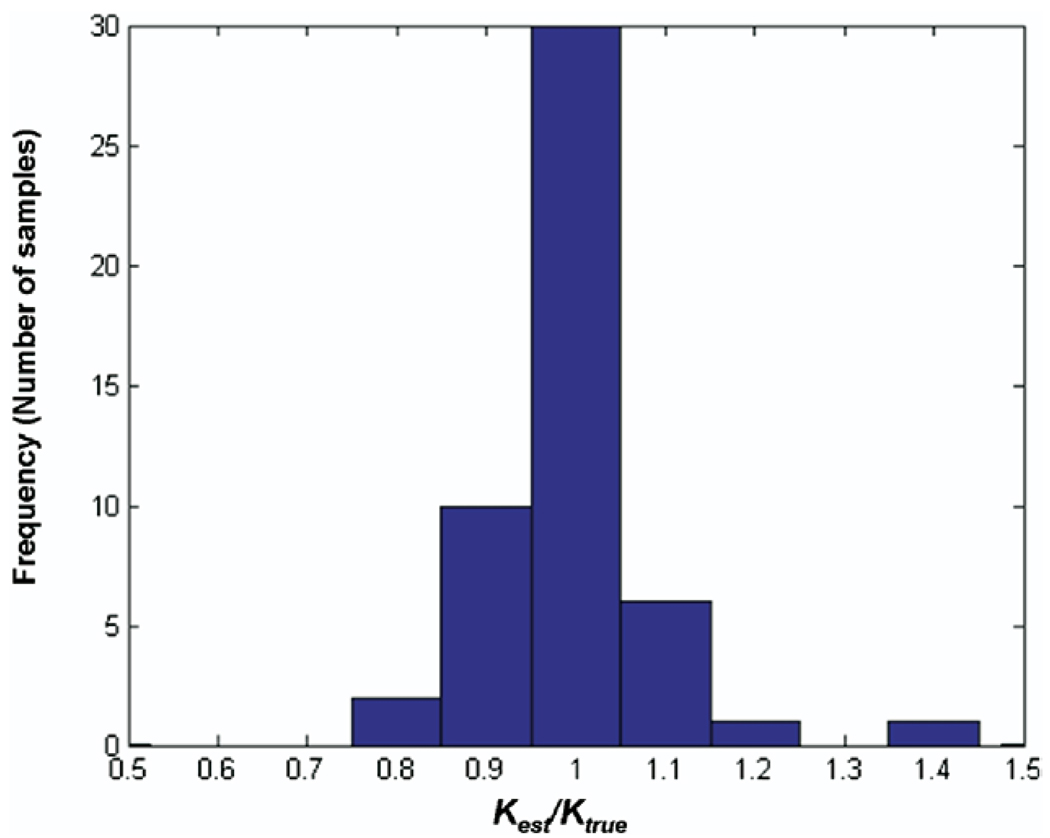
Fig. 9 illustrates the histogram of the ratio of estimated thermal diffusivity (K_est) and the true diffusivity (K_true) for 50 realizations in the simulation. The estimated mean value was 0.994 and the standard deviation was 0.089. This close match between the noninvasive estimate and true value illustrates the precision of the estimator used in the ultrasound based noninvasive technique for estimating K and suggests very little bias in the method.

Fig. 9.

Histogram illustrating distribution of estimated thermal conductivity (K_est) relative to true value (K_true) under simulated conditions at an ultrasonic SNR of 20 dB over 50 independent trials.

In vitro turkey breast muscle experiments

A plot of R(t) as a function of time during cool down (beginning immediately after heating was turned off) is shown in Fig. 10a for one of the samples tested. The slope of the linear fit to the data points leads to the thermal diffusivity: 1.42 × 10⁻⁷ m²/s for this sample. The uncertainty in this estimate at the 95% confidence level is 0.3 × 10⁻⁷ m²/s. The thermal diffusivity estimates obtained for the remaining samples tested are 1.18 × 10⁻⁷, 1.3 × 10⁻⁷ and 1.55 × 10⁻⁷ m²/s. The variation in the diffusivity values is possibly due to the local heterogeneities and inter-sample variability that would be expected between independent tissue samples. Fig. 10b is a plot of the mean value of R(t) for the four different tissue samples as a function of time. The error bars represent the standard deviation in the R(t) estimate at each time instant. For comparison, the reported range of thermal diffusivity values in the literature for muscle is 1.25–1.54 × 10⁻⁷ m²/s (Duck 1990). The values estimated from our experimental noninvasive measurements for turkey breast tissue fall in this range.

Fig. 10.

(a) Plot of R(t) versus time t estimated from a RF data set acquired in turkey breast muscle. The straight line represents a least squares linear fit to the data points. (b) Plot of the mean value of R(t) vs. t from data collected in four turkey breast tissue samples. The error bars represent the standard deviation in R(t).

DISCUSSION

The noninvasive estimation of tissue thermal and acoustic properties using ultrasound backscatter has been previously proposed. Yao and Ebbini (Hui et al. 2004) demonstrated that the ultrasound backscatter provides information to estimate the acoustic absorption and the tissue perfusion following a short ultrasound heating pulse. However, no quantitative estimates of these parameters were presented. Recently, Sumi and Yanagimura (2005 and 2007) proposed a technique for reconstructing the thermal properties such as thermal conductivity and diffusivity. The temperature rise in the sample was induced using a heated waterbath. Practical application of the methods in noninvasive therapy modalities such as HIFU was not presented in that study. Unique to this article is the development of a noninvasive ultrasound based approach to obtain quantitative absolute estimates of the thermal diffusivity by focused ultrasound heating. Furthermore, ultrasound strain estimation is performed using a new iterative heat transfer model-based signal processing algorithm. The method is intended to facilitate HIFU therapy planning but the small transverse beam width of the HIFU focus and the ease of delivering a short duration heating pulse present distinct advantages for general estimation of thermal diffusivity, and perhaps for capillary bed perfusion. In our experimental set-up, the ultrasound imaging scanlines are oriented transverse to the HIFU beam (Fig. 1). It is advantageous to image the temperature evolution in this direction since the thermal gradients are greater (compared with imaging in parallel with the HIFU beam), thus, providing greater sensitivity to spatial rates of thermal dissipation. The estimation approach was demonstrated in an in vitro experimental set-up in a gel phantom and in turkey breast tissue. Using a short ultrasound heating pulse permits simplification of the solution to the BHTE such that the diffusivity and the tissue perfusion can be separately estimated, provided the underlying BHTE model in eqn 1 is valid. The presence of large blood vessels in the region of interest would invalidate assumptions of homogeneity of acoustic and thermal parameters near the HIFU focus.

The results from the numerical simulations of HIFU induced acoustic strain demonstrated that under realistic ultrasound signal-to-noise conditions, K can be estimated compared to the ground truth value input in the simulations with a variation of less than 10%. The simulations provide a means to select the signal processing parameters and predict the lower bound of the estimation accuracy that can be expected with the algorithm. Experimental variation in the estimate of diffusivity would be expected to be greater than that obtained through these simulations which used Gaussian particle distribution statistics. In phantoms, the estimates of K independently obtained using the invasive transient hot-wire method and the noninvasive method showed a difference of approximately 15%. The hot-wire method was used for comparison because it is a standard method of estimating the thermal properties of solid materials in the heat transfer literature. However, there exist significant discrepancies between the governing equation describing the heat flow (eqn 20) and the experimental arrangement for the hot-wire method. For example, the estimation procedure includes a number of assumptions regarding the geometry of the heat source and sample, thermal properties of the heating wire, and heat transfer between the heating wire and the sample being tested (indeed, boiling at the wire surface is difficult to avoid). Based on a detailed quantitative error analysis incorporating model errors and experimental measurement errors, Hammerschmidt and Sabuga (2000) showed that the expected uncertainty in the thermal diffusivity from a hot-wire technique can be on the order of 30%. Another major source of uncertainty in the hotwire method specific to our experimental set-up is the distance between the thermocouples and the heating wire and orientation of the thermocouples. Since r²/4K appears as a lumped term in eqn 20, any errors in the measured distance strongly influences the diffusivity estimate. For example, an error of 0.2 mm in a thermocouple placed 2 mm from the wire results in an error of 20% in the estimated diffusivity. Given these challenges with the hot-wire method, we can only conclude that the two independent methods are in experimental agreement. In fact, the ultrasonic estimation technique using a HIFU source has significant advantages: i) the diffusivity estimation is based on data collected at multiple points along a complete scanline compared with a set of discrete thermocouple measurements, ii) the presence of the heating source (HIFU beam) does not affect the integrity of the sample as long as the temperature rise is small to prevent irreversible damage, and iii) the heat transfer from the HIFU focus to the surrounding medium is continuous. Finally, the ultrasonic approach is noninvasive. Experiments were also performed in excised turkey breast. The hot-wire method was not used in these turkey breast experiments because of experimental difficulty in visualizing the thermocouples amid the field of bright tissue scatterers present in the background. The estimates of K obtained in excised turkey breast samples showed good agreement with the published literature values.

Accurate estimation of echo location shifts s(r,t) is important to minimize errors in the ultrasonic estimates of K. In this study, no attempt was made to optimize the signal processing parameters such as RF data sampling rate, imaging and HIFU transducer frequency, cross-correlation window length (N) and thresholds in the optimization routines used in the estimation technique. A detailed error analysis would be necessary in a future study to understand how choice of these parameters affect s(r,t) estimates and, consequently, the uncertainties in K. Nevertheless, the results of this study clearly demonstrate that the local thermal diffusivity can be noninvasively estimated from the RF data acquired during brief HIFU exposures at subablative intensities.

A scanline based (one-dimensional [1D]) RF processing scheme was adopted in this article to estimate K with the lateral scan direction of the imaging transducer oriented parallel to the HIFU beam propagation direction. RF lines near the center of the HIFU focal region were used in the analysis. This is consistent with the orientation recommended by Simon and Ebbini (Simon et al. 1998) to minimize the acoustic thermal lens effect (decorrelation in the RF signal due to refraction and refocusing of the US beam during heating) because the thermal gradients across the imaging transducer aperture are smaller near the center as compared to the edges of the HIFU focal region. Extension of the 1D based approach to a 2D estimation technique performed over multiple adjacent scan lines in the heated region might benefit from incorporating the thermal lens effect in an appropriate numerical model (Alaniz et al. 2002) to minimize model inconsistencies. Additional signal processing and filtering could be performed on the raw ultrasound backscatter data to reduce the spatial ripple introduced by the thermal lens effect (Simon et al. 1998). In another recent approach proposed to mitigate the effect, the conventional beamforming on transmit was replaced by multiple steered plane wave insonifications using several subapertures. The results demonstrated that the artifact is reduced by averaging the 2D maps from the multiple steered plane wave insonifications. The averaged temperature induced strain map could be combined with the proposed approach presented in this article to estimate R(t) and the thermal diffusivity (Pernot et al. 2004). Nevertheless, in the experiments presented here, thermal lens aberration was not severe enough to preclude strain estimation using the new BHTE-constrained algorithm, both proximal and distal to the HIFU focal zone.

In this analysis, the medium was considered to be spatially homogenous and isotropic and the anisotropy of thermal properties in muscle is unknown and was neglected. In heterogeneous media, spatial variations in the thermal properties can be expected. To account for these spatial variations, measurements of the local thermal diffusivity at a number of spatial locations within the region of interest can be repeated to construct a spatial map of thermal properties. The maximum temperature rise induced in the sample to perform the thermal diffusivity estimation was less than 10°C and it was assumed that the thermal diffusivity remains constant with respect to temperature in this range. For the in vitro experimental results presented in this study, the excellent fit to the linear model (Fig. 7 and Fig. 10) provide confidence in the validity of this key assumption. The threshold for thermal ablation is typically close to 60–70°C (i.e., 20–30°C temperature rise from 37°C). Further experimental studies are required to understand whether the temperature dependence of thermal diffusivity is significant in the regimes involved in ablative thermal therapy in vivo. The proposed methods in this article could be used to perform repeat measurements of the diffusivity to understand its temperature sensitivity at elevated temperatures. The diffusivity can be estimated for small local temperature rises starting from an elevated baseline temperature and these measurements can be carried out successively over small temperature ranges for which the diffusivity is constant until the coagulation threshold is reached. The temperature dependence beyond the ablation threshold is less relevant in HIFU therapy since the clinical goal is to be able to monitor the treatment accurately until ablation has been reached. The temperature dependence of diffusivity was also not considered by a number of previous authors who developed simulation programs to predict the temperature rise during HIFU (Meaney et al. 1998; Curra 2001). Their results showed good agreement between simulated temperature profiles and measured temperature estimates from thermocouples in vitro.

The methods developed in this article can be used in therapy planning applications to compute the thermal dose at the treatment site for a given exposure protocol. Currently, these therapy planning procedures typically use standard values for the thermal parameters derived from the literature. In situ estimates can reduce the uncertainty in the knowledge of these parameters and thus improve the accuracy of the predicted results, and the new method is performed noninvasively without ablating the tissue. The experimental results in this article were limited to the estimation of thermal diffusivity. In an in vivo setting, tissue perfusion and its variability would play a significant role in the local temperature evolution. Future work would address the estimation of tissue perfusion in vivo by extending the methods developed in this article. In the absence of large blood vessels resulting in a directional heat sink, an exponential decay term would adequately model the perfusion in capillary beds and predict the temperature evolution. The method presented here improves upon conventional elastographic processing techniques for estimating strain because it constrains the solution using the heat transfer model. This approach has application in noninvasive estimation of temperature rise as well and we use this thermal diffusivity estimation algorithm as part of a calibration procedure for HIFU therapy monitoring (Kaczkowski and Anand 2004).

This study examined the feasibility of a noninvasive ultrasonic estimation of thermal diffusivity under in vitro conditions. Convective heat loss due to proximity to a blood vessel requires detailed study and the next step in the research is to extend the method to in vivo conditions. In addition to heat loss from vascularity and perfusion, potential complications include motion artifacts from respiration, cardiac pulsation and bulk motion of transducer assembly (especially for freehand scanning) that can preclude cross-correlation analysis. Although the experimental methods developed in this article employed HIFU devices, the same techniques can be applied to other forms of thermal ablation including radio-frequency ablation and microwave therapy. The heat transfer equations would need to be modified accordingly to include the geometry of the heat source and appropriate boundary conditions.

CONCLUSIONS

A noninvasive technique for estimating local thermal diffusivity using ultrasound backscatter data is developed and presented in this article. The method uses a highly focused ultrasonic source to develop a localized heat impulse in a medium and deduces the diffusivity from ultrasonic backscatter measurements of spatial and temporal rates of heat dissipation. The maximum temperature rise is small (less than 10°C) and the sound speed is assumed to vary linearly with temperature; thus, temperature variations induce proportional apparent displacements of scatterers in the medium that shift the backscattered waveforms over the dissipation time. A heat transfer model that takes advantage of the impulsive heat source is used to develop a spatio-temporal template for the dissipation of the heat pulse. A significant advance in acoustic strain estimation provided by the method presented here is the use of the heat transfer model to constrain the estimation of the heat diffusivity by fitting the ultrasonic RF waveform curves using the model templates and, thus, optimally compensate for the temperature induced strain. The applicability of this technique to estimate the diffusivity parameter can be extended to assess the heterogeneity of biological tissue and to construct spatial maps of the variation of this and other tissue specific thermal parameters. The techniques developed in this article have potential applications in thermal therapy planning and monitoring, by noninvasively and nondestructively determining tissue thermal properties specific to the patient and organ at the site of interest. Extension of the method to in vivo conditions is nontrivial, as motion artifacts and variable vascularization and perfusion rates will require modification of the model. Furthermore, validation of the method in vivo will require significantly more complicated experimental arrangements.