Abstract
The electrophysiological basis underlying the genesis of the U wave remains uncertain. Previous U wave modeling studies have generally been restricted to one or two dimensional geometries, and it is not clear whether the U waves generated by these models would match clinically observed U wave body surface potential distributions (BSPDs). We investigated the role of M cells and transmural dispersion of repolarization (TDR) in a two dimensional, fully ionic heart tissue slice model and a realistic three dimensional (3-D) heart/torso model. In the 2-D model, while a U wave was present in the ECG with dynamic gap junction conductivity, the ECG with static gap junctions did not exhibit a U wave. In the 3-D model, TDR was necessary to account for the clinically observed potential minimum in the right shoulder area during the U wave peak. Peak T wave simulations were also run. Consistent with clinical findings, the body surface maximum of the U wave was shifted to the right compared to the T wave maximum. We conclude that TDR can account for the clinically observed U wave BSPD, and that dynamic gap junction coupling of M cells is required to produce realistic U waves generated by M cells.
Keywords: electrocardiography, transmural dispersion of repolarization, U wave, computer modeling
INTRODUCTION
The electrocardiographic U wave (Figure 1A) has been recognized for over 100 years.1 Clinically, the body surface potential distribution (BSPD) of U waves in normal subjects is similar to that of T waves, which are characterized by positive potentials in the left anterior precordium and negative potentials in the right shoulder region2, 3 (Figure 1B). A recent study suggests that the U wave exists in most normal subjects.4 Yet, the electrophysiological basis underlying the genesis of the U wave has not been precisely elucidated, and several hypotheses have been proposed. The Purkinje hypothesis ascribes the origin of the U wave to delayed repolarization of the subendocardial Purkinje bers.5 The after-potential hypothesis argues that the U wave results from after-potentials possibly caused by mechanoelectrical feedback.6,7 The most recent hypothesis is the M cell hypothesis, which claims that the U wave is caused by delayed repolarization of mid-myocardial M cells in the setting of transmural dispersion of repolarization (TDR).8
Figure 1. Normal U wave.
A. U wave in surface electrocardiogram (solid arrow) in a healthy volunteer. B. U wave body surface potential distribution (BSPD) in normal subjects. The distributions of maxima and minima over a number of subjects are shown in the stippled and shaded regions, respectively. Dashed lines indicate average zero potential. Modified from Spach MS et al.2
The M cell hypothesis is supported by the observation that the timing of human M cell repolarization coincides with that of the U wave.9 It is also supported by one-dimensional (1-D)10 and two-dimensional (2-D) modeling studies of an electrically isotropic heart.11 However, other studies report that U waves can be generated without M cells by varying the terminal repolarization rates of endocardial and epicardial cells12 or adding after-potentials to action potentials.13 Most importantly, the M cell hypothesis as implemented in prior computer models cannot account for the negative U waves in the right shoulder region (Figure 1B). As we will demonstrate, a decreasing transmembrane potential gradient within the M cell layer will tend to decrease the current flowing into the right shoulder region, which would cause the body surface potentials there to tend toward the baseline (0 potential) level. In contrast, in at least some normal humans, the potentials in the right shoulder region are increasingly negative during the initial portion of the U wave. Therefore, the evidence to support the essential role of M cells in the genesis of the U wave is questionable unless some other mechanism, operating in conjunction with delayed M cell repolarization, can explain the negative U wave deflection over the right shoulder area.
The primary aim of the present study was to investigate the role of M cells in the genesis of the clinically observed U wave BSPD. More specifically, we investigated what types of transmembrane potential distributions would generate the clinically observed U wave BSPD (Figure 1B). To achieve this aim, we ran two sets of simulations. First, to determine whether delayed repolarization of M cells could generate a U wave in an ionic model, we ran one set of simulations in a 2-D, fully ionic heart tissue slice model that included important features of the 3-D heart/torso volume conductor. With the 2-D ionic model, we ran simulations with and without dynamic gap junction conductivity, which we hypothesized could explain the clinically observed negative U wave deflection over the right shoulder. Second, to determine the type of BSPD that could result from delayed M cell repolarization, we ran another set of simulations in a 3-D heart/torso model of the U wave peak. We also ran simulations of the peak T wave. The peak U wave and peak T wave BSPDs were qualitatively similar, except that that the maximum of the peak U wave was shifted to the right and superiorly compared to the T wave BSPD. A rightward shift in the U wave maximum compared to the T wave maximum has been clinically observed.2, 3 Our results suggest that delayed M cell repolarization can explain the clinically observed U wave BSPD and time course if gap junction conductivity is dynamic.
METHODS
2-D ionic model
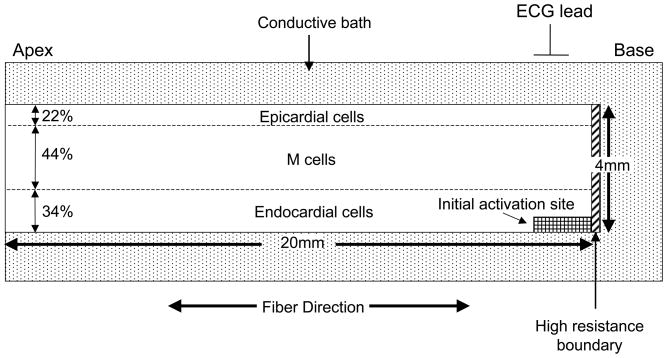
We implemented a variation of the ten Tusscher model14 to simulate a single activation/repolarization sequence, with and without delayed M cell repolarization, in a slice (20 mm × 4mm) of ventricular tissue (Figure 2). The source code of the ten Tusscher model (http://www-binf.bio.uu.nl/khwjtuss/SourceCodes/) was translated from C++ to Matlab and then modified as described below. The tissue was embedded in a conductive bath, which corresponds to the torso and intraventricular blood. The ventricular tissue was separated from the bath/atrium at the base by a thin layer of highly resistive tissue. To explore the effect of ventricular tissue anisotropy on extracellular potentials, fiber direction was set in an apex-base direction. In addition, to examine the effect of a base to apex repolarization sequence, the base of the tissue was configured to repolarize earlier than the apex by initiating activation from the base.15
Figure 2. Geometry of 2-D ionic model.
See text for details.
Different sets of repolarization conductivities in the transverse fiber direction were applied to the endocardial, M cell and epicardial regions, respectively, which qualitatively match the transmural resistance profile estimated for canine left ventricle.16 The values for longitudinal conductivity, and intracellular and extracellular transverse repolarization conductivities for the endocardial/M cell region are all within the range of estimates of these parameters for human myocytes17(Table 1).
Table 1.
Ionic model conductivities
| Parameter | Value |
|---|---|
| Cell capacitance/area | 1 μF/cm2 |
| slow delayed rectifier current (IKs) conductance GKs | 0.380 nS/pF (epicardium) 0.128 nS/pF (M cells) 0.290 nS/pF (endocardium) |
| minimum value of the calcium inactivation gate (fCa) | 0.25 (endocardium) 0.4 (M cells) |
| maximum ICaL conductance | 1.58−4 cm3 μF−1 s−1 (epicardium) |
| delayed rectifier current (IK1) conductance GK1 | 1 nS/pF (M cells) |
| M cell/Endocardial intracellular longitudinal conductivity (σil) | 0.18–0.36(S/m) (repolarization) |
| M cell/Endocardial extracellular longitudinal conductivity (σel) | 0.36(S/m) (repolarization) |
| M cell/Endocardial intracellular transverse conductivity (σit) | 0.003–0.006(S/m) (repolarization) |
| M cell/Endocardial extracellular transverse conductivity (σet) | 0.07(S/m) (repolarization) |
| Epicardial intracellular longitudinal conductivity (σil) | 0.18–0.36(S/m) (repolarization) |
| Epicardial extracellular longitudinal conductivity (σel) | 0.36(S/m) (repolarization) |
| Epicardial intracellular transverse conductivity (σit) | 0.0015–0.003(S/m) (repolarization) |
| Epicardial extracellular transverse conductivity (σet) | 0.02(S/m) (repolarization) |
| σel || σil* | 0.3(S/m)(propagation) |
| σet || σit* | 0.15(S/m)(propagation) |
| Atrio-ventricular conductivity | 0.018(S/m)q |
| Surrounding bath conductivity | 0.44 S/m |
Propagation conductivities were chosen solely to obtain a reasonable activation sequence. Propagation velocity is a function of the effective parallel conductivity of the intracellular and extracellular conductivities. Thus, only the parallel conductivity values, which affect propagation velocity, are shown in the table.
In baseline simulations, endocardial, M cell and epicardial cells were assigned to the corresponding inner, middle and outer layers of the tissue, accounting for 34%, 44% and 22% of tissue thickness, respectively.9
The implemented bidomain model involved iteratively solving the following equations
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
In equation (1), Jion is ionic current density (current/length2) which is the sum of all the ionic currents that pass through ion channels within the cell membrane. These currents are a function of the transmembrane potential Vt. Specifically, f(Vt) is a set of differential equations, specified by the ten-Tusscher model,14 that relate the ionic currents to Vt. In equation (2), Cm is membrane capacitance/unit area and Jm is total transmembrane current density. Equation (2) models the cell membrane as a capacitor, such that the capacitance Cm of the cell wall multiplied by the change in voltage across the cell wall with respect to time (dVt/dt) is equal to the net current available (Jm- Jion) available to charge the capacitor. In Equation (3), Vt is transmembrane potential and Ve is extracellular potential. The transmembrane potential Vt is the difference between intracellular potential (Vi) and Ve such that Vt.=Vi -Ve. (Equation (4)). Di and De are the intracellular and extracellular conductivity tensors (conductivity/distance), respectively. Equation (3) is a Poisson type equation that relates extracellular voltage on the left hand side of the equation to current sources on the right hand side of the equation. In this regard, increases in the magnitude of Di with respect to the magnitude of De are equivalent to an increase in the strength of the current source for a given distribution of transmembrane potentials. Equation (3) may also be regarded as a voltage divider equation, which effectively states that the transmembrane potential is divided between the intracellular and extracellular spaces according to the relative conductivities of those spaces.
In Equation (5), β is the myocyte membrane surface/volume ratio (1/distance). Equation (5) states that the change (divergence) in intracellular current Di∇Vi must appear as transmembrane current, i.e., all current entering/leaving the intracellular space must leave/enter as transmembrane current.
Following ten Tusscher et al.,14 the Rush and Larsen method18 was used to solve for Jion in Equation (1) and the forward Euler method was used to solve Equation (2). The Galerkin-based finite element method19 was used to solve Equation (3), with the stiffness matrix for each element computed by Gauss quadrature. Jm in Equation (5) was computed with the same finite element stiffness matrix corresponding to Di as was used in the solution of Equation (3). Table 1 sets forth the conductivity values associated with Di and De.
As noted in Table 1, different parameter values were employed for propagation and repolarization because the conductivities required to obtain reasonable propagation speed were far greater than the maximum conductivities that allowed for substantial transmembrane gradients during repolarization. Because the primary time interval of interest of the current study is repolarization, we modified propagation parameters simply to set up a reasonable activation sequence.
At the boundary between the tissue and the conductive bath, the extracellular potential in the tissue and the potential in the bath were constrained to equal one another and the intracellular current density was constrained to equal 0.20
To test our hypothesis that dynamic gap junction conductivity could underlie the genesis of the U wave, a linear function of the transmembrane potential was used to model a rise in intracellular conductivity with decreases in transmembrane potential during terminal repolarization. A linear function was chosen for convenience; our aim was to qualitatively determine whether dynamic gap junction coupling could explain the initial U wave downstroke over the basal portion of the tissue slice, which corresponds to the right shoulder in the human torso.
To compare the results of dynamic gap junction coupling with static gap junctions, another set of simulations was conducted with the intracellular conductivity held constant.
The ten Tusscher model was modified as follows. First, to enhance the action potential dispersion between the cell types, conductance GKs of the slow delayed rectifier current (IKs) was increased from 0.264 nS/pF to 0.380 nS/pF in the epicardium, and from 0.264 nS/pF to 0.290 nS/pF in the endocardium. Second, to lengthen the action potential durations of endocardial and M cells, respectively, the amount of depolarizing calcium current (ICaL) during the plateau was increased by increasing the baseline minimum value of the calcium inactivation gate (fCa) from approximately 0.21 to 0.25 and 0.4 for endocardial and M cells, respectively. This resulted in M cell action potentials that were too long. Consequently, M cell conductance GKs of the slow delayed rectifier current (IKs) was increased from 0.064 nS/pF to 0.128 nS/pF in the M cell region.
To further decrease epicardial action potential duration, maximum ICaL conductance was reduced by 10%. Finally, to decrease the slope of the terminal repolarization portion of the M cell action potential, maximal conductance of M cell delayed rectifier current was decreased from 5.405 nS/pF to 1 nS/pF. It is emphasized that the above changes were made for convenience to achieve desired action potential durations and shapes; other types of changes could have been made to achieve the same effects.
3-D heart/torso model
We used a static bidomain, 3-D monoventricular heart/torso model21 to calculate 3-D U wave BSPD with and without delayed M cell repolarization. A single point in time, corresponding to the peak of the U wave, was simulated by assigning transmembrane potentials (TMPs) to endocardial, M cell and epicardial heart layers, respectively. A monoventricular model was chosen because it enabled a simple division of the heart wall into three layers: endocardium, M cell and epicardium. A realistic torso shape was chosen because the aim of the current study was to match the torso BSPD reported by Spach et al.2
The heart torso/model is described elsewhere.21 Briefly, the ventricle was based on the epicardium of the Auckland canine heart,22 and the endocardial surface was a scaled version of the epicardium. The baseline scaling resulted in an approximate wall thickness of 1cm. Fiber angles rotated linearly from approximately −60 degrees to +60 degrees from epicardium to endocardium. Fibers were constrained to lie on the surface of each heart shell. The ventricular chamber was filled with blood. When a transmembrane potential gradient exists between different transmural layers, extracellular current flows in long loops through both the torso and the blood in the ventricular chamber. This current is responsible for the potentials on the body surface. Thus, the presence of ventricular chamber blood was critical to the simulations.
The heart was immersed in a realistic torso according to a coupling method described previously20 (Table 2.). An electrically resistive layer was interposed between the ventricles and an atrial cap.
Table 2.
Conductivity values (ratios) for 3-D heart/torso model
| Parameter | Symbol | Value |
|---|---|---|
| longitudinal extracellular conductivity | σel | 1 |
| longitudinal intracellular conductivity | σil | 1(homogeneous) 0.1–1 (anisotropic) |
| transverse extracellular conductivity | σet | 1(homogeneous) 0.1–1 (anisotropic) |
| transverse intracellular conductivity | σit | 1(homogeneous) 0.1–1 (anisotropic) |
| Ventricular chamber(blood) conductivity | σb | 4 |
| torso conductivity | σb | 2 |
| Atrio-ventricular junction conductivity | σt | 0.01–1 |
The heart was meshed by dividing it into 40 nested shells from endocardium to epicardium and creating hexahedral elements defined by a spherical coordinate system, where each element was parameterized by polar and azimuthal angle divisions, and consecutive shells. The Galerkin finite element method and Gauss quadrature were used to create the finite element stiffness matrix.
The 3-D U wave BSPDs were calculated by assigning transmembrane potentials to different cell types with and without M cells as in the 2-D ionic model. The transmural transmembrane potential distribution of the peak U wave was characterized by fully repolarized epicardial and endocardial cells, and relatively depolarized M cells. We experimented with a variety of apical/basal and anterior/posterior transmembrane potential distributions.
For a given set of transmembrane potentials, the computer model solved Equation (3). In particular, the computer solved for the extracellular potential (Ve), where the transmembrane potential of each node in the myocardium (Vt) was set manually. The resulting linear system of equations was solved using the pre-conditioned conjugate gradient method with an incomplete (0 fill in) Cholesky decomposition as a preconditioner.
To compare the U wave BSPD with the T wave BSPD, we also ran simulations with epicardial cells set to relatively more repolarized transmembrane potentials than endocardial cells, and with M cells remaining relatively more depolarized than both epicardial and endocardial cells.
RESULTS
2-D ionic model
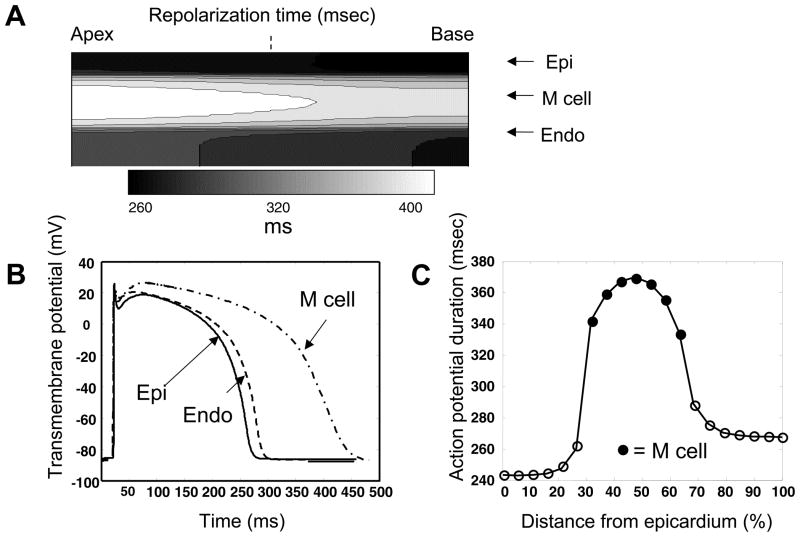
Simulation results of the 2-D ionic model are shown in Figure 3. Repolarization time, defined as the time the transmembrane potential reached −75mV during repolarization, was earliest at the epicardial layer. The endocardial layer then repolarized, followed much later by M cells (Figure 3A). For any given layer, the basal repolarization preceded the apical repolarization. Action potentials of epicardial, M cell and endocardial cells along a transmural section midway through the tissue, as indicated by the dashed line in Figure 3A, is shown in Figure 3B. As expected, the difference between cell types in action potential duration (APD), defined as the difference between activation onset and repolarization times, was primarily a function of plateau duration. Activation onset was defined as the time a cell’s transmembrane potential reached −75mV from its resting potential. Along the same transmural section, APD was the shortest in epicardial cells, longest in M cells, and intermediate in endocardial cells (Figure 3C). A sharp transition in APD was observed between epicardial and M cells, whereas a more gradual transition was observed between endocardial and M cells.
Figure 3. Simulation results of the 2-D ionic model.
A. Repolarization times, defined as the time the transmembrane potential reached −75mV during repolarization. B. Action potentials of epicardial (Epi), M cell and endocardial (Endo) cells along a transmural section midway through the tissue, as indicated by the dashed line in A. C. Action potential duration (APD), defined the difference between activation onset and repolarization times, which in turn were defined as the time a cell’s transmembrane potential reached −75mV from its resting potential and during repolarization, respectively.
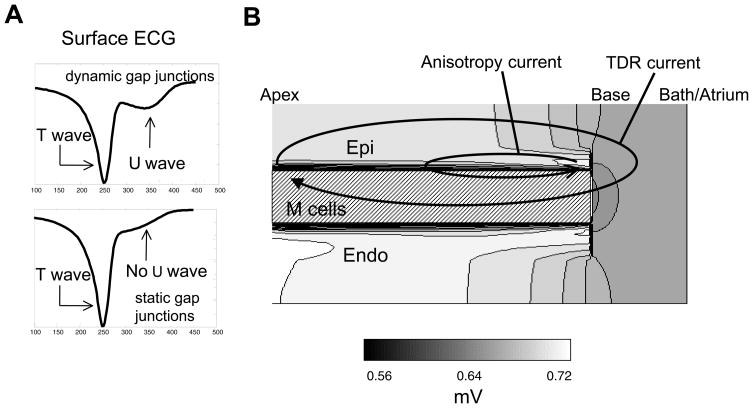
The ECGs in the simulations with both dynamic and static gap junction conductivity are shown in Figure 4A. While a U wave is present in the ECG with dynamic gap junctions, the ECG with static gap junction does not exhibit a U wave. More specifically, in the static gap junction case, the end of the T wave has a hump that results from delayed M cell repolarization. In the dynamic gap junction signal, the initial downstroke of the U-wave in Figure 4A is approximately 70ms long while the return to baseline from the U wave peak is approximately 90ms.
Figure 4. Simulation results of the 2-D ionic model (cont’d).
A. Surface ECG with dynamic and static gap junctions. B. Extracellular U wave potential distribution. TDR=transmural dispersion of repolarization. Abbreviations as in Figure 3.
The extracellular peak U wave potential distribution associated with the dynamic gap junction simulations is shown in Figure 4B. We found two main potential distributions outside of the heart tissue. One is positive at apex and negative at base (labeled TDR current), which resulted from TDR. The other is negative at the apex and positive at the base (labeled anisotropy current), which resulted from the anisotropy of cardiac tissue conductivity. The potentials along the top of the tissue slice exhibited a positive to negative pattern from the region over the apex to the region over the base. The TDR current was necessary to produce a potential minimum (relative to the potentials along the top of the tissue) in the region over the base.
When the atrio-ventricular border was given an infinite resistance, the TDR current disappeared after the endocardial and epicardial cells had both completely repolarized, while the anisotropy current still remained (data not shown). Along the top of the tissue, the anisotropy current produced positive U waves over the base and negative U waves over the apex (data not shown). When tissue anisotropy was removed while maintaining an infinite resistance at the atrio-ventricular border, both the TDR current and the anisotropy current disappeared; thus, the U wave was abolished (data not shown).
In Figure 4B, both the endocardium and epicardium are characterized by positive potentials while the M cell layer is characterized by negative potentials. Endocardial/M cell TDR current mirrors the epicardial/M cell current. The endocardial/M cell TDR current is not indicated on the diagram to emphasize the importance of the epicardial/M cell current.
3-D heart/torso model
The U wave BSPD and the potentials through a cross section of the heart are shown in Figure 5. The potential distribution that resulted solely from the current sources at the boundary between epicardial and M cell layers (Epi/M) was calculated by turning off the current sources at the boundary between endocardial and M cell layers (Figure 5, left panel). Similarly, by turning off the current sources at the boundary between epicardial and M cell layers, the potential distribution that resulted solely from the current sources at the boundary between endocardial and M cell layers (Endo/M) was calculated (Figure 5, middle panel). By superposition, these distributions were added together to form the distribution resulting from both current sources (Figure 5, right panel). The Epi/M distribution (Figure 5, left panel) is characterized by an anterior left precordial maximum over the heart and a minimum over the right superior torso.
Figure 5. Simulation results of the 3-D heart/torso model.
U-wave potential distributions on the torso (top) and within the heart (bottom) for transmural current sources restricted to the epi/M cell layer (left panels) and the endo/M cell layer (center panels). The right panels show the potentials associated with current sources along both epi/M cell and endo/M cell sources. By superposition, the right hand potentials are a sum of the left (epi/M cell) and center (endo/M cell) potentials. The black dashed line shows the torso midline.
The body surface maximum associated with the Epi/M pattern is shifted to the right compared to the T wave BSPD (Figure 6). Otherwise, the Epi/M and T wave BSPDs are somewhat similar. The Endo/M distribution (Figure 5, middle panel) is also similar to the Epi/M distribution but with a reverse polarity. In the resultant U wave distribution (Figure 5, right panel), the Epi/M and Endo/M distributions partially cancel each other, resulting in a distribution similar to the T wave BSPD but being characterized by smaller magnitudes than the Epi/M or Endo/M potentials, and having a maximum that was shifted towards the right and superiorly.
Figure 6. T wave BSPD along with the potentials through a cross section of the heart and the epicardial/atrial potential distribution.
In concordance with clinical observations, the body surface distribution is characterized by an anterior left precordial maximum over the heart and a minimum over the right superior torso. The black dashed line shows the torso midline.
In the heart, the potential drop across the Epi/M and the Endo/M layers was approximately 25mV (Figure 5, bottom panels). The transmural dispersion of repolarization created long loops of current (red solid loops), similar to the TDR current in the 2-D ionic model (Figure 4B). The TDR currents resulting from the Epi/M layers and the Endo/M layers partially cancel one other. The cancellation is not complete because the Epi/M source layer is closer to the torso than the Endo/M source layer. In the combined source model (Figure 5, right panel), current flows through the atrio-ventricular border from both the Epi/M sources and the Endo/M sources. The net result is a basal shift in the maximum potential on the epicardium which accounts for at least part of the basal shift of the maximum on the U wave BSPD.
As in the 2-D ionic model, when the resistance of the atrio-ventricular border was infinity, and the heart tissue had isotropic conductivity, the combined source distribution resulted in no current flow and therefore no U wave BSPD was observed (data not shown). When the resistance of the atrio-ventricular border was infinity and the heart tissue had anisotropic conductivity, current flowed according to the direction of heart fiber orientation but no type of transmembrane potential gradient (anterior/posterior or apical/basal) could produce a minimum on the torso near the right shoulder (data not shown).
The T wave BSPD shown in Figure 6 was discussed above. The lower left panel in Figure 6 shows the epicardial/atrial potential distribution, which was characterized by positive epicardial potentials with negative potentials on the atria.
DISCUSSION
Our results clearly demonstrate that delayed M cell repolarization in our model can produce the clinically observed U wave BSPD. Moreover, our results also suggest that some type of transmural transmembrane potential gradient is necessary to generate negative potentials over the right shoulder that characterizes clinical U wave BSPD in humans.2 This novel finding accords with other simulations pertaining to the T wave;23,24 in these simulations, models that implemented an epicardial to endocardial repolarization gradient generated T waves that were in good agreement with normal T waves in the standard 12 lead ECG. Further, the 3-D model produced a rightward shift in the body surface maximum of the U wave compared to the T wave, a phenomenon described in clinical studies.2, 3
TDR
Although the concept of TDR, or electrical heterogeneity, of the ventricular myocardium has provided a framework to understand normal and abnormal cardiac electrophysiology, it is still unclear whether TDR is present in vivo, where myocardial cells are electrically coupled.25 While some studies have shown little or no TDR across the heart wall,26 other in vivo studies showed a transmural repolarization gradient, with a potential minimum at the end of the T wave in the ventricular midwall towards the apex,27 consistent with delayed repolarization of M cells in mid-myocardium. Our results serve as indirect evidence for the delayed repolarization of M cells and TDR in humans in vivo. Our T wave simulation results (Figure 6) are also supported by experimental data that show generally positive T wave epicardial potentials with a rather abrupt transition to negative potentials on the atria.27
However, as mentioned in the Introduction section, if delayed M cell repolarization causes the U wave, the initial U wave downstroke in the upper right shoulder region would appear to be at odds with a decrease in the transmembrane potential gradient as M cells repolarize. A decreasing transmembrane potential gradient within the M cell layer will decrease the strength of the TDR current and therefore should decrease the magnitude of the potential in the upper right shoulder region.
Dynamic gap junction coupling
One potential explanation to this problem lies in dynamic gap junction conductivity; if the onset of the U wave coincides with an increase in gap junction conductivity, the strength of the current sources along the Epi/M and Endo/M layers can increase even if the transmembrane potential gradient decreases. This is a direct consequence of the bidomain model that relates extracellular potential to transmembrane potential gradients. According to this model, the strength of current sources is a function of both transmembrane potential gradient and gap junction conductivity. Our results from the 2-D ionic model showed that dynamic gap junction conductivity can produce a U wave downstroke at the base despite a decrease in the transmembrane potential gradient (Figure 4A).
More specifically, if |Di| is a function of Vt, for example |Di| = 1 - Vt/b where b is a positive constant chosen such that Vt/b is always less than 1, then the current source strength is proportional to Vt *(1 - Vt/b), which reaches a maximum value at: Vt = b/2. The current sources increase as Vt decreases from a high (depolarized) value to b/2, and then decrease as Vt decreases beyond this value. (For ease of illustration, endocardial and epicardial cells are assumed to have a Vt =0 so that the gradient of Vt is solely a function of the transmembrane potential of M cells.)
In addition, dynamic gap junction coupling could help explain how M cells can remain at a relatively high transmembrane potential while epicardial and endocardial cells have already repolarized.
Some form of dynamic gap junction conductivity has been demonstrated by Noma and Tsuboi,28 who showed that gap junction conductance decreases at intracellular calcium concentrations at the level that occur during a normal action potential. One cell model that incorporated calcium gated gap junctions exhibited a 15% decrease in gap junction conductivity just after the firing of an action potential.29 In this model, gap junction conductivity recovered steadily throughout diastole.
Resistance at the Atrio-Ventricular border
We did not find any negative U wave over the right shoulder when the resistance at the atrio-ventricular border was infinity. This resistance must be finite to allow TDR current arising from the M cell boundaries to flow along the loops shown in the bottom right panel of Figure 5. In our model, the U wave amplitude was approximately a linear function of this resistance when it was varied over a range between 1–100 times the extracellular resistance of cardiac tissue; within this range, a tenfold increase in atrio-ventricular border resistance resulted in approximately a 5-fold decrease of the U wave amplitude.
Apical/Base repolarization gradients; volume conductor effects
A repolarization time gradient in the apex-base direction could produce a U wave that is upright in the earlier to repolarize region and inverted and the later to repolarize region. Thus, if the apex repolarizes before the base, the U wave could be upright at the apex and inverted over the base. In our 3D heart torso model, no type of apex to base gradient resulted in negative potentials over the right clavicle; the closest distribution we could produce had negative potentials that were inferior to the right shoulder/clavicle line (data not shown). These results are consistent with other simulation studies of the T-wave23,24 which suggest that TDR current is required to produce a realistic T wave (and therefore U wave) BSPD.
However, we can not rule out the possibility that an apical to base repolarization gradient is a source of the U wave. It is possible that a more realistic torso model that includes lungs and other tissues, could shift body surface potentials associated with an apical/basal gradient in such a manner as to match the clinically observed U wave BSPD. A more realistic heart model, e.g. one with a septum and different anisotropy properties, could also affect generated BSPDs.
Mechanical implications
Schimpf et al.30 recently reported that the U wave is coincident with end systole in patients with short QT syndrome, implying that mechanoelectrical feedback has an impact on U wave formation. This mechanoelectrical hypothesis and the M cell hypothesis of the U wave are not mutually exclusive, and both may affect the generation of clinically observed U waves. In particular, TDR would provide a prolonged period of active ventricular relaxation during early diastole, which may strengthen ventricular suction manifested clinically as a high E/A ratio in transmitral velocity by Doppler echocardiography. Mechanical feedback could play a role in this process. More generally, by affecting heart tissue compliance during slow filling, delayed M cell repolarization, which could be modulated by mechanical feedback, could serve other mechanical functions that would require further study to establish.
Limitations
In general, computer models are tools to help to test specific hypotheses and explore possible mechanisms underlying observed phenomena, rather than to substitute for a real heart. Our simulations were based on simplified 2-D and 3-D models, and many of the parameter values regarding the ionic characteristics and conductivity of heart tissue are uncertain. In the 3-D model, we used a monoventricular heart and assumed that M cells comprise a continuous layer throughout the heart; if instead the M cells separately surround the right and left ventricles respectively, the BSPD would shift somewhat compared to the current model, although the maximum and minimum would still occur in the left precordium and upper right shoulder regions, respectively.
Our 2-D model did not include many features (e.g. pertaining to calcium handling) of more detailed models of epicardial, M cell and endocardial cell types.31 Further, gap junctions exhibit transjunctional voltage gating32 that we did not incorporate into our model. Incorporation of these more realistic features could affect the genesis of the U wave in the 2-D ion model.
We cannot rule out the endocardial to epicardial transmembrane potential gradients as the cause of the U wave. Our results suggest that the relationship between the endo/epi gradient and the body surface potentials is roughly linear, so that a U wave would require the slopes of the endocardial and epicardial transmembrane potentials to overlap one another multiple times during repolarzation. This type of overlapping generated U waves in the model of Depolli et al.12 However, for purely epicardial/endocardial transemembrane potential gradients to explain the clinically observed shift in the location of the U wave maximum (compared to the T wave maximum) would appear to require some sort of change in anterior/posterior or apical/basal repolarization sequence of the epicardium or endocardium.
Conclusions
We demonstrate that delayed M cell repolarization can produce realistic U waves if gap junction coupling between myocardial cells is dynamic and the resistance of the tissue at the atrio-ventricular border is finite.
Acknowledgments
The authors thank Elliot McVeigh, PhD for financial and spiritual support for the study.
SOURCES OF FUNDING
This work was supported by grants from the NHLBI (Z01-HL004609 to Elliot R. McVeigh, PhD). This work was made possible in part by the facilities of the NIH/NCRR Center for Integrative Biomedical Computing (P41-RR12553).
Footnotes
DISCLOSURES
Bruce Hopenfeld None
Hiroshi Ashikaga None
References
- 1.Einthoven W. Le elecardiogramme. Arch Int Physiol. 1906;4:132–164. [Google Scholar]
- 2.Spach MS, Barr RC, Warren RB, Benson DW, Walston A, Edwards SB. Isopotential body surface mapping in subjects of all ages: emphasis on low-level potentials with analysis of the method. Circulation. 1979;59(4):805–821. doi: 10.1161/01.cir.59.4.805. [DOI] [PubMed] [Google Scholar]
- 3.Lepeschkin E. Physiological basis of the U wave. In: Schlant RC, Hurst JW, editors. Advances in Electrocardiography. New York: Grune and Stratton; 1972. pp. 431–447. [Google Scholar]
- 4.Goernig M, Haueisen J, Liehr M, Schlosser M, Figulla HR, Leder U. Detection of U wave activity in healthy volunteers by high-resolution magnetocardiography. J Electrocardiol. 2009;43(1):43–47. doi: 10.1016/j.jelectrocard.2009.06.004. [DOI] [PubMed] [Google Scholar]
- 5.Hoffman BF, Cranefield PF. Electrophysiology of the Heart. New York: McGraw-Hill; 1960. [Google Scholar]
- 6.Surawicz B. U wave: facts, hypotheses, misconceptions, and misnomers. J Cardiovasc Electrophysiol. 1998;9(10):1117–1128. doi: 10.1111/j.1540-8167.1998.tb00890.x. [DOI] [PubMed] [Google Scholar]
- 7.Antzelevitch C. Modulation of transmural repolarization. Ann N Y Acad Sci. 2005;1047:314–323. doi: 10.1196/annals.1341.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Antzelevitch C, Sicouri S. Clinical relevance of cardiac arrhythmias generated by afterdepolarizations. Role of M cells in the generation of U waves, triggered activity and torsade de pointes. J Am Coll Cardiol. 1994;23(1):259–277. doi: 10.1016/0735-1097(94)90529-0. [DOI] [PubMed] [Google Scholar]
- 9.Drouin E, Charpentier F, Gauthier C, Laurent K, Le Marec H. Electrophysiologic characteristics of cells spanning the left ventricular wall of human heart: evidence for presence of M cells. J Am Coll Cardiol. 1995;26(1):185–192. doi: 10.1016/0735-1097(95)00167-x. [DOI] [PubMed] [Google Scholar]
- 10.Nesterenko VV, Antzelevitch C. Simulation of the electrocardiographic U wave in heterogeneous myocardium: effect of local junctional resistance. Proc Computers in Cardiology. 1992 Oct 11–14;:43–46. [Google Scholar]
- 11.Ritsema van Eck HJ, Kors JA, van Herpen G. The U wave in the electrocardiogram: a solution for a 100-year-old riddle. Cardiovasc Res. 2005;67(2):256–262. doi: 10.1016/j.cardiores.2005.04.010. [DOI] [PubMed] [Google Scholar]
- 12.Depolli M, Avbelj V, Trobec R. Computer-simulated alternative modes of U-wave genesis. J Cardiovasc Electrophysiol. 2008;19(1):84–89. doi: 10.1111/j.1540-8167.2007.00978.x. [DOI] [PubMed] [Google Scholar]
- 13.di Bernardo D, Murray A. Origin on the electrocardiogram of U-waves and abnormal U-wave inversion. Cardiovasc Res. 2002;53(1):202–208. doi: 10.1016/s0008-6363(01)00439-4. [DOI] [PubMed] [Google Scholar]
- 14.ten Tusscher KH, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. Am J Physiol Heart Circ Physiol. 2004;286(4):H1573–1589. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- 15.Opthof T, Coronel R, Janse MJ. Is there a significant transmural gradient in repolarization time in the intact heart?: Repolarization Gradients in the Intact Heart. Circ Arrhythmia Electrophysiol. 2009;2:89–96. doi: 10.1161/CIRCEP.108.825356. [DOI] [PubMed] [Google Scholar]
- 16.Yan GX, Antzelevitch C. Cellular basis for the normal T wave and the electrocardiographic manifestations of the long-QT syndrome. Circulation. 1998;98(18):1928–1936. doi: 10.1161/01.cir.98.18.1928. [DOI] [PubMed] [Google Scholar]
- 17.Stinstra JG, Hopenfeld B, Macleod RS. On the passive cardiac conductivity. Ann Biomed Eng. 2005;3(12):1743–1751. doi: 10.1007/s10439-005-7257-7. [DOI] [PubMed] [Google Scholar]
- 18.Rush S, Larsen H. A practical algorithm for solving dynamic membrane equations. IEEE Trans Biomed Eng. 1978;25(4):389–392. doi: 10.1109/TBME.1978.326270. [DOI] [PubMed] [Google Scholar]
- 19.Hoffman JD. The Finite Element Method. In: Hoffman JD, editor. Numerical Methods for Engineers and Scientists. 2. New York: Marcel Dekker; 2001. pp. 711–774. [Google Scholar]
- 20.Muzikant AL, Hsu EW, Wolf PD, Henriquez CS. Region specific modeling of cardiac muscle: comparison of simulated and experimental potentials. Ann Biomed Eng. 2002;30(7):867–883. doi: 10.1114/1.1509453. [DOI] [PubMed] [Google Scholar]
- 21.Hopenfeld B. ST segment depression: the possible role of global repolarization dynamics. Biomedical engineering online. 2007;6:6. doi: 10.1186/1475-925X-6-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nielsen PM, I, Le Grice J, Smaill BH, Hunter PJ. Mathematical model of geometry and fibrous structure of the heart. Am J Physiol. 1991;260(4 Pt 2):H1365–1378. doi: 10.1152/ajpheart.1991.260.4.H1365. [DOI] [PubMed] [Google Scholar]
- 23.Miller WT, Geselowitz DB. Simulation studies of the electrocardiogram. I. The normal heart. Circ Res. 1978;43(2):301–315. doi: 10.1161/01.res.43.2.301. [DOI] [PubMed] [Google Scholar]
- 24.di Bernardo D, Murray A. Computer model for study of cardiac repolarization. J Cardiovasc Electrophysiol. 2000;11(8):895–899. doi: 10.1111/j.1540-8167.2000.tb00069.x. [DOI] [PubMed] [Google Scholar]
- 25.Ashikaga H, Coppola BA, Hopenfeld B, Leifer ES, McVeigh ER, Omens JH. Transmural dispersion of myofiber mechanics: implications for electrical heterogeneity in vivo. J Am Coll Cardiol. 2007;49(8):909–916. doi: 10.1016/j.jacc.2006.07.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Taggart P, Sutton P, Opthof T, Coronel R, Kallis P. Electrotonic cancellation of transmural electrical gradients in the left ventricle in man. Prog Biophys Mol Biol. 2003;82(1–3):243–254. doi: 10.1016/s0079-6107(03)00025-7. [DOI] [PubMed] [Google Scholar]
- 27.Spach MS, Barr RC. Ventricular intramural and epicardial potential distributions during ventricular activation and repolarization in the intact dog. Circ Res. 1975;37(2):243–257. doi: 10.1161/01.res.37.2.243. [DOI] [PubMed] [Google Scholar]
- 28.Noma A, Tsuboi N. Dependence of junctional conductance on proton, calcium and magnesium ions in cardiac paired cells of guinea-pig. J Physiol. 1987;382:193–211. doi: 10.1113/jphysiol.1987.sp016363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oka C, Matsuda H, Sarai N, Noma A. Modeling the calcium gate of cardiac gap junction channel. J Physiol Sci. 2006;56(1):79–85. doi: 10.2170/physiolsci.r2139. [DOI] [PubMed] [Google Scholar]
- 30.Schimpf R, Antzelevitch C, Haghi D, Giustetto C, Pizzuti A, Gaita F, Veltmann C, Wolpert C, Borggrefe M. Electromechanical coupling in patients with the short QT syndrome: further insights into the mechanoelectrical hypothesis of the U wave. Heart Rhythm. 2008;5(2):241–245. doi: 10.1016/j.hrthm.2007.100.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Campbell SG, Flaim SN, Leem CH, McCulloch AD. Mechanisms of transmurally varying myocyte electromechanics in an integrated computational model. Philosophical transactions. 2008;366(1879):3361–3380. doi: 10.1098/rsta.2008.0088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lin X, Gemel J, Beyer EC, Veenstra RD. Dynamic model for ventricular junctional conductance during the cardiac action potential. Am J Physiol Heart Circ Physiol. 2005;288(3):H1113–1123. doi: 10.1152/ajpheart.00882.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]