Validation, In-Depth Analysis, and Modification of the Micropipette Aspiration Technique

Abstract

The micropipette aspiration technique (MAT) has been successfully applied to many studies in cell adhesion such as leukocyte-endothelium interactions. However, this technique has never been validated experimentally and it has been only employed to impose constant forces. In this study, we validated the force measurement of the MAT with the optical trap and analyzed two technical issues of the MAT, force-transducer offset and cell-micropipette gap, with finite element simulation. We also modified the MAT so that increasing or decreasing forces can be applied. With the modified MAT, we studied tether extraction from endothelial cells by pulling single tethers at increasing velocities and constant force loading rates. Before the onset of tether extraction, an apparently-linear surface protrusion of a few hundred nanometers was observed, which is likely related to membrane receptors pulling on the underlying cytoskeleton. The strength of the modified MAT lies in its capability and consistency to apply a wide range of force loading rates from several piconewtons per second up to thousands of piconewtons per second. With this modification, the MAT becomes more versatile in the study of single molecule and single cell biophysics.

INTRODUCTION

Small forces ranging from tens of femtonewtons to hundreds of nanonewtons are involved in extending single molecules, rupturing single receptor-ligand bonds, and deforming cellular surfaces. Therefore, measuring or applying these forces is of great importance in biophysics and bioengineering. As such, several techniques have been developed since the late eighties, including the atomic force microscope³, the optical trap (OT)¹, the magnetic force apparatus³³, the microneedle technique¹⁶, the biomembrane force probe⁷(BFP), and the micropipette aspiration technique (MAT)^26,30. Although these techniques were employed in earlier studies where the importance of the force loading rate was not recognized, they have made huge impacts in various fields of biology and medicine.

Both the BFP and the MAT are based on a micropipette manipulation system. The difference between these two techniques is that the BFP is based on the principles of solid mechanics, whereas the MAT is based on the principles of fluid mechanics. The BFP uses a bead affixed on an inflated red cell or liposome as the force transducer, whereas the MAT uses a spherical bead or cell placed inside a micropipette (a glass tube) as the force transducer. The red cell or liposome in the BFP serves like a spring, whereas the force in the MAT is applied by creating fluid flow in the micropipette. One advantage of the MAT is that it can be easily applied to cell-cell interactions. Although the MAT has been applied to many interesting studies, including the extensional stiffness of single neutrophil microvilli, tether extraction from neutrophils and endothelial cells, bond formation with contact stress, and single receptor anchoring strength, only constant forces were employed because it was technically limited by a constant pressure^{11,18,26,28,34}. With the MAT, the force (F) imposed through a spherical force transducer can be calculated from²⁶

$$F=\pi R_p^2\Delta p\left(1-\frac{4}{3}\stackrel{‒}{\epsilon }\right)\left(1-\frac{U_t}{U_f}\right),$$ (1)

where Δp is the suction pressure, R_p is the radius of the micropipette, U_f is the transducer velocity when it is moving freely under Δp, U_t is the transducer velocity when it is adherent to a cell or surface, and

$$\stackrel{‒}{\epsilon }=\left(R_p-R_b\right)∕R_p,$$ (2)

where R_b is the radius of the transducer. Equation 1 was obtained by analyzing the motion of an adherent or freely-moving sphere inside a uniform cylindrical tube with low Reynolds number hydrodynamics. Although no calibration of the MAT with another technique is required for its application, the validity of Eq. 1 has never been compared experimentally with another well-established technique.

One important problem that has been studied extensively with the MAT is tether extraction from leukocytes and endothelial cells (ECs)^{6,10–12,19,34}. Tethers are small membrane tubes that stabilize leukocyte rolling on the endothelium, which is a key step for the ensuing leukocyte arrest on the endothelium^20,36. Under a constant aspiration pressure, most tethers are extracted at a constant velocity. Since the diameters of tethers extracted from normal leukocytes and ECs are only in tens of nanometers, the existence of tethers is often perceived by a smaller transducer velocity (U_t) that accelerates to a larger free motion velocity (U_f) after tether extraction is terminated. From the study of tether extraction at many different pressures, a linear relationship between the pulling force (F) and the tether growth velocity (U_t) can be established¹⁵

$$F=F_0+2\pi {\eta }_{\mathit{eff}}{U}_t,$$ (3)

where F₀ is the threshold force and η_eff is the effective viscosity. For passive human neutrophils, F₀ is 45 pN and η_eff is 1.8 pN·s/μm, both of which are affected by cytokine stimulation^26,31. For human umbilical vein endothelial cells (HUVECs), F₀ is around 50 pN and η_eff is only 0.5 pN·s/μm, neither of which is affected by TNF-α or IL-1 stimulation¹¹. The comparatively-smaller effective viscosity for HUVECs indicates that ECs can contribute much more to the composite tether length when simultaneous tethers are extracted from both leukocytes and ECs³⁸.

Despite the potential of the MAT in single molecule, single cell, and cell-cell adhesion studies, two concerns in its application have never been addressed. One is that the spherical force transducer is sometimes offset from the axisymmetric axis of the cylindrical micropipette. This may occur in any MAT study and there are many possible causes. For example, during tether extraction, tethers may not be exactly pulled out from a point on the cell that is located on the axis of symmetry. Although a small and gentle contact between the cell and the force transducer prevents the adhesive bond from being too far from the axis of symmetry, a small deviation can easily occur. Since Eq. 1 was established with an axisymmetric model, how accurately the actual force applied on the offset transducer can be calculated with Eq. 1 is still unknown. The other concern is related to the studies of attached cells using the MAT (e.g., tether extraction from attached endothelial cells). In those studies, a nearly flat endothelial cell surface was placed close to the micropipette tip, creating a small gap between the micropipette tip and the endothelial cell. The pressure drop over this small gap may compromise one critical assumption made during the derivation of Eq. 1, i.e., the major pressure drop in the whole flow field occurs mainly inside the micropipette. Consequently, it may greatly affect the force calculation with Eq. 1.

In this paper, we first validated the MAT by the OT and then analyzed the two concerns associated with the MAT application by finite element analysis. We also modified the MAT to impose increasing or decreasing forces at a constant force loading rate on single cells or molecules. With the modification, we extracted tethers from HUVECs using beads coated with anti-PECAM-1 (platelet-endothelial cell adhesion molecule-1 or CD31) as the force transducer. Our results showed that, under an increasing force, the transducer moved at a constant acceleration, which indicates a linear relationship between the pulling force and the tether growth velocity. More importantly, a linear surface protrusion was observed before tether extraction and it is likely related to CD31 pulling on the underlying cytoskeleton. With the modified MAT, a large range of force loading rates from several piconewtons per second up to more than ten thousand piconewtons per second can be applied. These additional capabilities of the MAT will certainly broaden its applicability in studying mechanical properties of single cells and molecules.

MATERIALS AND METHODS

Cell Preparation

Neutrophils were isolated from the blood of healthy donors by finger prick. Briefly, a few drops of blood were collected into a heparinized capillary glass tube (Fisher Scientific, Hampton, NH) and overlaid on 200-μl mono-poly resolving medium (MP Biomedicals, Irvine, CA). The sample was then centrifuged at 300×g for 15 minutes at room temperature. Afterwards, 0.1 ml of neutrophil-containing medium above the red blood cell pellet was collected and washed in 1-ml Hanks balanced salt solution (HBSS; Sigma, Saint Louis, MO) at 300×g for 5 min. After wash, the cells were resuspended in 0.1-ml 50% autologous plasma-HBSS solution, a fraction of which was transferred into the experimental chamber.

HUVECs were purchased from Cambrex Biosciences (Walkersville, MD) and cultured in 6-well plates with endothelial cell medium-2 (Cambrex Biosciences). For experiments with suspended HUVECs, confluent cells were detached with 5 mM EDTA (Sigma), washed with 0.1% bovine serum albumin (BSA), and then resuspended in CO₂-independent medium (Invitrogen Corporation, Carlsbad, CA) for immediate use. For experiments with attached HUVECs, cells were first cultured on a cell-culture-treated coverslip (NUNC, Naperville, IL), which was mounted on the inner side wall of the experimental chamber with silicone adhesive (Dow Corning Corporation, Midland, MI). The whole chamber was then kept in an incubator for 12 hours for the cells to attach and spread. Prior to experiment, the chamber was removed from the incubator, washed, and refilled with CO₂-independent medium.

Validation of the MAT with the OT

The OT combined with a micropipette manipulation system was described previously³⁵. Briefly, an infrared laser (wavelength 1064 nm) was expanded, directed into the epifluorescence port of an inverted microscope (Zeiss, Germany), and focused into a tiny spot by an objective with a high numerical aperture. The focal spot can trap particles in the experimental chamber and serve as a mechanical spring. As shown in Fig. 1a, an anti-PSGL-1 (P-selectin glycoprotein ligand-1)-coated polystyrene bead (~4.5 μm in diameter) was trapped. The trap stiffness, calibrated with Stokes' drag, was ~0.08 pN/nm. Close to the trapped bead was a micropipette holding a passive human neutrophil as the force transducer of the MAT. A constant aspiration pressure of 2 pN/μm² was applied in the MAT to extract tethers from the neutrophil. When a tether was extracted from the neutrophil, the pulling force was measured simultaneously by the OT and the MAT. All the experiments were recorded on a DVD for post-analysis.

FIGURE 1.

(a) One video micrograph showing tether extraction from a human neutrophil using the OT and the MAT simultaneously. An antibody-coated bead and a passive human neutrophil were used as the force transducers of the OT and the MAT, respectively. (b and c) Two video micrographs showing tether extraction from a suspended (b) or attached (c) HUVEC with an antibody-coated bead (the force transducer of the MAT). A voltage stamp of 5V (shown actually as “+05.08”) was used to indicate the instant when the stage started to move and the suction pressure started to increase.

Finite Element Simulation

To evaluate the accuracy of using Eq. 1 to calculate the force when the bead is offset from the axisymmetric axis or when there is an attached cell close to the micropipette tip, the force exerted on the transducer bead should be determined by another reliable means first. To this end, finite element analysis was chosen since no precise solutions were available. The simulations were performed with FIDAP (Fluent Incorporated, Lebanon, NH). Two models (Model I and II) were developed corresponding to the two scenarios described above.

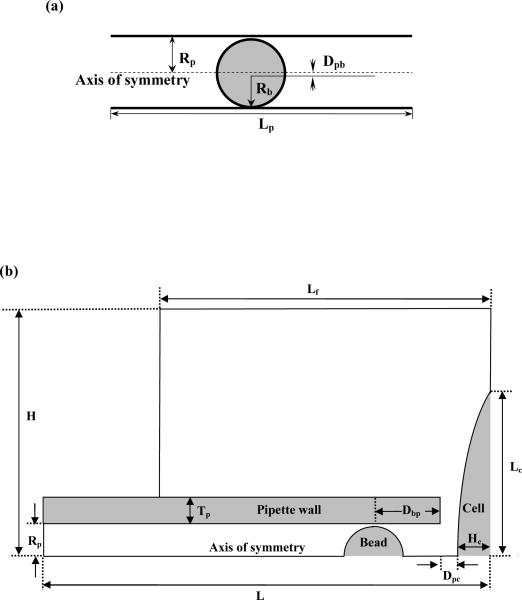
In Model I, a three-dimensional (3-D) model was developed for examining the effect of the transducer offset on the force calculation with Eq. 1 in the MAT. A schematic illustrating the geometrical parameters for this model is shown in Fig. 2a. In the simulation, the bead radius was 3.9 μm, the pipette inner radius was 4 μm, and the pipette length was 60 μm. To simulate the flow field accurately, finer meshes were generated at the small gap between the bead and the micropipette inner wall, where more dramatic changes in pressure and velocity were expected. Altogether, ~500,000 elements were generated in this model.

FIGURE 2.

Geometric dimensions used in the finite element simulations. (a) Model I: L_p = 60 μm, R_p = 4 μm, R_b = 3.9 μm, and D_pb = 0–0.08 μm. (b) Model II: H = 30 μm, L_f = 40 μm, R_p = 4 μm, R_b = 3.9 μm, T_p = 3 μm, D_bp = 8 μm, H_c = 4 μm, and L_c = 20 μm. The total pipette length was 650 μm and only part of the pipette is shown. For this particular case, the distance between the cell apex and the pipette tip (D_pc) was 2 μm. The size of the entire simulation area outside the pipette was 30 μm × 40 μm.

In Model II, a 2-D axisymmetric model was developed for examining how accurate the force calculation with Eq. 1 is when an opposing surface is positioned close to the micropipette tip. Figure 2b shows the typical geometry. The pipette inner radius was 4 μm and its wall thickness was 3 μm, both of which were determined experimentally. The bead radius was 3.9 μm and the bead center was 8 μm inside from the micropipette tip. The endothelial cell surface was approximated by an arc, which was characterized by the maximum thickness (H_c) and the half length (L_c) of the cell. The pipette length in this model (L) was about 650 μm (note that only part of the pipette is shown in Fig. 2b). Altogether, ~30,000 elements were generated with finer mesh grading specified at both the micropipette tip (the right end of the micropipette as shown in Fig. 2b) and in and around the small gap between the bead and the micropipette.

In both models, appropriate pressure boundary conditions were imposed to simulate actual experiments. In Model I, the pressures at the pipette inlet and outlet were set to zero and a negative value, respectively. In Model II, a total pressure drop was set between the pipette outlet and the far field boundary. On the surfaces of the cell, bead, pipette, and substrate, no-slip boundary condition was imposed. In all the simulations, the density and the viscosity of the medium were set to 10⁻⁹ pN·s²/μm⁴ (equivalent to10⁻⁹ mg/μm³) and 10⁻³ pN·s/μm² (equivalent to10⁻³ N·s /m²), respectively.

Modification of the MAT

The micropipette manipulation system and how it is used in the MAT have been described in detail elsewhere^26,30,31. Briefly, it is composed of an inverted microscope, two micropipettes (glass tubes), two micromanipulators for positioning the micropipettes in the experimental chamber, and two manual manometers for controlling the pressures inside the micropipettes. With the manual manometers, only constant suction pressures can be applied without disturbance, resulting in constant forces. In this study, we replaced one of the manual manometers with a motorized system where two vertical translational stages (one motorized (Physik Instrumente, Auburn, MA. Model M-501.1PD) and the other manual) are assembled together in series. The motorized stage is controlled with a program written in LabView (National Instruments, Austin, TX). With this modification, an increasing pressure or any pressure pattern can be applied in the micropipette, thus allowing us to impose forces with different loading rates and patterns.

Latex beads coated with goat-anti-mouse antibodies (~8 μm in diameter; Sigma, Saint Louis, MO) were washed twice in PBS and incubated with mouse anti-human antibodies (anti-CD31; R&D Systems, Minneapolis, MN) for 1 hour at 37°C. The beads were washed twice and resuspended in PBS prior to use. Glass micropipettes of desired diameters (~8 μm in diameter) were prepared with a vertical pipette puller and a microforge as described elsewhere²⁶. The narrow opening of the micropipette was filled with 1% BSA and the rest of it was backfilled with PBS. The bead and micropipette diameters were determined by dividing their optical diameters by their corresponding correction factors³¹. The gap between the bead and the micropipette was ~0.2 μm on average.

Surface Protrusion and Tether Extraction from HUVECs

For tether extraction with the MAT, spherical latex beads coated with mouse antibodies against human receptors were used as the force transducer. As shown in Fig. 1b, for suspended HUVECs, the force transducer (i.e., the antibody-coated bead) was aspirated into a micropipette that has a slightly larger diameter than the bead. An endothelial cell was held by another micropipette with an aspiration pressure that does not deform the cell much. For surface-attached HUVECs, a single micropipette that contains the force transducer was used (Fig. 1c). In both cases, a positive pressure was first used to drive the transducer bead to contact the cell and then an increasing aspiration pressure starting from zero was applied to pull the transducer bead away from the cell. The increasing pressure was applied by moving the motorized stage at a constant speed. This procedure was repeated for about 50 times per cell-bead pair at each stage speed. To record the instant when the stage started to move in each contact event, an NI-DAQ board (6024E, NI, Austin, TX) was installed on the same computer and incorporated into the LabView program that controls the motorized stage as a virtual instrument. When an electrical signal was sent through the computer to trigger the stage movement, another 5V TTL signal was transmitted simultaneously to a multiplexer through the NI-DAQ board. A voltage stamp of 5V was then printed on the monitor along with the image signal transmitted from the camera until the stage movement stopped (Fig. 1c). The whole experiment was recorded onto a DVD with a Sony DVD recorder. Typically, the adhesion frequency (the number of adhesion events divided by the number of contact) was low (< 25%, achieved by decreasing the antibody concentration on the bead), indicating dominant single-bond interaction and single-tether extraction between the bead and the cell^22,25,29.

Data Analysis

The analysis procedure of the tether-extraction experiments has been described in detail elsewhere^26,31. Briefly, the DVD recorded during the tether-extraction experiments was played in a DVD player and the signal was transmitted to a Windows computer through a monochrome frame grabber. Individual adhesion events were stored in separate movie files. The displacement of the force transducer was then tracked with the single particle tracking technique⁹, which has a tracking resolution of ~5 nm.

In the experiments where the OT and the MAT were employed simultaneously, the displacements of both the bead in the trap and the cell in the micropipette were tracked with the single particle tracking technique and saved in separate ASCII files. The tether growth velocity (U_t) and the corresponding free motion velocity of the cell (U_f) were calculated by linear regression from the cell displacement data. Then the magnitude of the force imposed on the cell was calculated with Eq. 1 by taking $\stackrel{‒}{\epsilon }$ to be zero since it is very small. The force magnitude was also calculated by multiplying the trap stiffness by the bead deflection.

In the experiments with the modified MAT, only the bead displacement was tracked. The magnitude of the force was calculated with Eq. 1. However, since an increasing aspiration pressure was applied in the micropipette, the bead was moving at an increasing velocity. Based on different behaviors of the bead displacement, different methods were employed to calculate its velocity (see RESULTS for detailed description).

RESULTS

Experimental Validation of the MAT with the OT

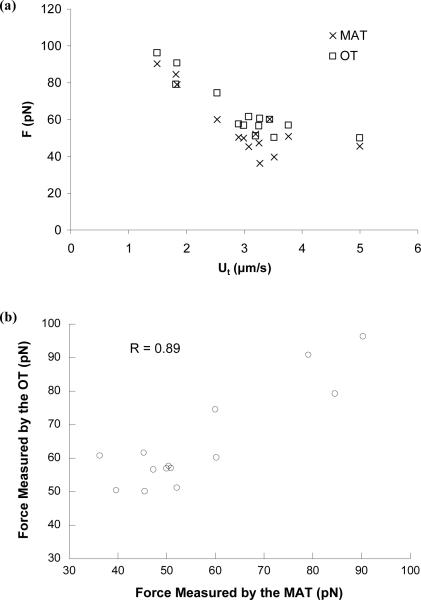
Tether extraction from human neutrophils has been investigated with the MAT using either a spherical bead or a neutrophil as the force transducer^26,31. In the current study, to save the bead for the optical trap, a spherical neutrophil was used as the force transducer of the MAT. The bead for the optical trap was coated with antibodies against PSGL-1. Overall 14 tethers were extracted under a constant suction pressure of 2 pN/μm². Due to the heterogeneity of the cells, the tether growth velocity varied from 1.5 μm/s to 5 μm/s (Fig. 3a). However, in most cases, the force magnitudes calculated from the MAT agreed well with the values obtained with the OT and the average difference was only 8.9 ± 6.4 pN (mean ± standard deviation). Linear regression through the forces obtained with these two techniques yielded statistically indistinguishable slopes, intercepts, and elevations. The strong correlation between the forces simultaneously measured with the OT and the MAT is shown in Fig. 3b. This demonstrates that the force measurement with the MAT is very accurate. The average tether growth velocity for the 14 cases shown in Fig. 3a was 3.0 μm/s and the corresponding pulling force was 57 pN, both of which are consistent with our previous results obtained from passive human neutrophils using the MAT^31,34.

FIGURE 3.

(a) Pulling forces (F) measured simultaneously with the MAT and the OT during tether extraction from human neutrophils. Although the force magnitudes distributed widely from 40 pN up to 100 pN due to the cell heterogeneity, the close agreement between the MAT and OT is clear. The stiffness of the OT was ~0.08 pN/nm and the suction pressure in the micropipette was 2 pN/μm². (b) Correlation between the pulling forces measured simultaneously with the OT and the MAT.

Finite Element Analysis of the MAT: 1. The Effect of the Transducer Offset on the Force Calculation

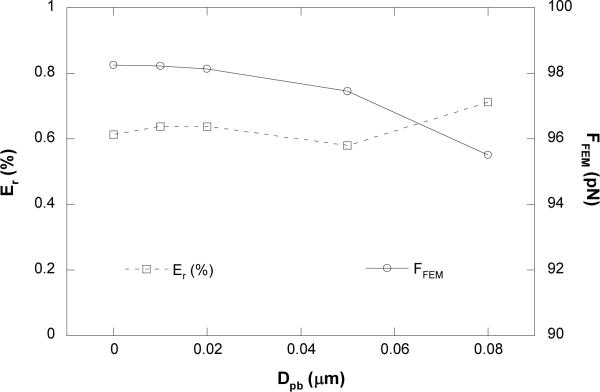
To determine whether the force calculation with Eq. 1 is accurate enough when the bead is offset from the pipette axis in the MAT, we developed a 3-D model with finite element analysis and compared its results with those from the MAT. Five cases with different offsets (i.e., different distances between the bead center and the micropipette axis of symmetry, D_pb; see Fig. 2a) were examined. For all the five values of D_pb ranging from 0 to 0.08 μm, the same total pressure drop of 2.5 pN/μm² and the bead velocity of 10 μm/s were used in the simulation. The force applied on the offset bead, F_FEM, was then calculated with FIDAP. To ensure that F_FEM is reliable and accurate, we refined the mesh for each model until the change in F_FEM was less than 0.1% after successive refinement. In addition, for the case when D_pb = 0, we compared F_FEM with the force calculated from a 2-D axisymmetric model and found the difference was less than 0.2%.

To calculate the force on the bead with Eq. 1, the bead free motion velocity (U_f) under the same pressure drop needs to be obtained in advance. By definition, the free motion velocity is the bead velocity when the hydrodynamic force imposed on the bead is zero. Due to the linear nature of low Reynolds number flow, the hydrodynamic force is linearly dependent on the bead velocity. Therefore, simulating the bead motion at two randomly-chosen velocities and calculating the forces on the bead at these two velocities allowed us to accurately identify the bead free motion velocity, at which the force on the bead is zero. This way of determining the free motion velocity was verified by simulating the bead moving at the identified free motion velocity and calculating the force applied on the bead, which was less than 0.01 pN for every case examined.

Denote the force on the bead calculated with Eq. 1 as F_Eq. The difference between F_Eq and F_FEM represents the error of using Eq. 1 to calculate the force when the bead center is offset from the micropipette axis. The relative error (E_r) is therefore defined as

$$E_{\mathrm{r}}=\mid \left(F_{Eq}-F_{FEM}\right)∕F_{FEM}\mid \times 100\%.$$ (4)

Figure 4 shows the dependence of the relative error and F_FEM on D_pb. At D_pb = 0, the relative error was only about 0.6%; even when the bead was offset for 0.08 μm (80% of the maximum offset since the gap between the pipette and the bead is generally ~0.1 μm), the relative error was still only 0.7%. These results show that the force calculation with Eq. 1 is fairly accurate even when the force transducer is a little off the micropipette axis of symmetry.

FIGURE 4.

Effect of D_pb on the relative error (E_r) between the two forces calculated from either Eq. 1 (F_Eq) or FIDAP simulation (F_FEM). F_FEM is also shown. Five different D_pb values in the range of 0 to 0.08 μm were examined at the constant total pressure drop of 2.5 pN/μm² and the tether growth velocity of 10 μm/s.

Finite Element Analysis of the MAT: 2. The Optimal Distance between the Micropipette Tip and Its Opposing Cell Surface

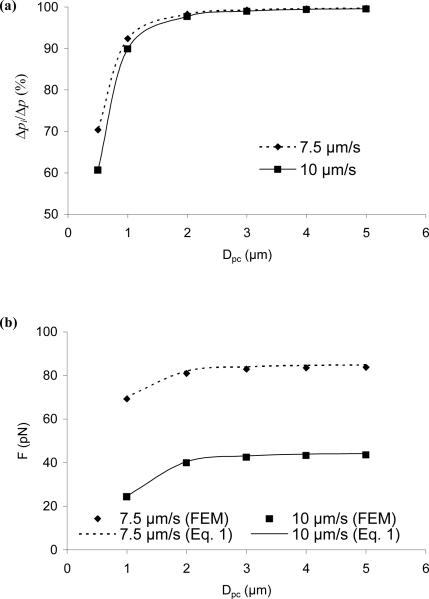
In the MAT experiment with an attached cell, the cell surface is positioned at a certain distance away from the micropipette tip. When this distance, i.e., the gap between the cell surface and the micropipette tip (D_pc), is getting smaller and smaller, the pressure drop around the micropipette tip, Δp_o (note that the total pressure drop Δp = Δp_o + Δp_i where Δp_i is the pressure drop inside the micropipette) will become larger and larger. Consequently, when this distance becomes so small that Δp_o becomes a significant portion of Δp, the force calculation with Eq. 1 will become inaccurate because the derivation of this equation requires the drag around the micropipette tip to be small so that Δp ≈ Δp_i. On the other hand, this distance cannot be too large because most of the transducer body needs to stay inside the micropipette for Eq. 1 to work. To identify an optimal distance between the cell and the micropipette tip, six different distances from 0.5 μm to 5 μm were examined in Model II. For all these cases, two different bead velocities (7.5 μm/s and 10 μm/s, simulating two different tether growth velocities) were simulated under a total pressure drop of 4.24 pN/μm². The thickness of the attached endothelial cell (H_c) was set to 4 μm, a typical value estimated from the actual experiments. The half length of the cell (L_c) was set at 20 μm. For every case considered, the bead free motion velocity was obtained as described in the previous section.

Shown in Fig. 5a is the comparison between the pressure drop inside the micropipette (Δp_i) and the total pressure drop (Δp). At a given bead velocity, the inner pressure drop decreased while the cell was positioned closer to the micropipette tip. When D_pc approached 0.5 μm, the inner pressure drop declined to ~60%~70% of the total pressure drop. In other words, the pressure drop outside the micropipette (mainly across the gap between the micropipette tip and the opposing cell surface when the micropipette length is not too long) increased substantially. To prevent this from happening, a minimum distance of 2 μm should be employed between the micropipette tip and the opposing cell surface. This conclusion was further supported by the observation that the force applied on the transducer bead (calculated using Eq. 1) was obviously decreased when the distance between the micropipette tip and the cell surface was less than 2 μm (Fig. 5b). When D_pc was larger than or equal to 2 μm, the calculated forces were not dependent on D_pc; when D_pc was 1 μm, the calculated forces at the bead velocities of 7.5 μm/s and 10 μm/s were significantly decreased by 17% and 44%, respectively. However, it is intriguing to note that Eq. 1 still predicts the force very well even at a distance less than 2 μm. One possible reason for this nice agreement is that the bead free motion velocity is also dependent on D_pc (see more explanation in Discussion).

FIGURE 5.

Effect of D_pc on the inner pressure drop in the MAT (a) and the force exerted on the transducer, F (b). Under the constant total pressure drop of 4.24 pN/μm², six different distances (D_pc) were simulated with the bead velocity at either 7.5 μm/s or 10 μm/s, simulating tether extraction at two different velocities.

Application of the Modified MAT to Surface Protrusion and Tether Extraction from HUVECs

Tether extraction from both suspended and attached HUVECs has been investigated with the MAT and a linear relationship between the pulling force (F) and the tether growth velocity (U_t) has been established¹¹. Previous experiments were carried out with either constant pulling force or constant pulling velocity. The linear relationship was acquired by fitting the tether data. With the modified MAT, we can easily extract tethers at an increasing velocity by applying an increasing aspiration pressure. The receptor we chose as the force handle was CD31, which is constitutively expressed on endothelial cells.

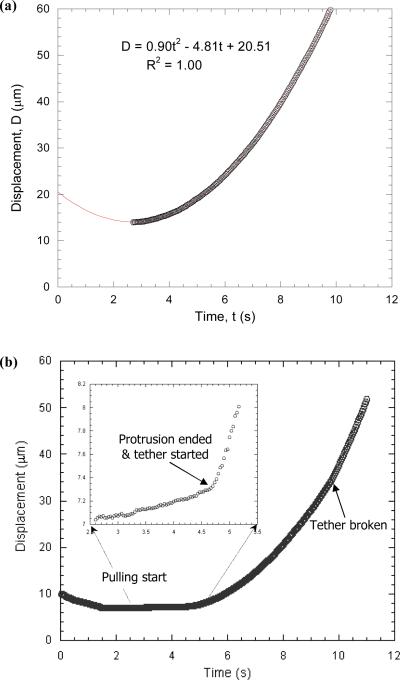
As shown in Fig. 6a, if there was no adhesion between the bead and the cell, the bead moved downstream in a parabolic fashion (D = 0.90t² − 4.81t + 20.51 where D is the bead displacement and t is time), i.e., at a constant acceleration under a linearly-increasing pressure. This behavior is expected due to the linear nature of low Reynolds number flow in these experiments. The free motion velocity at each pressure can be obtained by differentiating the parabolic equation. On the other hand, if adhesion did occur between the bead and the cell, the bead moved downstream as shown in Fig. 6b where the stage speed of the manometer was 75 μm/s. In this case, two different dynamic regimes can be identified from the bead motion.

FIGURE 6.

(a) A typical case of the bead free motion obtained with the modified MAT at the stage speed of 75 μm/s. A quadratic equation was used to fit the bead displacement and the resulting correlation coefficient is also shown in the figure. (b) A typical case of the bead displacement acquired at the stage speed of 75 μm/s when there was adhesion between the bead and a suspended HUVEC. Both (a) and (b) were acquired with the same pair of bead and micropipette. Two different regimes, surface protrusion and tether extraction, were identified from the bead displacement. The termination of the initial surface protrusion could be clearly identified in the inset figure, which also indicates the onset of tether extraction.

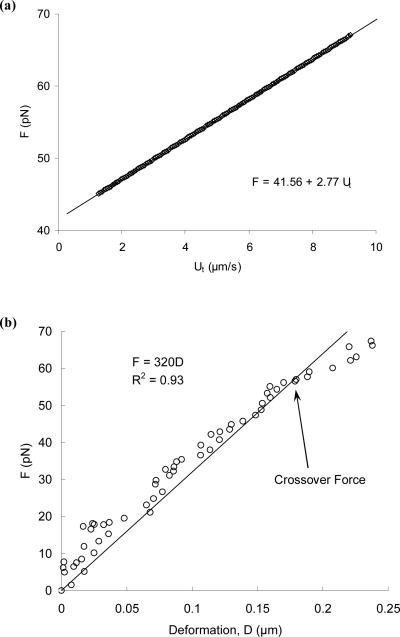
In the second regime (starting from ~4.7 s), a tether was extracted for more than 20 μm before the adhesion was ruptured at about 9.5 s. After tether extraction was terminated by adhesion rupture, the bead quickly accelerated to its free motion indicating the complete separation of the bead and the cell. Further analysis showed that, in this regime, the bead also moved in a parabolic fashion, but with a significantly smaller acceleration, which indicates that tethers were actually extracted at a linearly-increasing velocity. To characterize the relationship between U_t and F, the tether growth velocity was first obtained by differentiating the displacement-time relationship (D = 0.80t² − 6.12t +18.30). The total aspiration pressure (Δp) at each time point was calculated from the stage speed and time, whereas the free motion velocity (U_f) at each pressure was determined from Fig. 6a. As shown in Fig. 7a, it is clear that F has a linear relationship with U_t, which could be directly derived theoretically (Eq. B10 in Appendix B). Moreover, it can be shown that tethers were extracted at a constant force loading rate (Eqs. B8 and B9 in Appendix B). The corresponding force loading rate, effective viscosity and threshold force can be obtained by directly fitting the free or tethered motion of the bead with quadratic equations (Appendix B).

FIGURE 7.

Further analysis of surface protrusion and tether extraction of the case shown in Fig. 6b. A quadratic equation was fitted very well to the bead displacement in the tether extraction regime (D = 0.80t² − 6.12t +18.30), so a linear relationship was found between the pulling force and the tether growth velocity (a). In the surface protrusion regime, the cell surface deformed linearly with a protrusional stiffness of 320 pN/μm (b) and a constant force loading rate of 34 pN/s (data not shown).

In the first regime shown in Fig. 6b, surface protrusion was observed before the onset of tether extraction. During surface protrusion, the bead translated for ~250 nm in about two seconds. Analyzing the force applied on the bead showed that the force increased linearly with time (data not shown). The force at the conclusion of surface protrusion was calculated as the crossover force, which represents the force at which surface protrusion transitions to tether extraction. The force loading rate during surface protrusion is represented by r_fm. As shown in Fig. 6b, the bead moved almost at a constant velocity during surface protrusion, which was also true in other cases of our experiments. Therefore, we fit the whole initial displacement with linear regression and used the obtained velocity in all the force calculation during surface protrusion. The free motion velocity (U_f) was again calculated from analyzing the bead free motion as described above. Further analysis of surface protrusion showed that the cell surface was extended linearly (Fig. 7b). For the case shown in Fig. 7b, the protrusional stiffness (represented by k_m) was ~320 pN/μm. The termination of the initial apparently-linear protrusion can be easily identified in the inset of Fig. 6b with a crossover force of ~70 pN (Fig. 7b).

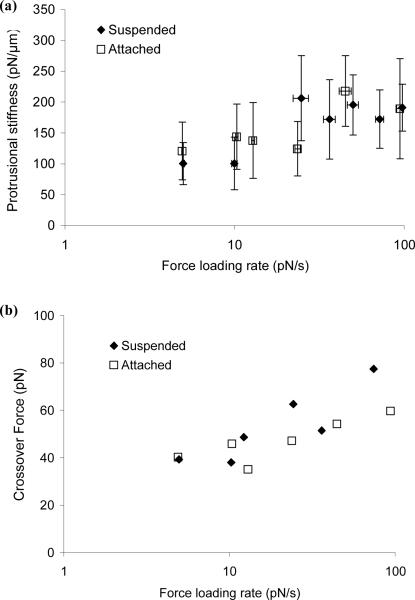
Shown in Figs. 8a and 8b were the protrusional stiffness and the crossover force obtained from both suspended and attached HUVECs during their surface protrusion. With an analogue camera, only a small range of manometer stage speeds can be examined (10 to 200 μm/s), which corresponds to a small range of force loading rates from 5 pN/s to 100 pN/s. As shown in Fig. 8a, the protrusional stiffness values for suspended and attached HUVECs were both within 100 and 200 pN/μm and they did not seem to depend on the force loading rate probably because the range of the force loading rate was not wide enough. However, the crossover force for both suspended and attached cells was dependent on the force loading rate evidently (Fig. 8b). These findings are similar to what was found in human neutrophils and they clearly show that forces at various loading rates can be applied with the enhanced MAT.

FIGURE 8.

Effect of the force loading rate on surface protrusion from HUVECs. Anti-CD31-coated beads were used as the force transducer to interact with both suspended and attached HUVECs. The corresponding protrusional stiffness (a) and crossover force (b) are all plotted as a function of the force loading rate. Each point here represents the mean value of 5~22 adhesion events obtained from three to ten cells. The error bars in (a) stand for the standard deviations in both directions.

DISCUSSION

Since its debut in 1996²⁵, the MAT has been applied to many interesting studies in cellular and molecular biophysics^14,30,34,35 and more capabilities are being added²⁴. In this paper, we summarize the most recent progress in the development and application of the MAT. First, with the OT, we validated the MAT by measuring tether pulling forces using these two techniques simultaneously. Second, with finite element simulations, we investigated how the force calculation in the MAT may be affected by the force-transducer offset from the micropipette axis and the gap between the micropipette tip and the opposing cell surface. Most importantly, we improved the MAT so we can impose increasing or decreasing forces on single cells or molecules with controlled force loading rates. With this new capability of the MAT, we pulled single membrane receptors on endothelial cells with forces loaded in the range of 5 to 100 pN/s. Two different regimes that characterize distinct cell behaviors were identified during the pulling process. In the first regime, short surface protrusion of several hundred nanometers was observed and the pulling force had an apparently-linear relationship with the cellular deformation (Fig. 7b). In the second regime, membrane tethers were extracted at linearly-increasing velocities under linearly-increasing forces (Fig. 7a).

The OT functions like a spring with an ultra small spring constant. For example, the trap stiffness used in this study was only 0.08 pN/nm. With a tracking resolution of ~5 nm for the bead deflection in the trap, the OT has a theoretical force resolution of ~0.4 pN. This high force sensitivity makes the OT an ideal candidate for validating the force measurement with the MAT. However, the transducer bead of the OT cannot be placed directly in the micropipette because of the potential optical effect of the pipette on the trap. Therefore, a separate force transducer (i.e., a human neutrophil) was used in the MAT and the two transducers were connected by a membrane tether when forces were imposed on them. It should be pointed out that the maximum force that can be applied with our OT setup is ~100 pN (other setups may be used to apply forces of a few hundred piconewtons), so we only applied a small suction pressure of 2 pN/μm² to keep the force below 100 pN although much larger forces (a few hundred nanonewtons) can be exerted with the MAT. One obvious advantage of the MAT over the OT is that the force transducer of the MAT is not heated by laser as in the OT.

The force calculation in the MAT is performed with Eq. 1, which was derived by a lubrication analysis with two major assumptions: 1)$\stackrel{‒}{\epsilon }$ is much smaller than one, and 2) the force transducer moves exactly along the axis of the micropipette. Although the first assumption is usually valid in the MAT experiments (~2%), the second one can easily become invalid. By approximating some terms with higher order series the ones used by Shao and Hochmuth²⁵, we derived more accurate solutions to this fluid flow problem (Appendix A), but it is still an approximate formula because many higher order terms are neglected because of the small gap between the pipette and force transducer. Although the asymptotic solution obtained by Bungay and Brenner with perturbation analysis can be applied to the bead offset from the pipette axis⁵, their solution is only accurate to the first order, so we chose to carry out finite element analysis to evaluate Eq. 1. As expected, our 3-D model (Model I) demonstrates that neglecting the higher order terms only cause a small deviation from the actual force on the force transducer. More importantly, our 3-D model demonstrates that even when the bead is a little offset from the micropipette axis, the force calculation with Eq. 1 is still very accurate. In addition, when a spherical object like a bead moves towards the micropipette wall, it will eventually experience a repulsive force that prevents the bead from getting too close to the wall²⁹. Therefore, it should be of little concern if the force transducer is occasionally offset from the axisymmetric axis in the MAT experiments, as long as the gap between the micropipette and the force transducer is small.

When the MAT is used to probe attached cells or large substrates, the opposing surface outside the micropipette may invalidate another assumption made during the derivation of Eq. 1: the major pressure drop occurs inside the micropipette. Using our 2-D axisymmetric model, we identified an optimal distance between the opposing surface and the micropipette tip in the MAT. In the simulation, we used an arc to approximate the cell curvature, so the cell is approximated by an axisymmetric disk with a curved surface. This may not always be the case for some cell types, such as HUVECs, which are not as elongated in the viewing direction as shown in Fig. 1c. Nevertheless, the higher curvature region of the cell (out of the focal plane in Fig. 1c) actually forms a larger gap with the micropipette tip and decreases its effect on the inner pressure drop. Therefore, the 2-μm gap criterion should still be valid in this situation. If the disk-shaped cell was replaced by a large flat surface, the results were similar (data not shown).

One intriguing outcome from our 2-D axisymmetric simulation (Model II) is that, although the inner pressure drop decreased significantly when the pipette-cell gap fell below 2 μm (Fig. 5a), the force calculation with Eq. 1 is still very accurate (Fig. 5b). It should be noted that, even when the pipette-cell gap was less than 2 μm, Eq. 1 should be accurate if we use Δp_i and its corresponding free motion velocity (U_fi) in Eq. 1. On the one hand, the pressure drop used in the force calculation with Eq. 1 (in both the simulation and the actual experiment) was the total pressure drop, Δp, which was larger than the value we should use, Δp_i. On the other hand, the bead free motion velocity used in the force calculation with Eq. 1 (again in both the simulation and the actual experiment), U_f, was smaller than the value we should use, U_fi. This is because, as in actual experiments, the free motion velocity (U_f) was obtained while keeping the effect of the pipette-cell gap. When the gap is small (less than 2 μm), the larger the bead velocity, the larger μp_o is because of the larger flow rate, so the smaller Δp_i is for a constant Δp (Fig. 5a). When the bead is moving freely, it has its maximum velocity, so Δp_i is at its minimum, making U_f the minimum value for U_fi. Therefore, we essentially used overestimated pressure drop and also overestimated free motion velocity in the force calculation with Eq. 1 when the bead was moving at 7.5 or 10 μm/s, which is smaller than U_f. The overestimated pressure drop would result in a larger force and the overestimated free motion velocity would result in a smaller force. These two effects canceled each other, resulting in a force magnitude that agrees well with the actual force on the transducer. However, we do not expect this to be true any more when the pipette-cell gap becomes comparable to the pipette-transducer gap.

Mechanical properties of tether extraction have been studied with several different techniques^13,23,26. Besides the linear relationship shown in Eq. 3, a power-law relationship between the pulling force and the tether growth velocity has also been proposed^4,13. In the present study, we extracted single tethers at increasing velocities with our modified MAT. Further analysis showed that the tether pulling force is linearly dependent on the tether growth velocity (Appendix B). However, due to the limited lifetime of the adhesion in our experiments, each tether was only extracted in a certain range of velocities, e.g., from 2 to 9 μm/s for the case shown in Fig. 7b. In a larger velocity range, this relationship should follow the power-law function, as in the data obtained from neutrophil tether extraction over a larger range of tether growth velocities, from 0.4 to 150 μm/s¹³. Nevertheless, our study shows that in a small velocity range, the linear relationship between the pulling force and tether growth velocity is still reasonable.

The surface protrusion before the onset of tether extraction from endothelial cells has not been observed in the previous studies with the MAT. One possible reason is that a constant aspiration pressure was applied in those experiments, resulting in large initial force loading rates. Since the force transducer was almost stationary at the beginning of pulling, the applied force could be so large that surface protrusion was terminated instantaneously without being recorded by an analogue camera, which only has a temporal resolution of ~ 0.033 s. Occasionally, we did observe brief pause before tether extraction between the cell and the force transducer when multiple bonds were formed, which may indicate surface protrusion at multiple locations. The underlying mechanism about surface protrusion is still not completely understood. However, the stiffness values obtained in our study are very close to the results obtained from neutrophils studied with the BFP⁸. In the BFP study, by analyzing the crossover force of the initial surface protrusion from neutrophils, Evans et al. discovered that the force distribution agreed well with the kinetic model of the rupture of a weak bond, which is likely the bond between the receptor and the cytoskeleton. Many receptors that function in leukocyte rolling have been found to be linked to the cytoskeleton via actin binding proteins^2,21,32,37. Truncation of the cytoplasmic tail of most of these receptors, which abolishes their linkage to the cytoskeleton, could severely undermine leukocyte rolling and the ensuing arrest on the endothelium^17,32. Therefore, further investigation of surface protrusion, especially its mechanical and kinetic properties, is important to understanding and manipulating leukocyte function.

One advantage of using the modified MAT to study the bond rupture or adhesion strength under a constant force loading rate is that the applied force loading rate is very consistent once the stage speed is set. For all the data shown in Fig. 8, the maximum standard deviation of the force loading rate was only ~10% of the average value with most of the standard deviations less than 5%. This is because the applied force loading rate is mainly determined by the stage speed, which is very consistent with its positional resolution of 8 nm. In the current study, only a small range of force loading rates of 5 to 100 pN/s was applied on the force transducer. This is because when the pressure drop is increased rapidly (stage velocity greater than 200 μm/s), the transducer speed becomes too large to allow good-quality image acquisition by an analog camera. Moreover, even at a moderate stage speed, some short speed fluctuations may be missed by an analogue camera. In theory, for a stationary 8-μm force transducer in the micropipette, a maximum force loading rate of approximately 7,500 pN/s can be obtained. This limit corresponds to the maximum allowable stage velocity of 15 mm/s. If higher force loading rates are desired, larger force transducers can be used. When the size of the force transducer is doubled, the maximum force loading rate that can be applied will be quadrupled, so the force loading rate of more than ten thousand piconewtons per second can be easily imposed with the modified MAT. Therefore, the modification presented in this work endowed the MAT with more potential in its application in cellular and molecular adhesion studies.

APPENDIX A

LOW REYNOLDS NUMBER MOTION OF A CONCENTRIC CLOSELY-FITTED SPHERE OR CAPSULE IN A CYLINDRICAL TUBE

In the MAT, the force transducer (a spherical object) moves back and forth in a cylindrical tube. If a spherical cell is employed as the force transducer and its diameter (R_c) is slightly larger than the pipette radius (R_p), it can be deformed slightly into a capsule shape, but an apparent gap between the cell and pipette still exists²⁷. Both scenarios (either a sphere or capsule) have been analyzed with the lubrication theory by Shao and Hochmuth²⁶,²⁷. However, in those analyses, some terms are not approximated with high accuracy. As a result, some equations are not very accurate, e.g., the equations for calculating the pressure drop over the sphere or capsule (Δp_s or Δp_c) and the force on it (F). In this appendix, we list the equations derived with more accurate approximations.

The pressure drop over the sphere, the pressure drop due to the fluid flow in the tube (Δp_f), and the total pressure drop in the whole tube (Δp) can be expressed by

$$\Delta p_s=\frac{\mu U}{R_p}\left[\frac{4\sqrt{2}\pi }{{\stackrel{‒}{\epsilon }}^{1∕2}}-32+\frac{2\sqrt{2}\pi }{3}{\stackrel{‒}{\epsilon }}^{1∕2}+O\left(\stackrel{‒}{\epsilon }\right)\right]+\frac{F}{\pi R_p^2}\left[1+\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{16}{9}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A1)

$$\Delta p_f=\frac{8\mu (L_{eq}-2R_s)U}{R_p^2}\left[1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{16}{9}{\stackrel{‒}{\epsilon }}^2+o\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right]+\frac{8(L_{eq}-2R_s)F}{\pi R_p^3}\left[\frac{2\sqrt{2}}{9\pi }{\stackrel{‒}{\epsilon }}^{5∕2}+O\left({\stackrel{‒}{\epsilon }}^{7∕2}\right)\right],$$ (A2)

$$\Delta p=\frac{\mu U}{R_p}\left[\left(\frac{4\sqrt{2}\pi }{{\stackrel{‒}{\epsilon }}^{1∕2}}-32+\frac{2\sqrt{2}\pi }{3}{\stackrel{‒}{\epsilon }}^{1∕2}\right)+\frac{8(L_{eq}-2R_s)}{R_p}\left(1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{16}{9}{\stackrel{‒}{\epsilon }}^2\right)\right]+\frac{F}{\pi R_p^2}\left[\left(1+\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{16}{9}{\stackrel{‒}{\epsilon }}^2\right)+\frac{8(L_{eq}-D_s)}{R_p}\left(\frac{2\sqrt{2}}{9\pi }{\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A3)

where μ, R_p, R_s and U are the viscosity, the tube radius, the sphere radius and the sphere velocity, respectively; $\stackrel{‒}{\epsilon }=(R_p-R_s)∕R_p$. For a stationary sphere (U = 0),

$$\pi R_p^2\Delta p_s=-\frac{9\sqrt{2}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1+\frac{1}{6}\stackrel{‒}{\epsilon }+\frac{59}{360}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A4)

$$F=-\frac{9\sqrt{2}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1-\frac{7}{6}\stackrel{‒}{\epsilon }-\frac{7}{120}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A5)

where Q is the volumetric flow rate. From Eqs. (A4) and (A5), we can get

$$\frac{F}{\pi R_p^2\Delta p_s}=1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{74}{15}{\stackrel{‒}{\epsilon }}^{5∕2}+O\left({\stackrel{‒}{\epsilon }}^3\right).$$ (A6)

For a capsule with its cylindrical length of 2l_s, the pressure drop over the capsule (Δp_c), the pressure drop due to the fluid flow in the tube, and the total pressure drop in the whole tube can be expressed by (when $\stackrel{‒}{\beta }$, which is defined as l_s/R_p, is on the order of 1 or larger)

$$\Delta p_c=\frac{\mu U}{R_p}\left[\left(\frac{10\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}+\frac{17\sqrt{2}\pi }{4{\stackrel{‒}{\epsilon }}^{1∕2}}\right)+\left(\frac{121\stackrel{‒}{\beta }}{10}-32-\frac{3{\pi }^2}{32\stackrel{‒}{\beta }}+\frac{243{\pi }^4}{4096{\stackrel{‒}{\beta }}^3}\right)\right]+\frac{F}{\pi R_p^2}\left[1+\stackrel{‒}{\epsilon }+\frac{\sqrt{2}\pi }{16\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^{3∕2}+O\left({\stackrel{‒}{\epsilon }}^2\right)\right],$$ (A7)

$$\Delta p_f=\frac{8\mu U}{R_p}\left[\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right]\left[1-\stackrel{‒}{\epsilon }-\frac{\sqrt{2}\pi }{16\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^{3∕2}+\left(\frac{1}{2}+\frac{3{\pi }^2}{128{\stackrel{‒}{\beta }}^2}\right){\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right]+\frac{8F}{\pi R_p^2}\left[\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right]\left[\frac{\pi }{12\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^3-\frac{\sqrt{2}\pi }{64{\stackrel{‒}{\beta }}^2}{\stackrel{‒}{\epsilon }}^{7∕2}+O\left({\stackrel{‒}{\epsilon }}^4\right)\right],$$ (A8)

$$\Delta p=\frac{\mu U}{R_p}\left[\left(\frac{10\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}+\frac{17\sqrt{2}\pi }{4{\stackrel{‒}{\epsilon }}^{1∕2}}\right)+\left(\frac{121\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}-32-\frac{3{\pi }^2}{32\stackrel{‒}{\beta }}+\frac{243{\pi }^4}{4096{\stackrel{‒}{\beta }}^3}\right)+8\left(\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right)\left(1-\stackrel{‒}{\epsilon }-\frac{\sqrt{2}\pi }{16\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^{3∕2}\right)\right]+\frac{F}{\pi R_p^2}\left[\left(1+\stackrel{‒}{\epsilon }+\frac{\sqrt{2}\pi }{16\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^{3∕2}\right)+8\left(\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right)\left(\frac{\pi }{12\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^3-\frac{\sqrt{2}\pi }{64{\stackrel{‒}{\beta }}^2}{\stackrel{‒}{\epsilon }}^{7∕2}\right)\right].$$ (A9)

If $\stackrel{‒}{\beta }$ is on the order of $\stackrel{‒}{\epsilon }$ or smaller, assume that $\stackrel{‒}{\epsilon }=\alpha \stackrel{‒}{\epsilon }$ (α is a constant which is on the order of 1 or smaller), we have:

$$\Delta p_c=\frac{\mu U}{R_p}\left[\frac{4\sqrt{2}\pi }{{\stackrel{‒}{\epsilon }}^{1∕2}}+\left(-32+\frac{34}{3}\alpha -\frac{2048{\alpha }^3}{9{\alpha }^2}\right)+O\left({\stackrel{‒}{\epsilon }}^{1∕2}\right)\right]+\frac{F}{\pi R_2^p}\left[1+\frac{4}{3}\stackrel{‒}{\epsilon }+\left(-\frac{8\sqrt{2}\alpha }{9\pi }+\frac{1024{\alpha }^3}{27{\pi }^3}\right){\stackrel{‒}{\epsilon }}^{3∕2}+\left(\frac{16}{9}-\frac{640{\alpha }^2}{27{\pi }^2}\right){\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A10)

$$\Delta p_f=\frac{8\mu U}{R_p}\left[\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right]\left[1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{8\sqrt{2}\alpha }{9\pi }{\stackrel{‒}{\epsilon }}^{3∕2}+\left(\frac{16}{9}-\frac{128{\alpha }^2}{27{\pi }^2}\right){\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right]+\frac{8F}{\pi R_p^2}\left[\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right]\left[\frac{2\sqrt{2}}{9\pi }{\stackrel{‒}{\epsilon }}^{5∕2}-\frac{32\alpha }{27{\pi }^2}{\stackrel{‒}{\epsilon }}^3+O\left({\stackrel{‒}{\epsilon }}^{7∕2}\right)\right],$$ (A11)

$${\Delta }_p=\frac{\mu U}{R_p}\left[\left(\frac{4\sqrt{2}\pi }{{\stackrel{‒}{\epsilon }}^{1∕2}}-32+\frac{34}{3}\alpha -\frac{2408{\alpha }^3}{9{\alpha }^2}\right)+8\left(\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right)\left(1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{8\sqrt{2}\pi }{9\pi }{\stackrel{‒}{\epsilon }}^{3∕2}\right)\right]+\frac{F}{\pi R_p^2}\left[\left(1+\frac{4}{3}\stackrel{‒}{\epsilon }\left(\frac{8\sqrt{2}\alpha }{9\pi }-\frac{1024{\alpha }^3}{27{\pi }^3}\right){\stackrel{‒}{\epsilon }}^{3∕2}\right)+8\left(\frac{L_{eq}}{R_p}-2(1-\stackrel{‒}{\epsilon })-2\stackrel{‒}{\beta }\right)\left(\frac{2\sqrt{2}}{9\pi }{\stackrel{‒}{\epsilon }}^{5∕2}-\frac{32\alpha }{27{\alpha }^2}{\stackrel{‒}{\epsilon }}^3\right)\right].$$ (A12)

For a stationary capsule (U = 0), when $\stackrel{‒}{\beta }$ is on the order of 1 or larger, the pressure drop over the body and the force on it are:

$$\pi R_p^2\Delta p_c=-\frac{9\sqrt{2}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1+\frac{1}{6}\stackrel{‒}{\epsilon }+\frac{59}{360}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right]-\frac{12\mu Q}{R_p}\frac{\stackrel{‒}{\beta }}{{\stackrel{‒}{\epsilon }}^3}\left[1+\frac{\stackrel{‒}{\epsilon }}{2}+\frac{7{\stackrel{‒}{\epsilon }}^2}{30}+\frac{{\stackrel{‒}{\epsilon }}^3}{10}+O\left({\stackrel{‒}{\epsilon }}^4\right)\right],$$ (A13)

$$F=-\frac{9\sqrt{2}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1-\frac{7}{6}\stackrel{‒}{\epsilon }-\frac{7}{120}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right]-\frac{12\mu Q}{R_p}\frac{\stackrel{‒}{\beta }}{{\stackrel{‒}{\epsilon }}^3}\left[1-\frac{\stackrel{‒}{\epsilon }}{2}-\frac{{\stackrel{‒}{\epsilon }}^2}{10}-\frac{{\stackrel{‒}{\epsilon }}^3}{20}+O\left({\stackrel{‒}{\epsilon }}^4\right)\right].$$ (A14)

The relative magnitude of these two equations is:

$$\frac{F}{\pi R_p^2\Delta p_c}=1-\stackrel{‒}{\epsilon }-\frac{\sqrt{2}\pi }{16\stackrel{‒}{\beta }}{\stackrel{‒}{\epsilon }}^{3∕2}+O\left({\stackrel{‒}{\epsilon }}^2\right).$$ (A15)

If $\stackrel{‒}{\beta }$ is on the order of $\stackrel{‒}{\epsilon }$ or smaller, the solution will be:

$$\pi R_p^2\Delta p_c=-\frac{9\sqrt{9}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1+\frac{8\sqrt{2}\alpha }{3\pi }{\stackrel{‒}{\epsilon }}^{1∕2}+\frac{1}{6}\stackrel{‒}{\epsilon }+\frac{4\sqrt{2}\alpha }{3\pi }{\stackrel{‒}{\epsilon }}^{3∕2}+\frac{59}{360}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right],$$ (A16)

$$F=-\frac{9\sqrt{9}\pi \mu Q}{4R_p{\stackrel{‒}{\epsilon }}^{5∕2}}\left[1+\frac{8\sqrt{2}\alpha }{3\pi }{\stackrel{‒}{\epsilon }}^{1∕2}-\frac{7}{6}\stackrel{‒}{\epsilon }-\frac{4\sqrt{2}\alpha }{3\pi }{\stackrel{‒}{\epsilon }}^{3∕2}-\frac{7}{120}{\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right)\right].$$ (A17)

The relative magnitude of these two equations is:

$$\frac{F}{\pi R_p^2\Delta p_c}=1-\frac{4}{3}\stackrel{‒}{\epsilon }+\frac{8\sqrt{2}\alpha }{9\pi }{\stackrel{‒}{\epsilon }}^{3∕2}-\left(\frac{128{\alpha }^2}{27{\pi }^2}+\frac{1684{\alpha }^4}{81{\pi }^4}\right){\stackrel{‒}{\epsilon }}^2+O\left({\stackrel{‒}{\epsilon }}^{5∕2}\right).$$ (A18)

APPENDIX B

CALCULATION OF THRESHOLD FORCE, EFFECTIVE VISCOSITY AND FORCE LOADING RATE DURING TETHER EXTRACTION

With the modified MAT, tethers can be extracted from cell membranes under an increasing suction pressure. During this process, both the tether growth velocity and the pulling force are increasing so that a relationship between F and U_t can be obtained from one tether event. The equation governing the force magnitude exerted on the force transducer is still the same:

$$F=\pi R_p^2\Delta p\left(1-\frac{4}{3}\stackrel{‒}{\epsilon }\right)\left(1-\frac{U_t}{U_f}\right).$$ (B1)

In the case of the modified setup, the total pressure drop Δp is determined by the speed of the moving stage (V_s) according to

$$\Delta p=\rho g{V}_s(t-t_0),$$ (B2)

where t₀ is the time when the stage starts to move, which can be determined from the reading of voltage stamp (Figs. 1b and 1c). The substitution of Eq. (B2) into Eq. (B1) gives

$$F=\alpha (t-t_0)\left(1-\frac{U_t}{U_f}\right),$$ (B3)

where

$$\alpha =\pi R_p^2\rho g{V}_s\left(1-\frac{4}{3}\stackrel{‒}{\epsilon }\right).$$ (B4)

At a certain stage speed, the free motion of the force transducer is parabolic and can be fitted well with an equation of the form D = a₂(t − t₀)²+ b₂, where D is the transducer displacement. Accordingly we can write the free motion velocity as

$$U_f=2a_2(t-t_0).$$ (B5)

The substitution of Eq. (B5) into Eq. (B3) leads to

$$F=\alpha (t-t_0)-\frac{\alpha }{2a_2}{U}_t.$$ (B6)

In an actual experiment, when a tether is extracted from an endothelial cell, the transducer also moves with a parabolic trajectory. By fitting the trajectory of the transducer with an equation of the form y = a₁t²+ b₁t + c₁, the tether growth velocity can be calculated by

$$U_t=2a_{1}t+b_1.$$ (B7)

The substitution of Eq. (B7) into Eq. (B6) then yields

$$F=\alpha \left(1-\frac{a_1}{a_2}\right)t-\alpha \left(\frac{b_1}{2a_2}+t_0\right).$$ (B8)

Because the stage is moving at a constant speed, V_s (i.e., α is a constant), the tether is actually extracted at a constant force loading rate, given by

$$r_{ft}=\alpha \left(1-\frac{a_1}{a_2}\right).$$ (B9)

Finally, the substitution of Eq. (B7) into Eq. (B8) yields

$$F=\frac{\alpha }{2a_1}\left(1-\frac{a_1}{a_2}\right)U_t-\alpha \left(\frac{b_1}{2a_1}+t_0\right).$$ (B10)

This expression demonstrates that at a constant force loading rate, the force required to extract a tether is linearly dependent on the tether growth velocity. Consequently, the threshold force and effective viscosity can be calculated by

$$F_0=-\alpha \left(\frac{b_1}{2a_1}+t_0\right),$$ (B11)

$${\eta }_{\mathit{eff}}=\frac{\alpha }{4\pi a_1}\left(1-\frac{a_1}{a_2}\right).$$ (B12)