Nonparametric Second-Order Theory of Error Propagation on Motion Groups

Abstract

Error propagation on the Euclidean motion group arises in a number of areas such as in dead reckoning errors in mobile robot navigation and joint errors that accumulate from the base to the distal end of kinematic chains such as manipulators and biological macromolecules. We address error propagation in rigid-body poses in a coordinate-free way. In this paper we show how errors propagated by convolution on the Euclidean motion group, SE(3), can be approximated to second order using the theory of Lie algebras and Lie groups. We then show how errors that are small (but not so small that linearization is valid) can be propagated by a recursive formula derived here. This formula takes into account errors to second-order, whereas prior efforts only considered the first-order case. Our formulation is nonparametric in the sense that it will work for probability density functions of any form (not only Gaussians). Numerical tests demonstrate the accuracy of this second-order theory in the context of a manipulator arm and a flexible needle with bevel tip.

1 Introduction

Error propagation on the Euclidean motion group arises in a surprising number of different areas. For example, consider a robotic manipulator for which each joint angle has some backlash. If we describe this backlash as a distribution of possible angles around the nominal one, how will these joint errors add up to produce pose errors at the end effector ? Similar problems arise in the study of chainlike biological macromolecules that undergo thermal fluctuations in solution. See, for example, [Zhou and Chirikjian 2006] and [Kim and Chirikjian 2005]. As another example, consider a nonholonomic mobile robot that executes an open loop trajectory. Uncertainties in pose will add up along the path, and if many trials are performed, what will the distribution of terminal poses be ? Many such problems in ‘probabilistic robotics’ can be imagined with the recent popularity of SLAM [Thrun, Burgard and Fox 2005].

If the errors are small, Jacobian-based methods or first-order error propagation theories can be used. But what if the errors are very large ? Here we address the propagation of large errors in rigid-body poses in a coordinate-free way. In this paper we show how errors propagated by convolution on the Euclidean motion group, SE(3), can be approximated to second order using the theory of Lie algebras and Lie groups. We then show how errors of moderate size (but not so small that linearization is valid) can be propagated by a recursive formula derived here. This formula takes into account errors to second-order, whereas prior efforts only considered the first-order case. Our formulation is nonparametric in the sense that it will work for probability density functions of any form (not only Gaussians).

In the remainder of this section we review the literature on error propagation, and review the terminology and notation used throughout the paper. In what follows, bold lower case letters denote vectors. N and n are positive integers. G denotes either the groups SO(3) or SE(3). All upper case letters (Roman or Greek) (except for N and G) denote matrices. Lower case letters denote scalars and group elements. A lower case letter followed by parenthesis denotes a scalar-valued function.

In Section 2, important definitions from the basic theory of Lie groups and probability and statistics are reviewed. In Section 3, several new theorems are proved. This forms the core of our paper. In Section 4, sampling is discussed and the theory is adapted for the case when a whole pdf is not available. Then numerical tests demonstrate the accuracy of this recursive second-order propagation formula relative to baseline truth generated by brute force. In Section 5 our conclusions are presented. Three appendices provide more detailed background material that is important for understanding the definitions and proofs presented in the main body of the paper. The remainder of the current section reviews the literature and basic definitions and notation used throughout the paper.

1.1 Literature Review

The Lie-group-theoretic notation and terminology which has now become standard vocabulary in the robotics community is presented in [Murray, Li and Sastry 1994], and Selig [Selig 1996]. In [Chirikjian 2001] many problems in robot kinematics and motion planning were formulated as the convolution of functions on the Euclidean group. The representation and estimation of spatial uncertainty has also received attention in the robotics and vision literature. Two classic works in this area are [Smith and Cheeseman 1986] and [Su and Lee 1992]. Recent work on error propagation describes the concatenation of Gaussian random variables on groups and applies this formalism to mobile robot navigation [Smith, Drummond and Roussopoulos 2003]. In all three of these works, errors are assumed to be small enough that co-variances can be propagated by the formula [Wang and Chirikjian 2006a, Wang and Chirikjian 2006b]

$${\Sigma }_{1\ast 2}=\mathit{Ad}\left(g_2^{-1}\right){\Sigma }_1{\mathit{Ad}}^T\left(g_2^{-1}\right)+{\Sigma }_2,$$ (1)

where Ad is the adjoint operator for SE(3) (See Appendix for a review of terminology). This equation essentially says that given two ‘noisy’ frames of reference g₁, g₂ ∈ SE(3), each of which is a Gaussian random variable with 6 × 6 covariance matrices³ Σ₁ and Σ₂, respectively, the covariance of g₁ ○ g₂ will be Σ_1*2. This approximation is very good when errors are very small. We extend this linearized approximation to the quadratic terms in the expansion of the matrix exponential parameterization of SE(3). The origin of (1) will become clear for the special case of small errors in our more general nonparametric derivation.

1.2 Review of Rigid-Body Motions

The Euclidean motion group, SE(3), is the semi-direct product of IR³ with the special orthogonal group, SO(3). We represent elements of SE(3) using 4 × 4 homogeneous transformation matrices

$$g=\left(\begin{array}{cc}\hfill R\hfill & \hfill \mathbf{t}\hfill \\ \hfill 0^T\hfill & \hfill 1\hfill \end{array}\right),$$

and identify the group law with matrix multiplication. The inverse of any group element is written as

$$g^{-1}=\left(\begin{array}{cc}\hfill R^T\hfill & \hfill -R^T\mathbf{t}\hfill \\ \hfill 0^T\hfill & \hfill 1\hfill \end{array}\right).$$

For small translational (rotational) displacements from the identity along (about) the i^th coordinate axis, the homogeneous transforms representing infinitesimal motions look like

$$g_i\left(∊\right)\triangleq \exp \left(∊{\tilde{E}}_i\right)\approx I_4+∊{\tilde{E}}_i$$

where I₄ is the 4 × 4 identity matrix and

$$\begin{array}{cc}\hfill & {\tilde{E}}_1=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\tilde{E}}_2=\left(\begin{array}{cccc}\hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);{\tilde{E}}_3=\left(\begin{array}{cccc}\hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);\hfill \\ \hfill & {\tilde{E}}_4=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right);{\tilde{E}}_5=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right);{\tilde{E}}_6=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).\hfill \end{array}$$

These are related to the basis elements {E_i} for so(3) (the Lie algebra corresponding to the rotation group, SO(3)) as

$${\tilde{E}}_i=\left(\begin{array}{cc}\hfill E_i\hfill & \hfill 0\hfill \\ \hfill 0^T\hfill & \hfill 0\hfill \end{array}\right)$$

when i = 1,2,3. Each Ẽ_i has a corresponding natural unit basis vector e_i ∈ IR⁶. For example, e₁ = [1, 0, 0, 0, 0, 0]^T, e₂ = [0, 1, 0, 0, 0, 0]^T, etc.

Large motions are also obtained by exponentiating these matrices. For example,

$$\exp \left(t{\tilde{E}}_3\right)=\left(\begin{array}{cccc}\hfill \cos t\hfill & \hfill -\sin t& \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sin t\hfill & \hfill \cos t& \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0& \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0& \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\text{and}\exp \left(t{\tilde{E}}_6\right)=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill t\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

More generally, it can be shown that every element in the neighborhood of the identity of a matrix Lie group G can be described with the exponential parameterization

$$g=g(x_1,x_2,\dots ,x_n)=\exp \left(\underset{i=1}{\overset{n}{\Sigma }}{x}_i{\tilde{E}}_i\right)$$ (2)

where n is the dimension of the group. For SO(3) and SE(3), n = 3 and 6, respectively, and the exponential parameterization extends over the whole group.

One defines the ‘vee’ operator, ∨, such that

$${\left(\underset{i=1}{\overset{n}{\Sigma }}{x}_i{\tilde{E}}_i\right)}^{\vee }=\left(\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \\ \hfill x_3\hfill \\ \hfill ⋮\hfill \\ \hfill x_n\hfill \end{array}\right)$$

The vector, x ∈ IRⁿ, can be obtained from g ∈ G from the formula

$$\mathbf{x}={\left(\log g\right)}^{\vee }.$$ (3)

For SO(3) and SE(3) this is defined except on a set of measure zero, which for all intents and purposes in the probability and statics problems that we will consider means that the exponential and logarithm maps are ‘effectively’ bijective. See the Appendix for details.

When integrating a function over SO(3) or SE(3), a weight w(x) is defined such that

$${\int }_{G}f\left(g\right)\mathit{dg}={\int }_{{\mathit{IR}}^n}f\left(g\left(\mathbf{x}\right)\right)w\left(\mathbf{x}\right)d\mathbf{x}.$$

The exact form of the weighting function is

$$w\left(\mathbf{x}\right)=\left|\det J_r\left(\mathbf{x}\right)\right|\text{where}{J}_r\left(\mathbf{x}\right)\left[{\left(g^{-1}\frac{\partial g}{\partial x_1}\right)}^{\vee },\cdots ,{\left(g^{-1}\frac{\partial g}{\partial x_n}\right)}^{\vee }\right].$$ (4)

This is derived for SO(3) and SE(3) in the Appendix. The weighting function is even in the sense that w(x) = w(−x).

1.3 The Baker-Campbell-Hausdorff Formula

Given any two elements of a Lie algebra, X and Y, the Lie bracket is defined as [X,Y] = XY − Y X. An important relationship called the Baker-Campbell-Hausdorff formula exists between the Lie bracket and matrix exponential (see [Baker 1904, Campbell 1897, Hausdorff 1906]). Namely, the logarithm of the product of two Lie group elements written as exponentials of Lie algebra elements can be expressed as

$$Z(X,Y)=\log \left(e^X{e}^Y\right)$$

where

$$\begin{array}{cc}\hfill Z(X,Y)=& X+Y\mathrm{zeroth}\mathrm{order}\hfill \\ \hfill & +\frac{1}{2}[X,Y]\mathrm{first}\mathrm{order}\hfill \\ \hfill & +\frac{1}{12}([X,[X,Y]]+[Y,[Y,X]])\mathrm{second}\mathrm{order}\hfill \\ \hfill & +\frac{1}{48}([Y,[X,[Y,X]]]+[X,[Y,[Y,X]]])\mathrm{third}\mathrm{order}\hfill \\ \hfill & +\cdots \hfill \end{array}$$ (5)

This expression is verified by expanding e^X and e^Y in Taylor series of the form in (37), and then substituting the result into (38) with g = e^Xe^Y. If the ∨ operation is applied (see Appendix for a review), (5) can be written as

$$\begin{array}{cc}\hfill \mathbf{z}=& \mathbf{x}+\mathbf{y}+\frac{1}{2}\mathit{ad}\left(X\right)\mathbf{y}+\frac{1}{12}(\mathit{ad}\left(X\right)\mathit{ad}\left(X\right)\mathbf{y}+\mathit{ad}\left(Y\right)\mathit{ad}\left(Y\right)\mathbf{x})\hfill \\ \hfill & +\frac{1}{48}(\mathit{ad}\left(Y\right)\mathit{ad}\left(X\right)\mathit{ad}\left(Y\right)\mathbf{x}+\mathit{ad}\left(X\right)\mathit{ad}\left(Y\right)\mathit{ad}\left(Y\right)\mathbf{x})+\cdots \hfill \end{array}$$

1.4 Probability and Statistics in IRⁿ: Multivariate Analysis

In IRⁿ, a probability density function (or pdf) is defined by the conditions

$$f\left(\mathbf{x}\right)\ge 0\forall \mathbf{x}\in {\mathit{IR}}^n\text{and}{\int }_{{\mathit{IR}}^n}f\left(\mathbf{x}\right)d\mathbf{x}=1$$

where dx = dx₁dx₂ … dx_n is the usual Lebesgue integration measure. The mean of a pdf, f(x), is defined as

$$\mu ={\int }_{{\mathit{IR}}^n}\mathbf{x}f\left(\mathbf{x}\right)d\mathbf{x}\text{or}{\int }_{{\mathit{IR}}^n}(\mathbf{x}-\mu )f\left(\mathbf{x}\right)d\mathbf{x}=0.$$ (6)

Note that μ minimizes the cost function

$$c\left(\mathbf{x}\right)={\int }_{{\mathit{IR}}^n}\Vert \mathbf{x}-\mathbf{y}{\Vert }^{2}f\left(\mathbf{y}\right)d\mathbf{y}$$ (7)

where $\Vert \mathbf{v}\Vert =\sqrt{\mathbf{v}\cdot \mathbf{v}}$ is the 2-norm in IRⁿ.

The covariance of the same pdf about the mean is defined as

$$\Sigma ={\int }_{{\mathit{IR}}^n}(\mathbf{x}-\mu ){(\mathbf{x}-\mu )}^{T}f\left(\mathbf{x}\right)d\left(x\right).$$ (8)

It follows that

$$C={\int }_{{\mathit{IR}}^n}{\mathbf{xx}}^{T}f\left(\mathbf{x}\right)d\mathbf{x}=\Sigma +\mu {\mu }^T$$ (9)

where C is the covariance about the origin and Σ is the covariance about the mean.

Pdfs are often used to describe distributions of errors. If these errors are concatenated, they ‘add’ by convolution:

$$(f_1\ast f_2)\left(\mathbf{x}\right)={\int }_{{\mathit{IR}}^n}{f}_1\left(\xi \right)f_2(\mathbf{x}-\xi )d\xi .$$ (10)

The mean and covariance of convolved distributions are found as

$${\mu }_{1\ast 2}={\mu }_1+{\mu }_2\text{and}{\Sigma }_{1\ast 2}={\Sigma }_1+{\Sigma }_2$$ (11)

In other words, these quantities can be propagated without explicitly performing the convolution computation, or even knowing the full pdfs. This is independent of the parametric form of the pdf. Often one does not have access to the full pdf, but only samples from a process with an underlying pdf. In this case, the unbiased sample mean and covariance are defined as [Anderson 2005]:

$${\mu }^{\left(N\right)}=\frac{1}{N}\underset{i=1}{\overset{N}{\Sigma }}{\mathbf{x}}_i\text{and}{\Sigma }^{\left(N\right)}=\frac{1}{N-1}\underset{i-1}{\overset{N}{\Sigma }}({\mathbf{x}}_i-{\mu }^{\left(N\right)}){({\mathbf{x}}_i-{\mu }^{\left(N\right)})}^T.$$

The reason for division by N − 1 rather than N is explained in texts on multivariate analysis such as [Anderson 2005]. As the sample size becomes large, the difference between N and N − 1 becomes negligible and these sampled quantities converge to those corresponding to the underlying pdf.

Our main purpose in this paper is to develop equations analogous to (11) to describe the propagation of error on the motion group SE(3). In the process we will also do so for the rotation group SO(3).

It is often convenient to use the Gaussian (or normal) distribution: to model errors in IRⁿ. This parametric distribution is completely defined by its mean and covariance. We will have no need to assume that densities are Gaussian. Our results are nonparametric, and therefore more general.

2 Definitions and Properties of Mean and Covariance on SE(3)

In this section we provide definitions of the mean and covariance of Lie-group-valued functions and illustrate some of their properties. We note in passing that a pdf that is a symmetric function, ρ(g) = ρ(g⁻¹), always satisfies the condition

$${\int }_G{\left(\log g\right)}^{\vee }\rho \left(g\right)\mathit{dg}=0,$$ (12)

for G = SO(3) or G = SE(3). This is easy to see if we let ρ₀(x) = ρ(e^X). Then ρ₀(x) = ρ₀(−x). This is an even function in the exponential coordinates, and so the odd function xρ₀(x) integrates to zero over a symmetric domain of integration in the space of exponential parameters that maps to G. See appendix for discussion of integration measures. In our case this domain is the ball of radius π (for SO(3)), or the Cartesian product of this ball with IR³. Both of which are symmetric. Hence the integral in (12) vanishes. More generally, if ρ(g) is a symmetric function on G = SO(3) or G = SE(3) then for ${\Sigma }_{i=1}^n{n}_i\text{odd}$,

$${\int }_G\prod _{i=1}^n{[{\left(\log g\right)}^{\vee }\cdot {\mathbf{e}}_i]}^{n_i}\rho \left(g\right)\mathit{dg}=0.$$ (13)

This is because the integrand is an odd function of the components of x. For example,

$${\int }_G{\left(\log g\right)}^{2k+1}\rho \left(g\right)\mathit{dg}=0_n.$$

DEFINITION 1: If a unique value μ ∈ G exists for which

$${\int }_G{\left[\log ({\mu }^{-1}\circ g)\right]}^{\vee }f\left(g\right)\mathit{dg}=0,$$ (14)

μ will be called the mean of a pdf f(g) on G, which is a straightforward extension of (6). Furthermore, the covariance about the mean will be computed as

$$\Sigma ={\int }_G\log {({\mu }^{-1}\circ g)}^{\vee }{\left[\log {({\mu }^{-1}\circ g)}^{\vee }\right]}^{T}f\left(g\right)\mathit{dg}.$$ (15)

Note that while in the case of Euclidean space (6) and minimization of (7) both give the same value of the mean, the minimization of a functional of the form

$$c\left(h\right)={\int }_G\Vert {\left[\log (h^{-1}\circ g)\right]}^{\vee }{\Vert }^{2}f\left(g\right)\mathit{dg}$$

does not generally return a value h_min that is equal to μ. However, in the special case when f(g) is unimodal and very concentrated, h_min ≈ μ.

The equality (12) can be thought of as a statement of when the mean is at the identity. If ρ(g) has mean at the identity, then f(g) = ρ(a⁻¹ ○ g) has mean at a. We will use ρ(g) to denote pdfs with mean at the identity, and f(g) to denote pdfs that can have the mean at some other group element.

THEOREM 1: If f(g) has mean μ and covariance Σ, then to second order

$$\mathbf{m}=[I+F_1\left(\Sigma \right)]\mu$$ (16)

where the following shorthand is used:

$$\mathbf{m}={\int }_G{\left(\log \left(g\right)\right)}^{\vee }f\left(g\right)\mathit{dg}\text{and}\mu ={\left(\log \left(\mu \right)\right)}^{\vee },$$ (17)

and the matrix-valued function F1(Σ) is defined as

$$F_1\left(\Sigma \right)=\frac{1}{12}\underset{i,j=1}{\overset{6}{\Sigma }}{\sigma }_{\mathit{ij}}\mathit{ad}\left({\tilde{E}}_i\right)\mathit{ad}\left({\tilde{E}}_j\right)$$ (18)

and

$$\begin{array}{cc}\hfill C& ={\int }_G{\left(\log \left(g\right)\right)}^{\vee }{\left({\left(\log \left(g\right)\right)}^{\vee }\right)}^{T}f\left(g\right)\mathit{dg}\hfill \\ \hfill & =\Sigma +{\left(\log \mu \right)}^{\vee }{\left({\left(\log \mu \right)}^{\vee }\right)}^T+\frac{1}{2}\left(\Sigma {\mathit{ad}}^T\left(\log \mu \right)+\mathit{ad}\left(\log \mu \right)\Sigma \right).\hfill \end{array}$$ (19)

Here C is the covariance about the identity, which is defined in an analogy with the concept of covariance about the origin in the context of probability and statistics in IRⁿ.

Proof: Let f(g) = ρ(μ⁻¹ ○ g) where ρ(g) has mean at the identity. Then

$${\int }_G{\left(\log g\right)}^{\vee }f\left(g\right)\mathit{dg}={\int }_G{\left(\log g\right)}^{\vee }\rho ({\mu }^{-1}\circ g)\mathit{dg}={\int }_G{\left(\log (\mu \circ g)\right)}^{\vee }\rho \left(g\right)\mathit{dg}.$$

Expanding using the BCH formula (5) with μ = exp X and g = exp Y, and using the linearity of the Lie bracket, we find that since ρ(g) is a pdf with mean at the identity,

$$\begin{array}{c}\hfill {\int }_G{\left[\log (\mu \circ g)\right)]}^{\vee }\rho \left(g\right)\mathit{dg}=\hfill \\ \hfill \mathbf{x}+\underset{i,j=1}{\overset{6}{\Sigma }}{\sigma }_{\mathit{ij}}{\left\{\frac{1}{12}[{\tilde{E}}_i,[{\tilde{E}}_j,X]]+\frac{1}{48}([{\tilde{E}}_i,[X,[{\tilde{E}}_j,X]]]+[X,[{\tilde{E}}_i,[{\tilde{E}}_j,X]]])\right\}}^{\vee }+\cdots \hfill \end{array}$$

The first expression in the statement of the theorem results from the definition of the adjoint. Likewise,

$$\begin{array}{c}\hfill {\int }_G{\left[\log (\mu \circ g)\right)]}^{\vee }{\left({\left[\log (\mu \circ g)\right)]}^{\vee }\right)}^T\rho \left(g\right)\mathit{dg}=\hfill \\ \hfill {\int }_G[\mathbf{x}+\mathbf{y}+\frac{1}{2}\mathit{ad}\left(X\right)\mathbf{y}+\cdots ]{[\mathbf{x}+\mathbf{y}+\frac{1}{2}\mathit{ad}\left(X\right)\mathbf{y}+\cdots ]}^T\rho \left(g\right)\mathit{dg}\hfill \end{array}$$

Expanding out the product and eliminating terms linear in y results in the second statement of the theorem.

3 Propagation of the Mean and Covariance of PDFs on SE(3)

Let μ₁, μ₂ ∈ SE(3) be two precise reference frames. Then μ₁₀○μ₂ is the frame resulting from stacking one relative to the other. Now suppose that each has some uncertainty. Let {h_i} and {k_j} be two sets of frames of reference that are distributed around the identity. Let the first have N₁ elements, and the second have N₂. What will the covariance of the set of N₁ · N₂ frames {(μ₁○μ₂)⁻¹○μ₁○h_i○μ₂○k_j} (which are also distributed around the identity) look like ?

Let ρ_i(g) be a unimodal pdf with mean at the identity and which has a preponderance of its mass concentrated in a unit ball around the identity (where distance from the identity is measured as ∥(log g)^∨∥). Then ${\rho }_i({\mu }_i^{-1}\circ g)$ will be a distribution with the same shape centered at μ_i. In general, the convolution of two pdfs is defined as

$$(f_1\ast f_2)\left(g\right)={\int }_G{f}_1\left(h\right)f_2(h^{-1}\circ g)\mathit{dh},$$

and in particular if we make the change of variables $k={\mu }_1^{-1}\circ h$, then

$$\rho ({\mu }_1^{-1}\circ g)\ast {\rho }_2({\mu }_2^{-1}\circ g)={\int }_G{\rho }_1\left(k\right){\rho }_2({\mu }_2^{-1}\circ k^{-1}\circ {\mu }_1^{-1}\circ g)\mathit{dk}.$$

Making the change of variables g = μ₁ ○ μ₂ ○ q, where q is a relatively small displacement measured from the identity, the above can be written as

$${\rho }_{1\ast 2}({\mu }_1\circ {\mu }_2\circ q)={\int }_G{\rho }_1\left(k\right){\rho }_2({\mu }_2^{-1}\circ k^{-1}\circ {\mu }_2\circ q)\mathit{dk}.$$ (20)

The essence of this paper is the efficient approximation of covariances about the mean of ρ_1*2 in (20) when the covariances about the means of ρ₁ and ρ₂ are known. In cases when μ_1*2 = μ₁ ○ μ₂, the problem reduces to the efficient approximation of

$$\begin{array}{cc}\hfill {\Sigma }_{1\ast 2}& ={\int }_G{\int }_G\log {\left(q\right)}^{\vee }{\left[\log {\left(q\right)}^{\vee }\right]}^T{\rho }_1\left(k\right){\rho }_2({\mu }_2^{-1}\circ k^{-1}\circ {\mu }_2\circ q)\mathit{dkdq}\hfill \\ \hfill & ={\int }_G{\int }_G\log {({\mu }_2^{-1}\circ k\circ {\mu }_2\circ q^{\prime })}^{\vee }{\left[\log {({\mu }_2^{-1}\circ k\circ {\mu }_2\circ q^{\prime })}^{\vee }\right]}^T{\rho }_1\left(k\right){\rho }_2\left(q^{\prime }\right){\mathit{dkdq}}^{\prime }.\hfill \end{array}$$ (21)

LEMMA 1: The convolution of pdfs with mean at the identity results (to second order) in a pdf with mean at the identity. Furthermore, if ρ₁ * ρ₂ = ρ₂ * ρ₁ and ρ_i(g) = ρ_i(g⁻¹), then this result becomes exact.

Proof:

$$\begin{array}{c}\hfill {\int }_G\left(\log g\right)({\rho }_1\ast {\rho }_2)\left(g\right)\mathit{dg}={\int }_G{\int }_G\left(\log g\right){\rho }_1\left(h\right){\rho }_2(h^{-1}\circ g)\mathit{dhdg}\hfill \\ \hfill ={\int }_G{\int }_G\log (h\circ k){\rho }_1\left(h\right){\rho }_2\left(k\right)\mathit{dhdk}.\hfill \end{array}$$

To second order, all terms in the BCH expansion of log(h ○ k) are linear in either log h or log k (or both), and therefore at least one of the above integrals integrates to zero.

If ρ₁ * ρ₂ = ρ₂ * ρ₁ and ρ_i(g) = ρ_i(g⁻¹) then it is easy to show that (ρ₁ * ρ₂)(g) = (ρ₁ * ρ₂)(g⁻¹), which automatically means that the function (ρ₁ * ρ₂)(g) has mean at the identity.

THEOREM 2: If f_i(g) has mean μ_i and covariance Σ_i for i = 1,2, then to second order, the mean and covariance of (f₁ * f₂)(g) are respectively

$${\mu }_{1\ast 2}={\mu }_1\circ {\mu }_2$$ (22)

and

$${\Sigma }_{1\ast 2}=A+B+F(A,B)$$ (23)

where

$$F(A,B)=\frac{1}{4}C(A,B)+\frac{1}{12}\left[A^{″}B+{\left(A^{″}B\right)}^T+B^{″}A+{\left(B^{″}A\right)}^T\right],$$

$A=\mathit{Ad}\left({\mu }_2^{-1}\right){\Sigma }_1{\mathit{Ad}}^T\left({\mu }_2^{-1}\right)$, B = Σ₂, and C(A,B) and A″ are computed as follows:

$$A^{″}=\left(\begin{array}{cc}\hfill A_{11}-\mathrm{tr}\left(A_{11}\right)I_3\hfill & \hfill 0_3\hfill \\ \hfill A_{12}+A_{12}^T-2\mathrm{tr}\left(A_{12}\right)I_3\hfill & \hfill A_{11}-\mathrm{tr}\left(A_{11}\right)I_3\hfill \end{array}\right).$$

B″ is defined in the same way with B replacing A everywhere in the expression. The blocks of C are computed as

$$\begin{array}{c}\hfill C_{11}=-D_{11,11}\hfill \\ \hfill C_{12}=-{\left(D_{21,11}\right)}^T-D_{11,12}=C_{21}\hfill \\ \hfill C_{22}=-D_{22,11}-D_{21,21}-{\left(D_{21,12}\right)}^T-D_{11,22}\hfill \end{array}$$

where D_ij,kl = D(A_ij, B_kl), and the matrix-valued function D(A′,B′) is defined relative to the entries in the 3 × 3 blocks A′ and B′ as

$$\begin{array}{c}\hfill d_{11}=-a_{33}^{\prime }{b}_{22}^{\prime }+a_{31}^{\prime }{b}_{32}^{\prime }+a_{23}^{\prime }{b}_{23}^{\prime }-a_{22}^{\prime }{b}_{33}^{\prime }\hfill \\ \hfill d_{12}=a_{33}^{\prime }{b}_{21}^{\prime }-a_{32}^{\prime }{b}_{31}^{\prime }-a_{13}^{\prime }{b}_{23}^{\prime }+a_{21}^{\prime }{b}_{33}^{\prime }\hfill \\ \hfill d_{13}=-a_{23}^{\prime }{b}_{21}^{\prime }+a_{22}^{\prime }{b}_{31}^{\prime }+a_{13}^{\prime }{b}_{22}^{\prime }-a_{12}^{\prime }{b}_{32}^{\prime }\hfill \\ \hfill d_{21}=a_{33}^{\prime }{b}_{12}^{\prime }-a_{31}^{\prime }{b}_{32}^{\prime }-a_{21}^{\prime }{b}_{13}^{\prime }+a_{21}^{\prime }{b}_{33}^{\prime }\hfill \\ \hfill d_{22}=-a_{33}^{\prime }{b}_{11}^{\prime }+a_{31}^{\prime }{b}_{31}^{\prime }+a_{13}^{\prime }{b}_{13}^{\prime }-a_{11}^{\prime }{b}_{33}^{\prime }\hfill \\ \hfill d_{23}=a_{23}^{\prime }{b}_{11}^{\prime }-a_{21}^{\prime }{b}_{31}^{\prime }-a_{13}^{\prime }{b}_{12}^{\prime }+a_{11}^{\prime }{b}_{32}^{\prime }\hfill \\ \hfill d_{31}=-a_{32}^{\prime }{b}_{12}^{\prime }+a_{31}^{\prime }{b}_{22}^{\prime }+a_{22}^{\prime }{b}_{13}^{\prime }-a_{21}^{\prime }{b}_{23}^{\prime }\hfill \\ \hfill d_{32}=a_{32}^{\prime }{b}_{11}^{\prime }-a_{31}^{\prime }{b}_{21}^{\prime }-a_{12}^{\prime }{b}_{13}^{\prime }+a_{11}^{\prime }{b}_{23}^{\prime }\hfill \\ \hfill d_{33}=-a_{22}^{\prime }{b}_{11}^{\prime }+a_{21}^{\prime }{b}_{21}^{\prime }+a_{12}^{\prime }{b}_{12}^{\prime }-a_{11}^{\prime }{b}_{22}^{\prime }\hfill \end{array}$$

Proof: The approximation in (22) follows directly from Lemma 1. Next, let $X=\log ({\mu }_2^{-1}\circ k\circ {\mu }_2)$ where k = exp K, and let Y = log q′. Using the Baker-Campbell-Hausdorff formula (5) to evaluate the log terms in the definition of covariance, and retaining all even terms to second order (since first order terms will integrate to zero), we get

$$\begin{array}{cc}\hfill {\left\{{\left(Z(X,Y)\right)}^{\vee }{\left[{\left(Z(X,Y)\right)}^{\vee }\right]}^T\right\}}_{\mathit{even}}& ={\mathbf{xx}}^T+{\mathbf{yy}}^T+\frac{1}{4}{[X,Y]}^{\vee }{\left({[X,Y]}^{\vee }\right)}^T\hfill \\ \hfill & +\frac{1}{12}\mathbf{y}{\left({[X,[X,Y]]}^{\vee }\right)}^T+\frac{1}{12}\mathbf{x}{\left({[Y,[Y,X]]}^{\vee }\right)}^T\hfill \\ \hfill & +\frac{1}{12}{[X,[X,Y]]}^{\vee }{\mathbf{y}}^T+\frac{1}{12}{[Y,[Y,X]]}^{\vee }{\mathbf{x}}^T\hfill \end{array}$$ (24) (25)

Each of these terms can be expanded using the adjoint concept. For example,

$${[X,Y]}^{\vee }{\left({[X,Y]}^{\vee }\right)}^T=\mathit{ad}\left(X\right){\mathbf{yy}}^T{\mathit{ad}}^T\left(X\right)\text{and}{[X,[X,Y]]}^{\vee }{\mathbf{y}}^T=\mathit{ad}\left(X\right)\mathit{ad}\left(X\right){\mathbf{yy}}^T.$$ (26)

In our formulation, $X={\mu }_2^{-1}K{\mu }_2$ (where k = e^K and so ${\mu }_2^{-1}\circ k\circ {\mu }_2=\exp \left({\mu }_2^{-1}K{\mu }_2\right)=e^X$). Defining the vector $\mathbf{x}=\mathit{Ad}\left({\mu }_2^{-1}\right)\mathbf{k}$, then

$$\begin{array}{cc}\hfill A& ={\int }_G{\mathbf{xx}}^T{\rho }_1\left(k\right)\mathit{dk}\hfill \\ \hfill & =\mathit{Ad}\left({\mu }_2^{-1}\right)\left[{\int }_G{\left(\log k\right)}^{\vee }{\left[{\left(\log k\right)}^{\vee }\right]}^T{\rho }_1\left(k\right)\mathit{dk}\right]{\mathit{Ad}}^T\left({\mu }_2^{-1}\right)\hfill \\ \hfill & =\mathit{Ad}\left({\mu }_2^{-1}\right){\Sigma }_1{\mathit{Ad}}^T\left({\mu }_2^{-1}\right)\hfill \end{array}$$

and since q′ = e^Y,

$$B={\int }_G{\mathbf{yy}}^T{\rho }_2\left(q^{\prime }\right){\mathit{dq}}^{\prime }={\int }_G{\left(\log q^{\prime }\right)}^{\vee }{\left[{\left(\log q^{\prime }\right)}^{\vee }\right]}^T{\rho }_2\left(q^{\prime }\right){\mathit{dq}}^{\prime }={\Sigma }_2.$$

.

The following complicated looking integral (which is nothing more than (21) written in exponential coordinates)

$$\begin{array}{cc}\hfill {\Sigma }_{1\ast 2}& ={\int }_{q^{\prime }\in G}{\int }_{k\in G}\left\{{\left(Z(X,Y)\right)}^{\vee }{\left[{\left(Z(X,Y)\right)}^{\vee }\right]}^T\right\}{\rho }_1\left(k\right){\rho }_2\left(q^{\prime }\right){\mathit{dkdq}}^{\prime }\hfill \\ \hfill & ={\int }_{q^{\prime }\in G}{\int }_{k\in G}{\left\{{\left(Z(X,Y)\right)}^{\vee }{\left[{\left(Z(X,Y)\right)}^{\vee }\right]}^T\right\}}_{\mathit{even}}{\rho }_1\left(k\right){\rho }_2\left(q^{\prime }\right){\mathit{dkdq}}^{\prime }\hfill \end{array}$$

can be simplified. This is because

$$x_i{x}_j={\mathbf{e}}_i^T\mathit{Ad}\left({\mu }_2^{-1}\right){\left(\log k\right)}^{\vee }{\left[{\left(\log k\right)}^{\vee }\right]}^T{\mathit{Ad}}^T\left({\mu }_2^{-1}\right){\mathbf{e}}_j$$

and

$$y_k{y}_l={\mathbf{e}}_k^T{\left(\log q^{\prime }\right)}^{\vee }{\left[{\left(\log q^{\prime }\right)}^{\vee }\right]}^T{\mathbf{e}}_l,$$

and since all terms in {(Z(X, Y))^∨[(Z(X, Y))^∨]^T}_even can be expressed as weighted sums of such products, it follows that after integration we get

$${\Sigma }_{1\ast 2}=A+B+F(A,B).$$ (27)

For the SE(3) case

$$\mathit{Ad}\left(g\right)=\left(\begin{array}{cc}\hfill R\hfill & 0_3\hfill \\ \hfill \mathit{TR}\hfill & R\hfill \end{array}\right)\in {\mathit{IR}}^{6\times 6}\text{and}\mathit{ad}\left(X\right)=\left(\begin{array}{cc}\hfill \Omega \hfill & 0_3\hfill \\ \hfill V\hfill & \Omega \hfill \end{array}\right)\in {\mathit{IR}}^{6\times 6}$$

where T^∨ = t, V^∨ = v and Ω^∨ = ω. Then (26) becomes:

$$\begin{array}{cc}\hfill {[X,Y]}^{\vee }{\left[{(X,Y)}^{\vee }\right]}^T& =\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{c}\hfill {\omega }_y\hfill \\ \hfill {\mathbf{v}}_y\hfill \end{array}\right)[{\omega }_y^T,{\mathbf{v}}_y^T]\left(\begin{array}{cc}\hfill -{\Omega }_x\hfill & \hfill -V_x\hfill \\ \hfill 0_3\hfill & \hfill -\Omega \hfill \end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\omega }_y{\omega }_y^T\hfill & {\omega }_y{\mathbf{v}}_y^T\hfill \\ \hfill {\mathbf{v}}_y{\omega }_y^T\hfill & {\mathbf{v}}_y{\mathbf{v}}_y^T\hfill \end{array}\right)\left(\begin{array}{cc}\hfill -{\Omega }_x\hfill & \hfill -V_x\hfill \\ \hfill 0_3\hfill & \hfill -\Omega \hfill \end{array}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {[X,[X,Y]]}^{\vee }{\mathbf{y}}^T& =\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{c}\hfill {\omega }_y\hfill \\ \hfill {\mathbf{v}}_y\hfill \end{array}\right)[{\omega }_y^T,{\mathbf{v}}_y^T]\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\Omega }_x\hfill & \hfill 0_3\hfill \\ \hfill V_x\hfill & \hfill \Omega \hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\omega }_y{\omega }_y^T\hfill & \hfill {\omega }_y{\mathbf{v}}_y^T\hfill \\ \hfill {\mathbf{v}}_y{\omega }_y^T\hfill & \hfill {\mathbf{v}}_y{\mathbf{v}}_y^T\hfill \end{array}\right)\hfill \end{array}$$

If we divide the 6 × 6 symmetric matrices $A=\mathit{Ad}\left({\mu }_2^{-1}\right){\Sigma }_1{\mathit{Ad}}^T\left({\mu }_2^{-1}\right)$ and B = Σ₂ into 3 × 3 blocks as

$$A=\left(\begin{array}{cc}\hfill A_{11}\hfill & \hfill A_{12}\hfill \\ \hfill A_{12}^T\hfill & \hfill A_{22}\hfill \end{array}\right)\text{and}B=\left(\begin{array}{cc}\hfill B_{11}\hfill & \hfill B_{12}\hfill \\ \hfill B_{12}^T\hfill & \hfill B_{22}\hfill \end{array}\right),$$

then using the specific form of ad(X) and integrating over q′ we get

$${\int }_G{[X,[X,Y]]}^{\vee }{\mathbf{y}}^T{\rho }_2\left(q^{\prime }\right){\mathit{dq}}^{\prime }=\left(\begin{array}{cc}\hfill {\Omega }_x^2\hfill & \hfill 0_3\hfill \\ \hfill V_x{\Omega }_x+{\Omega }_x{V}_x\hfill & \hfill {\Omega }_x^2\hfill \end{array}\right)B$$

and

$$\begin{array}{c}\hfill {\int }_G{[X,Y]}^{\vee }{\left({[X,Y]}^{\vee }\right)}^T{\rho }_2\left(q^{\prime }\right){\mathit{dq}}^{\prime }=\hfill \\ \hfill \left(\begin{array}{cc}\hfill -{\Omega }_x{B}_{11}{\Omega }_x\hfill & \hfill -{\left(V_x{B}_{11}{\Omega }_x\right)}^T-{\Omega }_x{B}_{12}{\Omega }_x\hfill \\ \hfill -V_x{B}_{11}{\Omega }_x-{\left({\Omega }_x{B}_{12}{\Omega }_x\right)}^T\hfill & \hfill -V_x{B}_{11}{\Omega }_x-V_x{B}_{12}{\Omega }_x-{\left(V_x{B}_{12}{\Omega }_x\right)}^T-{\Omega }_x{B}_{12}{\Omega }_x\hfill \end{array}\right)\hfill \end{array}$$

Then integrating over k ∈ G gives

$$\begin{array}{c}\hfill {\int }_G{\int }_G{[X,[X,Y]]}^{\vee }{\mathbf{y}}^T{\rho }_1\left(k\right){\rho }_2\left(q^{\prime }\right){\mathit{dkdq}}^{\prime }=A^{″}B\hfill \\ \hfill {\int }_G{\int }_G{[X,Y]}^{\vee }{\left({[X,Y]}^{\vee }\right)}^T{\rho }_1\left(k\right){\rho }_2\left(q^{\prime }\right){\mathit{dkdq}}^{\prime }=C(A,B)=\left(\begin{array}{cc}\hfill C_{11}\hfill & \hfill C_{12}\hfill \\ \hfill C_{12}^T\hfill & \hfill C_{22}\hfill \end{array}\right).\hfill \end{array}$$

The BCH formula yields several such terms, each of which can be obtained by either transposing those given above or switching the roles of B and A.

4 Sampled Distributions and Numerical Examples

Evaluating the robustness of the first-order (1) and the second-order (23) covariance propagation formula over a wide range of kinematic errors is essential to understand effectiveness of these formulas. In this section, we test these two covariance propagation formulas with concrete numerical examples.

In many practical situations, discrete data are sampled from ρ₁ and ρ₂ rather than having complete knowledge of the distributions themselves. Therefore, sampled covariances can be computed by making the following substitutions:

$${\rho }_1\left(g\right)=\underset{i=1}{\overset{N_1}{\Sigma }}{\alpha }_i\Delta (h_i^{-1}\circ g)$$ (28)

and

$${\rho }_2\left(g\right)=\underset{j=1}{\overset{N_2}{\Sigma }}{\beta }_j\Delta (k_j^{-1}\circ g)$$ (29)

where

$$\underset{i=1}{\overset{N_1}{\Sigma }}{\alpha }_i=\underset{j=1}{\overset{N_2}{\Sigma }}{\beta }_j=1.$$

Here Δ(g) is the Dirac delta function for the group G, which has the properties

$${\int }_{G}f\left(g\right)\Delta (h^{-1}\circ g)\mathit{dg}=f\left(h\right)\text{and}\Delta (h^{-1}\circ g)=\Delta (g^{-1}\circ h).$$

Using these properties, if we substitute (28) and (29) into (21), the result is

$${\Sigma }_{1\ast 2}=\underset{i=1}{\overset{N_1}{\Sigma }}\underset{j=1}{\overset{N_2}{\Sigma }}{\alpha }_i{\beta }_j\log {({\mu }_2^{-1}\circ h_i\circ {\mu }_2\circ k_j)}^{\vee }{\left[\log {({\mu }_2^{-1}\circ h_i\circ {\mu }_2\circ k_j)}^{\vee }\right]}^T.$$ (30)

While this equation is exact, it has the drawback of requiring O(N₁ · N₂) arithmetic operations. In the first-order theory of error propagation, we made the approximation

$$\log (k^{-1}\circ q)=X-Y,$$

or equivalently

$${\left[\log (k^{-1}\circ q)\right]}^{\vee }=\mathbf{x}-\mathbf{y},$$

where k = exp Y and q = exp X are elements of the Lie group SE(3). This decouples the summations and makes the computation O(N₁ + N₂). However, the first-order theory breaks down for large errors. Therefore, we explore here the numerical accuracy of the second-order theory developed in the previous section.

4.1 Error Propagation in a PUMA Manipulator

Consider a spatial serial manipulator, PUMA 560. The link-frame assignments of PUMA 560 for D-H parameters is the same as those given in [Craig 2005]. Table 1 lists the D-H parameters of PUMA 560, where a₂ = 431.8 mm, a₃ = 20.32 mm, d₃ = 124.46 mm, and d₄ = 431.8 mm. The solution of forward kinematics is the homogeneous transformations of the relative displacements from one D-H frame to another multiplied sequentially.

Table 1.

DH Parameters of the PUMA 560

i	αi−1	ai−1	di	θ i
1	0	0	0	θ 1
2	−90°	0	0	θ 2
3	0	a 2	d 3	θ 3
4	−90°	a 3	d 4	θ 4
5	90°	0	0	θ 5
6	−90°	0	0	θ 6

In order to test these covariance propagation formulas, we first need to create some kinematic errors. Since joint angles are the only variables of the PUMA 560, we assume that errors exist only in these joint angles. We generated errors by deviating each joint angle from its ideal value with uniform random absolute errors of ±∊. Therefore, each joint angle was sampled at three values: θ_i − ∊, θ_i, θ_i + ∊. This generates N = 3⁶ different frames of references $\left\{g_{\mathit{ee}}^i\right\}$ that are clustered around desired g_ee. Here g_ee denotes the position and orientation of the distal end of the manipulator relative to the base in the form of homogeneous transformation matrix.

It is important to note that while the cloud of frames $\left\{g_{\mathit{ee}}^i\right\}$ is clustered around g_ee, it may not be the case that g_ee is actually the mean of this cloud. In the first-order theory, the cloud is assumed to be so tightly focused around g_ee that the approximation μ_ee ≈ g_ee can be made without causing significant errors. However, in the second order theory, one needs to be more precise. We can update our estimate of the mean as:

$${\mu }_{\mathit{ee}}=g_{\mathit{ee}}\circ \exp \left[\frac{1}{N}\underset{i=1}{\overset{N}{\Sigma }}\log (g_{\mathit{ee}}^{-1}\circ g_{\mathit{ee}}^i)\right].$$ (31)

In practice, for errors of moderate magnitude, only one such update is required to obtain the exact mean. For very large errors this formula can be iterated with the output, μ_ee, from one iteration serving as the input, g_ee, for the next iteration. A similar update to obtain μ₁ and μ₂ from the frame clouds around the frames g₁ and g₂ (the relative frames from base to mid point and mid point to distal end of the manipulator such that g₁ ○ g₂ = g_ee) should also be performed.

Three different methods for computing the same error covariances for the whole manipulator are computed. The first is to apply brute force enumeration, which gives the actual covariance of the whole manipulator:

$$\Sigma =\frac{1}{N}\underset{i=1}{\overset{N}{\Sigma }}{\mathbf{x}}_i{\mathbf{x}}_i^T$$ (32)

where ${\mathbf{x}}_i={\left[\log \left({\mu }_{\mathit{ee}}^{-1}\circ g_{\mathit{ee}}^i\right)\right]}^{\vee }$, and (32) is used for all of the 3⁶ different frames of references $\left\{g_{\mathit{ee}}^i\right\}$. The second method is to apply the first-order propagation formula (1). The third is to apply the second-order propagation formula (23). For the covariance propagation methods, we only need to find the mean and covariance of each individual link. Then the covariance of the whole manipulator can be recursively calculated using the corresponding propagation formula.

In order to quantify the robustness of the two covariance approximation methods, we define a measure of deviation of results between the first/second order formula and the actual covariance using the Hilbert-Schmidt (Frobenius) norm as

$$\text{deviation}=\frac{\Vert {\Sigma }_{\mathit{prop}}-{\Sigma }_{\mathit{actual}}\Vert }{\Vert {\Sigma }_{\mathit{actual}}\Vert },$$ (33)

where Σ_prop is the covariance of the whole manipulator calculated using either the first-order (1) or the second-order (23) propagation formula, Σ_actual is the actual covariance of the whole manipulator calculated using (32), and ∥ · ∥ denotes the Hilbert-Schmidt (Frobenius) norm.

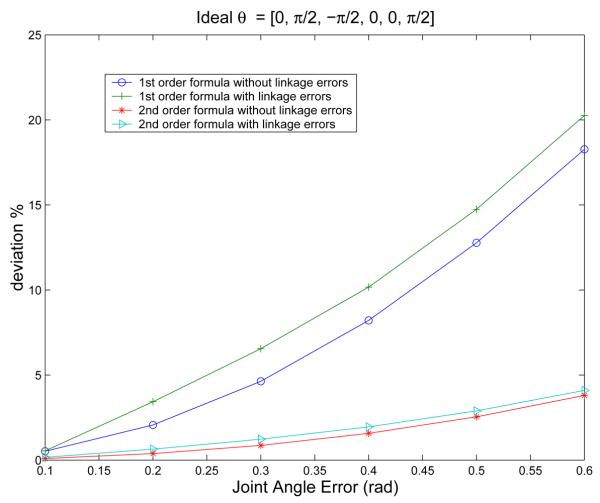
With all the above information, we now can conduct the specific computation and analysis. The results of two different configurations of the manipulator are illustrated here. The ideal joint angles of one configuration from θ₁ to θ₆ were taken as [0, π/2, −π/2, 0, 0, π/2]. The ideal joint angles of the other configuration were taken as [π/4, π/5, −π/4, π/10, π/8, π]. As an initial test, the joint angle errors ∊ were taken from 0.1 rad to 0.6 rad, and the static DH parameters of the links were assumed to be error free. The covariances of the whole manipulator corresponding to these kinematic errors were then calculated through the three aforementioned methods. The resulting deviations between the covariance matrices computed directly using (32) and the first-order and second-order propagation formulas are plotted in Figures 1 and 2 with (33) on the y-axis for different amounts of noise on the x-axis.

Figure 1.

The Deviation of the First and Second-order Propagation Methods for Configuration I

Figure 2.

The Deviation of the First and Second-order Propagation Methods for Configuration II

Since physical manipulators cannot be manufactured with exact design parameters, and their real linkage parameters such as the static DH parameters (α_i, a_i, d_i) may have errors, the propagation theory is applied now to the case with both joint angle errors and linkage errors. The same sets of calculations that were conducted for the case with only joint angles are now conducted for this case with the additional linkage errors. Our numerical simulations have shown that if the only static DH parameters that have errors are the translational parameters a_i and d_i, then they have essentially no effect the value of the deviation. In other words, both the first and second order propagation formulas capture the covariances resulting from these translational errors. However, the linkage errors in the angular DH parameters such as α_i create observable effects on the accuracy of the propagation formulas. In the given example, we assume that DH parameters α₀, α₁, and α₅ deviate from their ideal values with uniform random absolute errors of ±0.2 rad. Therefore, they are sampled at three values: α_i − 0.2, α_i, α_i + 0.2. Together with the six joint angle errors, this generates N = 3⁹ different frames of references $\left\{g_{\mathit{ee}}^i\right\}$ that are clustered around the baseline g_ee. The results of the first-order and second-order propagation formula of these cases were also graphed in Figures 1 and 2.

The numerical simulation results demonstrate that the propagation formula can efficiently deal with all kinematic errors including errors in joint angles and linkage parameters. It is also clear that the second-order propagation formula makes significant improvements in terms of accuracy when compared to the first-order formula. The second-order propagation theory is much more robust than the first-order formula over a wide range of kinematic errors. These two methods both work well for small errors, and deviate from the actual value more and more as the errors become large. However, the deviation of the first-order formula grows rapidly and breaks down while the second-order propagation method still retains a reasonable value.

To give the readers a sense of what these covariances look like, we listed the values of the covariance of the whole manipulator for the joint angle error ∊ = 0.3 rad below.

The ideal pose of the end effector can be found easily via forward kinematics to be

$$g_{\mathit{ee}}=\left(\begin{array}{cccc}\hfill 0.0000\hfill & \hfill -1.0000\hfill & \hfill 0\hfill & \hfill 0.0203\hfill \\ \hfill -1.0000\hfill & \hfill -0.0000\hfill & \hfill 0\hfill & \hfill 0.1245\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1.0000\hfill & \hfill -08636\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.0000\hfill \end{array}\right).$$

The actual covariance of the whole manipulator calculated using equations (32) is

$${\Sigma }_{\mathit{actual}}=\left(\begin{array}{cccccc}\hfill 0.1748\hfill & \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill -0.0755\hfill & \hfill -0.0024\hfill \\ \hfill 0.0000\hfill & \hfill 0.0078\hfill & \hfill 0.0000\hfill & \hfill 0.0034\hfill & \hfill -0.0000\hfill & \hfill 0.0003\hfill \\ \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0.1747\hfill & \hfill 0.0012\hfill & \hfill -0.0072\hfill & \hfill -0.0000\hfill \\ \hfill 0.0000\hfill & \hfill 0.0034\hfill & \hfill 0.0012\hfill & \hfill 0.0025\hfill & \hfill -0.0001\hfill & \hfill 0.0001\hfill \\ \hfill -0.0755\hfill & \hfill -0.0000\hfill & \hfill -0.0072\hfill & \hfill -0.0001\hfill & \hfill 0.0546\hfill & \hfill 0.0015\hfill \\ \hfill -0.0024\hfill & \hfill 0.0003\hfill & \hfill -0.0000\hfill & \hfill 0.0001\hfill & \hfill 0.0015\hfill & \hfill 0.0011\hfill \end{array}\right),$$

the covariance using the first-order propagation formula (1) is

$${\Sigma }_{\mathit{prop},1\mathit{st}}=\left(\begin{array}{cccccc}\hfill 0.1800\hfill & \hfill 0.0000\hfill & \hfill 0\hfill & \hfill 0.0000\hfill & \hfill -0.0777\hfill & \hfill -0.0024\hfill \\ \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0\hfill & \hfill 0.0000\hfill & \hfill -0.0000\hfill & \hfill -0.0000\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.1800\hfill & \hfill 0.0012\hfill & \hfill -0.0075\hfill & \hfill 0\hfill \\ \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0.0012\hfill & \hfill 0.0000\hfill & \hfill -0.0002\hfill & \hfill -0.0000\hfill \\ \hfill -0.0777\hfill & \hfill -0.0000\hfill & \hfill -0.0075\hfill & \hfill -0.0002\hfill & \hfill 0.0569\hfill & \hfill 0.0016\hfill \\ \hfill -0.0024\hfill & \hfill -0.0000\hfill & \hfill 0\hfill & \hfill -0.0000\hfill & \hfill 0.0016\hfill & \hfill 0.0000\hfill \end{array}\right),$$

and the covariance using the second-order propagation formula (23) is

$${\Sigma }_{\mathit{prop},2\mathit{nd}}=\left(\begin{array}{cccccc}\hfill 0.1748\hfill & \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill -0.0743\hfill & \hfill -0.0024\hfill \\ \hfill 0.0000\hfill & \hfill 0.0079\hfill & \hfill 0.0000\hfill & \hfill 0.0034\hfill & \hfill -0.0000\hfill & \hfill 0.0003\hfill \\ \hfill 0.0000\hfill & \hfill 0.0000\hfill & \hfill 0.1747\hfill & \hfill 0.0012\hfill & \hfill -0.0072\hfill & \hfill 0.0000\hfill \\ \hfill 0.0000\hfill & \hfill 0.0034\hfill & \hfill 0.0012\hfill & \hfill 0.0025\hfill & \hfill -0.0001\hfill & \hfill 0.0001\hfill \\ \hfill -0.0743\hfill & \hfill -0.0000\hfill & \hfill -0.0072\hfill & \hfill -0.0001\hfill & \hfill 0.0546\hfill & \hfill 0.0015\hfill \\ \hfill -0.0024\hfill & \hfill 0.0003\hfill & \hfill 0.0000\hfill & \hfill 0.0001\hfill & \hfill 0.0015\hfill & \hfill 0.0011\hfill \end{array}\right).$$

4.2 Continuous-Time Covariance Propagation: The Stochastic Flexible Needle with Bevel Tip

The previous example in this paper illustrated how to obtain the mean and covariance of error pdfs resulting from convolutions of densities centered around discrete joints in a manipulator arm. In contrast, applications such as SLAM can be better described with a model in which the error accumulates continuously over time. This section addresses that problem. In particular, estimates of the mean and covariance of a process described by a stochastic differential equation can be obtained for small time intervals by numerical integration. The second-order propagation formulas derived earlier in the paper are then used to propagate these estimates for larger values of time. The example that is used to illustrate this technique is flexible needle steering.

Recently, a number of works have been concerned with the steering of flexible needles with bevel tips through soft tissue for minimally invasive medical treatments. See, for example, [Webster et al. 2006], [Park et al. 2005], [Alterovitz, Simeon and Goldberg 2007]. In this problem, a flexible needle is rotated with the angular speed ω(t) around its tangent while it is inserted with translational speed v(t) in the tangential direction. Due to the bevel tip, the needle will not follow a straight line when ω(t) = 0 and v(t) is constant. Rather, in this case the tip of the needle will approximately follow a circular arc with curvature κ when the medium is very firm and the needle is very flexible. The specific value of the constant κ depends on parameters such as the angle of the bevel, how sharp the needle is, and properties of the tissue. In practice κ is fit to experimental observations of the needle bending in a particular medium during insertions with ω(t) = 0 and v(t) is constant. Using this as a baseline, and building in arbitrary ω(t) and v(t), a nonholonomic kinematic model then predicts the time evolution of the position and orientation of the needle tip [Webster et al. 2006, Park et al. 2005].

In a reference frame attached to the needle tip with the local x₃ axis denoting the tangent to the “backbone curve” of the needle, and x₁ denoting the axis orthogonal to the direction of infinitesimal motion induced by the bevel (i.e., the needle bends in the x₂ − x₃ plane), the nonholonomic kinematic model for the evolution of the frame at the needle tip was developed in [Webster et al. 2006, Park et al. 2005] as:

$$\xi ={\left(g^{-1}\stackrel{.}{g}\right)}^{\vee }={\left[\kappa 0\omega \left(t\right)00v\left(t\right)\right]}^T.$$ (34)

If everything were certain, and if this model were exact, then g(t) could be obtained by simply integrating the ordinary differential equation in (34). However, in practice a needle that is repeatedly inserted into a medium such as gelatin (which is used to simulate soft tissue) will demonstrate an ensemble of slightly different trajectories.

A simple stochastic model for the needle is obtained by letting [Park et al. 2005, Park et al. 2008]:

$$\omega \left(t\right)={\omega }_0\left(t\right)+{\lambda }_1{w}_1\left(t\right),$$

and

$$v\left(t\right)=v_0\left(t\right)+{\lambda }_2{w}_2\left(t\right).$$

Here ω₀(t) and v₀(t) are what the inputs would be in the ideal case, w₁(t) and w₂(t) are uncorrelated unit Gaussian white noises, and λ_i are constants.

Thus, a nonholonomic needle model with noise is

$${\left(g^{-1}\stackrel{.}{g}\right)}^{\vee }\mathit{dt}=\left[\begin{array}{c}\hfill \kappa \hfill \\ \hfill 0\hfill \\ \hfill {\omega }_0\left(t\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill v_0\left(t\right)\hfill \end{array}\right]\mathit{dt}+\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\lambda }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill \end{array}\right)\left[\begin{array}{c}\hfill {\mathit{dW}}_1\hfill \\ \hfill {\mathit{dW}}_2\hfill \end{array}\right]$$ (35)

where dW_i = W_i(t + dt) − W_i(t) = w_i(t)dt are the non-differentiable increments of a Wiener process W_i(t). This noise model is a stochastic differential equation (SDE) on SE(3). As shorthand, we write this as

$${\left(g^{-1}\stackrel{.}{g}\right)}^{\vee }\mathit{dt}=\mathbf{h}\left(t\right)\mathit{dt}+\mathit{Hd}\mathbf{W}\left(t\right).$$

In this subsection, the second-order covariance propagation formula is demonstrated by “pasting together” two ensembles of needle trajectories from t = 0 to t = 1/2 and t = 1/2 to t = 1 to get the mean and covariance of needle trajectories from t = 0 to t = 1. These needle trajectories are generated by integrating the SDE in (35) for these three time periods with Δt = 0.01 using a modified version of the Euler-Maruyama method for generating sample paths of SDEs [Higham 2001]. The mean and covariance resulted from the second-order propagation formula are then compared with those obtained by integrating the SDE from t = 0 to t = 1 as detailed below.

The reference frame g(t) is generated from ξ(t) = (g^−ldg)^∨ by the product of exponentials formula at multiples of the small time step Δt as:

$$g\left(n\Delta t\right)=\exp \widehat{\xi }\left(\Delta t\right)\exp \widehat{\xi }\left(2\Delta t\right)\cdots \exp \widehat{\xi }\left(n\Delta t\right).$$

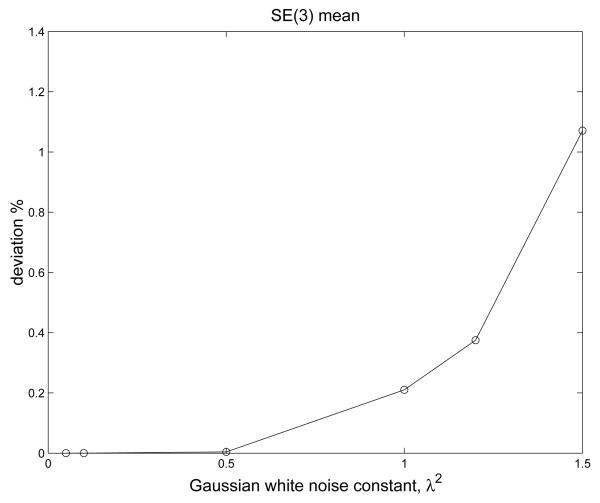
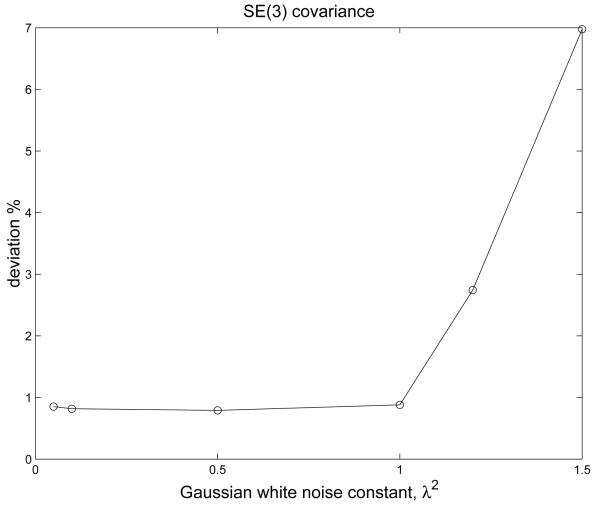
A cloud of frames {g⁽ⁱ⁾(nΔt)} for the trials i = 1, …, 10,000 are created with κ = 0.05 and a certain value of λ₁ and λ₂. The actual SE(3) means and covariances of the cloud of frames {g⁽ⁱ⁾(nΔt)} are then computed using brute force enumeration for the three time periods: t₁ = [0, 1/2], t₂ = [1/2, 1], and t₃ = [0, 1] by applying (31) and (32) respectively. With the actual means and covariances of needle trajectories for t₁ = [0, 1/2] and t₂ = [1/2, 1], the estimated means and covariances of needle trajectories for t₃ = [0,1] are derived using the second-order propagation formula (22) and (23). These estimated means and covariances for period t₃ = [0, 1] are compared with their corresponding actual values. The comparison results are quantitively expressed through a definition on deviation. The measure of deviation on the covariance is defined as (33). Similarly, the measure of deviation on the mean is defined as

$$\text{deviation}=\frac{\Vert {\mu }_{\mathit{prop}}-{\mu }_{\mathit{actual}}\Vert }{\Vert {\mu }_{\mathit{actual}}\Vert },$$ (36)

where μ_prop is the mean calculated using second-order propagation formula (22), μ_actual is the actual mean calculated using (31), and ∥ · ∥ denotes the Hilbert-Schmidt (Frobenius) norm.

A range of values of λ₁ and λ₂ are tested to verify the effectiveness of the second order propagation formula. These values are ${\lambda }_1^2={\lambda }_2^2=0.05,0.1,0.5,1,1.2,1.5$. These comparison results are illustrated through the graphs of deviation versus Gaussian white noise constant λ² as shown in Figures 3 and 4. It can be observed that the deviation of the mean is less than 0.3% and the deviation of the covariance is less than 1% for λ < 1, where λ = 1 is a fairly large noise constant. These comparisons have shown that the mean and covariance computed from the second-order propagtion formula are very good approximations to those obtained by integrating the SDE from t = 0 to t = 1.

Figure 3.

The Deviation of the Mean

Figure 4.

The Deviation of the Covariance

5 Conclusions

In this paper, first-order kinematic error propagation formulas are modified to include second-order effects. This extends the usefulness of these formulas to errors that are not necessarily small. In fact, in the example to which the methodology is applied, errors in orientation can be as large as a radian or more and the second-order formula appears to capture the error well. The second-order propagation formula makes significant improvements in terms of accuracy than that of the first-order formula. The second-order propagation theory is much more robust than the first-order formula over a wide range of kinematic errors. This is demonstrated with the example of a PUMA manipulator arm with substantial errors in the joints, as well as stochastic trajectories of a nonholonomic kinematic model of a flexible needle.

A Matrix Lie Groups in General

A matrix Lie group is a Lie group where G is a set of square matrices and the group operation is matrix multiplication. In this work, only the groups SO(3) and SE(3) will be considered.

A.1 The Exponential and Logarithm Maps

Given a general matrix Lie group, elements sufficiently close to the identity are written as g(t) = e^tX for some X ∈ 𝒢 (the Lie algebra of G) and t near 0. Explicitly,

$$e^X=\underset{k=0}{\overset{\infty }{\Sigma }}\frac{X^k}{k!}.$$ (37)

The matrix logarithm is defined by the Taylor series about the identity matrix:

$$\log \left(g\right)=\log (I+(g-I))=\underset{k=1}{\overset{\infty }{\Sigma }}{(-1)}^{k+1}\frac{{(g-I)}^k}{k}.$$ (38)

For matrix Lie groups, operations such as g − I and division of g by a scalar are well defined. The exponential map takes an element of the Lie algebra and produces an element of the Lie group. This is written as:

$$\exp :𝒢\to G.$$

The logarithm map does just the opposite:

$$\log :G\to 𝒢.$$

In other words, log(exp X) = X, and exp(log(g)) = g.

Given any smooth curve g(t) ∈ G, we can compute $g^{-1}\frac{\mathit{dg}}{\mathit{dt}}$ and $\frac{\mathit{dg}}{\mathit{dt}}{g}^{-1}$. These will be elements of 𝒢.

A.2 The Lie Bracket and the Adjoint Matrices Ad(g) and ad(X)

The adjoint operator is defined as

$$\mathit{Ad}\left(g_1\right)X=\frac{d}{\mathit{dt}}\left(g_1{e}^{\mathit{tX}}{g}_1^{-1}\right){\mid }_{t=0}=g_1{\mathit{Xg}}_1^{-1}.$$ (39)

This gives a homomorphism Ad : G → GL(𝒢) from the group into the set of all invertible linear transformations of 𝒢 onto itself. It is a homomorphism because

$$\mathit{Ad}\left(g_1\right)\mathit{Ad}\left(g_2\right)X=g_1\left(g_2{\mathit{Xg}}_2^{-1}\right)g_1^{-1}=\left(g_1{g}_2\right)X{\left(g_1{g}_2\right)}^{-1}=\mathit{Ad}\left(g_1{g}_2\right)X.$$

It is linear because

$$\begin{array}{cc}\hfill \mathit{Ad}\left(g\right)(c_1{X}_1+c_2{X}_2)& =g(c_1{X}_1+c_2{X}_2)g^{-1}=c_1{\mathit{gX}}_1{g}^{-1}+c_2{\mathit{gX}}_2{g}^{-1}\hfill \\ \hfill & =c_1\mathit{Ad}\left(g\right)X_1+c_2\mathit{Ad}\left(g\right)X_2.\hfill \end{array}$$

In the special case of a 1-parameter subgroup when g = g(t) is an element close to the identity. ⁴, we can approximate g(t) ≈ I + tX for small t. Then we get Ad(I + tX)Y = Y + t(XY − YX). The quantity

$$\mathit{XY}-\mathit{YX}=[X,Y]=\frac{d}{\mathit{dt}}\left(\mathit{Ad}\left(g\left(t\right)\right)Y\right){\mid }_{t=0}$$ (40)

is called the Lie bracket of the elements X, Y ∈ 𝒢.

It is clear from the definition in (40) that the Lie bracket is linear in each entry:

$$[c_1{X}_1+c_2{X}_2,Y]=c_1[X_1,Y]+c_2[X_2,Y]$$

and

$$[X,c_1{Y}_1+c_2{Y}_2]=c_1[X,Y_1]+c_2[X,Y_2].$$

Furthermore, the Lie bracket is anti-symmetric:

$$[X,Y]=-[Y,X],$$ (41)

and hence [X, X] = 0. Given a basis {E₁, .…, E_n} for the Lie algebra 𝒢, any arbitrary element can be written as

$$X=\underset{i=1}{\overset{n}{\Sigma }}{x}_i{E}_i.$$

The Lie bracket of any two elements will result in a linear combination of all basis elements. This is written as

$$[E_i,E_j]=\underset{k=1}{\overset{n}{\Sigma }}{C}_{\mathit{ij}}^k{E}_k.$$

The constants $C_{\mathit{ij}}^k$ are called the structure constants of the Lie algebra 𝒢. Note that the structure constants are antisymmetric: $C_{\mathit{ij}}^k=-C_{\mathit{ji}}^k$.

It can be checked that for any three elements of the Lie algebra, the Jacobi identity is satisfied:

$$[X_1,[X_2,X_3]]+[X_2,[X_3,X_1]]+[X_3,[X_1,X_2]]=0.$$ (42)

It is often convenient to write the independent entries of any X ∈ 𝒢 as a column vector using the notation x = X^∨ where the rule ${\mathbf{e}}_i=E_i^{\vee }$ is used. The particular details of the ∨ operator for the cases of SO(3) and SE(3) are given in the following appendices.

A matrix denoted as ad(X) can then be defined such that for any X, Y ∈ 𝒢

$$[X,Y]=\mathit{ad}\left(X\right)\mathbf{y}.$$

From (41), it follows that

$$\mathit{ad}\left(X\right)\mathbf{y}=-\mathit{ad}\left(Y\right)\mathbf{x}.$$

B The Rotation Group, SO(3)

The Lie algebra so(3) consists of skew-symmetric matrices of the form

$$X=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -x_3\hfill & \hfill x_2\hfill \\ \hfill x_3\hfill & \hfill 0\hfill & \hfill -x_1\hfill \\ \hfill -x_2\hfill & \hfill x_1\hfill & \hfill {}_0\hfill \end{array}\right)=\underset{i=1}{\overset{3}{\Sigma }}{x}_i{E}_i.$$ (43)

The skew-symmetric matrices {E_i} form a basis for the set of all such 3 × 3 skew-symmetric matrices, and the coefficients {x_i} are all real. The ∨ operation is defined to extract these coefficients from a skew symmetric matrix to form a column vector [x₁, x₂, x₃]^T ∈ IR³ such that Xy = x × y for any y ∈ IR³, where × is the usual vector cross product.

In this case, the adjoint matrices are

$$\mathit{Ad}\left(R\right)=R\text{and}\mathit{ad}\left(X\right)=X.$$

Furthermore,

$${[X,Y]}^{\vee }=\mathbf{x}\times \mathbf{y}.$$

It is well known (see [Chirikjian 2001] for derivation and references) that

$$R\left(\mathbf{x}\right)=e^X=I+\frac{\sin \Vert \mathbf{x}\Vert }{\Vert \mathbf{x}\Vert }X+\frac{(1-\cos \Vert \mathbf{x}\Vert )}{\Vert \mathbf{x}{\Vert }^2}{X}^2$$ (44)

where $\parallel \mathbf{x}\parallel ={(x_1^2+x_2^2+x_3^2)}^{\frac{1}{2}}$. Clearly, since the instantaneous rotation axis is preserved under a rotation, R(x)x = x.

An interesting and useful fact is that except for a set of measure zero, all elements of SO(3) can be captured with the parameters within the open ball defined by ∥x∥ < π, and the matrix logarithm of any group element parameterized in this range is also well defined. It is convenient to know that the angle of the rotation, θ(R), is related to the exponential parameters as |θ(R)| = ∥x∥. Furthermore,

$$\log \left(R\right)=\frac{1}{2}\frac{\theta \left(R\right)}{\sin \theta \left(R\right)}(R-R^T)$$

where

$$\theta \left(R\right)={\cos }^{-1}\left(\frac{\text{trace}\left(R\right)-1}{2}\right).$$

Invariant definitions of directional (Lie) derivatives and integration measure for SO(3) can be defined. When computing these invariant quantities in coordinates (including exponential coordinates), a Jacobian matrix comes into play. There are two such Jacobian matrices:

$$J_l\left(\mathbf{x}\right)=\left[{\left(\frac{\partial R}{\partial x_1}{R}^T\right)}^{\vee },{\left(\frac{\partial R}{\partial x_2}{R}^T\right)}^{\vee },{\left(\frac{\partial R}{\partial x_3}{R}^T\right)}^{\vee }\right].$$

and

$$J_r\left(\mathbf{x}\right)=\left[{\left(R^T\frac{\partial R}{\partial x_1}\right)}^{\vee },{\left(R^T\frac{\partial R}{\partial x_2}\right)}^{\vee },{\left(R^T\frac{\partial R}{\partial x_3}\right)}^{\vee }\right].$$

The subscripts r and l denote the side where the partial derivative appears (right or left).

These two Jacobian matrices are related as

$$J_l={\mathit{RJ}}_r.$$ (45)

Relatively simple analytical expressions have been derived by Park [?] for the Jacobian J_l and its inverse when rotations are parameterized as in (44). These expressions are

$$J_l\left(\mathbf{x}\right)=I+\frac{1-\cos \Vert \mathbf{x}\Vert }{\Vert \mathbf{x}{\Vert }^2}X+\frac{\Vert \mathbf{x}\Vert -\sin \Vert \mathbf{x}\Vert }{\Vert \mathbf{x}{\Vert }^3}{X}^2$$ (46)

and

$$J_l^{-1}\left(\mathbf{x}\right)=I-\frac{1}{2}X+\left(\frac{1}{\Vert \mathbf{x}{\Vert }^2}-\frac{1+\cos \Vert \mathbf{x}\Vert }{2\Vert \mathbf{x}\Vert \sin \Vert \mathbf{x}\Vert }\right)X^2.$$

The corresponding Jacobian J_r and its inverse are then calculated using (45) as [Chirikjian 2001]

$$J_r\left(\mathbf{x}\right)=I-\frac{1-\cos \Vert \mathbf{x}\Vert }{\Vert \mathbf{x}{\Vert }^2}X+\frac{\Vert \mathbf{x}\Vert -\sin \Vert \mathbf{x}\Vert }{\Vert \mathbf{x}{\Vert }^3}{X}^2$$

and

$$J_r^{-1}\left(\mathbf{x}\right)=I-\frac{1}{2}X+\left(\frac{1}{\Vert \mathbf{x}{\Vert }^2}-\frac{1+\cos \Vert \mathbf{x}\Vert }{2\Vert \mathbf{x}\Vert \sin \Vert \mathbf{x}\Vert }\right)X^2.$$

Note that

$$J_l=J_r^T.$$

The determinants are

$$\left|\det \left(J_l\right)\right|=\left|\det \left(J_r\right)\right|=\frac{2(1-\cos \Vert \mathbf{x}\Vert )}{\Vert \mathbf{x}{\Vert }^2}.$$

Given a square-integrable function of rotation, f(R) ∈ L²(SO(3)), the proper (invariant) way to integrate using exponential coordinates is

$${\int }_{\mathit{SO}\left(3\right)}f\left(R\right)\mathit{dR}=\frac{1}{8{\pi }^2}{\int }_{\Vert \mathbf{x}\Vert <\pi }f\left(R\mathbf{x}\right)\left|\det J\left(\mathbf{x}\right)\right|d\mathbf{x}$$

where dx = dx₁dx₂dx₃ and J can denote either J_r or J_l. The normalization by 8π² ensures that ∫_SO(3) 1dR = 1.

C The Special Euclidean Group, SE(3)

The Lie algebra se(3) consists of “screw” matrices of the form

$$X=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill -x_3\hfill & \hfill x_2\hfill & \hfill x_4\hfill \\ \hfill x_3\hfill & \hfill 0\hfill & \hfill -x_1\hfill & \hfill x_5\hfill \\ \hfill -x_2\hfill & \hfill x_1\hfill & \hfill 0\hfill & \hfill x_6\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)=\underset{i=1}{\overset{6}{\Sigma }}{x}_i{\tilde{E}}_i.$$ (47)

The matrices {Ẽ_i} form a basis for the set of all such 4×4 screw matrices, and the coefficients {x_i} are all real. The tilde is used to distinguish between these basis elements and those for SO(3). The ∨ operation is defined to extract these coefficients from a screw matrix to form a column vector X^∨ = [x₁, x₂, x₃, x₄, x₅, x₆]^T ∈ IR⁶. The double use of ∨ in the so(3) and se(3) cases will not cause confusion, since the object to which it is applied defines the sense in which it is used.

It will be convenient to define ω= [x₁, x₂, x₃]^T, and v = [x₄, x₅, x₆]^T, so that

$$X^{\vee }=\mathbf{x}=\left(\begin{array}{c}\hfill \omega \hfill \\ \hfill \mathbf{v}\hfill \end{array}\right).$$

It can be shown that [Chirikjian 2009]

$$g\left(X^{\vee }\right)=\exp X=\left(\begin{array}{cc}\hfill R\left(\omega \right)\hfill & \hfill J_l\left(\omega \right)\mathbf{v}\hfill \\ \hfill 0^T\hfill & \hfill 1\hfill \end{array}\right).$$ (48)

This follows from the expression for the matrix exponential given in [Murray, Li and Sastry 1994] and the definition of the SO(3) Jacobian in (46). From the form of (48), it is clear that if g has rotational part R, and translational part t, then the matrix logarithm can be written in closed form as

$$X=\log \left(g\right)=\left(\begin{array}{cc}\hfill \log R\hfill & \hfill J_l^{-1}\left({\left(\log R\right)}^{\vee }\right)\mathbf{t}\hfill \\ \hfill 0^T\hfill & \hfill 0\hfill \end{array}\right),$$

and

$$X^{\vee }=\left(\begin{array}{c}\hfill {\left(\log R\right)}^{\vee }\hfill \\ \hfill J_l^{-1}\left({\left(\log R\right)}^{\vee }\right)\mathbf{t}\hfill \end{array}\right).$$ (49)

The adjoint matrices for SE(3) are

$$\mathit{Ad}\left(g\right)=\left(\begin{array}{cc}\hfill R\hfill & \hfill 0_3\hfill \\ \hfill \mathit{TR}\hfill & \hfill R\hfill \end{array}\right)\in {\mathit{IR}}^{6\times 6}$$

where T^∨ = t and

$$\mathit{ad}\left(X\right)=\left(\begin{array}{cc}\hfill \Omega \hfill & \hfill 0_3\hfill \\ \hfill V\hfill & \hfill \Omega \hfill \end{array}\right)\in {\mathit{IR}}^{6\times 6}$$

where V^∨ = v and Ω^∨ = ω.

The Jacobians for SE(3) using exponential parameters are then

$${𝒥}_l\left(\mathbf{x}\right)=\left[{\left(\frac{\partial g}{\partial x_1}{g}^{-1}\right)}^{\vee },{\left(\frac{\partial g}{\partial x_2}{g}^{-1}\right)}^{\vee },\cdots ,{\left(\frac{\partial g}{\partial x_6}{g}^{-1}\right)}^{\vee }\right].$$

and

$${𝒥}_r\left(x\right)=\left[{\left(g^{-1}\frac{\partial g}{\partial x_1}\right)}^{\vee },{\left(g^{-1}\frac{\partial g}{\partial x_2}\right)}^{\vee },\cdots ,{\left(g^{-1}\frac{\partial g}{\partial x_6}\right)}^{\vee }\right].$$

The right Jacobian for SE(3) in exponential coordinates can be computed from (48) as

$${𝒥}_r\left(\mathbf{x}\right)=\left(\begin{array}{cc}\hfill J_r\omega \hfill & \hfill 0_3\hfill \\ \hfill e^{-\Omega }\frac{\partial }{\partial \omega }\left(J_l\left(\omega \right)\mathbf{v}\right)\hfill & \hfill J_r\omega \hfill \end{array}\right).$$ (50)

where 0₃ is the 3 × 3 zero matrix. It becomes immediately clear that

$$\left|\det \left({𝒥}_r\left(\mathbf{x}\right)\right)\right|=|\det \left(J_r\left(\omega \right)\right){|}^2.$$

Given a square-integrable function of motion, f(g) ∈ L²(SE(3)), the proper (invariant) way to integrate using exponential coordinates is

$${\int }_{\mathit{SE}\left(3\right)}f\left(g\right)\mathit{dg}=\frac{1}{8{\pi }^2}{\int }_{\mathbf{v}\in {\mathit{IR}}^3}{\int }_{\Vert \omega \Vert <\pi }f\left(e^X\right)|\det \left(J_r\left(\omega \right)\right){|}^{2}d\omega d\mathbf{v}.$$

The normalization by 8π² is an artifact of the SO(3) case, which is retained since SE(3) is not compact.