Abstract
We measured accuracy of object identification across illuminations on the basis of color cues. Four similarly shaped real objects, three of the same reflectance, were separated into pairs under distinct colored real lights. Observers were asked to pick the odd object. Correct and incorrect identifications formed systematic patterns that could not be explained by color-constancy, contrast-constancy, inverse-optics or neural-signal matching algorithms. The pattern of results were simulated by an algorithm that purposely made the incorrect assumption that color constancy holds, and used similarity between perceived object colors, along the difference vector between illuminant colors, to identify objects of the same reflectance across illuminants. The visual system may use this suboptimal strategy because the computational costs of an optimal strategy outweigh the benefits of more accurate performance.
Keywords: Color constancy, Object identification, Object recognition, Color algorithms, Opportunistic Bayesian observers
1. Introduction
The human brain creates a world of colored objects and illuminants in which perceived colors are functions of light spectra. For each retinotopic location, this operation requires multiple classes of neurons tuned to different spectral distributions. The cost for this is not only decreased spatial resolution, but also added neural computation. One of the main benefits of these computations is thought to be reliable identification of objects and materials under different lighting conditions (Healey & Slater, 1994; Slater & Healey, 1996), especially when objects do not differ in shape or texture, such as fruits of different degrees of ripeness.
When confronted with a scene like that shown in Fig. 1, observers feel confident that they can divide the scene into sunny and shaded segments. Since the scene is imaged from above, it consists wholly of terrain, and no sources of light are visible. Observers use the geometrical cue of long fairly straight transitions between brighter and darker segments to infer higher probabilities of illuminant change and lower probabilities of material changes. The segments on the brighter and/or yellower sides of these transitions are identified as sunny, based on memory. Despite the fact that segments of the image under sunlight appear yellower and brighter, observers feel confident that they can identify similar foliages from sunny to shady parts of the scene.
Fig. 1.
“Sundance” by Ketchum (1993). Can you identify which parts are sunny and which shady? How? Why do you infer illuminant rather than material changes? Can you identify similar foliages from sunny to shady parts?
The first purpose of this paper is to test this ability with quantitative measurements of the accuracy of identification of real objects/materials across real illuminants. The second purpose of this paper is to identify a simple observer strategy that accounts for both correct and incorrect identifications.
A number of theories have been put forward that could explain observer performance, and if correct would justify observer confidence. The oldest such theory goes under the rubric of “color constancy”, i.e., constancy of subjective appearance. Although the idea predates him, Ives (1912) was the first to show that modeling adaptation to the illuminant as multiplicative changes in independent color channels leads to approximate constancy in chromaticities of object colors, and thus by implication in subjective appearance. Under prolonged adaptation to a single illuminant, such constancies have been shown to hold quantitatively (Bramwell & Hurlbert, 1996; de Almeida, Fiadeiro, Teixeira, Nascimento, & Zaidi, 2007; Smithson & Zaidi, 2004), and to be due to temporally extended but spatially local adaptation processes (Schulz, Doerschner & Maloney, 2006; Smithson & Zaidi, 2004). Since foliage appears yellower under sunlight than in the shade (where the main illuminant is reflected skylight), it is obvious that constancy of color appearance does not hold for scenes with multiple illuminants (Fig. 1).
An alternative is to assume, in an analogy with brightness constancy (Wallach, 1948), that the subjective constancy is not at the level of isolated colors but at the level of color-contrasts or color-differences. Under many conditions, color-contrast is the major determinant of appearance (Shapiro, 2008). Unlike brightness which varies along a single dimension, color is multi-dimensional, so color differences can vary in a multitude of directions, to many of which neurons may be tuned (Gegenfurtner, Kiper, Fenstemaker, & Gegenfurtner, 1997; Kiper, Fenstemaker, & Gegenfurtner, 1997; Lennie, Krauskopf, & Sclar, 1990). Khang and Zaidi (2002) suggested that observers would be generally, but not universally, successful at material identification across illuminants, if they picked materials whose chromaticity difference was parallel to the chromaticity difference between the illuminants. This strategy seemed to account for most correct and incorrect identifications in a post-hoc analysis of their data, but the conditions of their experiments were not sufficient to provide a critical test.
Instead of relying on constancy of percepts, other approaches have built on invariance of physical properties. Since the spectral reflectance of most materials is constant in the short-term (prolonged exposure to light can change the spectral reflectance of many materials, e.g., human skin and fruits), extracting the spectral reflectance of each material would lead to perfect object identification across illuminants (Maloney, 1999). To achieve this purpose, a number of deterministic and probabilistic inverse-optics models have been proposed to first extract the spectrum of the illuminant and then the spectra of materials under the illuminant for a variety of conditions (e.g., Brainard & Freeman, 1997; Maloney & Wandell, 1986). It makes little sense for the human visual system to extract high-dimensional spectra because subsequent color computations would be high-dimensional and costly. However, it is still worthwhile to consider such models as computational, in the sense defined by Marr (1982), and to test for object identification accuracy in situations where recovery of stable surface descriptors would be predicted, such as identical sets of objects under two distinct lights (D'Zmura and Iverson, 1993a, 1993b).
An alternative to the inverse-optics approach is to compare cone-absorptions and subsequent neural signals from objects across spectrally different illuminants. A number of studies have plotted human L, M and S cone-absorptions from a variety of natural and man-made materials under one light against absorptions under a spectrally different light, and found that the points all fall close to straight lines joining the origin to the cone-absorptions of the illuminants (Dannemiller, 1993; Foster & Nascimento, 1994; Zaidi, Spehar, & DeBonet, 1997). A shift in illuminant spectra is thus associated with a neural invariant that can be described as a diagonal transform in cone-absorptions, an affine transform in second-stage neural signals (Zaidi et al., 1997), and preservation of rank-orders of cone-absorptions (Dannemiller, 1993) and cone-contrast ratios (Foster & Nascimento, 1994). This invariant explains why Ives-type discounting of the illuminant is computationally successful for color constancy, and why temporally extended adaptation in individual cones leads to color constancy under single illuminants (de Almeida et al., 2007; Smithson, 2005; Smithson & Zaidi, 2004; Zaidi, 2005). More interestingly, for multiple illuminant cases like Fig. 1, many affine-deformable matching algorithms can be devised that can successfully identify reflectances across illuminants by relying on the affine transform as an invariant (Zaidi, 1998, 2001).
All four classes of theories predict that identification performance should be generally accurate, but make different predictions about the nature of systematic identification errors. We introduce a method using real objects and lights that provides a general test for all of these theories.
2. Color-based object identification
Observers looked with both eyes at the apparatus pictured in Fig. 2(a). They were informed that the backgrounds in the two boxes were made from the same material, but the lights were spectrally distinct. A pair of real objects was presented in each box. Three of the four objects were made from the same material, and the observer was asked to identify the object made from the odd material. Readers can try out the same experiment and pick the numbers corresponding to their choice of odd materials in Fig. 2(a) and then in (b). In Fig. 3(a) and (b), all four objects have been moved to the same box, and readers can compare their picks with the correct choices (Objects # 1 and #4, respectively). Readers who made incorrect choices, should be aware that this demo has been presented to many audiences, and the vast majority of observers make incorrect choices. Given that in Fig. 2(a), neither #1 nor #2 looks exactly like #s 3 and 4, readers are urged to introspect about their identification strategy and compare it to the strategies discussed later in the paper.
Fig. 2.
(a) Observer's view of the apparatus. The pair of boxes are lined with the same materials but the lights in them differ spectrally. Three of the objects are made from the same material (Standards), while one is made from a material of a different color (Test). Observers (and readers) are asked to pick the object number corresponding to the odd material. (b) Another view of the apparatus. The Test is now under a different light than in the panel above.
Fig. 3.

(a) The objects in Fig. 2(a) have all been moved to one box revealing that the odd object was #1. (b) The objects in Fig. 2(b) have all been moved to one box revealing that the odd object was #4.
2.1. Methods
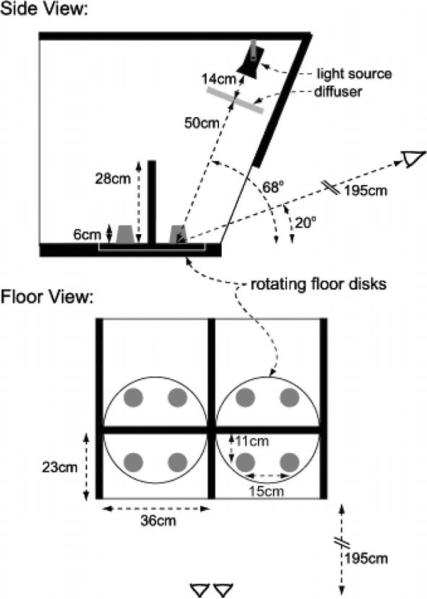
Schematics of the side view and the floor of the apparatus are shown in Fig. 4. Complete details of the apparatus can be found in Robilotto and Zaidi (2006). The observer sat in front of the apparatus in a dark room, was allowed to take as much time as needed on each trial, and given one practice session before collecting data. Feedback about correct or incorrect answers was not provided during the practice or actual sessions.
Fig. 4.
Side and top plans of the apparatus. For details see Robilotto and Zaidi (2006).
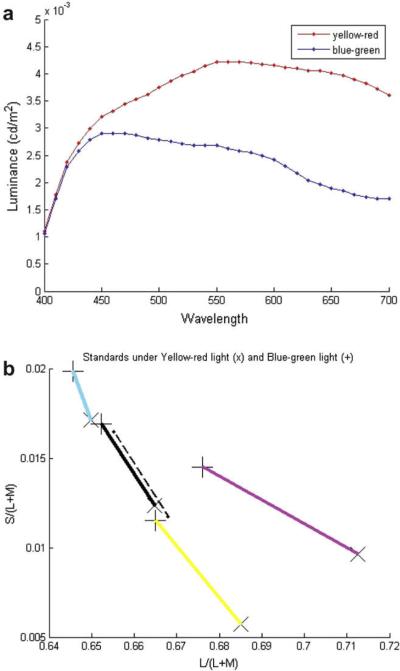
We would have liked to use the spectra of Sunlight and Skylight (Taylor & Kerr, 1941) for the two illuminants, but given the limitations of available color-correcting filters, we settled for two lights whose spectra (measured directly with a Photo-Research SpectraScan PR-704 at 2 nm intervals) are shown in Fig. 5(a), and whose MacLeod and Boynton (1979) chromaticities are shown in Fig. 5(b). The spectra were obtained by filtering 50-W SoLux light bulbs (color temperature = 4700 K; beam-spread = 36°; Tailored Lighting, Rochester, NY) with Kodak color-correcting filters, and passing the lights through holographic diffusers to ensure uniform illuminant intensity (diffusion angles = 30°; Physical Optics Corporation, Torrance, CA). The lamps were not visible to the observers. In isolation, one of the lights appeared blue-green and the other yellow-red, as is expected from their chromaticities in the Macleod–Boynton diagram where the achromatic point is at (.66, .015).
Fig. 5.
(a) Spectra of the yellow-red and blue-green lights. (b) MacLeod-Boynton chromaticity diagram. The dashed line connects the chromaticity of the illuminants. The colored lines connect the chromaticities of each Standard under the two lights.
The sides, backs, and floors of the two boxes were covered with a pattern of colored ellipses and lines that averaged to a gray under neutral light. The three objects in each trial that are made of identical materials, are called Standards, the odd object is called the Test. All objects in this study were made by printing chosen colors on a laser color-printer. Given nonlinearities in combinations of inks and the variations in inks from batch to batch, we found that even the use of professional inks did not allow us to calibrate the printer to the accuracy required by vision experiments. Therefore, we used the best approximate color coordinates for the printer, but the spectrum of light reflected by each paper under each illuminant was measured directly with a Photo-Research SpectraScan PR-704 at 2 nm intervals using flat papers in a fixed stand. The papers were rolled to make cylinders. The Standards were chosen to sample different parts of color space. We used four Standards, gray, cyan, magenta, and yellow in appearance. Their chromaticities under each of the lights (converted from spectral measurements) are shown in Fig. 5(b). Besides the gray standard we used standards close to the printer's primaries because this provided colors of reasonable saturation spread over the chromaticity diagram, which allowed a range of tests to be printable. We intended to derive discrimination and identification thresholds as was done by Khang and Zaidi (2002) and Robilotto and Zaidi (2004), so a number of Tests were compared to each Standard, some of which we expected not to be reliably discriminable from the Standard (Total number of Tests = 120). We intended to use Tests that differed from the Standards along a color line parallel to the line joining the illuminant chromaticities or orthogonal to it, but given the limitations of control over colored dye mixtures, we could only approximate such lines. To use the same Tests under both lights, the Tests were distributed in chromaticity on both sides of the Standards. Each Standard–Test–Illuminant condition was run 10 times per observer. Each session consisted of a trial each for all conditions. Given the limitations of stimulus generation and data collection (each trial required the experimenter to manually change the stimuli out of the observer's sight), it was not possible to collect sufficient data to estimate thresholds.
Two color-normal female observers were run in this experiment. They were informed about the purpose of the experiment only at the conclusion of data collection. Observer RH had previously participated in lightness constancy experiments in a different institution. Observer KS had previously participated in a color difference study using a CRT.
2.2. Results
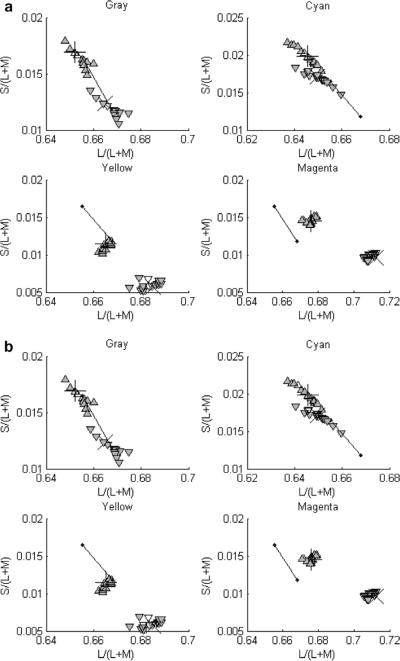
When observers are asked to identify the odd object, they first have to decide which box is more likely to contain two objects that differ in materials. For any Test–Standard–Illuminant combination, if the observer chooses an object in the correct box for at least 8 out of 10 trials, then this is sufficient to reject the null hypothesis of chance selection of boxes with a probability greater than .95, and to accept that the observer can reliably discriminate between that Test and that Standard under that Illuminant (Using a binomial distribution with p = .5). The discrimination results for the two observers are shown in Fig. 6(a) and (b). The points flanking the chromaticity of each Standard are the chromaticities of all the Tests. A few of the Tests could not be discriminated from the Standards, so identification performance for these Tests is not relevant, and they are left out of the subsequent analysis.
Fig. 6.
Each panel presents discrimination results for each Standard under each of the two lights. The line connects the chromaticities of the illuminants. This line has the same coordinates in all four panels, so it provides a landmark for the chromaticities of the other stimuli. The + and X represent the chromaticities of the Standard under the blue-green and yellow-red lights, respectively. The triangles pointing up are the chromaticities of the Tests under the blue-green light, and the triangles pointing down are the chromaticities of the Tests under the yellow-red light. The gray triangles represent Tests that could be reliably discriminated from the Standards (p > .95), whereas the open triangles represent Tests that could not be reliably discriminated from the Standards. (a) Observer RH. (b) Observer KS.
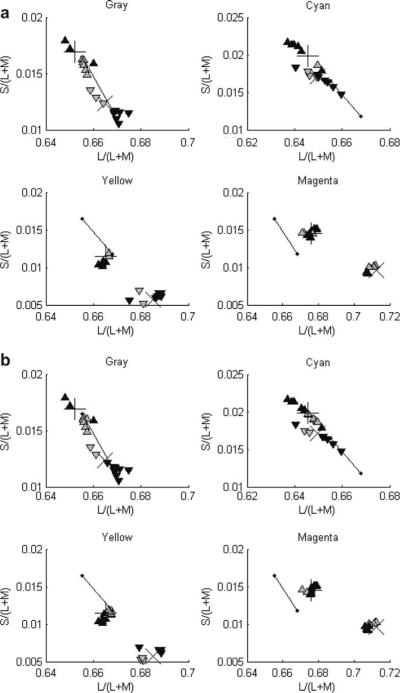
If observers can discriminate between two objects in one of the two boxes, then they have to decide which object in that box is less likely to be made from the same material as the two objects in the other box. In the data analysis, the Tests that could be reliably discriminated as derived from the proportion of box-correct responses can then be divided into three classes according to the proportion of object-correct responses. If the odd object was picked correctly on enough trials so that the null hypothesis of chance selection of objects given the correct box can be rejected with a probability greater than .95 with a one-tailed test, then the Test was considered to be correctly identified. Since we only considered objects that were reliably discriminated, i.e., 8, 9 or 10 box-correct responses out of 10, using the binomial distribution with p = .5, this means identifying the Test object correctly for at least 8 out of the 10, 7 out of the 9 or 6 out of the 8 box-correct trails. On the other hand, if the Standard in the correct box was incorrectly chosen as the odd object on enough trials that the null hypothesis of chance selection of objects given the correct box can be rejected with a probability greater than .95 on the other tail, then the Test was considered to be reliably misidentified. If the null hypothesis cannot be rejected on either tail, then despite being discriminable from the Standard, the Test was considered neither correctly identified nor misidentified. Identification results are plotted in Fig. 7(a) and (b)
Fig. 7.
Each panel presents identification results for each Standard under each of the two lights for those Tests that could be reliably discriminated. Symbols are used in the same manner as Fig. 6, except that dark triangles represent Tests that were correctly identified (p > .95), gray triangles represent Tests that were misidentified (p > .95). Tests that were neither correctly identified nor misidentified, clustered around the Standard, and are not shown. (a) Observer RH. (b) Observer KS.
There are a number of patterns that stand out in the results. First, identification across illuminants is more difficult than discrimination within illuminants, as some Tests that were reliably discriminated from the Standards were neither correctly identified nor misidentified. This is unlikely to be a deficit in chromatic discrimination which survives gaps in time and space (Danilova & Mollon, 2006; Sachtler & Zaidi, 1992). These points have been omitted from Fig. 7 to highlight the important results, but can be inferred by comparisons to Fig. 6 Second, there are a significant number of reliable misidentifications where the Standard is chosen as the odd object. Third, as would be expected, at sufficient color distances from the Standard, Tests on both sides of the Standard along a color line are reliably identified. Fourth, and most importantly, close to the color of the Standard, misidentified and correctly identified Tests tend to fall on opposite sides, and to switch sides across illuminants.
2.3. Implications
These results have a number of implications for theories of color constancy. First, since the Standard object was present on every trial, if subjective color constancy existed in this situation, the observer should have no problem picking the Test as the odd reflectance on every trial where it can be discriminated from the Standard under the same light. It is possible that due to color adaptation, Standards across the two light appear more similar than they would without adaptation, but clearly this partial adjustment is not sufficient to support precise object identification. Similarly, to the extent that contrast-constancy holds, it too is not sufficient. The result that misidentified objects switch sides around the Standard under the two illuminants, serves to rule out a number of models. If Ives-type adaptation underlies color constancy, then certain reflectances will not be “corrected” as well as others. However, if this is the main problem, the same materials should be misidentified under either illuminant, and that is clearly not the case.
In addition, there was sufficient information in the scene for both the inverse-optics and the neural-invariants based matching approaches to solve the identification problem. D'Zmura and Iverson (1993a, 1993b) showed that recovery of constant surface descriptors is possible for a system with three classes of photoreceptors, given three distinct reflectances under two different illuminants, if surface reflectances and illuminant spectra are well described by three-dimensional linear models. Given the variegated backgrounds, the conditions in Exp 1 consist of two illuminants and many more than three reflectances, so reflectance recovery is formally possible, if spectra are three-dimensional. Similarly, Zaidi (1998) showed that when the same collection of reflectances is presented under two illuminants, the chromaticities of the objects are related by an affine transform across illuminants, and it is easy to identify reflectance correspondence by estimating parameters of the affine transform. This is true for Lambertian surfaces and non-Lambertian surfaces in constant positions (Zaidi, 2001). However, since adequate representation of surface spectra require more than three dimensions (Nascimento, Foster, & Amano 2005), departures from perfect reflectance identification in the inverse-optics approaches could be attributed to imperfect representation. Similarly, identification errors would be predicted for those materials whose reflectances deviate from the affine transform in the matching algorithms (Zaidi, 1998). However, such deviations cannot explain the result that different sets of reflectances are systematically misidentified under different illuminants. In addition, the result that the patterns of identifications and misidentifications are similar for color lines parallel or orthogonal to the difference between the illuminant chromaticities, rules out the idea that misidentifications are caused by object matches on color lines parallel to the illuminant change (Khang & Zaidi, 2002).
Given the carnage of existing theories above, we decided to test whether a simple perceptual strategy could account for the distinct patterns of identifications and misidentifications under the different illuminants. In similar experiments on achromatic objects, Robilotto and Zaidi (2004) showed that perceived relative brightness could account for lightness identification performance. In the next section, we test whether perceived relative colors can account for color based identification performance.
3. Relative color percepts and object identification
Our purpose in measuring relative colors is to test the relation of correct identifications (and misidentifications) to relative color categories. Besides the two observers from Exp 1, to insure that judgments in the relative measurements were not contaminated by the identification judgments, we also used a different observer (the first author) for the categorizations. Measuring perceived relative colors is tricky, and the choice of color names can be idiosyncratic. When a red material is compared to an orange one, most observers call the orange yellower than the red, but the red redder than the orange. Similarly pink is called whiter than red, but red is called redder than pink. Observers are more likely to report increments of hues rather than decrements, and inferring decrements, e.g., on the basis of opponent colors, is problematic. Asking observers whether a yellow (or pink) is greener than a red, elicits looks of incomprehension. After piloting a number of different procedures, we chose the following because it gave reasonable concordance across observers. To measure relative color percepts for our experimental objects, we used only one of the boxes at a time. A Standard and a Test were placed in the box, and the observer was instructed to say whether the Test was predominantly greener, redder, yellower, or bluer than the Standard. Observer QZ's results are shown in Fig. 8 It is interesting that the observer chose to use yellower–bluer distinctions for the Tests that were compared to the Gray and Magenta Standards and redder–greener distinctions for the Tests that were compared to the Cyan and Yellow Standards. This implies that the salience of relative hues depend not only on color direction, but also on location in chromaticity space. In general, Tests separated into opposing relative color groups around the chromaticity of the Standard, but there were exceptions, particularly when the color-line of Tests did not pass through the chromaticity of the Standard. Also, in general, the division was similar for each Standard under both illuminants. Results of the other two observers were similar to Observer QZ's, differing mainly in the number of Tests each observer perceived as too similar to the Standard for reliable classification.
Fig. 8.
Each panel presents relative color-categorization results for each Standard under each of the two lights. Symbols are used in the same manner as Fig. 6, except that the color of the triangle represents the perceived color of the Test relative to the color of the Standard.
3.1. Color-similarity based object-identification algorithm
In explaining reflectance identification (and misidentification) of achromatic objects under achromatic lights, we showed that observers do not have any access to surface albedos, so they use similarity in perceived brightness as a surrogate for reflectance similarity (Robilotto & Zaidi, 2004), which would be an optimal strategy only if lightness constancy was a valid assumption. In the present experiment, the difference between the illuminants is spectral and not just intensive. To test whether observers identify objects across colored illuminants on the basis of color similarity, we tested the following algorithm which gives primacy to similarity along the color axis between the two illuminants:
STEP 1. Identify the illuminant on the test (It) by finding the side on which the two objects have different colors.
STEP 2. Compare the colors of the backgrounds to judge the change in color from It to the illuminant on the two Standards (Is).
STEP 3. Pick as the odd object, the object that is most dissimilar to the others when the relative colors are projected onto the perceived It – Is color direction.
The algorithm can be expressed in terms of perceived relative colors as follows. For Tests under the blue-green light, e.g., Fig. 2(a), the algorithm predicts that Tests perceived as bluer or greener than the Standard under the same light, will be picked correctly as the odd object, but Tests perceived as yellower or redder than the Standard under the same light, will not be picked as the odd object, unless they are perceived to be at least as yellow or red as the Standards under the yellow-red light in the other box. For Tests under the yellow-red light, e.g., Fig. 2(b), Tests perceived as yellower or redder than the Standard under the same light, will be picked correctly as the odd object in the identification experiment, but Tests perceived as bluer or greener than the Standard under the same light, will not be picked as the odd object unless they are perceived to be at least as blue or green as the Standards under the blue-green light in the other box.
We used the relative color categorization results to predict correct and incorrect object identifications by using the above algorithm, and compared them to the identification results. The cross-tabulation of predicted and observed identifications is shown in Table 1a and Table 1b. Combined over the two observers RH and KS, of the Tests that could be discriminated reliably from the Standard in Exp 1 and Exp 2, 86% of correct identifications and 96% of misidentifications were predicted correctly by the algorithm using observer QZ's categorizations. These numbers are similar to those predicted correctly when each observer's identifications are compared with their own categorizations, i.e., 88% of correct identifications and 93% of misidentifications for he two observers combined. It is clear that the similarity-based algorithm accounts for most of the identification results.
Table 1a.
Relative color categorization results of QZ were used in the similarity-based algorithm to predict object identification results for RH and KS
| Predicted | Observed |
|||
|---|---|---|---|---|
| I | G | M | Total | |
| I | 80 | 2 | 2 | 84 |
| M | 13 | 16 | 48 | 77 |
| Total | 93 | 18 | 50 | 161 |
I, correct identification; M, misidentification; G, neither correct nor incorrect identification.
Table 1b.
Relative color categorization results of RH and KS were used in the similarity-based algorithm to predict their own object identification results
| Predicted | Observed |
|||
|---|---|---|---|---|
| I | G | M | Total | |
| I | 65 | 5 | 3 | 73 |
| M | 9 | 12 | 42 | 63 |
| Total | 74 | 17 | 45 | 136 |
I, correct identification; M, misidentification; G, neither correct nor incorrect identification.
4. Discussion
The voluminous literature on color constancy has been summarized in many places (e.g., Brainard, 2004). Interest in color constancy is generally implicitly, but sometimes explicitly, driven by the putative role of color in object recognition and identification (Hurlbert, 1998), but the methods have generally been confined to subjective appearance measurements (Foster, 2003). In this paper, we have directly tackled object identification/recognition on the basis of color, using a forced-choice performance measure. This performance may incorporate volitional judgments as well as perceptual factors. In fact, the proposed similarity-based strategy requires perceiving the relative colors of the illuminants, and the relative colors of the objects, and then making judgments on the basis of perceived similarities of color differences.
In perceiving colors of illuminants, Khang and Zaidi (2004) showed that for scenes with a single illuminant, observers use the spatial average to infer the color of the illuminant. In the present study, the achromatic spatial average of the backgrounds would give decent estimates of the illuminant colors. It would be interesting to see if identification performance would change if the average color of the background was not achromatic, and if this would be due to biased estimates of the color difference between the illuminants.
In perceiving colors of objects, adaptation to a single illuminant does lead to the color of a material appearing similar in different lights, but complete adaptation to a single illuminant is unlikely to occur in natural settings, and cognitive factors seem to play a part in even simple color reports (Smithson, 2005; Zaidi, 2005). A role is also often suggested for simultaneous color induction in color constancy, but the presence of high spatial frequencies in variegated color backgrounds drastically reduces the amount of induction on uniformly colored objects (Hurlbert, & Wolf, 2003; Zaidi, 1999; Zaidi, Yoshimi, Flanigan, & Canova, 1992)
The use of a suboptimal similarity-based strategy by observers raises some important questions. First, why do observers use color similarity for object identification despite the demonstrable absence of color constancy? It is a common experience that the same material looks different indoors than outdoors, so a color match across illuminants is actually a more reliable indicator of material difference than of material identity, and for optimal functioning, the visual system should learn to use such false matches. Second, why are other more accurate strategies not used? As stated earlier, there is sufficient information in the experimental situation in this study, that simple algorithms using justifiable prior assumptions could solve the identification problem accurately. It remains to be explained why the visual system does not learn such strategies, when it seems to have learned quite complex strategies for solving stereo correspondence, including the use of false matches (Read & Cumming, 2007). Is there a lack of negative reinforcement for wrong decisions because objects that are misidentified across illuminants have similar enough properties to suffice for each other, or was there little evolutionary pressure because changes in natural lights are predominantly along the yellow–blue axis (Mollon, 2006) and do not hamper identification across the red–green axis that defines the distinction between many ripe and unripe fruits. Third, how does this suboptimal performance relate to recent attempts to model human perceptual performance in terms of optimal statistical models (e.g., Knill, & Richards, 1996)? It is possible to think of the visual system in a more general way than as just a combiner of prior probabilities and data likelihoods. In choosing between strategies, the visual system could behave as a statistically optimal model selector which incorporates Occam's razor so that the operations or costs of computations are weighted in strategy selection (MacKay, 2003). If more accurate algorithms require more computations than the similarity-based algorithm, the additional costs may outweigh the benefits of improved identification, especially if there is time–pressure and more important computations need to be completed. A much simpler but almost optimal strategy would be preferred to a computationally intensive optimal strategy by such an opportunistic Bayesian.
Looking ahead, this study shows that it is worthwhile to directly study color-based object identification/recognition, because it raises interesting issues that go beyond questions of constant subjective percepts. The resolution of some of these issues may provide clues to the efficient functioning of the visual system in areas broader than color perception.
Acknowledgments
We thank Robin and Katherine for hours of patient careful observation. This work was supported by NEI Grants EY07556 and EY13312 to Qasim Zaidi.
References
- Brainard DH. Color constancy. In: Chalupa L, Werner J, editors. The visual neurosciences. MIT Press; 2004. pp. 948–961. [Google Scholar]
- Brainard DH, Freeman WT. Bayesian color constancy. Journal of the Optical Society of America A. 1997;14(7):1393–1411. doi: 10.1364/josaa.14.001393. [DOI] [PubMed] [Google Scholar]
- Bramwell DI, Hurlbert AC. Measurements of colour constancy using a forced choice matching technique. Perception. 1996;25:229–241. doi: 10.1068/p250229. [DOI] [PubMed] [Google Scholar]
- Danilova MV, Mollon JD. The comparison of spatially separated colours. Vision Research. 2006;46(6–7):823–836. doi: 10.1016/j.visres.2005.09.026. [DOI] [PubMed] [Google Scholar]
- Dannemiller JL. Rank orderings of photoreceptor photon catches from natural objects are nearly illuminant-invariant. Vision Research. 1993;33:131–140. doi: 10.1016/0042-6989(93)90066-6. [DOI] [PubMed] [Google Scholar]
- de Almeida VMN, Fiadeiro PT, Teixeira M, Nascimento SMC, Zaidi Q. Color constancy of real 3-D objects and the roles of spatial and temporal mechanisms. International color vision society, annual meeting; Belem, Brazil. 2007. [Google Scholar]
- D'Zmura M, Iverson G. Color constancy. I. Basic theory of two-stage linear recovery of spectral descriptions for lights and surfaces. Journal of the Optical Society of America A. 1993a;10:2148–2165. doi: 10.1364/josaa.10.002148. [DOI] [PubMed] [Google Scholar]
- D'Zmura M, Iverson G. Color constancy. II. Results for two-stage linear recovery of spectral descriptions for lights and surfaces. Journal of the Optical Society of America A. 1993b;10:2166–2180. doi: 10.1364/josaa.10.002166. [DOI] [PubMed] [Google Scholar]
- Foster DH. Does colour constancy exist? Trends in Cognitive Sciences. 2003;7(10):439–443. doi: 10.1016/j.tics.2003.08.002. [DOI] [PubMed] [Google Scholar]
- Foster DH, Nascimento SMC. Relational colour constancy from invariant cone-excitation ratios. Proceedings of the Royal Society of London Series B Biological Sciences. 1994;257:115–121. doi: 10.1098/rspb.1994.0103. [DOI] [PubMed] [Google Scholar]
- Gegenfurtner KR, Kiper DC, Levitt JB. Functional properties of neurons in macaque area V3. Journal of Neurophysiology. 1997;77:1906–1923. doi: 10.1152/jn.1997.77.4.1906. [DOI] [PubMed] [Google Scholar]
- Healey G, Slater D. Global color constancy: Recognition of objects by use of illumination-invariant properties of color distributions. Journal of the Optical Society of America A. 1994;11:3003. [Google Scholar]
- Hurlbert AC. Computational models of colour constancy. In: Walsh V, Kulikowski J, editors. Perceptual constancy: Why things look as they do. Cambridge University Press; 1998. pp. 283–322. [Google Scholar]
- Hurlbert A, Wolf K. Color contrast: A contributory mechanism to color constancy. Progress in Brain Research. 2003;144:147–160. doi: 10.1016/s0079-6123(03)14410-x. [DOI] [PubMed] [Google Scholar]
- Ives HE. The relation between the color of the illuminant and the color of the illuminated object. Transactions of Illumination Engineering Society. 1912;7:62–72. Reprinted in Color Research and Application 20, 70–75 (1995) [Google Scholar]
- Ketchum RG. The legacy of wilderness: The photographs of Robert Glenn Ketchum. Aperture Foundation; New York: 1993. [Google Scholar]
- Khang BG, Zaidi Q. Cues and strategies for color constancy: Perceptual scission, image junctions and transformational color matching. Vision Research. 2002;42(2):211–226. doi: 10.1016/s0042-6989(01)00252-8. [DOI] [PubMed] [Google Scholar]
- Khang BG, Zaidi Q. Illuminant color perception of spectrally filtered spotlights. Journal of Vision. 2004;4(9):680–692. doi: 10.1167/4.9.2. [DOI] [PubMed] [Google Scholar]
- Kiper DC, Fenstemaker SB, Gegenfurtner KR. Chromatic properties of neurons in macaque area V2. Visual Neuroscience. 1997;14:1061–1072. doi: 10.1017/s0952523800011779. [DOI] [PubMed] [Google Scholar]
- Knill DC, Richards W. Perception as Bayesian inference. Cambridge University Press; 1996. [Google Scholar]
- Lennie P, Krauskopf J, Sclar G. Chromatic mechanisms in striate cortex of macaque. Journal of Neuroscience. 1990;10:649–669. doi: 10.1523/JNEUROSCI.10-02-00649.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay DJC. Information theory, inference, and learning algorithms. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- MacLeod DIA, Boynton RM. Chromaticity diagram showing cone excitation by stimuli of equal luminance. Journal of the Optical Society of America A. 1979;69:1183–1187. doi: 10.1364/josa.69.001183. [DOI] [PubMed] [Google Scholar]
- Maloney LT. Physics-based approaches to modeling surface color perception. In: Gegenfurtner KR, Sharpe LT, editors. Color vision: From genes to perception. Cambridge University Press; Cambridge, UK: 1999. pp. 387–422. [Google Scholar]
- Maloney LT, Wandell BA. Color constancy: A method for recovering surface spectral reflectance. Journal of the Optical Society of America A. 1986;3(1):29–33. doi: 10.1364/josaa.3.000029. [DOI] [PubMed] [Google Scholar]
- Marr D. Vision. W. H. Freeman; San Francisco, CA: 1982. [Google Scholar]
- Mollon J. Monge: The Verriest lecture. Visual Neuroscience. 2006;23(3–4):297–309. doi: 10.1017/S0952523806233479. [DOI] [PubMed] [Google Scholar]
- Nascimento SM, Foster DH, Amano K. Psychophysical estimates of the number of spectral-reflectance basis functions needed to reproduce natural scenes. Journal of the Optical Society of America. A, Optics, Image Science, and Vision. 2005;22(6):1017–1022. doi: 10.1364/josaa.22.001017. [DOI] [PubMed] [Google Scholar]
- Read JC, Cumming BG. Sensors for impossible stimuli may solve the stereo correspondence problem. Nature Neuroscience. 2007;10:1322–1328. doi: 10.1038/nn1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robilotto R, Zaidi Q. Limits of lightness identification for real objects under natural viewing conditions. Journal of Vision. 2004;4(9):779–797. doi: 10.1167/4.9.9. [DOI] [PubMed] [Google Scholar]
- Robilotto R, Zaidi Q. Lightness identification of patterned three-dimensional real objects. Journal of Vision. 2006;6(1):18–36. doi: 10.1167/6.1.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachtler W, Zaidi Q. Chromatic and luminance signals in visual memory. Journal of the Optical Society of America A. 1992;9:877–894. doi: 10.1364/josaa.9.000877. [DOI] [PubMed] [Google Scholar]
- Schultz S, Doerschner K, Maloney LT. Color constancy and hue scaling. Journal of Vision. 2006;6:1102–1116. doi: 10.1167/6.10.10. [DOI] [PubMed] [Google Scholar]
- Shapiro AG. Separating color from color contrast. Journal of Vision. 2008;8:1–18. doi: 10.1167/8.1.8. [DOI] [PubMed] [Google Scholar]
- Slater D, Healey G. The illumination-invariant recognition of 3D objects using local color invariants. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1996;18(2):206–210. [Google Scholar]
- Smithson HE. Sensory, computational and cognitive components of human colour constancy. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 2005;360:1329–1346. doi: 10.1098/rstb.2005.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smithson H, Zaidi Q. Colour constancy in context: Roles for local adaptation and levels of reference. Journal of Vision. 2004;4(9):693–710. doi: 10.1167/4.9.3. [DOI] [PubMed] [Google Scholar]
- Taylor AH, Kerr GP. The distribution of energy in the visible spectrum of daylight. Journal of the Optical Society of America. 1941;31:3. [Google Scholar]
- Wallach H. Brightness constancy and the nature of achromatic colors. Journal of Experimental Psychology. 1948;38:310–324. doi: 10.1037/h0053804. [DOI] [PubMed] [Google Scholar]
- Zaidi Q. Identification of illuminant and object colors: Heuristics based algorithms. Journal of the Optical Society of America A. 1998;15:1767–1776. doi: 10.1364/josaa.15.001767. [DOI] [PubMed] [Google Scholar]
- Zaidi Q. Color and brightness induction: From Mach bands to 3-D configurations. In: Gegenfurtner K, Sharpe L, editors. Color vision: From genes to perception. Cambridge University Press; New York: 1999. pp. 317–344. [Google Scholar]
- Zaidi Q. Color constancy in a rough world. Color Research and Application. 2001;26:S192–S200. [Google Scholar]
- Zaidi Q. The role of adaptation in color constancy. In: Clifford C, Rhodes G, editors. Fitting the mind to the world adaptation and aftereffects in high-level vision advances in visual cognition series. Vol. 2. Oxford University Press; 2005. pp. 103–131. [Google Scholar]
- Zaidi Q, Spehar B, DeBonet JS. Color constancy in variegated scenes: The role of low-level mechanisms in discounting illumination changes. Journal of the Optical Society of America A. 1997;14:2608–2621. doi: 10.1364/josaa.14.002608. [DOI] [PubMed] [Google Scholar]
- Zaidi Q, Yoshimi B, Flanigan N, Canova A. Lateral interactions within color mechanisms in simultaneous induced contrast. Vision Research. 1992;32:1695–1707. doi: 10.1016/0042-6989(92)90162-c. [DOI] [PubMed] [Google Scholar]