Young’s Modulus Reconstruction for Radio-frequency Ablation Electrode-induced Displacement Fields: A Feasibility Study

Abstract

Radiofrequency (RF) ablation is a minimally invasive treatment for tumors in various abdominal organs. It is effective if good tumor localization and intra-procedural monitoring can be done. In this paper, we investigate the feasibility of using an ultrasound-based Young’s modulus reconstruction algorithm to image an ablated region whose stiffness is elevated due to tissue coagulation. To obtain controllable tissue deformations for abdominal organs during and/or intermediately after the RF ablation, the proposed modulus imaging method is specifically designed for using tissue deformation fields induced by the RF electrode. We have developed a new scheme under which the reconstruction problem is simplified to a two-dimensional problem. Based on this scheme, an iterative Young’s modulus reconstruction technique with edge-preserving regularization was developed to estimate the Young’s modulus distribution. The method was tested in experiments using a tissue-mimicking phantom and on ex vivo bovine liver tissues. Our preliminary results suggest that high contrast modulus images can be successfully reconstructed. In both experiments, the geometries of the reconstructed modulus images of thermal ablation zones match well with the phantom design and the gross pathology image, respectively.

I. Introduction

Radiofrequency (RF) ablation is receiving increasing attention as a minimally invasive treatment for tumors in various organs, such as the liver, kidney and prostate [1-5]. During RF ablation, an interstitial electrode delivers high frequency electric current (~500 kHz) to a targeted zone. Heat generated by the flow of current and ionic agitation is conducted into the surrounding tissue, ultimately causing coagulative necrosis. While effective, the adoption of RF ablation is hampered by the lack of a reliable imaging modality to effectively localize the tumor and monitor treatment progression [3, 6]. Attempts to monitor ablation with conventional B-mode ultrasound have been largely unsuccessful. Hyperechoic areas caused by micro-bubbles and gas formed during tissue heating have been used as a surrogate for the ablation zone but do not correlate well with the actual ablation zone [7]. In addition, these hyperechoic areas gradually disappear within 30 minutes after ablation, thereby making post-treatment evaluation difficult. Computed Tomography (CT) has also been used to monitor RF ablation procedures [8]. However, repeated exposure to ionizing radiation to both the physician and patient hamper the use of CT to provide real-time guidance during the treatment. Although Magnetic Resonance Imaging (MRI) generally provides excellent contrast between tumor and normal tissue, and can be used to monitor thermal ablation therapies [3, 9, 10], this modality is expensive and not easily incorporated into real-time or near real-time guidance. Moreover, the availability of magnetically-compatible RF ablation equipment and interventional MRI suites is still limited.

During RF ablation, protein denaturation during heating results in an increase in the elastic modulus of tissue [11]. Therefore, thermal ablation zones appear to be stiffer than the surrounding untreated tissue and can be differentiated by elasticity imaging methods. Thus, elasticity imaging has emerged as a modality that can be used to assess the dimensions, areas and volumes of thermal ablation zones [12, 13].

Methods for estimating tissue strain and elastic constants (e.g. shear or Young’s modulus, Poison’s ratio) are being developed, and many are summarized in several review papers [14-17]. Among them, ultrasonic strain imaging is a technique that emulates the manual palpation technique used to determine differences in tissue stiffness. With strain imaging, an ultrasound transducer is used to scan an object within a ROI both before and after an applied deformation. Resulting tissue displacements are then estimated by comparing the pre- and post-deformation echo fields. Object strain and/or elastic constants (e.g. shear or Young’s modulus) can then be computed from the estimated displacement field. Compared to strain, a relative measure, the Young’s or shear modulus values are intrinsic material properties of the tissue being studied, thereby providing unambiguous information of tissue elasticity [18]. Furthermore, the modulus of the treated tissue is believed to be related to the ablation temperature [13, 19, 20]. Therefore, estimating the Young’s modulus in this case may potentially provide additional information to monitor and to quantitatively evaluate the formation of thermal necrosis.

One of challenges to using ultrasound-based modulus imaging techniques in abdominal organs is that controllable displacements or deformations are difficult to be applied to the site being imaged. It is well understood (e.g. [21, 22]) that large errors among displacement estimates obtained from complex in vivo tissue motion may significantly hamper our efforts in obtaining accurate modulus images. To overcome this, we adopted a RF electrode displacement method [12]. In this method, controllable and reproducible local deformation of tissue is achieved by pulling or pushing the RF electrode from which forces are transmitted across the tissue being imaged through the adherence of treated soft tissue to the metal electrode [23]. Strain images from in vivo experiments [12] have demonstrated the effectiveness of this method. However, this method has not been used for modulus imaging.

The purpose of this study was to assess the feasibility of estimating Young’s moduli of thermal ablation zones using RF ablation electrode-induced displacement fields in 2-D image planes. In this paper, we first describe a manner by which the complex three-dimensional mechanical interaction between the RF ablation electrode and surrounding tissue can be simplified using a two-dimensional approximation. Keys in this approximation are the assumptions that the RF ablation electrode is bound to the treated tissue and the perturbation provided by the electrode can be accurately enforced as displacement boundary conditions during modulus reconstruction. Using three-dimensional finite element simulations we recently demonstrated that the above-mentioned 2-D approximation retains sufficient accuracy in terms of the patterns of tissue deformation (i.e. displacement and strain) [24]. Based on this approximation, we formulate an iterative modulus reconstruction technique to image tissue moduli using 2D axial (parallel to the acoustic beam direction) displacement estimates. Finally, we tested the proposed method with ultrasound data collected from a tissue-mimicking (TM) ablation phantom and ablated ex vivo bovine liver tissues.

II. Materials and Methods

A. Tissue Mimicking (TM) Ablation Phantom

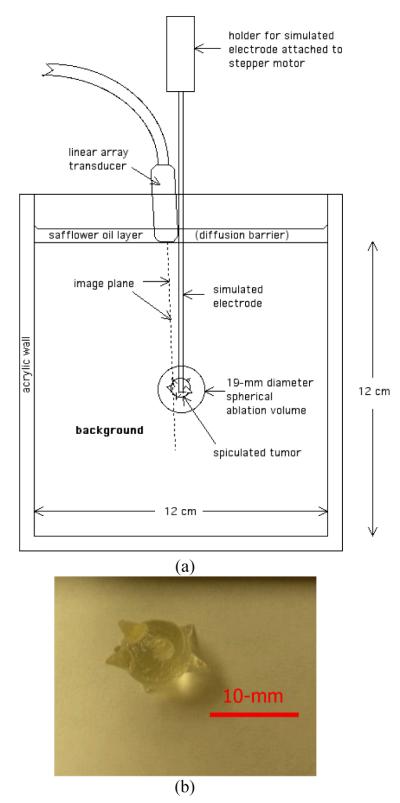
Young’s modulus reconstruction was initially applied to ultrasound data collected from a cubic TM phantom designed for assessing strain imaging using the electrode displacement technique [12]. A schematic diagram of the TM phantom for inducing electrode-displacement deformation is shown in Figure 1(a). It contains a large (19-mm diameter) spherical inclusion centered in a 120-mm × 120-mm × 120-mm cube of background TM material to simulate the overall ablated area. The large inclusion contains a smaller spiculated inclusion mimicking an ablated liver cancer i.e. an 8-mm (in diameter) spherical core with multiple 4-mm long cone-shaped protrusions (see Fig. 1(b)). Both inclusions were bonded to a 1.6-mm diameter stainless steel rod that simulates an ablation electrode. The terminal end of the rod had been roughened to enhance bonding between the TM material and the stainless steel rod.

Fig. 1.

(a) A schematic drawing illustrating the configuration of the tissue-mimicking phantom; (b) a photograph showing a silicone facsimile of the simulated liver tumor.

The TM materials used in the phantom have been previously described by Madsen et al. in [25] and consist of dispersions of microscopic safflower oil droplets in an aqueous gelatin matrix. In this study, adjustments of oil concentration among TM materials (not RF ablation) were utilized to change their stiffness because stiffness decreases with increasing volume percent of oil. The volume percentage of oil is as low as 30% for a simulated ablated liver cancer (i.e. the spiculated tumor) and as high as 70% for the simulated normal liver tissue (i.e. the background). Here we used a 50% oil-in-gelatin dispersion to simulate the ablated normal tissue (i.e. the spherical target excluding the spiculated inclusion). Storage modulus (real part of the complex shear modulus) values were measured at 0.1 Hz for the three materials using a Bose EnduraTEC ® model 3200 ElectroForce system (Bose Corporation, ElectroForce Group, Eden Prairie, MN, USA) [26], as listed in Table 1. The phantom design is motivated by the fact that practitioners tend to strive for a negative margin (i.e. the creation of an ablated region larger than the actual tumor) around the targeted cancerous tumor to ensure the death of all cancerous cells. Since there are, to our knowledge, no reported stiffness values of ablated cancerous tissues in the literature, we stipulated that ablated cancerous liver tissue would be harder than ablated normal liver tissue.

TABLE 1.

MEASURED STRORAGE MODULUS VALUES FOR THREE DIFFERENT MATERIALS FROM WHICH THE ABLATION PHANTOM WAS CONSTRUCTED

Material	Description	Measured Modulus (mean ± std; unit: kPa)
1	70% (volume percentage) of safflower droplets in aqueous gelatin	12.9 ± 0.6
2	50% of safflower droplets in aqueous gelatin	53.4 ± 3.7
3	30% of safflower droplets in aqueous gelatin	73.2 ± 6.2

B. Ex Vivo Bovine Liver Tissue Containing a Thermal Ablation Zone

In addition to testing with collected ultrasound data on the TM phantom, the method was also evaluated on an ex vivo thermal ablation zone. The RF ablation was performed on an excised bovine liver using a 17-guage cooled needle electrode (Valleylab Inc., CO, USA) with a 30-mm electrically-active tip. The ablation was performed for three minutes total - two minutes with active electrode cooling followed by a one minute “cautery” without active cooling. The ”cautery” mode was used to ensure sufficient contact between the electrode and tissue for electrode displacement. Clinically, the “cautery” mode is often operated prior to the removal of the needle electrode for preventing bleeding. Following the experiment, a gross pathology image was obtained at approximately the same position and orientation as that of the ultrasound B-mode image.

C. Data Acquisition and Processing

The set-up for imaging the ablation TM phantom and the ex-vivo bovine liver tissue using a linear array transducer is illustrated in Figure 2. The transducer was placed adjacent to the RF electrode on the upper surface of the phantom or the ex vivo bovine liver tissue. The RF electrode was then manually displaced along the vertical direction by approximately ± 0.5-mm and radiofrequency echo data were collected using a Siemens Antares scanner equipped with a linear array transducer (VFX9-4) pulsed at 6 MHz and an Axius direct™ Ultrasound Research Interface (URI) package (Siemens Medical Solution (USA) Inc., Mountain View, CA, USA) for data acquisition. To avoid damage to the phantom or loss of the contact between the electrode and the ex vivo liver tissue, the RF electrode was not displaced more than 0.5 mm from its initial position. Two consecutive (pre- and post-deformation) RF echo frames were recorded as inputs for motion tracking and then the deformation field was estimated using a modified block matching algorithm [27] to track motion between these two frames. A small two-dimensional non-overlapping kernel 0.96 × 0.40 mm (length by width) was used to obtain the axial displacements. Axial strain images were obtained by fitting the local estimated axial displacement data to a line (i.e. linear regression) whose slope provides the local strain at the center of a small (1.6 mm) region. The absolute axial strains are displayed in all strain images shown below.

Fig. 2.

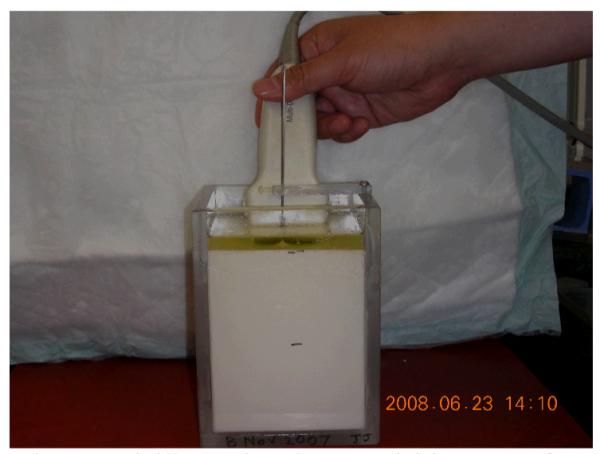
A photograph illustrating data acquisition setup for the phantom experiment under freehand scanning. An imaging plane (typically 3-mm away from the needle electrode) is chosen to maximize the cross-sectional area of the spherical lesion without introducing reflection from the metal

To measure the size of the ablated areas, images were manually segmented in Matlab (Mathworks Inc., MA), and areas of thermal ablation zones were digitally measured by counting the number of pixels in the segmented region.

D. Modulus Reconstruction Method

A finite element-based iterative reconstruction algorithm was used to obtain modulus distributions. Here we assume that the tissue being imaged is linearly elastic as a first approximation [28]. This is reasonable because the frame-to-frame deformation is small (<0.5% frame-average strain). Formally, we consider the following constrained minimization problem,

$$J_{\alpha }\left(\widehat{E}\right)=\arg \min \left\{\frac{1}{2}{\Vert T\left(\widehat{E}\right)-U\Vert }^2+\alpha V\left(\widehat{E}\right)\right\}$$ (1)

where

$$V\left(\widehat{E}\right)={\int }_{\Omega }\phi \left(\mid \nabla \widehat{E}\mid \right)d\Omega$$ (2)

$$\phi \left(t\right)=\sqrt{{\mid t\mid }^2+{\beta }^2}$$ (3)

subject to

$$E_{\min }\le \widehat{E}\le E_{\max }$$ (4)

and where Ê denotes the estimated modulus distribution, ▽ is a gradient operator, and U is the estimated axial displacement using the ultrasound-based speckle tracking algorithm [27]. T (E) is the predicted axial displacement by a forward FEA simulation and V (Ê) is a regularization function to penalize the image roughness. Here ||•|| denotes the standard L₂ norm and $\mid (x,y)\mid =\sqrt{x^2+y^2}$ is the Euclidean norm. Note that the first item in J_α (Ê) represents the fidelity of the measured displacement data U , and α is a positive parameter controlling the trade-off between the fidelity and variability in Ê.

To stabilize the solution of Eqn. (1), regularization is often used, and the resulting solution is then a tradeoff between fidelity to the measured displacement data and bias due to the regularity of the solution constrained through the regularization function. This implies that a regularization parameter is set a priori information in a way that balances this tradeoff for a given situation. In the original modulus reconstruction technique described by Kallel and Bertrand [21], they used the Tikhonov regularization [29] to deal with the ill-posed nature of Young’s modulus reconstruction. Because they defined a ultra-smooth modulus distribution as a prior information, their original formulation tends to produce blurred images [21, 29]. In our experience in handling ablated tissues, we have found that the transition of tissue stiffness between the normal and the ablated region is fairly sharp. To use this knowledge as prior information, an edge-preserving regularization technique [30, 31] was selected. This would provide improved depiction of the boundary of the thermal ablation region in the reconstructed modulus map to enable accurate determination of the size of the thermal ablation zone. In particular, φ(t) (see Eqn. (3)), a smooth differentiable approximation of the total variation operator [31] known for preserving shape edges, was adopted.

Historically, ultrasound elasticity imaging systems have utilized linear array transducers to scan tissue and have only estimated the axial (parallel to the acoustic beam) tissue deformation. This was due to inability to accurately track lateral (perpendicular to the acoustic beam) motion or deformation. Therefore, only the axial component of the estimated displacement was used in this study.

Motivation and Justification for 2-D simplification

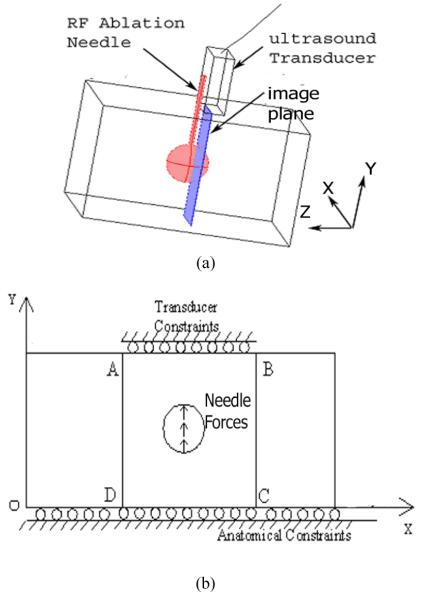
There are two practical difficulties involved in solving the forward problem (i.e. obtaining T(Ê) in Eqn. (1)). First, as detailed in Appendix A, the solution to the interfacial contact between the electrode and the ablated tissue is a complex and numerically expensive process. Second, a typical interaction problem in this work, e.g. the phantom shown in Fig. 1(a), is three dimensional in nature. Modeling cylindrical (needle electrode) and spherical (ablation zone) volumes with FEA is a demanding task because such shapes have to be approximated with a larger number of basic elements (e.g. brick- or tetrahedron-shaped three-dimensional elements). Very dense meshes typically lead to a larger number of degrees of freedom (DOF), i.e. a large linear algebraic system. Indeed, as the number of DOF increases, computational complexity associated with matrix evaluation becomes overwhelming. Therefore, in this work, we were motivated to reduce the computational burden by simplifying the reconstruction problem into its equivalent two-dimensional case.

More specifically, we aimed to establish a modeling approximation for tissue deformation captured by ultrasound data acquired in an image plane (see Fig. 3(a)). We assumed that the RF ablation electrode is bound to the treated tissue. Therefore, in a two-dimensional image plane, we will likely observe that the perturbation provided by the electrode can be accurately enforced either as equivalent force or displacement boundary conditions during the solution of the FEA model, as shown in Fig. 3(b). This simplification is reasonable because the dimension of the needle electrode (≈ 1-mm) used for RF ablation is much smaller than typical thermal ablation zones (e.g. >15 mm). It is, therefore, easy to conclude that for small deformations the perturbation introduced by the needle electrode is limited to areas where the needle is bound or attached to the thermal ablation zone. In other words, it is justified that the RF ablation electrode in our FEA models and corresponding reconstruction was approximated as uniformly distributed external forces applied to a small region, as shown in Fig. 3(b). We manually select the small region in the displacement field where displacement gradients are low, such that rigid body motion can be assumed to approximate the needle perturbation. In the current study, we enforce estimated displacements from that region onto the two dimensional FEA model for the forward solution (i.e. T(Ê) in Eqn. (1)). Since no absolute force information was obtained, only the relative modulus distribution can be obtained, wherein it is assumed the normal liver tissue has a modulus value of 1.

Fig. 3.

(a) A schematic drawing illustrating the configuration of a typical Cool-tip RF electrode for liver tumor ablation; (b) a simplified mechanical model for modulus reconstruction for ultrasound data acquired on an image plane described below. The surface of the electrode tip is conductive; the electrode can create a coagulation zone. An image plane where RF echo fields are acquired by an ultrasound transducer is 3 mm - 5 mm away from the needle electrode.

This simplification eliminates modeling details that impose increased computational complexity when their presence has little effect on the overall mechanical behavior. Our recent study [24] demonstrated that the two-dimensional finite element model under the plane stress condition exhibited similar mechanical behavior (i.e. axial displacement and strain patterns) compared to a full three-dimensional mechanical model at an image plane. In all reconstructions, the plane stress state was used for the forward solution.

Minimization Algorithm

In practice, the Young’s modulus of ex vivo soft tissue typically ranges from 1-kPa to 300-kPa based on reported mechanical testing data [11, 32, 33]. Hence, the reconstructed modulus values were limited to lie in a reasonable range (i.e. shear modulus of 0.1-40 kPa for ex vivo normal and ablated liver tissue [11]), and this constraint (see Eqn. (4)) was enforced during the reconstruction by a bound trust region method [34, 35]. More specifically, this constrained optimization problem (see Eqns. (1) - (4)) was solved by the “fmincon” function provided by the Matlab (Mathworks Inc., MA) optimization toolbox.

Starting from a uniform modulus distribution (e.g. 5-kPa for each finite element as the initial guess), this algorithm updates values for each element in the parameter vector Ê, so that Eqn. (1) is iteratively minimized. The basic steps involved are as follows:

1. Subdivide the domain (2D imaging plane) into finite elements where the Young’s modulus is assumed to be constant within each element.

2. Assume an initial Young’s modulus distribution. The displacement solution of the simplified model under the specified boundary conditions represents predicted theoretical estimations of tissue deformation T(Ê).

3. Compare these predicted displacements with the measured displacements obtained using the ultrasonic speckle tracking algorithm [27]. Simultaneously, the assumed modulus distribution is updated algorithmically until one or all criteria are satisfied. Usually, the criteria for convergence can be set with pre-determined thresholds ε₁ and ε₂ such that, delta(Ê) < ε₁ and/or J_α(Ê) < ε₂. delta(Ê) above denotes the difference in modulus distribution between two consecutive iterations.

Implementation details for updating the modulus distribution are similar to that described in the Kallel and Bertrand’s original approach [21] and are included in Appendix B for completeness. As discussed above, modifications were made so that the total variational regularization [31] can be incorporated into the formulation. It is worth noting that computational efficiency can be further improved if the scheme of fast gradient estimation developed by Oberai et al. [36, 37] is adopted.

In all reconstructions, the units for displacement (i.e. U and T(Ê) in Eqn. (1)) and modulus Ê are mm and Pa, respectively. The regularization parameter α was empirically chosen and was approximately 10⁻⁶. In the literature, statistical methods [38], such as generalized cross validation (GCV) or L-curve, may be used to determine an appropriate α. Nevertheless, these methods do not guarantee an optimal α, as shown in the simple example illustrated by Vogel [38].

Handling Nearly Incompressible Tissue

In this study, we treated all materials as nearly incompressible media by assuming the Poisson’s ratio to be 0.49. We used four-node linear elements. Therefore, in the reconstruction, the only unknown for each element is the Young’s modulus. To avoid “volumetric locking” [39] that often accompanies incompressible or nearly incompressible finite element formulation, the generalized “B-bar” method where a selective integration technique was used for the volumetric terms [40] was adopted with the bilinear four-node elements in this study.

Robustness in Reconstruction

For the ex vivo case, the actual underlying composition of the thermal ablation zone was not known, and uniqueness of the proposed method cannot be mathematically proven [41]. In this study, we randomly selected four different regions of interest (ROIs A through D) that all include the thermal ablation zone but have different sizes. For each ROI, the speckle tracking algorithm [27] provides a different estimated displacement field as the input to the modulus reconstruction algorithm. More specifically, these four realizations of the same thermal ablation zone should be considered independent because each displacement field has a unique measurement uncertainty. Starting with a uniform modulus distribution for each ROI, multiple reconstructions using the method described above provided four independent modulus maps. Consistent geometries of the thermal ablation zone delineated among these four independent modulus images suggest the robustness of the proposed reconstruction method.

Dependency on Mesh Density

It is important to assess the degree to which the discretization specifics of the numerical solution affect the results. Rectilinear meshes of 1600 (approximate element size of 1-mm²) and 3600 (approximate element size of 0.44-mm²) elements were examined for the reconstruction of the ex vivo tissue case. The results shown in the next section highlight that there is not a large discrepancy between results on these two computational meshes. Using this method we investigated the sensitivity of the mesh density aiming to perform reconstructions with a mesh that was adequate but that did not require unrealistic computational times for a reconstruction. Therefore, the coarse mesh (i.e. 1-mm square elements) was used throughout this paper except for results presented in Fig. 6 below where mesh independency was examined.

Fig. 6.

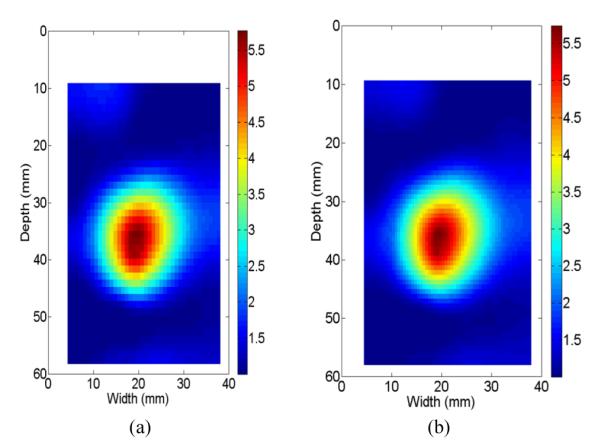
Reconstructed relative Young’s modulus images of the ex vivo thermal lesion using two different mesh sizes: (a) 1-mm square elements and (b) 2/3-mm square element.

III. Results

In this section, we evaluate the proposed method with the TM phantom and the thermal ablation zone created from ex vivo bovine liver tissues. The TM phantom experiment was designed as the first task to examine the accuracy of the proposed modulus reconstruction algorithm, given the ground truth. The second task was to use displacement data from an ablation experiment of ex vivo bovine liver tissues, where data are corrupted by noise, as would be found in a typical clinical setting due to electronic noise, motion tracking errors and other instrumentation sources. By varying the regions of interest (ROIs) from which the displacements were estimated, the third task involved testing the reliability of reconstructing the thermal ablation zone’s modulus distribution. Modulus images shown in this section were interpolated up to a pixel size of approximately 0.2-mm using the “Spline” function in MATLAB (Mathworks Inc., MA), except Figs. 6(a)-(b) where the raw modulus distributions were displayed to show the difference because of the two mesh sizes.

A. TM Phantom Results

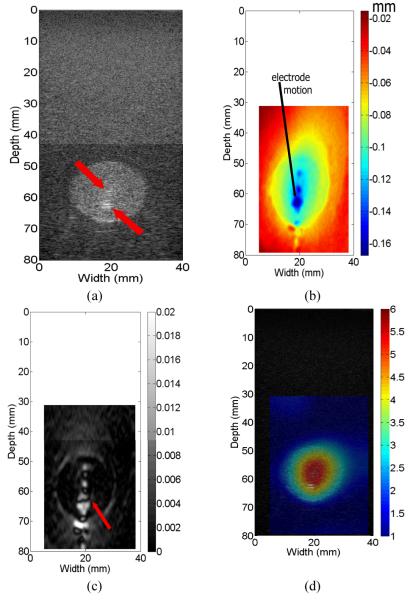
Figure 4(a) shows a B-mode image of the ablation phantom. Since the two inclusions have similar acoustic properties resulting in very similar echogenicity, it is easy to visualize the spherical inclusion but very difficult to see the smaller spiculated inclusion. We identified the location of the spiculated thermal ablation zone via specular reflections [See arrows on Fig. 4(a)]. The estimated axial displacements from a ROI are displayed in Fig. 4(b). Here an area having large rigid-body motion (i.e. large displacements and low displacement gradients) can be easily identified (see the arrow) and manually input into the forward FEA model (see Fig. 3(b)) as displacement boundary conditions during modulus reconstruction. It is worth noting that characteristics of the axial displacement image (see Fig. 4(b)) are fairly similar to those obtained using a three-dimensional finite element model in our previous work [24].

Fig. 4.

(a) B-mode, (b) estimated axial displacement, (c) axial strain and (d) relative Young’s modulus images from the TM phantom. Unit used for displacements is mm, while measured Young’s moduli (in kPa) have been normalized to normal liver tissue. The arrows in (a) and (c) point to the specular reflection and complex strain patterns, respectively. In (d), 1-mm square elements were used for reconstruction.

Figures 4(c) - (d) show, respectively, the axial strain field and the modulus distribution reconstructed from the input displacement field shown in Fig. 4(b). It is difficult to interpret the strain field, given the complexity in strain patterns shown in Fig. 4(c), whereas both targets can be visualized in the resultant modulus image (Fig. 4(d)). The phantom ablation zone (i.e. relative modulus value > 2.5) manually segmented from Fig. 4(d) was digitally measured to be 269.7 mm², found by summing pixel areas within the segmented region. The area of the overall simulated spherical ablation zone as measured from the B-mode image obtained at the same time as the modulus image was 276.8 mm² or within 2.5% of the ideal 283.5 mm² for the maximal cross-section of the 19-mm sphere. It is also easy to see from Fig. 4(d) that the relative elastic contrast (defined as the modulus of the target divided by the modulus of the background) between the spherical inclusion excluding the spiculated inclusion and the background is roughly 3.1, while the relative elastic contrast between the spiculated inclusion and the background is roughly 5.5. Both values were consistent with the mechanical testing results shown in Table 1.

B. Reconstruction with displacement obtained from ex vivo liver data

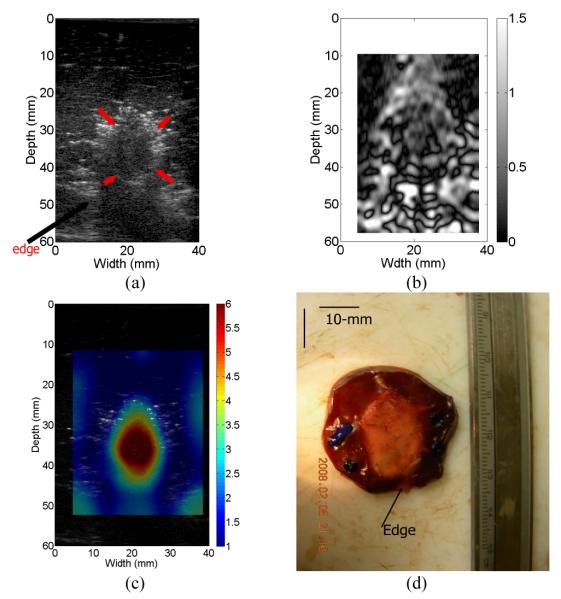
Figure 5(a) shows a B-mode image of the ex vivo thermal ablation zone, where the thermal ablation zone is located near the boundary of the liver tissue (see the arrows on Fig. 5(a)). The combination of the low signal-to-noise ratio in the RF echo signal (see the B-mode image in Fig. 5(a)) due to shadowing and complex tissue motion around the tissue boundary result in large noise in the strain image (see Fig. 5(b)). Consequently, compared to the post-ablation B-mode image (see Fig. 5(a)), detectability of the thermal ablation zone in the strain image doesn’t appear to be enhanced. Figures 5(c) - (d) display the reconstructed modulus distribution and the gross pathology image obtained for the ex vivo thermal ablation zone, respectively. The overall ablated area (i.e. relative modulus value > 2.5) manually segmented from Fig. 5(c) was 237.4 mm² and the area of the thermal ablation zone as measured from the gross pathology image was 227.4 mm². The overestimation is about 4.3%. The averaged elastic contrast between the thermal ablation zone and the background normal liver tissue is about 1:6.5, consistent with experimental measurements results from our group [11].

Fig. 5.

(a) B-mode, (b) estimated axial strain, (c) relative Young’s modulus and optical gross pathology images of the ablated ex vivo thermal lesion. The arrows in the B-mode image (a) point to the thermal lesion and the edge of the liver tissue, respectively. In (c), 1-mm square elements were used for reconstruction.

C. Results on Mesh Dependency

The Young’s moduli of the TM phantom were reconstructed for two different mesh sizes (1-mm square elements and 2/3-mm square element) and results are shown in Figs. 6(a)-(b), respectively. During the reconstruction, all parameters were the same except that the regularization parameter was proportionally scaled to accommodate the change of element size. There are almost no measurable changes between these two modulus images (Figs. 6(a)-(b)), and the shape and size of the ablation zone are very consistent.

D. Robustness of the Modulus Reconstruction

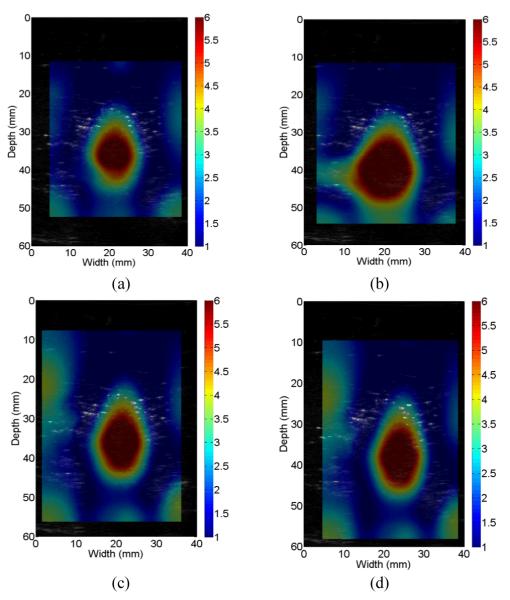
Axial displacement estimates were obtained for four randomly chosen ROIs containing the ex vivo ablated zone and the displacement estimates were re-interpolated onto the finite element mesh grid consisting of 1600 elements (40 × 40). Starting from a uniform modulus distribution (5-kPa), the algorithm described in Section II-D was used to estimate the modulus distribution. Figures 7(a)-(d) show four resultant modulus images from these four different ROIs (A-D). Figures 7(a)-(d) demonstrate that the reconstructed shape and size of the ablation zone are very consistent. The measured areas from Figs. 7(a)-(d) are 237.4-mm², 275.4-mm², 222.9-mm², and 240.3-mm², respectively. Of note, all coherent pixels in the modulus image where the relative modulus values are greater than 2.5 were regarded as the ablation region. Consistent geometries of the same thermal ablation zone obtained from four independent realizations demonstrate the proposed method is indeed robust.

Fig. 7.

Reconstructed relative Young’s modulus images of the ex vivo thermal lesion from four randomly-selected regions of interest (ROIs): (a) ROI A; (b) ROI B; (c) ROI c and (d) ROI (d). In all images, 1-mm square elements were used for reconstruction.

IV. Discussions

There is a need to monitor and assess results of minimally invasive clinical percutaneous RF and microwave ablation treatments. Compared to conventional B-mode imaging, strain imaging is effective in delineating the boundaries of thermal ablation zones both in vivo [12] and ex vivo [42]. Modulus imaging has several advantages over its corresponding strain imaging counterpart since modulus values are proportional to the ablation temperature [11, 13, 19, 20]. Therefore, estimating the Young’s modulus, especially absolute measurements of the tissue moduli, may provide additional information to monitor and evaluate the formation of necrosis in a quantitative manner. Certainly, work is needed to thoroughly understand how the electrode force information should be modeled to accurately assess the absolute Young’s modulus. In addition, local strains correlate to true elastic moduli only under limited circumstances [18]. Using the ablation electrode to apply tissue deformation results in a complicated field (see Figs. 4(c) and 5(b)) compared to that induced by conventional compression techniques. As is well understood in the literature [18], local strains can be used as surrogates for tissue moduli only in the presence of a uniform stress distribution. This fundamental limitation places a burden on identifying the complete contour of the thermal ablation zone in strain images whereas the thermal ablation zone can be easily identified in the corresponding modulus image (Figs. 4(d) and 5(c)).

To reduce the computational complexity of three-dimensional reconstruction, a two-dimensional simplification was proposed. Another reason for this simplification is that data is often only collected from a two-dimensional (2D) image plane in ultrasonic elasticity imaging. In such a situation, we have to use two-dimensional reconstruction techniques that may result in errors. Two common two-dimensional simplifications (plane stress and plane strain), can be used to simplify the problem. Plane strain conditions assume that the strains parallel to the out-of-plane direction are zero. This condition is ideal when the object is well confined in the out-of-plane direction or the beam dimension along the out-of-plane direction is long enough to ignore the deformation in this direction. Plane stress conditions assume that the stresses parallel to the out-of-plane-direction vanish. Plane stress conditions may be suitable for objects that are thin in the out-of-plane direction. Unfortunately, neither of these conditions accurately represent the RF ablation electrode displacement approach [18]. Our recent simulation results [24] suggest that the plane stress condition approximates the three-dimensional deformation with less error, given a cube with a single inclusion at the center. From phantom and ex vivo results, this simplification appears to give acceptable accuracy.

Modulus reconstruction is an attempt to infer quantities that cannot be imaged directly using clinical ultrasound systems. In theory, this inverse problem may be ill-posed. Often the problem is not whether a solution exists; on the contrary, there may be too many solutions that fit the measured displacement data. As demonstrated by Barbone and colleagues [41] in several idealized cases, vastly different modulus distributions can all produce exactly the same axial displacement fields, whereby our current method (Eqn. (1)) would fail. Interestingly, two reports [41, 43] for different inverse problem solutions both confirm that additional information is needed to obtain unique solutions. In particular, Barbone and colleagues [41] analytically demonstrated that additional force boundary conditions (e.g. pressure sensors) or multiple deformation fields (e.g. compression + shear) could provide the unique solutions for the modulus reconstruction problem for some idealized cases. The practical concern regarding the use of acoustically-opaque pressure sensors is that they would interfere with ultrasound data acquisition. Alternatively, the use of shear deformation requires that we dramatically improve our ability to track lateral motion. We are interested in using the pressure sensor approach described earlier because it may enable us to obtain absolute modulus information that correlates with the thermal dosage [13, 19, 20]. It is also worth noting that, given that the frame rate with clinical ultrasound scanners is reasonably high (> 20 frames/second for typical abdominal imaging), it is unlikely that temporal changes in tissue stiffness during the ablation procedures in a short interval (e.g. 0.1 second) will affect our ability to estimate the modulus distribution.

In this study, we initiated the iterative modulus reconstruction (Eqn(1)) from a uniform modulus distribution as the initial guess. The optimization function (i.e. fmincon in MATLAB) is a local minimizer [34, 35] and therefore could not guarantee to find the global minimum. Given a small (e.g. 2) number of unknowns, plotting the cost function with respect to these unknowns as a multi-dimensional surface plot will assist us to determine how well the solution converges to the global minimum of the cost function [44]. However, it would be difficult to do so in our case where unknowns are in the order of a few thousands. In this sense, one weakness of this study is that the imaging results were not rigorously compared to high resolution mechanical measurements (e.g. nano-indentation test) in the ex vivo tissue experiment because RF ablation will likely produce a heterogeneous hard (compare to the untreated tissue) ablation zone. Unfortunately, nano-indentation tests with high resolution (1-2 mm spacing between adjacent testing sites) are very time consuming (greater than 10 hours for a typical 2 × 2-cm thermal ablation zone). Rapid degradation of tissue properties due to sample desiccation defeated our initial attempts to conduct such validations. The ability to validate reconstruction of heterogeneous ablation zones is still under investigation.

This ill-posed condition also implies that small errors in the measured displacement data may cause prohibitively large variations in the estimates of tissue modulus without appropriate regularization techniques. When we changed displacement fields by choosing different (four) ROIs, the estimated size of the ablation zone changed by about 15% in one instance (ROI B; See Fig. 6(b)). In three other ROIs (i.e. A, C and D), the shape and size of the ablation zone remained consistent (See Figs. 6(a),(c) and (d)). One possible scenario is that the estimated displacements around the boundary of ROI B in Figure 6(d) were less accurate than those for ROIs A, C and D. Inaccurate displacements around the boundary will challenge the reconstruction algorithm, because these displacement estimates are rigorously enforced in the forward solution. This situation could be remedied by more intelligent regularization methods (e.g. [45]) and better motion estimation/filtering algorithms (e.g. [46]). Here an edge-preserving regularization functional [30, 31, 38] was employed to obtain a physically meaningful solution. The results appear to be reliable when different regions of interests are used. Furthermore, the use of multiple realizations may also provide a practical way to investigate the robustness of our image reconstruction method using current technique in a clinical setting.

V. CONCLUSION

A new method of using the RF ablation electrode displacement to reconstruct tissue modulus has been proposed and tested with a TM ablation phantom and a thermal ablation zone created using ex vivo bovine liver tissues. The RF ablation electrode can be tightly bound to the treated tissue and thus the complex three-dimensional contact problem can be treated as a two-dimensional inverse problem under a simplifying assumption. Theoretically, this assumption leads to the inclusion of additional noise into the displacement estimates utilized in the modulus reconstruction. Our preliminary results obtained from the TM ablation phantom and the ex vivo thermal ablation zone are encouraging as a feasibility study. Compared to strain images estimated through RF ablation electrode displacement, the reconstructed modulus images improve the ability to determine accurate contours or boundaries of thermal ablation zones. In the TM phantom, both the sizes and modulus values of the simulated thermal ablation zone are fairly close to the “ground truth” (i.e. known modulus distributions of TM materials). The underestimation in size is only about 5%. However, variations among estimated moduli for the same TM materials are greater than that in mechanical testing and this aspect requires further investigation. In the ex vivo thermal ablation zone, the size of thermal ablation zone obtained from the modulus image is comparable to that in the gross pathology image.

In this work, we concentrated on the reconstruction of a relative modulus distribution. Our future work will seek to measure the perturbation force information and modeling the distribution of the contact force. Collectively, these efforts will lead to obtaining the absolute Young’s modulus distributions which might be more valuable for treatment monitoring and diagnosis.

In vivo biological tissue experiments are indispensable for accurate clinical studies. However, TM phantom and ex vivo results presented in this study provide valuable information regarding what one should expect from in vivo tissue experiments. This method will be further verified in phantoms with more complex geometries and in vivo biological tissue. Several challenges still remain but the RF ablation electrode-induced displacement for modulus imaging provides encouraging results for abdominal ablation applications.

APPENDIX A

The biomechanical interaction between the needle electrode and surrounding tissue belongs to the class of classical contact mechanics problems. Without considering the frictional sliding along the contact interface, the basic formulation starts with the minimization of the total energy of for two hyperelastic bodies ${\stackrel{‒}{B}}_1$ and ${\stackrel{‒}{B}}_2$ in contact (see Figure A-1), where Ω = Ω₁ ⋃ Ω₂ denotes the boundaries and Γ = Γ₁ ⋃ Γ₂ denotes the respective volumes [47]:

$$\min \left(\sum _{\gamma =1}^2\left\{{\int }_{B_{\gamma }}{W}_{\gamma }\left(C\right)d{\Omega }_{\gamma }-{\int }_{B_{\gamma }}{\stackrel{‒}{f}}_{\gamma }{\phi }_{\gamma }d{\Omega }_{\gamma }-{\int }_{{\Gamma }_{\gamma }}{\stackrel{‒}{t}}_{\gamma }{\phi }_{\gamma }dA\right\}+{\Pi }_C\right)$$ (A-1)

where W_γ(C) is the strain energy function related to body B_γ(γ = 1,2), φ_γ denotes the deformation related to body B_γ, and the energy contribution due to the contact constraints are enclosed in Π_C. ${\stackrel{‒}{f}}_{\gamma }$ is the body force related to body B_γ and ${\stackrel{‒}{t}}_{\gamma }$ is the traction acted on the boundary Γ_γ. The first three terms combined in Eqn. (A-1) denote the total energy potential for Ω, including strain energy of elastic distortion and potential possessed by the external applied loads, and the forth term in Eqn. (A-1) represents nonlinear physical constraints that prevent local penetration between the contact interface. Since no analytical solutions of Eqn. (A-1) are available and a large variety of algorithms have been developed. Two main strategies [47], i.e. the penalty method and the LAGRANGE multiplier method, can be used with Eqn. (A-1) to enforce the physical constraints Π_C for obtaining a solution. However, these algorithms are all nonlinear processes and numerically expensive to resolve. Note that typical finite element formulations deal with the first three terms of Eqn. (A-1), resulting in a linear algebraic system that is relatively easy to solve. Moreover, the inclusion of frictional sliding will make the solution path-dependent and much more challenging to solve, because the frictional sliding occurred along the interface Γ_γ is energy dissipative.

Fig. A-1.

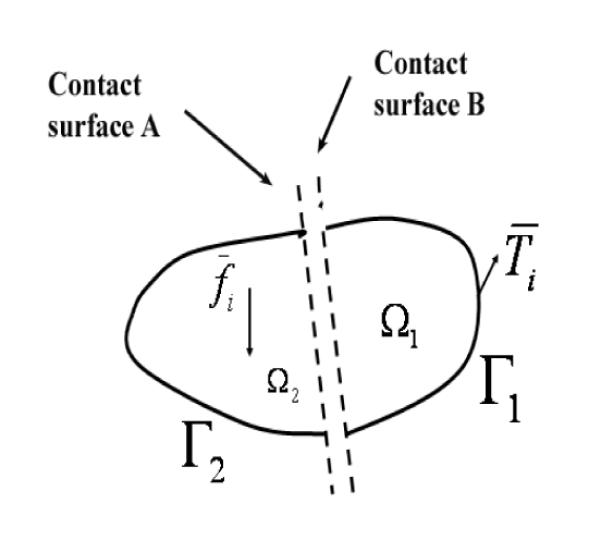
Formation of a contact interface between volumes Ω₁ and Ω₂ containing a pair of contact surfaces, A and B. Surface Γ₁ is the outside boundary of volume Ω₁ and surface Γ₂ is the outside boundary volume Ω₂. Note that this representation is a simple generalization of FEA simulations with a contact interface.

APPENDIX B

Formally, the elasticity reconstruction problem for a continuum under quasi-static compression can be considered as follows; given that the displacement field $U(x,y)$ in a medium Ω is governed by certain constitutive equations, we determine the elasticity parameters of the governing constitutive equations of the domain Ω. If we also assume tissue to be linear elastic, isotropic, and nearly incompressible (i.e. assuming a constant Poison’s ratio ≈ 0.5), the inverse problem is then simplified to the shear (or Young’s) modulus reconstruction problem. In this work, following the original approach proposed by Kallel and Bertrand [21], we modeled the inverse problem to be a constrained optimization problem to minimize the cost function below

$$J_{\alpha }\left(\widehat{E}\right)=\arg \min \left\{\frac{1}{2}{\Vert T\left(\widehat{E}\right)-U\Vert }^2+\alpha V\left(\widehat{E}\right)\right\}$$ (B-1)

where V(Ê) and α are a regularization term and a constant regularization parameter, respectively. We intended to use a gradient-based optimization approach to find solution for a given axial displacement field U. The gradient of J_α(Ê) has a matrix form and can be written as follows,

$$\frac{\partial J_{\alpha }\left(\widehat{E}\right)}{\partial \widehat{E}}=\frac{\partial T}{\partial \widehat{E}}\left\{T\left(\widehat{E}\right)-U\right\}+\alpha \frac{\partial V\left(\widehat{E}\right)}{\partial \widehat{E}}$$ (B-2)

Similar to Kallel and Bertrand’s approach [21],, the second order Hessian matrix of J_α(Ê) is approximated as follows,

$$\frac{{\partial }^2{J}_{\alpha }\left(\widehat{E}\right)}{\partial {\widehat{E}}^2}={\left[\frac{\partial T}{\partial \widehat{E}}\right]}^T\left[\frac{\partial T}{\partial \widehat{E}}\right]+\alpha \frac{{\partial }^{2}V\left(\widehat{E}\right)}{\partial {\widehat{E}}^2}$$ (B-3)

In Eqns. (B-2) and (B-3), $\frac{\partial V\left(\widehat{E}\right)}{\partial \widehat{E}}$ and $\frac{{\partial }^{2}V\left(\widehat{E}\right)}{\partial {\widehat{E}}^2}$ were calculated using a finite difference scheme for the discrete data Ê, as described by Vogel (Page 133-134; [38]).

Once the gradient and the Hessian matrices of the cost function are obtained, we can call the “fmincon” function implemented in Matlab (MathWorks Inc., MA) to perform the iterative optimization