Abstract
This study developed an improved motion estimation algorithm for ultrasonic strain imaging that employs a dynamic programming technique. In this paper, we model the motion estimation task as an optimization problem. Since tissue motion under external mechanical stimuli often should be reasonably continuous, a set of cost functions combining correlation and various levels of motion continuity constraint were used to regularize the motion estimation. To solve the optimization problem with a reasonable computational load, a dynamic programming technique that does not require iterations was used to obtain displacement vectors in integer precision. Then, a sub-sample estimation algorithm was used to calculate local displacements in fractional precision. Two implementation schemes were investigated with in vivo ultrasound echo data sets.
We found that the proposed algorithm provides more accurate displacement estimates than our previous algorithm for in vivo clinical data. In particular, the new algorithm is capable of tracking motion in more complex anatomy and increases strain image consistency in a sequence of images. Preliminary results also suggest that a significantly longer sequence of high contrast strain images could be obtained with the new algorithm compared to the previous algorithm. The new algorithm can also tolerate larger motion discontinuities (e.g. cavity in an anthropomorphic uterine phantom).
Keywords: strain imaging, elasticity imaging, elastography, speckle tracking, motion tracking, motion estimation, dynamic programming, optimization
Introduction
Elasticity imaging is a method for the assessment of stiffness changes in biological tissue that correlate with pathological changes and can be an indicator of many diseases, such as cancer and cardiovascular disease (Fung 1993). Different types of perturbation or mechanical stimuli, such as quasi-static compression (Hall et al. 2003; O'Donnell et al. 1994; Ophir et al. 1991), dynamic vibration (Parker et al. 1990) or acoustic radiation force (Fatemi et al. 2002; Nightingale et al. 2001), have been used to assess local profiles of tissue deformation. The quasi-static method employing unmodified clinical equipment and techniques similar to standard clinical examinations is termed ultrasonic strain imaging. Development of real-time strain imaging systems (Hall et al. 2003; Pesavento et al. 2000; Shiina et al. 2002) offers instant feedback to the operator (i.e., high frame rate, high quality strain images) thereby helping this modality rapidly gain popularity as it moves out of the research environment and into the clinical setting. Recent studies (Garra et al. 1997; Hall et al. 2003; Itoh et al. 2006; Regner et al. 2006) show, in breast imaging, strain imaging under real-time guidance has the capacity to demonstrate lesion size difference between the B-mode and the strain images, thereby helping differentiate benign from malignant masses. The desmoplasia that surrounds most malignant breast tumors (Tavassoli 1999) forms a layer of dense collagenous stroma (Walker 2001), thereby stiffening the tissue surrounding malignant lesions and making them palpable. Desmoplasia often exhibits different acoustical features (e.g. highly echogenic) compared to its adjacent breast malignancies (Muradali and Kulkarni 2005, Stavros 2004). Consequently, desmoplasia is the likely cause for some breast lesions to appear larger in the strain images as compared to the sizes of the hypoechoic mass in the corresponding B-mode images.
Strain imaging is performed using phase-sensitive echo signals (either radio frequency (RF) or quadrature data) as maps of anatomy and these signals are tracked as the anatomy is deformed. Thus, displacement estimates from a speckle tracking algorithm are the fundamental data available for most strain imaging systems. Due to the real-time image formation constraint, only efficient correlation-based speckle tracking algorithms had been used in real-time strain imaging systems (Hall et al. 2003; Pesavento et al. 2000; Shiina et al. 2002). In one system, to reduce computational cost, Pesavento et al. (Pesavento et al. 2000) used an iterative phase-seeking method without time shift compensation, limiting frame-to-frame deformation to be fairly small (e.g 0.1%) strain and this resulted in relatively low signal-to-noise ratio in strain images. Shiina et al. (Shiina et al. 2002) proposed a combined autocorrelation method where time shift compensation can be performed in parallel to a phase-seeking technique. Therefore, this approach has the advantages of producing strain images of relatively high quality with real-time processing and being applicable to large displacements. In another real-time strain imaging system, using a motion continuity assumption, Hall and his colleagues (Hall et al. 2003; Zhu and Hall 2002) modified the classic block-matching algorithm using a strategy of predictive search to improve frame rate. In particular, the motion continuity assumption was used to reduce the search region at a spatial location to a 3×3 grid once the displacement estimate at its immediate neighbor is known. These two real-time strain imaging systems (Hall et al. 2003; Shiina et al. 2002) have been successfully applied to breast lesion characterization (Burnside et al. 2007; Hall et al. 2003; Itoh et al. 2006).
To date, consistently obtaining high quality in vivo strain images is still a challenge. Although correlation-based estimators are simple and effective, they may suffer from echo signal decorrelation induced by out-of-plane motion, non-rigid motion and non-uniform motion of sub-resolution scatters, resulting in large errors in displacement estimates. Some echo signal decorrelation errors are due to large lateral motion or axial deformation and can be reduced by signal processing. For instance, companding (Chaturvedi et al. 1998) and stretching (Varghese and Ophir 1996) have been successfully applied. However, each of those techniques increases computation time by a significant factor, making real-time implementation on current ultrasound scanners difficult. Since signal processing of echo data alone cannot resolve ambiguities in motion tracking, approaches integrated with different forms of smoothness constraints have also been reported (Pellot-Barakat et al. 2004; Revell et al. 2005; Yeung et al. 1998; Zhu et al. 1999). Although these approaches provide higher quality strain images without losing contrast or spatial resolution and are less sensitive to local echo signal decorrelation, there are still two main problems. First, motion discontinuity in certain locations (e.g. radial deformation near arteries) within the image plane may limit the use of smoothness constraints (Shi and Varghese 2007). Second, the time constraint in a clinical setting (i.e. real-time or near real-time display) limits our ability to use those more sophisticated motion estimation algorithms. This paper reports our effort to develop a more generalized fast block-matching algorithm (BMA) to address the above mentioned problems.
In this work, motion tracking is also treated as an optimization problem where displacement vectors in a neighborhood will be determined by a cost function (see Eqn. (2) below) to maximize the correlation between the pre- and post-compression echo signals while maintaining their local motion continuities (i.e. smoothness constraint). However, moderate motion discontinuity among these displacement vectors can be tolerated by formulating a set of cost functions based on a modified total variation functional (Vogel 2002). An integral part of the formulation of this optimization problem is a solution technique that balances the tradeoff between the reliability and the computational cost. In this paper, the optimization problem is solved by a dynamic programming technique named the Viterbi algorithm (Viterbi 1967). To test the effect of the regularization, we compare its performance with an un-regularized real-time BMA (Zhu and Hall 2002).
The rest of the paper is structured as follows. A detailed description of the proposed regularized BMA and it applications in real-time strain imaging is given in Method and Material Section. This section focuses on the description of the specific regularization model and the associated optimization strategy using the Viterbi algorithm (Viterbi 1967) to reconstruct displacement fields between the pre- and post-deformation RF echo fields. Experiments with in vivo breast and thyroid tissue data are also given in this section. Subsequent analyses of our in vivo data are conducted in Results Section. In particular, the adjustment of the cost function (see Eqn. (2) below) and the subsequent displacement and strain images from in vivo data are presented in this section. Finally, discussions are given followed by some closing remarks.
Methods and Materials
A. A Regularized Block-Matching Algorithm
Formally, we estimate a dense (nominally 0.2-mm spacing in axial [parallel to the acoustic beam] and lateral [perpendicular to the acoustic beam] directions) displacement field between a reference RF echo field {RFref}and a target echo field {RFt arg et}. A block matching algorithm (BMA) is designed to match patterns in {RFref} with patterns in {RFt arg et} using a search kernel. Each search kernel consists of a short axial segment of echo data from several beam lines that is used to determine displacements at the center of the search kernel. To reduce computational cost, a small search kernel (0.2-mm (axial) × 0.9-mm (lateral)) is used. In the framework of a BMA, the set Λ of possible displacements (i.e. search region) is defined as
| (1) |
where Da and Dl are maximum possible axial and lateral displacement estimates in a search grid of M × K, respectively, as specified by the user. ⊗ in Eqn. (1) denotes an operation to form a combined set whose elements (lk, am) represent displacement vectors. The motion tracking for a small neighborhood Ω can be formulated as an optimization problem by minimizing the following cost function in the framework of a typical BMA:
| (2) |
where the first item EC is a penalty term for speckle decorrelation, assuming echo signals can be fully restored, and the second term Φ(Es) is a penalty term for losing motion continuity where Es is the motion smoothness measure in a neighborhood. The normalized cross-correlation coefficient (NCC) is used to measure the local pattern similarity between the search kernels on the reference and the target echo fields and Ec is set to be 1 - NCC to penalize the loss of signal coherence. The NCC is chosen because it provides normalized values between -1 and 1 for convenience. α is a positive regularization parameter and is set to unity in this study for all chosen cost functions (Eqn. 3(a)-(c)) below.
The major difference between this approach and a classic BMA is that Eqn. (2) simultaneously determines a sequence of estimated displacement vectors rather than a single displacement vector based on local correlation values. For many applications such as breast elasticity imaging, the tissue being imaged is assumed, as a first approximation, to be a continuum such that the displacement field under mechanical stimuli is nearly a continuous function. But the presence of complex anatomy (e.g. large blood vessels, tissue interfaces) within the image plane will cause discontinuous motion. Typically, such motion discontinuities will present falsely large deformation in a displacement field (e.g. one RF sample difference between two adjacent axial displacement estimates separated 8 RF samples could result in more than 10% axial strain in the deformation field where the average deformation is only 1%), because local strains are typically calculated by relative displacement differences between two adjacent locations. In this paper, we propose the use of a specially-designed penalty function Φ(ES) (Eqns. 3(a)-(b)) to impose minimal, intermediate and maximum motion continuity constraints for adaptively regularizing motion estimation under different circumstances (e.g., different target organs as discussed in Results and Discussion Sections):
| (3a) |
| (3b) |
| (3c) |
| (3d) |
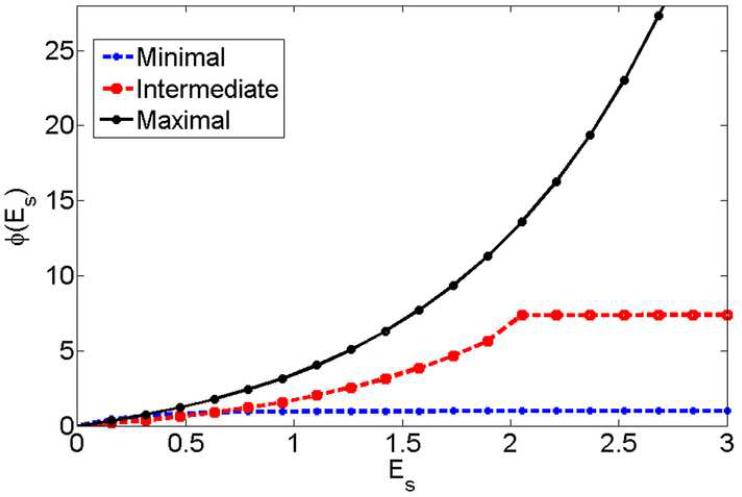
where β is a small positive number (e.g. 0.1) and is the estimated multi-dimensional displacement vector. In this paper, the derivatives of the displacement vector were estimated using a simple forward finite difference scheme. It is worth noting that we regularize motion estimation at the integer sample level for both axial and lateral directions. Plots shown in Fig. 1 demonstrate different penalties of motion discontinuity can be imposed.
Figure 1.
Three proposed penalty functions Φ(ES ) which impose different amount of penalties for losing motion continuity.
B. Solution to This Optimization Problem
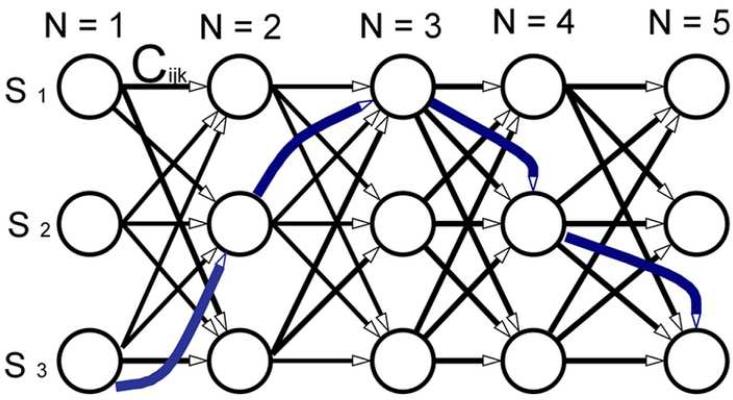
We model the block matching-based motion estimation as an optimization problem maximizing (1) signal correlation and (2) motion continuity among displacement vectors in a small neighborhood. Determining a sequence of displacement vectors corresponding to a segment of closely-spaced physical points in the framework of a BMA is equivalent to determining a best possible motion sequence for this segment of points, each having S (S = M × K) possible states (i.e. possible displacements from a search grid M × K) by the combination of the correlation and the continuity constraint. Mathematically, this problem can be modeled as a fully developed Hidden Markov Model (HMM) built on Bayes' theorem (Rabiner 1989). Since real probability density functions are difficult to determine, we instead write this as an optimization problem using a simple cost function (Eqn. (2)). This optimization problem was solved by a dynamic programming technique named the Viterbi algorithm (Viterbi 1967) as follows. As shown in a simplified example (Fig. 2), all costs will be estimated in a forward fashion between two adjacent data points using Eqn. (2) and be stored in a three-dimensional matrix Cijk to save computing time. The Viterbi algorithm (Viterbi 1967) can efficiently trace the cost matrix for obtaining a global “optimal” solution for these five points (See the solid line path in Fig. 2). This algorithm was selected because of its efficiency and simplicity. It is important to note that this optimization process will only be used to determine the displacement vector in integer precision due to the nature of the Viterbi algorithm. Then, a sub-sample estimation algorithm (Cespedes et al. 1995) (e.g. quadratic interpolation) will be used to obtain fractional displacement estimates.
Figure 2.
An illustration of the Viterbi algorithm. On this illustration, “N” represents different locations where the displacement vectors need to be simultaneously estimated and “Sm”represents m possible selections of the displacement vector for each location. Therefore, in the framework of block-matching, each circle represents one possible choice in the search window for each location. The cost of choosing a target circle (where the arrow is pointing toward) at the next location is determined by Eqn. (2), given the current choice (i.e. the circle which the arrow is originating from). The resultant cost function value is one element of the three dimensional cost matrix Cijk and this process is repeated until all elements of Cijk are determined. If all possible combinations are considered, there will be a large solution pool. The Viterbi algorithm can be utilized to find the “best” set of displacement vectors (the solid blue line) in a cost-effective manner. Of note, small numbers for m and N are used to reduce the size of this illustration.
C. Implementation
Two methodologically different schemes were considered and implemented, as illustrated in Fig. 3(a)-(b). Both implementations use the predictive search strategy analogous to that developed by Zhu and Hall (Zhu and Hall 2002). The basic idea of predictive search is to use an estimated displacement vector in one spatial location to guide speckle tracking in its immediate neighborhood because of the local motion continuity. Limiting the search region improves computational efficiency while simultaneously eliminating phase ambiguity (“peak hopping”) errors in the displacement estimation. Use of this idea in elasticity imaging was first proposed by Zhu and Hall (Zhu and Hall 2002) and successfully implemented into a real-time breast strain imaging system (Hall et al. 2003).
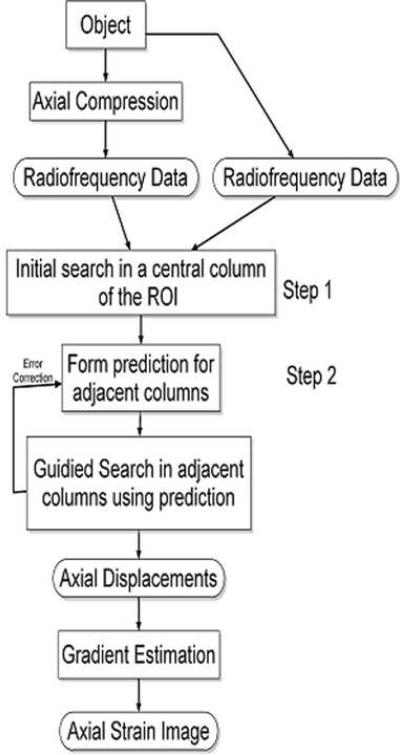
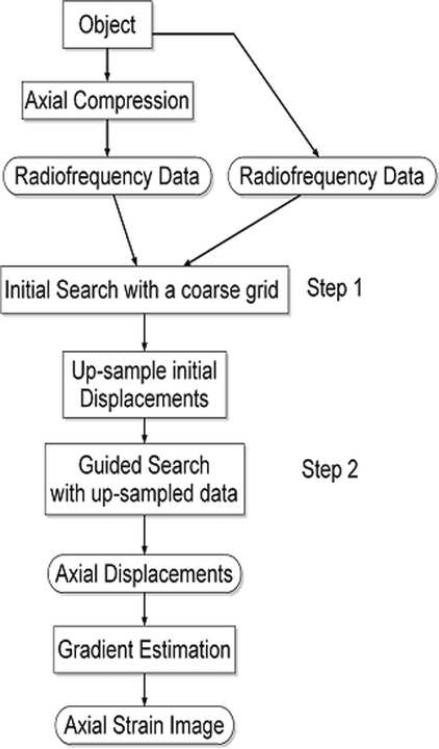
Figure 3.
Flow charts summarizing two implementations of the proposed speckle tracking method for strain imaging: (a) the lateral guidance approach and (b) the multi-grid approach.
In the first implementation (hereafter referred to as the “lateral-guidance” approach; see Fig. 3(a)), we combined the proposed method with a “lateral-guidance” block matching algorithm (Jiang and Hall 2007). In the first step, searching with relatively large 2-D (approx. 0.5-mm long by 1-mm wide) search kernels along the central column ROI is performed using the Viterbi algorithm (Viterbi 1967) to obtain displacement estimates with integer precision. To further reduce the computational cost, the initial column can be divided into small segments (e.g. 20 points spaced by 0.2-mm per segment). Then, the displacements estimated at the end of each segment can be used to guide motion tracking for the subsequent segment. In this step, the lateral (perpendicular to the acoustic beam) search region for each segment is fixed at three beam lines and the axial search region is determined to allow 6% local axial strain. In the second step, for each column, the search region can be reduced to a 3 by 3 sample grid (corresponding to 6% allowable local axial strains) under the guidance of its adjacent column of displacement estimates (i.e. displacement predictions), thereby drastically improving computational efficiency. To avoid errors among displacement predictions, displacement estimates from an adjacent column will be filtered by a moving linear regression method (Jiang and Hall 2007). Smaller search kernels (0.2-mm long and 1-mm wide) are used in this step to improve displacement estimate sensitivity and spatial resolution. The first implementation of this approach was reported in (Jiang and Hall 2006).
In the second implementation (hereafter referred to as the “multi-grid” approach), the proposed method is implemented in the framework of “multi-grid” motion tracking (Li and Lee 2002, Shi and Varghese 2007). As shown by the schematic diagram in Fig. 3(b), in the first step, the pre- and post-deformation RF echo frames will first be down-sampled by a pre-determined factor that may be dataset dependent. For all datasets tested in this paper, we set the down-sample factor at two. Then, the BMA algorithm using the Viterbi algorithm described above will be performed in a column-wise manner to obtain displacement estimates in a coarse grid. In the second step, the displacement estimates in the coarse grid will be up-sampled to a fine grid (typically 0.2-mm by 0.2-mm) using a fast B-spline algorithm (Thevenaz et al. 2000). Then, using the predictive search, the up-sampled displacement vectors will allow us to limit the motion tracking in a 3 by 3 sample grid. In this step, motion estimation was performed with the pre- and post-deformation RF echo frames with original size.
Both approaches described above have been implemented in MATLAB (Mathworks Inc., MA) for data processing using a standard gateway interface (MEX) in conjunction with ANSI C. All tests were performed on a windows-based dual-CPU (1.8-GHz) workstation equipped with 2-Gbytes of memory. All strain imaging examples presented below in Results Section were estimated off-line by the regularized BMA (both the multi-grid and lateral-guidance approaches) described above and the un-regularized BMA axial-guidance algorithm (Zhu and Hall 2002) with a small search kernel (0.9-mm (lateral) × 0.2-mm (axial)) and a 1.6-mm linear regression window used to estimate displacements and strains, respectively. All algorithm comparisons were also performed using exactly the same pairs of RF echo frames.
D. Displacement Quality Assessment
Comparing the performance of different strain imaging systems among in vivo data sets is a difficult task due to lack of knowledge regarding the modulus distribution in and around the pathology. An automatic method (Jiang et al. 2006) based on a displacement quality metric (DQM) has demonstrated that estimated DQM values were consistent with the visual assessment by experienced researchers actively involved in elasticity imaging. The DQM is the product of the cross correlations among the pre-deformation and motion-compensated post-deformation RF echo fields (a measure of motion tracking accuracy applied to the entire region of interest) and the cross correlation between two consecutive motion-compensated strain images (a measure of strain image consistency) (Jiang et al. 2006). In this paper, the DQM method was used to compare the performance of both implementations of the proposed algorithm and our original guided-search speckle tracking algorithm (henceforth referred to as axial guidance algorithm) (Zhu and Hall 2002).
E. Phantom and In vivo Tissue Experiments
To demonstrate the usefulness of the proposed speckle tracking algorithm, two different kinds of data were acquired. The first includes an in vivo breast with a fibroadenoma and an in vivo thyroid with a follicular adenoma (roughly 200 frames of RF echo fields in total). The human subjects provided informed consent with the procedure approved by the local institutional review boards. During data acquisition, the real-time strain imaging system (Hall et al. 2003; Zhu and Hall 2002) was used to maintain nearly uni-axial deformation with minimal elevation motion under freehand scanning. The strain imaging system used for data acquisition consisted of a Siemens Elegra scanner (Siemems Medical Solution USA, Inc., Mountain View, CA) with a 10 MHz linear array transducer (VFX13-5) and a real-time strain imaging software package. The details of data acquisition can be found in (Hall et al. 2003). All frame-average axial strains reported below in the Results Section were estimated by the multi-grid approach to provide the estimated deformation for each data set.
The second kind of data was acquired from an anthropomorphic uterine phantom (Hobson et al. 2008) manufactured at the University of Wisconsin (Madison, Wisconsin, USA). Radiofrequency echo data was acquired using a Siemens SONOLINE Antares (Siemens Medical Solution USA, Inc., Mountain View, CA) equipped with a 10 MHz linear array transducer (VFX13-5) and the Axius Direct Ultrasound Research Interface (URI) software package. During data acquisition, the ultrasound transducer was held steady and saline was injected into the simulated uterine cavity to push the simulated uterine wall apart, similar to the saline-infused sonohysterography (SIS) method (Berridge and Winter 2004). The expansion of the simulated uterus within the image plane resulted in a discontinuous motion field. The data is used to demonstrate that this motion tracking algorithm does not require the assumption of global motion continuity. The details of phantom production and data acquisition can be found in (Hobson et al. 2008).
Results
A. Influence of Deformation
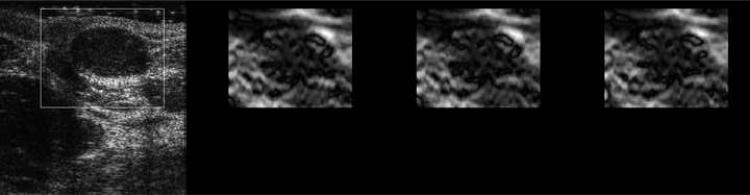
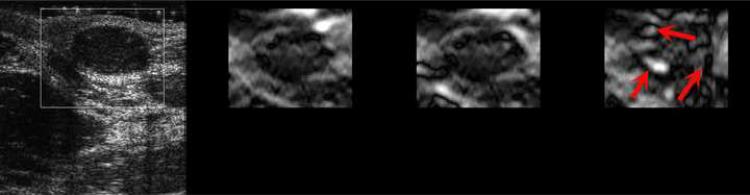
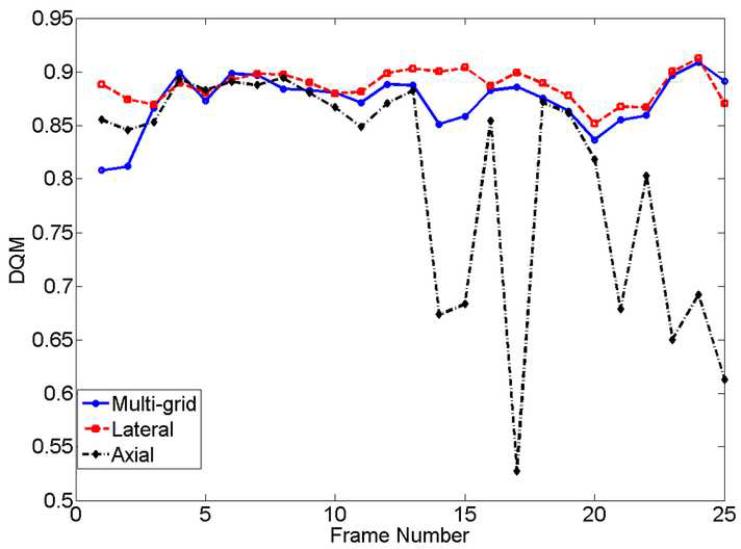
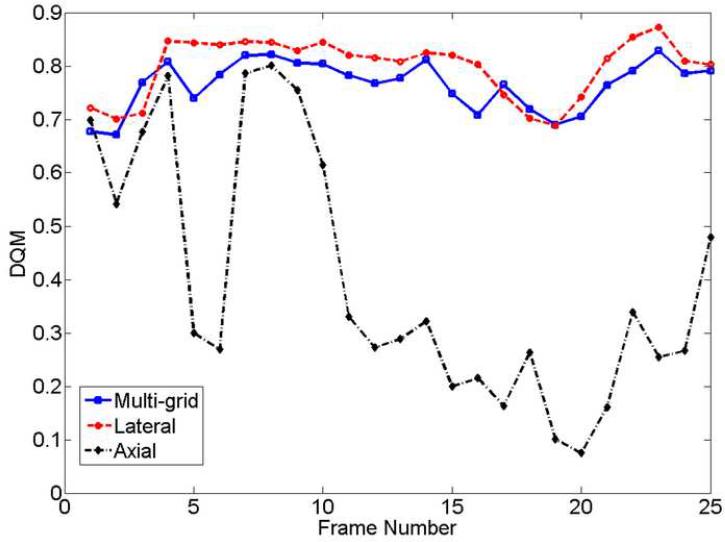
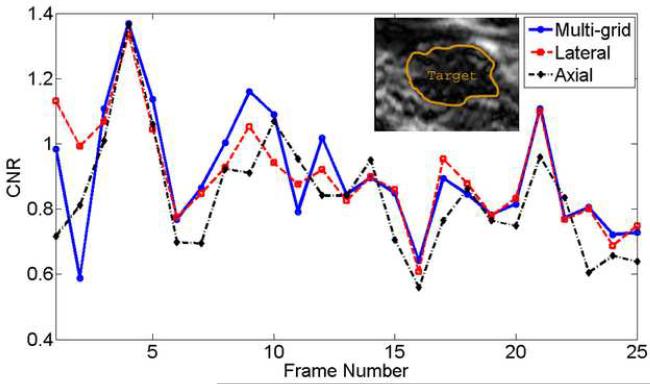
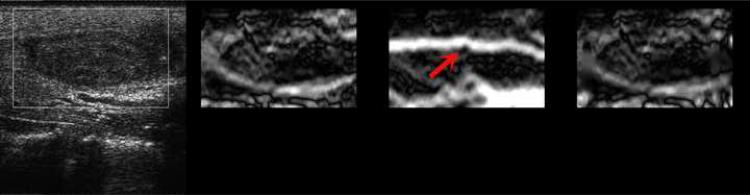
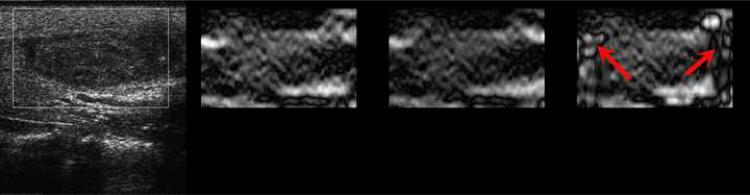
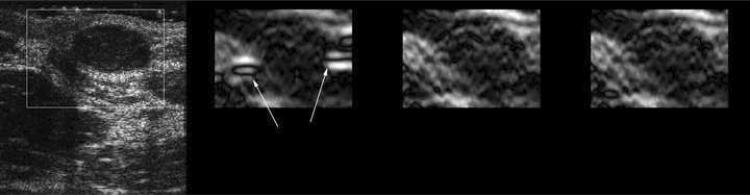
Figure 4(a) displays representative strain images from an in vivo breast fibroadenoma using two implementations of the proposed algorithm (i.e. the multi-grid approach and the lateral-guidance approach) and the axial-guidance algorithm (Zhu and Hall 2002), where the frame-average axial strain is 0.8%. In both implementations, the intermediate cost function was chosen for data analysis presented in this subsection. Strain images obtained by the three methods for 1.5% frame-average strain for the same in vivo breast lesion are shown side by side in Fig. 4(b). As shown in Figs. 4(a), all three methods perform equally well for a small deformation (0.8%) for most data. However, both the multi-grid approach and the lateral-guidance approach outperform the un-regularized axial-guidance algorithm for large and more complex motion (see Movies 1 and 2, and Figs. 5(a)-(b)). The decorrelation noise (see arrows) in the strain image (far right in Fig. 4(b)) is apparent. The decorrelation noise typically resulted from large motion estimation errors and may hamper accurately tracing the lesion boundary in the strain image. In Fig. 4(b), consistent with visual perception, the strain images with 1.5% frame-average axial strain obtained by the multi-grid approach and the lateral guidance approach achieve DQM values of 0.77 and 0.81, respectively, whereas the strain image obtained using the axial guidance algorithm achieved a DQM value of only 0.27. In Movie 1 (0.8% strain) and Movie 2 (1.5% strain), two sequences of strain images (each 25 frames) as well as the estimated corresponding DQM values (Figs. 5(a)-(b)) confirm these observations. Note that for each comparison among algorithms the same pairs of the pre- and post-deformation RF echo fields and the same strain processing parameters (kernel size, separation, etc.) were used. Two different frame pairings (nominally 0.8% and 1.5% frame-average strains (Hall et al. 2002; Lubinski et al. 1999) were used to compare algorithm performance at different amounts of strain.
Figure 4.
B-mode (far left) and strain images using three different speckle tracking methods (middle left: the multi-grid approach; middle right: the lateral-guidance approach; and far right: the axial-guidance approach) of an in vivo breast fibroadenoma with (a) 0.8% and (b) 1.5% frame-average axial strain. The white box in the B-mode image defines the ROI for strain images. The order of images is the same for Movies 1 and 2. The arrows in the far-right image point to decorrelation noise in the strain images resulted from large speckle tracking errors.
Figure 5.
Plots of the DQM (a and b) and CNR (c and d) values versus the frame number for the in vivo fibroadenoma shown in Fig. 4 obtained with the “multi-grid” approach (solid line), the “lateral-guidance” approach (dashed line) and the “axial-guidance” algorithm (dash-dotted line) for frame-average strains of (a and c) 0.8%, corresponding to Movie 1 and (b and d) 1.5% corresponding to Movie 2.
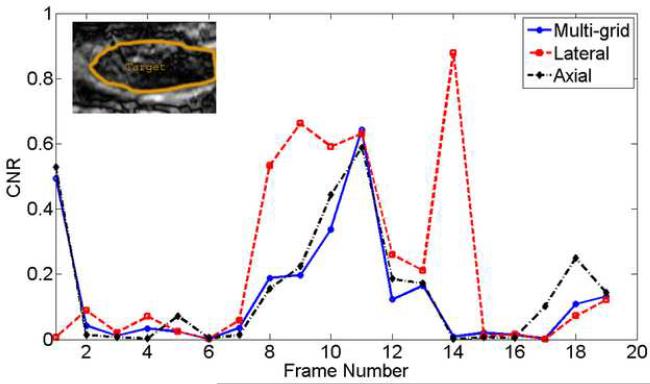
One measure of image quality (lesion detectability) is the contrast-to-noise ratio (CNR) (Song et al. 2004):
| (4) |
where S and σ 2 denote means and variances of signals, and subscripts b and t represent the background and target, respectively. To calculate the CNR using Eqn. (4) for each strain image, we used the manually-segmented breast fibroadenoma lesion (see Figs. 5(c) and 5(d)) and the rest of strain image as the target and the background, respectively. w is a weighting of the area of the target and the background to the total area given by wx = areax / areatotal . The inclusion of the weighted area is necessary because the target and the background contribute in different amounts to the noise estimates (Song et al. 2004). The estimated CNR values for the breast fibroademoa lesion using these three above-mentioned motion tracking approaches for Movies 1 and 2 are shown in Fig. 5(c) and (d). Similar to what demonstrated by the DQM values, the estimated CNRs also clearly indicated that the multi-grid and lateral-guidance approaches outperformed the axial-guidance approach in these two cases.
B. Influence of Anatomy
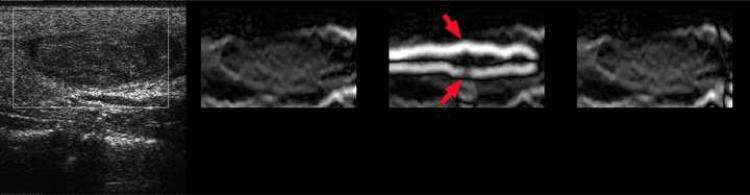
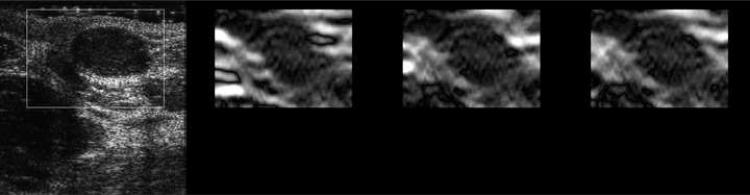
Representative strain images from the in vivo thyroid follicular adenoma using the same three motion tracking approaches are shown in Figs. 6(a)-(c) where the frame-average axial strain is roughly 0.8%. In both the multi-grid approach and the lateral guidance approach, the intermediate cost function was chosen for data analysis presented in this subsection. In Fig. 6(a), the lateral-guidance approach failed to correctly predict tissue motion after the initial estimation, resulting in large horizontal “banding” artifacts (see arrows in the middle right strain images) due to fairly complex interfacial tissue motion near the thyroid lesion.
Figure 6.
B-mode (far left) and strain images of an in vivo thyroid follicular adenoma using three different speckle tracking methods (middle left: the multi-grid approach; middle right: the lateral-guidance approach; and far right: the axial-guidance approach) with 0.8% frame-average axial strain. There are instances where (a,b) the lateral guidance implementation and (c) the axial guidance had difficulties in predicting tissue motion (arrows in the strain images point to decorrelation noise). The white box in the B-mode image defines the ROI for strain images. The order of images is the same for Movie 3.
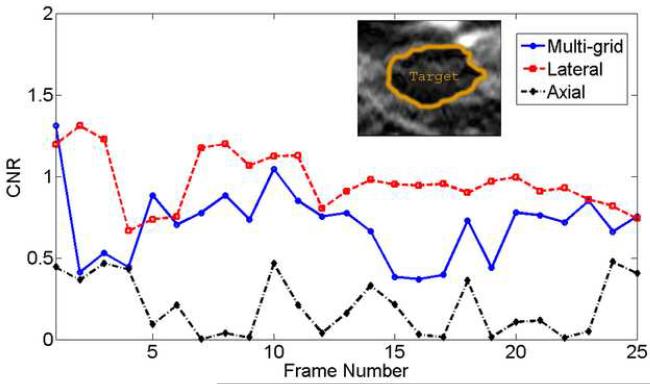
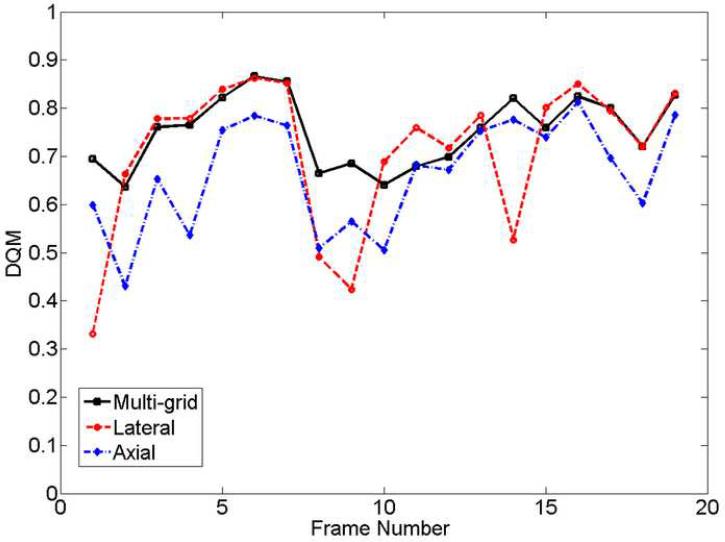
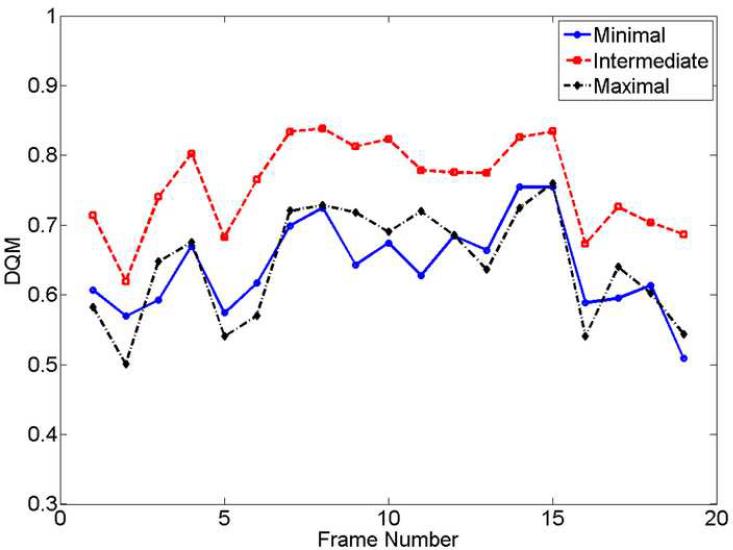
A sequence of strain images (19 frames) of the thyroid follicular adenoma are shown in Movie 3 where the frame-average strain is also 0.8% and the strain image noise is higher compared with the in vivo breast lesions. We found that the DQM values in the thyroid data (Fig. 7(a)) were lower (i.e. 0.75 [mean] ± 0.07 [standard deviation]) than the DQM values obtained in the breast data in Fig. 5a (0.87 ± 0.03) for the same frame-average strain (0.8%) both using the multi-grid implementation. The reason is not clear. However, in our experience, the presence of the carotid artery and trachea (not in the image plane shown in Figs. 6(a)-(c) and Movie 3) adjacent to the thyroid gland often causes very complex (i.e. rotation, shear and discontinuous motion patterns around the gland interface) and more out-of-plane motion. These sources of signal decorrelation challenge our motion tracking algorithm. The high noise strain image may make identifying the lesion boundary more difficult, as shown in Figs. 6(a)-(c). This example shows that when the tissue motion is complex, as we expected, the multi-grid approach considerably outperforms the other two methods (see Movie 3). As evident in Figs. 6(a)-(c), there are instances where the lateral guidance implementation (See Figs. 6(a) and (b)) and the axial guidance algorithm (See Fig. 6(c)) had difficulties in predicting tissue motion. Consequently, the multi-grid implementation appears to be more reliable in some cases.
Figure 7.
Plots of the (a) DQM and (b) CNR values versus the frame number for the in vivo thyroid follicular adenoma lesion shown in Figs. 6(a)-(c) with 0.8% frame-average strain.
It is apparent that the estimated CNR values from the in vivo thyroid follicular adenoma in Fig. 7(b) from all strain images in Movie 3 are not consistent with our visual perception. In particular, in Fig. 6(b) where the lateral guidance approach showed signs of "prediction errors", the estimated CNR value was falsely high because of the presence of large decorrelation noise (see arrows in Fig. 6(b)). The comparison between the estimated DQM and CNR values for Figs. 4 and 6 is summarized in Table 1.
Table 1.
Comparison of estimated DQM values to the calculated CNR values for the in vivo breast fibroadenoma and thyroid follicular carcinoma lesions. M, L and A denote multi-grid, lateral-guidance and axial-guidance approaches, respectively.
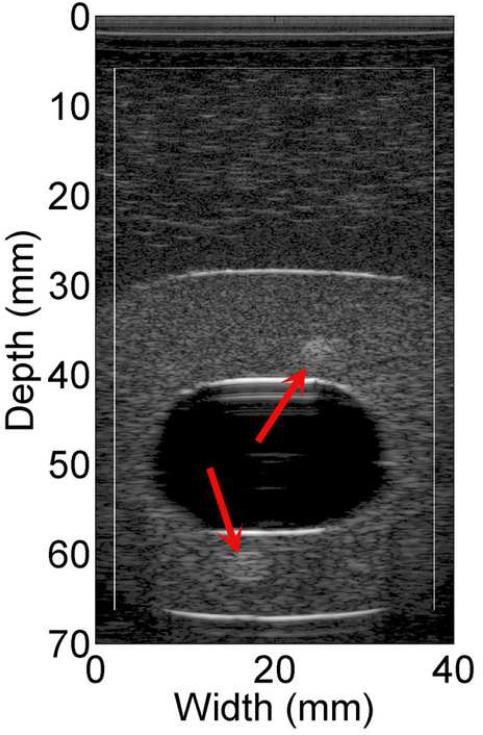
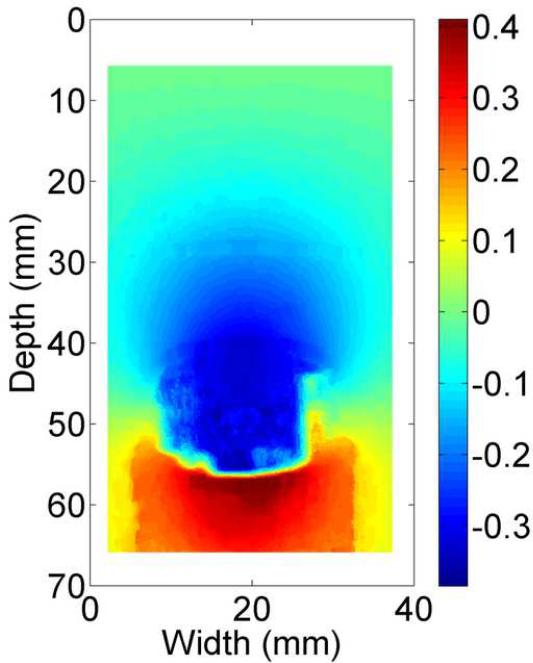
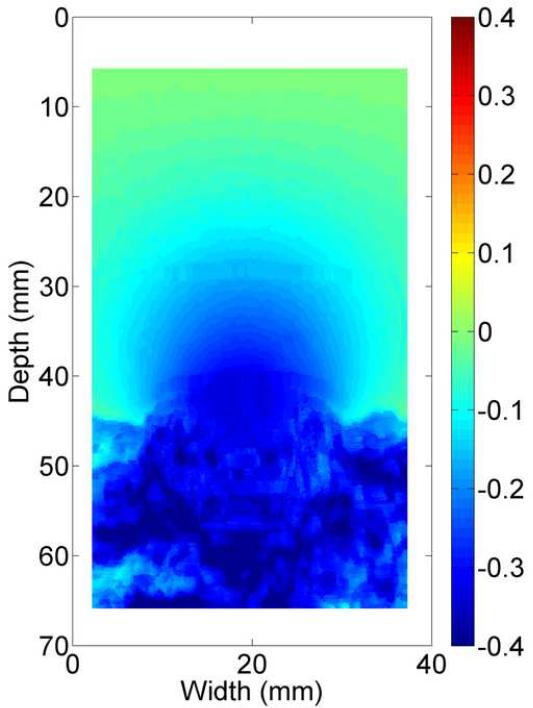
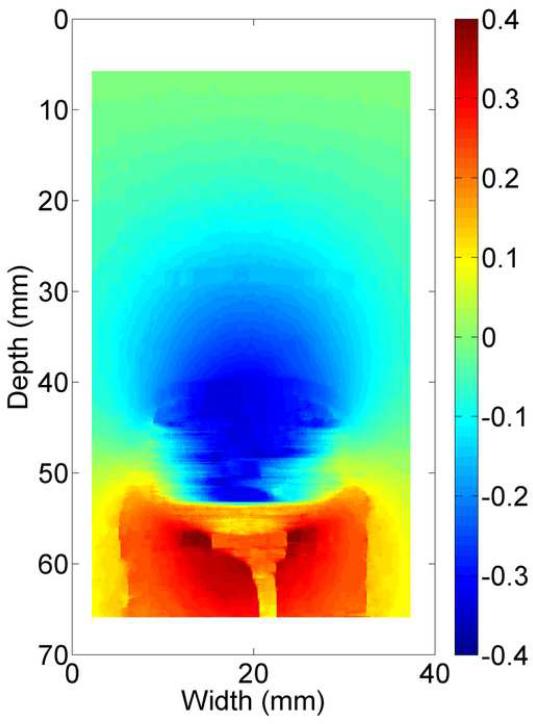
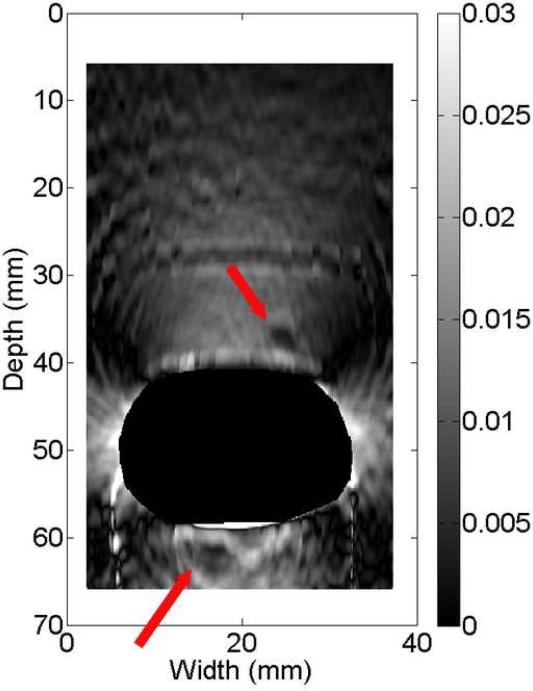
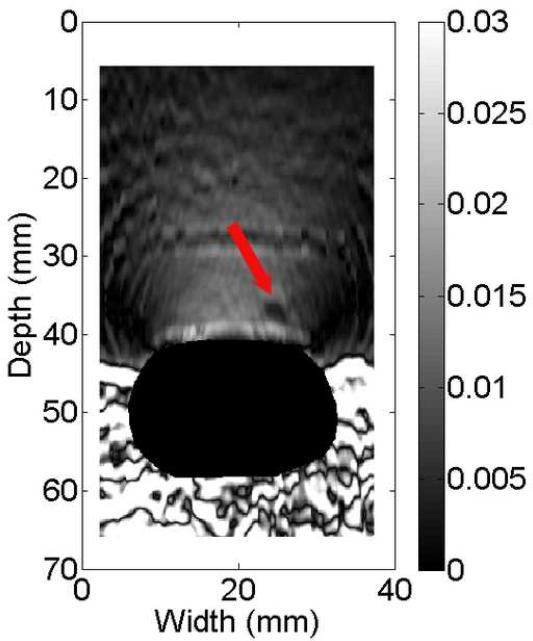
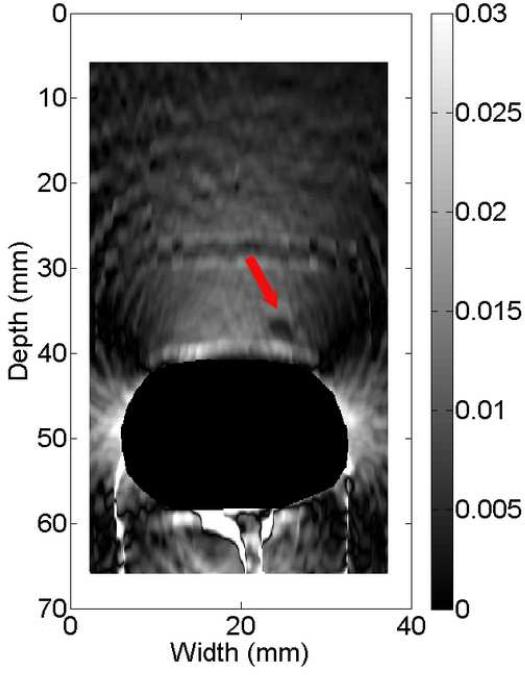
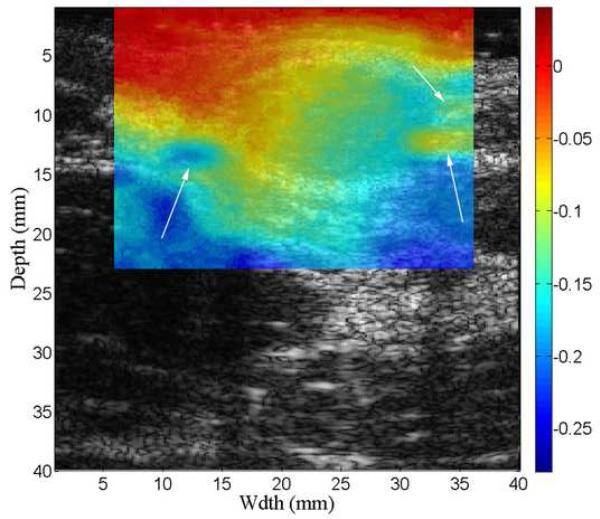
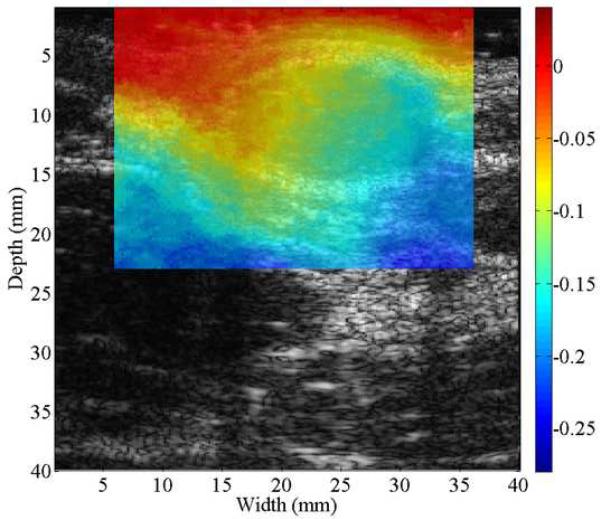
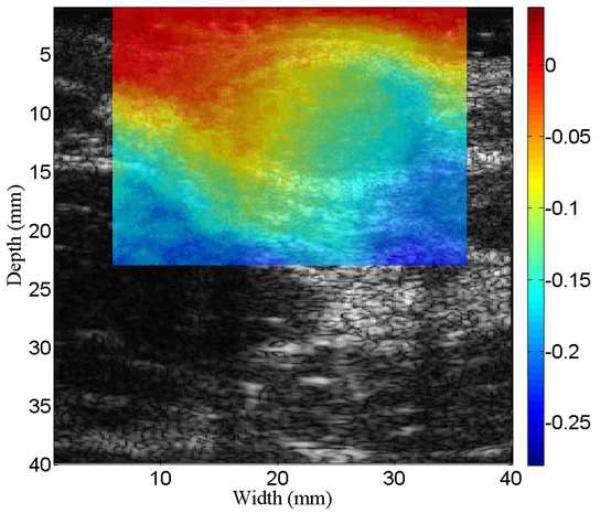
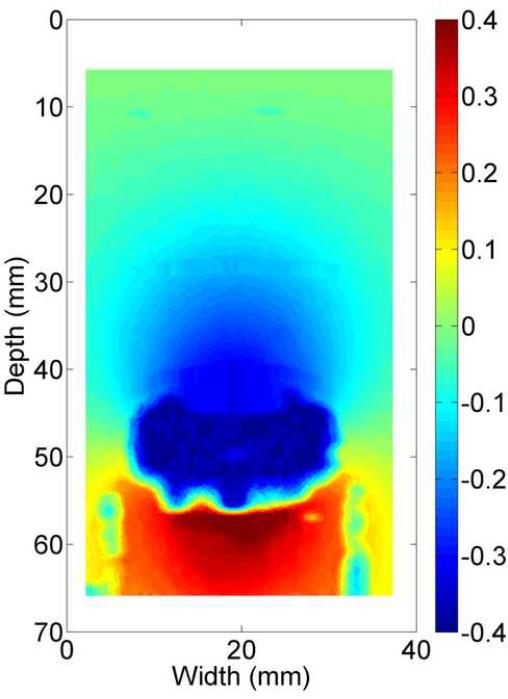
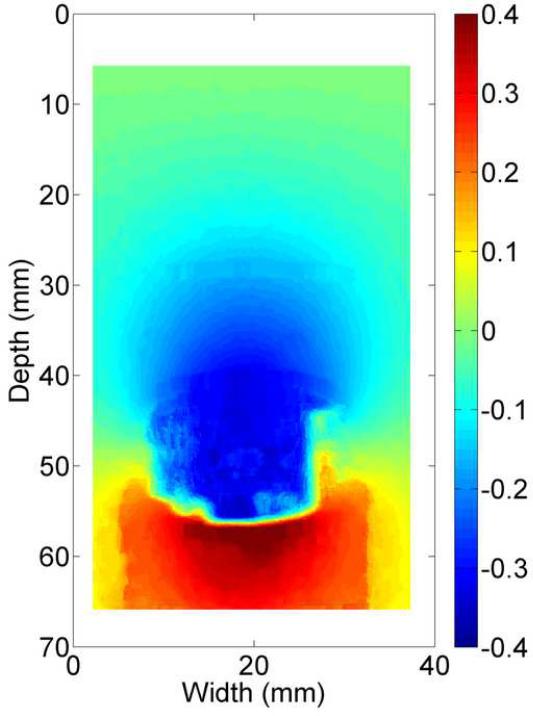
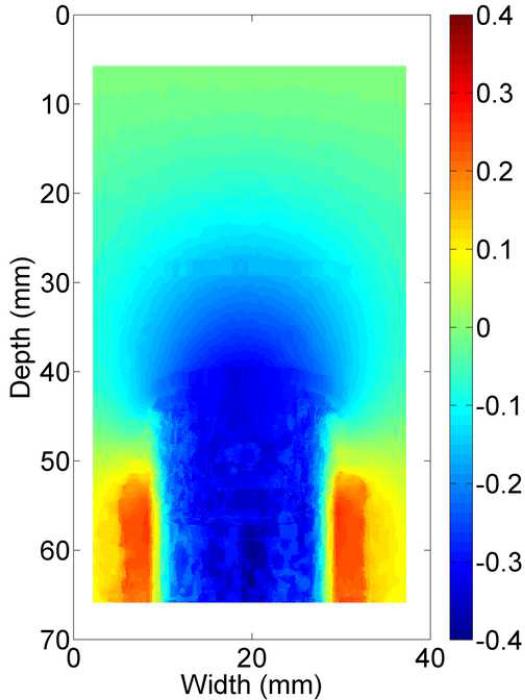
The B-mode image of the tissue-mimicking uterine phantom is shown in Fig. 8(a). Figs. 8 (b)-(d) show the displacement fields estimated by the multi-grid approach, the lateral-guidance approach and the axial-guidance method, respectively. In the image plane, there are two 3-mm spherical inclusions (one above the cavity and one below the cavity; see arrows in Fig. 8(a)). Both inclusions can be visually identified in strain image (Fig. 8(e)) obtained using the multi-grid, but the lower inclusion cannot be seen in strain images (See Fig. 8(f)-(g)) obtained using the lateral and axial guidance methods. Consistent with expectation, three methods performed equally well among regions above the simulated cavity. However, the lateral-guidance approach and the axial-guidance method failed to accurately track motion in the region below the cavity because the assumption of global motion continuity is no longer valid as explained in subsection E of the Materials and Methods Section. From Figs. 8(b)-(d), estimated displacements below the simulated cavity were larger than those above the simulated cavity, though the cavity was symmetric and pressure induced by the injection of safflower oil was likely uniform. The difference noted in Fig. 8 is likely due to gravity, i.e. the upward pressure induced by the injection may be offset by the gravity acting on the upper portion the simulated uterine body whereas the lower portion is supported by the container. The "high" negative displacement region below and around the large cavity (see Fig. 8c) shows results of the wrong predictions by the lateral guidance approach. The normalized cross correlation (NCC) coefficients between pairs of the pre- and motion-compensated post-deformation RF echo fields using the estimated displacement vector fields provide an objective measure of motion tracking accuracy (Jiang et al. 2006). The NCC values for displacement fields displayed in Fig. 8(b)-(d) are 0.989, 0.759 and 0.867, respectively, while the estimated DQM values for the strain images displayed in Figs. 8(e)-(g) are 0.87, 0.67, 0.80, respectively. Furthermore, the estimated NCC values (mean ± standard deviation) among these 10 realizations (i.e. 10 displacement fields under similar deformations) for these three methods are 0.975 ± 0.0001, 0.763 ± 0.002 and 0.889 ± 0.06, respectively. For these same 10 realizations, the estimated DQM values (mean ± standard deviation) among resulting strain images for these three methods (i.e. multi-grid, lateral-guidance and axial-guidance) are 0.898 ± 0.019, 0.656 ± 0.008 and 0.885 ± 0.074, respectively.
Figure 8.
B-mode (a), axial displacement in mm (b-d) and strain (e-g) images obtained from an anthropomorphic uterine phantom using three different speckle tracking methods: (b and e) the multi-grid approach; (c and f) the lateral-guidance approach and (d and g) the axial-guidance approach. The white box on the B-mode image defines the ROI from which the displacements and strains were estimated. The saline with the simulated cavity provides no internal echo signals resulting in signal decorrelation, motion tracking errors and high noise on the strain images. Arrows point to spherical inclusions. The simulateduterine cavity was masked out in all strain images [(e)-(g)] to avoid visual distraction.
C. Influence of Cost Functions
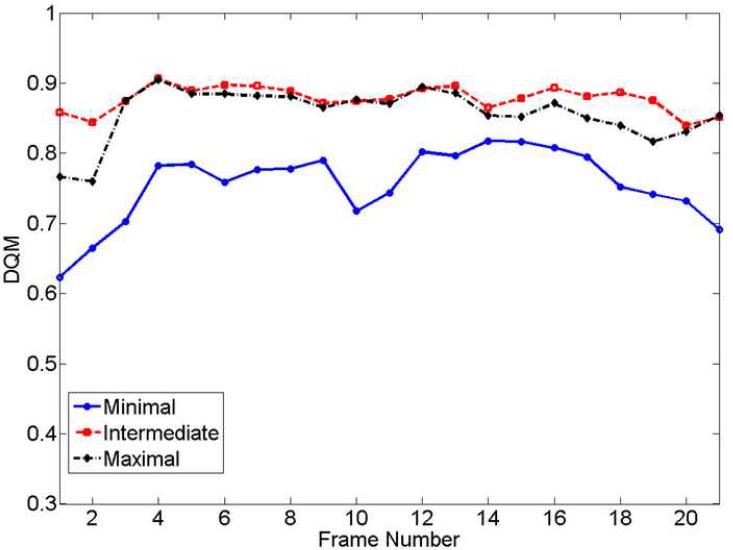
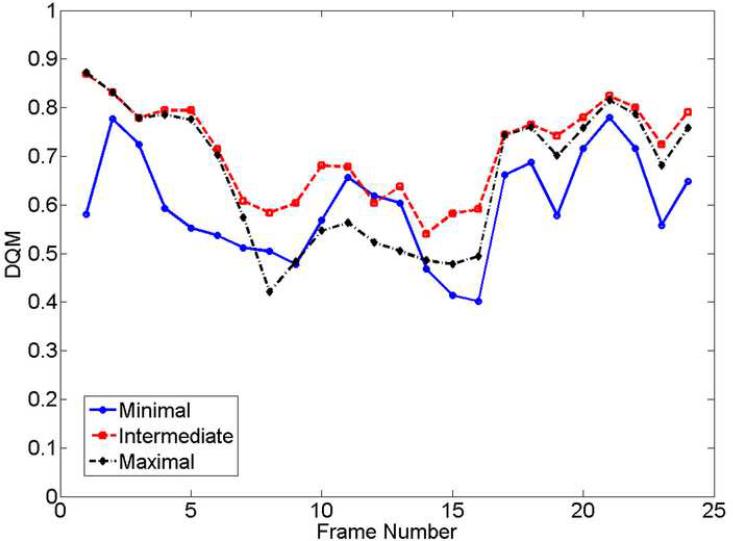
Representative strain images from the in vivo breast fibroadenoma using the multi-grid approach with three different cost functions are displayed in Fig. 9(a)-(b) where the frame-average axial strains are 0.8% and 1.5%, respectively. From the strain images in Fig. 9(a)-(b), we found the intermediate and the maximal constraint cost functions perform equally well, but the minimal constraint function occasionally makes mistakes (see arrows in Figs. 9(a)-(b)). From the displacement images corresponding to the strain images displayed in Fig. 9(a), there are regions on the estimated displacement field (see arrows in Fig. 9(c)) where the minimal constraint cost function doesn't provide sufficient constraint, as compared with the other two cost functions (see Fig. 9(d)-(e)). Such motion discontinuities appeared to be unreasonable given relatively continuous motion presented in this breast data (see the B-mode images in Movie 4). By comparing the DQM values (Fig. 10(a)-(b)) and visual analysis of Movies 4 (0.8%; 21 frames) and Movie 5 (1.5%; 19 frames) there is higher noise in the strain images obtained by using the minimal constraint cost function for this data set.
Figure 9.
B-mode (far left in (a)-(b)) and strain images obtained from in vivo breast fibroadenoma displayed in Fig. 4 using the multi-grid approach with three different cost functions. The strain images in (a) and (b) were obtained by the minimal constraint cost function (middle left), the intermediate constraint cost function (middle right) and the maximal cost function (far right), respectively. The corresponding displacement images (c)-(e) from which the strain images in (a) are also shown. Arrows point to decorrelation noise on strain images resulted from tracking errors on displacement images.
Figure 10.
Plots of the DQM values versus the frame number for the in vivo breast fibroadenoma shown in Fig. 4 obtained using the multi-grid approach with three different cost functions for two frame-average strains: (a) 0.8% and (b) 1.5%.
Fig. 11(a) shows representative strain images of the in vivo thyroid follicular adenoma obtained using the multi-grid approach with three different cost functions. The strain image obtained with a minimal constraint cost function appears to have artifacts (see arrows) due to errors in motion tracking similar to those shown in Fig. 9(c). The entire sequence of the strain images (Movie 6) and the corresponding DQM values are plotted out in Fig. 11(b). The pairing of the pre- and post-deformation RF echo frames was targeted to obtain 0.8% frame-average strains. Both the DQM values and the visualization confirm that the intermediate constraint cost function gives the best overall performance for this thyroid data. In this data set, certain motion discontinuities and large shearing/rotation due to complexity in anatomy are evident (see B-mode images in Movie 6). Therefore, both under-constraint (i.e. minimal constraint cost function) and over-constraint (i.e. maximal constraint cost function) may be prone to errors in the displacement estimation, as expected.
Figure 11.
B-mode (far left) and strain images (a) of an in vivo thyroid follicular adenoma lesion estimated by the multi-grid approach with (middle left image) the “minimal constraint” cost function, (middle right image) the “intermediate constraint” cost function and (far right image) the “maximal constraint” cost function. (b) DQM values versus the frame number. Strain images were obtained by pairing RF frames of data to reach 0.8% of frame-average strain. Arrows in (a) point to the decorrelation noise on strain images.
In the phantom data studied in subsection (b) of Results Section, the presence of the simulated uterine cavity and the wall expansion due to saline injection in the image plane results in a large motion discontinuity but a fairly simple motion field elsewhere. The minimal and intermediate constraint cost functions perform equally well based on the displacement images shown in Fig. 12(a)-(c). Again, the normalized cross correlation (NCC) values estimated between pairs of the pre- and motion-compensated post-deformation RF echo fields using the estimated displacement vector fields is employed to quantitatively assess motion tracking accuracy (Jiang et al. 2006). The NCC values for displacement fields displayed in Fig. 12(a)-(c) are 0.985, 0.973 and 0.796, respectively. The estimated NCC values (mean ± standard deviation) among these 10 realizations (similar deformations) for these three cost functions (minimal, intermediate and maximum) are 0.986 ± 0.0001, 0.975 ± 0.0001 and 0.793 ± 0.06, respectively.
Figure 12.
Displacement images obtained from the TM uterine phantom using the multi-grid approach with: (a) the “minimal constraint” cost function, (b) the “intermediate constraint” cost function and (c) the “maximal constraint” cost function. The corresponding B-mode image of the uterine phantom is shown in Fig. 8(a). Displacement unit is mm.
Discussion
In this work, we demonstrate that a regularized block-matching algorithm with different levels of motion continuity constraints can be effectively used to compute local displacements and strains in media with complex motion. One contribution of this work is the methodological change in providing “prediction” seeds for the later predictive search stage. When the regularized speckle tracking is performed in a coarse grid (5-mm spacing for the multi-grid approach presented above), there are high probabilities for planting several good prediction seeds in each region with disjoint motion patterns. On the other hand, the lateral-guidance and the axial-guidance approaches only provide prediction seeds in much smaller regions, thereby having less chances of success for more complex motion patterns. That is the fundamental reason why both the axial and lateral guidance algorithms failed to predict the tissue motion in regions below the simulated cavity in the uterine phantom (roughly a 2-cm [long axis] by 1.5-cm [short axis] ellipse), resulting in large errors in the displacement estimates. We found that the multi-grid approach accurately calculates local displacements around the simulated cavity, while making large errors within the cavity because of weak scattering signals from the safflower oil (Hobson et al. 2008).
However, the robustness of the multi-grid approach comes with penalties in computational speed, as summarized in Table 2. Our previous work (Hall et al. 2003; Jiang and Hall 2007), demonstrated that both the axial guidance algorithm and the lateral guidance algorithm could achieve real-time frame rates (roughly 15 frames/second) with common computing platforms and employing surrogates for NCC (sum-absolute difference or sum-squared difference cost functions). For a typical 3-cm by 3-cm region of interest, the multi-grid approach requires approximately 9 times the computing time compared to the other two approaches. Of note, all testing was performed with un-optimized code in Matlab (MathWorks Inc. MA) as described in Methods and Materials Section. For example, if the original echo fields were down-sampled by a factor of 4 (instead of the factor of 2 used in current implementation), the computational efficiency could be significantly enhanced. Furthermore, the search on a coarse grid in the multi-grid approach is independent among individual columns in the grid and therefore can be fully parallelized without inter-process communication to avoid problems such as large overhead and deadlock (Tanenbaum and Steen 2002). Therefore, if the code of the multi-grid approach is optimized and runs as a standalone program in a state-of-the-art system, its computational efficiency can be significantly improved toward real time operation.
Table 2.
Comparison of frame rates among three speckle tracking approaches for a typical 3-cm × 3-cm region of interest
| Frame Rate (Frames/Second) | |
|---|---|
| Multi-grid (not being optimized) | 2 |
| Lateral-guidance | 15-20 |
| Axial-guidance | 10-15 |
Overall, we found that the multi-grid approach also gave consistent results for the all data tested, though the improvement of the multi-grid approach compared to the lateral-guidance approach is minimal for some example data (i.e., uni-axial compression used with freehand breast examination; see Figs. 5(a)). With sufficient complexity in the anatomy (i.e. the thyroid follicular adenoma example), the motion prediction based on a column of displacement estimates at the center of ROI is no longer very reliable without a sophisticated error detection and correction algorithm. That is why the axial guidance algorithm, which employs a computationally intensive method for error detection and correction, occasionally performs better than the lateral-guidance approach (see Fig. 7 and Movie 3). In this sense, a more sophisticated error detection and correction scheme without the real-time constraint that we imposed on the axial and lateral-guidance approaches could improve their performance. Nevertheless, obtaining regularized and highly reliable displacement estimation in a coarse grid (i.e. multi-grid approach) covering multiple relatively disjoint motion regions and using that information for motion prediction eliminates the great need for a sophisticated error detection and correction method. That is the reason why the multi-grid approach performs better for the thyroid data.
Another contribution is that we applied the motion regularization (Eqn. (2)) to eliminate large “inter-wavelength” errors (e.g. 10 samples) in motion tracking. When correlation-based methods are used to track tissue motion, if the underlying echo signals were moderately or significantly decorrelated, secondary correlation peaks (typically random) between the pre- and post-compression echo signals could actually be higher than the primary peaks, resulting in large errors in the motion tracking. Appropriate constraints will help to eliminate the large tracking errors resulting from these random secondary correlation peaks. That is why both the lateral guidance and the multi-grid approaches outperform the axial guidance algorithm where the motion regularization (i.e. Eqn.(2)) is not applied. The ideas of using multi-resolution/scale estimation and smoothness constraints to regularize speckle tracking are not new. Several groups (Chaturvedi et al. 1998; Pellot-Barakat et al. 2004; Shi and Varghese 2007; Yeung et al. 1998; Yeung et al. 1998; Zhu et al. 1999) have applied smoothness constraints (with or without multiscale) to speckle tracking. Work presented in this paper focuses on two new directions. First, we modeled the motion estimation problem as an optimization problem that can be solved by a dynamic programming technique, potentially in real-time. To our knowledge, optimization with dynamic programming technique has not been reported in ultrasound-based elasticity imaging, although it has been used in stereo matching problem (Ohta and Kanade 1985). Second, we attempted to use cost functions with different levels of continuity constraints, leading toward an “organ-specific” algorithm design. For instance, for breast elasticity imaging (Pellot-Barakat et al. 2004; Zhu et al. 1999), motion continuity through tight smoothness constraints (i.e. maximal cost function) has been assumed and successfully applied. However, for organs like thyroid, there are tissue interfaces and complex anatomical structures (i.e. trachea, cervical spine, and musculature) in the image plane resulting in more complex motion. Our work shows that a different cost function (i.e. the intermediate cost function) can be designed to improve the speckle tracking. We thought the minimal cost function could help in situations where there is little need to constrain tissue motion estimates. These situations include the presence of large vessels, the existence of inter-organ gap (e.g. liver, kidney and prostate) and intra-organ cavity (e.g. uterine cavity and common carotid artery). Although only limited success has been found in the current minimal constraint cost function, the results reported in this paper certainly warrant further investigations. More importantly, our ongoing research is working toward a heuristic speckle tracking algorithm that is intelligent enough to determine spatially-variant continuity constraints.
One limitation of this study is that the underlying modulus distributions of two in vivo benign lesions were unknown. Without knowing the anticipated strain images, we mainly used the DQM (Jiang et al. 2006) for comparing algorithm performance. We believe it is a judicious choice because the DQM combines the motion tracking accuracy and the consistency among consecutive strain images to assess the fidelity of strain image formation, thereby being relevant for the purpose of this study. As discussed in our previous work (Jiang et al. 2006), the elastographic SNRe (Varghese 1998) is only valid for uniform phantoms and is not applicable for heterogeneous in vivo tissues. As shown in our previous work (Jiang et al. 2006), the DQM values are expected to correlate well with single targets embedded in relatively uniform background in tissue-mimicking phantoms. Our in vivo results (e.g. Figs. 5(c) and 5(d) and Table 1) showed that CNR values are consistent with the DQM values estimated from the breast fibroadenoma lesion where the background is relatively uniform. We are not surprised that the DQM and CNR values are not consistent in the case of the thyroid follicular adenoma (see Table 1 and Fig. 7(b)), because the DQM and CNR are different performance metrics representing the fidelity of strain image formation and target detectability, respectively. We think, in this case, the use of CNR metric for the in vivo thyroid follicular adenoma is problematic because speckle tracking errors often result in very bright spots (i.e. decorrelation noise) in the strain images and significantly affect our ability of interpreting these CNR values.
It is worth noting that the two in vivo lesions provide low contrast strain images (Figs. 4a and 9a) under the 0.8% frame-average strain. The contrast in some strain images will be enhanced under high compressions (e.g. Fig. 9(a) vs. Fig. 9(b)). In this case, more sophisticated motion estimation algorithms are needed because signal decorrelation will likely become more significant under higher compressions. For instance, the un-regularized BMA (i.e. axial-guidance approach) or inappropriately regularized (overconstrained vs. under-constrained) algorithms failed to provide meaningful strain images under the high compression. The contrast of the strain image shown in Figs. 6b-c, where the pathology is a benign thyroid follicular adenoma, is also low (the estimated mean strain ratio between the target and the background is only 0.9) for two possible reasons. First, according to limited mechanical testing results by Lyshchik et al. (2005), the mean elastic modulus ratio between the benign thyroid nodule and the normal thyroid tissue was 2.3 ± 1.7 ( ± standard deviation). When the lesion is only slightly stiffer than its surrounding tissues, strain image contrast will be low. Second, after reviewing Movie 3, contrast change (incremental frame-average strains are both 0.8%) may be related to a nonlinear stress strain relationship. In particular, the relative elastic contrast between the target and background can change as tissue is compressed. Similar contrast changes were observed by our group (Hall et al. 2003) in many benign breast lesions. Unfortunately there is very limited stress-strain data available for thyroid pathologies in the literature to really understand this problem.
In our formulations, Eqn. 3(a) is a total variation function (Vogel 2002) where β will change the shape of the minimal and the intermediate (only the first portion; see Eqn. 3(b)) penalty functions. Since we only regularize motion tracking at the integer sample level (Eqn. (1)), we found results were not sensitive to the selection of β . Therefore, we selected β to be 0.1 for all cases reported above. Referring to the overall cost function, Eqn. (2), different choices of α are equivalent to adjusting the contribution of Φ(Es) to the overall cost. In this study, we selected α to be unity so that both items (i.e. correlation and smoothness constraint) of the cost function were of the same order and effectively used for regularizing tissue motion.
In the future, we plan to extend elasticity imaging to abdominal organs (e.g. liver and kidney) and prostate. These applications require accurate motion estimation in RF echo data sampled in a sector field using curve-linear and phase array transducers. Therefore, the search kernel will be highly distorted if the speckle tracking is performed on RF echo data prior to the scan conversion. Typical block-matching algorithm assumes rigid body motion of the search kernel. However, this assumption is no long valid if a highly distorted search kernel is used to track motion over a large search region. To date, the proposed algorithm and many other speckle tracking algorithms (Pellot-Barakat et al. 2004; Shi and Varghese 2007; Yeung et al. 1998; Zhu and Hall 2002) have only been tested with linear array ultrasound transducers. Further development is underway to extend the proposed algorithm to abdominal elasticity imaging (Fisher et al. 2007) in an application-specific fashion. To deal with non-uniform spacing between adjacent samples in a sector-shaped image plane, we could adaptively choose appropriate tracking parameters (e.g. kernel size and requirements for motion continuity) based on certain local criteria (e.g. depth, center frequency and the nature of the applicable organ). For instance, kernel size can be adaptively adjusted to account for the beam hardening effect.
Conclusions
A modified block-matching algorithm integrated with the Viterbi algorithm for motion regularization is presented. Two implementation schemes were investigated. The multi-grid approach has potential to be a real-time algorithm, while the lateral-guidance approach operates in real-time. The experimental results investigated show that the proposed algorithm outperforms Zhu and Hall's algorithm (Zhu and Hall 2002) for in vivo breast and thyroid data acquired. Our results also demonstrated that the proposed algorithm is capable of tracking in the presence of a large motion discontinuity, thereby enhancing its potential usability in abdominal organs.
Supplementary Material
Acknowledgment
We gratefully acknowledge the support by NIH grants R01CA100373 and R21CA133488 as well as funding from the University of Wisconsin. We are also grateful to colleagues at the Mayo Clinic in Rochester, MN (especially Drs. Nicholas Hangiandreou and Gina Hesley) for the in vivo thyroid data and at the University of Wisconsin (especially Prof. Ernest Madsen and Dr. Maritza Hobson) for providing the uterine phantom data. Last, but not the least, we want to thank Dr. Liexiang Fang at the Ultrasound Division of the Siemens Medical Solution (USA) Inc. for his helpful discussion on dynamic programming.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Reference
- Berridge DL, Winter TC. Saline infusion sonohysterography: technique, indications, and imaging findings. J Ultrasound Med. 2004;23:97–112. doi: 10.7863/jum.2004.23.1.97. [DOI] [PubMed] [Google Scholar]
- Burnside ES, Hall TJ, Sommer AM, Hesley GK, Sisney GA, Svensson WE, Fine JP, Jiang J, Hangiandreou NJ. Differentiating benign from malignant solid breast masses with US strain imaging. Radiology. 2007;245:401–10. doi: 10.1148/radiol.2452061805. [DOI] [PubMed] [Google Scholar]
- Cespedes I, Huang Y, Ophir J, Spratt S. Methods for estimation of subsample time delays of digitized echo signals. Ultrason Imaging. 1995;17:142–71. doi: 10.1177/016173469501700204. [DOI] [PubMed] [Google Scholar]
- Chaturvedi P, Insana MF, Hall TJ. 2-D companding for noise reduction in strain imaging. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1998;45:179–91. doi: 10.1109/58.646923. [DOI] [PubMed] [Google Scholar]
- Fatemi M, Wold LE, Alizad A, Greenleaf JF. Vibro-acoustic tissue mammography. IEEE Trans Med Imaging. 2002;21:1–8. doi: 10.1109/42.981229. [DOI] [PubMed] [Google Scholar]
- Fisher T, Jiang J, Hall TJ. Volumetric strain imaging. 2007 IEEE Ultrasonics Symposium; 27-31 Oct. 2007; New York City, NY, USA: IEEE; 2007. [Google Scholar]
- Fung YC. Biomechanics : mechanical properties of living tissues. Springer-Verlag; New York: 1993. [Google Scholar]
- Garra BS, Cespedes EI, Ophir J, Spratt SR, Zuurbier RA, Magnant CM, Pennanen MF. Elastography of breast lesions: initial clinical results. Radiology. 1997;202:79–86. doi: 10.1148/radiology.202.1.8988195. [DOI] [PubMed] [Google Scholar]
- Hall TJ, Jiang J, Zhu Y, Cook LT. Noise reduction strategies in freehand elasticity imaging. Proceedings of 2002 IEEE International Ultrasonics Symposium; 8-11 Oct. 2002; Munich, Germany: IEEE; 2002. pp. 1877–80. [Google Scholar]
- Hall TJ, Zhu Y, Spalding CS. 2003;29:427–35. doi: 10.1016/s0301-5629(02)00733-0. [DOI] [PubMed] [Google Scholar]
- Hobson M, Madsen E, Frank G, Shi H, Jiang J, Hall T, Varghese T. Anthropomorphic uterine phantoms for US strain imaging. Ultrasound in Medicine & Biology. 2008;34:1622–37. doi: 10.1016/j.ultrasmedbio.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itoh A, Ueno E, Tohno E, Kamma H, Takahashi H, Shiina T, Yamakawa M, Matsumura T. Breast disease: clinical application of US elastography for diagnosis. Radiology. 2006;239:341–50. doi: 10.1148/radiol.2391041676. [DOI] [PubMed] [Google Scholar]
- Jiang J, Hall TJ. A regularized real-time motion tracking algorithm using dynamic programming for ultrasonic strain imaging. 2006 IEEE Ultrasonics Symposium; 3-6 Oct. 2006; Vancouver, BC, Canada: IEEE; 2006. p. 4. [Google Scholar]
- Jiang J, Hall TJ. A parallelizable real-time motion tracking algorithm with applications to ultrasonic strain imaging. Phys Med Biol. 2007;52:3773–90. doi: 10.1088/0031-9155/52/13/008. [DOI] [PubMed] [Google Scholar]
- Jiang J, Hall TJ, Sommer AM. A novel performance descriptor for ultrasonic strain imaging: a preliminary study. IEEE Trans Ultrason Ferroelectr Freq Control. 2006;53:1088–102. doi: 10.1109/tuffc.2006.1642508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li PC, Lee WN. An efficient speckle tracking algorithm for ultrasonic imaging. Ultrason Imaging. 2002;24:215–28. doi: 10.1177/016173460202400402. [DOI] [PubMed] [Google Scholar]
- Lubinski MA, Emelianov SY, O'Donnell M. Adaptive strain estimation using retrospective processing. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1999;46:97–107. doi: 10.1109/58.741428. [DOI] [PubMed] [Google Scholar]
- Lyshchik A, Higashi T, Asato R, Tanaka S, Ito J, Mai J, Pellot-Barakat C, Insana MF, Brill AB, Saga T, Hiraoka M, Togashi K, Yshchik A. Thyroid gland tumor diagnosis in US elastography. Radiology. 2005;237:202–211. doi: 10.1148/radiol.2363041248. [DOI] [PubMed] [Google Scholar]
- Muradali D, Kulkarni S. Sonography of the breast: to core or not to core? Can Assoc Radiol J. 2005;56:276–88. [PubMed] [Google Scholar]
- Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J Acoust Soc Am. 2001;110:625–34. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- O'Donnell M, Skovoroda AR, Shapo BM, Emelianov SY. Internal displacement and strain imaging using ultrasonic speckle tracking. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 1994;41:314–25. [Google Scholar]
- Ohta Y, Kanade T. STEREO BY INTRA- AND INTER-SCANLINE SEARCH USING DYNAMIC PROGRAMMING. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1985;PAMI:7–139. doi: 10.1109/tpami.1985.4767639. [DOI] [PubMed] [Google Scholar]
- Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrason Imaging. 1991;13:111–34. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- Parker KJ, Huang SR, Musulin RA, Lerner RM. Tissue response to mechanical vibrations for “sonoelasticity imaging”. Ultrasound Med Biol. 1990;16:241–6. doi: 10.1016/0301-5629(90)90003-u. [DOI] [PubMed] [Google Scholar]
- Pellot-Barakat C, Frouin F, Insana MF, Herment A. Ultrasound elastography based on multiscale estimations of regularized displacement fields. IEEE Trans Med Imaging. 2004;23:153–63. doi: 10.1109/TMI.2003.822825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesavento A, Lorenz A, Siebers S, Ermert H. New real-time strain imaging concepts using diagnostic ultrasound. Phys Med Biol. 2000;45:1423–35. doi: 10.1088/0031-9155/45/6/302. [DOI] [PubMed] [Google Scholar]
- Rabiner LR. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proceedings of the IEEE. 1989;77:257–86. [Google Scholar]
- Regner DM, Hesley GK, Hangiandreou NJ, Morton MJ, Nordland MR, Meixner DD, Hall TJ, Farrell MA, Mandrekar JN, Harmsen WS, Charboneau JW. Breast lesions: evaluation with US strain imaging--clinical experience of multiple observers. Radiology. 2006;238:425–37. doi: 10.1148/radiol.2381041336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revell J, Mirmehdi M, McNally D. Computer vision elastography: speckle adaptive motion estimation for elastography using ultrasound sequences. IEEE Trans Med Imaging. 2005;24:755–66. doi: 10.1109/TMI.2005.848331. [DOI] [PubMed] [Google Scholar]
- Shi H, Varghese T. Two-dimensional multi-level strain estimation for discontinuous tissue. Phys Med Biol. 2007;52:389–401. doi: 10.1088/0031-9155/52/2/006. [DOI] [PubMed] [Google Scholar]
- Shiina T, Nitta N, Ueno E, JC B. Real Time Tissue Elasticity Imaging Using the Combined Autocorrelation Method. Journal of Medical Ultrasonics. 2002;26:119–28. doi: 10.1007/BF02481234. [DOI] [PubMed] [Google Scholar]
- Song XM, Pogue BW, Jiang SD, Doyley MM, Dehghani H, Tosteson TD, Paulsen D. Automated region detection based on the contrast-to-noise ratio in near-infrared tomography. Applied Optics. 2004;43:1053–1062. doi: 10.1364/ao.43.001053. [DOI] [PubMed] [Google Scholar]
- Stavros AT. Breast ultrasound. Lippincott Williams & Wilkins; Philadelphia: 2004. [Google Scholar]
- Tanenbaum AS, Steen Mv. Distributed systems : principles and paradigms. Prentice Hall; Upper Saddle River, N.J.: 2002. [Google Scholar]
- Tavassoli FA. Pathology of the breast. McGraw-Hill; New York: 1999. [Google Scholar]
- Thevenaz P, Blu T, Unser M. Interpolation revisited. IEEE Transactions on Medical Imaging. 2000;19:739–58. doi: 10.1109/42.875199. [DOI] [PubMed] [Google Scholar]
- Varghese T, Ophir J. Performance optimization in elastography: multicompression with temporal stretching. Ultrason Imaging. 1996;18:193–214. doi: 10.1177/016173469601800303. [DOI] [PubMed] [Google Scholar]
- Varghese T, Ophir J. Theoretical framework for performance characterization of elastography: The strain filter. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 1997;44:164–172. doi: 10.1109/58.585212. [DOI] [PubMed] [Google Scholar]
- Viterbi AJ. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 1967;IT-13:260–69. [Google Scholar]
- Vogel CR. Computational methods for inverse problems. Society for Industrial and Applied Mathematics; Philadelphia: 2002. [Google Scholar]
- Yeung F, Levinson SF, Fu D, Parker KJ. Feature-adaptive motion tracking of ultrasound image sequences using a deformable mesh. IEEE Trans Med Imaging. 1998;17:945–56. doi: 10.1109/42.746627. [DOI] [PubMed] [Google Scholar]
- Yeung F, Levinson SF, Parker KJ. Multilevel and motion model-based ultrasonic speckle tracking algorithms. Ultrasound Med Biol. 1998;24:427–41. doi: 10.1016/s0301-5629(97)00281-0. [DOI] [PubMed] [Google Scholar]
- Walker RA. The complexities of breast cancer desmoplasia. Breast Cancer Res. 2001;3:143–5. doi: 10.1186/bcr287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y, Chaturvedi P, Insana MF. Strain imaging with a deformable mesh. Ultrason Imaging. 1999;21:127–46. doi: 10.1177/016173469902100204. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Hall TJ. A modified block matching method for real-time freehand strain imaging. Ultrason Imaging. 2002;24:161–76. doi: 10.1177/016173460202400303. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.