Abstract
Mediation models are widely used, and there are many tests of the mediated effect. One of the most common questions that researchers have when planning mediation studies is, “How many subjects do I need to achieve adequate power when testing for mediation?” This article presents the necessary sample sizes for six of the most common and the most recommended tests of mediation for various combinations of parameters, to provide a guide for researchers when designing studies or applying for grants.
Since the publication of Baron and Kenny’s (1986) article describing a method to evaluate mediation, the use of mediation models in the social sciences has increased dramatically. Using the Social Science Citation Index, MacKinnon, Lockwood, Hoffman, West, and Sheets (2002) found more than 2,000 citations of Baron and Kenny’s article. A more recent search of the Social Science Citation Index that we conducted found almost 8,000 citations, though a number of these publications examined moderation rather than mediation.
Although there are a number of methods to test for mediation, including structural equation modeling (SEM; Cole & Maxwell, 2003; Holmbeck, 1997; Kenny, Kashy, & Bolger, 1998) and bootstrapping (MacKinnon, Lockwood, & Williams, 2004; Shrout & Bolger, 2002), many researchers prefer to use regression-based tests. MacKinnon et al. (2002) investigated power empirically for common sample sizes for many of these tests. However, for researchers planning studies, it would be more useful to know the sample size required for .8 power to detect an effect. The purpose of this article is to offer guidelines for researchers in determining the sample size necessary to conduct mediational studies with .8 statistical power.
MEDIATION
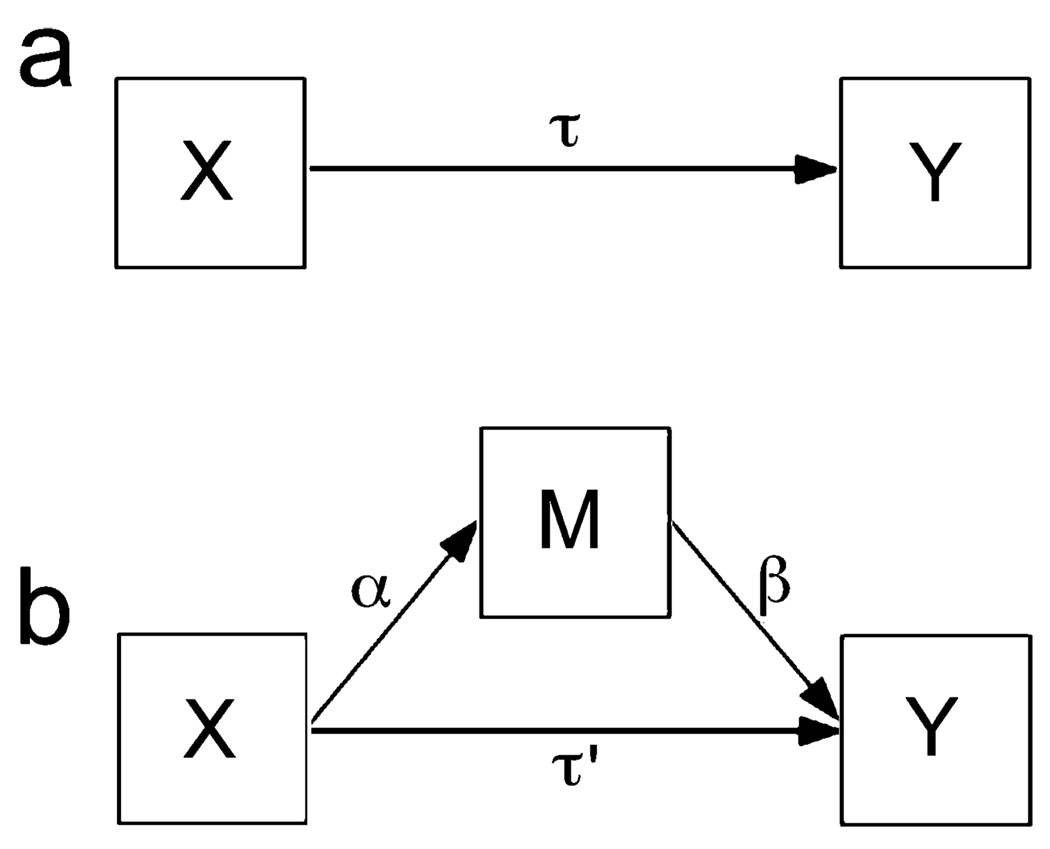
In a mediation model, the effect of an independent variable (X) on a dependent variable (Y) is transmitted through a third intervening, or mediating, variable (M). That is, X causes M, and M causes Y. Figure 1 shows the path diagrams for a simple mediation model; the top diagram represents the total effect of X on Y, and the bottom diagram represents the indirect effect of X on Y through M and the direct effect of X on Y controlling for M. If M is held constant in a model in which the mediator explains all of the variation between X and Y (i.e., a model in which there is complete mediation), then the relationship between X and Y is zero.
Fig. 1.
Path diagrams for (a) the total effect of the independent variable on the dependent variable and (b) the indirect effect of the independent variable on the dependent variable through the mediator variable.
The path diagrams in Figure 1 can be expressed in the form of three regression equations:
| (1) |
| (2) |
| (3) |
where τ̂ is the estimate of the total effect of X on Y, τ̂′ is the estimate of the direct effect of X on Y adjusted for M, β̂ is the estimate of the effect of M on Y adjusted for X, and α̂ is the estimate of the effect of X on M. ζ̂1, ζ̂2, and ζ̂3 are the intercepts. The product α̂β̂ is known as the mediated or indirect effect.
TESTS OF THE MEDIATED EFFECT
MacKinnon et al. (2002) placed the different regression tests of mediation into three categories: tests of causal steps, tests of the difference in coefficients, and tests of the product of coefficients. In the causal-steps approach, each of the four steps in the causal process must be true for mediation to be present (Judd & Kenny, 1981a, 1981b). The four steps are as follows:
The total effect of X on Y (τ̂) must be significant.
The effect of X on M (α̂) must be significant.
The effect of M on Y controlled for X (β̂) must be significant.
The direct effect of X on Y adjusted for M (τ̂′) must be non-significant.
Models in which all four steps are satisfied are called fully mediated models. A model in which Step 4 is relaxed so that the requirement is only |τ̂′| < |τ̂|, rather than that τ̂′ be nonsignificant, is called a partially mediated model (Baron & Kenny, 1986).
Difference-in-coefficients tests are conducted by taking the difference between the overall effect of X on Y and the direct effect of X on Y adjusted for M, τ̂ − τ̂′, and dividing by the standard error of the difference. This value is then compared against a t distribution to test for significance. The main difference between the various difference-in-coefficients tests is that they use different formulas for calculating the standard error of the difference.
In the product-of-coefficients tests, the product of the coefficient from the independent variable to the mediator, α̂, and the coefficient from the mediator to the dependent variable adjusted for the independent variable, β̂, is divided by the standard error of the product to create a test statistic. This test statistic is then compared against a normal distribution to test for significance. Despite conceptual differences between the product-of-coefficients tests and the difference-in-coefficients tests, MacKinnon, Warsi, and Dwyer (1995) showed that τ̂ − τ̂′ is equal to α̂β̂ for ordinary least squares regression, although this relationship does not hold for logistic regression models. Much as the difference-in-coefficients tests vary in the formulas used to calculate the standard error of the difference, the main difference among the various product-of-coefficients tests is the formula used to calculate the standard error of the product. A variation on the product-of-coefficients tests uses resampling. If a large number of samples are taken from the original sample with replacement, the parameter of interest, in this case the indirect effect αβ, can be calculated for each new sample, forming a bootstrap distribution of that parameter, and confidence intervals can be formed to test for mediation.
LITERATURE SURVEY
Given the large number of methods to test for mediation, we conducted a literature survey to examine which methods were most often used by psychologists. We examined articles in two psychological journals, the Journal of Consulting and Clinical Psychology and the Journal of Applied Psychology. To be included in the literature survey, an article had to be published between 2000 and 2003 and test at least one mediational relationship; meta-analyses and articles mentioning mediation, but not directly testing for mediation, were not included.
The survey identified a total of 166 articles reporting mediation studies of 189 independent samples. The studies were coded by the method used to test for mediation (as reported by the author or authors): (a) causal-steps tests not using SEM software (e.g., hierarchical regression), (b) tests of the indirect effect (i.e., non-SEM product-of-coefficients tests), (c) causal-steps tests using SEM software to fit nested models, (d) tests of overall model fit using SEM software, and (e) resampling tests. Researchers reported using some form of the non-SEM causal-steps test of mediation 5 times more than any of the other methods, and no studies utilized resampling tests (Table 1).
TABLE 1.
Results of the Literature Survey: Methods Used to Test for Mediation
| Method | Frequency | Percentage of studies |
Median sample size |
Upper and lower quartiles of sample size |
|---|---|---|---|---|
| Causal steps (non-SEM) | 134 | 70.90 | 159.5 | [86, 325] |
| Indirect effect | 22 | 11.64 | 142.5 | [115, 285] |
| SEM—nested models | 26 | 13.76 | 239.5 | [152, 413] |
| SEM—overall model fit | 26 | 13.76 | 340.5 | [189.5, 778] |
| Resampling | 0 | 0.00 | — | — |
| All methods | — | — | 187 | [107, 352] |
Note. Dashes indicate that the value was not applicable. Percentages add up to more than 100% because some of the studies used more than one method to test for mediation. SEM = structural equation modeling.
In addition to coding the methods used, we examined the sample sizes of the studies in the survey. Table 1 shows the median sample size for each method. Methods not employing SEM software had smaller median sample sizes than methods that did use SEM software. Table 2 lists the frequency of sample sizes for all methods combined. The smallest sample size was 20, and the largest sample size was 16,466. The median sample size for all experiments was 187 subjects (lower quartile = 107, upper quartile = 352), and 18 of the studies used samples larger than 1,000.
TABLE 2.
Results of the Literature Survey: Frequency of Sample Sizes for Mediational Testing
| Sample size | Frequency | Percentage of studies |
Cumulative percentage |
|---|---|---|---|
| 20–50 | 11 | 5.82 | 5.82 |
| 51–100 | 31 | 16.40 | 22.22 |
| 101–150 | 34 | 17.99 | 40.21 |
| 151–200 | 25 | 13.23 | 53.44 |
| 201–250 | 14 | 7.41 | 60.85 |
| 251–300 | 15 | 7.94 | 68.78 |
| 301–350 | 11 | 5.82 | 74.60 |
| 351–400 | 10 | 5.29 | 79.89 |
| 401–500 | 3 | 1.59 | 81.48 |
| 501–600 | 10 | 5.29 | 86.77 |
| 601–750 | 2 | 1.06 | 87.83 |
| 751–1,000 | 5 | 2.65 | 90.48 |
| 1,001–1,250 | 8 | 4.23 | 94.71 |
| 1,251–1,500 | 1 | 0.53 | 95.24 |
| > 1,500 | 9 | 4.76 | 100.00 |
PRIOR RESEARCH
Although the non-SEM causal-steps tests were found to be used 5 times more often than any of the other tests, concerns over the statistical power of these methods in certain situations have been raised. Statistical power refers to the sensitivity of a null-hypothesis test to detect an effect when an effect is present (Neyman & Pearson, 1933). Power is equal to 1 minus the Type II error rate (i.e., the probability of failing to reject the null hypothesis when an effect is present; Cohen, 1988). In psychology, power is conventionally considered adequate at .8 (Cohen, 1990).
MacKinnon et al. (2002) conducted a simulation study to compare 14 tests of mediation: 3 causal-steps tests, 4 difference-in-coefficients tests, and 7 product-of-coefficients tests. Empirical statistical power for select sample sizes (i.e., 50, 100, 200, 500, and 1,000) was found to be very low for the causal-steps tests and low for the rest of the tests except for 4 tests also found to have inflated Type I error rates.
MacKinnon et al. (2004) compared the confidence limits for the indirect effect, αβ, from MacKinnon and Lockwood’s (2001) asymmetric confidence-interval test with more traditional symmetric confidence intervals and with confidence intervals from six resampling methods. For the selected sample sizes, power was lowest and Type I error rates the highest for the jackknife and traditional z tests, followed by the percentile bootstrap, bootstrap T, and Monte Carlo test. Power and Type I error rates were better for the bootstrap Q and the asymmetric confidence-interval test. The bias-corrected bootstrap had the highest power of the tests, although it was found to have elevated Type I error rates in some conditions.
METHOD
The goal of this article is to present sample sizes necessary for .8 power for the most common (according to the literature survey) and the most recommended tests of mediation. To that end, we discuss six tests.
The Tests
Baron and Kenny’s Causal-Steps Test
Baron and Kenny’s (1986) causal-steps test is by far the most commonly used test of mediation. As Baron and Kenny suggested, in the social sciences, partial mediation is a more realistic expectation than complete mediation. Hence, the four steps tested are
The total effect of X on Y (τ̂) must be significant.
The effect of X on M (α̂) must be significant.
The effect of M on Y controlled for X (β̂) must be significant.
The effect of X on Y controlled for M (τ̂′) must be smaller than the total effect of X on Y (τ̂).
For one to conclude that mediation is present, each of the four steps must be satisfied using Equations 1, 2, and 3.
Joint Significance Test
A variation of Baron and Kenny’s (1986) causal-steps test is the joint significance test, described by MacKinnon et al. (2002). The joint significance test ignores τ̂ and uses the significance of the α̂ and β̂ coefficients to analyze mediation. If both α̂ and β̂ are found to be significant, mediation is present.
Sobel First-Order Test
The Sobel (1982) first-order test is the most common product-of-coefficients test and assesses the presence of mediation by dividing the indirect effect, α̂β̂, by the first-order delta-method standard error of the indirect effect:
| (4) |
This value is then compared against a standard normal distribution to test for significance. If significance is found, mediation is considered to be present.
PRODCLIN
One problem with the product-of-coefficient tests, like the Sobel (1982) test, is that they rely on normal theory, and the distribution of the product of two normally distributed random variables, in this case α and β, is not normally distributed for most values of those variables (Lomnicki, 1967; Springer & Thompson, 1966). MacKinnon and Lockwood (2001) developed a method of testing mediation by using tables of critical values in Meeker, Cornwell, and Aroian (1981) to create asymmetric confidence intervals based on the distribution of the product of two variables. We (MacKinnon, Fritz, Williams, & Lockwood, in press) have since improved on this method by computing the critical values directly using a Fortran program called PRODCLIN, which was derived from a previous Fortran program called FNPROD (Miller, 1997). PRODCLIN is available for download on the Web (http://www.public.asu.edu/~davidpm/ripl/Prodclin/).
PRODCLIN requires standardized value of α̂ and β̂ (i.e., zα = α̂/σ̂α, zβ = β̂/σ̂β) and the Type I error rate as input. PRODCLIN then returns the corresponding standardized critical values. These standardized values are then converted back into the original metric of α̂ and β̂ using the formula
| (5) |
Then, confidence limits are computed using the formula
| (6) |
for each standardized critical value from Equation 5, where σ̂αβ is the Sobel first-order standard error from Equation 4. If the confidence interval does not contain zero, then the mediated effect is significant. A newer version of the program, PRODCLIN2, allows the user to input the values of α̂, β̂, σ̂α, and σ̂β directly and returns the corresponding asymmetric confidence interval automatically.
Percentile Bootstrap
The percentile bootstrap test of mediation requires a random sample to be taken from the original data with replacement. The values for α̂ and β̂ are then found for this new, bootstrap sample, and the indirect effect, α̂β̂, is computed. This process of taking bootstrap samples and computing the indirect effect is then repeated a large number of times. The large number of estimates of the indirect effect forms a bootstrap distribution. The percentile bootstrap test takes the bootstrap estimates of the indirect effect that correspond to the ω/2 and the 1 − ω/2 percentiles of the bootstrap sample distribution to form a 100(1 − ω)% confidence interval, where ω is equal to the Type I error rate (Efron & Tibshirani, 1993; Manly, 1997). Mediation is said to occur if this confidence interval does not contain zero.
Bias-Corrected Bootstrap
The bias-corrected bootstrap test of mediation is the same as the percentile bootstrap test of mediation, except that it corrects for skew in the population. The problem with the percentile bootstrap is that it is possible that the confidence interval will not be centered on the true parameter value. The bias-corrected bootstrap contains a correction for the bias created by the central tendency of the estimate (Efron & Tibshirani, 1993; Manly, 1997). The correction is made under the assumption that there is a monotonically increasing function T such that T(θ̂) is normally distributed with
| (7) |
| (8) |
where z0 is the bias, or the proportion of bootstrap-sample parameter estimates that are below the parameter estimate of the original sample. The resulting upper and lower confidence limits are
| (9) |
| (10) |
where p = 1 − ω/2 and zp = 100 * p. Mediation is tested by determining whether or not the confidence interval contains zero.
Empirical Power
The method for estimating power in this project was empirically based. Simulations were used to empirically compute power for the six different tests of mediation. All single-sample simulations were conducted using SAS Version 8.2 (SAS Institute, 2004), and all resampling simulations were conducted using R Version.2.2.0 (R Development Core Team, 2006). For each simulation, the values for parameters α, β, and τ′ were varied. For all three, the parameter values included 0.14, 0.39, and 0.59, corresponding to Cohen’s (1988) criteria for small (2% of the variance), medium (13% of the variance), and large (26% of the variance) effect sizes, respectively.1 For α and β, the value 0.26, approximately halfway between the values for small and medium effects, was also used; for τ′, the value 0, simulating complete mediation, was added. All 64 possible combinations of α, β, and τ′ (small-small-zero, small-small-small, small-small-medium, small-small-large, small-medium-zero, etc.) were investigated.
To estimate power empirically for the nonresampling tests, we generated a sample of size N from a normal distribution with a mean of 0 and a variance of 1 using the random-number generator (RANNOR) in SAS. Next, X was used to calculate scores for both the mediating variable, M, and the dependent variable, Y, using Equations 2 and 3; random residual error was added from a normal distribution with a mean of 0 and a variance of 1. All of the variables, X, M, and Y, were modeled as continuous variables.
Each of the four single-sample tests was then used to determine the presence of mediation in the simulated data. This process of generating data sets for a specific sample size, running regression analyses, and then testing for significance was repeated a total of 100,000 times for each sample size. The proportion of the replications in which the effect was deemed significant was the measure of power for that sample size. Initial sample sizes were estimated using results from MacKinnon et al. (2002, 2004). Empirical power results from the simulations for the initial sample-size estimates were then compared to .8, and the sample sizes were adjusted accordingly; that is, if the empirical power estimate was larger than .8, the sample size for the next simulation was decreased, and if the empirical power estimate was smaller than .8, the sample size was increased. This iterative process was repeated until the empirical power estimate was within .001 of .8. All fractional sample sizes were rounded up to the next whole number.
For the percentile and bias-corrected bootstrap tests of mediation, 2,000 bootstrap samples of size N were taken from the original sample of size N with replacement, and the value of the indirect effect was calculated for each bootstrap sample. These 2,000 bootstrap estimates were used to construct confidence intervals for the indirect effect for both the percentile and the bias-corrected bootstrap tests; these confidence intervals were then tested for significance by examining whether or not they contained zero. This process of generating data sets, taking bootstrap samples, and then testing for significance was done a total of 1,000 times for each sample size. Power was then equal to the number of times out of 1,000 that the resampling confidence intervals detect the mediated effect.
RESULTS
Complete results are shown in Table 3. The sample sizes necessary to achieve .8 power in Baron and Kenny’s (1986) test were very large for all of the complete-mediation (τ′ = 0) conditions compared with the partial-mediation conditions; the largest sample size was 20,886, for the small-small-zero condition (α = 0.14, β = 0.14, τ′ = 0). As τ′ increased, the required sample size decreased for all combinations of α and β. Even allowing τ′ to be only slightly larger than zero (i.e., τ′ = 0.14) reduced the sample-size requirement to 562 when α and β were both small.
TABLE 3.
Empirical Estimates of Sample Sizes Needed for .8 Power
| Condition | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | SS | SH | SM | SL | HS | HH | HM | HL | MS | MH | MM | ML | LS | LH | LM | LL |
| BK (τ′ = 0) | 20,886 | 6,323 | 3,039 | 1,561 | 6,070 | 1,830 | 883 | 445 | 2,682 | 820 | 397 | 204 | 1,184 | 364 | 175 | 92 |
| BK (τ′ = .14) | 562 | 445 | 427 | 414 | 444 | 224 | 179 | 153 | 425 | 178 | 118 | 88 | 411 | 147 | 84 | 53 |
| BK (τ′ = .39) | 531 | 403 | 402 | 403 | 405 | 158 | 124 | 119 | 405 | 125 | 75 | 59 | 405 | 122 | 60 | 38 |
| BK (τ′ = .59) | 530 | 404 | 402 | 403 | 406 | 158 | 124 | 120 | 405 | 125 | 74 | 58 | 404 | 122 | 59 | 36 |
| Joint significance | 530 | 402 | 403 | 403 | 407 | 159 | 124 | 120 | 405 | 125 | 74 | 58 | 405 | 122 | 59 | 36 |
| Sobel | 667 | 450 | 422 | 412 | 450 | 196 | 144 | 127 | 421 | 145 | 90 | 66 | 410 | 129 | 67 | 42 |
| PRODCLIN | 539 | 402 | 401 | 402 | 402 | 161 | 125 | 120 | 404 | 124 | 74 | 57 | 404 | 121 | 58 | 35 |
| Percentile bootstrap | 558 | 412 | 406 | 398 | 414 | 162 | 126 | 122 | 404 | 124 | 78 | 59 | 401 | 123 | 59 | 36 |
| Bias-corrected bootstrap | 462 | 377 | 400 | 385 | 368 | 148 | 115 | 118 | 391 | 116 | 71 | 53 | 396 | 115 | 54 | 34 |
Note. All sample sizes have been rounded up to the next whole number. In the condition labels, the first letter refers to the size of the α path, and the second letter refers to the size of the β path; S = 0.14, H = 0.26, M = 0.39, and L = 0.59 (e.g., condition SM is the condition with α = 0.14 and β = 0.39). All results, except for those for Baron and Kenny’s (1986) test (BK), have been collapsed across τ′ conditions.
Results for the Sobel (1982) first-order test show that it was more powerful than Baron and Kenny’s (1986) test for all of the τ′ = 0 conditions. However, for conditions where τ′ > 0, Baron and Kenny’s test performed either the same as the Sobel test or better, requiring a smaller sample size to attain the same statistical power.
The joint significance and the PRODCLIN tests required approximately the same sample sizes for all conditions. They were more powerful than Baron and Kenny’s (1986) test for the τ′ = 0 and τ′ = 0.14 conditions and more powerful than the Sobel test for all parameter combinations. It should be noted that the sample-size requirement for .8 power did not change for the joint significance, Sobel, or PRODCLIN tests as τ′ increased, so the results in Table 3 have been collapsed across τ′ conditions for these tests.
The results from the resampling tests are also shown in Table 3. The percentile bootstrap was found to require a smaller sample size than the Sobel test and Baron and Kenny’s (1986) tests for many conditions when τ′ = 0, but a slightly larger sample size than many of the other tests. The results for the bias-corrected bootstrap showed it to be consistently the most powerful test across conditions. As did the Sobel, joint significance, and PRODCLIN tests, the percentile and bias-corrected bootstrap yielded identical results for the different τ′ conditions, and results are therefore collapsed across these conditions in the table.
DISCUSSION
The most important result from this study is the finding that for Baron and Kenny’s (1986) test, a sample size of at least 20,886 is necessary to achieve .8 power in the small-small-zero (α = 0.14, β = 0.14, τ′ = 0) condition. Although this seems to be an incredibly large sample-size requirement, it is important to remember that when τ′ = 0, τ is equal to the product of α and β. When these paths are small (i.e., 0.14), then τ is equal to 0.0196. Using Cohen, Cohen, West, and Aiken’s (2003, p. 92) method for computing power for regression coefficients, we get
| (11) |
where n is the sample size; k is the number of predictors in the regression equation; f is an effect size measure for ordinary least squares regression and, in this case, is equal to the regression coefficients used (i.e., 0.14, 0.26, 0.39, and 0.59); and L is a tabled value corresponding to a specific power value. For a one-predictor ordinary least squares regression with a Type I error of .05 and power of .8, L is equal to 7.85. Using this value, the sample size necessary for .8 power to detect the α path when α equals 0.14 is 403. However, by the same formula, the sample size necessary to test the τ path when α equals 0.14, β equals 0.14, and τ′ equals 0 is 20,436, a value very close to the empirical result.
Another critical finding is that the empirical power results suggest that for the six tests of mediation investigated in this study, 75% of the studies in the literature survey had less than .8 power to find a mediated effect including a small α or β path (given that across methods, 352 was the upper quartile for sample size in the survey).2 The literature survey also showed a lack of studies using resampling methods. The most likely explanation of this finding is that most researchers do not know how to use resampling methods to test for mediation or are uncomfortable using them. As more articles present the benefits of resampling and give example programs (e.g., MacKinnon et al., 2004; Shrout & Bolger, 2002), more researchers are likely to utilize these methods.
On the basis of the literature survey and the results of the empirical power simulations, we propose two recommendations for researchers. First, given the increased power of the bias-corrected bootstrap test, the joint significance test, and the PRODCLIN asymmetric confidence-intervals test, one of these three methods should be used to test for mediation, unless it is known that the direct path is large, in which case the Baron and Kenny (1986) test has the same power as the joint significance test. A word of caution is needed for the bias-corrected bootstrap test, however, as it has been found to have larger-than-normal Type I error rates in certain conditions (see MacKinnon et al., 2004, for more information). Although the simulations were carried out for continuous variables, MacKinnon et al. (2002) found that models in which the independent variable was modeled as dichotomous produced results almost identical to those of models with a continuous independent variable when effect size was made equivalent for the model parameters (Cohen, 1983). Second, researchers should use the empirical sample sizes from this study as a lower limit of the number of subjects needed for .8 power, not as a guarantee of .8 power. These variables were modeled without measurement error, but few variables in the social sciences are measured without error. If variables are measured with error, larger sample sizes will be needed to maintain .8 power (Hoyle & Kenny, 1999).
For example, consider a researcher interested in testing whether intentions mediate the relation between attitudes and behaviors, as proposed by the theory of planned behavior (Ajzen, 1985). The researcher believes that in the study, the effect of attitudes on intentions will be of medium size, the effect of intentions on behaviors will be small, and intentions will completely mediate the effect of attitudes on behavior. Using the empirical power tables, the researcher can see that for the joint significance test, a sample size of 405, or a larger sample if measurement error is present, is required for .8 power.
Given the recent increase in requirements for statistical power calculations when applying for grants and other types of funding, performing power analyses has become particularly important. The current study gives researchers a reference for determining the sample sizes necessary for adequate power in single-mediator models. In addition, the programs used to calculate these results are available (http://www.public.asu.edu/~davidpm/ripl/mediate.htm) to researchers who would like to estimate necessary sample sizes for power values other than .8 or other parameter combinations not discussed here.
Acknowledgments
The authors wish to thank Steve West, Joanna Gorin, Chondra Lockwood, and Jason Williams. This research was supported by a Public Health Service grant (DA06006). Portions of this project were presented at the May 2005 meeting of the Society for Prevention Research in Washington, DC.
Footnotes
Note that these values hold for the α and β paths only. Given these regression coefficients, the effect size for the τ′ path is smaller than the effect size for the other two paths. For example, when α = β = .39 and τ′ = .14, ρXY = .263, ρXM = .363, ρYM = .422, , and 1.69% (i.e., .132) of variance is explained—slightly less than the 2% Cohen designated as a small effect. We have taken this decrease in effect size into consideration in reporting the results from this study.
We should note, however, as one reviewer pointed out, that many psychological studies are underpowered and there is no reason to expect mediation studies to be an exception.
REFERENCES
- Ajzen I. From intentions to actions: A theory of planned behavior. In: Kuhl J, Beckman J, editors. Action-control: From cognition to behavior. Heidelberg, Germany: Springer; 1985. pp. 11–39. [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Cohen J. The cost of dichotomization. Applied Psychological Measurement. 1983;7:249–253. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Cohen J. Things I have learned (so far) American Psychologist. 1990;45:1304–1312. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Mahwah, NJ: Erlbaum; 2003. [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani TJ. An introduction to the bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- Holmbeck GN. Toward terminological, conceptual, and statistical clarity in the study of mediators and moderators: Examples from the child-clinical and pediatric psychology literatures. Journal of Consulting and Clinical Psychology. 1997;65:599–610. doi: 10.1037//0022-006x.65.4.599. [DOI] [PubMed] [Google Scholar]
- Hoyle RH, Kenny DA. Sample size, reliability, and tests of statistical mediation. In: Hoyle RH, editor. Statistical strategies for small sample research. Thousand Oaks, CA: Sage; 1999. pp. 195–222. [Google Scholar]
- Judd CM, Kenny DA. Estimating the effects of social interventions. Cambridge, England: Cambridge University Press; 1981a. [Google Scholar]
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981b;5:602–619. [Google Scholar]
- Kenny DA, Kashy DA, Bolger N. Data analysis in social psychology. In: Gilbert DT, Fiske ST, Lindzey G, editors. The handbook of social psychology. Vol. 1. New York: Oxford University Press; 1998. pp. 233–265. [Google Scholar]
- Lomnicki ZA. On the distribution of the product of random variables. Journal of the Royal Statistical Society. 1967;29:513–524. [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODCLIN. Behavioral Research Methods. doi: 10.3758/bf03193007. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM. Distribution of products tests for the mediated effect. Arizona State University, Tempe; 2001. Unpublished manuscript. [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–103. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate Behavioral Research. 2004;39:99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate Behavioral Research. 1995;30:41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manly BF. Randomization and Monte Carlo methods in biology. New York: Chapman and Hall; 1997. [Google Scholar]
- Meeker WQ, Jr., Cornwell LW, Aroian LA. The product of two normally distributed random variables. In: Kennedy WJ, Odeh RE, editors. Selected tables in mathematical statistics. Vol. VII. Providence, RI: American Mathematical Society; 1981. [Google Scholar]
- Miller AJ. [Retrieved September 14, 2004];FNPROD [Computer program] 1997 from http://users.bigpond.net.au/amiller/
- Neyman J, Pearson ES. The testing of statistical hypotheses in relation to probabilities a priori. Proceedings of the Cambridge Philosophical Society. 1933;24:492–510. [Google Scholar]
- R Development Core Team. R (Version 2.2.0) [Computer program] Vienna: R Foundation for Statistical Computing; 2006. [Google Scholar]
- SAS Institute. SAS (Version 8.02) [Computer program] Cary, NC: Author; 2004. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7:422–445. [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. In: Leinhardt S, editor. Sociological methodology, 1985. Washington, DC: American Sociological Association; 1982. pp. 290–312. [Google Scholar]
- Springer MD, Thompson WE. The distribution of independent random variables. SIAM Journal on Applied Mathematics. 1966;14:511–526. [Google Scholar]